Why hunter-gatherer populations do not show signs of Pleistocene demographic expansions (original) (raw)

Abstract

The mitochondrial DNA diversity of 62 human population samples was examined for potential signals of population expansions. Stepwise expansion times were estimated by taking into account heterogeneity of mutation rates among sites. Assuming an mtDNA divergence rate of 33% per million years, most populations show signals of Pleistocene expansions at around 70,000 years (70 KY) ago in Africa and Asia, 55 KY ago in America, and 40 KY ago in Europe and the Middle East, whereas the traces of the oldest expansions are found in East Africa (110 KY ago for the Turkana). The genetic diversity of two groups of populations (most Amerindian populations and present-day hunter-gatherers) cannot be explained by a simple stepwise expansion model. A multivariate analysis of the genetic distances among 61 populations reveals that populations that did not undergo demographic expansions show increased genetic distances from other populations, confirming that the demography of the populations strongly affects observed genetic affinities. The absence of traces of Pleistocene expansions in present-day hunter-gatherers seems best explained by the occurrence of recent bottlenecks in those populations, implying a difference between Pleistocene (≈1,800 KY to 10 KY ago) and Holocene (10 KY to present) hunter-gatherers demographies, a difference that occurred after, and probably in response to, the Neolithic expansions of the other populations.

A wealth of data on human mtDNA diversity has accumulated over the past few years, with more than 4,000 sequences from the first hypervariable region (HV1) being available (1). Previous analyses of some of these data have led to important results about the evolution of the mtDNA molecule, such as a very rapid evolutionary rate (2–5) associated with a strong heterogeneity of mutation rates (6). These data have also led to important conclusions about human evolution, e.g., a probably recent and unique African origin for all modern humans (7), a recent origin of Amerindian populations from North East Asia (see, for example, ref. 8), or the occurrence of large population expansions as inferred from the observed pattern of molecular diversity and the star-shape of phylogenetic trees (9, 10). Past demographic events seem to have had a profound effect on the amount and the pattern of mtDNA and on nuclear diversity (11–14). Current calibrations of those expansions point to the Pleistocene (15), with the oldest expansions apparently having occurred in Africa; this conclusion could partly explain the increased diversity observed on that continent (16, 17).

In this paper, we report on an extensive study of the molecular diversity in 62 worldwide population samples. We looked for genetic signals of population growth and estimated the timing of the putative demographic expansions. Most human populations show significant signs of Pleistocene expansion, although there are interesting exceptions, such as some Amerindian populations and some hunter-gatherer populations (HGPs) from different continents. A multivariate analysis of genetic distances reveals that the most divergent populations do not show signs of Pleistocene expansions, particularly in Africa and in America. Otherwise, the genetic affinities among populations are found in good agreement with geography. The puzzling lack of signal of Pleistocene expansions in hunter-gatherers is discussed. We propose that the Holocene HGPs lost previous signals of Pleistocene expansions because of post-Neolithic population bottlenecks; this conclusion is supported by computer simulations.

MATERIALS AND METHODS

Samples.

The 62 population samples analyzed consist of a total of 2,778 individuals; these populations are listed in Table 1. Ethnically heterogeneous population samples and samples with fewer than 20 individuals were not considered in this study.

Table 1.

Fu’s _F_S statistics and expansion times (τ) estimated from mtDNA HV1 sequences

Samples Abbr.* n _F_S P(_F_S)† τ‡ P§ t,KY t 95%CI, KY‖ Ref.
Asia and Oceania
Asia Asi 24 −19.87 0.000 8.94 0.994 73 46–87 55
Australia Desert AusD 51 −11.76 0.000 6.35 0.510 48 26–68 56
Australia Riverine AusR 63 −3.91 0.131 10.08 0.144 76 44–107 56
Hong-Kong H-K 20 −15.58 0.000 7.71 0.667 58 35–82 57
Japan Jap 61 −25.03 0.000 6.00 0.368 40 25–76 58
Luzon Philippines Luz 36 −19.72 0.000 5.38 0.006 86 51–105 55
Papua New Guinea 1 PNG1 20 −5.56 0.012 9.61 0.861 97 39–168 3
Papua New Guinea 2 PNG2 24 −8.16 0.004 10.30 0.599 84 48–151 59
Sabah Borneo Sab 37 −10.63 0.000 4.88 0.126 78 44–95 55
Taiwan Tai 33 −10.52 0.000 4.84 0.783 77 38–115 55
Vanuatu Melanesia Van 51 −20.83 0.000 5.45 0.423 87 46–124 55
America
Chile Chi 45 −12.33 0.000 10.79 0.754 59 26–99 8
Colombia Col 20 −0.74 0.374 9.89 0.020 67 34–99 8
Kuna Panama Kun 63 2.78 0.868 5.29** 0.054 43 13–87 37
Mapuche Argentina Map 39 −0.39 0.490 7.52 0.009 76 41–106 60
Ngobe Panama Ngo 46 3.39 0.902 5.50** 0.056 45 15–140 36
Nuu-Chah-Nulth Canada Nuu 63 −11.29 0.002 7.20 0.465 55 28–82 3
Africa
!Kung Botswana Kng 25 −1.74 0.198 1.14** 0.138 9 0–81 7
East Pygmies Rep. Congo Pyg 20 −0.02 0.520 9.95 0.004 81 37–129 7
Fulbe Ful 61 −23.51 0.000 7.20 0.444 59 35–112 40
Hausa Nigeria Hau 20 −13.64 0.000 7.18 0.833 59 33–77 40
Herero Botswana Her 27 0.24 0.589 5.09** 0.205 51 16–67 7
Kikuyu Kenya Kik 25 −13.70 0.000 9.38 0.258 77 44–145 40
Mandenka Senegal Man 119 −25.03 0.000 6.72 0.847 68 36–154 61
Somali Som 27 −14.89 0.000 8.90 0.786 73 45–91 40
Tuareg Niger Tua 26 −10.26 0.001 5.83 0.177 48 30–93 40
Turkana Kenya Tur 37 −24.47 0.000 13.40 0.523 110 73–138 40
Yoruba Nigeria Yor 34 −25.15 0.000 7.78 0.764 64 39–104 7, 40
Europe, Middle East, India
Albania Alb 42 −25.54 0.000 3.62 0.638 37 21–76 Unpubl.
Algeria Alg 85 −12.06 0.002 6.51 0.074 66 35–95 62
Basques 1 Ba1 45 −22.54 0.000 2.17 0.267 18 6–58 63
Basques 2 Ba2 61 −26.58 0.000 2.07 0.491 21 8–60 62
Bavaria Bav 49 −25.96 0.000 3.97 0.771 40 24–50 64
Bulgaria Bul 30 −14.40 0.000 4.11 0.435 34 19–67 65
Cornwall Cor 69 −26.11 0.000 1.91 0.612 19 6–44 64
Denmark Den 33 −18.79 0.000 6.25 0.320 63 33–92 64
England Eng 100 −25.71 0.000 2.98 0.771 24 11–68 66
Estonia Est 28 −18.77 0.000 2.80 0.766 23 9–52 67
Finland Fin 50 −25.94 0.000 4.21 0.754 34 20–42 67
Germany Ger 106 −25.54 0.000 4.22 0.402 43 32–62 64
Havik India Hav 48 −18.27 0.000 4.60 0.495 35 20–80 68
Iceland Ice 39 −22.19 0.000 4.61 0.223 38 24–60 67
German speakers Italy ItG 20 −12.50 0.000 6.83 0.815 56 34–94 69
Trento Italy ItT 20 −17.20 0.000 6.80 0.506 56 32–70 69
Karelian Russia Kar 83 −25.94 0.000 3.43 0.626 28 17–62 67
Ladin Italy Lad 20 −11.13 0.000 7.11 0.515 58 32–80 69
Middle East MdE 42 −25.02 0.000 7.90 0.586 60 40–72 70
Moksha Russia Mok 21 −6.89 0.002 4.70 0.211 38 20–77 67
Mukhri India Muk 43 0.24 0.567 10.32 0.073 78 40–115 68
Portugal Por 54 −26.11 0.000 3.70 0.914 37 19–78 62
Saami Inari Finland Sal 22 −0.38 0.450 10.89 0.428 89 40–142 67
Saami Karasjok Norway Sak 21 0.75 0.681 5.07** 0.041 38 13–78 67
Saami Norrbotten Sweden SaN 25 −2.56 0.110 6.01** 0.589 49 16–94 67
Saami Skolt Finland SaS 47 0.28 0.597 5.77** 0.071 47 15–96 67
Sardinia Sar 69 −25.81 0.000 4.06 0.687 31 16–68 70
Spain Spa 41 −6.51 0.017 6.35 0.764 52 27–76 62
Switzerland Swi 76 −23.96 0.000 3.84 0.348 31 20–42 71
Tenerife Ten 54 −25.37 0.000 4.88 0.688 40 20–110 72
Turcs 1 Tk1 29 −19.68 0.000 6.27 0.577 51 32–86 73
Turcs 2 Tk2 45 −25.43 0.000 5.72 0.826 47 29–59 65
Tuscany Italy Tus 52 −25.54 0.000 5.62 0.610 46 26–63 74
Wales Wel 92 −26.39 0.000 1.41 0.820 14 3–46 64

Detecting Demographic Expansions.

Traces of population expansions were examined by using two different approaches. First, we computed Fu’s F_S statistic (18) in all samples. This statistic is particularly sensitive to population growth. It is based on the probability of having a number of alleles greater or equal to the observed number in a sample drawn from a stationary population with parameter θ = 2_Nu (where N is the population effective size, and u is the mutation rate for the whole sequence). Here, θ is estimated by equating it with the average number of observed pairwise differences. The _F_S significance was tested with a coalescent simulation program (modified from ref. 19), as implemented in a new version of the computer program arlequin (20). Basically, the testing procedure consisted of random samples generating from a stationary population with estimated parameter θ̂, and of recomputing the _F_S statistic for each sample. Five thousand simulations were carried out to obtain the null distribution of the _F_S statistic and its P value. Significantly large negative F_S values are interpreted here as evidence for population expansion (18). Secondly, the distribution of the number of pairwise differences between sequences within a sample (the mismatch distribution) was used to estimate the timing of demographic expansion (the method proposed by Rogers and Harpending in ref. 9). This method is based on an infinite-site model and assumes that a stepwise expansion occurred some time in the past from a small stationary population to a large stationary population; this seems to be a good approximation of exponential or logistic growth (9). Although the infinite-site model is adequate under small departures from a pure infinite-site model (21), we have recently extended the Rogers and Harpending model to accommodate a more realistic mutation model (22): we have used a Kimura two-parameter mutation model (23), with 90% of the substitutions being transitions, and with a gamma distribution of mutation rates with shape parameter α = 0.26, as previously estimated for the HV1 human sequences (24). Confidence intervals (CIs) for the expansion time, τ, expressed in mutational units (τ = 2_ut, where u is the mutation rate for the whole sequence, and t is the number of generations since the expansion) were obtained by using a parametric bootstrap approach (see, for example, Chapter 13 in ref. 25). In this approach, the estimated parameters of the expansion τ, _θ_0 = 2_uN_0, and _θ_1 = 2_uN_1 (_N_0 and _N_1 being the population sizes before and after the expansion) are used to perform coalescent simulations of stepwise expansions from which new parameters τ*, _θ_0*, and _θ_1* are estimated (22). The overall validity of the estimated demographic model is tested by obtaining the distribution of a test statistic SSD (the sum of squared differences) between the observed and the estimated mismatch distribution by a bootstrap approach similar to that described above. The P value of the SSD statistic is computed as the proportion of simulated cases that show a SSD value larger than the original (22). A significant SSD value is taken here as evidence for departure from the estimated demographic model, which can be either a model of population expansion (if τ̂ > 0 and θ̂1 > θ̂0) or a model of population stationarity (if τ̂ = 0 or θ̂1 = θ̂0).

Genetic Affinities.

Genetic distances between pairs of populations were computed by using the arlequin program as pairwise _Φ_ST statistics obtained under the analysis of molecular variance (AMOVA) framework (26), linearized with divergence time as d = _Φ_ST/(1 − _Φ_ST) (27). The molecular distances between pairs of sequences necessary for the AMOVA analysis were computed under the Kimura two-parameter/gamma model (28), assuming α equal to 0.26 (24). Genetic distances were used in a multidimensional scaling (MDS) analysis (29) performed with the software package ntsys-pc, ver. 2.02 (30).

RESULTS AND DISCUSSION

Pleistocene Expansions.

The results of the detection of population expansions are reported in Table 1. Overall, results obtained from Fu’s _F_S statistic closely parallel those obtained from the mismatch analysis: significantly large negative _F_S values, indicative of recent population growth (18), are associated with a demographic model implying a large and sudden expansion as inferred from the mismatch distribution. As previously reported (15, 31), most human populations show signs of Pleistocene population expansions. Although the populations with the oldest expansion times are found in East Africa (Turkana, 110 KY), we find that average expansion times are slightly larger in Asia and Oceania (72 KY) than in sub-Saharan Africa (70 KY), America (57 KY), and in Europe, the Middle East, and India (42 KY). These averages were computed only for those populations with an accepted model of demographic expansion; the relative rank of the regions remains the same when we also remove samples that show, by Fu’s test, no significant expansion signal. These ancient Asian expansions are compatible with recent results obtained from Y chromosome (32) or _β_-globin (33) studies, evidence that a significant portion of human diversity arose in Asia. The average expansion time (≈57 KY) found for the Americas precedes the oldest dates generally accepted for the earliest evidence of colonization in the New World, approximately 30–35 KY ago (ref. 34, pp. 302–304), but these ages are included in the 95% CI of the expansion time for the two Amerindian samples that show clear signs of past expansions (Chile and Nuu-Chah-Nulth).

Accuracy of the Estimations. The expansion times inferred by taking into account a more realistic mutation model are, on average, 5% larger (minimum = −4%, maximum = 23%) than those inferred from the infinite-site model (results not shown). The difference is more pronounced for larger expansion times, but even for those cases, the τ value inferred from the infinite-site model is always included in the 95% CI around the value inferred with the more realistic mutation model (results not shown). Therefore, the improved mutation model does not drastically alter the point estimates obtained under the infinite-site model. The accuracy of the expansion times (expressed in years) strongly depends on the calibration of the molecular clock, which is still a subject of debate (4, 5). Most human populations must have expanded in the Pleistocene at similar times in Asia and Africa, approximately 60–70 KY ago, if one accepts the rate of 33% divergence per million years (3). However, those absolute dates should be read with caution until better estimates of mutation rates are available for HV1. The relatively large CI associated with those dates does not allow us to say whether demographic expansions spread from a geographical center by demic or cultural diffusion, or whether they occurred simultaneously and independently in different regions. The similarity of the dates for Africa and Asia suggests that if the demographic expansions spread from a given region, they did so rapidly. Alternatively, independent expansions could have arisen at the same time, for example, as a response to some global climatic change.

Simulation studies (22) have shown that the bootstrap CI around the estimated expansion time τ has good coverage (see, for example, p. 96 of ref. 35) in the sense that the true parameter is included in a 100 × (1 − α) percentage CI with a probability close to 1 − α. Assuming no error in the mutation rate, we can therefore give some credence to the limits of the 95% CI reported in Table 1 (Column 9), with upper limits lower than 100 KY, except in Africa and Asia. However, the bootstrap percentile CI intervals we have computed rely on the assumption that the dispersion of the estimations around the parameters does not depend on the values of the parameters. This does not seem to be the case for _θ_0 and _θ_1, but it is almost true for the expansion time τ (see figure 4 in ref. 22). The consequence is that the bootstrap CIs for _θ_0 and _θ_1 are usually too large; however, our conclusions depend mainly on the times of the expansions and not on their exact magnitude.

Genetic Diversity Not Explained by Stepwise Expansions.

Whereas the expansion model seems to be established for most human populations, a few populations (shown in boldface in Table 1) do not show signs of recent expansions. They can be divided into three categories.

The four Amerindian populations.

As indicated by the SSD statistic, the stationary or expansion model is rejected for the Colombian (P = 0.02) and the Mapuche (P = 0.009) samples and is very close to being rejected for the Kuna (P = 0.054) and the Ngobe (P = 0.056) from Panama. Alternative demographic scenarios must be invoked for these populations, e.g., (i) a strong founder effect at the time of the colonization of the Americas from the Bering Strait that would have erased previous diversity except for a few major lineages, (ii) a recent population crash after the European invasions, or (iii) a combination of these scenarios (36–38).

The Luzon Sample (Philippines) and the Herero (Botswana).

These samples do not fit with a simple expansion model. The Herero seem to have undergone a drastic and recent founder effect (39), which has depleted its genetic diversity and erased any sign of previous demography. On the other hand, the Luzon sample presents an overly leptokurvic unimodal mismatch distribution, which even a large expansion seldom reproduces.

The current or previous HGPs.

The remaining eight samples that do not show evidence of population expansions are HGPs from different continents (see Table 1): Australian aborigines (Riverine sample), !Kung and Pygmies from Africa, Mukhri from India, and four Saami populations from Northern Europe. Note that a visual difference between the shapes of the mismatch distribution found for food gatherers and food producers has been noted previously (40), but this observation has not been quantified or tested, and it has been criticized for its lack of statistical rigor (41).

Population Genetic Affinities.

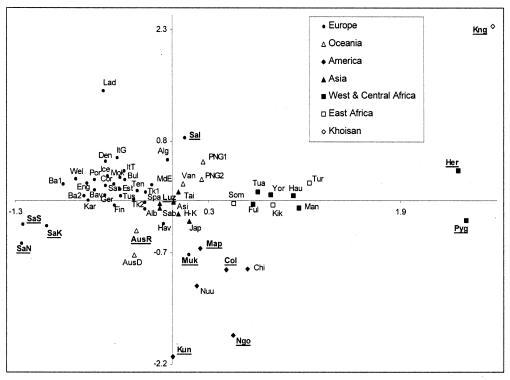
In Fig. 1, we show the pattern of genetic affinities among 61 populations (the Swiss population was removed because it did not have enough overlapping nucleotides with other populations). Overall, we observe a good congruence between geographic and genetic differentiation (i.e., the population cluster on the genetic plane accords with their geographic proximity), which is in keeping with results obtained from conventional markers (34). In Fig. 1, the abbreviated names of the populations that show no sign of population growth as inferred from Table 1 are underlined. They are mainly outliers in the genetic plane, suggesting that differential demography is at least partly responsible for their large genetic distances from other populations (42). In particular, sub-Saharan African populations showing signs of Pleistocene expansions become relatively closer to non-African populations, and the distinction between Africans and non-Africans is greatly reduced.

Figure 1.

Figure 1

Multidimensional analysis of 61 populations analyzed for mtDNA HV1 diversity. The abbreviated names of populations whose genetic diversity is not compatible with a simple past demographic expansion are underlined.

Hunter-Gatherers and Pleistocene Expansions. The lack of signs of demographic growth in HGPs would make perfect sense if the expansion times estimated for all of the other populations pointed to the Neolithic (5 to 10 KY ago) instead of to the Pleistocene (60–70 KY ago). We are thus confronted with a conceptual difficulty: why do the present-day HGPs show no signs of Pleistocene expansions?

The first possibility is that the molecular clock used to transpose τ into years is too slow, and that the expansions we see actually occurred in the Neolithic rather than in the Paleolithic. Several recent studies of mutations in pedigrees have proposed a much faster mutation rate than the one obtained by comparing human and chimpanzee diversity (4, 5). The last proposed pedigree-based rate (1.35 × 10−6 per site per year; see ref. 5) would nicely convert Pleistocene expansions into Neolithic expansions, but it would also mean that the time to the mitochondrial Eve must be significantly shortened (43). Moreover, such a fast mutation rate would require an effective female world population size that was approximately 10 times smaller before the expansion (Alan Rogers, Univ. of Utah, personal communication), corresponding to a total of approximately 500 females instead of the generally acknowledged total of 5,000 (44) and imposing an unreasonably low effective size for the human species during the Pleistocene.

A second possibility assumes that the molecular clock is correct but that the split between the HGPs and the future Neolithic populations is much earlier than previously thought. Under this scenario, Pleistocene HGPs would consist of two categories: those entering a demographic expansion phase and those remaining approximately constant in size until today. Why only the former group would undergo the Neolithic expansion is difficult to explain.

Finally, a third possibility is that the signs of Pleistocene expansions were erased in populations that did not go through the Neolithic transition. This possibility might be associated with a potential instability of HGP demography, such as a series of recurring founder events or population crashes. This view is supported by a recent analysis of the molecular diversity of the BiAka (West) Pygmies indicating a recent decrease in population (45). However, understanding how the signs of expansion persisted during the long period of hunter-gatherer existence of present-day Neolithic populations remains a difficult problem, unless the demographies of the Pleistocene and the Holocene HGPs were drastically different. Stable demography among Pleistocene HGPs indicates the maintenance of large effective population sizes achieved through high migration rates among subpopulations. A reduction of effective population sizes in Holocene HGPs does not necessarily imply a drastic reduction of their absolute census size; it could be achieved by a fragmentation of the environment. Most present-day HGPs live in unfavorable habitats (46) or refuge areas not easily exploitable by farmers or pastoralists. It is therefore likely that the rise of competing Neolithic farmers caused the Holocene HGPs to enter a metapopulation phase with a much smaller effective size (for an example, see ref. 47).

The Neolithic transition is usually studied for its effects on the populations that ultimately became farmers (see ref. 48); little or no attention is given to its consequences on the remaining HGPs. This study suggests that the demographic structure of the HGPs has been altered since and perhaps by the Neolithic transition. The fact that present-day HGPs differ from their Pleistocene forebears has been recognized, it is therefore misleading to think of present-day HGPs as living relics of Pleistocene populations (49). Some of their present (cultural or biological) characteristics may have been acquired recently and would therefore not represent pre-Neolithic adaptations. Moreover, the view that HGPs suffered less parasitic load than farmers because of their assumed smaller group size (see ref. 50) could be revised; some modern infectious diseases may have been widespread before the Neolithic transition (51).

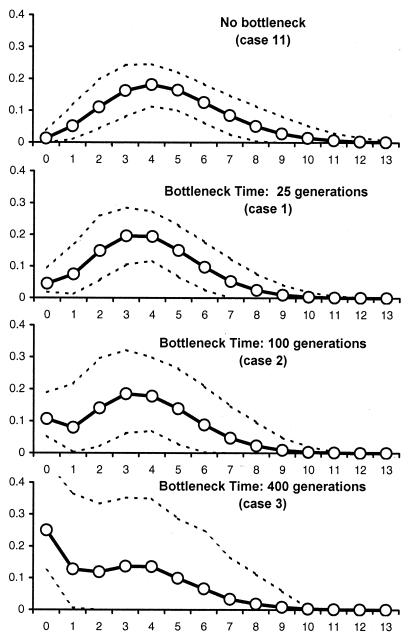
Recent Bottlenecks Can Erase Signals of Past Population Growth. To sustain the hypothesis that the absence of signs of population growth could be due to post-Neolithic bottlenecks, we have simulated the molecular diversity of populations that have completed a population expansion followed by a recent bottleneck (Table 2). The average mismatch distributions obtained for a few cases are shown in Fig. 2. We find that population bottlenecks can alter the signs of past population expansions: they tend to reduce the number of significant _F_S statistics, and they lead to a larger proportion of significant SSD statistics computed from the mismatch distributions (Table 2). We find that earlier bottlenecks have a more pronounced effect, in keeping with classical results concerning the amount of genetic variability maintained after a bottleneck (52). In Fig. 2, two main effects of the age of the bottleneck on the mismatch distribution can be seen: (i) the expected frequency of the low difference classes (0 and 1) increases with bottleneck age, and (ii) the variance of the mismatch distribution also increases with bottleneck age. These effects are caused by a longer period of increased genetic drift after the bottleneck. As expected, large bottlenecks have more effect than small bottlenecks (cases 9 and 10). Finally, it is interesting to note that postbottleneck population size is important; a bottleneck of identical magnitude will have less effect in populations that have a larger postbottleneck size (compare cases 1–3 to cases 4–6 in Table 2).

Table 2.

Population expansion signs in populations after an early demographic expansion and a recent bottleneck

Case Bottleneck time* Bottleneck factor Present population size No. of significant _F_S tests No. of significant SSD tests
1 25 100 1,000 996 103
2 100 100 1,000 279 448
3 400 100 1,000 21 416
4 25 100 5,000 1,000 46
5 100 100 5,000 998 72
6 400 100 5,000 763 270
7 100 10 1,000 165 243
8 100 10 5,000 997 78
9 400 1,000 1,000 3 478
10 400 1,000 5,000 119 490
11 Pure stepwise expansion 500,000 1,000 12

Figure 2.

Figure 2

Average distributions of the number of pairwise differences in simulated populations after a large stepwise demographic expansion 2,000 generations ago and a recent bottleneck. The number of pairwise differences are on the x axis, and their frequencies are on the y axis. The case numbers correspond to those described in Table 2. The dashed lines delimit a region incorporating 90% of the simulated points.

Although studies of nuclear markers show that HGPs are different from Neolithic populations (for example, see refs. 34, 53, and 54), this difference is not always linked to a decrease in molecular diversity as would be expected after a bottleneck. African HGPs in particular present a high level of diversity (53, 54), e.g., the Pygmies studied for mtDNA. Even though recent bottlenecks may have erased the traces of demographic expansions in most HGPs, the magnitudes and the causes of these bottlenecks depend on various ecological constraints and may be heterogeneous. We should therefore not expect to see the same pattern of diversity in all HGPs; the age of the bottleneck affects the diversity patterns and their variability (Fig. 2), and nuclear markers may be less sensitive than mtDNA to bottlenecks (Table 2) because they are associated with larger effective postbottleneck population sizes.

Acknowledgments

We thank Naruya Saitou, Evelyne Heyer, Alain Gallay, and André Langaney for stimulating discussions. We are grateful to Henry Harpending, Guido Barbujani, and Alan Rogers for their helpful comments on the manuscript. This work was supported by grants (32-047053.96 and 31-039847.93) to L.E. from the Swiss National Foundation for Scientific Research. Data and software programs are available from the authors on request.

ABBREVIATIONS

CI

confidence intervals

HGP

hunter-gatherer population

HV1

hypervariable region 1

KY

1,000 years

SSD

sum of squared differences

Footnotes

A Commentary on this article begins on page 10562.

References