Genome Scan to Detect Genetic Structure and Adaptive Genes of Natural Populations of Cryptomeria japonica (original) (raw)
Abstract
We investigated 29 natural populations of Cryptomeria japonica using 148 cleaved amplified polymorphic sequence markers to elucidate their genetic structure and identify candidate adaptive genes of this species. In accordance with the inferred evolutionary history of the species during and after the last glacial episode, the genetic diversity was higher in western populations than in northern populations. The results of phylogenetic and genetic structure analyses suggest that populations of the two main varieties of the species have clearly diverged from each other and that two of the examined loci are strongly associated with the differentiation between the two varieties. Using a coalescent simulation based on _F_ST and _H_e values, we detected five genes that had higher, and two that had lower, values than the respective 99% confidence intervals (C.I.s) that are theoretically expected intervals under a neutral infinite-island model. We also detected 13 outlier loci using a coalescent simulation based on the assumption that the 2 varieties originated from the splitting of an ancestral population. Four of these loci were detected by both methods, two of which were detected in a genetic structure analysis as loci associated with differentiation between the two varieties of the species, and are strong candidates for genes that have been subject to selection.
GENETIC structure has been studied in many plant species using several kinds of nuclear and organelle DNA markers. Analyses of the phylogeographical structure of various plant species based on organelle DNA polymorphisms have clearly illustrated the migration patterns of various species during the postglacial recolonization of several continents (Petit et al. 2003). Polymorphisms of organelle DNA markers are informative and useful for surveying the postglacial recolonization of continents because they are neutral and have low mutation rates. However, to obtain a detailed understanding of the population genetic structure and genetic diversity of species, large numbers of loci in their nuclear genomes should be analyzed (Nei 1987). Nevertheless, small numbers of loci have been examined in most studies of the population genetic structure of plant species because of limitations in the numbers of markers (e.g., allozymes) that were available (Hamrick et al. 1992). To identify key genes involved in adaptation to local environments or speciation, it is also necessary to investigate genes in the nuclear genome because it contains most of the genes related to these processes. Evolutionary scientists interested in adaptation and speciation have attempted to identify genome regions or genes associated with these processes using several different methods (see the review by Vasemägi and Primmer 2005), such as quantitative trait loci (QTL) analysis (Mauricio 2001), admixture mapping (Rieseberg et al. 1999), and neutrality tests such as Tajima's D (Tajima 1989), the Fu and Li test (Fu 1996), the HKA test (Hudson et al. 1987), and the MK test (McDonald and Kreitman 1991) based on sequence variations of specific genes. Another population-based method involving analyses of multiple loci is to evaluate the relationship between _F_ST and _H_e in an island model (Wright 1931), describing the expected distribution of Wright's inbreeding coefficient (_F_ST) vs. heterozygosity (_H_e) under an island demographic model with neutral selection and using this distribution to detect outlier loci that may have been subject to selective pressure (Beaumont and Nichols 1996). Another method is to use the coalescent-simulation approach developed by Vitalis et al. (2001), based on the assumption that current populations originated from the splitting of an ancestral population, to detect outlier loci that may have been affected by selection.
Such genomewide surveys have been conducted in several species (Storz 2005; Vasemägi and Primmer 2005; Vasemägi et al. 2005) to identify regions associated with adaptation and/or speciation. These kinds of approaches have also been applied in studies of several forest tree species, and some important regions of their genomes associated with adaptation have been identified (Scotti-Saintagne et al. 2004). However, most of these studies have been based on anonymous markers such as RAPD and AFLP markers, since linkage maps can be constructed much more rapidly with them than when using other markers like EST-based markers. However, EST information has rapidly accumulated in public databases recently and is used to identify convenient and informative DNA markers that are useful for linkage map construction and population studies. Using EST-based markers in genomewide surveys may also be a convenient way of clarifying genetic structure and identifying genes associated with local adaptation or speciation.
Cryptomeria japonica is an allogamous coniferous species with wind-mediated pollen and seed dispersal systems. Modern natural forests of the species are distributed in moist temperate regions from Aomori Prefecture (40° 42′ N) to Yaku Island (30° 15′ N) in the Japanese Archipelago (Hayashi 1960). However, its distribution is discontinuous and scattered among small, restricted areas as a result of its extensive exploitation during the past thousand years (Ohba 1993). Geographical variations among natural forests of C. japonica have been investigated using both morphological traits (needle length, needle curvature, and other features; Murai 1947) and diterpene components (Yasue et al. 1987). The results of these studies suggest that there are two main lines: ura-sugi (C. japonica var. radicans, found near the Sea of Japan) and omote-sugi (C. japonica, located near the Pacific Ocean). The ura-sugi variety has slender branchlets with soft leaves, while the omote-sugi variety has rough branchlets with hard leaves (Yamazaki 1995). However, no clear differences between the two varieties have been detected in previous studies using genetic markers (Tomaru et al. 1994; Tsumura and Tomaru 1999). We have already developed EST-based cleaved amplified polymorphic sequence (CAPS) markers for this species (Tsumura et al. 1997; Iwata et al. 2001; Nikaido et al. 2000) and constructed a linkage map using them (Tani et al. 2003).
In this study, we attempted to elucidate the genetic structure of this species and to identify key genes associated with its genetic divergence and adaptation in a genomewide survey using CAPS markers that have been mapped on a linkage map of the species.
MATERIALS AND METHODS
Plant materials:
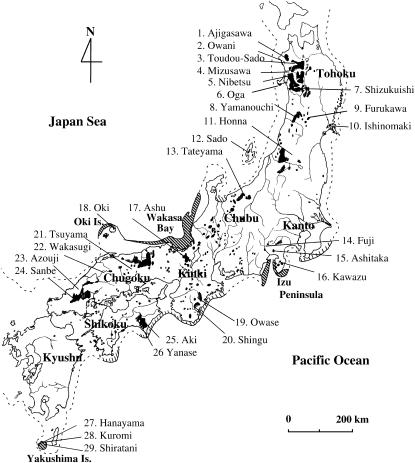
Fresh needle tissues were collected from 576 trees representing 29 natural populations. All trees sampled were in national forests that were candidates for in situ gene conservation programs (Figure 1, Table 1). The locations of the sampled populations covered most of the natural distribution of C. japonica. We collected small branches from individual trees spaced at least 50 m apart to avoid sampling related individuals. In addition, because C. japonica has been widely planted since 1945 in Japan, we sampled only relatively large, old trees that were presumed to predate the widespread planting programs. All individuals were rescued by transferring cuttings to a cutting bed, and in the following spring, the resulting seedlings were transplanted to a nursery. After sprouting, we collected shoots from each individual. Collected needle tissues were stored at −30° prior to DNA extraction.
Figure 1.—
Natural distribution of C. japonica in Japan (shaded areas; from Hayashi 1960) and the locations of the 29 natural populations surveyed in the present study. The dotted line indicates the coastline ∼18,000 years ago. Areas shaded in bold or within thin diagonal lines show refugia (Izu Peninsula, Wakasa Bay, Oki Island, and Yakushima Island) and probable refugia, respectively, at that time (Tsukada 1986).
TABLE 1.
Information on the investigated populations and their population genetic parameters
| No. | Population | Symbol | District | Latitude | Longitude | Altitude (m) | No. of investigated individuals | Conservation area (ha) | Pl | _N_a | _R_s | _H_e | _F_IS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Ajigasawa | JS-01 | Tohoku | 40.44.53 | 140.12.54 | 210–320 | 22 | 8.5 | 0.797 | 1.973 | 1.837 | 0.324 | −0.011 |
| 2 | Owani | JS-02 | Tohoku | 40.30.44 | 140.34.43 | 200–400 | 20 | 33.4 | 0.818 | 1.959 | 1.845 | 0.316 | −0.038 |
| 3 | Toudou-Sado | JS-03 | Tohoku | 39.57.37 | 140.26.28 | 700–800 | 20 | 229.2 | 0.804 | 1.939 | 1.795 | 0.300 | −0.064 |
| 4 | Mizusawa | JS-04 | Tohoku | 40.11.54 | 140.13.53 | 160–250 | 22 | 18.5 | 0.824 | 1.939 | 1.828 | 0.312 | −0.060 |
| 5 | Nibetsu | JS-05 | Tohoku | 39.42.55 | 140.7.2 | 200–396 | 22 | 20.5 | 0.838 | 1.986 | 1.848 | 0.319 | −0.002 |
| 6 | Oga | JS-06 | Tohoku | 39.55.35 | 139.49.4 | 400–500 | 22 | 29.9 | 0.811 | 1.973 | 1.816 | 0.297 | −0.050 |
| 7 | Shizukuishi | JS-07 | Tohoku | 39.40.48 | 140.57.19 | 300–500 | 20 | 15.0 | 0.838 | 1.973 | 1.847 | 0.323 | −0.043 |
| 8 | Yamanouchi | JS-08 | Tohoku | 38.44.5 | 140.10.20 | 300–600 | 20 | 43.0 | 0.851 | 1.939 | 1.834 | 0.312 | −0.033 |
| 9 | Furukawa | JS-09 | Tohoku | 38.44.19 | 140.42.14 | 300–800 | 20 | 19.8 | 0.831 | 1.966 | 1.818 | 0.309 | 0.002 |
| 10 | Ishinomaki | PO-01 | Tohoku | 38.19.43 | 141.29.31 | 40–60 | 20 | 8.7 | 0.858 | 2.034 | 1.882 | 0.323 | −0.001 |
| 11 | Honna | JS-10 | Tohoku | 37.25.37 | 139.30.32 | 410–700 | 20 | 25.0 | 0.872 | 2.007 | 1.861 | 0.318 | −0.036 |
| 12 | Sado | JS-11 | Chubu | 38.2.10 | 138.22.44 | 653–822 | 20 | 473.3 | 0.824 | 1.973 | 1.843 | 0.309 | −0.039 |
| 13 | Tateyama | JS-12 | Chubu | 36.38.51 | 137.19.49 | 1800–2000 | 20 | 62.4 | 0.811 | 1.959 | 1.823 | 0.314 | −0.018 |
| 14 | Fuji | PO-02 | Kanto | 35.29.8 | 138.36.44 | 800–1000 | 11 | 1.0 | 0.804 | 1.926 | 1.830 | 0.307 | −0.078 |
| 15 | Ashitaka | PO-03 | Kanto | 35.13.30 | 138.49.9 | 1100–1200 | 20 | 4.7 | 0.885 | 1.973 | 1.861 | 0.327 | 0.052 |
| 16 | Kawazu | PO-04 | Kanto | 34.48.18 | 139.3.28 | 600–700 | 17 | 0.8 | 0.899 | 1.980 | 1.873 | 0.329 | 0.001 |
| 17 | Ashu | JS-13 | Kinki | 35.18.28 | 135.46.26 | 600–800 | 32 | 2000.0 | 0.851 | 2.054 | 1.874 | 0.330 | −0.007 |
| 18 | Oki | JS-14 | Chugoku | 36.16.6 | 133.19.45 | 400–500 | 20 | 14.0 | 0.892 | 1.925 | 1.829 | 0.321 | 0.016 |
| 19 | Owase | PO-05 | Kinji | 34.20.41 | 136.18.20 | 800–1000 | 18 | 427.0 | 0.939 | 2.081 | 1.929 | 0.338 | 0.018 |
| 20 | Shingu | PO-06 | Kinki | 33.49.24 | 135.45.36 | 350–850 | 19 | 20.0 | 0.912 | 2.081 | 1.920 | 0.337 | −0.029 |
| 21 | Tsuyama | JS-15 | Chugoku | 35.17.35 | 133.58.4 | 700–900 | 18 | 9.0 | 0.858 | 1.986 | 1.873 | 0.329 | −0.033 |
| 22 | Wakasugi | JS-16 | Chugoku | 34.40.31 | 131.58.37 | 600–700 | 19 | 3.0 | 0.912 | 1.993 | 1.860 | 0.322 | −0.055 |
| 23 | Azouji | JS-17 | Chugoku | 34.46.7 | 132.6.12 | 920–1100 | 20 | 5.0 | 0.845 | 2.014 | 1.858 | 0.320 | −0.012 |
| 24 | Sanbe | JS-18 | Chugoku | 33.31.35 | 133.55.2 | 700–1000 | 19 | — | 0.865 | 2.034 | 1.863 | 0.325 | −0.042 |
| 25 | Aki | PO-07 | Shikoku | 35.9.31 | 132.30.56 | 580–870 | 19 | — | 0.885 | 1.993 | 1.859 | 0.320 | −0.060 |
| 26 | Yanase | PO-08 | Shikoku | 33.35.4 | 134.5.8 | 700–900 | 20 | 92.2 | 0.899 | 2.027 | 1.897 | 0.339 | −0.071 |
| 27 | Hanayama | PO-09 | Kyushu | 30.19.36 | 130.27.36 | 1200–1400 | 21 | 1219.0 | 0.919 | 2.034 | 1.895 | 0.339 | −0.007 |
| 28 | Kuromi | PO-10 | Kyushu | 30.19.1 | 130.30.37 | 1700–1800 | 20 | >1000.0 | 0.892 | 2.034 | 1.900 | 0.347 | −0.001 |
| 29 | Shiratani | PO-11 | Kyushu | 30.22.41 | 130.34.24 | 650–800 | 21 | 424.0 | 0.892 | 2.061 | 1.922 | 0.344 | 0.009 |
| Mean | 20.1 | 0.860 | 1.994 | 1.914 | 0.322 | −0.024 | |||||||
| SE | 0.039 | 0.044 | 0.033 | 0.012 |
Investigated loci:
Total DNA was extracted from all samples using the slightly modified CTAB method of Tsumura et al. (1995). We adopted a genomewide approach to detect the genetic diversity of, and differentiation between, populations of C. japonica, using 148 CAPS markers based on cDNA sequences from C. japonica (Tsumura et al. 1997; Iwata et al. 2001) (supplemental Table S1 at http://www.genetics.org/supplemental/). Most of these loci had already been mapped on a linkage map (Tani et al. 2003). The markers were amplified by the method of Iwata et al. (2001). The PCR products were digested with restriction enzymes specific for each CAPS marker (supplemental Table S1) and their restriction patterns were checked by electrophoresis in 2% agarose gels followed by staining with ethidium bromide.
Inference of putative functions and copy numbers of CAPS loci:
Sequences of CAPS loci in C. japonica were compared to known amino acid sequences in the NCBI NR database using a BLASTX search with <10−10 expected value (_E_-value) limits to infer their putative functions (Ujino-Ihara et al. 2005). We also searched for tentative unique genes with significant similarity to infer the copy number of each gene in the nonredundant C. japonica, Pinus taeda, Arabidopsis thaliana, and Oryza sativa cDNA databases using the method of Ujino-Ihara et al. (2005).
Genetic diversity and differentiation between and within populations:
To evaluate the within-population variation, we used the following measures calculated from the allele frequencies of all loci analyzed: the proportion of polymorphic loci (Pl) at the 95% probability level, the average number of alleles per locus (_N_a), unbiased heterozygosity (_H_e) (Nei 1978), and allelic richness (_R_s). Allelic richness was measured by the method of El Mousadik and Petit (1996) with a reference sample size of 11. The fixation indices, _F_IS = 1 – _H_e /_H_o, for Pl and their averages over all loci were determined to compare the observed genotype frequencies with expectations based on the Hardy–Weinberg equilibrium (HWE) (Wright 1922; Nei 1977; Nei and Chesser 1983). Deviations from such expectations were analyzed using Fisher's exact test. Total gene diversity (_H_T) consists of the genetic variation within (_H_S) and among (_D_ST) populations, _H_T = _H_S + _D_ST. Coefficients of gene differentiation, _G_ST, among populations were then calculated to determine how gene diversity was partitioned at each level using the equation _G_ST = _D_ST /_H_T (Nei 1973). These analyses were done using the GDA (Lewis and Zaykin 2002) and FSTAT programs (Goudet 2000).
Genetic structure:
Nei's unbiased genetic distances (Nei 1972, 1978) between all pairs of population were calculated. Dendrograms were also constructed by the neighbor-joining method (Saitou and Nei 1987) and bootstrap values were calculated using PHYLIP (Felsenstein 1995). To examine the genetic differentiation between two groups representing the two varieties C. japonica and C. japonica var. radicance, we performed a hierarchical analysis of molecular variance (AMOVA) (Excoffier et al. 1992) with the program Arlequin (Schneider et al. 1997), in which the significance levels for variance components were tested through the use of permutations.
To detect population structure and infer the most appropriate number of subpopulations (K) for interpreting the data without prior information on the number of locations at which the populations were sampled, we used the Bayesian clustering approach proposed by Pritchard et al. (2000). For this analysis, we carefully excluded all loci that appeared to have a dominant mode of inheritance or to not be in HWE, since their inclusion would complicate interpretation of the results. Consequently, we used 139 loci for this analysis. Ten independent runs of K = 1–10 were performed at 2 × 106 Markov chain Monte Carlo sampling after a burn-in period of 50,000 iterations. The posterior probability was then calculated for each value of K using the estimated log-likelihood of K to choose the optimal K.
The “isolation by distance” pattern was assessed by comparing genetic distances to geographic distances between pairs of populations. The geographic distance between populations was measured as the shortest distance between them on the map. The significance of the association between the 2 types of distance was determined by the Mantel test (Mantel 1967) with 10,000 permutations.
Methods for detecting candidate loci for divergence:
We also compared the distribution of the _G_ST values over all loci to their expected distributions under the assumption of neutrality. In this analysis, we only used codominant loci showing HWE to obtain exact estimates of _H_e values. Beaumont and Nichols (1996) have shown that the distribution of _F_ST as a function of heterozygosity in the context of an island model is quite robust, i.e., insensitive to variations in factors such as population structure, demographic structure, and mutation level. Therefore, we applied this method to identify markers deviating from the null hypothesis of neutral evolution. All _G_ST values were transformed to _F_ST values using the Cockerham and Weir (1987) transformation, _F_ST = n _G_ST /(_G_ST + n − 1), where n is the number of populations, and _F_ST values were plotted as a function of expected heterozygosity. This analysis was done in a two-step procedure (Beaumont and Nichols 1996; Scotti-Saintagne et al. 2004). The first envelope of neutral expectation was based on the overall mean value of _F_ST. Markers with _F_ST values outside the 99% envelope were removed and a new analysis was done based on the mean _F_ST value. Markers with _F_ST values outside the 99% envelope after the second analysis were considered as outliers. Calculations were done using the Fdist2 program (Beaumont and Nichols 1996) for all populations and populations belonging to each variety (18 and 11 populations of the ura-sugi and omote-sugi varieties, respectively) to detect candidate species- and variety-specific nonneutral genes.
The coalescence simulation approach, developed by Vitalis et al. (2001), was also used to detect outlier loci in this species. Since this method involves pair-wise comparison, the populations considered in this analysis consisted of the individuals representing the ura-sugi and omote-sugi varieties, respectively. The expected joint distributions of Fpop1 (all individuals representing the ura-sugi variety) and Fpop2 (all individuals representing the omote-sugi variety) were generated by performing 500,000 coalescent simulations using DETSEL v. 1.0 software (Vitalis et al. 2003). The following nuisance parameters were used to generate null distributions with similar numbers of allelic stages as in the observed data set: mutation rates (infinite allele model) 1 × 10−3, 1 × 10−4, 1 × 10−5, and 1 × 10−6; ancestor population sizes 1000, 10,000, and 100,000; times since an assumed bottleneck event 100, 1000, and 10,000 generations; and population size before the split 50 and 500.
RESULTS
Characterization of CAPS markers:
Three-quarters of our CAPS markers were probably based on low-copy-number genes, but a quarter of the loci were highly redundant, not only in the C. japonica database but also in the P. taeda, A. thaliana, and O. sativa databases (supplemental Table S1 at http://www.genetics.org/supplemental/). However, the CAPS patterns of most highly redundant loci can be easily converted into genotypes. Of the 148 loci, 9 (CC0973, CC1204, CC2752, CC1319, CC2700, CC1189, CD1875, CC2831, and CC0337) showed dominant inheritance patterns. We identified putative functions for 98 of the 148 CAPS markers (supplemental Table S1). One hundred twenty-eight of the CAPS loci used have been mapped on a linkage map (Tani et al. 2003).
Genetic diversity and differentiation between populations:
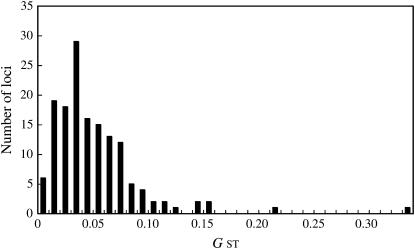
We measured the genetic diversity of the 29 natural C. japonica populations using 4 population genetic parameters: Pl, _N_a, _H_e, and _R_s (Table 1). The Pl values ranged from 0.797 to 0.939 with an average of 0.860. All of the southern populations (population nos. 15–29) had higher than average values except numbers 17, 21, 22, and 24. The _N_a values ranged from 1.926 to 2.081 with an average of 1.994, and the southern populations tended to have higher values than the northern populations. The _R_s values also varied, from 1.795 to 1.929, with an average of 1.914, and populations in southern Japan had higher values than northern populations. The _H_e values ranged from 0.297 to 0.347 with an average of 0.322. The geographical trend of this diversity was similar to those of the other population genetic parameters; Pl, _N_a and _R_s. However, the observed heterozygosity (_H_o) did not completely follow the trend for _H_e. The differences between _H_e and _H_o in each population are represented by the value of _F_IS = 1 – _H_o/_H_e. The average _F_IS value for the 148 loci was negative (but not the nonnegative values of 6 populations) and was not significantly different from expectations under the HWE. Thus, almost all of the populations had a slight, nonsignificant excess of _H_e. The overall genetic differentiation among populations at the 148 loci was low (_G_ST = 0.0500), but the _G_ST value varied among loci, ranging from 0.000 at locus CC0973 to 0.336 at locus CC0539 (Figure 2). The _G_ST values for 11 loci were >0.100, and the allele frequency of 2 of these loci, CC0539 and CC1176, clearly differed between the groups representing the 2 varieties. Ten of the 148 loci (CD1761, CC1127, CC0462, CC0719, CC3393, CC1774, CC0539, CC1176, CC1798, and CD1111) are likely to reflect a genetic differentiation related to the geographic location of each population.
Figure 2.—
Distribution of _G_ST values between 29 natural populations for 148 CAPS loci.
Genetic structure:
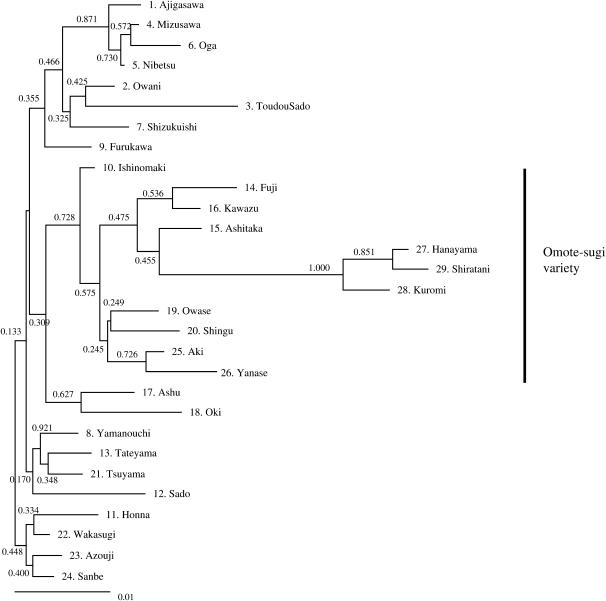
We constructed a phylogenetic tree for the natural populations of C. japonica using the neighbor-joining method (Figure 3). Populations within the same district or group of districts were generally clustered and thus showed a clear geographic trend; omote-sugi variety (Pacific Ocean side) populations cluster together in a clade with relatively high bootstrap support (0.728). However, the positions of 2 populations, JS-15 (no. 21) in Chugoku district and JS-10 (no. 11) in south Tohoku, were not consistent with their geographical locations (here and elsewhere in the text, the abbreviations JS and PO refer to the Japan Sea and Pacific Ocean sides of Japan, respectively). The branching points of 3 populations (nos. 27–29) on Yakushima Island were also inconsistent with their geographical locations. The bootstrap value of each branch was not high, but the divergence point of the 2 main groups was relatively high, 0.728.
Figure 3.—
Phylogenetic tree for 29 natural C. japonica populations created using the neighbor-joining method and a genetic distance matrix based on Nei's genetic distance (Nei 1978); the scale bar at the bottom represents Nei's genetic distance. Values on the horizontal lines in the tree represent bootstrap probabilities.
We also conducted an AMOVA to determine the variation within and among groups (the two varieties) and populations and to test the significance of the among-population variation (Table 2). The variation among populations was 0.0595 and was highly significant (P < 0.001), while the proportions of variance among groups and among populations within groups were 2.08 and 3.87%, respectively.
TABLE 2.
Summary of the AMOVA in 148 CAPS loci
| Source of variation | d.f. | Sum of squares | Variance components | % of variation |
|---|---|---|---|---|
| Among groups | 1 | 306.133 | 0.46701 | 2.08 |
| Among populations within groups | 27 | 1,515.492 | 0.86933 | 3.87 |
| Within populations | 1139 | 24,077.577 | 21.13923 | 94.05 |
| Total | 1167 | 25,899.203 | 22.47556 |
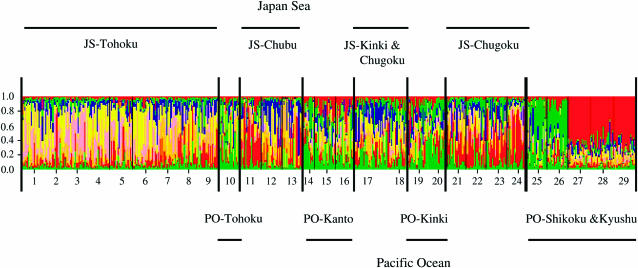
Bayesian clustering of the information from the 139 loci demonstrated that only the model with K = 8 explained the data satisfactorily (this simulation had the highest log-likelihood value). This finding suggests that the most probable number of populations was 8 based on our data for 582 individuals from 29 populations. Populations within the Tohoku district had relatively high frequencies of groups 1 and 2 (colored pink and yellow, respectively, in Figure 4). The frequency of group 3 (colored green in Figure 4) was relatively high in the PO side populations and was especially frequent in populations from the Shikoku district. Group 4 (blue color in Figure 4) was slightly higher in populations located on the Japan Sea side than in populations located on the Pacific Ocean side. Group 5 (colored red in Figure 4) was characteristic of 3 populations (nos. 27–29) from the Yakushima Island and was found in the genomes of more than one-half of the individuals analyzed in these populations. The other three groups were minor and did not show any clear distributional trends.
Figure 4.—
Genetic relationships among the 29 populations surveyed in this study, including 582 individuals, estimated using STRUCTURE (Pritchard et al. 2000) and data on 139 CAPS loci. The model with K = 8 showed the highest log-likelihood value.
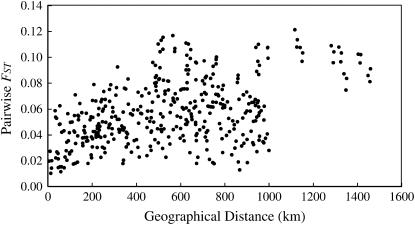
We also investigated the association between the pairwise _F_ST values and the geographical distances between populations, which represents the magnitude of isolation by distance (IBD) (Figure 5). The association was highly significant (r = 0.481, Mantel test, P < 0.001); thus, IBD was clearly a feature of the genetic structure of this species.
Figure 5.—
Relationship between geographical distance and the overall pairwise _F_ST for 148 CAPS loci. The significance of this relationship, which represents the magnitude of IBD, was tested using the Mantel test (r = 0.481, P < 0.001).
Outlier loci:
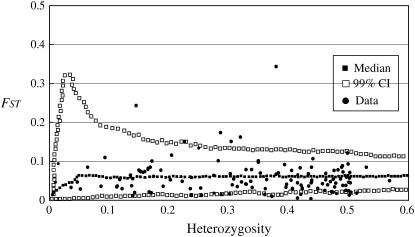
We used the overall mean _F_ST value (0.06258) over 139 loci to construct the expected distribution of _F_ST in an infinite-allele model based on an island demographic model in Fdist. Seven loci were identified as outliers, 5 of which (CC0539, CC0300, CC0924, CC1784, and CC1176; Table 3) had _F_ST values exceeding the upper 99% C.I. (Figure 6), while the other 2, CC0731 and CC0501, had _F_ST values lower than the 99% C.I. envelope.
TABLE 3.
Candidate loci of adaptive genetic divergence between populations in different habitats and varieties
| Fdist | DetSel: | |||||
|---|---|---|---|---|---|---|
| Locus | All populations | Among populations in ura-sugi variety | Among populations in omote-sugi variety | Between ura-sugi and omote-sugi | _F_ST | Putative function |
| CC0539 | ** | ** | ** | *** | 0.347 | — |
| CC0300 | ** | — | ** | ** | 0.242 | — |
| CC0924 | ** | — | ** | ** | 0.174 | Aspartic proteinase 1 |
| CC1784 | ** | ** | ** | — | 0.163 | Nine-cis-epoxycarotenoid oxygenase |
| CC1176 | ** | — | — | *** | 0.150 | — |
| CC0734 | ** | — | — | — | 0.004 | — |
| CC0501 | ** | — | — | — | 0.006 | Monooxygenase, putative (MO2) |
| CC1921 | — | — | — | ** | 0.036 | Pleckstrin homology domain protein |
| CD 1111 | — | — | — | ** | 0.074 | — |
| CC2846 | — | — | — | ** | 0.090 | — |
| CC1127 | — | — | — | ** | 0.084 | Calmodulin |
| CD0657 | — | — | — | ** | 0.033 | Chitinase class I |
| CC1774 | — | — | — | ** | 0.078 | — |
| CD 1761 | — | — | — | ** | 0.056 | Acyl carrier protein 1 |
| CC0462 | — | — | — | ** | 0.061 | CBL-interacting protein kinase 10 |
| CD0041 | — | — | — | ** | 0.116 | Aconitate hydratase |
Figure 6.—
Distribution of _F_ST values as a function of the within-population heterozygosity (_H_S) based on 139 CAPS loci in C. japonica. The envelope of values corresponds to neutral expectations (with _F_ST = 0.06258) in the infinite-allele model constructed according to the method of Beaumont and Nichols (1996).
Two genes, CC0539 and CC1784, were detected as outlier genes with values exceeding the 99% C.I. limits within ura-sugi populations, and 4 such genes (CC0539, CC0300, CC0924, and CC1784) were detected within omote-sugi populations. The two genes that were detected as outliers within ura-sugi populations were also detected as outliers within omote-sugi populations, and only one (CC1176, which was detected as an outlier when including all populations in the analysis) was not detected within populations of each variety as an outlier.
The coalescent simulation, which was based on a population split model (Vitalis et al. 2003), identified 13 loci as outliers (P < 0.01) in a comparison of the populations representing the 2 varieties, 4 of which were also identified by the Fdist test (Table 3).
DISCUSSION
CAPS markers:
The CAPS markers were developed using sequence data from cDNA clones, and we were able to infer the putative functions of two-thirds of the genes using existing DNA databases. Therefore, when we find loci that appear to be associated with adaptation to local conditions and/or differentiation, we should be able to infer their function and to assess their role in these processes. Most of the markers also show codominant inheritance in C. japonica, and the copy number of each locus is not related to its inheritance mode. The average _G_ST might have been underestimated when we included loci with a dominant inheritance mode, but excluding these loci from calculations of the population genetic parameters had little effect on the resulting genetic structure of this species.
Genetic diversity in CAPS markers between populations:
According to our data, 10 of the 148 loci are likely to exhibit a genetic differentiation related to the geographic location of each population, 7 of which were identified as outlier loci, although no such tendencies have been found in previous studies using allozyme and CAPS markers (Tomaru et al. 1994; Tsumura and Tomaru 1999). Populations located in western parts of Japan tended to have higher genetic diversity at these 10 loci than populations in northern Japan. These results probably strongly reflect the historical distribution of C. japonica populations and their migration from the west to the northeast during the most recent postglacial period. According to fossil pollen data (Tsukada 1983, 1988), the refugial areas of this species in the last glacial period (∼18,000 years ago) were located in the Izu peninsula, along the Wakasa Bay to Oki Island, Yakushima Island, and (probably) the southern Kii peninsula and Shikoku Island (Figure 1). Most of these refugia were in western parts of Japan, in accordance with both our data and the results of a previous microsatellite marker-based population study (Takahashi et al. 2005). The populations in the refugia of the last glacial period still show higher than average genetic diversity. Meanwhile, the more remote northern populations, such as the JS-03 (no. 3) and JS-06 (no. 6) populations, and others located at high elevations or more marginal areas such as peninsulas showed lower genetic diversity. A previous population analysis using microsatellite markers showed similar results, especially in the frequencies of rare alleles (Takahashi et al. 2005). These northern populations are thought to have been established ∼6000 years ago by migration from refugial areas, based on inferences from fossil pollen data (Tsukada 1986). Therefore, the genetic diversity of the most northern marginal forests has probably been reduced by bottleneck effects. However, a few populations in northern areas have relatively high genetic diversity compared to the other northern populations, suggesting that small populations may have remained in the northern area even in the last glacial period (Takahara 1998).
The variation among populations was 0.0595 (while the variation among groups and among populations within groups was 2.08 and 3.87%, respectively), very similar to the level found in previous studies (_G_ST = 0.060; Tomaru et al. 1994; Tsumura and Tomaru 1999) and to values reported for other conifers with similar ecological characteristics (Hamrick et al. 1992). These values imply that the 2 variety groups might have exchanged genes more frequently than populations within them because some populations belonging to the different varieties, such as populations in the Kinki district [the JS-13 (no. 17) population of the ura-sugi variety] and the PO-05 and PO-06 (nos. 19 and 20) populations of the omote-sugi variety, are geographically very close to each other (Figure 1).
Genetic structure of natural populations of C. japonica:
The JS-15 (no. 21), JS-10 (no. 11), and PO-9, -19, and -11 (nos. 27–29) populations had phylogenetic locations that were not consistent with their geographical locations. These deviations may reflect the effects of small refugial areas in the last glacial period, migration routes in the postglacial age, random genetic drift, and/or human activities. Our Bayesian analysis of the genetic structure defined eight groups. Populations (nos. 1–9) in the Tohoku district on the Japan Sea side, which contain many individuals with genotypes belonging to pink and yellow groups (Figure 4), are considered to have established in the postglacial period. However, Takahara (1998) recently inferred, from fossil pollen data (Kawamura 1977), that isolated Cryptomeria forests were present in the northern Tohoku district at the beginning of the postglacial period, ∼9500 years ago. Such isolated forests in the past may have continuing effects on the genetic structure of current natural populations. Groups labeled with green and blue colors are relatively frequent in each population along the Pacific Ocean and Japan Sea sides, respectively. These frequency distributions may reflect the locations of refugial populations in the last glacial period. The red-labeled group is especially frequent in the Yakushima populations, which are isolated from the main islands of Japan. In the last glacial period, ∼20,000 years ago, this island was connected to Kyushu Island and then became isolated during the postglacial period, ∼10,000 years ago. In the last glacial period, no C. japonica populations are thought to have been present on Kyushu Island, so C. japonica forests on Yakushima Island have presumably been isolated for a long time from those of the mainland. Consequently, this forest has a unique structure and higher diversity than the other natural forests (Tsumura and Ohba 1993; Takahashi et al. 2005) because the area of natural C. japonica forest on this island is quite large, ∼6000 ha, and the species is dominant in this forest.
However, this species has probably undergone repeated shrinkage and expansion of its distribution as a result of climatic fluctuations since it was first established in Japan. The eight groups might have migrated and exchanged genes between populations, leading to the current genetic structure of this species.
The average _F_IS value indicates that the populations as a whole were not distorted from the HWE, even though some loci were significantly distorted within each population. Three populations (JS-01, JS-07, and PO-09) in widely separated parts of Japan had relatively high numbers of loci with significantly negative _F_IS values. However, 6 populations (JS-09, JS-12, JS-13, PO-05, PO-07, and PO-09) in widely separated parts of Japan showed positive values >10 of these loci. This finding is consistent with the linkage disequilibrium results (data not shown) since these populations were probably subject to severe bottlenecks during the course of their expansion in the postglacial period or logging in recent years, which may have dramatically reduced their size.
IBD was demonstrated in the C. japonica populations, especially among geographically close populations, but the IBD appears to be weaker in this species than in C. obtusa (Tsumura et al. 2007). The genetic isolation of the Yakushima populations from the others contributed strongly to the IBD, but significant IBD was still detected when Yakushima populations were excluded. These findings suggest that natural populations of C. japonica still retain genetic structure in Japan, and this structure can be seen in the phylogenetic tree that we created (Figure 3).
Outlier loci:
We detected 7 outlier loci, 2 of which had _F_ST values lower than the 99% C.I.s in the Fdist test. The _F_ST values for these loci were fairly low (_F_ST < 0.01). Balancing selection (Strobeck 1983; Hudson and Kaplan 1988) or stabilizing selection (Endler 1986) may be responsible for these outliers. In such cases, very similar degrees of polymorphism of the genes involved should theoretically be maintained in stable equilibrium, and their _F_ST values should also be low. In accordance with these theoretical considerations, the allele frequencies of both of these loci in the examined populations are very similar. Some of these loci are ubiquitously expressed and have putative roles in cell maintenance, like housekeeping genes, and thus their _F_ST values might be low because of the importance of their functions, but there are other possible explanations for this finding. In contrast, 5 loci had _F_ST values exceeding the 99% confidence limits (Figure 6). When we examined the status of outlier loci within groups representing the two varieties, only one (CC1176, which was found in all populations) was not detected within populations of each variety as an outlier. This gene might be important in adaptation to different environments for the two varieties, since snow falls abundantly on the Japan Sea but the Pacific Ocean side is quite dry in the winter. The ura-sugi variety on the Japan Sea side has short needles with narrow angles, which are thought to have selective advantages in areas with heavy snowfall in the winter. Two outlier genes, CC0539 and CC1784, were detected in both groups, so these genes are candidate genes related to species adaptation.
The Detsel test revealed a much higher number of outlier loci than the Fdist test, as found in a salmon study (Vasemägi et al. 2005). We identified 13 outlier loci in the Detsel test, and the overlap was only 4, which were identified by the Fdist test, and 2 of these (CC539 and CC1176) deviated highly significantly from neutral expectations (P < 0.001, Table 3).
The test to detect outlier loci that deviate from neutral expectations is not able to identify false positives (type I errors). Thus, we conducted Fdist and Detsel tests, setting a 99% P level criterion for the identification of genes under selective pressure, at which the expected number of false positive loci is 139 × 0.01 = 1.39. We still found 7 and 13 outlier loci in these Fdist and Detsel tests, respectively, indicating that some, at least, of the outlier loci are unlikely to be false positives (due to type I errors). However, only 4 loci were detected in both tests; the other 12 loci were identified by one, but not the other, neutrality test, suggesting that the status of these 16 loci as genes under selective pressure must be regarded with considerable caution (Vasemägi et al. 2005). However, the 4 loci identified by both tests are good candidate loci, especially 2 for which the results were highly significant (P < 0.001). Putative functions can generally be identified for about two-thirds of the genes analyzed in BLAST searches (Ujino-Ihara et al. 2000, 2005). We identified possible functions for only one-half of the 16 candidate genes, suggesting that these candidate genes for adaptation may be conifer or C. japonica specific. Whether or not this is the case, these genes are candidate nonneutral genes and may have specific roles in local adaptation or differentiation in this species. To obtain clear evidence for the adaptive value of these genes, we must analyze nucleotide variations in them between populations located in contrasting environments.
Implications of the results for genetic resources of C. japonica:
We detected several candidate genes for adaptation of this species and/or populations in this study. These genes are likely to be important not only for conservation of the species but also in efforts to develop seedling transfer guidelines. Two of these genes, CC1176 and CC0539, are probably associated with the differentiation between populations of the two varieties. Populations of the ura-sugi variety were mostly homozygous at these loci, implying that they may confer a selective advantage in this variety. We need further information regarding the divergence of the two varieties, such as sequence variation data and gene expression data, but these loci must be considered in attempts to conserve the two varieties. The results of the phylogenetic and STRUCTURE analyses are also consistent with the divergence of the two varieties. However, plantations of this species account for ∼45% of the total 10 million ha of artificial plantations in Japan because of its importance in Japanese forestry. This means that pollen from the artificial forests will increasingly enter the natural forests and consequently affect the seedlings produced by natural regeneration. Thus, gene flow from the artificial forests will greatly modify the genetic structure of the natural populations, even in cases where the clones have been selected from the same region as the natural populations; even in a best-case scenario, the genetic diversity will be decreased because the limited number of clones in the seed orchards represents a strong bottleneck for future generations.
Conservation of natural C. japonica forests is currently an important issue, and these forests must be protected from pollen contamination. Fortunately, forest tree species are long-lived and can maintain their populations for several hundred years, even if the newly produced seedling populations cause gene contamination. Therefore, an ex situ conservation program is currently the best way to conserve the genetic diversity and structure of natural populations of C. japonica. Materials conserved in this manner could be used as future sources of breeding materials and to facilitate the discovery of single nucleotide polymorphisms associated with important traits, because the species currently retains a clear genetic structure.
Acknowledgments
We thank H. Tachida for insightful comments and discussion concerning earlier versions of this manuscript and H. Takahara for helpful comments regarding the fossil pollen data. We also thank M. Koshiba, M. Koyano, and Y. Taguchi for their excellent technical assistance. We also thank two anonymous reviewers for useful comments and suggestions in an early version of this manuscript. This study was partly supported by the Japan Society for the Promotion of Science, Grant-in-Aid for Scientific Research (B) no. 16380112 and Research on Genetic Guideline for Restoration Programs using Genetic Diversity Information from the Ministry of Environment, Japan.
References
- Beaumont, M. A., and R. A. Nichols, 1996. Evaluating loci for use in the genetic analysis of population structure. Proc. R. Soc. Lond. Ser. B 263**:** 1619–1626. [Google Scholar]
- Cockerham, C. C., and B. S. Weir, 1987. Correlations, descent measures: drift with migration and mutation. Proc. Natl. Acad. Sci. USA 84**:** 8512–8514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Mousadik, A., and R. J. Petit, 1996. High level of genetic differentiation for allelic richness among populations of the argan tree [Argania spinosa (L.) Skeels] endemic to Morocco. Theor. Appl. Genet. 92**:** 832–839. [DOI] [PubMed] [Google Scholar]
- Endler, J. A., 1986. Natural Selection in the Wild. Princeton University Press, Princeton, NJ.
- Excoffier, L., P. E. Smouse and J. M. Quattro, 1992. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 131**:** 479–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein, J., 1995. PHYLIP (phylogeny inference package). Ver. 3.57c. Department of Genetics, University of Washington, Seattle.
- Fu, Y. X., 1996. New statistical tests of neutrality for DNA samples from a population. Genetics 143**:** 557–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudet, J., 2000. FSTAT: a program to estimate and test gene diversities and fixation indices. Ver. 2.9.1. (http://www2.unil.ch/popgen/softwares/fstat.htm).
- Hamrick, J. L., M. J. W. Godt and S. L. Sherman-Broylers, 1992. Factors influencing levels of genetic diversity in woody plant species. New Forests 6**:** 95–124. [Google Scholar]
- Hayashi, Y., 1960. Taxonomical and phytogeographical study of Japanese conifers. Norin-Shuppan, Tokyo (in Japanese).
- Hudson, R. R., and N. Kaplan, 1988. The coalescent process in models with selection and recombination. Genetics 120**:** 831–840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., M. Kreitman and M. Aguade, 1987. A test of neutral molecular evolution based on nucleotide data. Genetics 116**:** 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwata, H., T. Ihara-Ujino, K. Yoshimura, K. Nagasaka and Y. Tsumura, 2001. Cleaved amplified polymorphic sequence markers in sugi, Cryptomeria japonica D. Don, and their locations on the linkage map. Theor. Appl. Genet. 103**:** 881–895. [Google Scholar]
- Kawamura, T., 1977. Fossil pollen study on distribution of Cryptomeria japonica forest. I. Akita Prefecture. Kafun 11**:** 8–20 (in Japanese). [Google Scholar]
- Lewis, P. O., and D. Zaykin, 2002. GDA. (http://hydrodictyon.eeb.uconn.edu/people/plewis/software.php).
- Mantel, N., 1967. The detection of disease clustering and a generalized regression approach. Cancer Res. 27**:** 209–220. [PubMed] [Google Scholar]
- Mauricio, R., 2001. Mapping quantitative trait loci in plants: uses and caveats for evolutionary biology. Nature Rev. Genet. 2**:** 370–381. [DOI] [PubMed] [Google Scholar]
- McDonald, J. H. and M. Kreitman, 1991. Adaptive protein evolution at the Adh locus in Drosophila. Nature 351**:** 652–654. [DOI] [PubMed] [Google Scholar]
- Murai, S., 1947. Major forestry tree species in the Tohoku region and their varietal problems, pp. 131–151 in Kokudo Saiken Zourin Gijutsu Kouenshu. Aomori Rinyukai, Aomori, Japan.
- Nei, M., 1972. Genetic distance between populations. Am. Nat. 106**:** 283–292. [Google Scholar]
- Nei, M., 1973. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 70**:** 3321–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., 1977. _F_-statistics and analysis of gene diversity in subdivided populations. Ann. Hum. Genet. 41**:** 225–233. [DOI] [PubMed] [Google Scholar]
- Nei, M., 1978. Estimation of average heterozygosity and genetic distance from a small number of individuals. Genetics 89**:** 583–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York.
- Nei, M., and R. K. Chesser, 1983. Estimation of fixation indices and gene diversities. Ann. Hum. Genet. 47**:** 253–259. [DOI] [PubMed] [Google Scholar]
- Nikaido, A. M., T. Ujino, H. Iwata, K. Yoshimura, H. Yoshimaru et al., 2000. AFLP and CAPS linkage maps of Cryptomeria japonica. Theor. Appl. Genet. 100**:** 825–831. [Google Scholar]
- Ohba, K., 1993. Clonal forestry with sugi (Cryptomeria japonica), pp. 66–90 in Clonal Forestry II, Conservation and Application, edited by M. R. Ahuja and W. J. Libby. Springer-Verlag, Berlin.
- Petit, R. J., I. Aguinagalde, J.-L. De Beaulieu, C. Bittkau, S. Brewer et al., 2003. Glacial refugia: hotspots but not melting pots of genetic diversity. Science 300**:** 1563–1565. [DOI] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. Inference of population structure using multilocus genotype data. Genetics 155**:** 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieseberg, L. H., J. Whitton and K. Gardner, 1999. Hybrid zones and the genetic architecture of a barrier to gene flow between two sunflower species. Genetics 152**:** 713–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saitou, N., and M. Nei, 1987. A neighbor-joining method: a new method for constructing phylogenetic trees. Mol. Biol. Evol. 44**:** 406–425. [DOI] [PubMed] [Google Scholar]
- Schneider, S., J. M. Kueffer, D. Roessli and L. Excoffier, 1997. Arlequin, Version 2.0: software for population genetic data analysis. Genetic and Biometry Laboratory, University of Geneva, Switzerland. (http://lgb.unige.ch/arlequin/).
- Scotti-Saintagne, C., S. Mariette, I. Porth, P. G. Goicoechea, T. Barreneche et al., 2004. Genome scanning for interspecific differentiation between two closely related oak species [Quercus robur L. & Q. petraea (Matt.) Liebl.]. Genetics 168**:** 1615–1626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz, J. F., 2005. Using genome scans of DNA polymorphism to infer adaptive population divergence. Mol. Ecol. 14**:** 671–688. [DOI] [PubMed] [Google Scholar]
- Strobeck, C., 1983. Expected linkage disequilibrium for a neutral locus linked to a chromosomal arrangement. Genetics 103**:** 545–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1989. Statistical-method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123**:** 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahara, H., 1998. Distribution history of Cryptomeria forest, pp. 207–223 in Vegetation History of the Japanese Archipelago, edited by Y. Yasuda and N. Miyoushi. Asakura-Shoten, Tokyo.
- Takahashi, T., N. Tani, H. Taira and Y. Tsumura, 2005. Microsatellite markers reveal high allelic variation in natural populations of Cryptomeria japonica near refugial areas of the last glacial period. J. Plant Res. 118**:** 83–90. [DOI] [PubMed] [Google Scholar]
- Tani, N., T. Takahashi, H. Iwata, Y. Mukai, T. Ujino-Ihara et al., 2003. A consensus linkage map for sugi (Cryptomeria japonica) from two pedigrees, based on microsatellites and expressed tags. Genetics 165**:** 1551–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomaru, N., Y. Tsumura and K. Ohba, 1994. Genetic variation and population differentiation in natural populations of Cryptomeria japonica. Plant Species Biol. 9**:** 191–199. [Google Scholar]
- Tsukada, M., 1983. Vegetation and climate during the last glacial maximum in Japan. Quatern. Res. 19**:** 212–235. [Google Scholar]
- Tsukada, M., 1986. Altitudinal and latitudinal migration of Cryptomeria japonica for the past 20,000 years in Japan. Quatern. Res. 26**:** 135–152. [Google Scholar]
- Tsukada, M., 1988. Japan, pp. 458–518 in Handbook of Vegetation Science, Vol. VII, Vegetation History, edited by B. Huntley and T. Webb III. Kluwer, Dordrecht, The Netherlands.
- Tsumura, Y., and K. Ohba, 1993. Genetic structure of geographical marginal populations of Cryptomeria japonica. Can. J. For. Res. 23**:** 859–863. [Google Scholar]
- Tsumura, Y., and N. Tomaru, 1999. Genetic diversity of Cryptomeria japonica using co-dominant DNA markers based on sequenced-tagged site. Theor. Appl. Genet. 98**:** 396–404. [Google Scholar]
- Tsumura, Y., K. Yoshimura, N. Tomaru and K. Ohba, 1995. Molecular phylogeny of conifers using RFLP analysis of PCR-amplified specific chloroplast genes. Theor. Appl. Genet. 91**:** 1222–1236. [DOI] [PubMed] [Google Scholar]
- Tsumura, Y., Y. Suyama, K. Yoshimura, N. Shirato and Y. Mukai, 1997. Sequence-tagged-sites (STSs) of cDNA clones in Cryptomeria japonica and their evaluation as molecular markers in conifers. Theor. Appl. Genet. 94**:** 764–772. [Google Scholar]
- Tsumura, Y., A. Matsumoto, N. Tani, T. Ujino-Ihara, T. Kado et al., 2007. Genetic diversity and the genetic structure of natural populations of Chamaecyparis obtusa: implication for management and conservation. Heredity (in press). [DOI] [PubMed]
- Ujino-Ihara, T., K. Yoshimura, Y. Ugawa, H. Yoshimaru, K. Nagasaka et al., 2000. Expression analysis of ESTs derived from the inner bark of Cryptomeria japonica. Plant Mol. Biol. 43**:** 451–457. [DOI] [PubMed] [Google Scholar]
- Ujino-Ihara, T., H. Kanamori, H. Yamane, Y. Taguchi, N. Namiki et al., 2005. Comparative analysis of expressed sequence tags of conifers and angiosperms reveals sequences specifically conserved in conifers. Plant Mol. Biol. 59**:** 895–907. [DOI] [PubMed] [Google Scholar]
- Vasemägi, A., and C. R. Primmer, 2005. Challenges for identifying functionally important genetic variation: the promise of combining complementary research strategies. Mol. Ecol. 14**:** 3623–3642. [DOI] [PubMed] [Google Scholar]
- Vasemägi, A., J. Nilsson and C.R. Primmer, 2005. Expressed sequence tag-linked microsatellites as a source of gene-associated polymorphisms for detecting signatures of divergent selection in Atlantic salmon (Salmo salar L.). Mol. Biol. Evol. 22**:** 1067–1076. [DOI] [PubMed] [Google Scholar]
- Vitalis, R., K. Dawson and P. Boursot, 2001. Interpretation of variation across marker loci as evidence of selection. Genetics 158**:** 1811–1823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitalis, R., K. Dawson, P. Boursot and K. Belkhir, 2003. DetSel 1.0: a computer program to detect markers responding to selection. J. Hered. 94**:** 429–431. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1922. Coefficients of inbreeding and relationship. Am. Nat. 56**:** 330–338. [Google Scholar]
- Wright, S., 1931. Evolution in Mendelian populations. Genetics 16**:** 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki, T., 1995. Cryptomeriaceae, pp. 264, in Flora of Japan. Vol I, Pteridophyta and Gymnospermae, edited by K. Iwatsuki, T. Yamazaki, D.E. Boufford and H. Ohba. Kodansha, Tokyo
- Yasue, M., K. Ogiyama, S. Suto, H. Tsukahara, F. Miyahara et al., 1987. Geographical differentiation of natural Cryptomeria stands analyzed by diterpene hydrocarbon constituents of individual trees. J. Jpn. For. Soc. 69**:** 152–156. [Google Scholar]