Virus dynamics and drug therapy (original) (raw)

Abstract

The recent development of potent antiviral drugs not only has raised hopes for effective treatment of infections with HIV or the hepatitis B virus, but also has led to important quantitative insights into viral dynamics in vivo. Interpretation of the experimental data depends upon mathematical models that describe the nonlinear interaction between virus and host cell populations. Here we discuss the emerging understanding of virus population dynamics, the role of the immune system in limiting virus abundance, the dynamics of viral drug resistance, and the question of whether virus infection can be eliminated from individual patients by drug treatment.

Several anti-HIV drugs are now available that act by inhibiting specific viral enzymes. Reverse-transcriptase inhibitors prevent infection of new cells; protease inhibitors stop already- infected cells from producing infectious virus particles. Antiviral drug treatment of HIV-infected patients leads to a rapid decline in the abundance of plasma virus (virus load) and an increase in the CD4 cells that represent the major target cells of the virus. The decline of virus load is roughly exponential and occurs with a half-life of around 2 days (1–8). Unfortunately, the effect of single-drug therapy is often only short-lived, as the virus readily develops resistance (9–16). This causes virus load to rise and CD4 cell counts to fall. Multiple-drug treatment is more successful. A combination of zidovudine (AZT) and 2′-deoxy-3′-thiacytidine (3TC) can maintain a roughly 10-fold reduction of virus load for at least a year (17, 18). Triple-drug therapy—using AZT, 3TC, and a protease inhibitor—can lead to a more than 10,000-fold reduction of virus load and can in many patients maintain plasma virus below detection limit for the whole duration of treatment.

In chronic hepatitis B virus (HBV) carriers, single-drug therapy with the reverse-transcriptase inhibitor lamivudine leads to an exponential decline of plasma virus load, with a half-life of about one day (19). Plasma virus is below detection limit for the duration of treatment (up to 6 months) (20). But when treatment is withdrawn, virus load rapidly resurges to pretreatment levels.

Analyzing the dynamics of decline in virus load during drug therapy and/or the rate of emergence of resistant virus can provide quantitative estimates of the values of crucial rate constants of virus replication in vivo. In this way, it has been shown for HIV-1 that the observed decay of plasma virus implies virus-producing cells have a half-life of about 2 days, whereas for HBV the rate of plasma virus decay suggests that free virus particles have a half-life of about 1 day. Such analyses can provoke further questions. In what follows, we will suggest explanations for the puzzling observation that there is little variation in the turnover rate of productively infected cells among HIV-infected patients, while there is large variation in the turnover rate of such cells in HBV carriers. We characterize the dynamics of different types of infected cells, including productively infected cells, latently infected cells, and cells harboring defective HIV provirus. We explore the rate of emergence of resistant virus, in relation to the frequency of resistant virus mutants before therapy is begun. Finally, we analyze the kinetics of multiple-drug therapy, exploring the crucial question of whether HIV can be eradicated from patients (and if so, how long it will take).

A Basic Model

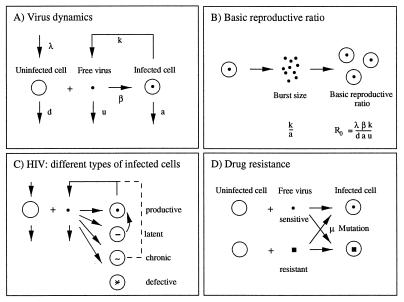
We begin with a very simple model, which captures some of the essentials. This basic model of viral dynamics has three variables: uninfected cells, x; infected cells, y; and free virus particles, v (Fig. 1A). Uninfected cells are produced at a constant rate, λ, and die at the rate dx. Free virus infects uninfected cells to produce infected cells at rate β_xv_. Infected cells die at rate ay. New virus is produced from infected cells at rate ky and dies at rate uv. The average life-times of uninfected cells, infected cells, and free virus are thus given by 1/d, 1/a, and 1/u, respectively. The average number of virus particles produced over the lifetime of a single infected cell (the burst size) is given by k/a. These assumptions lead to the differential equations:

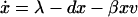
graphic file with name M1.gif

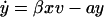
graphic file with name M2.gif

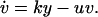graphic file with name M3.gif 1

Before infection (y = 0, v = 0), uninfected cells are at the equilibrium _x_0 = λ/d. An intuitive understanding of the properties of these equations can be obtained, along lines familiar to ecologists and epidemiologists (22, 23). A small initial amount of virus, _v_0, can grow if its basic reproductive ratio, _R_0, defined as the average number of newly infected cells that arise from any one infected cell when almost all cells are uninfected, is larger than one (Fig. 1B). Here R_0 = βλ_k/(adu). The initial growth of free virus is exponential, given roughly by v(t) = _v_0exp[a(_R_0 − 1)t_] when u ≫ a. Subsequently the system converges in damped oscillations to the equilibrium x* = (au)/(β_k), y* = (R_0 − 1)(du)/(β_k), v* = (_R_0 − 1)(d/β). At equilibrium, any one infected cell will, on average, give rise to one newly infected cell. The fraction of free virus particles that manage to infect new cells is thus given by the reciprocal of the burst size, a/k. The probability that a cell (born uninfected) remains uninfected during its lifetime is 1/_R_0. Hence the equilibrium ratio of uninfected cells before and after infection is _x_0/x* = _R_0.

Figure 1.

Figure 1

Models of virus dynamics are based on ordinary differential equations that describe the change over time in abundance of free virus, uninfected, and infected cells. (A) In the simplest model, we assume that uninfected cells, x, are produced at a constant rate, λ, and die at rate dx. Free virus is produced by infected cells at rate ky and dies at rate uv. Infected cells are produced from uninfected cells and free virus at rate β_xv_ and die at rate ay. This leads to Eq. 1 in the text. (B) The average number of virus particles (burst size) produced from one infected cell is k/a. The basic reproductive ratio of the virus, defined as average number of newly infected cells produced from any one infected cell if most cells are uninfected (x = λ/d), is given by R_0 = (λβ_k)/(adu). (C) In HIV-1 infection, there are different types of infected cells. Productively infected cells have half-lifes of about 2 days and produce most (>99%) of plasma virus. Latently infected cells can be reactivated to become virus-producing cells; their turnover rate and abundance may vary among patients depending on the rate of immune activation of CD4 cells. Preliminary results suggest half-lifes of 10–20 days (21). Infected macrophages may be long-lived, chronic producers of virus particles. More than 90% of infected PBMC contain defective provirus. Their half–live was estimated to be around 80 days (2, 21). (D) The simplest models of drug resistance include a sensitive wild-type virus and a resistant mutant (Eq. 3). Mutation between wild type and mutant occurs at rate μ.

Virus Decline Under Drug Therapy

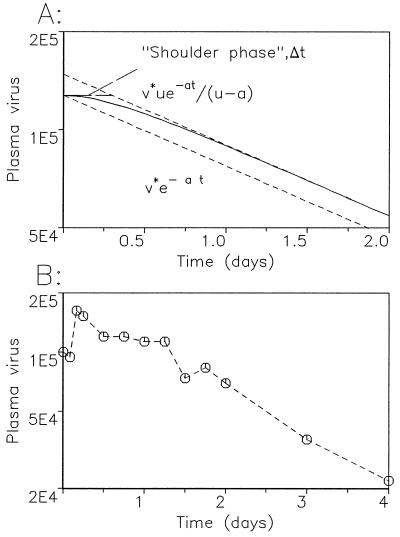
In HIV infection, reverse-transcriptase inhibitors prevent infection of new cells. Suppose first, for simplicity, that the drug is 100% effective and that the system is in equilibrium before the onset of treatment. Then we put β = 0 in Eq. 1, and the subsequent dynamics of infected cells and free virus are given by ẏ = −ay and v̇ = ky − uv. This leads to y(t) = y*e_−_at and v(t) = v*(ue_−_at − ae_−_ut)/(u − a). Infected cells fall purely as an exponential function of time, whereas free virus falls exponentially after an initial shoulder phase. If the half-life of free virus particles is significantly shorter than the half-life of virus-producing cells, u ≫ a, then (as illustrated in Fig. 2A) plasma virus abundance does not begin to fall noticably until the end of a shoulder phase of duration Δ_t_ ≈ 1/u [more precisely, from Fig. 2A, Δ_t_ = −(1/a)ln(1 − a/u)]. Thereafter virus decline moves into its asymptotic phase, falling as e_−_at. Hence, the observed exponential decay of plasma virus reflects the half-life of virus-producing cells, while the half-life of free virus particles determines the length of the shoulder phase. [Note that the equation for v(t) is symmetric in a and u, and therefore if a ≫ u the converse is true.]

Figure 2.

Figure 2

Short-term dynamics of virus decline during anti-HIV-1 treatment. (A) For a drug that reduces cell infection rates from β to s_β (s < 1), we find the amount of free virus, _v_(_t_)/_v_*, declines asymptotically as [Λ2/(Λ2 − Λ1)]exp(−Λ1_t_), where 2Λ1,2 = (_u_ + _a_) ± 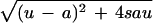Inline graphic (providing _d_ ≪ _a_, _u_). Thus the asymptotic slope of ln[_v_(_t_)] versus _t_ gives a measure of Λ1, while the duration of the shoulder phase, Δ_t_, can be assessed from Δ_t_ = (1/Λ1)ln(Λ2/(Λ2 − Λ1)]. In the limit _s_ → 0 (drug 100% effective), we have Λ1 = _a_ and Δ_t_ = (1/_a_)ln[_u_/(_u_ − _a_)], for _u_ > a. More generally, for positive s < 1 and u ≫ a, we see that the asymptotic decay rate is approximately Λ1 ≈ a(1 − s)[1 − (sa/u) + O (a_2/u_2)] and the shoulder phase duration is correspondingly Δ_t ≈ (1/u)[1 + (a/2_u)(1 − 3_s) + O (_a_2/_u_2)]. (B) Plasma virus decline in a patient treated with the protease inhibitor ritonavir. Data are from ref. 7. Virus load starts to fall exponentially around 30 to 40 h after initiating treatment. This time span is a combination of the shoulder phase described in A, a pharmacological delay of the drug and the intracellular phase of the virus life-cycle (7, 8).

In the more general case when reverse-transcriptase inhibition is not 100% effective, we may replace β in Eq. 1 with β̄ = s_β, with s < 1 (100% inhibition corresponds to s = 0). If the time-scale for changes in the uninfected cell abundance, 1/d, is longer than other time-scales (d ≪ a, u), then we may approximate x(t) by x*. It follows that the decline in free virus abundance is still described by Fig. 1a, except now the asymptotic rate of decay is exp[−_at(1 − s)] for u ≫ a; the duration of the shoulder phase remains Δ_t_ ≈ 1/u (exact expressions for arbitrary a/u and s < 1 are given in the legend to Fig. 2). Thus the observed half-life of virus producing cells, _T_1/2 = (ln 2)/[a(1 − s)], depends on the efficacy of the drug.

Protease inhibitors, on the other hand, prevent infected cells from producing infectious virus particles. Free virus particles, which have been produced before therapy starts, will for a short while continue to infect new cells, but infected cells will produce noninfectious virus particles, w. The equations become ẏ = β_xv_ − ay, v̇ = −uv, ẇ = ky − uw. The situation is more complex, because the dynamics of infected cells and free virus are not decoupled from the uninfected cell population. However, we can obtain analytic insights if we again assume that the uninfected cell population remains roughly constant for the time-scale under consideration. This gives the total virus abundance as v(t) + w(t) = v*[e_−_ut + {(e_−_at − e_−_ut)u/(a − u) + ate_−_ut}u/(a − u)] (ref. 7). As in Fig. 1A, for u ≫ a this function describes a decay curve of plasma virus with an initial shoulder (of duration Δ_t_ = −(2/a)ln(1 − a/u) ≈ 2/u) followed by an exponential decay as e_−_at. The situation is very similar to reverse-transcriptase inhibitor treatment. The main difference is that the virus decay function is no longer symmetric in u and a, and therefore a formal distinction between these two rate constants can be possible; if a > u, the asymptotic behavior is no longer simply exponential, but rather v(t)/v* → [a/(a − u)]ute_−_ut.

Sequential measurements of virus load in HIV-1-infected patients treated with reverse-transcriptase or protease inhibitors usually permit a good assessment of the slope of the exponential decline, which reflects the half-life of infected cells, (ln 2)/a. This half-life is usually found to be between 1 and 3 days (1, 2, 6, 7). Very frequent and early measurements (Fig. 2B) also have provided a maximum estimate of the half-life of free virus particles, (ln 2)/u, of the order of 6 hr (7).

Half-life of Infected Cells and CTL Response

In all HIV-1-infected patients analyzed so far the half-life of virus-producing cells is roughly the same, around 2 days. This rough constancy of half-lives seems puzzling. If the lifespan of productively infected cells is determined by CTL-mediated lysis (24, 25), then it is surprising to find so little variation in the observed half-life in different patients. Alternatively, if we assume that all cell death is caused by virus-induced killing, then CTL-mediated lysis could not limit virus production.

We see two potential explanations why different levels of CTL activity may not result in different half-lifes of infected cells: (i) Measurements of turnover rates based on plasma virus decay strictly imply only that those cells producing most of the plasma virus have a half-life of about 2 days (26). In an individual with a strong CTL response, many infected cells may be killed by CTL before they can produce large amounts of virus (27). A small fraction of cells, however, escapes from CTL killing; these produce most of the plasma virus and are killed by viral cytopathicity after around 2 days. In a weak immune responder, on the other hand, most infected cells may escape from CTL-mediated lysis, produce free virus, and die after 2 days. Thus in both kinds of infected individuals, the half-life of virus-producing cells is the same, but in the strong CTL responder a large fraction of virus production is inhibited by CTL activity. (ii) A second possible explanation is based on the fact that the virus decay slope actually reflects the slowest phase in the viral life cycle (26). If, for example, it takes on average 2 days for an infected cell to become a target for CTL and to start production of new virus, but soon afterwards the cell dies (either due to CTL or virus-mediated killing), then the observed decay slope of plasma virus may reflect the first phase of the virus life cycle, before CTL could attack the cell. In this event, variation in the rate of CTL-mediated lysis would have no effect on the virus decay slope during treatment.

Long-Lived Infected Cells

Only a small fraction of HIV-1-infected cells have a half-life of 2 days. These short-lived cells produce about 99% of the plasma virus present in a patient. But most infected peripherial blood mononuclear cells (PBMC) live much longer (Fig. 1C). We estimated the half-life of these cells by measuring the rate of spread of resistant virus during lamivudine therapy (2, 21). While it takes only about 2 weeks for resistant virus to grow to roughly 100% frequency in the plasma RNA population, it takes around 80 days for resistant virus to increase to 50% frequency in the provirus population. This suggests that most HIV-1-infected PBMC have half-lives of around 80 days. In fact more than 90% of infected PBMC seem to contain defective provirus (21). It is likely that most of these cells are not targets for CTL-mediated lysis and their lifespan is similar to the lifespan of uninfected CD4 cells. The large fraction of defectively infected cells is mostly a consequence of their long lifetime, not because they are produced so frequently.

Less than 10% of infected PBMC harbor replication competent provirus (21). Some of these cells are actively producing new virus particles (and have a half-life of 2 days) while others harbor latent provirus, which can be reactivated to enter virus production. In two patients we estimated the half-life of latently infected cells to be around 10–20 days (21). This suggests that in an HIV-infected patient 50% of latently infected CD4 cells get reactivated on average after 10–20 days. In addition, there may be long-lived, infected macrophages in tissue, which may chronically produce new virus particles.

During triple-drug therapy, plasma virus load declines during the first 1 or 2 weeks with a half-life of less than 2 days and subsequently enters a second phase of slower decline. This second phase has a half-life of around 10 to 20 days (28, 29) and reflects the decay of either latently infected cells or slow, chronic producers. Triple-drug therapy also has led to an improved estimate for the half-life of defectively infected cells by direct observation of HIV-1 provirus decline; an average half-life of around 140 days was observed (28).

Dynamics of Resistance

A main problem with antiviral therapy is the emergence of drug-resistant virus (Fig. 1D). Several mathematical models have been developed to describe the emergence of drug-resistant virus (30–35). An appropriate model that captures the essential dynamics of resistance is:

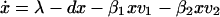
graphic file with name M4.gif

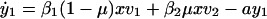
graphic file with name M5.gif

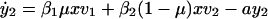
graphic file with name M6.gif

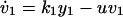
graphic file with name M7.gif

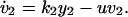graphic file with name M8.gif 2

Here _y_1, _y_2, _v_1, and _v_2, denote, respectively, cells infected by wild-type virus, cells infected by mutant virus, free wild-type virus, and free mutant virus. The mutation rate between wild-type and mutant is given by μ (in both directions). For small μ, the basic reproductive ratios of wild-type and mutant virus are _R_1 = β1λ_k_1/(adu) and _R_2 = β2λ_k_2/(adu). If we assume _R_1 > _R_2, then the equilibrium abundance of cells infected by wild-type virus, y*1, is roughly given as earlier (following Eq. 1), while the corresponding value of y*2 is smaller by a factor of order μ:

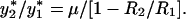graphic file with name M9.gif 3

Suppose drug treatment reduces the rates at which wild-type and mutant virus infect new cells, β1 and β2, to β′1 and β′2, and correspondingly reduces the basic reproductive ratios to _R_′1 and _R_′2.

An important question is whether mutant virus is likely to be present in a patient before drug treatment begins (5, 36). Let σ denote the selective disadvantage of resistant mutant virus compared to wild-type virus before therapy. In terms of the basic reproductive ratios, we have _R_2 = _R_1(1 − σ). If wild type and mutant differ by a single point mutation, then the pretreatment frequency of mutant virus is given by μ/σ. Using a standard quasi-species model and assuming that all (intermediate) mutants have the same selective disadvantage, we find that the approximate frequency of two- and three-error mutant is, respectively, 2(μ/σ)2 and 6(μ/σ)3 (R. M. Ribeiro, S.B., and M.A.N., unpublished work). If the point mutation rate is about 3 × 10−5 (38) and if, for example, the selective disadvantage is σ = 0.01, then for a one-error mutant the pretreatment frequency is about 3 × 10−3, for a two-error mutant 2 × 10−5 and for a three error mutant 2 × 10−7. Thus the expected pretreatment frequency of resistant mutant depends on the number of point mutations between wild-type and resistant mutant, the mutation rate of virus replication, and the relative replication rates of wild-type virus, resistant mutant, and all intermediate mutants. Whether or not resistant virus is present in a patient before therapy will crucially depend on the population size of infected cells (39).

Pre-existing Mutant.

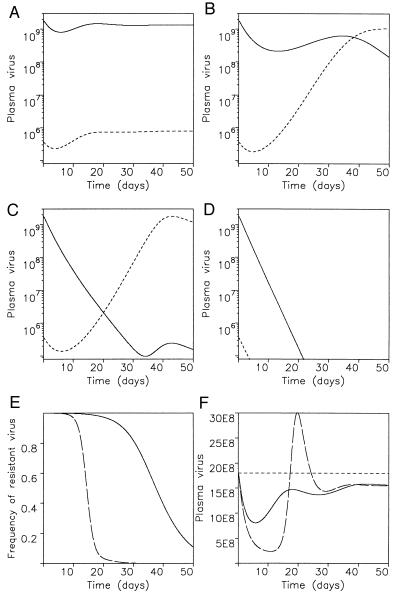
First, we study the consequences of drug therapy in situations where resistant mutants are present before therapy begins. This will usually apply to drugs (or drug combinations) where one- or two-point mutations confer resistance. Suppose _R_1 > _R_2 > 1 before therapy. There are now four possibilities (Fig. 3 A–D): (i) A very weak drug (low dose or low efficacy) may not reduce the rate of wild-type reproduction below mutant reproduction, i.e., _R_′1 > _R_′2 > 1. In this case the mutant virus will not be selected. Nothing much will change. (ii) A stronger drug may reverse the competition between wild type and mutant such that _R_′2 > _R_′1 > 1. Here the mutant virus will eventually dominate the population after long-term treatment, but the initial resurgence of virus can be mostly wild type. (iii) A still stronger drug may reduce the basic reproductive ratio of wild type below one, _R_′2 > 1 > _R_′1. Here wild-type virus should decline roughly exponentially after start of therapy and be maintained in the population at very low levels (only because of mutation). (iv) In this happy case, a very effective drug may reduce the basic reproductive ratio of both wild type and mutant below one, 1 > _R_1 > _R_2, and eliminate the virus population.

Figure 3.

Figure 3

Dynamics of drug treatment if resistant virus is present before therapy. Before treatment, the basic reproductive ratios of wild-type and mutant virus are given by _R_1 and _R_2, respectively. Drug therapy reduces the basic reproductive ratios to _R_′1 and _R_′2. There are four possibilities depending on dosage and efficacy of the drug: (A) If _R_′1 > _R_′2, then mutant virus is still outcompeted by wild type. Emergence of resistance will not be observed. Equilibrium virus abundance during treatment is similar to the pretreatment level. (B) If _R_′2 > _R_′1 > 1, resistance will eventually develop, but the initial resurgence of virus can be due to wild type. (C) If _R_′2 > 1 > _R_′1, resistant virus rises rapidly. In B and C the exponential growth rate of resistant virus is approximately given by a(_R_′2 − 1), thus providing an estimate for the basic reproductive ratio of resistant virus during treatment. (D) If 1 > _R_′1, R_′2, then both wild-type and resistant virus will disappear. (E) A stronger drug will lead to a faster rise of resistant virus, if it exerts a larger selection pressure. (F) The total benefit of drug treatment, as measured by the reduction of virus load during therapy integrated over time, ∫_t (v(t) − v*)dt, is largely independent of the efficacy of the drug to inhibit wild-type replication. A stronger drug leads to a larger initial decline of virus load, but causes faster emergence of resistance. Parameter values: λ = 107, d = 0.1, a = 0.5, u = 5, _k_1 = _k_2 = 500, β1 = 5 × 10−10, β2 = 2.5 × 10−10. Hence, _R_1 = 10 and _R_2 = 5. Treatment reduced β1 and β2 such that: (A) _R_′1 = 3, _R_′2 = 2.5; (B) _R_′1 = 1.5, _R_′2 = 2.25; (C) _R_′1 = 0.5, _R_′2 = 2; (D) _R_′1 = 0.1, _R_′2 = 0.5; and (E and F) _R_′1 = 3, _R_′2 = 4.5 (continuous line) and _R_′1 = 1.5, _R_′2 = 4.5 (broken line). In A–D the continuous line is wild-type virus, whereas the broken line denotes mutant.

Some interesting points emerge from the above dynamics. (i) The resurgence of (wild-type or mutant) virus during treatment is a consequence of an increasing abundance of target cells (31). There is experimental evidence that rising target cell levels can lead to a rebound of wild-type virus during zidovudine treatment (16). Preventing target cell increase therefore could maintain the virus at low levels (40). (ii) The more effective the drug, the more intense the selection, and thus the faster the emergence of resistant virus (41) (Fig. 3E). (iii) The eventual equilibrium abundance of (resistant) virus under drug therapy will usually be very similar to that of wild-type virus before therapy, even if the drug markedly reduces the basic reproductive ratio of the virus population (42) (the abundances for μ ≪ 1, are (λ/a)(1 − 1/_R_1) and (λ/a)(1 − 1/R_′_i) with i = 1 or 2, respectively; these are both roughly λ/a, unless either _R_1 or R_′_i gets close to unity, much less below it). (iv) Finally, the total benefit of drug treatment—as measured by the total reduction of virus load over time (or by the increase of uninfected cells)—is roughly constant, independent of the efficacy of the drug (Fig. 3F).

Non-Pre-Existing Mutant.

Second, we consider the situation where three or more point mutations are necessary for the virus to escape from drug treatment. Here the equilibrium abundance of resistant mutant, y*2, as given by Eq. 3, may be smaller than one. That is, the deterministic model represented by Eq. 2 leads to the conclusion that, on average, less than one cell infected with mutant virus is present before therapy. In this case, the deterministic description is no longer valid; a stochastic model is necessary (41). Assuming a standard Poisson process, the probability that no mutant virus exists before therapy is exp(−y*2).

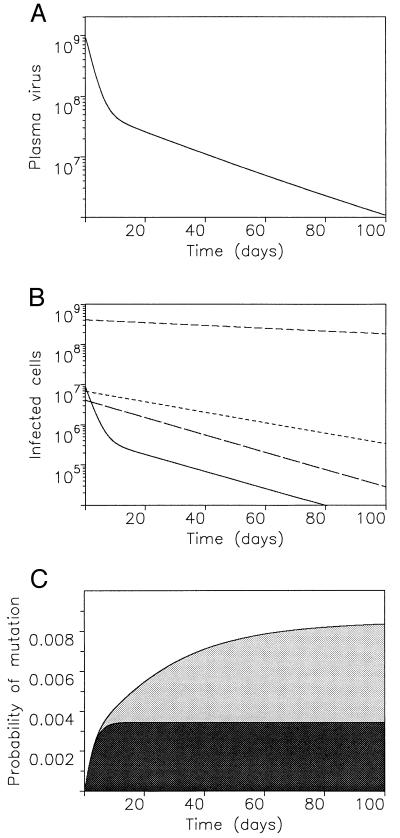
If the drug is strong enough to eliminate wild-type virus, _R_′1 < 1, then we can calculate the probability that mutant virus is produced by the declining wild-type population, even if it is initially absent. We find that this probability is roughly sy*2, under the reasonable assumption that uninfected cells live noticeably longer than infected ones, which in turn live longer than free virus (u ≫ a ≫ d). Here s is the efficacy of the drug on wild-type virus, defined as s = _R_′1/_R_1. Thus, if it is unlikely that mutant virus exists before therapy (y*2 < 1), then for small s it is even less likely that it will be produced by the declining wild-type population. This conclusion, based on an analytic approximation, is supported more generally by numerical studies (Fig. 4).

Figure 4.

Figure 4

Decay of plasma virus and different types of infected cells and probability to produce resistant virus during anti-viral treatment. (A) The first phase of plasma virus decay occurs with a half-life of about 2 days and reflects the turnover rate of productively infected cells. The second phase occurs with a longer half-life (10–30 days) reflecting the decay of latently infected cells or long-lived chronic producers. (B) Productively infected cells disappear rapidly, followed by latently infected cells and chronic producers. Most infected cells may carry defective provirus and decline slowly with a half-life of about 80 days. (C) What is the probability that resistant virus is generated during therapy? Assume treatment reduces wild-type reproduction by a factor s = _R_′1/_R_1. Using the simplified model (2), we can calculate the total amount of mutant virus, _Y_2, which is produced by mutation from wild-type virus after onset of therapy: Y_2 = ∫0∞ β′1μ_x(τ)_v_1(τ)_d_τ. If u ≫ a, we have _v_1(t) ≈ _k_1_y_1/u. If a ≫ d, we have x(t) ≈ x*. During therapy y_1(t) ≈ y*1exp(−_at). Using these approximations, we obtain _Y_2 = s_μ_y*1. A more accurate approximation can be obtained by assuming ẋ ≈ λ − dx during treatment (41). The probability that resistant virus exists before treatment is P_0 = 1 − exp(−_y*2), which is for small y*2 approximately _P_0 = y*2. Similarily the probability that resistant mutant is generated during therapy is P = 1 − exp(−_Y_2) ≈ Y_2. Because y*2 > μ_y*1, we have P < _sP_0. For an effective drug (small s), the probability that resistant mutant is generated during therapy is much smaller than the probability that it already existed before therapy. We can also take into account the possibility that resistant virus is generated by mutation events during production of free virus from infected cells. If this mutation rate is given by v, we find with a similar calculation that _Y_2 = svy*1. If both mutations are possible, then _Y_2 = s(μ + v)y*1. The mutation rates simply add up. The final result, P < sP_0, remains the same. The dark shaded area shows Y_2(t) for a simple model ignoring latency. The lighter shaded area shows the same quantity computed from a model with latency. Model equations are: uninfected cells ẋ = λ − dx − β_xv; productively infected cells ẏ1 = β_q_1_xv − _a_1_y_1 + a_2_y_2; latently infected cells ẏ2 = β_q_2_xv − a_2_y_2; chronic producers ẏ3 = β_q_3_xv − a_3_y_3; defectively infected cells ẏ4 = β_q_4_xv − _a_4_y_4; free virus v̇ = _k_1_y_1 + _k_3_y_3 − uv. Parameter values: λ = 107, d = 0.1, _a_1 = 0.5, _a_2 = 0.05, _a_3 = 0.03, _a_4 = 0.008, u = 5, _k_1 = 500, _k_3 = 10, _q_1 = 0.55, _q_2 = _q_3 = 0.025, _q_4 = 0.4, β = 5 × 10−10 before therapy and β′ = 0.01β during therapy.

If, on the other hand, the drug is unable to eliminate wild type, _R_′1 > 1, then mutant virus will certainly be generated after some time, and will dominate the population provided _R_′2 > _R_′1.

If resistant virus is not present before therapy, then a stronger drug can reduce the chance that a resistant mutant emerges and can prolong the time until resistant virus is generated. (On the other hand, if resistant virus is present then a stronger drug usually leads to a faster rise of resistant virus.)

The above model can be expanded to include a large number of virus mutants with different basic reproductive ratios and different susceptibilities to a given antiviral therapy. Some of these mutants may pre-exist in most patients, while others may not be present before therapy. The basic question is whether a given antiviral drug combination manages to supress the basic reproductive ratios of all pre-existing variants to below one or not. This question is central to hopes for effective long-term treatment against viral infections.

Why Treatment Should Be as Early as Possible and as Hard as Possible.

The outcome of therapy should depend on the virus population size before treatment. The lower the virus load, the smaller the probability that resistant virus is present. Consequently, treatment will be more succesful in patients with lower virus load. Therefore treatment should start early in infection as long as virus load is still low.

The above models also suggest that antiviral therapy should immediately start with as many drugs as clinically possible. Using several drugs at once reduces the probability that resistant virus is present in a patient before therapy. Starting with one drug and then adding other drugs, or cycling between different drugs, creates an evolutionary scenario, which favors the emergence of multiple-drug resistant virus, because at any time virus mutants will be present with basic reproductive ratios larger than one. Similarily, drug holidays or irregular drug consumption are very disadvantageous.

Virus Eradication

Consider a combination treatment that reduces the basic reproductive ratio of all virus variants in a given patient to below one. For how long do we have to treat in order to eliminate HIV infection? Latently infected cells have half-lifes of about 10 to 20 days. Treatment for 1 year may thus reduce the initial population of latently infected cells by a factor of 10−8, which could mean extinction (Fig. 4).

There is one problem, however. Suppose the average half-life of infected PBMC is around 140 days. Most of these cells carry defective provirus, but some may contain replication-competent provirus integrated in a CD4 cell that has not been stimulated since it became infected. Such unstimulated latently infected cell may have half-lifes equivalent to cells carrying defective provirus. With respect to eliminating this cell population, the relevant half-life is therefore about 140 days. Treatment for one year will reduce this cell population to about 16% of its initial value; treatment for 2 years to 3%. Extinction seems difficult. It might be important to develop treatment strategies that reactivate latently infected CD4 cells, so as to reduce their half-life. In addition, it is possible that virus replication persists in specific sites where drugs do not acchieve high concentration.

HBV

In the life cycle of HBV, the virus-encoded reverse transcriptase is responsible for transcribing the unspliced viral mRNA into the DNA genome of new virus particles. Therefore the reverse-transcriptase inhibitor, lamivudine, stops already-infected cells from producing new virus particles. During drug therapy, the dynamics of infected cells and free virus are given by ẏ = β_xv_ − ay and v̇ = −uv. Thus plasma virus, v, simply falls as an exponential function of time. Hence the slope of the virus decay reflects the half-life of free virus particles, which turns out to be about 24 hr (19).

The half-life of infected cells in HBV infection has been estimated from the decay of virus production (comparing the rate of virus production before and after therapy) or from the decline of hepatitis E antigen levels during therapy. In contrast to HIV, virus producing cells in HBV are long-lived. There is also great variation in turnover rates in different patients, ranging from about 10 days to more than 100 days (19). HBV is considered to be noncytopathic, and the difference in infected cell half-lives can be attributed to different CTL activities. In HBV infection it is also possible that infected cells lose their HBV DNA and can thus become uninfected. CTL may accelerate this process (43, 44). Thus our estimated turnover rates of infected cells may not simply describe cell death, but rather the time span a cell remains infected or in the state of virus production.

Emergence of resistance to lamivudine in HBV infection is slower and rarer than in HIV infection. There was no indication of resistance in 50 chronic HBV carriers treated for 24 weeks (19, 20), whereas the same drug usually induces HIV resistance in a few weeks (4). HBV resistance, however, is possible and was observed after about 30 weeks in three patients receiving liver transplantation (45, 46). The 10- to 100-day half-life of HBV-producing cells suggests that the generation time is 5 to 50 times longer in HBV than in HIV, which could explain the slower adaptive response.

What Next?

A combination of experimental techniques and mathematical models has provided new insights into virus population dynamics in vivo. The effect of antiviral treatment on the decline of plasma virus and infected cells, and on the emergence of drug-resistant virus, can be largely understood in quantitative terms. This has consequences for interpreting success or failure of long-term therapy and for designing optimal treatment schedules. Essentially all mathematical models so far suggest that HIV should be hit as early as possible and as hard as possible.

Measurement of changes in plasma virus during therapy should ideally be complemented by quantification of infected cells in those tissues that contain most of the virus population [the lymph-system for HIV (47, 48) and the liver for HBV]. Determining the abundance of infected cells in those tissues before and during therapy should lead to a more direct assessment of their turnover rates. It also may provide estimates of further parameters of virus dynamics, such as the rate of infection of new cells, β, and the rate of virus production from infected cells, k (49). It will also be important to illuminate the spatial dynamics of virus infections (50).

Another important step will be to monitor changes in immune cell populations (specific CTL or B cells) during drug therapy, to gain insights into the rates of turnover of various cells of the immune system and their rates of proliferation in response to antigenic stimulation in vivo. In addition, it would be helpful to have experimental techniques that determine the fraction of infected cells (or free virus) eliminated by specific immune responses in a given length of time. Such information is essential for a quantitative understanding of immune response dynamics in vivo.

The dynamics of drug resistance also provides further insights into theories of viral population genetics and antigenic variation (51–61). The main difference between escape from drug treatment and escape from immune responses is that drugs provide a constant selection pressure, while the immune response is sensitive to changes in the antigenic structure of the virus population (37) and also may shift between different viral epitopes (53).

The approach developed here is, of course, not limited to HIV or HBV, but can easily be adapted to other persistant infections with replicating parasites (viruses, bacteria, protozoa, helminths) and also to various kinds of drug treatment such as interferons, chemokines, or antibiotics. The ultimate aim is to derive a detailed understanding of the dynamics of the interactions between populations of viruses (or other infectious agents) and populations of immune system cells. Such nonlinear population dynamics often can defy any intuition based on interactions between individual cells and virus.

Acknowledgments

Support from the Wellcome Trust (M.A.N. and S.B.) and the Royal Society (S.B. and R.M.M.) is gratefully acknowledged.

ABBREVIATIONS

HBV

hepatitis B virus

CTL

cytotoxic T cell

PBMC

peripherial blood mononuclear cells

References