Velvet: Algorithms for de novo short read assembly using de Bruijn graphs (original) (raw)

Abstract

We have developed a new set of algorithms, collectively called “Velvet,” to manipulate de Bruijn graphs for genomic sequence assembly. A de Bruijn graph is a compact representation based on short words (_k_-mers) that is ideal for high coverage, very short read (25–50 bp) data sets. Applying Velvet to very short reads and paired-ends information only, one can produce contigs of significant length, up to 50-kb N50 length in simulations of prokaryotic data and 3-kb N50 on simulated mammalian BACs. When applied to real Solexa data sets without read pairs, Velvet generated contigs of ∼8 kb in a prokaryote and 2 kb in a mammalian BAC, in close agreement with our simulated results without read-pair information. Velvet represents a new approach to assembly that can leverage very short reads in combination with read pairs to produce useful assemblies.

Sequencing remains at the core of genomics. Applications include determining the genome sequence of a new species, determining the genome sequence of an individual within a population, sequencing RNA molecules from a particular sample, and using DNA sequence as a readout assay in molecular biology techniques. Determining the complete genome sequence of a species remains an important application of sequencing, and despite the success in determining the human (International Human Genome Sequencing Consortium 2001; Venter et al. 2001), mouse (Waterston et al. 2002), and numerous other genomes, this is a tiny sample of the millions of species in the biosphere.

Recently, new sequencing technologies have emerged (Metzker 2005), for example, pyrosequencing (454 Sequencing) (Margulies et al. 2005) and sequencing by synthesis (Solexa) (Bentley 2006), both commercially available. Compared to traditional Sanger methods, these technologies produce shorter reads, currently ∼200 bp for pyrosequencing and 35 bp for Solexa. Until recently, very short read information was only used in the context of a known reference assembly, either for sequencing individuals of the same species as the reference, or readout assays—for example, STAGE (Kim et al. 2005) and ChIPSeq (Johnson et al. 2007).

A critical stage in genome sequencing is the assembly of shotgun reads, or piecing together fragments randomly extracted from the sample, to form a set of contiguous sequences (contigs) representing the DNA in the sample. Algorithms are available for whole-genome shotgun (WGS) fragment assembly, including: Atlas (Havlak et al. 2004), ARACHNE (Batzoglou et al. 2002), Celera (Myers et al. 2000), PCAP (Huang et al. 2003), phrap (P. Green, http://www.phrap.org), or Phusion (Mullikin and Ning 2003). All these programs rely on the overlap-layout-consensus approach (Batzoglou 2005), representing each read as a node and each detected overlap as an arc between the appropriate nodes. These methods have proved their use through numerous de novo genome assemblies.

Very short reads are not well suited to this traditional approach. Because of their length, they must be produced in large quantities and at greater coverage depths than traditional Sanger sequencing projects. The sheer number of reads makes the overlap graph, with one node per read, extremely large and lengthy to compute. With long reads, repeats in the data are disambiguated by careful metrics over long overlaps that distinguish repeat matches from real overlaps, using, for example, high-quality base disagreements. With short reads, and correspondingly short overlaps to judge from, many reads in repeats will have only a single or no base differences. This leads to many more ambiguous connections in the assembly.

The EULER assembler (Pevzner et al. 2001) adopted a fundamentally different approach using de Bruijn graphs. In this representation of data, elements are not organized around reads, but around words of k nucleotides, or _k_-mers. Reads are mapped as paths through the graph, going from one word to the next in a determined order. Several teams (Shah et al. 2004; Bokhari and Sauer 2005; Myers 2005; Jiang et al. 2007) have since expanded on the use of de Bruijn graphs for sequence assembly. The fundamental data structure in the de Bruijn graph is based on _k_-mers, not reads, thus high redundancy is naturally handled by the graph without affecting the number of nodes. In addition, each repeat is present only once in the graph with explicit links to the different start and end points. Depending on available information, it can be either resolvable or not, but it is readily identifiable. Mis-assembly errors are therefore more easily avoided than with overlap graphs. Finally, searches for overlaps are simplified, as overlapping reads are mapped onto the same arcs and can easily be followed simultaneously.

Despite the attractiveness of the de Bruijn graph data structure for short read assemblies, it has not been used extensively in current production-based assembly methods. Chaisson et al. (2004) and Sundquist et al. (2007) suggested ways of using these graphs specifically for short read assembly (100–200 bp), but not for very short reads (25–50 bp). More recently, programs such as SSAKE (Warren et al. 2007), SHARCGS (Dohm et al. 2007), and VCAKE (Jeck et al. 2007) implicitly use this framework, but at a local level. With the advent of highly cost effective very short reads, de Bruijn graph-based methods will grow in utility. However, it is necessary to develop efficient and robust methods to manage experimental errors and repeats.

In this study, we present a set of algorithms, collectively named “Velvet,” that manipulates these de Bruijn graphs efficiently to both eliminate errors and resolve repeats. These two tasks are done separately: first, the error correction algorithm merges sequences that belong together, then the repeat solver separates paths sharing local overlaps. We have assessed Velvet on both simulated and real data. Using only very short paired simulated reads, Velvet is capable of assembling bacterial genomes, with N50 contig lengths of up to 50 kb, and simulations on 5-Mb regions of large mammalian genomes, with contigs of ∼3 kb.

Results

The de Bruijn graph

Structure

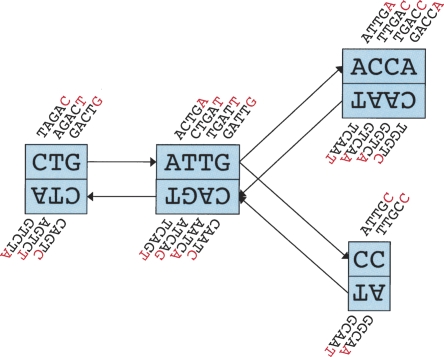
In the de Bruijn graph, each node N represents a series of overlapping _k_-mers (cf. Fig. 1 for a small example). Adjacent _k_-mers overlap by k − 1 nucleotides. The marginal information contained by a _k_-mer is its last nucleotide. The sequence of those final nucleotides is called the sequence of the node, or s(N).

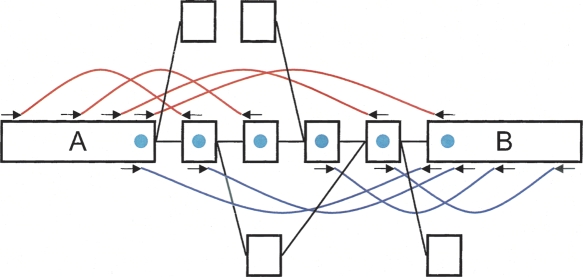
Figure 1.

Schematic representation of our implementation of the de Bruijn graph. Each node, represented by a single rectangle, represents a series of overlapping _k_-mers (in this case, k = 5), listed directly above or below. (Red) The last nucleotide of each _k_-mer. The sequence of those final nucleotides, copied in large letters in the rectangle, is the sequence of the node. The twin node, directly attached to the node, either below or above, represents the reverse series of reverse complement _k_-mers. Arcs are represented as arrows between nodes. The last _k_-mer of an arc’s origin overlaps with the first of its destination. Each arc has a symmetric arc. Note that the two nodes on the left could be merged into one without loss of information, because they form a chain.

Each node N is attached to a twin node N, which represents the reverse series of reverse complement _k_-mers. This ensures that overlaps between reads from opposite strands are taken into account. Note that the sequences attached to a node and its twin do not need to be reverse complements of each other.

The union of a node N and its twin N is called a “block.” From now on, any change to a node is implicitly applied symmetrically to its twin. A block therefore has two distinguishable sides, in analogy to the “_k_-mer edges” described in Pevzner et al.’s 2001 paper.

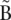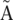Nodes can be connected by a directed “arc.” In that case, the last _k_-mer of an arc’s origin node overlaps with the first of its destination node. Because of the symmetry of the blocks, if an arc goes from node A to B, a symmetric arc goes from to . Any modification of one arc is implicitly applied symmetrically to its paired arc.

On these nodes and arcs, reads are mapped as “paths” traversing the graph. Extracting the nucleotide sequence from a path is straightforward given the initial _k_-mer of the first node and the sequences of all the nodes in the path.

Construction

The reads are first hashed according to a predefined _k_-mer length. This variable k is limited on the upper side by the length of the reads being hashed, to allow for a small amount of overlap, usually k = 21 for 25-bp reads. Smaller _k_-mers increase the connectivity of the graph by simultaneously increasing the chance of observing an overlap between two reads and the number of ambiguous repeats in the graph. There is therefore a balance between sensitivity and specificity determined by k (cf. Methods).

For each _k_-mer observed in the set of reads, the hash table records the ID of the first read encountered containing that _k_-mer and the position of its occurrence within that read. Each _k_-mer is recorded simultaneously to its reverse complement. To ensure that each _k_-mer cannot be its own reverse complement, k must be odd. This first scan allows us to rewrite each read as a set of original _k_-mers combined with overlaps with previously hashed reads. We call this new representation of the read’s sequence the “roadmap.”

A second database is created with the opposite information. It records, for each read, which of its original _k_-mers are overlapped by subsequent reads. The ordered set of original _k_-mers of that read is cut each time an overlap with another read begins or ends. For each uninterrupted sequence of original _k_-mers, a node is created.

Finally, reads are traced through the graph using the roadmaps. Knowing the correspondence between original _k_-mers and the newly created nodes, Velvet proceeds from one node to the next, creating a new directed arc or incrementing an existing one as appropriate at each step.

Simplification

After constructing the graph, it is generally possible to simplify it without any loss of information. Blocks are interrupted each time a read starts or ends. This leads to the formation of “chains” of blocks, or linear connected subgraphs. This fragmentation of the graph costs memory space and lengthens calculation times.

These chains can be easily simplified. Whenever a node A has only one outgoing arc that points to another node B that has only one ingoing arc, the two nodes (and their twins) are merged. Iteratively, chains of blocks are collapsed into single blocks.

The simplification of two nodes into one is analogous to the conventional concatenation of two character strings, and also to some string graph based methods (Myers 2005). This straightforward transformation involves transferring arc, read, and sequence information as appropriate.

Error removal

Errors are corrected after graph creation to allow for simultaneous operations over the whole set of reads. In our framework, errors can be due to both the sequencing process or to the biological sample, for example, polymorphisms. Distinguishing polymorphisms from errors is a post-assembly task. A naive approach to error removal would be to use the difference between the expected coverage of genuine sequences and that of random errors. Therefore removing all the low coverage nodes (and their corresponding arcs) would remove the errors. However, this relies on the differences being due to genuine errors and not to biological variants present at a reasonable frequency in the sample, and errors being randomly distributed in the reads.

Instead, Velvet focuses on topological features. Erroneous data create three types of structures: “tips” due to errors at the edges of reads, “bulges” due to internal read errors or to nearby tips connecting, and erroneous connections due to cloning errors or to distant merging tips. The three features are removed consecutively.

Removing tips

A “tip” is a chain of nodes that is disconnected on one end. Removing these tips is a straightforward task. Discarding this information results in only local effects, as no connectivity is disrupted. Nonetheless, some restraint must be applied to the process to avoid eroding genuine sequences that are merely interrupted by a coverage gap. To deal with this issue, we define two criteria: length and minority count.

A tip will only be removed if it is shorter than 2_k_. This arbitrary cutoff length was chosen because it is greater than the length in k_-mers of an individual very short read. Erroneous constructs involving entire short reads are presumably extremely rare. In the case of long reads, this cutoff is set to be the maximum length tip that can be created by two nearby mistakes. A tip longer than 2_k therefore represents either genuine sequence or an accumulation of errors that is hard to distinguish from novel sequence. In the latter case, clipping the read tips more stringently might be necessary.

We define “minority count” as the property that, at the node where the tip connects to the rest of the graph, the arc leading to that tip has a multiplicity inferior to at least one of the other arcs radiating out of that junction node. In other words, starting from that node, going through the tip is an alternative to a more common path.

This ensures that, at the local level, tips are removed in increasing order of multiplicity. Velvet progressively uncovers chains of high coverage nodes that are not destroyed by virtue of the previous criteria, thus preserving the graph from complete erosion.

Velvet iteratively removes tips from the graph under these two criteria. When there are no more tips to remove, the graph is simplified once again.

Removing bubbles with the Tour Bus algorithm

We consider two paths redundant if they start and end at the same nodes (forming a “bubble”) and contain similar sequences. Such bubbles can be created by errors or biological variants, such as SNPs or cloning artifacts prior to sequencing. Erroneous bubbles are removed by an algorithm called “Tour Bus.” The criteria for deciding whether two paths justify simplification can be complex, taking into account error models of the sequence or (for the case of mixed haplotype samples) other features of the sequence and graph, such as coverage. Currently, we apply simple sequence identity and length thresholds.

Detection of redundant paths is done through a Dijkstra-like breadth-first search. The algorithm starts from an arbitrary node and progresses along the graph, visiting nodes in order of increasing distance from the origin. In this application, the distance between two consecutive nodes A and B is the length of s(B) divided by the multiplicity of the arc leading from A to B. This ad hoc metric gives priority to higher coverage, more reliable, paths.

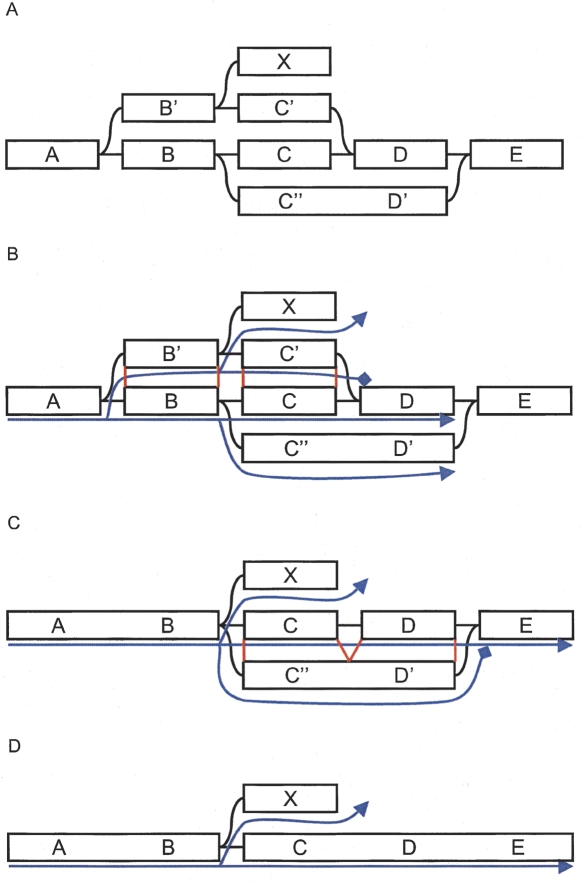
Whenever the process encounters a previously visited node, it backtracks from both the current node and the previously visited node, to find their closest common ancestor. From the two retraced paths, the sequences are extracted and aligned. If judged similar enough, they are merged. The path that reached the end node first in the search, “shortest” according to the metric, is used as the consensus path because of its higher coverage. The metric implicitly imposes a majority vote in choosing the consensus sequence. Figure 2 shows how the iteration proceeds on a small example graph.

Figure 2.

Example of Tour Bus error correction. (A) Original graph. (B) The search starts from A and spreads toward the right. The progression of the top path (through B′ and C′) is stopped because D was previously visited. The nucleotide sequences corresponding to the alternate paths B′C′ and BC are extracted from the graph, aligned, and compared. (C) The two paths are judged similar, so the longer one, B′C′, is merged into the shorter one, BC. The merging is directed by the alignment of the consensus sequences, indicated in red lines in B. Note that node X, which was connected to node B′, is now connected to node B. The search progresses, and the bottom path (through C′ and D′) arrives second in E. Once again, the corresponding paths, C′D′ and CD are compared. (D) CD and C′D′ are judged similar enough. The longer path is merged into the shorter one.

Merging two paths is a complex operation, as all the underlying graph structures must be remapped while maintaining their connections with other nodes. The positioning of the different elements is based on the sequence alignment of the paths. Although straightforward on linear paths, that is, when no block is visited more than once, this transformation is subtler in the presence of palindromes. Palindromes create “hairpin folds,” paths that go through a block one way, then go through it again, in the opposite direction. The need to preserve connectivity forbids projecting hairpins onto linear paths.

To merge two paths, Tour Bus creates a chain of markers along both of them, node by node. The paths are merged progressively from one end to the next. At each step, the first unmapped minority node is compared to the corresponding majority consensus node, using the local sequence alignment produced previously. All the information attached to that node, including coverage, sequence identifiers, and arcs, is then mapped accordingly onto the majority node. The presence of markers allows Tour Bus to dynamically modify the marked path as it corrects the graph. This can be especially useful when a path goes through node A, then later through its twin node. After remapping A, Velvet remaps 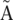, and diverts the path markers accordingly.

Removing erroneous connections

Erroneous connections are removed after Tour Bus. These unwanted connections do not create any recognizable loop or structure, so they cannot be readily identified from the topology of the graph as with tips and bubbles. Also, they cannot be associated directly to a corresponding correct path. Therefore, Velvet removes them with a basic coverage cutoff. Currently this cutoff is set by the user, based on plots of node coverage after the removal of bubbles.

It is important to stress that this simple node removal, because it is done after Tour Bus, does not contradict the cautious approach in the design of that algorithm. Indeed, the purpose of Tour Bus is to remove errors without destroying unique regions with low coverage. Once this algorithm has run, most unique regions are simplified into long straight nodes, where, by virtue of the law of large numbers, the average coverage is close to the expected value. Genuine short nodes that cannot be simplified correspond to low-complexity sequences that are generally present multiple times in the genome. Their overall coverage is therefore proportionally higher. This means that with a high probability, any low-coverage node left after Tour Bus is a chimeric connection, due to spurious overlaps created by experimental errors.

Testing error removal on simulated data

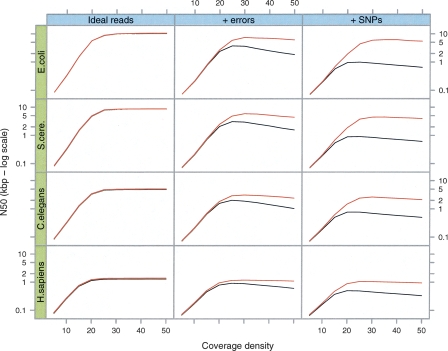
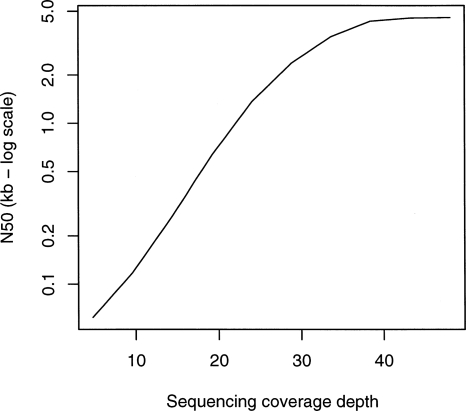
We simulated reads from four different reference genomes: Escherichia coli, Saccharomyces cerevisiae, Caenorhabditis elegans, and Homo sapiens. In the last three species, we chose 5-Mb regions of each genome, corresponding to the approximate amount of DNA that can be sequenced with a 50× coverage depth by a single Solexa lane. Five megabytes is therefore the largest amount of continuous data that could be present on current machine formats in a single lane; currently there are significant laboratory challenges to generate normalized clone pools for a complete 5-Mb region, but smaller units of genome, such as BACs, (potentially using indexing technology to track each clone) will present an easier assembly problem. Reads 35 bp long were randomly generated at different coverage values, from 5× to 50×, then hashed by 21-mer words. We only considered substitution errors as these are reported as the most common class of error for current short read sequencing technologies. The evolution of the N50, or median length-weighted contig length, against coverage is displayed in Figure 3.

Figure 3.

Simulations of Tour Bus. The genome of E. coli and 5-Mb samples of DNA from three other species (S. cerevisiae, C. elegans, and H. sapiens, respectively) were used to generate 35-bp read sets of varying read depths (_X_-axis of each plot). We measured the contig length N50 (_Y_-axis, log scale) after tip-clipping (black curve) then after the subsequent bubble smoothing (red curve). In the first column are the results for perfect, error-free reads. In the second column, we inserted errors in the reads at a rate of 1%. In the third column, we generated a slightly variant genome from the original by inserting random SNPs at a rate of 1 in 500. The reads were then generated with errors from both variants, thus simulating a diploid assembly.

In the first test, the reads do not contain errors. Initially coverage increases exponentially, as predicted by the Lander-Waterman statistic (Lander and Waterman 1988). Then, when coverage is sufficient, the N50 abruptly stops increasing, as it is limited by the natural repetition of the reference genome. This barrier has a different level depending on the reference genome. Obviously, the more repetitive and complex the genome is, the lower the maximum N50.

The second test is identical to the first, with the introduction of errors at a 1% rate. The results are consistent with the first test, except that the maximum N50 is lower than with error-free reads. In fact, as coverage rises to 50×, the N50 decreases slightly, owing to the adjunction of errors without the closing of any coverage gap.

Finally, the third test is identical to the second, but with reads (with 1% error) generated from two copies of the reference genome: the original one and one with SNPs randomly added at a rate of 1/500 bp. Velvet is not significantly affected by these variations.

Testing error removal on experimental data

A 173,428-bp human BAC was sequenced using Solexa sequencing machines, with an average coverage of 970×. The BAC was also sequenced to finished quality using conventional methods. The reads were 35 bp long, and the ensuing analysis was done with 31-mers.

We removed errors using Velvet’s error correction algorithm (cf. Table 1). Because of repeats, the Tour Bus method merged similar paths in the finished sequence, smoothing out similar (but not identical) repeats. The overcollapsing of repeats is not drastic and potentially could be avoided with more sophisticated detection of repeat differences.

Table 1.

Efficiency of the Velvet error-correction pipeline on the BAC data set

To test the performance of Velvet against a virtual ideal assembler, we built a de Bruijn graph from the known finished sequence of the BAC. This is equivalent to an error-free, gap-free assembly.

Not only did the Tour Bus method significantly increase the sensitivity and specificity of the correction, but it also preserved the integrity of the graph structure. Indeed, the median and maximum node lengths in the short read graph are comparable to those in the finished BAC graph. The N50 for all nodes of the graph was 1958 bp; for nodes >100 bp, 2041 bp; and for nodes >1000 bp, 3266 bp. Direct sequence alignment showed that nodes of length 100 bp or more from the short read graph covered 90.0% of the BAC with 99.989% sequence identity and no mis-assembly. In comparison, in the ideal graph, nodes longer than 100 bp represent 91.9% of the genome. Only one indel (2-bp deletion) was observed.

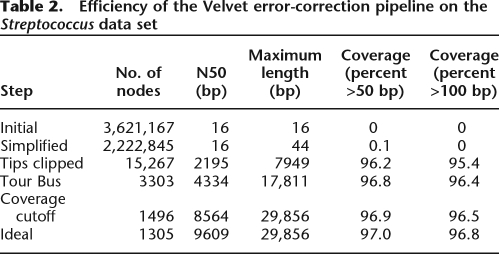
Two million seven hundred thousand 36-bp reads were sequenced from the 2-Mb genome of Streptococcus suis P1/7, for a mean coverage depth of 48×. The statistics of the resulting graph are in Table 2. Again, no mis-assembly was created, while 96.5% of the genome was covered with 99.996% identity. In the ideal graph, 96.8% of the genome is covered by contigs longer than 100 bp. The N50 for all nodes of the graph was 8564 bp; for nodes >100 bp, 8742 bp; and for nodes >1000 bp, 8871 bp. Excluding contigs that mapped onto multiple copies of a repeat, only six indels, up to 2 bp long, were observed.

Table 2.

Efficiency of the Velvet error-correction pipeline on the Streptococcus data set

On this data set, we tested the effect of coverage on the N50. We built the graph for subsets of reads of various sizes. Figure 4 shows how the results with experimental reads are similar to those of our simulations. The N50 goes up exponentially, then hits a limit. To avoid biasing the results by setting an arbitrary parameter for each data point, the removal of erroneous connections by coverage cutoff was omitted, hence the difference with the results in Table 2.

Figure 4.

Effect of coverage on contig length with experimental Streptococcus data.

Breadcrumb: Resolution of repeats with short read pairs

The previous simulations show that the short read assembly is limited by the intrinsic repeat structure of the genome being sequenced. It is therefore necessary to resolve these repeats; in other words, to correctly extend and connect contigs through repeated regions, which otherwise create “tangles” in the de Bruijn graph. To do so, we developed another module within Velvet, called “Breadcrumb” (Fig. 5), to exploit paired end read information.

Figure 5.

Breadcrumb algorithm. Two long contigs produced after error correction, A and B, are joined by several paired reads (red and blue arcs). The path between the two can be broken up because of a repeat internal to the connecting sequence, because of an overlap with a distinct part of the genome, or because of some unresolved errors. The small square nodes represent either nodes of the path between A and B, or other nodes of the graph connected to the former. Finding the exact path in the graph from A to B is not straightforward because of all the alternate paths that need to be explored. However, if we mark all the nodes that are paired up to either A or B (with a blue circle), we can define a subgraph much simpler to explore. Ideally, only a linear path connects both nodes.

We suppose that the insert length distribution has a small variance. We then determine a cutoff length longer than practically all inserts and designate as “long nodes” all the nodes longer than that cutoff. The objective of this definition is to include as many nodes of the graph as possible, while ensuring that very few read pairs span over such chosen nodes. Note that uniqueness is not an issue at this stage.

Using the read pairs, Breadcrumb starts by pairing up the long nodes. Because we did not set any restriction on uniqueness, some long nodes may consistently connect to several other long nodes, but they are simply flagged as ambiguous and left untouched. This selection therefore eliminates duplicated nodes, but not necessarily all of them.

For each of the unambiguous long nodes, Breadcrumb flags all the nodes containing the mate reads of the reads in that long node. If a single opposite long node is available, then all the nodes that pair up to it are also flagged. Because of the node length constraint, between two long contigs nearly all paired reads map onto a read on either of the long reads. With low probability, there will be mate pairs that are both in the low-complexity region between the reads, which are essentially unusable.

Breadcrumb then extends the unique node by going as far as possible from one connected flagged node to the next and stopping if there are no, or several, options. In the best case, a simple path can be found to the opposite long node, and the two contigs can be merged.

To be robust, such a method must allow for erroneous reads. First, Breadcrumb marks all the reads detected while removing erroneous connections (cf. above) as unreliable and does not use the corresponding read pairs. Second, despite this precaution, several long nodes may be erroneously connected by very few (<5) read pairs. Breadcrumb discards such weak connections between long nodes. Finally, because errors occur also in low-complexity regions, it is necessary to apply a Tour Bus-like process to the flagged nodes, unflagging them instead of destroying them.

Testing the use of read pairs

Using the same four species used previously, we tested the Breadcrumb algorithm on artificially generated reads. We generated random 35-bp reads with 50× coverage of the selected 5-Mb samples. Our simulated read pair set assumes complete coverage in read pairs with no mispairing rate and a restricted length distribution, which is an admittedly ideal scenario, although the algorithm does not explicitly utilize the coverage or length distribution of read pairs.

Figure 6 shows the evolution of N50 against insert length. We see that whereas insert lengths must be long enough to step over obstacles in the graph, if they are too long, scaffolding the contigs becomes problematic. Mis-assemblies were infrequent, <0.5% for the most challenging case, i.e., the assembly of human reads with errors and SNPs.

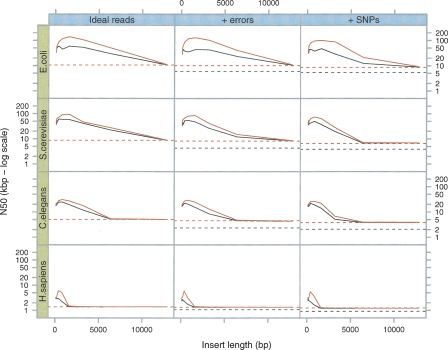
Figure 6.

Breadcrumb performance on simulated data sets. As in Figure 3, we sampled 5-Mb DNA sequences from four different species (E. coli, S. cerevisiae, C. elegans, and H. sapiens, respectively) and generated 50× read sets. The horizontal lines represent the N50 reached at the end of Tour Bus (see Fig. 3) (broken black line) and after applying a 4× coverage cutoff (broken red line). Note how the difference in N50 between the graph of perfect reads and that of erroneous reads is significantly reduced by this last cutoff. (Black curves) The results after the basic Breadcrumb algorithm; (red curves) the results after super-contigging.

The errors generated by Velvet are concentrated in the repeat regions reconstructed by Breadcrumb. This is because in its current implementation, Tour Bus simplifies small local variation and errors alike, creating consensus sequences for repeated regions. There is therefore a discrepancy between the reads being used to resolve a repeat and the sequence of the nodes they are mapped onto. This effect could be corrected by post-analysis of the contigs and the reads they contain, or by training Tour Bus to distinguish errors from biological variation.

Upon visual inspection of the actual contigs, we found that the N50 in human is mainly limited by Alu repeats and other common repeated structures. In other words, Breadcrumb resolves numerous short repeats and is blocked by the sparser and more complex ones. These structures are present in large quantities, sufficiently similar to present numerous overlaps, yet sufficiently polymorphic to resist simplification by Tour Bus. Therefore, they produced many long ambiguous loops that could not be resolved by Breadcrumb.

We attempted to use paired reads to help scaffold the contigs together, but rather than generating traditional super contigs (which are separated by a gap of unknown sequence), in this case we have complete, but unresolved, sequence between the two contigs. We describe these super contigs as “Sequence Connected Super Contigs” (SCSCs). This unresolved sequence could be used to classify the repeat class of the intervening sequence or be used in alignment of a novel sequence to the region, allowing one to definitively exclude a novel sequence from a region, despite not resolving the complete sequence of the region. The results of the previous test with the addition of this rule are also shown in Figure 6. The increase in N50 obtained by reporting SCSCs is particularly marked in human and E. coli, where the N50 is raised from 3 kb to 6 kb (for human) and from 50 kb to 100 kb in E. coli. This is indicative of the different repeat structures with dispersed repeats containing ambiguous central regions present in both of these genomes. In contrast, the S. cerevisiae or C. elegans repeat structure is either resolvable or not.

Complexity and scaling issues

Velvet has four stages: hashing the reads into _k_-mers, constructing the graph, correcting errors, and resolving repeats. Each stage has different computational requirements.

The main bottleneck, in terms of time and memory, is the graph construction. The initial graph of the Streptococcus reads needs 2.0 Gb of RAM. The scale of the problem will eventually require memory persistent data structures for whole-genome assemblies. Admittedly, access times would be greater, but the amount of storable data would be virtually unlimited.

The time complexity of Tour Bus depends primarily on the number N of nodes in the graph, which itself depends on the read coverage, error rate, and number of repeats. Idury and Waterman (1995) estimated N but neglected to consider repeats. The search itself is based on the Dijkstra algorithm, which has a time complexity of O(N log_N_) when implemented with a Fibonacci heap (Gross and Yellen 2004). The cost of individual path comparisons and the corresponding graph modifications can be limited by a length cutoff. In the latest implementation, correction of the human BAC reads took 18 sec on a single processor, and tests on large data sets have shown behavior close to the theoretical complexity.

The time cost of the Breadcrumb algorithm is also dependent on the number of nodes, as a test is run for every long node. The time for each test is proportional to the number of nodes spanned by a read. This depends on the average length of inserts and that of nodes. The latest implementation of the algorithm run on a whole-genome shotgun data set of E. coli data took 1.5 sec.

Comparison to other very short read assemblers

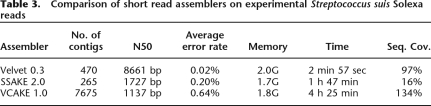
We compared Velvet to recently published short read assemblers SSAKE (Warren et al. 2007) and VCAKE (Jeck et al. 2007; Table 3). These differ from each other mainly in the way they deal with errors. SSAKE and VCAKE implicitly explore a de Bruijn graph step by step by searching for reads in a hash table. Whereas Velvet uses slightly more memory, it is significantly faster and produces larger contigs, without mis-assembly. Furthermore, it covers a large area of the genome with high precision.

Table 3.

Comparison of short read assemblers on experimental Streptococcus suis Solexa reads

We also tried using SHARCGS (Dohm et al. 2007) and EULER (Pevzner et al. 2001) but were not able to make these programs work with our data sets. This is probably due to differences in the expected input, particularly in terms of coverage depth and read length.

Discussion

We have developed Velvet, a novel set of de Bruijn graph-based sequence assembly methods for very short reads that can both remove errors and, in the presence of read pair information, resolve a large number of repeats. With unpaired reads, the assembly is broken when there is a repeat longer than the _k_-mer length. With the addition of short reads in read pair format, many of these repeats can be resolved, leading to assemblies similar to draft status in bacteria and reasonably long (∼5 kb) SCSCs in eukaryotic genomes.

For the latter genomes, the short read contigs will probably have to be combined with long reads or other sequencing strategies such as BAC or fosmid pooling. Simulations of Breadcrumb produced virtually identical N50 lengths on both a continuous 5-Mb region and a discontinuous 5-Mb region made up of random 150-kb BACs, with twofold variation in BAC concentration (data not shown). This approach would then require merging local assemblies.

Sequence connected supercontigs have considerably more information than gapped supercontigs, in that the sequence content separating the definitive contigs is an unresolved graph. One can easily imagine methods that can exclude the presence of a novel sequence in the SCSC completely by considering the potential paths in the unresolved sequence regions, in contrast to traditional supercontigs, where one can never make such a claim. In addition, the unresolved regions will often be dispersed repeats, and as such the classification of such regions as repeats is more important than their sequence content for many applications.

It is important to emphasize that assembly is not a solved problem, in particular with very short reads, and there will continue to be considerable algorithmic improvements. Velvet can already convert high-coverage very short reads into reasonably sized contigs with no additional information. With additional paired read information to resolve small repeats, almost complete genomes can be assembled. We believe the Velvet framework will provide a rich set of different algorithmic options tailored to different tasks and thus provide a platform for cheap de novo sequence assemblies, eventually for all genomes.

Methods

Velvet parameters

Velvet was implemented in C and tested on a 64-bit Linux machine.

The results of Velvet are very sensitive to the parameter k as mentioned previously. The optimum depends on the genome, the coverage, the quality, and the length of the reads. One approach consists in testing several alternatives in parallel and picking the best.

Another method consists in estimating the expected number X of times a unique _k_-mer in a genome of length G is observed in a set of n reads of length l. We can link this number to the traditional value of coverage, noted C, with the relations:

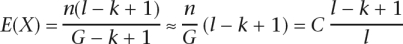
Experience shows that all the parameters should be set so that E(X) is between 10 and 15. In practice, given the limited number of possible values for k, it is common to try out various values in parallel then choose the one that produces the highest N50 contig length.

The Tour Bus algorithm decides whether to merge two paths based on three thresholds. Firstly, both paths must contain less than 200 nodes; secondly, their respective sequences must be shorter than 100 bp; and thirdly, the sequences must be at least 80% similar.

Experimental data

The experimental trials were run on human BAC bCX98J21 by Illumina. The reads are available from Illumina at info@ solexa.com. The 4,805,808 35-bp reads came from the 200 tiles of lane 5 in Flowcell 2012M. They were selected by Illumina’s in-house “purity filter.” Velvet was run with a hash length of 31 bp and a coverage cutoff of 15×.

The experiments on S. suis were run by the Sanger Center on strain P1/7. The data are available at http://www.sanger.ac.uk/Projects/S_suis/. The 2,726,374 36-bp reads came from the 200 tiles of a single lane. The first lane of the flow cell was used, and the reads were those passing the purity filter, but no other filter, as supplied by the Solexa software. Velvet used a hash length of 21 and a final coverage cutoff of 7×. The test on coverage was done with 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%, respectively, of the reads.

Both data sets will be publicly available through the Short Read Archive when it will be in service.

Comparative tests were run on SSAKE version 2.0, VCAKE version 1.0, SHARCGS, EULER version 2.0, and Velvet version 0.3. To settle different definitions, we only considered contigs longer than 100 bp. SSAKE and VCAKE were run with default options.

Simulations

Simulations were run on_: E. coli_ K12 genome (GenBank: U00096); S. cerevisiae chromosomes I to VIII (SGD1.01 assembly); C. elegans chromosome V, between positions 5,000,000 and 10,000,000 (WS170 assembly); human chromosome 20, between positions 40,000,000 and 45,000,000 (NCBI 36 assembly).

The first (i.e., unpaired) simulations were run with coverage depths of 5×, 10×, 15×, 20×, 25×, 30×, 35×, 40×, 45×, and 50×. The 35-bp reads were randomly placed and randomly orientated on the genome.

Errors were simulated by random mutations uniformly distributed over the reads, at a rate of 1%.

The paired read simulations were all run with random 35-bp reads, for a coverage of 50×. All the reads were paired and insert lengths varied with a standard deviation of 5%.

Alignments of SCSCs onto the reference were done with exonerate (Slater and Birney 2005). With the non-equivalenced regions (ner) model, exonerate is able to jump over the buffer regions that connect the SCSCs, thus forming long alignments.

Acknowledgments

D.R.Z. conceived the algorithms in discussions with E.B. All the programming and analysis was done by D.R.Z. The paper was written jointly by D.R.Z. and E.B. Both D.R.Z. and E.B. are funded by EMBL central funds. We thank John-Mark Gurney for the use of the BSD licensed Fibonacci heap method for the Dijkstra search, Guy Slater for his C methods, and M. Pop for discussions on AMOS. E.B. thanks Gene Myers, David Jaffe, and Phil Green for insightful discussions on assembly methods. D.R.Z. thanks Alison Meynert for her careful proofreading. We especially would like to thank all the users for their comments and encouragement. We apologize to authors of other assemblers for not having the space to discuss the analogies between Velvet and their programs.

Footnotes

References

1. Batzoglou S. Algorithmic challenges in mammalian genome sequence assembly. In: Dunn M., et al., editors. Encyclopedia of genomics, proteomics and bioinformatics. John Wiley and Sons; New York: 2005. Part 4. [Google Scholar]
2. Batzoglou S., Jaffe D.B., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Jaffe D.B., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Berger B., Mesirov J.P., Lander E.S., Mesirov J.P., Lander E.S., Lander E.S. ARACHNE: A whole genome shotgun assembler. Genome Res. 2002;12:177–189. doi: 10.1101/gr.208902. [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Bentley D.R. Whole-genome re-sequencing. Curr. Opin. Genet. Dev. 2006;16:545–552. doi: 10.1016/j.gde.2006.10.009. [DOI] [PubMed] [Google Scholar]
4. Bokhari S.H., Sauer J.R., Sauer J.R. A parallel graph decomposition algorithm for DNA sequencing with nanopores. Bioinformatics. 2005;21:889–896. doi: 10.1093/bioinformatics/bti129. [DOI] [PubMed] [Google Scholar]
5. Chaisson M., Pevzner P.A., Tang H., Pevzner P.A., Tang H., Tang H. Fragment assembly with short reads. Bioinformatics. 2004;20:2067–2074. doi: 10.1093/bioinformatics/bth205. [DOI] [PubMed] [Google Scholar]
6. Dohm J.C., Lottaz C., Borodina T., Himmelbauer H., Lottaz C., Borodina T., Himmelbauer H., Borodina T., Himmelbauer H., Himmelbauer H. SHARCGS, a fast and highly accurate short-read assembly algorithm for de novo genomic sequencing. Genome Res. 2007;17:1697–1706. doi: 10.1101/gr.6435207. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Gross J.L., Yellen J., Yellen J. Handbook of graph theory. CRC Press LLC; Boca Raton, FL: 2004. [Google Scholar]
8. Havlak P., Chen R., Durbin J., Egan A., Ren Y., Song X.-Z., Weinstock G.M., Gibbs R.A., Chen R., Durbin J., Egan A., Ren Y., Song X.-Z., Weinstock G.M., Gibbs R.A., Durbin J., Egan A., Ren Y., Song X.-Z., Weinstock G.M., Gibbs R.A., Egan A., Ren Y., Song X.-Z., Weinstock G.M., Gibbs R.A., Ren Y., Song X.-Z., Weinstock G.M., Gibbs R.A., Song X.-Z., Weinstock G.M., Gibbs R.A., Weinstock G.M., Gibbs R.A., Gibbs R.A. The Atlas genome assembly system. Genome Res. 2004;14:721–732. doi: 10.1101/gr.2264004. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Huang X., Wang J., Aluru S., Yang S.-P., Hillier L., Wang J., Aluru S., Yang S.-P., Hillier L., Aluru S., Yang S.-P., Hillier L., Yang S.-P., Hillier L., Hillier L. PCAP: A whole-genome assembly program. Genome Res. 2003;13:2164–2170. doi: 10.1101/gr.1390403. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Idury R.M., Waterman M.S., Waterman M.S. A new algorithm for DNA sequence assembly. J. Comput. Biol. 1995;2:291–306. doi: 10.1089/cmb.1995.2.291. [DOI] [PubMed] [Google Scholar]
11. International Human Genome Sequencing Consortium Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
12. Jeck W.R., Reinhardt J.A., Baltrus D.A., Hickenbotham M.T., Magrini V., Mardis E.R., Dangl J.L., Jones C.D., Reinhardt J.A., Baltrus D.A., Hickenbotham M.T., Magrini V., Mardis E.R., Dangl J.L., Jones C.D., Baltrus D.A., Hickenbotham M.T., Magrini V., Mardis E.R., Dangl J.L., Jones C.D., Hickenbotham M.T., Magrini V., Mardis E.R., Dangl J.L., Jones C.D., Magrini V., Mardis E.R., Dangl J.L., Jones C.D., Mardis E.R., Dangl J.L., Jones C.D., Dangl J.L., Jones C.D., Jones C.D. Extending assembly of short DNA sequences to handle error. Bioinformatics. 2007;23:2942–2944. doi: 10.1093/bioinformatics/btm451. [DOI] [PubMed] [Google Scholar]
13. Jiang Z., Tang H., Ventura M., Cardone M.F., Marques-Bonet T., She X., Pevzner P.A., Eichler E.E., Tang H., Ventura M., Cardone M.F., Marques-Bonet T., She X., Pevzner P.A., Eichler E.E., Ventura M., Cardone M.F., Marques-Bonet T., She X., Pevzner P.A., Eichler E.E., Cardone M.F., Marques-Bonet T., She X., Pevzner P.A., Eichler E.E., Marques-Bonet T., She X., Pevzner P.A., Eichler E.E., She X., Pevzner P.A., Eichler E.E., Pevzner P.A., Eichler E.E., Eichler E.E. Ancestral reconstruction of segmental duplications reveals punctuated cores of human genome evolution. Nat. Genet. 2007;39:1361–1368. doi: 10.1038/ng.2007.9. [DOI] [PubMed] [Google Scholar]
14. Johnson D.S., Mortazavi A., Myers R.M., Wold B., Mortazavi A., Myers R.M., Wold B., Myers R.M., Wold B., Wold B. Genome-wide mapping of in vivo protein-DNA interactions. Science. 2007;316:1497–1502. doi: 10.1126/science.1141319. [DOI] [PubMed] [Google Scholar]
15. Kim J., Bhinge A.A., Morgan X.C., Iyer V.R., Bhinge A.A., Morgan X.C., Iyer V.R., Morgan X.C., Iyer V.R., Iyer V.R. Mapping DNA-protein interactions in large genomes by sequence tag analysis of genomic enrichment. Nat. Methods. 2005;2:47–53. doi: 10.1038/nmeth726. [DOI] [PubMed] [Google Scholar]
16. Lander E.S., Waterman M.S., Waterman M.S. Genomic mapping by fingerprinting random clones: A mathematical analysis. Genomics. 1988;2:231–239. doi: 10.1016/0888-7543(88)90007-9. [DOI] [PubMed] [Google Scholar]
17. Margulies M., Egholm M., Altman W.E., Attiya S., Bader J.S., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Egholm M., Altman W.E., Attiya S., Bader J.S., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Altman W.E., Attiya S., Bader J.S., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Attiya S., Bader J.S., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Bader J.S., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Bemben L.A., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Berka J., Braverman M.S., Chen Y.-J., Chen Z., Braverman M.S., Chen Y.-J., Chen Z., Chen Y.-J., Chen Z., Chen Z., et al. Genome sequencing in microfabricated high-density picolitre reactors. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Metzker M.L. Emerging technologies in DNA sequencing. Genome Res. 2005;15:1767–1776. doi: 10.1101/gr.3770505. [DOI] [PubMed] [Google Scholar]
19. Mullikin J.C., Ning Z., Ning Z. The Phusion assembler. Genome Res. 2003;13:81–90. doi: 10.1101/gr.731003. [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Myers E.W. The fragment assembly string graph. Bioinformatics. 2005;21:ii79–ii85. doi: 10.1093/bioinformatics/bti1114. [DOI] [PubMed] [Google Scholar]
21. Myers E.W., Sutton G.G., Delcher A.L., Dew I.M., Fasulo D.P., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Sutton G.G., Delcher A.L., Dew I.M., Fasulo D.P., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Delcher A.L., Dew I.M., Fasulo D.P., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Dew I.M., Fasulo D.P., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Fasulo D.P., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Flanigan M.J., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Kravitz S.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Mobarry C.M., Reinert K.H.J., Remington K.A., Reinert K.H.J., Remington K.A., Remington K.A., et al. A whole-genome assembly of Drosophila. Science. 2000;287:2196–2204. doi: 10.1126/science.287.5461.2196. [DOI] [PubMed] [Google Scholar]
22. Pevzner P.A., Tang H., Waterman M.S., Tang H., Waterman M.S., Waterman M.S. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. 2001;98:9748–9753. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Shah M.K., Lee H., Rogers S.A., Touchman J.W., Lee H., Rogers S.A., Touchman J.W., Rogers S.A., Touchman J.W., Touchman J.W. Computational Systems Bioinformatics Conference. IEEE; New York: 2004. An exhaustive genome assembly algorithm using k-mers to indirectly perform n-squared comparisons in O(n) pp. 740–741. [Google Scholar]
24. Slater G.S.C., Birney E., Birney E. Automated generation of heuristics for biological sequence comparison. BMC Bioinformatics. 2005;6:31. doi: 10.1186/1471-2105-6-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Sundquist A., Ronaghi M., Tang H., Pevzner P., Batzoglou S., Ronaghi M., Tang H., Pevzner P., Batzoglou S., Tang H., Pevzner P., Batzoglou S., Pevzner P., Batzoglou S., Batzoglou S. Whole-genome sequencing and assembly with high throughput, short-read technologies. PLoS ONE. 2007;2:e484. doi: 10.1371/journal.pone.0000484. [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Venter J.C., Adams M.D., Myers E.W., Li P.W., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Adams M.D., Myers E.W., Li P.W., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Myers E.W., Li P.W., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Li P.W., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., Smith H.O., Yandell M., Evans C.A., Holt R.A., Yandell M., Evans C.A., Holt R.A., Evans C.A., Holt R.A., Holt R.A., et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
27. Warren R.L., Sutton G.G., Jones S.J.M., Holt R.A., Sutton G.G., Jones S.J.M., Holt R.A., Jones S.J.M., Holt R.A., Holt R.A. Assembling millions of short DNA sequences using SSAKE. Bioinformatics. 2007;4:500–501. doi: 10.1093/bioinformatics/btl629. [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Waterston R.H., Lindblad-Toh K., Birney E., Rogers J., Abril J.F., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Lindblad-Toh K., Birney E., Rogers J., Abril J.F., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Birney E., Rogers J., Abril J.F., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Rogers J., Abril J.F., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Abril J.F., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Agarwal P., Agarwala R., Ainscough R., Alexandersson M., An P., Agarwala R., Ainscough R., Alexandersson M., An P., Ainscough R., Alexandersson M., An P., Alexandersson M., An P., An P., et al. Initial sequencing and comparative analysis of the mouse genome. Nature. 2002;420:520–562. doi: 10.1038/nature01262. [DOI] [PubMed] [Google Scholar]