Decoy Methods for Assessing False Positives and False Discovery Rates in Shotgun Proteomics (original) (raw)

. Author manuscript; available in PMC: 2009 Jul 1.

Published in final edited form as: Anal Chem. 2009 Jan 1;81(1):146–159. doi: 10.1021/ac801664q

Abstract

The potential of getting a significant number of false positives (FPs) in peptide-spectrum matches (PSMs) obtained by proteomic database search has been well-recognized. Among the attempts to assess FPs, the concomitant use of target and decoy databases is widely practiced. By adjusting filtering criteria, FPs and false discovery rate (FDR) can be controlled at a desired level. Although the target-decoy approach is gaining in popularity, subtle differences in decoy construction (e.g., reversing vs. stochastic methods), rate calculation (e.g., total vs. unique PSMs), or searching (separate vs. composite) do exist among various implementations. In the present study, we evaluated the effects of these differences on FP and FDR estimations using a rat kidney protein sample and the SEQUEST search engine as an example. On the effects of decoy construction, we found that, when a single scoring filter (XCorr) was used, stochastic methods generated a higher estimation of FPs and FDR than sequence reversing methods, likely due to an increase in unique peptides. This higher estimation could largely be attenuated by creating decoy databases similar in effective size, but not by a simple normalization with a unique-peptide coefficient. When multiple filters were applied, the differences seen between reversing and stochastic methods significantly diminished, suggesting multiple filterings reduce the dependency on how a decoy is constructed. For a fixed set of filtering criteria, FDR and FPs estimated by using unique PSMs were almost twice those using total PSMs. The higher estimation seemed to be dependent on data acquisition setup. As to the differences between performing separate or composite searches, in general, FDR estimated from separate search was about three times that from composite search. The degree of difference gradually decreased as the filtering criteria became more stringent. Paradoxically, the estimated true positives in separate search were higher when multiple filters were used. By analyzing a standard protein mixture, we demonstrated that the higher estimation of FDR and FPs in separate search likely reflected an overestimation, which could be corrected with a simple merging procedure. Our study illustrates the relative merits of different implementations of the target-decoy strategy, which should be worth contemplating when large-scale proteomic biomarker discovery is to be attempted.

Keywords: True positives (TPs), False positives (FPs), False discovery rates (FDRs), Decoy database, Protein identification, Separate search, Composite search

Introduction

One of the primary goals of proteomic studies is to identify protein constituents in a complex biological sample. High-throughput analytical technologies such as MudPIT 1 and other LC/MS methods have significantly facilitated such analyses. Once mass spectrometry data are acquired, subsequent data analysis focuses on matching observed spectra to theoretical spectra of peptides generated in silico from a protein sequence database (i.e., finding peptide-spectrum matches or PSMs), using search engines such as SEQUEST 2, Mascot 3, or OMSSA 4. Hundreds or even thousands of proteins can now be routinely identified in a single experiment 5;6. Due to complex procedures involved in sample preparation and the automated nature of data-dependent spectral acquisition, a significant portion of acquired spectra may represent chemical or electrical noises. In essence, search engines are looking for the best "matches" between acquired spectra and those predicted from numerous peptide sequences using various algorithms. As a consequence, it is not unusual to have peptides “identified” with high scores yet the identifications are due to random matching. If not properly controlled, such false positives (FPs) may lead to misinterpretation of experimental results 7.

To reduce the number of FPs and control the false discovery rate (FDR), several approaches have been reported. Manual validation remains a common practice, especially for those identifications based on a single peptide 5. This approach is however rather subjective and impractical, as it lacks an operable standard and could hardly cope with the large amount of data requiring verification. Though empirically determined numerical score thresholds are shown to be effective in reducing FPs while preserving high-quality PSMs 1, they provide little information regarding the amount of FPs in the final identification list. Probabilistic models have been developed to compute the likelihood that an identified peptide or protein is a result of random matching 3;8;9. The resulting probability scores have been used as a guide to assess the reliability of identifications. But the underlying assumptions of some models may not be universally applicable to all data sets, nor are they readily translatable between different proteomic instrument platforms. Thus an instrument- and search algorithm-independent FP filtering and FDR estimation method is desirable. The approach using target-decoy database search seems to offer these features. Since initial publication 10, it has been widely adopted by investigators 5–7;11–18. In this approach, spectral data are searched against a protein sequence database (the target) and a database comprised of reversed or random amino acid sequences (the decoy). The number of positive identifications from the decoy database is used to estimate FPs in the target database search, assuming an equal probability of incorrect PSMs from the target or the decoy database. This underlying assumption has been demonstrated to be valid 14;19. By adjusting score thresholds, the number of FPs and FDR can be controlled at desired levels. Moreover, the error of FDR estimation using target-decoy search can be predicted 13;14. Despite its popularity due largely to the simplicity and effectiveness of application, there exist subtle differences in target-decoy search methods implemented in different laboratories. We are particularly interested in how those differences might affect FP filtering and FDR estimation. Specifically, we are interested in assessing how decoy sequence-generating strategies, such as reversing and stochastic methods, affect FDR estimation. We also want to know how FDR estimation is affected by the use of total PSMs versus unique PSMs in the calculation, and how search outcomes might be different when the target and decoy sequences are searched independently or simultaneously.

Our results indicated that FPs and FDR estimated using the reversing strategy were different from those using the stochastic strategy, but both strategies were similarly effective in FDR estimation when multiple filters were applied. We also found that using unique PSMs for calculation led to a much higher estimation of FDR, which probably depended upon data acquisition method setup. Finally, separate search might overestimate FDR, as supported by the analysis of a mixture of known proteins. We were able to use a simple corrective procedure in separate search, which yielded estimations comparable to those from composite search.

Materials and Methods

Sample preparation

Rat kidney proteins were prepared from adult male rats which were perfused with PBS. Freshly harvested kidneys were homogenized in a homogenization buffer containing 250 mM sucrose and protease inhibitors. Proteins (30 µg) were separated by SDS-PAGE using 10% Tris-HCl gels. The Coomasie-stained protein lane was excised into seven blocks and proteins in each gel block were in-gel digested with trypsin following reduction and alkylation with DTT and iodoacetamide, respectively, using the protocol described at http://www.donatello.ucsf.edu/ingel.html. Tryptic peptides were purified with C18 Ziptips before LC-MS/MS analysis. Standard peptides were prepared from a protein mixture containing an equal molar quantity of alpha-lactalbumin (from bovine milk), lysozyme (from chicken white), beta-lactoglobulin B (from bovine milk), hemoglobin (human), bovine serum albumin, apotransferrin (human), and beta-galactosidase (from E. coli). The proteins were reduced with DTT and alkylated with iodoacetamide before trypsinization. The peptides were analyzed (500 fmole of each protein) by LC-MS/MS.

LC-MS/MS analysis

Tryptic peptides were subject to LC-MS/MS analysis using an Agilent 1100 LC system (Santa Clara, CA) connected to a Finnigan LTQ ion trap mass spectrometer (Thermo Fisher Scientific, Inc., San Jose, CA), as described previously 20. Briefly, the peptide mixture was injected, using an autosampler (Agilent), and loaded onto a C18 peptide trap (Agilent). After washing, peptides were eluted from the trap with a gradient of acetonitrile (0 – 60% in 35 min) at a flow rate of 250 nL/min. The eluted peptides were then separated in a C18 PicoFrit column (New Objectives, Boston, MA) positioned directly in front of the orifice of an ion transfer tube of the LTQ mass spectrometer. Spectra were acquired in a data-dependent manner with dynamic exclusion option enabled. Each survey MS scan was followed by five MS/MS scans.

Database search was carried out with the BioWorks software package (Thermo Fisher Scientific, Inc.) running SEQUEST algorithm on an 8-node computer cluster. Peptide tolerance and fragment ion tolerance were set at 2.5 and 1 mass unit, respectively. Two missed tryptic cleavages were allowed. Top 500 candidate peptides in preliminary scoring were selected for XCorr calculation. Rat RefSeq protein sequences (i.e., target database) were downloaded from NCBI (36133 entries). Decoy versions of this database were created as detailed below. For separate search, the target database and each decoy database were searched separately. For composite search, a decoy database was appended to the target database to create a composite database before searching. In any case, only the top PSM (the candidate peptide with the highest XCorr) for each spectrum was retained for further analysis.

Construction of decoy databases

The following eight strategies were employed to generate decoy databases from a target database. Each method produces a decoy database of the same size (i.e., number of amino acids) and also the same number of proteins as the original.

  1. Protein sequence reversal (reverseProtein): a simple reverse of the amino acid sequence of each protein. This has been by far the most frequently used method for decoy database creation for its simplicity.
  2. Peptide sequence reversal (reversePeptide): the order of amino acids of each in silico tryptic peptide is reversed, except that Lysine (K) and arginine (R) remain at their original positions.
  3. Protein sequence randomization (randomAA): each amino acid is generated randomly according to their occurrence frequencies in the target database using a uniform distribution random number generator that can accommodate the generation of billions of random numbers 21.
  4. Peptide sequence randomization (randomAATrypsin): as in peptide sequence reversal, the tryptic cleavage sites (K or R) and positions are preserved in the new decoy database. All other amino acids are generated randomly according to their occurrence frequencies in the target database, as in randomAA method. Randomly generated K or R is ignored, therefore no new trypsin cutting sites are introduced.
  5. Protein sequence randomization based on dipeptide frequency (randomDipep): for each protein, an amino acid is randomly chosen according to their frequency distribution as the N-terminal. Each amino acid generated thereafter is based on the occurrence frequency of each dipeptide that starts with its preceding neighboring amino acid 22. Decoy sequences created this way are expected to have similar amino acid composition and nearest-neighbor frequencies of the target database.
  6. Peptide sequence randomization based on dipeptide frequency (randomDipepTrypsin): except amino acid K or R that has the same positions as in the target database, all other amino acids are randomly generated according to dipeptide frequency, as in randomDipep method.
  7. Protein sequence shuffle (shuffleProtein): the order of amino acids in each protein sequence is randomly shuffled using a uniform distribution random number generator. The random shuffle algorithm of the C++ standard library is used for this purpose.
  8. Peptide sequence shuffle (shufflePeptide): the amino acid order of each in silico tryptic sequence (excluding K or R) is randomly shuffled as described for shuffleProtein.

In the event that a non-redundant (i.e., each in silico tryptic peptide appears only once) decoy database is desired, the chosen construction strategy is modified slightly to ensure the uniqueness of tryptic peptides. During the process of construction, if a newly generated peptide already exists, it is ignored and the algorithm repeats until a unique tryptic sequence is generated.

False discovery rate

For peptide identification, FDR is a measure of the percentage of FPs (incorrect PSMs) in the final accepted PSM list. For both separate search and composite search, FDR is defined as the number (Nd) of PSMs from decoy sequences (decoy PSMs) divided by the number (Nt) of PSMs from target sequences (target PSMs), i.e., FDR = Nd / Nt. Nd is an estimate of the number of FPs resulting from random matching in target PSMs. The estimated number of true positives (TPs) is then Nt – Nd. Unless explicitly specified, PSMs (or total PSMs) refer to the redundant count of all PSMs, while unique PSMs refer to the count of identified unique peptides in a collection of PSMs (though strictly speaking, each PSM is unique).

Results

I. Decoy database construction: reversing vs. randomization (stochastic) methods

To examine the effect of database construction on FP and FDR estimations, we generated 2 reversed and 6 random decoy databases from a rat RefSeq database (see Materials and Methods for details). Data (70,791 dta files) from 7 LC-MS/MS analyses of an in-gel digested rat kidney sample were searched against the target RefSeq database and each of the decoy databases separately using the SEQUEST algorithm. Unless explicitly specified, data presented were derived from separate search (target and decoy databases are searched separately), as opposed to composite or concatenated search.

Ia. Differences in FP and FDR estimations using reversed and random decoy Databases

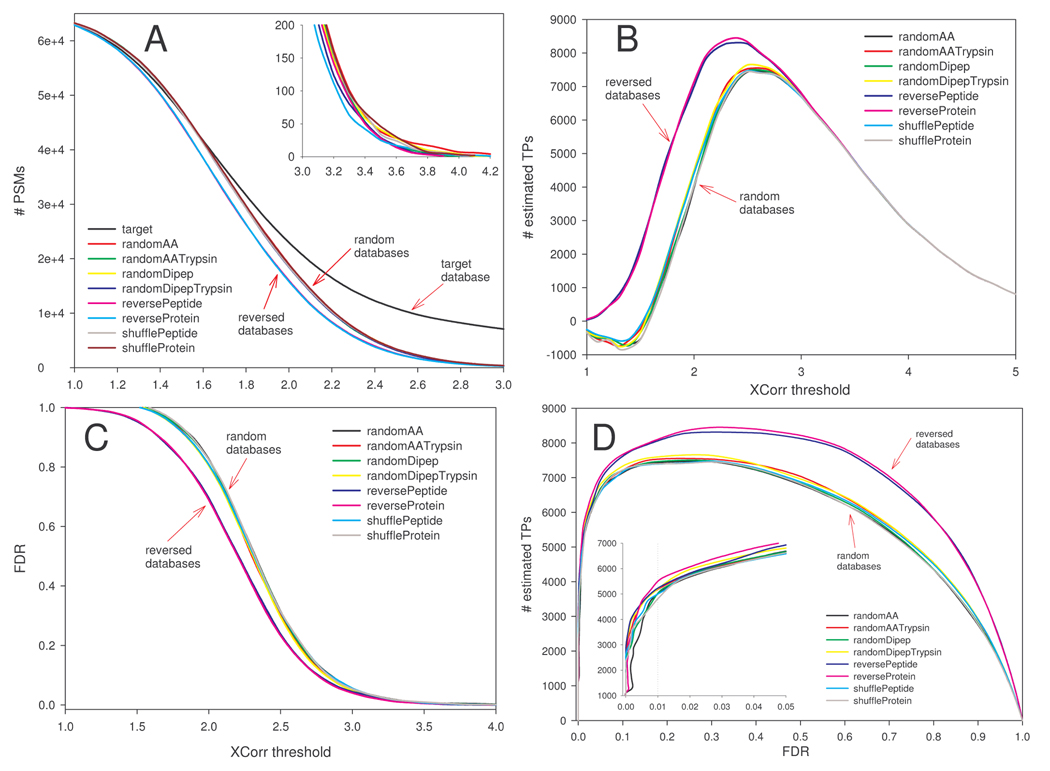
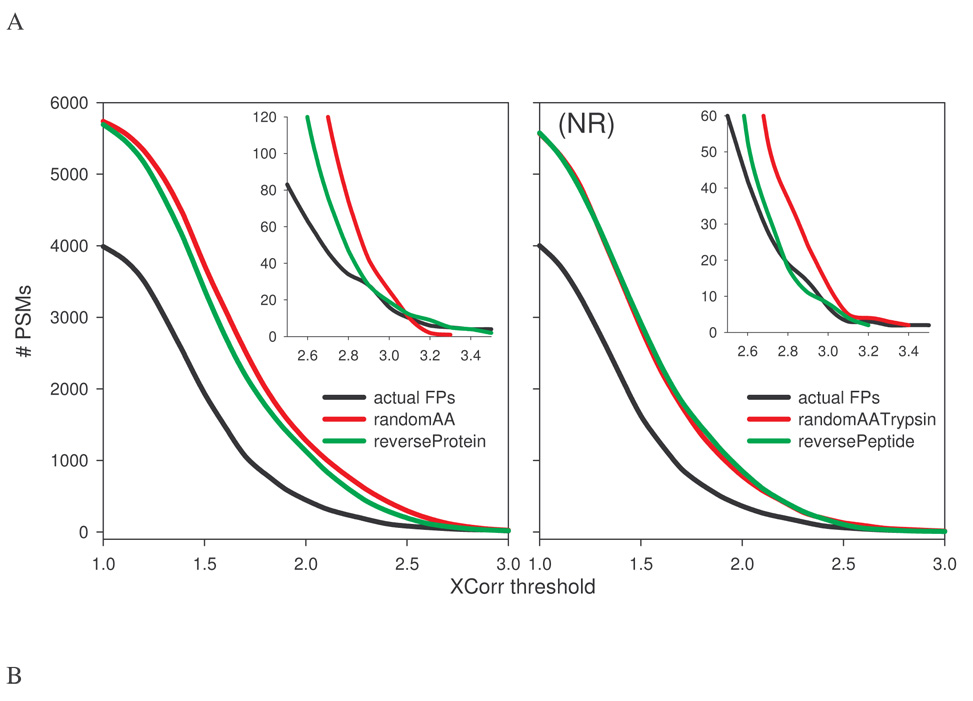
Fig. 1A shows the number of PSMs as a function of XCorr threshold. At low XCorr, the number of PSMs for each random database was similar to that of the target until XCorr was about 1.6, suggesting no discrimination between true and false positives at XCorr<1.6. As the XCorr threshold gradually increased, the target PSM curve started to deviate from those of the random databases. Between XCorr 1.0 and 2.8, the PSM curves for the two reversed databases (arrow marked reversed databases) overlapped but were divergent from those of the random decoys (arrow marked random databases). The numbers of PSMs of reversed databases were consistently lower. At XCorr >2.8, curves for all decoy databases converged, although subtle differences still existed as can be seen from the inset (zoom view).

Figure 1.

Figure 1

False positives, true positives, and FDR estimated from separate searches of target and decoy databases. Decoy databases were created by reversing and stochastic methods from a target rat RefSeq database. SEQUEST searches of the rat kidney protein data set were carried out against each database separately. A, The number of total PSMs from each database as a function of XCorr threshold. PSMs from the target database consist of true positives and false positives. PSMs from a decoy database are used to estimate the number of false positives in target PSMs. B, Estimated true positives (target PSMs – decoy PSMs) as a function of XCorr threshold. C, Estimated FDR (decoy PSMs divided by target PSMs) as a function of XCorr threshold. D, Estimated true positives plotted against estimated FDR (similar to sensitivity-specificity curves).

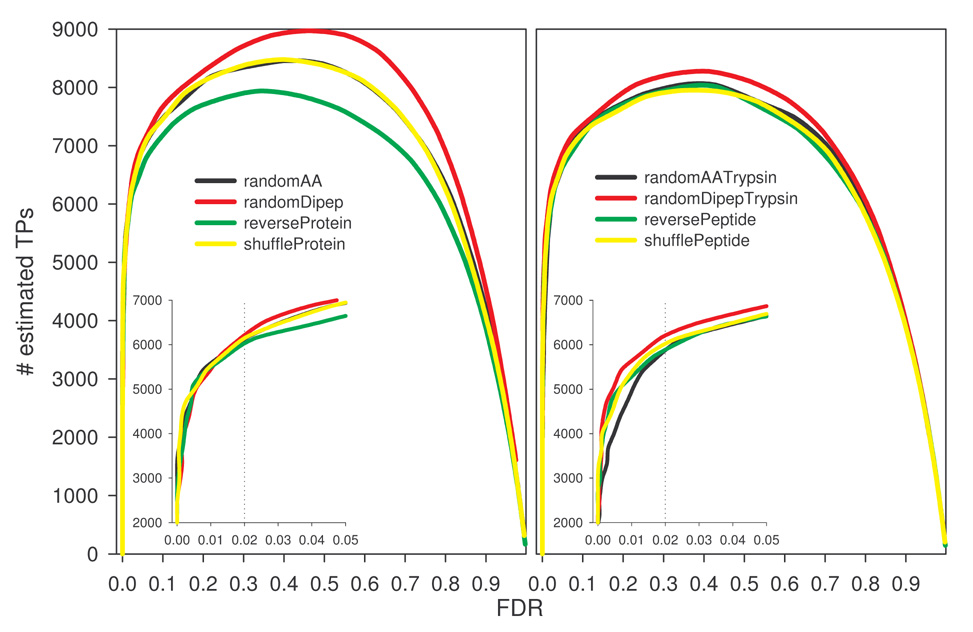
Compared to the random decoys, XCorr-dependent TP estimations were higher for the reversed decoys until XCorr reached 3.0 (Fig. 1B), consistent with lower decoy PSMs observed for the reversed decoys in the same region (Fig. 1A). Interestingly, TPs estimated by random decoys were negative at XCorr <1.5 (Fig. 1B), suggesting that decoy PSMs outnumber target PSMs, presumably due to a larger effective size of the database, as will be discussed later. TPs estimated by all decoys peaked around similar XCorr, 2.4 for reversePeptide and reverseProtein, 2.5 for shufflePeptide and shuffleProtein and 2.6 for others. The same trend differentiating reversed from random decoys was also seen in XCorr-dependent FDR estimations (Fig. 1C). Fig. 1D shows a plot of estimated TPs (approximately equivalent to sensitivity) against estimated FDR (roughly equivalent to 1-specificity). At a certain FDR, TPs estimated by the reversed databases were generally more than those by the random decoys. In other words, using the reversing strategies in decoy construction could achieve a similar number of estimated TPs with a smaller FDR. The difference between reversing and stochastic methods became less prominent in the low FDR region (FDR<0.05, inset), consistent with limited variations in estimated FPs, TPs, and FDRs observed at higher XCorr threshold in Fig. 1A–C. Overall, these data suggest that decoys created with the reversing methods behave differently from those from randomization methods, and that FPs and FDR estimated by the reversed decoys are lower when mild to moderate filtering criteria are used. At more stringent thresholds (e.g., XCorr >3), all methods yield similar outcomes.

Ib. Higher FP and FDR estimations could be attributed in part to increased unique peptides in random databases

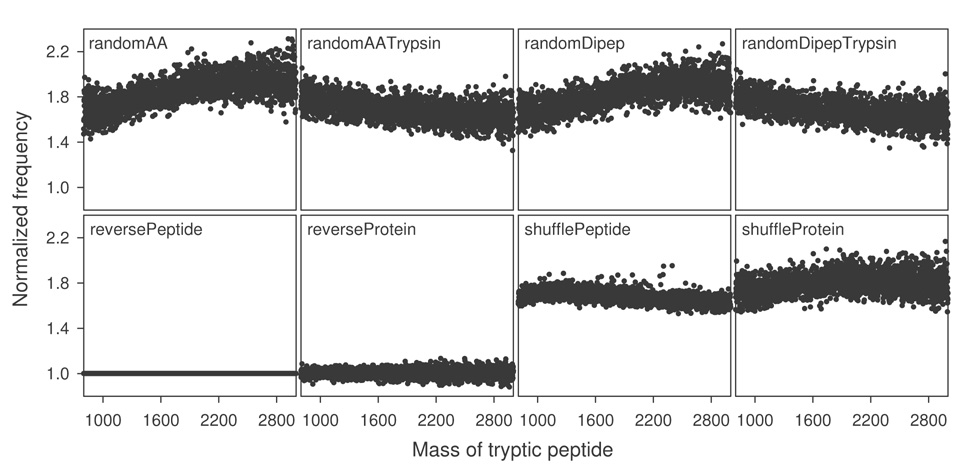
The observed differences in FP and FDR estimations between reversed and random decoys are unlikely due to changes in amino acid frequencies, as no statistically significant difference in amino acid frequencies between the target database and each decoy was observed (p>0.99; data not shown). The number of peptides with a certain mass (i.e., mass frequency) is an important characteristic of a database, as database search starts with finding peptides that match the precursor mass of an MS/MS spectrum. Fig. 2 displays normalized peptide mass frequency distribution for each decoy database between 800 and 3000 daltons. The mass frequency distribution in reversePeptide database, as expected, did not change, while that of reverseProtein deviated slightly (~10%) from the target database. However, the number of peptides in decoy databases created from stochastic methods was, on average, about 80% more than the target database, suggesting that sequences in the target database are highly redundant and that considerably more unique peptides exist in random databases. In other words, despite similar apparent sizes (i.e., number of amino acids), reversing methods led to decoys of approximately the same effective size as the target database, while stochastic methods created decoy databases of much larger effective size and less redundancy (as measured by the number of unique peptides).

Figure 2.

Figure 2

Peptide mass frequencies of the target and eight decoy databases. Protein sequences in each database were in silico digested (allowed maximally two miscleavages). The number of unique peptides in the mass range between 800 and 3000 daltons was counted with a bin width of 1.0 and normalized against that of the target database.

Ic. FDR estimation differences can be minimized by using decoy databases of equal number of unique peptides

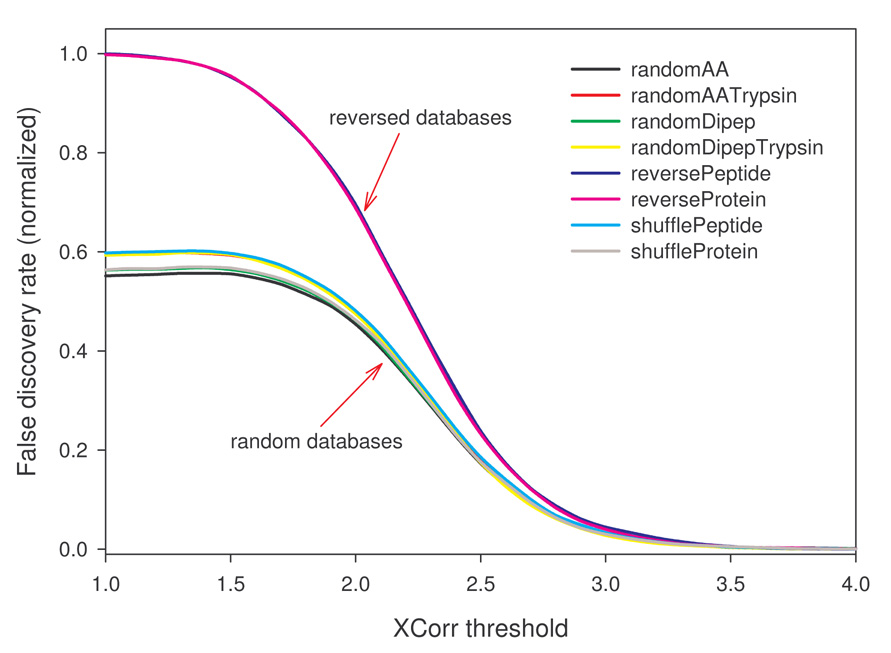
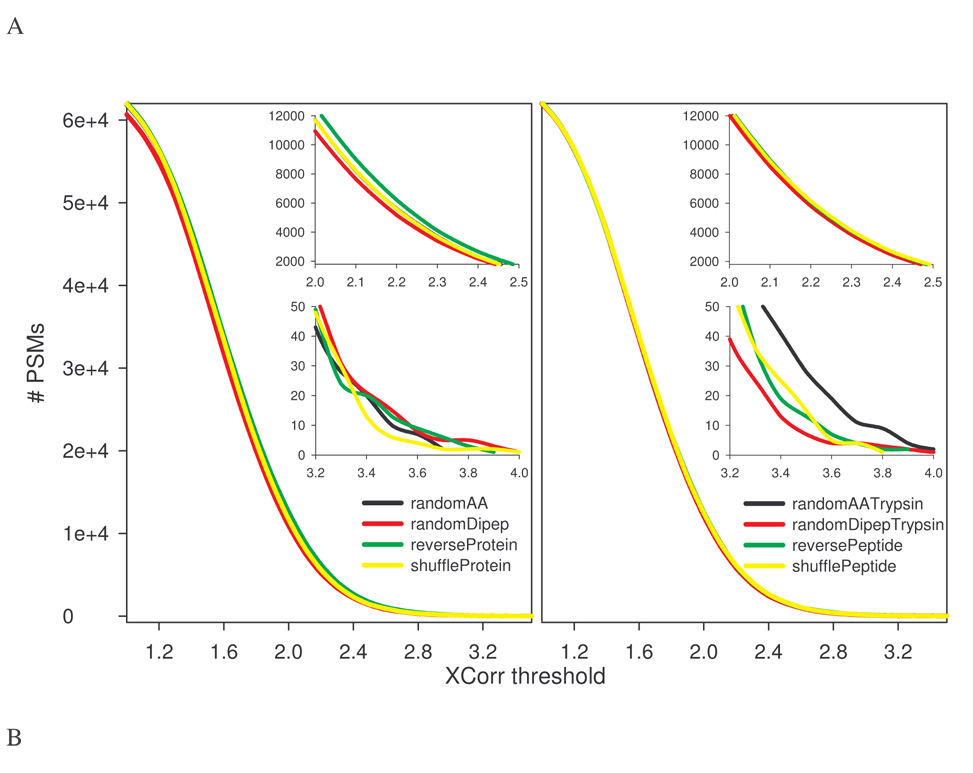
If increased decoy PSMs from random decoys result from an increase in unique peptides, then FDR overestimation could be corrected either by normalization with a coefficient of uniqueness or by generating decoys with sequence redundancy similar to the target database. These approaches should diminish differences in FDR estimations between databases created from reversing and stochastic methods. Uniqueness coefficient is the number of unique in silico tryptic peptides in a decoy database divided by that in the target database. Fig. 3 shows the normalized FDR for each decoy database as a function of XCorr threshold for the kidney protein data set used. It suggests that a simple global normalization fails to bring the FDR estimations to a similar level, consistent with the fact that differences in estimated FPs or FDR are not constant (see Fig. 1C). To test the effect of sequence redundancy, redundant tryptic peptides (assuming no miscleavages) were removed from the target database to generate a non-redundant (NR) target database. Decoy databases were then created from this new target database. As expected, randomAA, randomDipep, and shuffleProtein methods could introduce some redundancy. Thus the randomAATrypsin, randomDipepTrypsin, and shufflePeptide methods were modified (see Materials and Methods) to produce non-redundant decoys containing in silico peptides identical, both in the number and the size, to the NR target database. The rat kidney protein data set was searched with these new databases. As shown in Fig. 4, the number of PSMs from reverseProtein was slightly more than those from randomAA, randomDipep, and shuffleProtein databases (Fig. 4A left panel), as the latter three contained redundant sequences and thus were smaller in effective size. The difference was also reflected in estimated TPs as a function of estimated FDR (Fig. 4B left panel), albeit in a reversed order. Interestingly, the four decoy databases of the same effective size followed a similar trend (Fig. 4A right panel). Worth noting is that, unlike previous observation (Fig. 1D where all random decoys behaved almost identically), TPs-FDR plots of the randomDipep (left panel of Fig. 4B) and randomDipepTrypsin (right panel of Fig. 4B) deviated from other random databases, suggesting that sequence redundancy is a significant but not the sole factor leading to differences observed for decoys created by reversing and stochastic strategies.

Figure 3.

Figure 3

Normalized FDR as a function of XCorr threshold. To correct the bias in FDR estimation by decoy databases with increased number of unique peptides, FDR (as shown in Fig. 1C) was normalized by a uniqueness coefficient. The coefficient is the number of unique peptides in a decoy database divided by the number of unique peptides in the target database. Data shown were based on in silico tryptic peptides with maximally two miscleavages in the mass range between 800 and 3000 daltons.

Figure 4.

Figure 4

Figure 4

Database sequence redundancy and estimation of FPs and FDR. Redundant in silico tryptic peptides (assuming no miscleavages) were removed from the rat RefSeq database, yielding a non-redundant (NR) target database. The corresponding reversed databases and random databases (randomAA, randomDipep, and shuffleProtein) were generated. Because these random databases will likely contain redundant peptides, a modified procedure was used to create randomAATrypsin, randomDipepTrypsin, reversePeptide, and shufflePeptide databases that contained the same number of unique peptides as the target database. The rat kidney protein data set was searched against each decoy database individually. A, The number of decoy PSMs as a function of XCorr threshold. B, Estimated true positives (target PSMs – decoy PSMs) plotted versus estimated FDR.

Id. Multiple filtering criteria reduce variations in FP or FDR estimation

The result above uses only XCorr as the filter. To see whether similar differences also present when multiple filters are used, three sets of filtering criteria, from moderate to high-stringency, were tested: RSp≤5, deltaCn≥0.1, and XCorr set according to the charge states so that the estimated FDR was below 10% (FDR_10%), 5% (FDR_5%), or 1% (FDR_1%) estimated using reverseProtein decoy database. Table I shows the number of PSMs from the target RefSeq database and eight decoy databases searched separately with the rat kidney protein data. At a moderate filtering (FDR_10%), decoy databases had an average PSMs of 917 and the average estimated FDR was 9.5% with a small CV (coefficient of variation) of 4.64%, suggesting there is a limited variation among these decoys. At higher filtering criteria, an increase in CV of estimated FDR was seen (11% at FDR_5% and 26% at FDR_1%). Whether this increase in CV had any practical significance was not obvious, as the CVs for estimated TPs were consistently low (CV of 0.49%, 0.55%, 0.24% for FDR_10%, FDR_5%, and FDR_1%, respectively), indicating no major difference in TP estimations. These observations suggest that all decoy databases are similarly effective in controlling the number of FPs, and no significant differences due to the method used for producing decoy are apparent when multi-filtering is applied.

Table I.

False positives and FDR estimated by total PSMs using separate searches of the target and decoy databases under mild- to high-stringency multi-criterion filtering.

FDR_10%a FDR_5%b FDR_1%c
#PSMs FDR #PSMs FDR #PSMs FDR
target 9653 8762 6519
randomAA 922 9.55% 453 5.17% 70 1.07%
randomAATrypsin 892 9.24% 395 4.51% 34 0.52%
randomDipep 884 9.16% 379 4.33% 50 0.77%
randomDipepTrypsin 854 8.85% 356 4.06% 44 0.67%
reversePeptide 918 9.51% 389 4.44% 57 0.87%
reverseProtein 957 9.91% 433 4.94% 63 0.97%
shufflePeptide 916 9.49% 466 5.32% 76 1.17%
shuffleProtein 990 10.26% 485 5.54% 76 1.17%
average 917 9.50% 420 4.79% 59 0.90%
CV 4.64% 4.64% 11.02% 11.02% 26.13% 26.13%

II. Estimation of FPs and FDR: total PSMs vs. unique PSMs

IIa. FDR calculated with unique PSMs is much higher than that with total PSMs

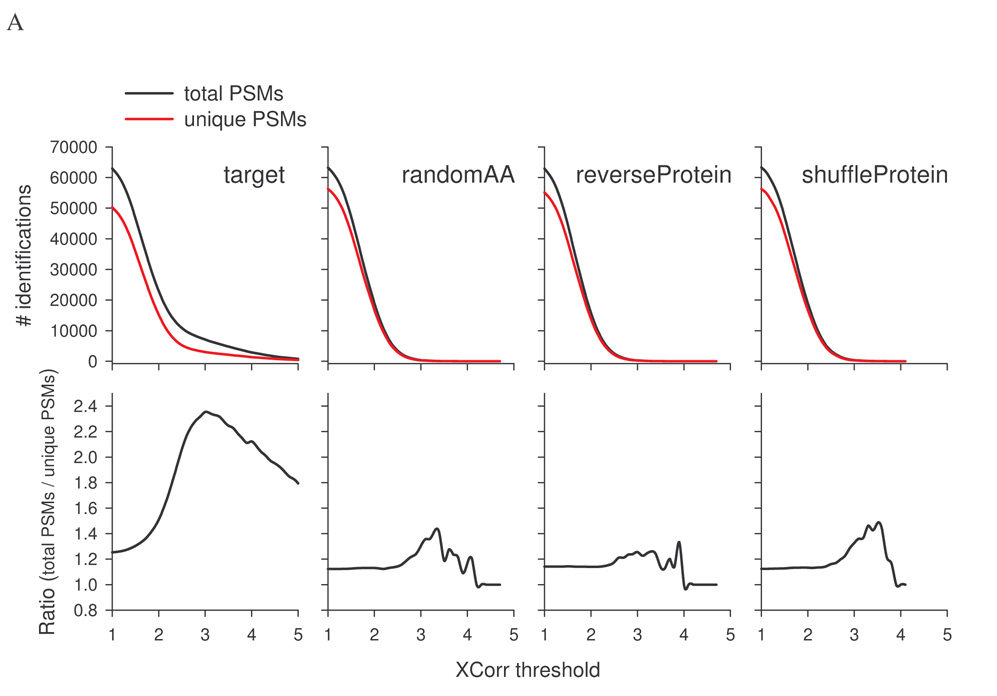
We have so far used the number of total PSMs (redundant count) in counting FPs and computing FDR (e.g., Fig. 1 and Table I). To examine the difference between using total and unique PSMs, the data in Table I were re-calculated using unique PSM counts. As shown in table II, FDRs estimated from unique PSMs under the three different filtering criteria showed slightly less variation than that using total PSMs (Table I). On average, the estimated FDR was about twice that using total PSMs (18.27 vs 9.5%, 8.98 vs 4.79%, and 1.61 vs 0.90% for the three respective filters of varying stringency). The increase in FDR could be attributed to a sharp decrease (~60%) in target PSMs (4215 vs 9653, 3708 vs 8762, 2780 vs 6519, for the three filters, respectively) from the non-redundant count approach. The decrease in decoy PSM count was surprisingly much less prominent (only about 20%). The results suggest that under the same filtering criteria, non-redundant count approach has a tendency to yield a much higher estimation of FDR.

Table II.

False positives and FDR estimated by unique PSMs identified from separate searches of target and decoy databases using mild- to high-stringency multi-criterion filtering.

FDR_10%a FDR_5%b FDR_1%c
# PSMs FDR # PSMs FDR # PSMs FDR
target 4215 3708 2780
randomAA 771 18.29% 356 9.60% 50 1.80%
randomAATrypsin 768 18.22% 329 8.87% 31 1.12%
randomDipep 738 17.51% 303 8.17% 34 1.22%
randomDipepTrypsin 764 18.13% 301 8.12% 40 1.44%
reversePeptide 798 18.93% 325 8.76% 49 1.76%
reverseProtein 797 18.91% 330 8.90% 49 1.76%
shufflePeptide 758 17.98% 358 9.65% 55 1.98%
shuffleProtein 767 18.20% 361 9.74% 49 1.76%
average 770 18.27% 333 8.98% 45 1.61%
CV 2.56% 2.56% 7.14% 7.14% 19.20% 19.20%

IIb. The extent of difference in FDR estimation correlates with the ratio between total and unique PSMs

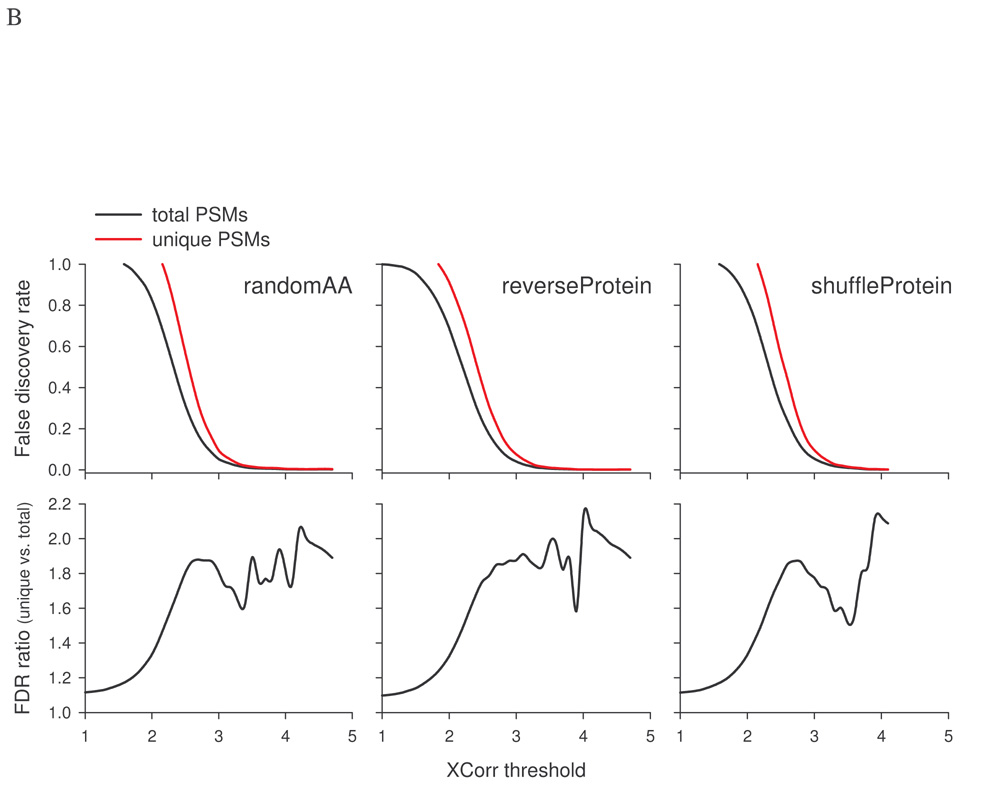
To further investigate the differences resulting from using total vs. unique PSMs in FDR calculation, total or unique PSMs were plotted against XCorr threshold for the rat kidney protein data set using search results from the target, randomAA, reverseProtein, or shuffleProtein databases. For the target database, the number of total PSMs was significantly higher than that of unique PSMs (Fig. 5A, upper panel). For decoy databases, the number of total PSMs was slightly more than that of unique PSMs at low XCorr. When XCorr was greater than 2.0, the difference was almost non-discernable. The ratio of total to unique PSMs was also plotted against XCorr threshold (Fig. 5A, lower panel). At lower XCorr, a ratio of ~1.25 and ~1.15 for the target database and the decoy databases, respectively, were observed. When XCorr threshold was >2.0, the ratio for the target database increased rapidly, exceeding 2.3 at XCorr of 3.0. In contrast, the ratios for decoy databases were relatively steady (~1 to 1.4) throughout the XCorr range. As expected, FDR estimated using unique PSMs was consistently higher than that using total PSMs (Fig. 5B, upper panels). At XCorr >2.5, the ratio stayed in the range between 1.6 to 2.2 (lower panels), suggesting FDR estimated with unique PSMs is about 60 to 120% higher than that with total PSMs, consistent with data presented in Table II.

Figure 5.

Figure 5

Figure 5

Comparison of using total PSMs or unique PSMs in the estimation of false positives and FDR. The rat kidney protein data set was searched against the target rat RefSeq database and three decoy databases separately. A, Identifications based on total or unique PSMs from each database as a function of XCorr threshold. B, FDR estimated based on total or unique PSMs as a function of XCorr threshold.

III. Target-decoy database search: separate or composite

Besides separate search, composite search (against a database consisting of a decoy database appended to the target database) is also commonly used. To compare the differences between these two searching methods, composite search was conducted with the same kidney protein data set.

IIIa. Separate search gives higher estimations of FPs and FDR when XCorr is the sole filter

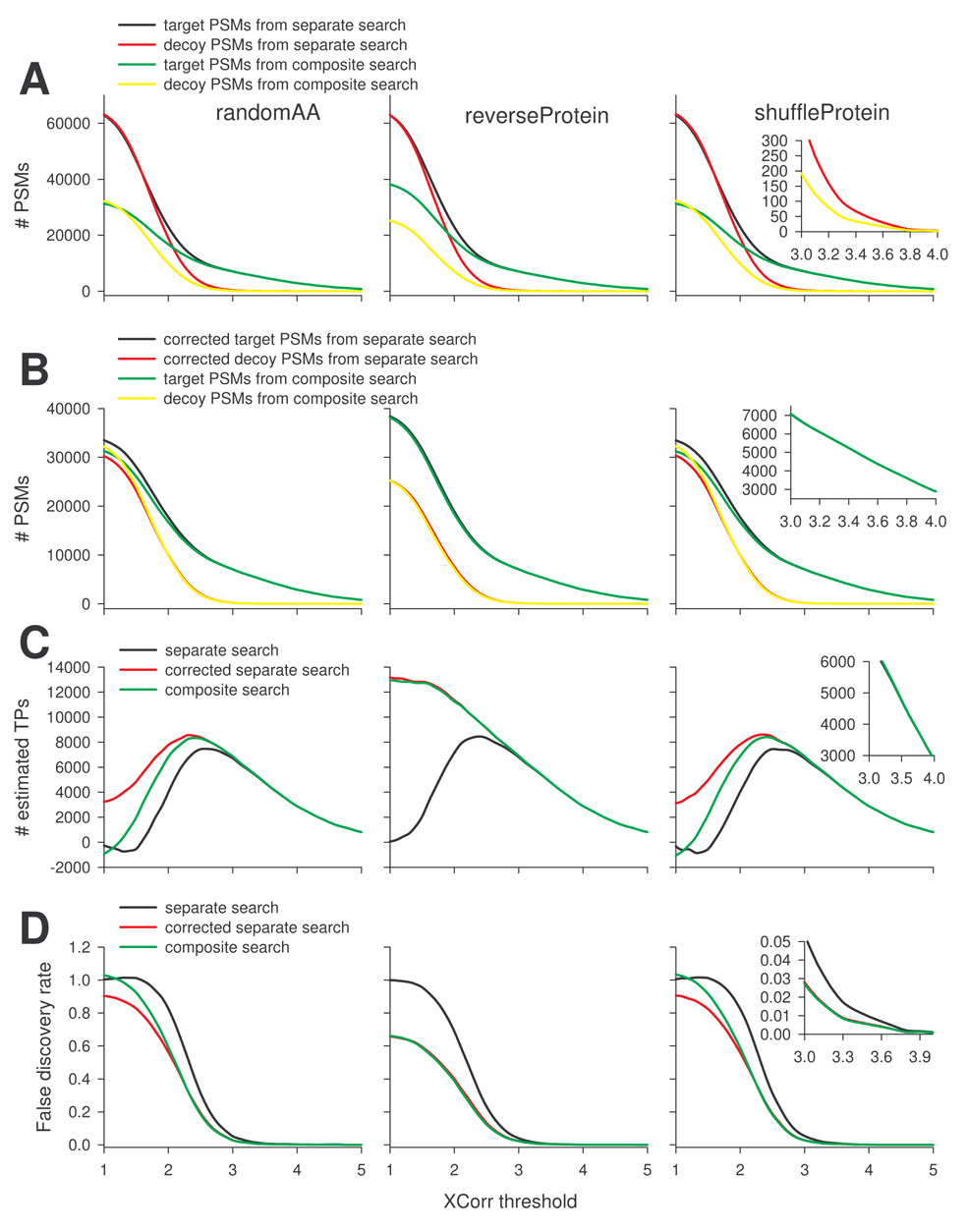
Fig. 6A shows target and decoy hits as a function of XCorr threshold from separate and composite searches, using randomAA, reverseProtein, and shuffleProtein decoy sequences. Both target and decoy PSMs of separate search were consistently higher than those of composite search. The differences between the two types of search gradually decreased as XCorr threshold increased, and became less significant as XCorr was greater than 3.0. The number of decoy PSMs using the separate search was however still higher than that using the composite search (Fig. 6A inset). Accordingly the number of estimated TPs was smaller (Fig. 6C) and FDR was higher (Fig. 6D) in separate search. In general when XCorr is the only filter used, separate search leads to higher estimations of FPs and FDR and a lower estimation of TPs.

Figure 6.

Figure 6

Comparison of separate search (with or without the proposed corrective measure) and composite search in FDR estimation. The rat kidney protein data set was searched against target and decoy databases by separate search or composite search. A corrective procedure was applied to separate search to minimize bias in the estimation of false positives and FDR. A, Target and decoy PSMs from separate or composite searches as a function of XCorr threshold. B, Target and decoy PSMs from composite and corrected separate searches as function of XCorr threshold. C, Estimated true positives based on separate search (with or without correction) or composite search as a function of XCorr threshold. D, Estimated FDR based on separate search (with or without correction) or composite search as a function of XCorr threshold.

IIIb. With multi-filtering, separate search produces higher estimated TPs than composite search does

To compare separate and composite searches under multiple filtering criteria, composite search results were filtered using the same three sets of multiple-filtering criteria mentioned previously. Comparing table III (composite search) with table I (separate search) when the same set of scoring criteria was used, a separate search gave higher estimation of FPs, with the estimated FDR about three times that from a composite search (on average 9.50 vs 2.95%, 4.79 vs 1.32%, and 0.90 vs 0.35%, for the three sets of filtering criteria, respectively). The variation of FDRs among the decoy databases was slightly higher for the composite search, suggesting higher dependency on decoy construction strategy. In addition, the average of estimated FPs from separate search was three to four times that from composite search (917 vs 255, 420 vs 107, and 59 vs 22, for the three filters, respectively). The TPs estimated by separate search were, however, slightly higher (on average 8736 vs 8394, 8342 vs 8029, 6460 vs 6322, for the three filters, respectively) due to a larger number of target PSMs.

Table III.

False positives and FDR estimated by total PSMs from composite search of concatenated target-decoy databases using mild- to high-stringency multi-criterion filtering.

FDR_10%a FDR_5%b FDR_1%c
target decoy FDR target decoy FDR target decoy FDR
PSMs PSMs PSMs PSMs PSMs PSMs
randomAA 8562 277 3.24% 8062 131 1.62% 6317 37 0.59%
randomAATrypsin 8590 260 3.03% 8097 100 1.24% 6330 14 0.22%
randomDipep 8584 254 2.96% 8095 102 1.26% 6326 24 0.38%
randomDipepTrypsin 8572 274 3.20% 8092 114 1.41% 6345 15 0.24%
reversePeptide 8862 213 2.40% 8289 81 0.98% 6391 21 0.33%
reverseProtein 8890 245 2.76% 8302 109 1.31% 6384 25 0.39%
shufflePeptide 8579 246 2.87% 8082 114 1.41% 6329 20 0.32%
shuffleProtein 8556 267 3.12% 8072 106 1.31% 6329 22 0.35%
average 8649 255 2.95% 8136 107 1.32% 6344 22 0.35%
CV 1.62% 8.08% 9.25% 1.22% 13.34% 13.98% 0.44% 32.03% 32.19%

IIIc. A model explaining the differences between separate and composite searches

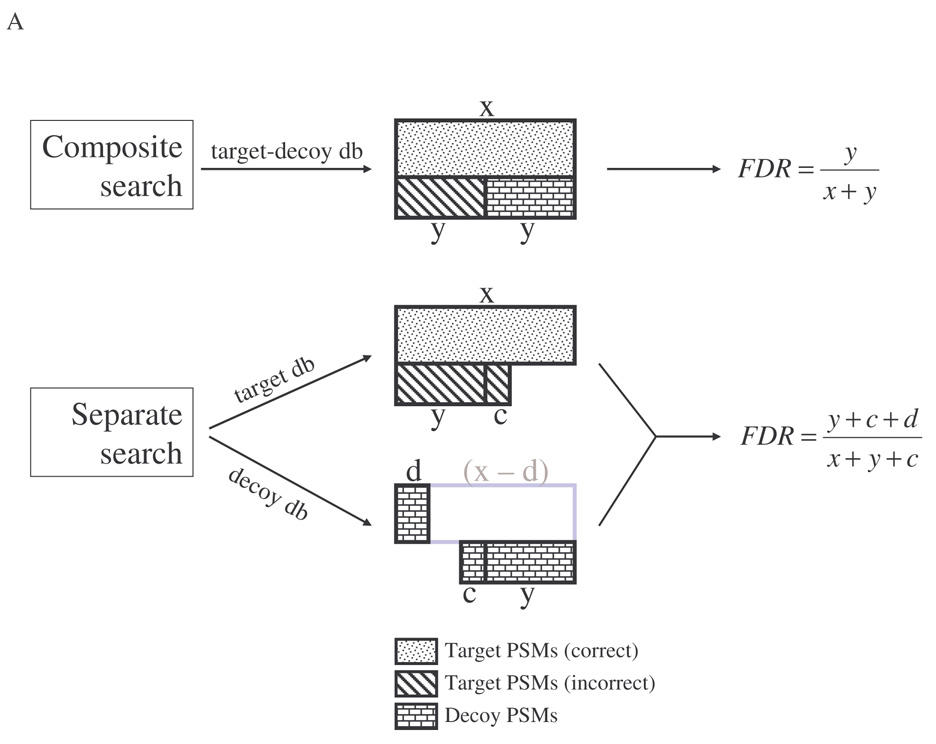
A simplified model to account for the difference between separate and composite searches was proposed in Fig. 7A. Here only the top-scoring PSM for each spectrum is considered. For simplicity, let us make a few reasonable assumptions. Let D represent the score distribution for correct PSMs, D1 represent the score distribution for incorrect PSMs from composite search, and D2 represent the score distribution for incorrect PSMs from separate target or decoy search. Let’s also assume that P, P1, and P2 represent the probability of a PSM attaining at least score T in D, D1, and D2, respectively. It is reasonable to assume that P1 ≥ P2 because in composite search in which the database size is doubled an incorrect PSM has a higher chance to attain score equal to or higher than T. Suppose we perform database search of S MS/MS spectra. In composite search, there are C correct PSMs and (S-C) incorrect PSMs. Given a threshold score T, the expected number of accepted correct PSMs is CP and the expected number of accepted incorrect PSMs is (S-C)P1. It is reasonable to expect that the incorrect PSMs evenly split between target and decoy PSMs. Let’s denote CP as x and (S-C)P1/2 as y. Let Nd denote the number of accepted decoy PSMs, and Nt denote the number of accepted target PSMs [which equals the number of TPs (Ntp) plus the number of FPs (Nfp)]. Then Nd ≈ (S-C)P1/2 = y, Nfp ≈ (S-C)P1/2 = y, Ntp = CP = x, and Nt = (Ntp+Nfp) ≈ (x+y). As shown in Fig. 7A (upper panel), there are x expected correct target PSMs, approximately y expected incorrect target PSMs, and approximately y expected decoy PSMs. The actual FDR is Nfp/Nt ≈ y/(x+y), and the estimated FDR is Nd/Nt ≈ y/(x+y). As can be seen, Nd is an unbiased estimate of Nfp in target PSMs, and the estimated FDR accurately reflects the actual FDR.

Figure 7.

Figure 7

Figure 7

A model for comparison of separate and composite searches and corrective procedures to minimize the differences. A, a simplified model explaining the difference between separate search and composite search. B, corrective procedures to correct the bias of separate search in overestimating FDR and false positives.

In separate search, it is slightly different (Fig. 7A lower panel). When searching the target database, suppose there are C’ correct PSMs. It is likely that C’≥C, as in the absence of competing decoy sequences, a true peptide spectrum has a slightly higher chance to match the true target sequence. For simplicity, let’s assume C’≈C. Now there are approximately C correct PSMs and (S-C) incorrect PSMs. When searching the decoy database, all S PSMs are incorrect. Given a threshold score T, one expects CP (or x) correct PSMs and (S-C)P2 incorrect PSMs in the accepted target PSMs, and SP2 accepted decoy PSMs. It is very likely that P1 ≥ 2P2, therefore (S-C)P2 ≥ (S-C)P1/2 (or y). Let’s denote (S-C)P2 as (y+c). In addition, SP2 = (C+S-C)P2 = CP2+(S-C)P2 = CP2+(y+c). Let’s denote CP2 as d, then SP2 = d+(y+c). In this case, Nd = SP2 = (y+c+d), Nfp = (S-C)P2 = (y+c), Ntp = CP = x, and Nt = (Ntp+Nfp) = (x+y+c). The actual FDR is Nfp/Nt = (y+c)/(x+y+c), and the estimated FDR is Nd/Nt = (y+c+d)/(x+y+c). Apparently Nd (i.e., y+c+d) overestimates Nfp (i.e., y+c) in target PSMs, and accordingly FDR is overestimated.

This simplified model shows that, in separate search, increase in estimated FPs could result from spectra of correct PSMs matching to decoy sequences (d) and from increased spectra of incorrect PSMs matching to decoy sequences (c). In fact c and d can be easily estimated: c is equal to the number of target PSMs from separate search (x+y+c) minus the number of target PSMs from composite search (x+y), while d is equal to the number of decoy PSMs from separate search (y+c+d) minus (c + the number of decoy PSMs from composite search (y)). As an example, at XCorr threshold of 2.5 (from Fig. 6A middle panel) the numbers of target and decoy PSMs for the rat kidney protein data set searched against the rat RefSeq target database and its reverseProtein decoy database by separate search or composite search were 10863, 2531, or 10405, 1286, respectively. In this case the c was estimated to be 458 (i.e., 10863-10405) and d estimated to be 787 (i.e., 2531-458-1286).

The model suggests that FDR estimated by separate search is higher than that by composite search as mathematically (y+c+d)/(x+y+c) is greater than y/(x+y) when c≥0, d≥0, and c+d>0. It also suggests that TPs estimated from composite search (x) is larger than that from separate search (x-d for d>0). The higher FDR and FPs predicted for separate search are consistent with experimental data (Table I and Table III, and Fig. 6A and 6D). The predicted TPs are consistent with experimental data with XCorr as the single filter (Fig. 6C), but not when multiple filters are used (Table I and Table III), likely because this simplified model does not consider the effects of relative scores (e.g., deltaCn). The discrepancy will be discussed in Discussion.

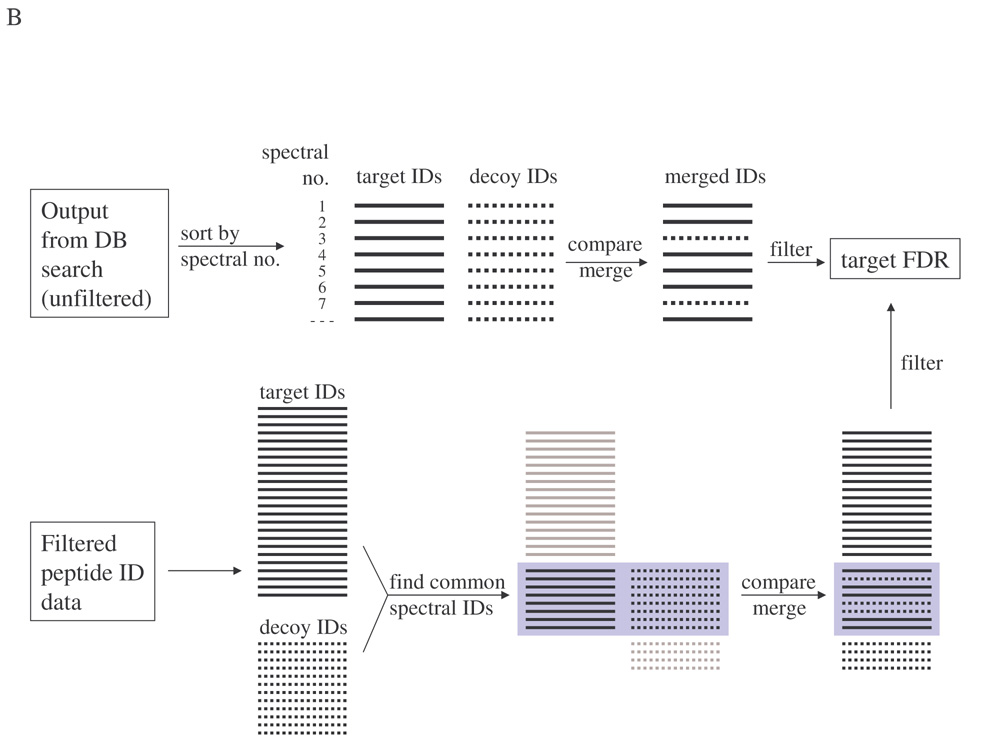
IIId. Differences in FP and FDR estimations between separate and composite searches can be minimized

From Fig. 6A, one way to obtain comparable search results from separate and composite searches is to use highly stringent XCorr threshold (e.g., >3.5). This is however impractical because such a high stringency will greatly increase the number of false negatives, resulting in lower sensitivity in protein identification. Two alternate procedures are proposed in Fig. 7B. In the first procedure (upper panel), using the raw outputs of SEQUEST database search as an example, two top hits, one from target and the other from decoy search, are obtained for each MS/MS spectrum. The one with a higher XCorr is retained. In this way the raw outputs from both target and decoy searches are merged, mimicking a composite search. It should be noted that sometimes the raw database search output may not be available. The second approach (lower panel) starts with two pre-filtered peptide/protein identification lists (one from target search and one from decoy search). For each MS/MS spectrum with peptide hits in both lists, the hit with a lower XCorr is discarded. The processed lists can either be merged into a single list or kept separate for FDR estimation.

Using the merge-raw-outputs procedure with the data set that yielded Fig. 6A, the corrected target and decoy PSM curves overlapped very well with those from composite search (Fig. 6B). For decoy search using reverseProtein database there was almost a complete overlapping in target and decoy PSMs and estimated TPs and FDR (Fig. 6C and 6D). For decoy search with randomAA and shuffleProtein databases, there was a clear difference between composite and corrected separate searches at lower XCorr thresholds, but the difference gradually diminished as XCorr threshold increased and finally almost disappeared at XCorr > 2.5 (Fig. 6B, 6C, and 6D). Actually in these cases the corrected separate search showed higher number of estimated TPs and lower FDR at moderate XCorr threshold (<2.5) before converging with composite search, due to the fact that corrected target PSMs were consistently higher and corrected decoy PSMs were consistently lower than those from composite search (Fig. 6B).

Table IV shows the results by applying the corrective approach to rat kidney protein data set using multi-criteria filtering. Compared with Table I, the corrective procedure reduced, on the average, estimated FPs and FDR by more than 50%. Because target PSMs were similar, the number of estimated TPs was higher. Furthermore, compared with Table III for composite search, the estimated FPs, TPs, and FDR were comparable (e.g., on average 30 vs 22, 6484 vs 6322, and 0.46% vs 0.35% at FDR_1% filtering, respectively).

Table IV.

False positives and FDR estimated with total PSMs from corrected separate searches of target and decoy databases using mild- to high-stringency multi-criterion filtering.

FDR_10%a FDR_5%b FDR_1%c
target decoy FDR target decoy FDR target decoy FDR
PSMs PSMs PSMs PSMs PSMs PSMs
randomAA 9547 431 4.51% 8721 197 2.26% 6514 43 0.66%
randomAATrypsin 9555 408 4.27% 8736 158 1.81% 6516 19 0.29%
randomDipep 9547 416 4.36% 8727 166 1.90% 6511 31 0.48%
randomDipepTrypsin 9550 450 4.71% 8718 177 2.03% 6515 19 0.29%
reversePeptide 9597 408 4.25% 8741 158 1.81% 6515 32 0.49%
reverseProtein 9579 434 4.53% 8736 175 2.00% 6514 37 0.57%
shufflePeptide 9547 397 4.16% 8723 169 1.94% 6517 25 0.38%
shuffleProtein 9547 418 4.38% 8724 176 2.02% 6510 33 0.51%
average 9559 420 4.40% 8728 172 1.97% 6514 30 0.46%
CV 0.20% 4.08% 4.10% 0.10% 7.33% 7.39% 0.04% 28.26% 28.27%

IV. Validation using a standard mixture of known proteins

Two interesting observations deserve further investigation: (1) random decoy databases tend to yield a higher estimation of FPs than reversed decoy databases, but the differences can be minimized by ensuring a similar number of unique peptides in the decoy databases; and (2) separate search produces higher FP and FDR estimates than composite search, but a simple corrective procedure can be applied to reconcile the differences. The question is whether the higher estimation is due to an overestimation by one method or an underestimation by the other. To gain insights into it, LC-MS/MS analysis of tryptic peptides from a mixture of known proteins was carried out and database search was performed against two representative decoy databases (randomAA and reverseProtein decoys constructed from a target database comprising of the known protein sequences inserted in the front of the rat RefSeq proteins). In addition, two decoy databases (randomAATrypsin and reversePeptide) with the same number of unique peptides, derived from the non-redundant version of the target database, were also searched.

IVa. Random database overestimates FPs to a higher degree than reversed Database

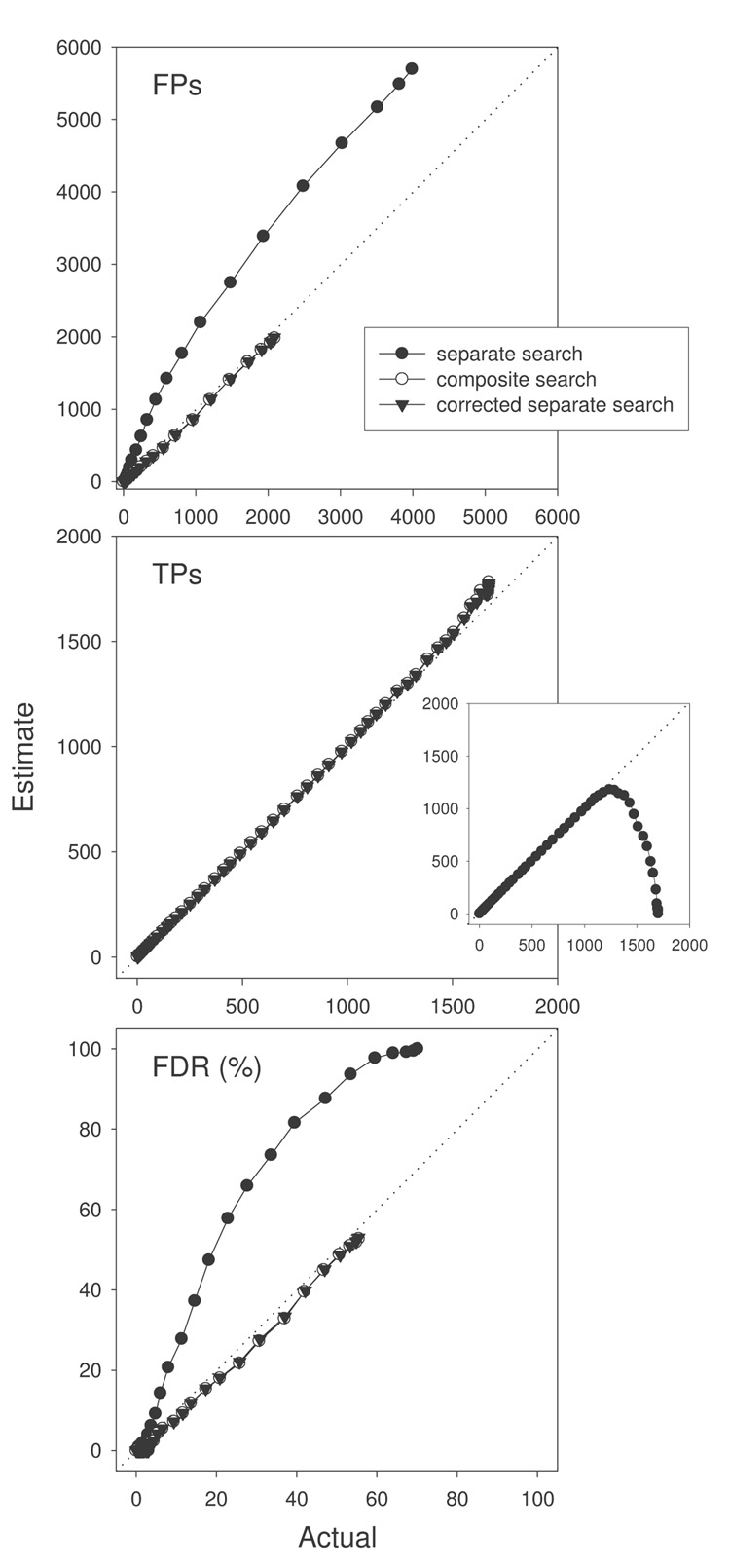
The number of decoy PSMs (i.e., FP estimates) obtained from separately searching the randomAA and reverseProtein databases as a function XCorr threshold is shown in Fig. 8A (left panel). The number of PSMs was consistently higher for randomAA decoy than for reverseProtein decoy until XCorr threshold of 3.0. When decoy databases with the same number of unique peptides were searched, the number of PSMs at a given XCorr threshold became similar (Fig. 8A right panel; though slight differences remained as suggested by the inset), confirming our earlier observation that differences in FP estimation can be minimized by ensuring similar levels of redundancy in decoy databases. Surprisingly, the actual FPs were much lower than the estimates by both decoy databases (Fig. 8A, left and right panels), suggesting both random and reversed databases overestimate FPs and that random decoy does it to a much greater degree.

Figure 8.

Figure 8

Figure 8

Validation using data from a standard mixture of known proteins. LC-MS/MS data of tryptic peptides from a mixture of 7 known proteins were searched against the databases described below. The sequences of these 7 known proteins were added to the beginning of the rat RefSeq database (36133 entries) to form the target database. The reverseProtein and randomAA decoy databases were generated from the target database. A non-redundant version of the target database and the corresponding non-redundant reversePeptide and randomAATrypsin decoy databases were also constructed. In addition, a composite database comprising the target and the reverseProtein decoy sequences was created. PSMs obtained from searching these databases are presented. PSMs for charge +1 or +3 made up only a very small portion of the data set (<5%) and were not included in the plots. PSMs are considered TPs if they are assigned to the 7 known proteins and FPs otherwise. A. Estimated FPs (PSMs from separate search of each decoy database) and actual FPs (PSMs assigned to proteins other than the 7 known proteins in the target database) are plotted as a function of XCorr threshold. B. Actual versus estimated FPs, TPs, and FDRs, from separate (with or without correction) and composite search of the target and the reverseProtein decoy databases, at various XCorr thresholds.

IVb. Separate search overestimates FPs and FDR

Fig. 8B shows actual vs. estimated FPs (upper panel), TPs (middle panel), and FDR (lower panel) at various XCorr thresholds (1.0 to 6.8 at 0.1 increments) from separate search (with or without correction) and composite search using the target and the reverseProtein decoy databases. If there is a high level of agreement between actual vs. estimates, data points will fall on or close to the y=x diagonal line. Indeed, separate search led to a much higher estimation of FPs at mild to relatively stringent XCorr threshold (1.0 to 3.0), and accordingly it underestimated TPs (inset of middle panel) and overestimated FDR. Note the exception that at very high XCorr threshold (>3.0), good agreement between actual vs. estimated TPs was obtained (left-side portion of the data points). In contrast, in composite search, the estimated FPs, TPs, and FDR were highly similar to the actual FPs, TPs, and FDR, respectively. Though theoretical discussions of the advantages and disadvantages of separate vs. composite search have been presented elsewhere16–18, we confirm here with experimental data that separate search tends to overestimate FPs and FDR while composite search gives much more accurate estimations. The nearly perfect overlapping of data points between composite search and corrected separate search in Fig. 8B demonstrates that a simple procedure can be applied to separate search to yield estimations of FPs and FDR comparable to composite search.

Overall, these data suggest that the differences in FP and FDR estimations between random and reversed decoy databases and between separate and composite searches seen with the more complex rat kidney protein data set are likely due to overestimations by using random databases or the separate search approach.

Discussion

The likelihood of having a significant number of FPs in large-scale proteomic identification represents a problem that requires serious attention 7. Target-decoy database search is a simple and effective way to estimate and control the FDR 14. Though conceptually straightforward, subtle differences exist in methods implemented in different laboratories. We undertook this study to better understand how different implementations might affect FDR estimation and FP filtering.

We first evaluated the effects of decoy construction. Sequence reversal is the most frequently used method in generating a decoy database 5;10;11;13, although stochastic methods have also been used 7;12. We generated 2 reversed and 6 stochastic decoys from a target database (see details in Materials and Methods). Despite the two reversed and the six random decoys behaved similarly as a group, there existed a distinctive difference between the two groups. Decoy PSMs and the corresponding estimated FDR from the reversed databases were significantly less than those from random databases when XCorr was used as the sole filter (Fig. 1). Examining the database characteristics suggests that sequence redundancy is an important factor. Others have reported increased number of peptides of specific lengths (i.e., length frequency) in databases generated by stochastic methods 14. Since database searching programs often start with the m/z of a precursor ion, we adopted a slightly different approach by counting the number of peptides of a specific mass (mass frequency) in a decoy database. Random databases were found to have similar mass frequencies, which were much higher (about 80%) than those of the target database for mass range between 800 and 3000 daltons. The mass frequencies of reversed databases were not significantly different from that of the target in the same range (Fig. 2).

We found that applying a global “uniqueness normalization” failed to correct the nonlinear differences in FDR estimation (Fig. 3). Similar attempts, applying a decoy factor or applying the reciprocal of the percentage of decoy PSMs in XCorr ranks two to ten as the normalization coefficient, have been reported by others 14;23. By removing redundant peptides from the target database and creating reversed and random databases with the same number of peptides as in the target, we showed that hit curves for decoys became largely merged irrespective of methods used for their generation (Fig. 4). But deviation of randomDipep and randomDipepTrypsin from other random databases was observed, suggesting redundancy is a significant contributing factor but specific stochastic methods may also play a role.

Filtering by various combinations of parameters (e.g., XCorr, charge state, RSp, and deltaCn) is a common practice in SEQUEST database searching 1;5;6;11. We showed that the differences between using reversed or random decoys when XCorr was the sole filter had largely disappeared when multiple filters (XCorr, deltaCn, and RSp) were employed (Table I). The merging in search outcomes was not fully expected. In the literature, opinions regarding using random databases are divergent, ranging from that a correction is needed to match reversed databases 14, that estimations between reversed and random databases are comparable 11, to that random databases are preferred over reversed databases 12. The discrepancies might be attributed in part to the different filters employed in those studies: XCorr and delta Cn 14, XCorr by charge state 11, and custom LIPS peptide score 12;24. On one hand, it suggests that differences among decoy databases rely partially on the types of filters used. On the other hand, as demonstrated from our results, multiple filters offer higher discriminating power in eliminating random PSMs which cannot consistently surpass each of the filtering thresholds. Overall, our study supports the notion that, when applied with cautions, decoy databases constructed by different methods can be similarly effective in controlling FPs 14.

A critical requirement for stochastic methods is a high reproducibility in estimating FPs and FDR. A stochastic procedure applied on the same target database at different time or in different laboratories may not produce the same randomized protein sequences. The FP and FDR estimations could still be comparable provided that the database characteristics are consistently similar. Among the methods used in this study, randomAA and shuffleProtein generate sequences more random in nature, as few constraints are imposed (e.g., preserving tryptic sites or dipeptide frequency). We had generated additional decoy databases from the rat RefSeq target database using randomAA or shuffleProtein approach. These independently generated decoys have highly similar mass frequency distributions (r=0.991 for randomAA and r=0.993 for shuffleProtein) and nearly perfect correlations in estimating FPs (r=0.999 for both methods) on the same kidney protein data set (results not shown). These data demonstrate that stochastic methods are capable of creating decoy databases with similar features as well as yielding similar FP and FDR estimations.

Though often not explicitly described, both total PSMs 5;15 and unique PSMs 11;14 have been used in FP and FDR estimation. We examined differences in both types of PSMs in estimating FPs and FDR and found that calculation using unique PSMs tended to give a much higher estimation of FPs and FDR (Table II and Fig. 5). Under moderate- to high-stringency XCorr threshold, peptide identifications from decoy databases were mostly non-redundant, while those from the target database were high in redundancy. On average, each peptide was identified more than 2 times in the target-database search which is in good agreement with the numbers reported by others (~2 6; 3–4 5). It is also consistent with our experimental setup allowing each ion to be sampled twice before being excluded for analysis. In practice, some abundant ions might have been sampled more than twice due to elution peaks spanning over the time window set for dynamic exclusion, while other lower abundant ions sampled only once. It is therefore reasonable to expect the total/unique PSM ratios to be ~2. In other words, a ratio of ~2 for total/unique PSMs in database searching suggests that the identifications likely reflect true positives. Chemical or machine noises, on the other hand, would appear randomly and unlikely be sampled more than once, thus yielding mostly one-hit identification. This is consistent with database search results from decoy databases. The inference is that spectra of real peptides rarely match well to decoy sequences, reiterating the validity of using decoy databases in FDR estimation. In general it is likely that the total/unique PSM ratio reflects the data acquisition method used. For this reason, it is reasonable to use total PSMs in the calculation of FDR. Out of the concern that a few frequently observed abundant peptides might skew the estimation, the use of non-redundant peptides in FDR estimation had also been proposed 14. But it has been shown that nearly half of all the peptides, not merely the abundant ones, have been identified more than once 6, consistent with our observation here that nearly 60% of the peptides (from searching the kidney protein data set against the rat RefSeq target database) were identified at least twice with the FDR_1% filter. The use of total PSMs is also meaningful from the perspective of false positive rate (FPR), a concept closely related to FDR. If we search a set of spectra against a decoy database, all PSMs can be considered FPs and FPR is the number of FPs divided by the number of spectra searched. In this case, it would be difficult to define the number of unique spectra among all of the spectra searched.

Two searching approaches have been used in target-decoy database search. One searches the target and the decoy databases separately, referred as separate search 6;7;10;11, while the other searches a composite database consisting of the target and decoy sequences, referred as composite search 5;12–14. Given the prevalent use of both approaches, we compared the different outcomes of using separate and composite searches and attempted to find a solution for reconciling or minimizing the differences. We showed that separate search led to higher estimated FPs and FDR (Fig. 6), consistent with the observation by others 12. The higher estimations could readily be explained by a simplified model (Fig. 7A). We further proposed a corrective measure for separate search (Fig. 7B) that yields estimations comparable to composite search with added advantages. In theory, one expects the corrected separate search approach (Fig. 7B) to yield the same result as that from a composite search. Our data however suggest that the outcomes were close but not identical. The discrepancies had to do with the algorithm of the search engine used. In SEQUEST search, a candidate peptide has to pass an RSp filter (top 500 in this study) before XCorr is calculated to avoid computational complexity. In separate search, a PSM with the highest XCorr has a better chance to pass the RSp filter than that from a composite search. For example, in composite search a PSM from target database may have a higher XCorr but could be excluded from calculation because PSMs from decoy database have higher Sp despite having a lower XCorr. Furthermore, the relative score, deltaCn, for a true PSM has a greater chance to be lower in the composite search. The shift in deltaCn in composite search has been recognized by others 14. They observed that the shifts were proportional between target and decoy databases and suggested that the shift as a reasonable cost in return for the overall benefit obtained in FDR estimation. However, since best matches to target sequences in general outnumber those to decoy sequences 14;19, the proportional shift implies that more target PSMs will eventually be affected. This could lead to the observed reduction in estimated TPs in composite search when multiple filters including deltaCn are applied (Table I and Table III). In other situations where search engines use database size-sensitive E-value 4 or P-value 3 to evaluate peptide hits, composite search could also be disadvantageous because the E-value or P-value of a PSM may be adversely affected when database size is doubled. Under such circumstances, separate search combined with the corrective measure we proposed has similar benefits as with composite search in FDR estimation, yet preserves the advantages of separate search in the estimation of TPs.

Conclusion

Confident assessment of FPs is a prerequisite in high-throughput protein identifications. In this study we investigated different implementations of the target-decoy database search to see how search outcomes and estimated FPs and FDR were affected, using a rat kidney protein data set and the SEQUEST search engine as examples. Several interesting findings from the study were: 1) When XCorr was used as the single filter, stochastic methods led to a higher estimation of FPs and FDR due to reduction in sequence redundancy; 2) the higher estimation could not be corrected by a simple global normalization with a unique peptide coefficient; 3) when filter combining multiple score thresholds was applied, reversed and random databases behaved similarly in FDR estimation; 4) using unique PSM count tended to give a much higher estimation of FDR, partially depending on the data acquisition method; 5) separate search generally led to a higher estimation of FPs and FDR; it, however, had more estimated TPs when multiple filters were employed; and 6) a simple corrective procedure could be incorporated into separate search to mimic the behavior of a composite search, which effectively corrected FDR overestimation and TP underestimation, as evidenced by data from a standard protein mixture. Overall, the effects of different implementations on FDR estimation using target-decoy search partially depend on factors specific to an experiment such as data acquisition method, database search engine, type of filters, and corrective post-processing. Understanding the roles of these factors should prove beneficial in designing large-scale proteomic marker discovery.

Acknowledgment

This research was supported by Intramural Research Programs of NHLBI, the National Institutes of Health.

Reference List