Robustness: mechanisms and consequences (original) (raw)
. Author manuscript; available in PMC: 2010 Sep 1.
Published in final edited form as: Trends Genet. 2009 Aug 28;25(9):395–403. doi: 10.1016/j.tig.2009.07.005
Abstract
Biological systems are robust to perturbation by mutations and environmental fluctuations. New data are shedding light on the biochemical and network-level mechanisms responsible for robustness. Robustness to mutation might have evolved as an adaptation to reduce the effect of mutations, as a congruent byproduct of adaptive robustness to environmental variation, or as an intrinsic property of biological systems selected for their primary functions. Whatever its mechanism or origin, robustness to mutation results in the accumulation of phenotypically cryptic genetic variation. Partial robustness can lead to pre-adaptation, and thereby might contribute to evolvability. The identification and characterization of phenotypic capacitors — which act as switches of the degree of robustness — are critical to understanding the mechanisms and consequences of robustness.
Robustness
Biological systems are subject to mutation, to environmental variation and to random fluctuations in the abundances of their component molecules. Many physiological and developmental systems are robust to such perturbations. That is, despite these natural perturbations, the systems produce relatively invariant outputs.
There is currently much interest in the role of robustness in multifactorial human disease [1] and in evolution [2]. Nevertheless, the mechanistic causes of robustness remain poorly understood. This is beginning to change, however, as researchers increasingly use high-throughput techniques to probe the mechanisms that generate complex traits [3]. These techniques not only provide quantitative details about the activities of individual genes and gene products, but they also enable a systems-level view. A systems-level view is crucial for robustness, which often emerges out of interactions between entities.
One of the earliest and most insightful thinkers on the subject of robustness was C.H. Waddington, who recognized decades ago that levels of phenotypic variation in natural populations tend to be small compared to what might be expected given typical levels of genetic and environmental variation [4]. It is not clear, however, what level of phenotypic variation one should expect. Waddington’s logic was based on the observation that a biological system (e.g., Drosophila wing development) perturbed by a major genetic or environmental insult (e.g., heat shock) exhibited greater variation than an unperturbed system. He therefore inferred that the original system was robust. Through artificial selection, Waddington showed that phenotypic variation initially seen only in the presence of a major perturbation had an underlying genetic basis. From this, he concluded that the experimental perturbation revealed the developmental system’s normal robustness to the everyday minor perturbations of genetic variation.
Perturbation experiments remain the dominant approach to probing the mechanistic basis of robustness. Whereas Waddington used simple environmental perturbations, such as exposing flies to heat shock [5], ether [6] or high salt concentrations [7], others have used mutations in key developmental genes [8,9]. More recent experiments have extended this paradigm to employ organisms genetically engineered to harbor loss-of-function [10] or gain-of-function [11,12] mutations. Varying doses of small interfering RNA (siRNA) have also been used to deplete each targeted gene product to different degrees, thereby creating a series of genetic perturbations that improves power to detect regulatory interactions that underlie robustness [13]. In all cases, relative robustness is quantified as the change in variation of one or more specific traits when the experimental perturbation is applied.
The measurement of robustness is specific to the sources of variation present in a particular experiment. For example, if a mutation causes greater phenotypic variation among genetically identical organisms raised in a carefully controlled environment, then the mutated gene product is inferred to contribute to robustness to either microenvironmental variation or stochastic fluctuations in the intracellular environment [10]. If, on the other hand, a mutation causes a greater increase in phenotypic variation across genetically divergent strains, then that gene product contributes to robustness to the underlying genetic variation present in those strains [8]. A key, unanswered question, which we will address here, is whether one set of mechanisms suppresses all types of genetic, environmental and stochastic variation, or instead whether mechanisms of robustness are specific to different sources of variation. The answer to this question has important evolutionary implications, because it has been argued that natural selection for environmental robustness is strong and continual. If mechanisms that provide robustness to environmental variation also provide robustness to genetic variation, then the latter might have evolved only as a side effect of selection for the former [14].
Regardless of why robustness to genetic variation exists, another major unanswered question is what effect it has on phenotypic evolution. One of Waddington’s major insights was that robustness to genetic variation need not constrain phenotypic adaptation, and indeed might promote it [4]. This is at first a counter-intuitive idea, as genetic robustness, by definition, reduces the phenotypic effects of new mutations. However, when a phenotype is robust to the effects of mutations, those mutations accumulate in the form of cryptic genetic variation. If robustness is later impaired, the cryptic genetic variation is revealed and might contribute to phenotypic evolution, a phenomenon known as capacitance (Box 1).
Box 1. Stabilizers and capacitors.
A “capacitor” is a biological switch capable of revealing previously cryptic heritable variation [8]. The analogy is drawn to an electrical capacitor, which stores and releases charge. Some but not all capacitors are gene products whose wild-type function contributes to robustness and, therefore, whose functional impairment reveals variation.
The term capacitor is usually modified by one of three adjectives — “phenotypic capacitor”, “genetic capacitor” or “evolutionary capacitor”. Unfortunately, precise definitions that distinguish the three are not usually given, so here we wish to propose guidelines for their usage. Evolutionary capacitor should only be used for mechanisms that store and release genetic variation and for which there is evidence that revealed variation contributes to adaptation (e.g. Box 4). When no claim is made about the contribution to adaptation, or when there is evidence against such a contribution, the more general term phenotypic capacitor should be used. Although genetic capacitor typically has the same meaning, we propose avoiding this shorthand because it potentially confuses the source of variation (genetic differences) with the agent of robustness (a gene or gene product).
The source of variation is important, because environmental and stochastic sources of variation do not accumulate in the way that genetic variation does, and therefore the capacitor analogy breaks down. Gene products that provide robustness to microenvironmental or intracellular stochastic variation have previously been termed “phenotypic capacitors of … ” these sources of variation [10]. We propose a less wordy and more apt term, “phenotypic stabilizer”, when dealing with non-heritable sources of variation. Here the analogy is to a voltage stabilizer, which maintains relatively steady output voltage despite variation in input voltage and load current.
Experimental identification and characterization of capacitors and stabilizers holds the promise of illuminating the mechanisms of robustness, the congruence between such mechanisms when different sources of variation are considered, and the potential for cryptic variation to contribute to evolutionary adaptation.
Robustness to different forms of natural perturbation
There are three major reasons that phenotypic robustness to a particular type of natural perturbation might exist [15]. Robustness might be adaptive, in the sense that it evolved primarily to limit phenotypic variation in response to a specific perturbation. Alternatively, robustness to the perturbation of interest might be a side effect of evolved robustness to a different perturbation. In such a case, the mechanism of robustness to one perturbation happens also to provide robustness to the other perturbation, and so the two forms of robustness are said to be congruent. The third possibility is that neither adaptive nor congruent selection occurred, but instead that robustness is an intrinsic property of the system that produces the phenotype. The prevalence of each reason for robustness remains to be determined. Theoretical studies, using computational simulations of gene-regulatory networks, suggest both that intrinsic robustness could be widespread and that natural selection can increase robustness under diverse and reasonable sets of parameter values and assumptions [16–22].
Theory predicts that adaptive robustness to mutations will evolve so long as Neμ, the product of the effective population size and the rate of mutations that would reduce fitness in the absence of a specific robustness mechanism, is greater than one [17,20]. Nevertheless, if mechanistic congruence is sufficiently great then robustness to genetic variation might still be largely a byproduct of robustness to environmental perturbations [14,23–25]. Neither genetic nor environmental perturbations should be considered as monolithic categories, however, and congruence should be considered both within and between the broad genetic and environmental categories of perturbations.
Genetic perturbations include not only spontaneous mutations, but also recombination, which brings existing mutations into new combinations. Genetic robustness to new point mutations might be a congruent side effect of genetic robustness to recombination [26]. New mutations can range from single-nucleotide changes to small insertions or deletions to genome rearrangements, and the different types and locations of mutations likely challenge regulatory systems in different ways.
Likewise, environmental variation can take many forms. In an experimental setting, environmental differences can either be macroenvironmental (i.e. systematic differences set by the experimenter) or microenvironmental (i.e. inevitable random fluctuations). In nature, this distinction is not so clear: it is more appropriate to consider the timescales at which changes occur and whether they are predictable or unpredictable. For example, seasonal changes in temperature can be anticipated, yet unexpectedly hot or cold days do occur. Moreover, different environmental variables are expected to impact regulatory systems differently, e.g. a temperature change will affect all kinetic processes, whereas a toxin might target a specific gene product.
One distinct source of perturbations, often included within the broader “microenvironmental” category, is intrinsic stochastic fluctuations due to the low copy numbers per cell of many biological molecules (Box 2). These perturbations are inevitable and universal, but the consequences will differ substantially depending on the cellular functions of particular molecules.
Box 2. Intrinsic stochasticity of gene expression.
When only a small number of molecules is present, variation in that number can be significant. For example, if the mean copy number per cell of a given mRNA is only 5, there is likely to be substantial variation between cells. Following cell division, one cell could easily receive zero copies of that mRNA. Similarly, a given DNA sequence is typically present in only one (haploid) or two (diploid) copies; thus there will be significant fluctuation between having 0, 1 or 2 copies transcriptionally active at any point in time.
If fluctuations are rapid, then their effects will average out even over the short timescales relevant to other kinetic processes of gene expression. However, fluctuations between transcriptionally active (open) and closed chromatin states are slow [83]. Following transcription, fluctuations in chromatin state are propagated into fluctuations in mRNA copy number, thereby creating a huge source of perturbations to which systems must be robust. Stochastic fluctuations can be damped directly by producing excess mRNA or proteins and degrading those not needed, or by increasing mRNA copy number while decreasing translational efficiency and hence keeping mean protein levels constant but less noisy [84]. Robustness to stochastic fluctuations can also arise at the network level.
Another inevitable constraint on living systems is that information cannot be propagated without some rate of error. DNA polymerase errors are familiar, as they cause mutations, but errors are also made during transcription [27] and translation [28]. Collectively, these errors can be seen as perturbations and can have substantial effects [29].
Mechanisms of robustness and their consequences for congruence
Some robustness mechanisms directly eliminate a specified perturbation. For example, at the biochemical level, one-step molecular processes will always suffer a high error rate, but when multiple simultaneous or sequential events are required, it is highly unlikely that they all contain errors. By exploiting this cooperativity, mechanisms to improve transcriptional and translational accuracy, such as kinetic proofreading [30], prevent errors and perturbations in one stage of a process from propagating through to the final stage of that process. In most cases, however, there is not a simple one-to-one relationship between sources of perturbation and mechanisms of robustness. Moreover, as a simple case study illustrates below, superficially minor details can dramatically alter mechanistic congruence.
A simple case study with low congruence
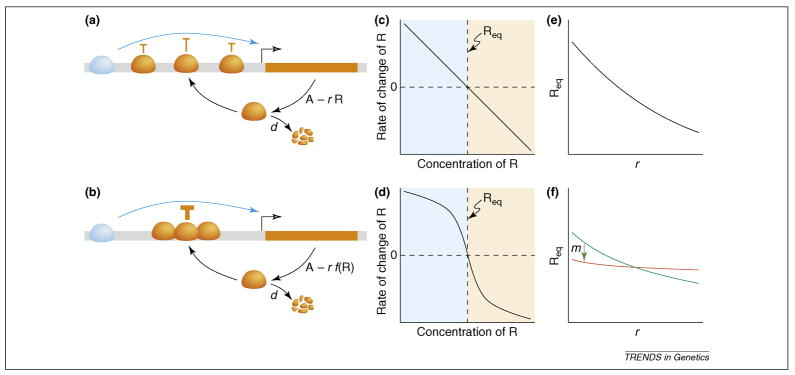
Consider an extremely simple “toy” gene-regulatory network consisting of just one gene, R, which forms a negative autoregulatory feedback loop by repressing its own expression in proportion to its concentration (Figure 1). At equilibrium, the protein concentration R = c/(r + d), where c is maximal production, r is a repression constant and d is a first-order degradation term. One form of robustness to environmental variation is homeostasis, meaning robustness to perturbations in the state of the system. This simple feedback loop is homeostatic: perturb the concentration of R above the equilibrium value and degradation will exceed production, perturb it below and production will exceed degradation.
Figure 1.
Robustness properties of a simple negative autoregulatory feedback loop. (a) A transcriptional repressor protein (orange) inhibits its own production by binding the _cis_-regulatory region (gray) of the gene that produces it (orange rectangle with promoter indicated by hollow arrow). The repressor counteracts the activity of an activator protein (blue), which binds to the same region and is present at constant concentration A. The repressor concentration, R, is determined by the regulatory circuit, which includes the negative feedback with repression constant r and degradation of the protein at rate d. In this simple example, we assume no post-transcriptional regulation and instantaneous transcription and translation. Each bound molecule of the repressor acts independently to counteract the activator. (b) A modification of the circuit in (a) is shown, in which repressor molecules act cooperatively. Without cooperativity the rate of change of R is a linear function of R (c). With cooperativity the rate of change of R is a non-linear function of R with a sigmoidal repression term, r f(R) (d). In the two cases there is the same stable equilibrium value of R, Req, at which the concentration of the repressor does not change. That is, both cases are robust to fluctuations in R. Req is a decreasing function of r. Without cooperativity, changes in r correspond to relatively large changes in Req (e). If we consider r to be genetically determined, e.g. by amino acids that determine the affinity of the repressor for its cognate DNA site, then this circuit is not robust to genetic variation. With increasing cooperativity, represented by increasing values of the Hill coefficient m, changes in r correspond to smaller changes in Req (f). This circuit is then more robust to genetic variation.
But is the network robust to genetic variation? Genetic variation most likely will affect the rate constants. The toy network is not particularly robust to perturbing rate constants. For example, as r increases, the equilibrium concentration of R decreases. That is, genetic variation changes the output of the network. Thus congruence is not universal, as robustness to stochastic microenvironmental perturbations can exist in the absence of robustness to genetic perturbations.
Such an incongruence is not limited to theoretical models. For instance, robustness to mutational perturbations and robustness to environmental perturbations are negatively correlated in strains of Escherichia coli [31]. Likewise, in one set of experiments in Drosophila, the phenotypic capacitor Hsp90 appeared to increase robustness to genetic variation but not to stochastic perturbations [32]. In neither case is the mechanistic basis of the disconnect understood. Moreover, the range of phenotypes assayed might strongly influence the resultant conclusions, e.g. the E. coli experiments only assayed one phenotype, growth rate. Other experiments on Hsp90 in Drosophila and Arabidopsis thaliana have indicated greater congruence. Thus, the question of congruence needs to be addressed on a case-by-case basis, and a large number of phenotypes must be studied, ideally using high-throughput measurements [10], to provide a comprehensive picture of the extent to which congruence exists.
Cooperativity can increase congruence
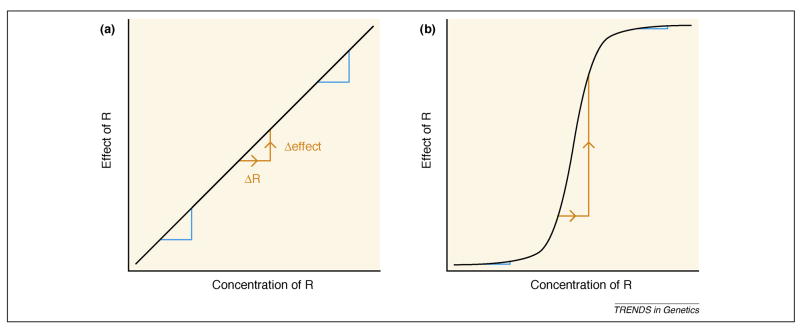
A simple addition to the toy model will render the network both more homeostatic (faster return to equilibrium) and more robust to genetic variation, thus providing greater congruence: sigmoidal response curves. As in the familiar example of oxygen binding to hemoglobin, cooperativity and other mechanisms can produce sigmoidal response curves, characterized by a sharp threshold between unbound and saturated states [33]. Cooperativity can be modeled in the simple network by introducing a Hill function so that repression occurs at rate r_R_m/(R_m_ + θm) rather than rate _r_R. With more cooperativity (a higher Hill coefficient, m), differences in r produce smaller differences in the equilibrium concentration of R (Figure 1). That is, the effects of genetic variation on the output are dampened by the existence of a threshold. Note, however, that although cooperative responses create significant robustness on either side of a threshold, they also magnify the effects of perturbations that cause that threshold to be crossed (Figure 2).
Figure 2.
Robustness properties of graded and sigmoidal relationships between the concentration of a factor and its effect. (a) With a graded response, the effect of a factor, R, is not robust to perturbations in its concentration; perturbations of the same magnitude have effects of the same magnitude, across the range of concentrations of R (as shown in orange and blue). (b) With a sigmoidal, switch-like response, the effect is highly robust in some regions (blue), but has catastrophic loss of robustness in others (orange).
Regulatory buffering provides congruent robustness to many perturbations
In addition to stochastic fluctuations in the state of a system, it is important to consider environmental variables that are external to the system. For example, virtually all organisms experience changes in external temperature. Temperature changes perturb all components of a regulatory system. Increased temperature has two primary effects. Firstly, all rate constants increase. If these increases were proportional, then the timescale of stochastic fluctuations would decrease and hence robustness to intrinsic noise would increase. Proportionality is unlikely, however, in light of entropic considerations. Increased temperature also favors free transcription factors over those bound to DNA, and free subunits over cooperative multi-subunit structures. The net effect is complex but likely will include correlated changes in activity of transcription factors that have similar binding specificities and similar requirements for oligomerization. If transcription is primarily regulated through the presence vs. absence of a single repressor or a single activator, it will be very sensitive to changes in temperature. If, however, transcription always represents a balance between competing activation and repression reactions, then temperature could have a more proportionate effect on both these reactions. In this case, the system will be more robust to changes in temperature.
We call this balance “regulatory buffering”. Just as the pH of a buffer solution changes very little when acid or base is added, because significant concentrations of both are already present, the same principle can apply to activating and repressing factors. Examples of regulatory buffering can be identified as cases in which knockout of a critical activtaor can be at least partially rescued by knockout of a repressor [34]. Note that in biology, “to buffer” is often used as synonymous for “to increase robustness”. Our usage here is more specific and aligns more closely with the term’s original meaning in chemistry.
Regulatory buffering mechanisms are highly congruent, potentially providing robustness to stochastic and genetic perturbations in addition to macroenvironmental factors such as temperature. A prime example of regulatory buffering in a complex network is temperature compensation of the circadian clock. The core oscillator tolerates major changes in both temperature and total cellular transcriptional activity, and the mechanisms of robustness to these changes appear to be linked [35]. Regulatory buffering is also observed at higher levels of biological organization, such as the textbook example of balance between sympathetic and parasympathetic nervous systems. As with cooperativity, buffering suppresses variation only within a certain range. Perturbations that exceed the range over which a system is buffered can cause extreme changes in phenotype (Figure 2).
Graded vs. switch-like responses
Most environmental perturbations will cause less-global effects than changes in temperature. Consider a case in which a nutrient’s concentration N is the relevant environmental variable. Assume that maximal transcription c is now proportional to N rather than constant. Now different values of N give rise to different equilibrium values of R, although this effect will be mitigated to some extent if repression is cooperative. This is known as a graded response, with low environmental robustness. By contrast, if the response to N is also cooperative and hence sigmoidal (i.e., very low c up to a threshold value of N, then maximum c above the threshold), then environmental robustness is high.
The degree to which signaling is graded vs. sigmoidal can itself be regulated. For example, although the Saccharomyces cerevisiae mitogen-activated protein kinase (MAPK) cascade responds to several signals with switch-like behavior, the response to mating pheromone is graded. This difference apparently relies upon a single scaffold protein, Sterile 5 (Ste5), which binds several kinases in the cascade [36]. Thus, congruence properties can differ dramatically across superficially similar networks and superficially similar environmental variables.
Sigmoidal responses can be generated not only by cooperative multi-subunit complexes, but also by thresholds or other non-linearities arising within complex networks. For example, bistable loops yield sigmoidal responses via mutual repression by two regulators [37]. Such switch-like networks should be highly sensitive to the magnitudes of input signals within a very narrow range, but highly insensitive to the magnitudes of input signals outside this range (Figure 2). Therefore many mutations that cause large changes in input signals might have little or no phenotypic effect, so long as their effects fall outside the key range.
Robustness of more complex regulatory networks
One seemingly straightforward mechanism of robustness is simple redundancy in the form of gene duplicates [38]. Compensation by a paralog need not be passive; indeed, upregulation of a duplicate in response to loss of its paralog might be a fairly widespread mechanism of robustness [39]. A prime recent example comes from the mammalian circadian clock network, in which knockdown of the products of the Cryptochrome 1 (Cry1), Rev-erb beta or Period 1 (Per1) genes leads to increased mRNA levels of their respective paralogs [13]. In addition, the widespread nature of copy number polymorphism [40] suggests that there might be significant genetic variation in the degree of redundancy-driven robustness.
Pathways can be redundant in more complex ways that need not involve gene duplicates [41,42]. Characterization of relevant network features remains a field in rapid flux, but candidate mechanisms for promoting robustness exist. At the local network topology level these mechanisms include “motifs” such as negative feedback and feed-forward loops [43,44]. An excellent recent example involves the microRNA miR-7, which is expressed during the development of several sensory organs in Drosophila, but is dispensable under standard laboratory conditions. miR-7 interacts with major signaling pathways in several feedback and feed-forward loops. The organization of these loops is consistent with a role in dampening fluctuations so that the pathways respond only to sustained signals. Confirmation of this notion was obtained by raising miR-7 mutants under conditions of fluctuating temperature: whereas wild-type flies are robust to this treatment, mutants display variable defects in specification of sensory cell fates [45].
Global network topology features, including the extent to which a network is organized with strong central hubs, might also affect robustness [46]; however a combination of topological and dynamical properties likely will be more informative [47]. For example, the observation that wild-type alleles of most genes tend to be dominant can be explained by the intrinsic properties of flux through biochemical networks [48].
Clearly, many distinct mechanisms contribute to robustness, and each might have different consequences for congruence. Future work must address the detailed mechanisms of robustness and the perturbations to which each mechanism is robust, as well as which, if any, of these mechanisms is most likely to have been the target of selection.
Perturbation approaches to studying robustness
Substantial difficulties arise when comparing robustness measures across different qualitative and quantitative perturbations, let alone across different phenotypic traits. Nevertheless, some kind of experimental perturbation analysis is critical to the study of robustness. Biological entities whose perturbation reduces genetic and environmental robustness are referred to as phenotypic capacitors and stabilizers, respectively (Box 1). A range of different perturbations can reveal variation, including environmental changes [5–7,9] and outcrossing, as illustrated by the ubiquity of transgressive segregation, in which progeny of hybrids show more extreme phenotypes than either parental strain [49]. Mutation and epimutation are, however, the perturbations most amenable to systematic analysis leading to mechanistic insight.
There are at least three approaches to using mutation-based phenotypic capacitors and stabilizers to study robustness. One is an unbiased genome-wide screen for genetic perturbations that affect the variance of a given trait, e.g. studies assaying cellular morphology in S. cerevisiae gene-knockout strains [10,50]. Naturally occurring perturbations can also be studied genome-wide by mapping quantitative trait loci (QTLs) that specify a particular measure of robustness; this has been done in both S. cerevisiae [51,52] and A. thaliana [53,54]. One limitation of QTL-based approaches is that they can only identify genes that contribute to robustness if the parental strains have different alleles of those genes. With either genome-wide approach, the trait(s) studied can be morphological [10,52,54], or physiological [31], or can take the form of RNA and protein concentrations [49,51,53]. A unique property of a study of robustness is the interest in the variance, rather than the mean, of the trait.
A second approach is to focus on a well-characterized model developmental system under the influence of a variety of perturbations. For example, the developmental lineage of the cells comprising the vulva is invariant within and between nematode species of the genus Caenorhabditis. Perturbation of C. elegans vulva development by mutation or major environmental change revealed variation in the underlying Ras, Notch and Wnt signaling pathways [55,56]. Compensatory interactions between the pathways might contribute to the robust developmental phenotype [55,56].
Some well-studied developmental systems can be modeled sufficiently well so that a large number of perturbations can be simulated in silico. The vulval network has been modeled in this way [57], as have different levels of the segmentation hierarchy in Drosophila [58–60]. Such models can illuminate mechanisms of robustness, for example by showing that robustness of the segment polarity network can be explained largely by positive feedback of gene products on their own expression [59]. New methods of quantifying gene expression with high precision [61], or indeed at the level of individual mRNA molecules [62], promise to bring empirical studies to the level of quantitative detail that has until now been only accessible through simulation, and thereby to bridge the gap between modeling and experiment.
The third complementary approach is to focus on a single well-characterized perturbation and the variety of developmental systems that it affects. Examples include perturbation of translation termination by the yeast prion [PSI+] [63–65] (Box 3), and the heat shock protein Hsp90, which affects a stunning variety of developmental processes [8,66].
Box 3. Evolution of [PSI+]-mediated evolvability.
The yeast prion [PSI+] is a well-characterized model system for the possible evolution of capacitance-driven evolvability. The presence of [PSI+] causes elevated rates of stop codon readthrough, revealing cryptic genetic variation both directly from the translation of 3′UTRs (untranslated regions) and indirectly from events further downstream [65,85,86].
Although [PSI+] is rarely found in wild yeast strains, the capacity to produce it has been conserved over long periods of evolution [87]. No candidate function other than evolvability is currently able to explain its long-term evolutionary persistence, and a variety of mutations can eliminate it in the short-term with no apparent ill effects [88]. [PSI+] will sometimes promote faster growth [65] and adaptation [63] in the lab in a manner that depends on the genetic background. Mathematical models using realistic parameters are compatible with natural selection for evolvability driving the origin [64] and maintenance [77,80,89,90] of the ability to form [PSI+].
[PSI+] is particularly attractive as a model system as its mechanism of action can be analyzed at the molecular level. 3′UTR sequences are amenable to bioinformatic analysis. One such analysis is consistent with [PSI+]-mediated adaptation events in the wild [91], in which in-frame 3′UTR sequences have been incorporated into coding regions at a higher rate than expected from mutational bias or than observed in other species.
Which gene products make potent phenotypic capacitors and stabilizers?
Do capacitors or stabilizers share particular properties, or do they constitute an eclectic set of unrelated factors, discovered only by serendipity or systematic screening? In other words, are some types of perturbations expected to reveal more variation? For example, effectors of protein quality control, such as [PSI+] and Hsp90, are expected to act as phenotypic capacitors [67].
Regulatory network components might also be particularly prone to act as capacitors, with nearly all such knockouts revealing variation in computationally simulated networks [68]. The identification of which genes are critical for robustness might therefore shed light on the molecular biology of the regulatory process. S. cerevisiae genes whose knockouts yield the most phenotypic variation are enriched for those involved in mRNA production, protein modification and chromatin modification [10], thus lending support to the idea that stabilizers are enriched for regulators, and providing an overview of the relevant regulatory mechanisms. A similar study in another eukaryote might be expected to identify RNAi-related factors (as S. cerevisiae lacks the RNAi system).
Any mutation that decreases cooperativity will convert a threshold response into a more graded one, thus allowing previously cryptic variation to have phenotypic consequences. One example of this effect might be reducing the propensity of a transcription factor to affect local chromatin structure and hence cooperatively recruit other factors. Even a self-repressor with highly cooperative activity can produce a graded output if its activity is controlled by a titratable factor, such as a small-molecule inhibitor, as negative feedback will stabilize the expression of the repressor at levels near the midpoint of its sigmoidal activity [69]. If regulatory factors tend to have high cooperativity due to their role in switches, then the tendency for congruence and an enrichment of regulatory factors as strong capacitors could be further accentuated.
Some regulatory genes are “hubs”, interacting with a large number of other genes. Regulatory hubs, by virtue of the sheer number of their pleiotropic effects, might be expected to be important for robustness [70]. Indeed, phenotypic stabilizers in S. cerevisiae tend to be highly connected in networks of protein interaction and genetic interaction [10]. However, a study of random vs. hub gene disruptions in E. coli found that hub genes were significantly more likely than random genes to contribute to environmental robustness but less likely to contribute to mutational robustness [31]. It will be important to determine whether this lack of congruence for hubs is seen in other systems.
Evolutionary consequences of robustness
Whatever its mechanistic cause or its evolutionary origin, robustness can have profound evolutionary consequences. When mutations have little effect in a robust system, they accumulate. Should robustness break down at some point in the future, this stock of genetic variation will then be phenotypically revealed. The distribution of fitness effects of new mutations is strongly bimodal [71]. One mode represents lethal mutations, which can never contribute to future adaptations. The raw material of evolution must, by a process of elimination, come from the second mode of mutations of smaller, typically slightly deleterious effect. When a system is robust and mutational effects are masked, both types of mutation will accumulate. Should they be revealed in the future, one lethal mutant is enough to poison an individual’s entire stock of variation. However, when variation spends time in a partially cryptic state, where mutations have low but non-zero penetrance, selection on partially cryptic lethals can still be effective, while mutations of small effect become effectively neutral. This shifts the ratio between these two categories of mutant alleles such that cryptic genetic variation becomes enriched for potential adaptations through a process of pre-adaptation [72]. Cryptic genetic variation might also be enriched for alleles adaptive at the spatial and temporal margins of a population, which could represent possible future environments [73].
Robustness can also lead to pre-adaptation even in the absence of cryptic genetic variation [74–76]. Low but appreciable levels of expression of cryptic genetic variation are closely analogous to low but appreciable rates of errors in translation [76,77] and protein folding [74]. The difference is that in the first case, pre-selection occurs after mutation but before full selection, whereas in the second, pre-selection occurs even before mutation, favoring genotypes for which mutation is less likely to be lethal.
Either way, robustness leads to an increase in the probability that new heritable phenotypic variation is adaptive, and therefore increases evolvability [72–75,78] (Box 3). This is especially true for adaptations that involve more than a single mutation [72,76,77] (Box 4). Note, however, that the extent to which cryptic genetic variation contributes to adaptation in wild populations has not yet been empirically determined [79].
Box 4. Hopeful monsters.
Evolutionary capacitance, whether evolved or intrinsic, reopens the idea, introduced by Richard Goldschmidt, of “hopeful monsters” in evolution [92]. Goldschmidt was one of the early proponents of the view that some differences between species reflected discontinuities that could not be explained by the standard neodarwinian account of long-term, stepwise fixation of alleles of small effect. Instead, Goldschmidt proposed that these “unbridgeable gaps” between species resulted from mutations of large effect, such as homeotic mutations, which transform one appendage type into another. Goldschmidt termed such mutants “hopeful monsters”, evoking the possibility that, under the right circumstances, individuals with extreme phenotypes could found new lineages.
A single capacitor mutation could have a large effect by phenotypically revealing a large number of pre-existing variants, each of small effect. Adaptations mediated by a capacitor often have a complex genetic basis involving multiple loci [9,93], and pre-adaptation of cryptic genetic variation dramatically increases the probability that such combinations will be adaptive [72]. This idea reconciles apparently contradictory views as to whether adaptation always proceeds through a series of small changes, or whether “hopeful monster” mutations of large effect could sometimes also be important. Large-effect mutations that participate in adaptation might simply arise in genes encoding capacitors that normally provide robustness to many small-effect mutations at other sites.
Any increase in evolvability is not necessarily a direct product of natural selection. An alternative hypothesis simply states that robustness, limits to robustness that allow preselection, and later breakdown of robustness through major genetic or environmental perturbation are all intrinsic processes, and require no adaptive explanation.
However, some ways of breaking down robustness are more likely to lead to adaptation than others, providing material for the evolution of evolvability. For example, a capacitor might be regulated to switch between states that confer more or less robustness. If the rate of switching is under genetic control, it is expected to evolve to an optimum rate equal to the probability that switching will be adaptive [80]. Moreover, for adaptation to be effective, revealed phenotypes must persist until selection has caused them to lose their dependence on the revealing mechanism (genetic assimilation) [77,81], a persistence that can be facilitated through the evolution of epigenetic inheritance systems. The yeast prion [PSI+] is a candidate for a capacitor that might have evolved to optimize its evolvability properties (Box 3).
Concluding remarks
It is impossible to understand whole biological systems without understanding their robustness. We are starting to understand the mechanisms of robustness at the biochemical, cellular network and multicellular developmental levels. Each of these mechanisms might have a different evolutionary origin, being either an adaptation to a particular form of commonly experienced perturbation, or an intrinsic property of a system that generates a primary phenotype. Each mechanism that provides robustness to one form of perturbation might also provide congruent robustness to a set of different perturbations.
Perturbation approaches will be critical for probing the contribution of each mechanism to observed robustness (Box of Questions). They are also critical for understanding the properties of cryptic genetic variation, which, via phenotypic revelation by evolutionary capacitors, could help explain the remarkable evolvability of biological systems.
Box of Questions.
Several questions will drive future work to understand robustness mechanisms and consequences. Answering these questions is likely to involve the use of perturbation approaches and a union of theoretical, experimental and bioinformatic approaches.
- What gene products are phenotypic stabilizers and capacitors?
Use genome-wide screens to identify gene products whose perturbation causes greater phenotypic variation. - How much mechanistic congruence is there between robustness to different sources of perturbation?
Assay a large number of stabilizers and capacitors across a range of environments and genetic backgrounds. - Which network features confer robustness to which perturbations?
Subject well-characterized regulatory and developmental networks to large numbers of perturbations, and assay variation in all network components and in ultimate phenotypes. - When is genetic variation pre-adapted?
Different approaches may be needed for different categories of variation and their phenotypic expression. In all cases, model evolution mathematically under circumstances under which low levels of expression are expected. Low levels of pre-adapting expression can result from errors in transcription, translation and protein folding, as well as rare combinations of segregating alleles that occasionally exceed a threshold. The extent of this expression may vary systematically, e.g. with temperature or codon usage, allowing model predictions to be compared to data with known patterns in the extent of expression. When a newly adaptive phenotypic variant is identified, assay its previous level of penetrance. - How does pre-adapted variation alter population-genetic and quantitative-genetic inference based on experimental data?
Develop methods for incorporating pre-adapted variation into population-genetic and quantitative models, and generate predictions and tests for its effects. - To what extent does pre-adapted variation, including newly released cryptic genetic variation, contribute to adaptation?
Finding an answer to this key empirical question is likely to involve a variety of approaches and to depend on further progress on the questions above.
Acknowledgments
The authors thank Richard Boyle, Taylor Kessinger, Sasha Levy, Grant Peterson, Joshua Richardson, Jason Slepicka, Pranidhi Sood and Ben Wilson for helpful comments on the manuscript. JM was supported by the National Institutes of Health (R01 GM076041). J.M. is a Pew Scholar in the Biomedical Sciences. MLS was supported by the National Science Foundation (IOS-0642999).
Glossary
Canalization
Evolved robustness of the final outcome to perturbations occurring during a developmental process. The system need not return to its pre-perturbation state, but instead returns to the same developmental trajectory
Cooperativity
A requirement for multiple subunits or multiple events for activity. This leads to sigmoidal rather than graded responses to a signal
Cryptic genetic variation
Mutations to whose effects a system is normally robust, so that selection does not prevent their accumulation through random drift. Following a major perturbation, a system might lose its robustness so that the phenotypic effects of cryptic genetic variation are revealed
Evolutionary capacitor
A phenotypic capacitor (see below) that, by revealing cryptic genetic variation, contributes to evolvability
Evolvability
Used in this paper to mean “the capacity to generate heritable phenotypic variation that could be adaptive in some contexts” [64]. For a systematic discussion of alternative definitions, see [82]
Homeostasis
Robustness to a perturbation in the state of a system, such that it returns to its previous state
Kinetic proofreading
Requirement for multiple sequential steps, with an overall error occurring only when every step contains an error. Kinetic proofreading is critical for replication, transcription and translation
Redundancy
Robustness arising from two interchangeable copies of a functional unit such as a gene, such that one compensates for deletion of the other
Regulatory buffering
A balance between simultaneous and opposing activation and repression, leading to greater robustness to changes in either
Robustness
The property of a system to produce relatively invariant output in the presence of perturbation. Sometimes “robustness” is used interchangeably with “canalization” and “buffering”, but see definitions of these more specialized terms in this Glossary
Phenotypic capacitor
A unit whose mutation or epigenetic switching serves as a major perturbation, resulting in the reduction of genetic robustness, and thus an increase in heritable phenotypic variation
Phenotypic stabilizer
A unit whose mutation or epigenetic switching serves as a major perturbation, resulting in the reduction of robustness to non-genetic sources of variation. Note that if congruence is widespread, most phenotypic stabilizers will also be phenotypic capacitors
References
- 1.Gibson G. Decanalization and the origin of complex disease. Nat Rev Genet. 2009;10:134–140. doi: 10.1038/nrg2502. [DOI] [PubMed] [Google Scholar]
- 2.Wagner A. Robustness and evolvability in living systems. Princeton University Press; 2005. [Google Scholar]
- 3.Ideker T, et al. A new approach to decoding life: Systems biology. Annu Rev Genomics Hum Genet. 2001;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
- 4.Waddington CH. The strategy of the genes. George Allen & Unwin; 1957. [Google Scholar]
- 5.Waddington CH. Genetic assimilation of an acquired character. Evolution. 1953;7:118–126. [Google Scholar]
- 6.Waddington CH. Genetic assimilation of the bithorax phenotype. Evolution. 1956;10:1–13. [Google Scholar]
- 7.Waddington CH. Canalization of development and genetic assimilation of acquired characters. Nature. 1959;183:1654–1655. doi: 10.1038/1831654a0. [DOI] [PubMed] [Google Scholar]
- 8.Rutherford SL, Lindquist S. Hsp90 as a capacitor for morphological evolution. Nature. 1998;396:336–342. doi: 10.1038/24550. [DOI] [PubMed] [Google Scholar]
- 9.Scharloo W. Canalization - genetic and developmental aspects. Annu Rev Ecol Syst. 1991;22:65–93. [Google Scholar]
- 10.Levy SF, Siegal ML. Network Hubs Buffer Environmental Variation in Saccharomyces cerevisiae. PLoS Biology. 2008;6:e264. doi: 10.1371/journal.pbio.0060264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dworkin I, et al. Evidence that Egfr contributes to cryptic genetic variation for photoreceptor determination in natural populations of Drosophila melanogaster. Curr Biol. 2003;13:1888–1893. doi: 10.1016/j.cub.2003.10.001. [DOI] [PubMed] [Google Scholar]
- 12.Polaczyk PJ, et al. Naturally occurring genetic variation affects Drosophila photoreceptor determination. Dev Genes Evol. 1998;207:462–470. doi: 10.1007/s004270050137. [DOI] [PubMed] [Google Scholar]
- 13.Baggs JE, et al. Network Features of the Mammalian Circadian Clock. PLoS Biology. 2009;7:e52. doi: 10.1371/journal.pbio.1000052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Meiklejohn CD, Hartl DL. A single mode of canalization. Trends Ecol Evol. 2002;17:468–473. [Google Scholar]
- 15.de Visser J, et al. Perspective: Evolution and detection of genetic robustness. Evolution. 2003;57:1959–1972. doi: 10.1111/j.0014-3820.2003.tb00377.x. [DOI] [PubMed] [Google Scholar]
- 16.Kim KJ, Fernandes VM. Effects of Ploidy and Recombination on Evolution of Robustness in a Model of the Segment Polarity Network. PLoS Comput Biol. 2009;5:e1000296. doi: 10.1371/journal.pcbi.1000296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Proulx SR, Phillips PC. The opportunity for canalization and the evolution of genetic networks. Am Nat. 2005;165:147–162. doi: 10.1086/426873. [DOI] [PubMed] [Google Scholar]
- 18.Siegal ML, Bergman A. Waddington’s canalization revisited: Developmental stability and evolution. Proc Natl Acad Sci USA. 2002;99:10528–10532. doi: 10.1073/pnas.102303999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Soyer OS, et al. Simulating the evolution of signal transduction pathways. J Theor Biol. 2006;241:223–232. doi: 10.1016/j.jtbi.2005.11.024. [DOI] [PubMed] [Google Scholar]
- 20.van Nimwegen E, et al. Neutral evolution of mutational robustness. Proc Natl Acad Sci USA. 1999;96:9716–9720. doi: 10.1073/pnas.96.17.9716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wagner A. Does evolutionary plasticity evolve? Evolution. 1996;50:1008–1023. doi: 10.1111/j.1558-5646.1996.tb02342.x. [DOI] [PubMed] [Google Scholar]
- 22.Wagner A. Circuit topology and the evolution of robustness in two-gene circadian oscillators. Proc Natl Acad Sci USA. 2005;102:11775–11780. doi: 10.1073/pnas.0501094102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ancel LW, Fontana W. Plasticity, evolvability, and modularity in RNA. J Exp Zool. 2000;288:242–283. doi: 10.1002/1097-010x(20001015)288:3<242::aid-jez5>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 24.Szoll si GJ, Derenyi I. Congruent Evolution of Genetic and Environmental Robustness in Micro-RNA. Mol Biol Evol. 2009;26:867–874. doi: 10.1093/molbev/msp008. [DOI] [PubMed] [Google Scholar]
- 25.Wagner GP, et al. A population genetic theory of canalization. Evolution. 1997;51:329–347. doi: 10.1111/j.1558-5646.1997.tb02420.x. [DOI] [PubMed] [Google Scholar]
- 26.Azevedo RBR, et al. Sexual reproduction selects for robustness and negative epistasis in artificial gene networks. Nature. 2006;440:87–90. doi: 10.1038/nature04488. [DOI] [PubMed] [Google Scholar]
- 27.Libby RT, Gallant JA. The role of RNA polymerase in transcriptional fidelity. Mol Microbiol. 1991;5:999–1004. doi: 10.1111/j.1365-2958.1991.tb01872.x. [DOI] [PubMed] [Google Scholar]
- 28.Kramer EB, Farabaugh PJ. The frequency of translational misreading errors in E. coli is largely determined by tRNA competition. RNA-Publ RNA Soc. 2007;13:87–96. doi: 10.1261/rna.294907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goldsmith M, Tawfik DS. Potential role of phenotypic mutations in the evolution of protein expression and stability. Proc Natl Acad Sci USA. 2009;106:6197–6202. doi: 10.1073/pnas.0809506106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hopfield JJ. Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity. Proc Natl Acad Sci USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cooper T, et al. Effect of random and hub gene disruptions on environmental and mutational robustness in Escherichia coli. BMC Genomics. 2006;7:237. doi: 10.1186/1471-2164-7-237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Milton CC, et al. Quantitative trait symmetry independent of Hsp90 buffering: Distinct modes of genetic canalization and developmental stability. Proc Natl Acad Sci USA. 2003;100:13396–13401. doi: 10.1073/pnas.1835613100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ferrell J. Q&A: Cooperativity. Journal of Biology. 2009;8:53. doi: 10.1186/jbiol157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pierce SB, et al. Drosophila growth and development in the absence of dMyc and dMnt. Dev Biol. 2008;315:303–316. doi: 10.1016/j.ydbio.2007.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.O’Neill JS. Circadian clocks can take a few transcriptional knocks. EMBO J. 2009;28:84–85. doi: 10.1038/emboj.2008.272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Takahashi S, Pryciak PM. Membrane localization of scaffold proteins promotes graded signaling in the yeast MAP kinase cascade. Curr Biol. 2008;18:1184–1191. doi: 10.1016/j.cub.2008.07.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Losick R, Desplan C. Stochasticity and cell fate. Science. 2008;320:65–68. doi: 10.1126/science.1147888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dean EJ, et al. Pervasive and Persistent Redundancy among Duplicated Genes in Yeast. PLoS Genet. 2008;4:e1000113. doi: 10.1371/journal.pgen.1000113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kafri R, et al. Transcription control reprogramming in genetic backup circuits. Nat Genet. 2005;37:295–299. doi: 10.1038/ng1523. [DOI] [PubMed] [Google Scholar]
- 40.Redon R, et al. Global variation in copy number in the human genome. Nature. 2006;444:444–454. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ihmels J, et al. Backup without redundancy: genetic interactions reveal the cost of duplicate gene loss. Mol Syst Biol. 2007;3:11. doi: 10.1038/msb4100127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wagner A. Distributed robustness versus redundancy as causes of mutational robustness. BioEssays. 2005;27:176–188. doi: 10.1002/bies.20170. [DOI] [PubMed] [Google Scholar]
- 43.Alon U. Network motifs: theory and experimental approaches. Nat Rev Genet. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- 44.Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- 45.Li X, et al. A MicroRNA Imparts Robustness against Environmental Fluctuation during Development. Cell. 2009;137:273–282. doi: 10.1016/j.cell.2009.01.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Barabasi AL, Oltvai ZN. Network biology: Understanding the cell’s functional organization. Nat Rev Genet. 2004;5:101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- 47.Siegal ML, et al. Functional and evolutionary inference in gene networks: does topology matter? Genetica. 2007;129:83–103. doi: 10.1007/s10709-006-0035-0. [DOI] [PubMed] [Google Scholar]
- 48.Kacser H, Burns JA. The molecular basis of dominance. Genetics. 1981;97:639–666. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Brem RB, Kruglyak L. The landscape of genetic complexity across 5,700 gene expression traits in yeast. Proc Natl Acad Sci USA. 2005;102:1572–1577. doi: 10.1073/pnas.0408709102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ohya Y, et al. High-dimensional and large-scale phenotyping of yeast mutants. Proc Natl Acad Sci USA. 2005;102:19015–19020. doi: 10.1073/pnas.0509436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ansel J, et al. Cell-to-Cell Stochastic Variation in Gene Expression Is a Complex Genetic Trait. PLoS Genet. 2008;4:e1000049. doi: 10.1371/journal.pgen.1000049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Nogami S, et al. Genetic Complexity and Quantitative Trait Loci Mapping of Yeast Morphological Traits. PLoS Genet. 2007;3:e31. doi: 10.1371/journal.pgen.0030031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fu J, et al. System-wide molecular evidence for phenotypic buffering in Arabidopsis. Nat Genet. 2009;41:166–167. doi: 10.1038/ng.308. [DOI] [PubMed] [Google Scholar]
- 54.Hall MC, et al. Genetics of microenvironmental canalization in Arabidopsis thaliana. Proc Natl Acad Sci USA. 2007;104:13717–13722. doi: 10.1073/pnas.0701936104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Braendle C, Felix MA. Plasticity and Errors of a Robust Developmental System in Different Environments. Dev Cell. 2008;15:714–724. doi: 10.1016/j.devcel.2008.09.011. [DOI] [PubMed] [Google Scholar]
- 56.Milloz J, et al. Intraspecific evolution of the intercellular signaling network underlying a robust developmental system. Genes & Development. 2008;22:3064–3075. doi: 10.1101/gad.495308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fisher J, et al. Predictive Modeling of Signaling Crosstalk during C. elegans Vulval Development. PLoS Comput Biol. 2007;3:e92. doi: 10.1371/journal.pcbi.0030092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Albert R, Othmer HG. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J Theor Biol. 2003;223:1–18. doi: 10.1016/s0022-5193(03)00035-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ingolia NT. Topology and Robustness in the Drosophila Segment Polarity Network. PLoS Biology. 2004;2:e123. doi: 10.1371/journal.pbio.0020123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.von Dassow G, et al. The segment polarity network is a robust developmental module. Nature. 2000;406:188–192. doi: 10.1038/35018085. [DOI] [PubMed] [Google Scholar]
- 61.Manu, et al. Canalization of Gene Expression in the Drosophila Blastoderm by Gap Gene Cross Regulation. PLoS Biology. 2009;7:e49. doi: 10.1371/journal.pbio.1000049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Raj A, et al. Imaging individual mRNA molecules using multiple singly labeled probes. Nat Methods. 2008;5:877–879. doi: 10.1038/nmeth.1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Joseph SB, Kirkpatrick M. Effects of the [PSI+] prion on rates of adaptation in yeast. J Evol Biol. 2008;21:773–780. doi: 10.1111/j.1420-9101.2008.01515.x. [DOI] [PubMed] [Google Scholar]
- 64.Masel J, Bergman A. The evolution of the evolvability properties of the yeast prion [PSI+] Evolution. 2003;57:1498–1512. doi: 10.1111/j.0014-3820.2003.tb00358.x. [DOI] [PubMed] [Google Scholar]
- 65.True HL, Lindquist SL. A yeast prion provides a mechanism for genetic variation and phenotypic diversity. Nature. 2000;407:477–483. doi: 10.1038/35035005. [DOI] [PubMed] [Google Scholar]
- 66.Queitsch C, et al. Hsp90 as a capacitor of phenotypic variation. Nature. 2002;417:618–624. doi: 10.1038/nature749. [DOI] [PubMed] [Google Scholar]
- 67.Sangster TA, et al. Under cover: causes, effects and implications of Hsp90-mediated genetic capacitance. BioEssays. 2004;26:348–362. doi: 10.1002/bies.20020. [DOI] [PubMed] [Google Scholar]
- 68.Bergman A, Siegal ML. Evolutionary capacitance as a general feature of complex gene networks. Nature. 2003;424:549–552. doi: 10.1038/nature01765. [DOI] [PubMed] [Google Scholar]
- 69.Nevozhay D, et al. Negative autoregulation linearizes the dose-response and suppresses the heterogeneity of gene expression. Proc Natl Acad Sci USA. 2009;106:5123–5128. doi: 10.1073/pnas.0809901106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lehner B, et al. Systematic mapping of genetic interactions in Caenorhabditis elegans identifies common modifiers of diverse signaling pathways. Nat Genet. 2006;38:896–903. doi: 10.1038/ng1844. [DOI] [PubMed] [Google Scholar]
- 71.Eyre-Walker A, Keightley PD. The distribution of fitness effects of new mutations. Nat Rev Genet. 2007;8:610–618. doi: 10.1038/nrg2146. [DOI] [PubMed] [Google Scholar]
- 72.Masel J. Cryptic genetic variation is enriched for potential adaptations. Genetics. 2006;172:1985–1991. doi: 10.1534/genetics.105.051649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Eshel I, Matessi C. Canalization, genetic assimilation and preadaptation: A quantitative genetic model. Genetics. 1998;149:2119–2133. doi: 10.1093/genetics/149.4.2119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bloom JD, et al. Protein stability promotes evolvability. Proc Natl Acad Sci USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.McBride RC, et al. Robustness promotes evolvability of thermotolerance in an RNA virus. BMC Evol Biol. 2008;8:231. doi: 10.1186/1471-2148-8-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Whitehead DJ, et al. The look-ahead effect of phenotypic mutations. Biol Direct. 2008;3:18. doi: 10.1186/1745-6150-3-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Griswold CK, Masel J. Complex adaptations drive the evolution of the capacitor [PSI+], even with realistic rates of yeast sex. PLoS Genet. 2009;5:e1000517. doi: 10.1371/journal.pgen.1000517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Wagner A. Robustness and evolvability: a paradox resolved. Proc R Soc B-Biol Sci. 2008;275:91–100. doi: 10.1098/rspb.2007.1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.McGuigan K, Sgro CM. Evolutionary consequences of cryptic genetic variation. 2009;24:305–311. doi: 10.1016/j.tree.2009.02.001. [DOI] [PubMed] [Google Scholar]
- 80.King O, Masel J. The evolution of bet-hedging adaptations to rare scenarios. Theor Pop Biol. 2007;72:560–575. doi: 10.1016/j.tpb.2007.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kim Y. Rate of adaptive peak shifts with partial genetic robustness. Evolution. 2007;61:1847–1856. doi: 10.1111/j.1558-5646.2007.00166.x. [DOI] [PubMed] [Google Scholar]
- 82.Pigliucci M. Is evolvability evolvable? Nat Rev Genet. 2008;9:75–82. doi: 10.1038/nrg2278. [DOI] [PubMed] [Google Scholar]
- 83.Raj A, et al. Stochastic mRNA synthesis in mammalian cells. PLoS Biology. 2006;4:e309. doi: 10.1371/journal.pbio.0040309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Karn M, et al. Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 85.Namy O, et al. Epigenetic control of polyamines by the prion [PSI+] Nat Cell Biol. 2008;10:1069–1075. doi: 10.1038/ncb1766. [DOI] [PubMed] [Google Scholar]
- 86.Wilson MA, et al. Genetic interactions between [PSI+] and nonstop mRNA decay affect phenotypic variation. Proc Natl Acad Sci USA. 2005;102:10244–10249. doi: 10.1073/pnas.0504557102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Harrison LB, et al. Evolution of Budding Yeast Prion-determinant Sequences Across Diverse Fungi. J Mol Biol. 2007;368:273–282. doi: 10.1016/j.jmb.2007.01.070. [DOI] [PubMed] [Google Scholar]
- 88.Masel J, Griswold CK. The Strength of Selection Against the Yeast Prion [PSI+] Genetics. 2009;181:1057–1063. doi: 10.1534/genetics.108.100297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Masel J. Evolutionary capacitance may be favored by natural selection. Genetics. 2005;170:1359–1371. doi: 10.1534/genetics.105.040493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Masel J, et al. The loss of adaptive plasticity during long periods of environmental stasis. Am Nat. 2007;169:38–46. doi: 10.1086/510212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Giacomelli MG, et al. The conversion of 3′ UTRs into coding regions. Mol Biol Evol. 2007;24:457–464. doi: 10.1093/molbev/msl172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Goldschmidt R. Some Aspects of Evolution. Science. 1933;78:539–547. doi: 10.1126/science.78.2033.539. [DOI] [PubMed] [Google Scholar]
- 93.True HL, et al. Epigenetic regulation of translation reveals hidden genetic variation to produce complex traits. Nature. 2004;431:184–187. doi: 10.1038/nature02885. [DOI] [PubMed] [Google Scholar]