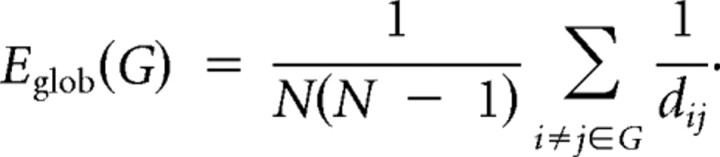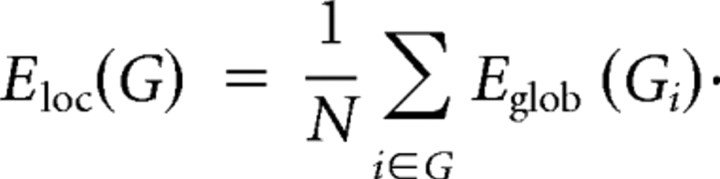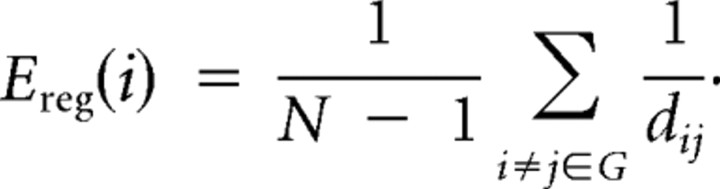Age- and Gender-Related Differences in the Cortical Anatomical Network (original) (raw)
Abstract
Neuroanatomical differences attributable to aging and gender have been well documented, and these differences may be associated with differences in behaviors and cognitive performance. However, little is known about the dynamic organization of anatomical connectivity within the cerebral cortex, which may underlie population differences in brain function. In this study, we investigated age and sex effects on the anatomical connectivity patterns of 95 normal subjects ranging in age from 19 to 85 years. Using the connectivity probability derived from diffusion magnetic resonance imaging tractography, we characterized the cerebral cortex as a weighted network of connected regions. This approach captures the underlying organization of anatomical connectivity for each subject at a regional level. Advanced graph theoretical analysis revealed that the resulting cortical networks exhibited “small-world” character (i.e., efficient information transfer both at local and global scale). In particular, the precuneus and posterior cingulate gyrus were consistently observed as centrally connected regions, independent of age and sex. Additional analysis revealed a reduction in overall cortical connectivity with age. There were also changes in the underlying network organization that resulted in decreased local efficiency, and also a shift of regional efficiency from the parietal and occipital to frontal and temporal neocortex in older brains. In addition, women showed greater overall cortical connectivity and the underlying organization of their cortical networks was more efficient, both locally and globally. There were also distributed regional differences in efficiency between sexes. Our results provide new insights into the substrates that underlie behavioral and cognitive differences in aging and sex.
Introduction
Age-related neuroanatomical changes have been well recognized and are thought to account for the cognitive declines in normal aging (Park and Reuter-Lorenz, 2009). The anatomical connectivity disturbance induced by white matter (WM) degeneration in aging would conceivably result in declines of functional integration between systems of brain areas. In particular, O'Sullivan et al. (2001) have proposed that cognitive deficits in aging emerge from the cortical “structural disconnection,” in addition to the dysfunction of specific gray matter (GM) areas.
Neuroanatomical differences between men and women have also been repeatedly observed (Sowell et al., 2007). For example, the male brain is larger but has a lower GM percentage at a population level (Leonard et al., 2008). As well as the neuroanatomical differences, sex differences in behaviors and cognitive performance have been well demonstrated. Statistically, men perform better in visuospatial perception processing, whereas women have advantages in language (Hamilton, 2008). Thus, there is the possibility that specific gender differences in cognitive performance arise from gender differences in the brain neuroanatomy (Gur et al., 1999).
To date, little is known about the differences of the organizational patterns of anatomical connectivity in aging and sex. Graph theoretical analysis provides a unique tool to reveal intrinsic attributes of the connectivity patterns in a complex network/graph and is being translated to explore brain organization (Bullmore and Sporns, 2009; He et al., 2009a). Such an anatomical network captures the structural substrate for distributed functional interactions between brain areas, forming the basis of cognitive processing (Sporns et al., 2005). Cortical network analysis across a population therefore provides a novel insight into the cortical organizational dynamics that may underlie cognitive variability in aging and sex.
Functional and morphological networks of human brains have been explored using a variety of structural and functional imaging methods (Achard et al., 2006; Bassett et al., 2006, 2008; He et al., 2007, 2008, 2009b; Stam et al., 2007). Recent advances in diffusion magnetic resonance imaging (MRI) and tractography methods have allowed for the noninvasive mapping of corticocortical anatomical connections, facilitating the construction of anatomical network at a macroscale (Hagmann et al., 2007; Iturria-Medina et al., 2008). Specifically, we have developed a population-based cortical network with diffusion tensor imaging (DTI) tractography (Gong et al., 2009). In this study, we extended the population-based unweighted network of the previous study to allow for an individual-based weighted network, using sophisticated probabilistic tractography. Importantly, the weighted network is specific to the individual, which therefore facilitates the network comparisons across the population.
To our knowledge, the present study is the first to explore the age- and sex-related dynamics of the anatomical network across a population. We focus on the network efficiency that characterizes how well the information is communicated within the cerebral cortex. Particularly, we hypothesized that the cortical network efficiency as well as the regional efficiency of selective cortical regions are different in aging and sex. Given the cognitive declines in older people, we further expected that the network efficiency would decrease with age.
Materials and Methods
Subjects
The present study included data from 95 normal subjects (males, 47; females, 48; age, 19–85 years). All subjects were recruited for the International Consortium of Brain Mapping (ICBM) dataset at Montreal Neurological Institute (MNI) and have no history of neurological and psychiatric disorders. Informed consent was obtained from each subject, and our protocol was approved by the Research Ethics Committee of the Montreal Neurological Institute and Hospital.
MRI acquisition
All scans were performed on the same Siemens Sonata 1.5 T MRI scanner. Diffusion MRI was acquired by using a single-shot echo planar imaging-based sequence with sensitivity encoding and a parallel imaging factor of 2.0: coverage of the whole brain; 2.5 mm slice thickness with no interslice gap; 60 axial slices; repetition time (TR), 8000 ms; echo time (TE), 94 ms; 30 optimal nonlinear diffusion weighting directions with b = 1000 s/mm2 (Jones et al., 1999) and five additional images without diffusion weighting (i.e., b = 0 s/mm2); average, 3; acquisition matrix, 96 × 96; field of view (FOV), 240 × 240 mm2. Three-dimensional T1-weighted images with high resolution were obtained by a three-dimensional gradient echo sequence with following parameters: 1 mm slice thickness with no interslice gap; 117 sagittal slices; TR, 22 ms; TE, 9.2 ms; flip angle, 30°; 1 average; acquisition matrix, 256 × 256; FOV, 256 × 256 mm2.
The construction of weighted cortical networks
Step 1: cortical parcellation.
In this study, we used the automated anatomical labeling (AAL) template (Tzourio-Mazoyer et al., 2002) to parcellate the entire cerebral cortex into 78 cortical regions (39 for each hemisphere), each representing a node of the cortical network. For each subject, the parcellation was conducted in the diffusion MRI native space. First, the T1-weighted image was coregistered to the _b_0 image in the diffusion MRI space using a linear transformation. The transformed T1-weighted image was then nonlinearly mapped to the T1 template of ICBM152 in MNI space (Collins et al., 1994). The resulting transformation was inversed and further applied to warp the AAL mask from MNI space to the diffusion MRI native space in which the discrete labeling values were preserved by using a nearest-neighbor interpolation method. We further refined the AAL mask by removing the WM voxels in the raw mask if they are not adjacent to GM voxels. This parcellation procedure has been applied previously (Gong et al., 2009). In this study, the linear and nonlinear registrations were implemented using local MNI registration tools embedded in CIVET pipeline (Ad-Dab'bagh et al., 2006).
Step 2: interregional connectivity probability derived from diffusion MRI probabilistic tractography.
The diffusion-weighted images were coregistered to a reference volume (i.e., _b_0 image) using an affine transformation for the correction of head motion and eddy current induced image distortion. After this preprocessing, the local probability distribution of fiber direction at each voxel was estimated (Behrens et al., 2003a). Here, we chose the computation model allowing for automatic estimation of two fiber directions within each voxel, which can significantly improve the tracking sensitivity of nondominant fiber populations in the human brain (Behrens et al., 2007).
To estimate the connectivity probability, probabilistic tractography was applied by sampling 5000 streamline fibers per voxel. For each sampled fiber, a sample direction was first drawn from the local direction distribution at the seed voxel, and then we proceeded a fixed distance of 0.5 mm along this direction to a new position and continued to draw a sample direction from the local distribution at this new position. This propagation procedure continued until the brain surface was reached or the path loops back on itself. The resulting fibers therefore account for the uncertainty in all local fiber orientations. The connectivity probability from the seed voxel i to another voxel j was defined by the number of fibers passing through voxel j divided by the total number of fibers sampled from voxel i (Behrens et al., 2007). This idea could be extended from the voxel level to the regional level. For a seed cortical region, 5000*n fibers were sampled (5000 fibers for each voxel), where n is the number of voxels in this region. The number of fibers passing through a given region divided by 5000*n is calculated as the connectivity probability from the seed region to this given region. The connectivity derived from this probabilistic tractography has been well recognized and applied in neuroscientific studies (e.g., connectivity-based parcellation) (Behrens et al., 2003b; Johansen-Berg et al., 2004).
In the present study, each cortical region was selected as the seed region and its connectivity probability to each of the other 77 regions was calculated. Notably, the probability from i to j is not necessarily equivalent to the one from j to i because of the tractography dependence on the seeding location. However, these two probabilities are highly correlated across the cerebral cortex for all subjects (the least Pearson r = 0.70, p < 10−50). Thus, we defined the undirectional connectivity probability Pij between region i and j by averaging these two probabilities. We implemented the voxel-by-voxel diffusion model estimation, probabilistic tractography, and the calculation of regional connectivity probability using FSL (http://www.fmrib.ox.ac.uk/fsl/) and in-house Matlab scripts.
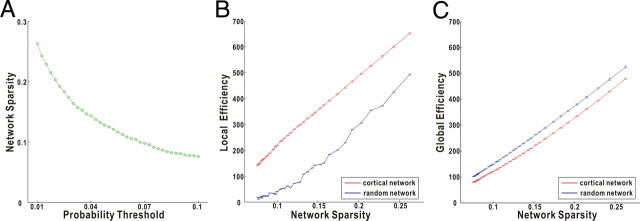
Because of the probabilistic nature of the tractography in our study, the vast majority of regional pairs were assigned a nonzero probability. The resultant nonsparse network is opposed to the classic anatomical view supporting sparse connectivity patterns within the human brain. To address this, we removed those obviously spurious connections that have extremely small probabilities by applying a thresholding. Specifically, two cortical regions were considered unconnected if the mean connectivity probability across subjects was >2 SDs below a given threshold [e.g., mean (Pij) + 2std (Pij) < threshold]. For a given threshold value, this scheme leads to an identical number and position of the connections within the cerebral cortex across subjects. Since there is no definitive choice for a single threshold, we chose a thresholding range between 0.01 and 0.1 at intervals of 0.0025 (resulting in 37 threshold intervals) (Fig. 1). This range maximizes the inclusion of real regional connections while minimizing the number of false connections and therefore is biologically plausible. The corresponding range of network sparsity (8∼27%) is similar to previous brain networks studies (Achard and Bullmore, 2007; Liu et al., 2008). As is described later, we then generated an integral summary statistic to compare the network efficiency across the entire threshold range.
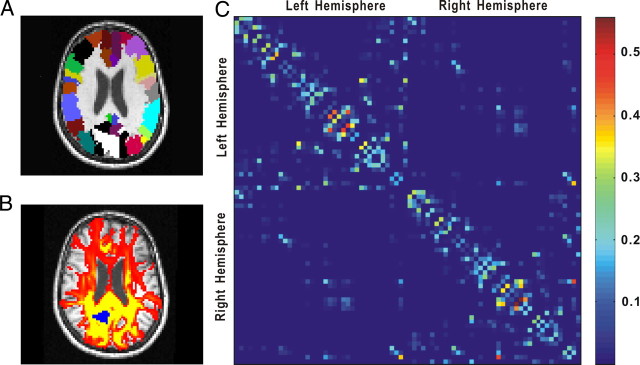
Figure 1.
The schematic image processing for the construction of the cortical weighted network. A, The AAL template masks in diffusion MRI space for one subject. Each color represents a cortical region. B, Connectivity probability using diffusion MRI tractography. The yellow–red color represents the resulting probability (yellow > red) from the left precuneus (marked as blue) to the other voxels. C, The regional probability matrix from the probabilistic tractography for the same subject. Each row or column represents one cortical region. The order of regions in the matrix is the same as in our previous study (Gong et al., 2009). For more details, see Materials and Methods.
Step 3: the weighted network/graph.
To construct a weighted network/graph, we need to define a distance/weight associated with each edge. In our case, high connectivity probability between cortical regions should be interpreted as short distances in a graph. Specifically, we computed wij = 1 − Pij as the distance/weight between cortical region i and j, as used in previous literature (Achard and Bullmore, 2007). It is important to note that the distance/weight here does not correspond to the physical length of the white matter pathway linking the cortical regions, or the physical distance between cortical regions in the real spatial space. [Notably, they are related to some extent. See supplemental Figure 1 (available at www.jneurosci.org as supplemental material).] For each subject, a 78 × 78 symmetric weighted cortical network/graph W was constructed, representing the anatomical organization of cerebral cortex.
The weighted network properties
Weighted network efficiency and small worldness.
Many real complex networks have been demonstrated to have “small-world” properties (i.e., characteristic path length L less than a regular lattice and local clustering C greater than a random graph) (Watts and Strogatz, 1998). The small-world concept was originally defined for unweighted networks, but has been recently generalized to weighted networks by introducing the concept of network efficiency (Latora and Marchiori, 2001). The local clustering C and characteristic path length L of unweighted networks conceptually correspond to the local and global efficiency of weighted networks, respectively (Latora and Marchiori, 2003). However, these two parameter sets are not computationally equivalent and therefore could provide different results.
Specifically, the inverse of the harmonic mean of shortest path length (dij) between each pair of nodes within the network is defined as the network global efficiency _E_glob as follows:
Furthermore, the local efficiency for each node could be calculated as the global efficiency of the neighborhood subgraph Gi of the node. The local efficiency represents how much the complex network is fault tolerant, indicating how well the information is communicated within the neighbors of a given node when this node is removed. The local efficiencies across all nodes within the network are further averaged to estimate the network local efficiency _E_loc as follows:
In terms of network efficiency, a small world network is the one with high _E_glob and _E_loc (i.e., very efficient both in global and local information transfer) (Latora and Marchiori, 2003). The network efficiency has a number of conceptual and technical advantages, compared with the original small-world parameters (i.e., local clustering C and characteristic path length L) (Latora and Marchiori, 2003; Achard and Bullmore, 2007). Practically, a weighted network could be categorized as small world if _E_glob is slightly less but _E_loc is much greater than a matched random network. Here, the matched random networks were generated using the random rewiring procedure described by Maslov and Sneppen (2002) that preserves the degree distribution. In particular, we retained the weight of each edge during the rewiring procedure such that the weight distribution of the entire network was preserved. For comparison, we generated 100 of these random networks per subject and calculated their mean _E_glob and _E_loc as described previously.
Weighted network cost.
The concept of network cost was originally defined by Latora and Marchiori (2003) to measure the expense for building up the connecting elements of a graph. Typically, the cost of a connection is proportional to its distance/weight, and therefore the overall cost of a graph is derived by taking the sum of distance/weight [i.e., cost = sum (wij)]. In the present study, higher values for distance/weight mean lower probability of fiber connection between the pairs of cortical nodes. Thus, a higher network cost corresponds to a lower overall connectivity within the cerebral cortex.
Of note, the network cost has an impact on the efficiency: networks with a higher cost tend to have lower network efficiency. To normalize for the cost effect, we divided the weights of a cortical network by its cost. The resultant weighted network captures the essential underlying organization of the raw weighted network since the contrast among weights remains the same but has a fixed unit cost and therefore is corrected for cost. Thus, the efficiency variability among the cost-normalized weighted networks represents the intrinsic organizational difference of the cortical networks across individuals. Specifically, in our study, the calculation of cost and the network normalization were performed after the thresholding procedure and separately for each sparsity level. Unless otherwise specified, the efficiency in this study refers to cost-normalized efficiency.
Regional efficiency.
The regional efficiency (_E_reg) for a given node i is defined as the inverse of mean harmonic shortest path length between this node and all other nodes in the network (Achard and Bullmore, 2007) as follows:
Likewise, we will focus on the regional efficiency of each node that is derived from the cost-normalized weighted network. This measure quantifies the importance of the nodes for the communication within the network and high regional efficiency implies the hub roles.
Statistical analysis
The objective of this study is to assess the relationship between the network properties (i.e., efficiency and cost) and age or sex. Since each of these network metrics has been computed for a specific sparsity range, a summary network metric is necessary. Here, we estimated the integrals of each metric curve over the range of the sparsity (∼8∼27%) as the summary metric. Such integrated metrics mathematically correspond to the areas under the metric curve (Fig. 2B,C) and have been applied in recent brain networks studies (Achard and Bullmore, 2007; Bassett et al., 2008; He et al., 2008). A general linear model (GLM) was then conducted to test age and sex effects on the network metrics. As reported previously (Leonard et al., 2008), brain size showed highly significant sex difference in our population (two-sample t test, p < 10−10). To remove the brain size effect, we included it as a covariate in the model. The interaction term between age and sex was first included in the model but showed no significant effects. Thus, this interaction term was excluded in our final model (Engqvist, 2005). The GLM analysis was first performed on the overall network metrics (_E_loc and _E_glob), and the age or sex effect was regarded as significant if the one-tailed p < 0.05. This analysis was then applied to the regional efficiency (_E_reg) of all 78 nodes respectively, and a false discovery rate (FDR) procedure was performed at a q value of 0.05 to correct for the multiple comparisons (Genovese et al., 2002).
Figure 2.
The small worldness of the cortical weighted networks. The weighted network is sparser as the probability threshold increases (A). The selected threshold range of 0.01∼0.1 approximately corresponds to a sparsity range of 8∼27%. The cortical network has much higher local efficiency than the matched random network (B) but similar global efficiency (C) over the entire sparsity range, indicating small-world character. The error bar indicates 1 SD of the network efficiency across subjects. Statistically, there are significant differences in both local and global efficiency between cortical and matched random networks, over the entire sparsity range.
Results
Small worldness of the human cortical networks
The characteristics of our weighted networks are specific to the choice of the probability threshold. If the threshold is high, the network will be more sparsely connected and have low number of edges (Fig. 2A). The selected thresholds (i.e., 0.01∼0.1) resulted in the networks over the sparsity range of 8∼27% that is similar to previous literature (Achard and Bullmore, 2007; Liu et al., 2008). All of the resulting networks are fully connected with no disconnected nodes. The local and global efficiencies of the cortical networks as well as those of the matched random networks are demonstrated as a function of the network sparsity (Fig. 2). As expected, the network efficiency increases when there are more edges in the network (i.e., less sparse). Compared with the matched random networks, the cortical networks have a much higher local efficiency but similar global efficiency over the entire range of the sparsity, suggesting small-world character of the weighted cortical networks (Fig. 2). This small-world character indicates that cortical anatomical networks of human brain, based on probabilistic tractography, are very efficient for both global and local information transfer. Specifically, high global efficiency reflects effective interactions or rapid transfers of information between and across remote cortical regions that are believed to form the basis of cognitive processes, whereas high local efficiency implies the modularized information processing among nearby regions. This underlying architecture of anatomical connectivity forms the substrates of the intrinsic small-world topology of functional or morphological networks in human brains (Stam, 2004; Achard et al., 2006; He et al., 2007).
Age effect on the cost and efficiency of cortical networks
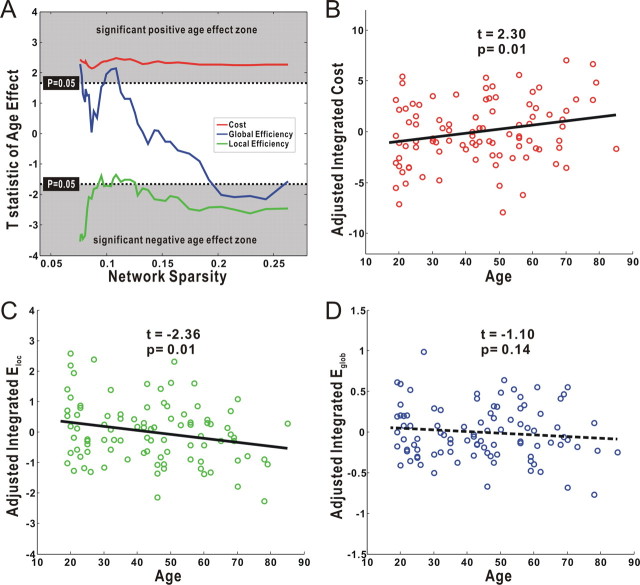
Using the GLM analysis, we found a significant age correlation (positive; t(91) > 1.66; p < 0.05) with the network cost over the entire range of the sparsity (Fig. 3A), suggesting a decline of overall cortical connectivity with age. We also observed significant age effect (negative; t(91) < −1.66; p < 0.05) on local efficiency across the majority of the sparsity range (Fig. 3A). However, there was no significant age effect on the global efficiency over a wide range. Consistently, the integrated results showed a significant age correlation with the integrated cost (positive; t(91) = 2.30; p = 0.01) (Fig. 3B) and integrated local efficiency (negative; t(91) = −2.36; p = 0.01) (Fig. 3C), but nonsignificant age effect on the integrated global efficiency (t(91) = −1.10; p = 0.14) (Fig. 3D). Notably, the measured efficiencies in the present study were obtained from the cost-normalized networks; therefore, the efficiency variability between subjects represents the intrinsic organizational difference of the cortical networks, rather than reflecting any differences in wiring cost. Interestingly, the three parameters of cortical anatomical networks (e.g., integrated cost, local efficiency, and global efficiency) were strongly correlated with one another across subjects (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).
Figure 3.
The age effect on the cost and efficiency of the cortical networks. A, Plots of the T statistic of the age effect on the network cost, local efficiency, and global efficiency as a function of the sparsity. Significant positive age effect on the cost was found over the entire sparsity. Local efficiency but not global efficiency showed significant age effect over the majority of the sparsity range. In accordance, significant age effect was observed on both the integrated network cost (B) and integrated local efficiency (C), but the integrated global efficiency showed no significant age effect (D). Notably, all results here were calculated after adjusting for the effects of brain size and sex, using a general linear model.
Sex effect on the cost and efficiency of cortical networks
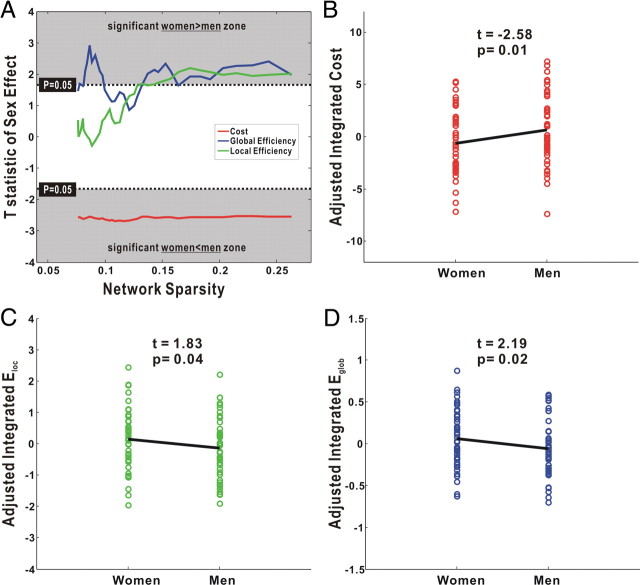
As shown in Figure 4A, the GLM analysis demonstrated a significant sex difference (women < men; _t_(91) < −1.66; _p_ < 0.05) in the network cost over the entire range of sparsity, indicating a higher overall connectivity in women. In addition, significant sex effects (women > men; t(91) > 1.66; p < 0.05) were found for both local and global efficiency over a wide range of sparsity (Fig. 4_A_). There were significant sex differences in the three integrated metrics: integrated cost (women < men; _t_(91) = −2.58; _p_ = 0.01) (Fig. 4_B_), integrated local efficiency (women > men; t(91) = 1.83; p = 0.04) (Fig. 4C) and integrated global efficiency (women > men; t(91) = 2.19; p = 0.02) (Fig. 4D). Notably, these results were obtained after factoring out the effect of brain size. Thus, it is unlikely that the sex differences in the cortical networks result from their difference in brain size (two-sample t test, p < 10−10).
Figure 4.
The sex effect on the cost and efficiency of the cortical networks. A, Plots of the T statistic of sex effect on the network cost, local efficiency, and global efficiency as a function of the sparsity. A significant women less than men effect was found on the cost over the entire sparsity. Both local efficiency and global efficiency showed sex effect over a wide range of the sparsity. In accordance, the integrated network cost (B), integrated local efficiency (C), and integrated global efficiency (D) all showed significant sex effect. Notably, all results here were calculated after adjusting for the effects of brain size and age, using a general linear model.
Regional efficiency of individual cortical nodes
The regional efficiency of each node measures its connectivity to all other nodes of the network. Likewise, the regional efficiency across all nodes increases when the network is less sparse (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). In this study, we specifically reported the results of the integrated regional efficiency for each node in the network. The regional efficiency specific to the sparsity showed similar relationships with the age and sex factors.
Centrally connected regions across population
High regional efficiency implies hub/core roles in a network (Achard and Bullmore, 2007). The 78 regional nodes were ranked in descending order of regional efficiency in Figure 5. Notably, the bilateral precuneus (PUN) and right posterior cingulate gyrus (PCG) consistently have the highest regional efficiency, regardless of age and sex. This observation is quite compatible with a recent study from Hagmann et al. (2008), who identified a structural core within posterior medial and parietal cortex in the cortical anatomical network (Hagmann et al., 2008). Moreover, the precuneus has been ranked as the most pivotal region in the population-based human cortical anatomical network in our previous study (Gong et al., 2009), and an equivalent region to the precuneus (i.e., area 7) was also observed as a hub in the macaque cortical network (Sporns et al., 2007). Furthermore, the precuneus/posterior cingulate cortex plays a pivotal role in the default mode network that represents intrinsic brain activity (Fransson and Marrelec, 2008).
Figure 5.
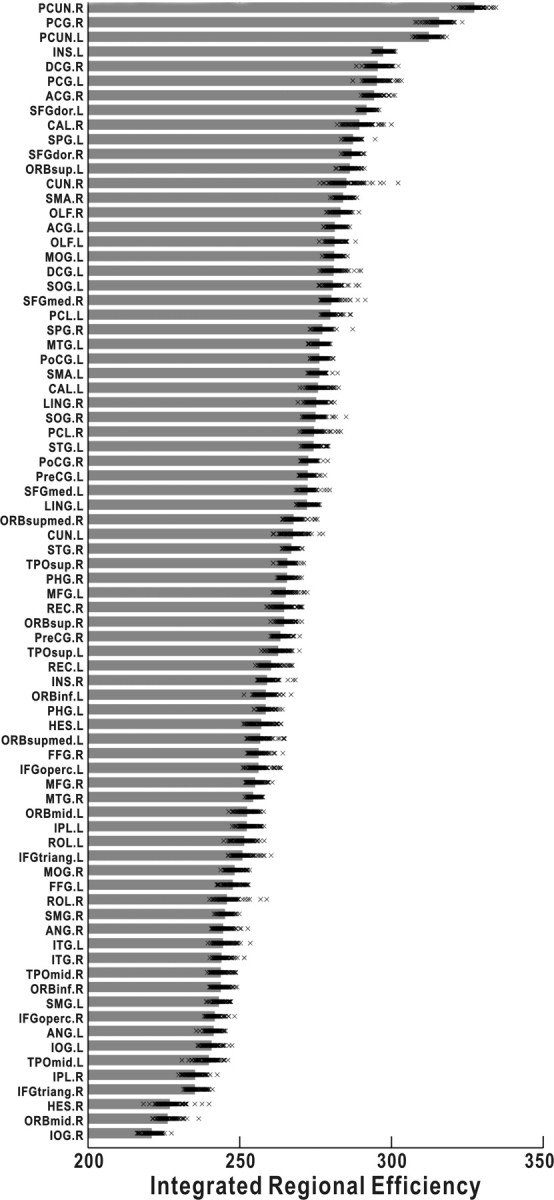
The integrated regional efficiency for all cortical regions. The cortical regions were ranked in the order of descending mean integrated regional efficiency across subjects. The gray bar represents the mean regional efficiency and each x mark corresponds to one subject. As shown, the PUN and PCG always have the highest regional efficiencies, regardless age and sex. For the abbreviations of cortical regions, see supplemental Table 1 (available at www.jneurosci.org as supplemental material).
Age effect on regional efficiency
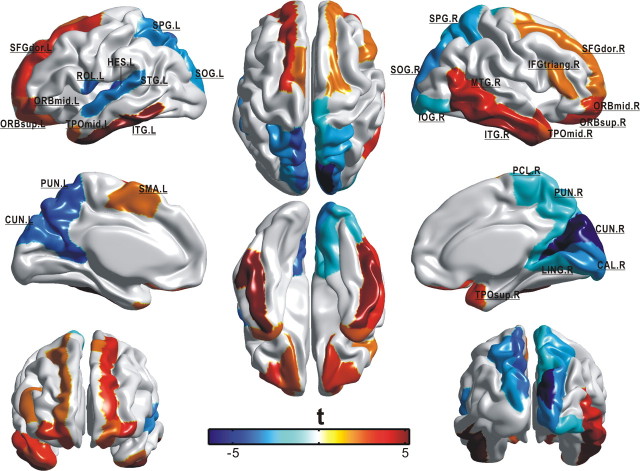
Both negative and positive age effects (p < 0.05, FDR corrected) were found on the integrated regional efficiency in selective cortical regions across the cerebral cortex (29 in total) (Table 1). The majority of these identified regions were distributed in association cortex (20 of 29), supporting the view that age-related changes are mainly characteristic of association cortex as opposed to primary cortex (Albert and Knoefel, 1994). It is noted that the negative age effect was mainly localized to the regions in the parietal and occipital neocortex (12 of 15), whereas the positive age effect concentrated on the regions in the frontal and temporal cortex (Table 1, Fig. 6). Among these regions, four with negative age effect (the precuneus, superior parietal gyrus, cuneus, and superior occipital gyrus) and five with positive age effect (the orbital middle frontal gyrus, orbital superior frontal gyrus, dorsolateral superior frontal gyrus, inferior temporal gyrus, and middle temporal pole) appeared in a bilaterally symmetric manner. Particularly, prominent reduction of regional efficiency in aging was observed in our identified hub regions (i.e., the bilateral precuneus).
Table 1.
Cortical regions showing significant age effect (p < 0.05, FDR corrected) on the integrated regional efficiency (_E_reg)
| Age effect on _E_reg | Regions | Class | T statistic |
|---|---|---|---|
| Negative effect | |||
| Frontal | ROL.L | Association | −3.58 |
| Temporal | HES.L | Primary | −4.29 |
| STG.L | Association | −3.18 | |
| Parietal | PCUN.L | Association | −3.93 |
| SPG.L | Association | −3.11 | |
| SPG.R | Association | −2.81 | |
| PCL.R | Association | −2.33 | |
| PCUN.R | Association | −2.32 | |
| Occipital | CUN.R | Association | −6.40 |
| CUN.L | Association | −3.65 | |
| SOG.R | Association | −3.20 | |
| CAL.R | Primary | −3.14 | |
| SOG.L | Association | −2.86 | |
| LING.R | Association | −2.42 | |
| IOG.R | Association | −2.39 | |
| Positive effect | |||
| Frontal | ORBmid.L | Paralimbic | 3.76 |
| SFGdor.L | Association | 3.49 | |
| ORBsup.R | Paralimbic | 3.20 | |
| ORBmid.R | Paralimbic | 3.09 | |
| SMA.L | Association | 2.29 | |
| ORBsup.L | Paralimbic | 2.59 | |
| IFGtriang.R | Association | 2.25 | |
| SFGdor.R | Association | 2.24 | |
| Temporal | ITG.L | Association | 5.24 |
| ITG.R | Association | 4.72 | |
| MTG.R | Association | 3.47 | |
| TPOsup.R | Paralimbic | 3.21 | |
| TPOmid.R | Paralimbic | 2.55 | |
| TPOmid.L | Paralimbic | 2.45 |
Figure 6.
The spatial distribution of cortical regions showing significant age effect (p < 0.05, FDR corrected) on the integrated regional efficiency. The color represents t statistic of the age effect that was calculated from the general linear model. Each identified region was marked out. Notably, negative age effect was mainly distributed in the parietal and occipital cortex (12 of 15), whereas the positive age effect was localized only in the frontal and temporal cortex. Note that nine regions (the PUN, SPG, CUN, SOG, ORBmid, ORBsup, SFGdor, ITG, and TPOmid) appeared in a bilateral manner. For the abbreviations of cortical regions, see supplemental Table 1 (available at www.jneurosci.org as supplemental material).
Sex effect on regional efficiency
Statistical analysis revealed significant sex difference (p < 0.05, FDR corrected) of the integrated regional efficiency in eight regions predominantly in association cortex (seven of eight). Six of them (left Heschl's gyrus, superior temporal gyrus, superior parietal gyrus, inferior parietal gyrus, insula, and right fusiform gyrus) have higher efficiency in women, but the other two (right rolandic operculum and triangular inferior frontal gyrus) showed higher efficiency in men (Table 2). These regions are predominantly in association cortex, supporting the view that sex cognitive differences mainly relate to higher level brain functions (Hamilton, 2008).
Table 2.
Cortical regions showing significant sex effect (p < 0.05, FDR corrected) on the integrated regional efficiency
| Sex effect on _E_reg | Region | Class | T statistic |
|---|---|---|---|
| Women > men | |||
| Temporal | HES.L | Primary | 3.07 |
| STG.L | Association | 2.65 | |
| Parietal | SPG.L | Association | 2.97 |
| IPL.L | Association | 2.88 | |
| Occipital | FFG.R | Association | 2.97 |
| Insula | INS.L | Association | 3.34 |
| Women < men | |||
| Frontal | ROL.R | Association | −3.34 |
| IFGtriang.R | Association | −2.85 |
Discussion
In this study, probabilistic tractography based on diffusion MRI was used to construct weighted networks that represent the anatomical connectivity organization of the human cerebral cortex at a regional level. Additional network comparison among individuals revealed significant age and sex effect on the network cost, network efficiency, and regional efficiency in selective cortical regions.
Cortical networks are less economical in aging
Cost is a graph-theoretical concept derived by taking the sum of the distance/weight within a graph (Latora and Marchiori, 2003). In our study, higher values for distance/weight mean lower probability of fiber connection between the pairs of cortical nodes. As shown in Figure 3, the network cost increases with age, corresponding to a reduction in overall cortical connectivity. The observation that the aging network becomes less connected (costs more) is expected, as previous studies have consistently demonstrated extensive WM degeneration in aging brains (Head et al., 2004; Pfefferbaum et al., 2005; Salat et al., 2005). The disruption of anatomical connectivity in aging may impair the functional integration between areas, eventually leading to selective cognitive declines. In particular, Andrews-Hanna et al. (2007) have demonstrated a direct relationship between the anatomical connectivity and cognitive score in aging people, strongly supporting the theory that cognitive deficit in aging arises from the “disconnection” of brain areas, in addition to selective GM dysfunction (O'Sullivan et al., 2001).
The underlying organization of cortical network is adapted in aging
Although the cortical networks retained small worldness regardless of age, the underlying organization of the cortical network was adapted, resulting in a decreased overall local efficiency but a preserved overall global efficiency in older people (Fig. 3). This is compatible with a recent finding showing conserved modular organization of the functional network but significant differences in composition and topological roles of specific modules in the aging brain (Meunier et al., 2009). Essentially, the network organizational change results from the differential decline and relative preservation of specific regional anatomical connections in aging brain. This interpretation is supported by recent DTI findings showing an approximately anterior-to-posterior gradient of WM degeneration in aging people (Head et al., 2004; Salat et al., 2005). Particularly, our findings are consistent with a recent functional network study showing reduced network efficiency of functional networks in normal aging using resting-state functional MRI techniques (Achard and Bullmore, 2007). The decreased local efficiency of cortical anatomical networks found in this study may provide the underlying substrate for the functional disturbance and cognitive deficit in aging.
Despite the preservation of overall global efficiency in aging, the regional efficiency showed extensive changes across the cerebral cortex in aging. As shown in Table 1 and Figure 6, reduced efficiency was found in 15 cortical regions predominantly in the parietal and occipital neocortex. In contrast, 14 regions localized to frontal and temporal cortex showed increased efficiency, indicating a putative compensation mechanism of cortical network reorganization in aging (Park and Reuter-Lorenz, 2009). Specifically, several regions (e.g., the Heschl's gyrus and superior temporal gyrus) consistently exhibited a reduction of regional efficiency both in our anatomical network and in the functional network (Achard and Bullmore, 2007). Of note, previous functional neuroimaging studies of aging have repeatedly revealed reduced occipital activity coupled with an elevation in frontal activity across a variety of cognitive functions. This phenomena was referred to as PASA (posterior–anterior shift in aging) (Davis et al., 2008). Likewise, the regional efficiency changes exhibited a clear shift from occipital and parietal to frontal and temporal cortices, possibly accounting for the shift pattern of functional reorganization in older people. In addition, our results suggested no direct relationship between the neuroanatomical deficit and the efficiency changes, at the regional level. For example, previous studies reported preferential age-related atrophy in the prefrontal cortex (Raz et al., 2005), whereas, in the present study, increased regional efficiency was found in this area. Conceptually, regional efficiency is based on the cortical connectivity pattern and therefore biologically depends on the axonal properties across the cerebral cortex. In contrast, regional neuroanatomical deficit (e.g., atrophy) typically reflects locally neuronal body declines in GM. Thus, it is unexpected to predict the regional efficiency change directly from its neuroanatomical deficit. However, we cannot rule out the possibility that specific neuroanatomical deficit is associated with the regional efficiency in some way.
Cortical networks are less economical in men
In addition to the age-related network changes, we found the cortical network is less economical (costs more) in men than in women, corresponding to a higher overall cortical connectivity of women. In accordance with our findings, previous studies have suggested a female advantage in cortical anatomical connectivity. For instance, a larger corpus callosum in women, after adjusting for the brain size, was repeatedly found (Allen et al., 2003; Leonard et al., 2008), suggesting greater interhemispheric connectivity and possibly accounting for the more bilateral pattern in language-related activation of women (Baxter et al., 2003). Recently, a DTI study revealed greater fractional anisotropy and leftward asymmetry of frontal lobe WM in women, indicating either denser or better packed axons in that area (Szeszko et al., 2003).
The underlying organization of cortical network is different between men and women
The present study also revealed sex differences in the underlying organization of the cortical networks. Specifically, women showed both higher overall global and local efficiency (Fig. 4). Using MRI, Gur et al. (1999) found a stronger association between cognitive performance and WM volume in women, and have therefore suggested the possibility that women may make more efficient use of the available WM. Using network efficiency indices, our study provides direct evidence for this hypothesis. However, the higher percentage of GM in women represents a computational advantage that requires effective signal transfer (Gur et al., 1999; Leonard et al., 2008). This requirement may be achieved by the more optimal anatomical organization coupled with the stronger cortical connectivity in women (Fig. 4). However, the disadvantage of overall anatomical connectivity pattern does not necessarily mean men's worse performance for all cognitive tasks. The submodular organization for specific functional domains may exhibit optimized patterns in men, leading to their better performance in corresponding cognitive tasks. In addition, other mechanisms such as area-specific GM differences are likely invoked to account for the sex differences in particular cognitive performance (Hamilton, 2008).
Likewise, the sex effect was further localized in terms of regional efficiency (Table 2). Of note, the sex differences in regional efficiency exhibited a clear hemispheric asymmetry: women had higher efficiency in five left-hemispheric and one right-hemispheric regions, but men had higher efficiency only in two right-hemispheric regions. Given that the left hemisphere is generally dominant in verbal and the right in spatial processing (Springer and Deutsch, 1997), this asymmetry of regional efficiency may underlie women's advantageous verbal processing and men's advantageous spatial processing (Hamilton, 2008). In particular, two well recognized language-related regions (i.e., left superior temporal gyrus and Heschl's gyrus) showed greater efficiency in women, which may directly contribute to the previously observed female advantage in language (Hamilton, 2008). Unexpectedly, we did not observe men's higher efficiency in visuospatial processing regions (e.g., right superior parietal gyrus), as has been previously reported (Zarahn et al., 2000). The visuospatial performance has shown a positive correlation with rightward laterality of related brain regions (Everts et al., 2009). Interestingly, we found less efficiency of left superior parietal gyrus in men, indicating a rightward laterality of this region and possibly underlying the men's advantage in visuospatial function. The sex differences in regional efficiency provide a new insight into our understanding of the functional and cognitive specificity between women and men.
Methodological issues
Several methodological issues need to be addressed. First, the probabilistic tractography used in our study has showed advantages in tracking specific WM tracts relating to fiber crossing (Behrens et al., 2007). However, it remains possible that we missed some biological connections or included spurious connections in the cortical network even after the thresholding procedure. Second, we confined the weighted network to the cerebral cortical system in current study. The deep GM structures such as the striatum and thalamus will be included in future. Third, the present study included only anatomical network analysis using diffusion MRI. It would be intriguing in future to explore how the anatomical network changes in aging are associated with the alteration of morphological/functional brain networks, by combining structural MRI and functional MRI. Finally, the age-related cortical network changes in our study were found using cross-sectional data and therefore could be influenced by potential cohort effects. The longitudinal network dynamics need to be examined in the future.
Conclusion
Our study revealed significant age- and sex-related effects on the underlying organization of the cortical anatomical network, as well as on the overall anatomical connectivity within the cerebral cortex. These findings provide new insights into the substrate that underlies the behavioral and cognitive variability in aging and sex. The present study, for the first time, reveals the dynamics of the cortical anatomical connectivity patterns across a population and provides a new way to evaluate the impairment of anatomical connectivity patterns for specific brain disorders.
Footnotes
This work was conducted as part of the International Consortium for Brain Mapping, funded by Consortium Grant NIH9P01EB001955-11 (principal investigator, John Mazziotta, University of California, Los Angeles, Los Angeles, CA). We thank Oliver Lyttelton for his editing of this manuscript.
References
- Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput Biol. 2007;3:e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ad-Dab'bagh Y, Lyttelton O, Muehlboeck J-S, Lepage C, Einarson D, Mok K, Ivanov O, Vincent RD, Lerch J, Fombonne E, Evans AC. The CIVET image-processing environment: a fully automated comprehensive pipeline for anatomical neuroimaging research. 12th Annual Meeting of the Organization for Human Brain Mapping; June; Florence, Italy. 2006. Paper presented at. [Google Scholar]
- Albert ML, Knoefel JE. Clinical neurology of aging. Ed 2. New York: Oxford UP; 1994. [Google Scholar]
- Allen JS, Damasio H, Grabowski TJ, Bruss J, Zhang W. Sexual dimorphism and asymmetries in the gray-white composition of the human cerebrum. Neuroimage. 2003;18:880–894. doi: 10.1016/s1053-8119(03)00034-x. [DOI] [PubMed] [Google Scholar]
- Andrews-Hanna JR, Snyder AZ, Vincent JL, Lustig C, Head D, Raichle ME, Buckner RL. Disruption of large-scale brain systems in advanced aging. Neuron. 2007;56:924–935. doi: 10.1016/j.neuron.2007.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Meyer-Lindenberg A, Achard S, Duke T, Bullmore E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc Natl Acad Sci U S A. 2006;103:19518–19523. doi: 10.1073/pnas.0606005103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, Meyer-Lindenberg A. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28:9239–9248. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baxter LC, Saykin AJ, Flashman LA, Johnson SC, Guerin SJ, Babcock DR, Wishart HA. Sex differences in semantic language processing: a functional MRI study. Brain Lang. 2003;84:264–272. doi: 10.1016/s0093-934x(02)00549-7. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. 2003a;50:1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Johansen-Berg H, Woolrich MW, Smith SM, Wheeler-Kingshott CA, Boulby PA, Barker GJ, Sillery EL, Sheehan K, Ciccarelli O, Thompson AJ, Brady JM, Matthews PM. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat Neurosci. 2003b;6:750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Berg HJ, Jbabdi S, Rushworth MF, Woolrich MW. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage. 2007;34:144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Collins DL, Neelin P, Peters TM, Evans AC. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J Comput Assist Tomogr. 1994;18:192–205. [PubMed] [Google Scholar]
- Davis SW, Dennis NA, Daselaar SM, Fleck MS, Cabeza R. Que PASA? The posterior-anterior shift in aging. Cereb Cortex. 2008;18:1201–1209. doi: 10.1093/cercor/bhm155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engqvist L. The mistreatment of covariate interaction terms in linear model analyses of behavioural and evolutionary ecology studies. Anim Behav. 2005;70:967–971. [Google Scholar]
- Everts R, Lidzba K, Wilke M, Kiefer C, Mordasini M, Schroth G, Perrig W, Steinlin M. Strengthening of laterality of verbal and visuospatial functions during childhood and adolescence. Hum Brain Mapp. 2009;30:473–483. doi: 10.1002/hbm.20523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P, Marrelec G. The precuneus/posterior cingulate cortex plays a pivotal role in the default mode network: evidence from a partial correlation network analysis. Neuroimage. 2008;42:1178–1184. doi: 10.1016/j.neuroimage.2008.05.059. [DOI] [PubMed] [Google Scholar]
- Genovese CR, Lazar NA, Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb Cortex. 2009;19:524–536. doi: 10.1093/cercor/bhn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gur RC, Turetsky BI, Matsui M, Yan M, Bilker W, Hughett P, Gur RE. Sex differences in brain gray and white matter in healthy young adults: correlations with cognitive performance. J Neurosci. 1999;19:4065–4072. doi: 10.1523/JNEUROSCI.19-10-04065.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Kurant M, Gigandet X, Thiran P, Wedeen VJ, Meuli R, Thiran JP. Mapping human whole-brain structural networks with diffusion MRI. PLoS One. 2007;2:e597. doi: 10.1371/journal.pone.0000597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6:e159. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton C. Cognition and sex differences. Basingstoke, UK; New York: Palgrave Macmillan; 2008. [Google Scholar]
- He Y, Chen ZJ, Evans AC. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 2007;17:2407–2419. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- He Y, Chen Z, Evans A. Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer's disease. J Neurosci. 2008;28:4756–4766. doi: 10.1523/JNEUROSCI.0141-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Gong G, Evans AC. Neuronal networks in Alzheimer's disease. Neuroscientist. 2009a;15:333–350. doi: 10.1177/1073858409334423. [DOI] [PubMed] [Google Scholar]
- He Y, Dagher A, Chen Z, Charil A, Lerch J, Zijdenbos A, Worsley K, Evans A. White matter lesions impair small-world topological efficiency in structural cortical networks in multiple sclerosis. Brain. 2009b doi: 10.1093/brain/awp089. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Head D, Buckner RL, Shimony JS, Williams LE, Akbudak E, Conturo TE, McAvoy M, Morris JC, Snyder AZ. Differential vulnerability of anterior white matter in nondemented aging with minimal acceleration in dementia of the Alzheimer type: evidence from diffusion tensor imaging. Cereb Cortex. 2004;14:410–423. doi: 10.1093/cercor/bhh003. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y, Sotero RC, Canales-Rodríguez EJ, Alemán-Gómez Y, Melie-García L. Studying the human brain anatomical network via diffusion-weighted MRI and graph theory. Neuroimage. 2008;40:1064–1076. doi: 10.1016/j.neuroimage.2007.10.060. [DOI] [PubMed] [Google Scholar]
- Johansen-Berg H, Behrens TE, Robson MD, Drobnjak I, Rushworth MF, Brady JM, Smith SM, Higham DJ, Matthews PM. Changes in connectivity profiles define functionally distinct regions in human medial frontal cortex. Proc Natl Acad Sci U S A. 2004;101:13335–13340. doi: 10.1073/pnas.0403743101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
- Latora V, Marchiori M. Efficient behavior of small-world networks. Phys Rev Lett. 2001;87:198701. doi: 10.1103/PhysRevLett.87.198701. [DOI] [PubMed] [Google Scholar]
- Latora V, Marchiori M. Economic small-world behavior in weighted networks. Eur Phys J B. 2003;32:249–263. [Google Scholar]
- Leonard CM, Towler S, Welcome S, Halderman LK, Otto R, Eckert MA, Chiarello C. Size matters: cerebral volume influences sex differences in neuroanatomy. Cereb Cortex. 2008;18:2920–2931. doi: 10.1093/cercor/bhn052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T. Disrupted small-world networks in schizophrenia. Brain. 2008;131:945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
- Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103. [DOI] [PubMed] [Google Scholar]
- Meunier D, Achard S, Morcom A, Bullmore E. Age-related changes in modular organization of human brain functional networks. Neuroimage. 2009;44:715–723. doi: 10.1016/j.neuroimage.2008.09.062. [DOI] [PubMed] [Google Scholar]
- O'Sullivan M, Jones DK, Summers PE, Morris RG, Williams SC, Markus HS. Evidence for cortical “disconnection” as a mechanism of age-related cognitive decline. Neurology. 2001;57:632–638. doi: 10.1212/wnl.57.4.632. [DOI] [PubMed] [Google Scholar]
- Park DC, Reuter-Lorenz P. The adaptive brain: aging and neurocognitive scaffolding. Annu Rev Psychol. 2009;60:173–196. doi: 10.1146/annurev.psych.59.103006.093656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfefferbaum A, Adalsteinsson E, Sullivan EV. Frontal circuitry degradation marks healthy adult aging: evidence from diffusion tensor imaging. Neuroimage. 2005;26:891–899. doi: 10.1016/j.neuroimage.2005.02.034. [DOI] [PubMed] [Google Scholar]
- Raz N, Lindenberger U, Rodrigue KM, Kennedy KM, Head D, Williamson A, Dahle C, Gerstorf D, Acker JD. Regional brain changes in aging healthy adults: general trends, individual differences and modifiers. Cereb Cortex. 2005;15:1676–1689. doi: 10.1093/cercor/bhi044. [DOI] [PubMed] [Google Scholar]
- Salat DH, Tuch DS, Greve DN, van der Kouwe AJ, Hevelone ND, Zaleta AK, Rosen BR, Fischl B, Corkin S, Rosas HD, Dale AM. Age-related alterations in white matter microstructure measured by diffusion tensor imaging. Neurobiol Aging. 2005;26:1215–1227. doi: 10.1016/j.neurobiolaging.2004.09.017. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Kan E, Woods RP, Yoshii J, Bansal R, Xu D, Zhu H, Thompson PM, Toga AW. Sex differences in cortical thickness mapped in 176 healthy individuals between 7 and 87 years of age. Cereb Cortex. 2007;17:1550–1560. doi: 10.1093/cercor/bhl066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kötter R. The human connectome: a structural description of the human brain. PLoS Comput Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Honey CJ, Kötter R. Identification and classification of hubs in brain networks. PLoS One. 2007;2:e1049. doi: 10.1371/journal.pone.0001049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springer SP, Deutsch G. Left brain, right brain: perspectives on cognitive neuroscience. Ed 5. New York: Freeman; 1997. [Google Scholar]
- Stam CJ. Functional connectivity patterns of human magnetoencephalographic recordings: a “small-world” network? Neurosci Lett. 2004;355:25–28. doi: 10.1016/j.neulet.2003.10.063. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. Small-world networks and functional connectivity in Alzheimer's disease. Cereb Cortex. 2007;17:92–99. doi: 10.1093/cercor/bhj127. [DOI] [PubMed] [Google Scholar]
- Szeszko PR, Vogel J, Ashtari M, Malhotra AK, Bates J, Kane JM, Bilder RM, Frevert T, Lim K. Sex differences in frontal lobe white matter microstructure: a DTI study. Neuroreport. 2003;14:2469–2473. doi: 10.1097/00001756-200312190-00035. [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Aguirre G, D'Esposito M. Replication and further studies of neural mechanisms of spatial mnemonic processing in humans. Brain Res Cogn Brain Res. 2000;9:1–17. doi: 10.1016/s0926-6410(99)00033-6. [DOI] [PubMed] [Google Scholar]