The incoherent feedforward loop can provide fold-change detection in gene regulation (original) (raw)
. Author manuscript; available in PMC: 2010 Dec 11.
SUMMARY
Many sensory systems, such as vision and hearing, show a response that is proportional to the fold-change in the stimulus relative to the background, a feature related to Weber’s law. Recent experiments suggest such a fold-change detection feature in signaling systems in cells: a response that depends on the fold-change in the input signal, and not on its absolute level (Cohen-Saidon et al., in press; Goentoro and Kirschner, submitted; both in this volume). It is therefore of interest to find molecular mechanisms of gene regulation that can provide such fold-change detection. Here we demonstrate theoretically that fold-change detection can be generated by one of the most common network motifs in transcription networks, the incoherent feedforward loop (I1-FFL), in which an activator regulates both a gene and a repressor of the gene.The fold-change detection feature of the I1-FFL applies to the entire shape of the response, including its amplitude and duration, and is valid for a wide range of biochemical parameters.
INTRODUCTION
Gene regulation networks are composed of a small set of recurring interaction patterns called network motifs (Milo et al., 2002; Shen-Orr et al., 2002). Each motif has been experimentally found to perform specific dynamical functions (reviewed in Alon, 2007). In cases studied so far, these motifs seem to preserve their autonomous functions even in their natural contexts, wired into the regulatory networks of the cell.
One of the most common network motifs is the incoherent type-1 feedforward loop (I1-FFL), which appears hundreds of times in bacteria (Eichenberger et al., 2004; Mangan et al., 2006; Milo et al., 2002) and yeast (Lee et al., 2002; Milo et al., 2002). In animal cells, the I1-FFL has been discovered in the transcriptional networks of human embryonic stem cell (Boyer et al., 2005) and hematopoietic stem stem cell (Swiers et al., 2006) and downstream of the Notch signaling pathway (Krejci et al., 2009).
An I1-FFL is a regulatory pattern in which an activator X controls a target gene Z, and also activates a repressor of that target gene, Y. The repressor Y may be a transcription factor, or microRNAs, such as found in c-Myc/E2F1 regulation (O’Donnell et al., 2005) and eye patterning in Drosophila (Li et al., 2009). Previous studies have demonstrated that the I1-FFL can generate a temporal pulse of Z response (Basu et al., 2004; Mangan and Alon, 2003; Mangan et al., 2006), accelerate the response time of Z (Mangan and Alon, 2003; Mangan et al., 2006), and act as a band-pass amplitude filter that provides maximal Z response for intermediate levels of X activity (Entus et al., 2007; Kaplan et al., 2008; Kim et al., 2008).
Here we demonstrate a new function for the I1-FFL: the I1-FFL can generate a response to fold-changes in the input signal, rather than absolute levels. This fold-change detection property means that the dynamics of the output (amplitude and duration of the transcription of gene Z) depends only on the relative change in input signal, not on its absolute levels. Figure 1 provides an example: a signal that changes from, say, level 1 to 2 provides exactly the same output as a signal that goes from 2 to 4, since both represent a 2-fold increase in input. In contrast, a non-fold-detection system results in different outputs for these two step stimuli.
Figure 1.
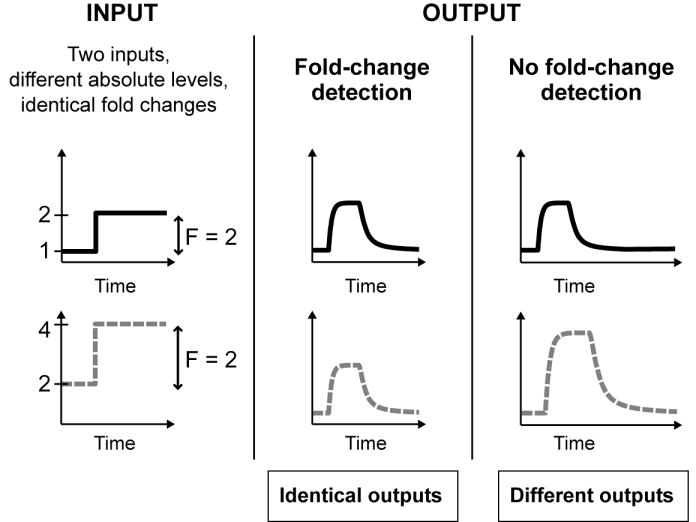
Fold-change detection means that the dynamics of the output (amplitude and duration of the transcription of gene Z) depends only on the fold-changes in the level of the input signal, not on the absolute levels of the input signal.
Although known in physiology for 150 years, evidence for such fold-change responsiveness was only recently demonstrated in mammalian signaling systems. In the Wnt signaling pathway, Goentoro and Kirschner (submitted, this volume) present evidence that gene expression and the embryonic phenotype appear to correlate with fold-changes, rather than absolute levels, of the activator β-catenin. In the ERK signaling system, Cohen-Saidon and colleagues (in press, this volume) present evidence that fold-changes in the doubly phosphorylated ERK (the activator X in our notation), as opposed to its absolute levels, is the more precise outcome of ligand stimulation.
Reading fold-changes intuitively requires that cells remember the past activity level of the transcription factor, and compare it to the present level, after stimulation. This comparison has to extend the entire duration of the dynamics (both transient and steady state) if the target gene’s dynamics are to be entirely dependent only on fold-changes in the transcription factor, and not on absolute levels. Current models of gene regulation do not show this property. This study demonstrates that such a perfect temporal comparison is theoretically feasible, and that the almost minimal circuit to accomplish this temporal comparison happens to be one of the recurrent motifs in transcriptional networks, the type-1 incoherent feedforward loop.
The fold-change detection property occurs for a wide range of biochemical parameters for the I1-FFL interactions, provided that the activator is in its linear regime, and the repressor saturates the promoter of the target gene (Z). The fold-change detection property of the I1-FFL can provide gene regulation with an analogue of the Weber’s law, a feature of many sensory systems (e.g., vision, smell, hearing, taste, touch), in which signal discrimination is relative to the background signal (Laming, 1986; Ross and Murray, 1996; Weber, 1905). Fold-change detection may help cells maintain sensitivity to noisy signals across a wide dynamic range and perhaps cope with variation in the regulatory protein concentrations.
RESULTS
The incoherent feedforward loop with strong repression responds to fold-changes in signal
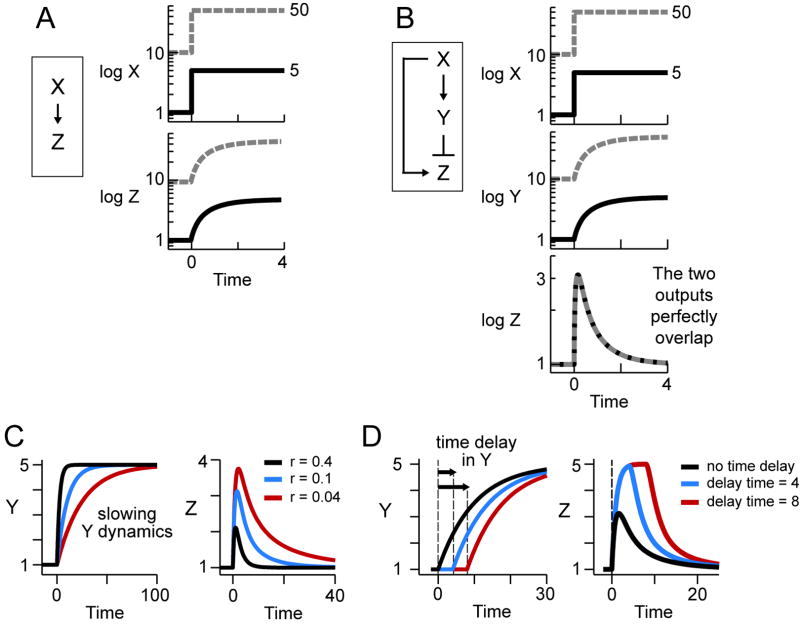
For illustration, Figure 2A shows how simple gene regulation, where a transcription factor X activates transcription of a target gene Z, responds to input steps. In simple regulation the amount of Z produced simply depends on the absolute level of the transcription factor X. The more transcription factor is around, the more Z is produced. A higher basal level of X corresponds to a higher basal transcription of Z (dashed lines).
Figure 2. The incoherent feedforward loop can provide fold-change detection.
(A) In a simple gene regulation, two inputs with different absolute levels but identical fold-changes give two different profiles of Z transcription.
(B) In a properly designed I1-FFL (see text), two inputs with different absolute levels but identical fold-changes give two identical profiles of Z transcription (dashed and full lines overlap).
(C-D) The amplitude and duration of the response Z can be increased by slowing the dynamics of Y (C) or by introducing a delay in the response of Y to X (D).
In all the plots, time is in arbitrary units. Using typical biochemical rate constants, the response time is in the range of minutes to hours (see text). The plots were generated using equations 7-8 in Box with r=0.1, except in Fig C where r varies.
In contrast, we now demonstrate that the I1-FFL, with proper design of its regulatory elements, can show a different type of response: the output Z depends on the fold-change in the input, and not on its absolute levels.
In the I1-FFL, a transcription factor X activates a target gene Z and also activates Y, which represses Z (Figure 2B). We consider here the case where Y represses Z strongly (Y nearly saturates the Z promoter), and where X acts in a linear fashion (X is far from saturating the Y and Z promoters; equations 1-2 in Box). In this case, we find that the response of Z depends only on the fold-change in the level of the activator X, and not on its absolute levels.
Box.

To demonstrate fold-change detection, we provide two input steps that have an identical fold-change, but different absolute levels (Figure 2B, X, solid and dashed lines). We find that the response of Z is a pulse that shows exact adaptation to its basal level. The shape of the pulse is identical for both input steps (Figure 2B, Z, the solid and dashed lines overlap). The height and the duration of the response thus depend on fold-changes in input, and not on its absolute levels. Variation in the basal activity level of the transcription factor X can be completely compensated, such that gene transcription depends only on the fold-changes.
The I1-FFL circuit with fold-change detection can maintain equal responses to a series of stimuli with identical steps (Figure S1). Such a property can be useful in the case that old signal is not cleared before the cells need to respond to a new stimulus. Our examples so far included sharp steps in X, but fold response is also seen for gradually changing signal profiles (Figure S1). For illustration, Figure S2 shows how all other network motifs, includes positive and negative auto-regulation, coherent FFLs and single-input modules, respond to the absolute levels of the input.
Fold-change detection in I1-FFL arises because the repressor Y acts as a memory of the activator X
The intuitive reason for the fold response property of the I1-FFL is that the repressor Y acts as a memory of the activator X (Friedland et al., 2009; Gardner et al., 2000). The I1-FFL with strong repression allows Y to act as a reference memory of previous levels of X, and to normalize the activation of Z accordingly. In this manner, Y mediates a continual temporal comparison between the present and past levels of X. At long time scales, the memory is adjusted to the new level of the activator X, and the response Z returns to its basal level (Figure 2C).
Mathematically, fold-change detection can be seen via dimensional analysis. The dynamic equations for Y and Z can be rescaled so that the stimulus X drops out, and only the fold-change in input level, F(t) = X(t) / X0, drives the dynamics of Z (equations 7-9 in Box). In a special case, an analytical solution can be obtained that explicitly shows the strict dependence on fold-changes in the input (please see Supplement).
Tuning the duration and amplitude of fold-change detection
The time scales for the dynamics of Z can be tuned to range from minutes to hours to days, by changing the degradation rates of Y and Z (α1 and α2 in equations 3-4 in Box). The time to reach the peak of the response is on the order of the half-life of the repressor Y, and the time for Z to adapt back to basal levels is on the order of the half-life of Z.
The amplitude of the Z response can be tuned in two ways. First, the slower the dynamics of the repressor Y compared to the dynamics of the target Z, the higher the amplitude of the response (Figure 3C). This may occur, for example, when the repressor is a relatively stable protein or inhibitory RNA, and Z is an unstable protein or mRNA.
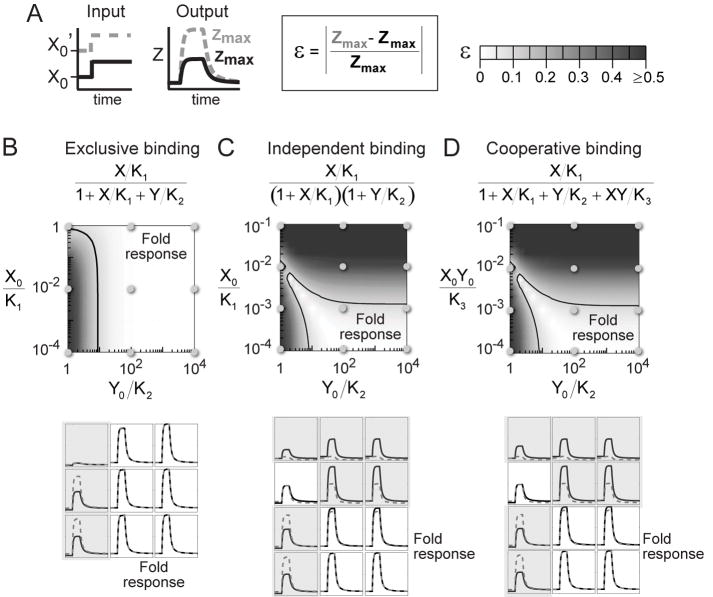
Figure 3. I1-FFL shows fold-change detection over a wide range of parameters.
(A) Model parameters were varied. For each choice of parameters, we provided two step inputs with the same fold-change F=10, and different absolute levels X0’=10 X0. As a measure of the fold-change detection property, we computed the relative difference (ε) in the amplitude of the Z response (Zmax) for the two step inputs.
(B-D) Three detailed designs of the Z promoter input function were considered, in which binding of X and Y is exclusive (B), independent (C), or cooperative (D). In all cases, the light region indicates the parameter range where fold-change detection occurs, in the sense that the two step inputs produce identical outputs within 10% (contour line delineates ε=0.1).
Parameters: Ki’s are binding constants, X0 is the basal input level, and Y0= β1X0/α1, with β1 and α1 defined in equation 3 in Box.
Second, the amplitude and duration of the Z response is increased when a time delay is incorporated so that Y is activated by X at a delay of relative to Z (Figure 3D). Such a delay in expression of a target gene is seen in diverse systems (e.g., Mdm2 expression is delayed by ~100 min relative to other genes activated by the same factor, p53) (Lahav et al., 2004). Such delays can be differentially controlled for different genes, by controlling delays in transcription, translation, localization, folding, splicing, and so on.
Fold-change detection occurs for a wide range of parameters in the I1-FFL
Up to now, we examined a model of the I1-FFL that is in the limit where Y saturates the Z promoter, and X is linear for the X and Z promoters (equation 2 in Box). To go beyond this limiting case, we tested the behavior of a more complete model of the I1-FFL. In this model, standard Michaelis-Menten-like terms describe the action of X and Y on the promoters (equation 1 in Box) (Alon, 2007; Bintu et al., 2005).
We tested the model by varying its biochemical parameters (e.g., binding affinities, degradation rates, production rates). We considered the three possible types of mechanisms for the way the two regulators X and Y bind the Z promoter: (i) binding of X and Y is mutually exclusive; (ii) binding of X and Y is independent; and (iii) binding of X and Y is cooperative. For each set of biochemical parameters, we computed the response to two step stimuli with different absolute levels but identical fold-changes (Figure 4A).
Figure 4. Fold-change detection may provide signaling advantages in noisy environment.
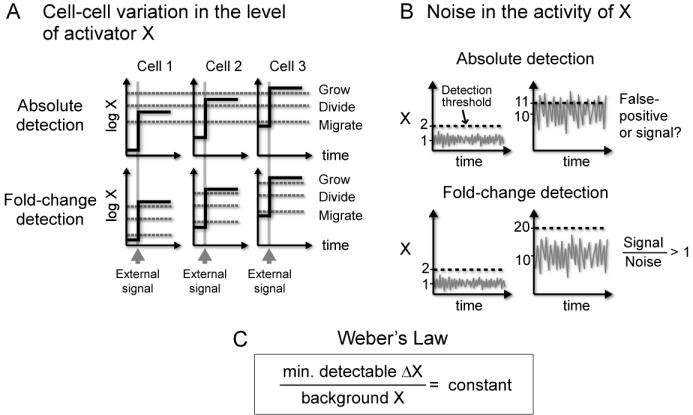
(A) Fold-change detection ensures that each cell responds reliably to an external signal despite variation in the basal level of X. In fold-change detection, cells sense relative changes from the basal level, and not absolute levels or absolute changes.
(B) Fold-change detection rescales the meaningful change in signal according to the background noise. In fold-change detection, ΔX = 1 when background X = 1 gives the same information as ΔX = 10 when background X = 10.
(C) Fold-change detection in the I1-FFL can provide a transcriptional analog of Weber’s Law in sensory system, which states that the minimal detectable change in signal scales linearly with the background signal.
In all three cases, there is a range of parameters that provides good fold-change detection (Figures 4B-D). The light-colored region in Figures 4B-D indicates the range of parameters in which the response to the two step stimuli is identical to within 10%. The lower panel of Figure 4 shows examples of Z dynamics across the parameter range. This suggests that the I1-FFL can be designed to show fold-change detection in a way that does not require fine-tuning of parameter values, and only requires that certain parameter ratios are large.
The parameter range for fold-change detection is greatest for the case where X and Y binding to the Z promoter is mutually exclusive. In this case, fold-change detection requires only that Y saturates the Z promoter (Y0/K2 ≫1, Figures 4B). If both X and Y can bind the promoter, such that their binding is independent of each other, fold-change detection requires also that X activation of the Z promoter is linear (X0/K1≪1, Figure 4C). If X and Y bind cooperatively, fold-change detection requires further that the simultaneous binding of both activators be relatively rare compared to the binding of Y alone (X0Y0/K3≪1, Figure 4D).
In short, fold-change detection requires that the ratio of Y concentration to its effective binding constant to the Z promoter is large, Y/K>~10. This can be achieved either by having high levels of Y, say Y=100 nM and affinity K=10 nM, or lower levels of Y and higher affinity, Y=10 nM, K=1 nM. (For reference, note that 10 nM represents ~10 molecules in a bacterium and ~1000 molecules in a fibroblast nucleus). In the cases considered here, fold-change detection also requires that X be in the linear regime in regulating the Y promoter.
Since Y strongly represses the promoter, fold-change detection operates at a small fraction of the promoter’s maximal strength. An appropriate combination of a strong promoter and strong repression can be used to provide the needed expression level of the output gene Z.
The present simulations indicate that the I1-FFL can also be designed in a way that it does not show fold-change detection properties. This is expected if X saturates the Y or Z promoter and is thus not in its linear regime, or if cooperative binding of X and Y to the Z promoter is near saturation. In these cases, the I1-FFL shows either a response that depends on the absolute level of the input, or a weak response.
We also tested a different way of implementing an I1-FFL. Here, instead of acting as a transcriptional repressor, Y promotes degradation of the target gene Z (Levchenko and Iglesias, 2002; Tyson et al., 2003). This is also similar to the ‘proportioner’ node in the adapting circuits discussed in (Ma et al., 2009). With appropriate choice of parameters, we find that this version of the I1-FFL can also show fold-change detection (Figure S3).
It is likely that additional circuits can provide fold-change detection. One possible direction is integral feedback circuits that provide precise adaptation (Barkai and Leibler, 1997; Ma et al., 2009; Yi et al., 2000). Not all circuits with precise adaptation, however, are expected to show fold-change detection. Figure 3 shows parameters in which I1-FFL displays almost precise adaptation but poor fold-change detection.
DISCUSSION
This study suggests that the I1-FFL, a common network motif, can provide fold-change detection. Fold-change detection means that the amplitude and duration, and indeed the entire shape of the response, depend on the fold-changes in the input, and not on its absolute levels. Fold-change detection occurs for a wide range of biochemical parameters of the I1-FFL, in which the repressor saturates its promoter, and the activator works in the linear regime.
Are there advantages to fold-change detection, rather than absolute detection, in gene regulation circuitry? One can suggest at least two advantages, related to cellular variation in the concentration of transcription factors, and to rapidly varying noise in their activity level (Figure 4).
The first potentially useful property of fold-change detection regards the observation that the nuclear level of transcription factors can vary by several folds between individual cells (Cohen-Saidon et al., in press; Sigal et al., 2006). For example, in the ERK system, the nuclear level of ERK2 (which corresponds to X in the present notation) varies by up to 4-fold across individual cells (Cohen-Saidon et al., in press). When an external signal arrives (the growth factor EGF), the nuclear level of ERK2 in each cell rises by the approximately same fold-change over the basal level (Figure 4A; (Cohen-Saidon et al., in press)). Thus, more ERK2 enters the nucleus in cells with a high basal ERK2 level than in cells with low level. An absolute-detection mechanism would generate different responses in different cells, due to the different absolute level of nuclear ERK2 (Figure 4A). In contrast, fold-change detection mechanism, such as that provided by the I1-FFL, can allow all cells to have identical response to the external signal, despite cell-cell variation in the basal level of the activator X (Figure 4A)
A second potentially useful property of fold-change detection is the ability to maintain sensitivity despite noise in the X activity (Figure 4B). Such noise can result from rapid fluctuations in the external signal level (e.g., external fluctuations in EGF concentration as it varies in space and time). Noise strength, defined as the standard deviation of a signal around its mean, is known to increase with signal strength. In many systems, the standard deviation of a signal increases proportionally to X. Thus, a background signal of 1 might have noise of ±0.1, whereas a background signal of 10 might have a higher noise of ±0.3. This increasing noise leads to a fundamental problem with absolute-detection mechanisms. If we had an absolute-detection mechanism, and would like it to detect changes of 0.3 above a background signal of 1, we would run into trouble when the background signal rises to 10—because noise in the signal would trigger false-positive responses (Figure 4B). Fold-change detection mechanism can address this problem: it allows detection of a signal that changes by 0.3 above a background of 1, but obtains a similar response only to changes of 3 above a background of 10.
Fold-change detection therefore assigns meaning to signal in reference to the background signal level, allowing responses only to signal that rises sufficiently above the noise. In other words, signal discrimination is proportional to the background level. This is analogous to Weber’s law in sensory systems, which states that the minimal detectable change in stimulus is linear in the background stimulus (Figure 4C) (Ross and Murray, 1996) , or more generally, that the response amplitude to a change in signal is inversely proportional to the background signal level. It would be fascinating to test whether naturally occurring incoherent FFLs, found in numerous systems, act as fold-change detection elements that, in analogy to Weber’s Law in sensory systems, provide gene regulation with the ability to reliably detect signals above a variable and noisy background.
Supplementary Material
01
Acknowledgments
For suggestions and critical reading of the manuscript, the authors thank Cellina Cohen-Saidon, Michael Springer, Eduardo Sontag, Jessica Gray, and Adam Palmer. OS is grateful to the Azrieli Foundation for the award of an Azrieli Fellowship. LG is a Robert Black Fellow of the Damon Runyon Foundation (DRG-1958-07). This work was supported by the Kahn Family Foundation (UA), R01 HD037277 (MWK) the Novartis-Harvard-Hebrew University program (MWK), and the Israel Science Foundation (UA).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alon U. An Introduction to Systems Biology. Boca Raton, FL: Chapman & Hall/CRC; 2007. [Google Scholar]
- Basu S, Mehreja R, Thiberge S, Chen MT, Weiss R. Spatiotemporal control of gene expression with pulse-generating networks. Proc Natl Acad Sci U S A. 2004;101:6355–6360. doi: 10.1073/pnas.0307571101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. Transcriptional regulation by the numbers: models. Curr Opin Genet Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyer LA, Lee TI, Cole MF, Johnstone SE, Levine SS, Zucker JP, Guenther MG, Kumar RM, Murray HL, Jenner RG, et al. Core transcriptional regulatory circuitry in human embryonic stem cells. Cell. 2005;122:947–956. doi: 10.1016/j.cell.2005.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen-Saidon C, Cohen AA, Sigal A, Liron Y, Alon U. Dynamics and variability in ERK2 response to EGF in individual living cells. Molecular Cell. doi: 10.1016/j.molcel.2009.11.025. in press. [DOI] [PubMed] [Google Scholar]
- Eichenberger P, Fujita M, Jensen ST, Conlon EM, Rudner DZ, Wang ST, Ferguson C, Haga K, Sato T, Liu JS, Losick R. The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis. PLoS Biol. 2004;2:e328. doi: 10.1371/journal.pbio.0020328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Entus R, Aufderheide B, Sauro HM. Design and implementation of three incoherent feed-forward motif based biological concentration sensors. Syst Synth Biol. 2007;1:119–128. doi: 10.1007/s11693-007-9008-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fechner GT. Elements of Psychophysics (Leipzig: Breitkopf & Hartel) H.S. Langfeld: H.S. Langfeld; 1860. [Google Scholar]
- Friedland AE, Lu TK, Wang X, Shi D, Church G, Collins JJ. Synthetic gene networks that count. Science. 2009;324:1199–1202. doi: 10.1126/science.1172005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Kaplan S, Bren A, Dekel E, Alon U. The incoherent feed-forward loop can generate non-monotonic input functions for genes. Mol Syst Biol. 2008;4:203. doi: 10.1038/msb.2008.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D, Kwon YK, Cho KH. The biphasic behavior of incoherent feed-forward loops in biomolecular regulatory networks. Bioessays. 2008;30:1204–1211. doi: 10.1002/bies.20839. [DOI] [PubMed] [Google Scholar]
- Krejci A, Bernard F, Housden BE, Collins S, Bray SJ. Direct response to Notch activation: signaling crosstalk and incoherent logic. Sci Signal. 2009;2:ra1. doi: 10.1126/scisignal.2000140. [DOI] [PubMed] [Google Scholar]
- Lahav G, Rosenfeld N, Sigal A, Geva-Zatorsky N, Levine AJ, Elowitz MB, Alon U. Dynamics of the p53-Mdm2 feedback loop in individual cells. Nat Genet. 2004;36:147–150. doi: 10.1038/ng1293. [DOI] [PubMed] [Google Scholar]
- Laming D. Sensory Analysis. London: Academic Press; 1986. [Google Scholar]
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- Levchenko A, Iglesias PA. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Cassidy JJ, Reinke CA, Fischboeck S, Carthew RW. A microRNA imparts robustness against environmental fluctuation during development. Cell. 2009;137:273–282. doi: 10.1016/j.cell.2009.01.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma W, Trusina A, El-Samad H, Lim WA, Tang C. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci U S A. 2003;100:11980–11985. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangan S, Itzkovitz S, Zaslaver A, Alon U. The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli. J Mol Biol. 2006;356:1073–1081. doi: 10.1016/j.jmb.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- O’Donnell KA, Wentzel EA, Zeller KI, Dang CV, Mendell JT. c-Myc-regulated microRNAs modulate E2F1 expression. Nature. 2005;435:839–843. doi: 10.1038/nature03677. [DOI] [PubMed] [Google Scholar]
- Sigal A, Milo R, Cohen A, Geva-Zatorsky N, Klein Y, Alaluf I, Swerdlin N, Perzov N, Danon T, Liron Y, et al. Dynamic proteomics in individual human cells uncovers widespread cell-cycle dependence of nuclear proteins. Nat Methods. 2006;3:525–531. doi: 10.1038/nmeth892. [DOI] [PubMed] [Google Scholar]
- Swiers G, Patient R, Loose M. Genetic regulatory networks programming hematopoietic stem cells and erythroid lineage specification. Dev Biol. 2006;294:525–540. doi: 10.1016/j.ydbio.2006.02.051. [DOI] [PubMed] [Google Scholar]
- Tyson JJ, Chen KC, Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- Weber EH. E.H. Weber on the Tactile Senses. East Sussex, UK: Erlbaum Taylor & Francis; 1996. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
01