The Biomass Objective Function (original) (raw)
. Author manuscript; available in PMC: 2011 Jun 1.
Published in final edited form as: Curr Opin Microbiol. 2010 Apr 27;13(3):344–349. doi: 10.1016/j.mib.2010.03.003
Abstract / Summary
Flux balance analysis (FBA) is a mathematical approach for analyzing the flow of metabolites through a metabolic network. To computationally predict cell growth using FBA, one has to determine the biomass objective function that describes the rate at which all of the biomass precursors are made in the correct proportions. Here we review fundamental issues associated with its formulation and use to compute optimal growth states.
Introduction
Flux balance analysis (FBA) [1] is a widely used approach for studying biochemical networks, in particular the genome-scale metabolic network reconstructions that have been built in the past decade [2,3]. These network reconstructions contain all of the known metabolic reactions in an organism and the genes that encode each enzyme. FBA calculates the flow of metabolites through this metabolic network, thereby making it possible to predict the growth rate of an organism or the rate of production of a biotechnologically important metabolite. An objective function, such as the biomass objective function, is necessary to compute an optimal network state and resulting flux distribution (unique or non-unique) in a constraint-based reconstruction as the solution space is often very large for genome-scale networks [4]. With metabolic models becoming available for a growing number organisms [5] and high-throughput technologies enabling the construction of many more each year [6], FBA is an important tool for harnessing the knowledge encoded in these models.
Genome-scale models are used to compute a variety of phenotypic states. How the genome-scale metabolic network supports the growth of a cell has been a topic of much interest. Here we, 1) discuss the computation of cellular yields and growth rates and how they differ, 2) outline the formulation of a detailed biomass objective function, and 3) review several studies that have focused on the use of the objective function.
Computing Cellular Yields and Growth Rates
Metabolic network reconstructions contain the known biochemical conversions inside the cell and allow for computation of both topological properties and biophysical capabilities. The vast majority of cellular metabolic conversions are enzymatically catalyzed with a few occurring spontaneously. A curated metabolic reconstruction can be utilized as a comprehensive parts list of the cell, allowing for detailed and accurate computation of the conversion of substrates into products by the cell.
Computation of yields
Metabolic reconstructions are an ideal platform for rapidly calculating the yield of any given product from single or multiple substrates. Most often, the product yield (the maximum amount of product that can be generated per unit of substrate, Yp/s) is of greatest interest (Figure 1). Calculation of biomass yields are different in that multiple biomass components (e.g., lipids) and biomass precursors (e.g., amino acids) have to be quantified in proportion to each other to form a biomass objective function (Figure 1). By detailing the molar content that makes up the biomass of the cell, stoichiometrically based biomass yields can be computed. The yield does not have a time dimension
Figure 1.

Calculation of yield and growth rate with a metabolic reconstruction
A substrate uptake rate can be utilized with a metabolic reconstruction to calculate yields (e.g., substrate-specific product yield, YP/S). In the absence of additional constraints on a network, the relationship between a measured uptake rate and yield is a constant (i.e., directly proportional). With the use of a biomass objective function, complete with growth and non-growth associated maintenance energies (GAM and NGAM), growth rates (μ) can be calculated based on measured substrate uptake rates (qsubstrate). Prediction of accurate growth rates often requires several input fluxes to the cell, with typically one or two limiting nutrient fluxes (e.g., glucose and oxygen).
Computation of growth rate
Optimal or sub-optimal actual growth rates can also be computed. The growth rate is constrained by the measured substrate uptake rates, with the uptake rate of the limiting substrate being critical, and by maintenance energy requirements (Figure 1). Simulating the generation of cellular biomass products from available inputs using the biomass objective function allows for the prediction of allowable growth rates for given substrate uptake rates and maintenance requirements. The non-growth associated maintenance and the substrate uptake rate introduce time and thus enable the computation of a growth rate.
The Formulation the Biomass Objective Function
The formulation of a detailed biomass objective function for use in examining metabolic networks is dependent on knowing the composition of the cell and energetic requirements necessary to generate biomass content from metabolic precursors (Figure 2). One can formulate biomass objective function at a different level of detail.
Figure 2.
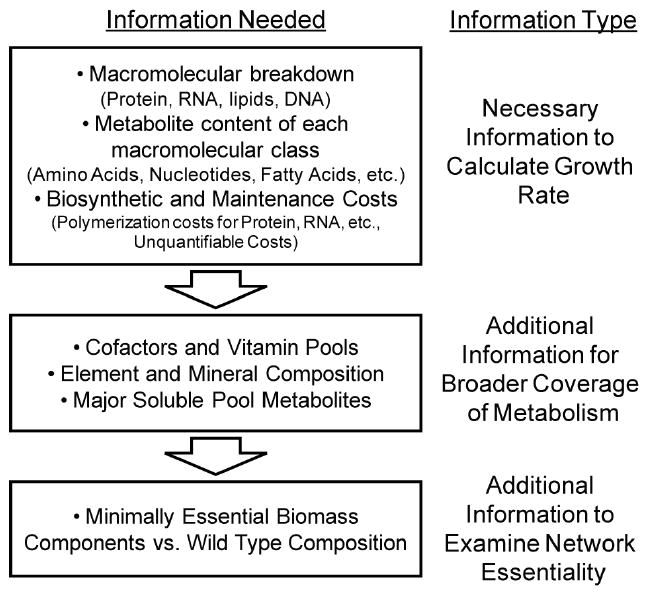
Information used to generate a detailed biomass objective
Different types of information are utilized in generating a biomass objective function. The top box contains the necessary information needed to accurately calculate a growth rate and this content determines the bulk of metabolic activity (i.e., flux). Addition of information from the second box enables a broader coverage of metabolism and increases the accuracy of predictions of the growth rate and network essentiality. The addition of information from the bottom box allows for the generation of a ‘core’ biomass objective function that can be used for even greater accuracy of network essentiality prediction.
Basic level
The formulation process starts with defining the macromolecular content on the cell (i.e., weight fraction of protein, RNA, lipid, etc.) and then the metabolites that make up each macromolecular group (e.g., amino acids, nucleotide triphosphates, etc.). With this information, it is possible to detail the required amount of metabolites (subsequently defining amounts of carbon, nitrogen, and additional elemental requirements) that are needed along with associated reaction pathways.
Intermediate level
It is possible to increase this level of resolution and calculate the necessary biosynthetic energy that is needed to synthesis the macromolecules whose building blocks are directly accounted for in a curated metabolic network. For example, it is known that it takes approximately 2 ATP molecules and 2 GTP molecules to drive the polymerization of each amino acid into a protein molecule [7]. More energy is required when considering processes such as RNA error checking in transcription. This energetic conversion is included in the biomass objective function and details the necessary energy that the cell has to make to drive these biosynthetic processes (often included as part of maintenance energies). This energy is, of course, over and above the energy that is necessary to synthesize the appropriate macromolecular building blocks (e.g., the amount of energy to make a building block, such as UTP, from a common substrate, such as glucose). An important detail to take into account in the biomass objective function is that it is necessary to include the products of macromolecular biosynthesis from building blocks included in a network (e.g., water from protein synthesis and diphosphate from RNA or DNA synthesis). These polymerization products are then directly available to the cell and reduce the amounts of resources the cell needs to take up from the media.
Advanced level
Advanced biomass objective functions can be formed by detailing the necessary vitamins, elements, and cofactors required for growth as well as determining core components necessary for cellular viability. Inclusion of vitamins, elements, and cofactors allow for the analysis of a broader coverage of network functionality and required network activity. Another advanced approach is to not only define the wild-type biomass content of the cell, but to generate a separate biomass objective function that contains the minimally functional content of the cell. This objective function (referred to as the ‘core’ biomass objective function [8]) can result in increased accuracy when predicting gene, reaction, and metabolite essentiality and is formulated using experimental data from genetic mutants and knockout strains. Workflows for how a biomass objective function is formulated have appeared [5,9]. Furthermore, a detailed spreadsheet of actual data used for formulating both a wild-type and core biomass objective function is available for E. coli [8] that can be used as a template for similar organisms.
The scope of network reconstructions continues to grow [5]. It should be noted that with full reconstructions of the entire protein synthesis machinery [10], that the level and detail in biomass objective functions can continue to grow.
Brief Review of Studies Examining Cellular Objective Functions
Over the past two decades, an number of studies have been carried out to examine the use of objective function optimization with reconstructed networks towards predicting biological outcomes (Table 1) [11-19]. These studies have utilized small-scale central metabolic networks, as well as genome-scale reconstructions of bacteria and eukaryotic organisms. This set of studies can roughly be divided into two categories: (1) studies examining hypotheses on presumed cellular objective functions through comparison to experimental data [11-13,15,16,19], and (2) studies examining optimization techniques to discover or algorithmically predict biological objective functions from experimental data [14,17,18]. Each category is described below.
Table 1.
Studies examining objective functions
| Ref | Objective Function(s) Examined | Modeling Approach | Metabolic Reconstruction and Model Used | Source of Experimental Data | Simple Statement |
|---|---|---|---|---|---|
| [11,12] 1992 | (1) Max. of growth rate, (2) Min. of ATP production, (3) Minimizing total nutrient uptake, and (4) Minimize redox metabolism through minimizing NADH production. | Linear Programming | Hybridoma cell line central metabolism (83 reactions, 42 metabolites) [11] | (1) aerobic batch bioreactor with growth, uptake, secretion, and protein production rates [20] | Optimization of biomass production can be used to examine growth characteristics and explain observed phenomena. |
| [13] 1997 | Max. or Min. of (1) growth rate, (2) ATP production rate, (3) substrate uptake, or (4) product formation | Linear Programming (iterative optimization) | E. coli central metabolsim model (300 reactions, 289 metabolites) [13] | Aerobic batch growth isotopomer based flux distribution on (1) acetate, and (2) glucose and acetate [38] | Optimization with a growth-rate dependent biomass objective function can accurately predict experimentally determined metabolic fluxes. |
| [14] 2003 | ObjFind Algorithm - Optimization-based framework to infer best objective function | Linear programming | E. coli core central metabolism model (62 reactions, 48 metabolites) (see [14]) | batch growth of (1) aerobic and (2) anaerobic growth isotopomer-based flux distributions [39] | Optimization of biomass production (growth) was identified as the most significant driving force in both cases examined. |
| [15] 2007 | (1) Max. of Growth rate, (2) Min. of the production rate of redox potential, (3) Min. of ATP production rate, (4) Max. of ATP production rate, and (5) Min. of nutrient uptake rate | Linear programming & Bayesian discrimination technique | E. coli genome-scale metabolic network iJR904 (1320 reactions, 625 metabolites) [40] | (1) batch aerobic growth, substrate, production rates [26] | Min. of the production rate of redox potential was determined to be the most probable objective function. |
| [16] 2007 | (1) Max. of biomass yield (production), (2) Max. of ATP yield (energy expenditure), (3) Min. of the overall intracellular yield, (4) Max. of ATP yield per unit flux, (5) Max. of biomass yield per unit flux, (6) Min. of glucose production, (7) Min. of reaction steps, (8) Max. of ATP yield per reaction step, (9) Min. of redox potential, (9) Min. of ATP producing reactions, (10) Max. of ATP producing fluxes | Linear programming & non-Linear programming | E. coli core central metabolism model (98 reactions, 60 metabolites) [16] | (1) Aerobic, (2) anaerobic, (3) anaerobic with nitrate growth in batch, and (4) carbon- and (5) nitrogen-limited limited growth in chemostat; Isotopomer-based flux distributions. [41-43] | No single objective describes the flux states under all conditions. Unlimited growth on glucose in oxygen or nitrate respiring batch cultures is best described by nonlinear Max. of the ATP yield per flux unit. Under nutrient scarcity in continuous cultures, in contrast, linear Max. of the overall ATP or biomass yields achieved the highest predictive accuracy. |
| [17] 2008 | Biological Objective Solution Search (BOSS) Algorithm - Optimization-based framework to infer best objective function | Linear programming | S. cerevisiae core central metabolism model (62 reactions, 60 metabolites) [44] | (1) Aerobic batch growth isotopomer-based flux distribution [44] | Growth is the best-fit objective function for the examined network and conditions. |
| [18] 2009 | GrowMatch Algorithm - Minimizes modifications (addition of reactions or activation of secretion of metabolites) in the metabolic model to match growth phenotype data | Linear programming (bi-level optimization) | _E. col_i genome-scale metabolic network iAF1260 (2077 reactions, 1039 metabolites) [8] | (1) growth phenotype data for wild type and mutant E. coli; (2) pathway content data; MetaCyc/KEGG [45-47] | GrowMatch is a useful model-refinement tool for curating/refining metabolic reconstructions and can be used to increase predictivity of phenotype data. |
| [19] 2009 | (1) Max. of biomass production (growth rate), (2) Max. of plasmid production rate (Max plasmid), and (3) maximizing maintenance energy expenditure (Max ATPm). | Linear programming | E. coli genome-scale metabolic network iJR904 (1320 reactions, 625 metabolites) with plasmid / protein product reactions [40] | Aerobic glucose-limited limited growth in chemostat of (1) wild-type and (2) plasmid-bearing cells with growth, substrate, and product rates and isotopomer-based flux | Wild-type can best be determined with the objective function of maximizing growth rate, and maximizing expenditure of ATP best predicts overall metabolism and phenotype of plasmid-bearing _E. col_i. |
Biased search for cellular objectives
Several studies have been conducted to examine which hypothesized cellular objective function best predicts cellular behavior through network optimization and comparison to experimental data. The first of these highlighted studies to appear (conducted in two parts [11,12]), considered growth of a hybridoma cell line with the intention of examining growth limiting substrate conditions and intracellular energy generation and utilization. This study utilized the wealth of information available for a known hybridoma cell line [20] to reconstruct its cellular network and investigate growth capabilities apparent from the stoichiometry of the network.
Later, studies in this category examined a number of additional cellular objectives to analyze growth characteristics of microorganisms and a growth-rate dependent biomass objective function [13]. One particular study performed a relatively comprehensive analysis of eleven different objective functions and compared each to growth of E. coli under six different growth conditions (the study also examined a number of different modeling parameters and their effect on phenotype prediction [16]). This combinatorial engineering approach of analyzing each objective functions towards predicting each experimental condition resulted in the findings that growth under batch (unlimited) and chemostat (limited) conditions are best described by two different cellular objectives. Another study in this category examined the metabolic burden of plasmid-based expression in a cell and has implications in biotechnology applications [19].
Examining the conclusions of each of these studies (see Table 1), two main points emerge: (1) the search for cellular objective functions is an ongoing area of research, and (2) objective functions for an organism are likely condition-dependent and training-data (comparison data) specific. Therefore, it is likely necessary to analyze the use of an objective function on a case-by-case basis for an intended application and useful to compare predicted fluxes to numerous input, output, and intracellular training-data fluxes in order to find the best overall predictive objective function.
Unbiased search for cellular objectives
Studies of metabolism have also been conducted which utilize computational algorithms to determine best-fit cellular objective functions [14,17,18]. The details of each algorithm will not be discussed her, but these optimization-based frameworks each approach the determination of a predictive objective function in a different manner, and can also be utilized as tools to improve reconstructed network content [18]. In contrast to the studies where objective functions are first identified and then tested (described above), two effectively unbiased studies where an objective function was not initially assumed, concluded that optimization of biomass production or growth is the best fit for predicting growth data in the microorganisms E. coli [14] and S. cerevisiae [17]. The third study in this category developed an algorithm to refine both reconstruction and biomass objective function content, and demonstrated that overall improvements in cellular phenotype predictions can be achieved in such an approach (e.g., an increase in growth phenotype prediction of mutants from 91.4% to 96.7% in E. coli [18]). These algorithmic tools are readily applicable towards additional organism-specific networks and should aid in discovery projects, as well as industrially relevant applied applications.
Conclusions
The biomass objective function describes the growth requirements of a cell. It is needed to perform a variety of Constraint-Based Reconstruction and Analysis (COBRA) methods [21]. It has a variety of uses ranging from the interpretation of evolutionary outcomes [22-24] to the introduction of a plasmid into a cell through the creation of additional metabolic burden [19]. Its use can allow for the computation of fluxes and provide insights into the functioning of cellular processes [25].
What does a microorganism try to do in a given environment? The answer to this question may be unknowable without understanding the evolutionary history of the target organism. Thus, we have a fundamental question associated with the selection of an appropriate objective function that is physiologically realistic. This issue was recognized in the very first paper on large scale network analysis using FBA [11,12] where a series of selected objective functions were used to find which one fit the data the best. Since then, a number of similar studies have appeared [13,15,16,19], along with the systematic evaluation of the space of all objective functions that match experimental data [14,17,18].
The cumulative data suggests that strains, such as the widely studied E. coli strains, that have been grown over long periods of time in laboratory settings, have acquired an optimal growth phenotype on commonly used substrates in growth media [26]. When confronted with an unfamiliar substrate, optimal growth phenotypes can be generated using laboratory adaptive evolution [27-30]. Evolved strains can then be re-sequenced to find all mutations generated, thus illuminating the underlying genetic and molecular biological basis for optimal growth phenotypes [31,32].
Nutritionally rich environments are probably the exception rather than the norm in natural environments. Thus, the studies just described may represent exceptions rather than the norm. In general, we might begin to conceptualize cellular survival strategies in order to formulate useful objective functions. Consider three different environments; 1) nutritionally rich, as above, 2) scarce nutritional environment, and 3) elementally limited environment. From a natural habitat standpoint and the experiences of microorganisms, these are perhaps listed from the least likely to the likeliest; however, no computational studies of the third case have appeared. For the first and second cases, data from batch growth (nutritionally rich, case one) and chemostat growth experiments (nutritionally scarce, case two) suggests that optimal biomass yield or growth rates are meaningful objectives [11-14,16,17,19]. However, cases have appeared indicating contrary objectives, such as maximization of ATP per unit flux, being better predictors of experimental data [16]. Nonetheless, maximal growth rate phenotype can still result after adaptive evolution, or through prolonged experimentation in the laboratory. It should be noted that a predictable phenomena becomes the basis for design. For example, growth coupling of a bioengineering production objective has emerged as a strain design strategy [33-36], with adaptive evolution being a tool to produce such designs [37].
The constraint-based formalism has been shown to work at the genome-scale [2,3]. It obviates the need for many details by incorporating an objective function and assuming optimal organism functions. Although, ‘everything in biology should be viewed through the eyes of evolution’ implies some optimal performance based on the organism's past history, we are only beginning to decipher what cellular objectives actually are. One can therefore anticipate that many studies of the objective function are to appear.
Acknowledgments
We would like to thank Jacob D. Feala and Daniel C. Zielinski for their valuable feedback on this manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Varma A, Palsson BO. Metabolic Flux Balancing: Basic concepts, Scientific and Practical Use. Nat Biotechnol. 1994;12:994–998. [Google Scholar]
- 2.Feist AM, Palsson BO. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat Biotech. 2008;26:659–667. doi: 10.1038/nbt1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Oberhardt MA, Palsson BO, Papin JA. Applications of genome-scale metabolic reconstructions. Mol Syst Biol. 2009;5:320. doi: 10.1038/msb.2009.77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Reed JL, Palsson BO. Genome-Scale In Silico Models of E. coli Have Multiple Equivalent Phenotypic States: Assessment of Correlated Reaction Subsets That Comprise Network States. Genome Res. 2004;14:1797–1805. doi: 10.1101/gr.2546004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Feist AM, Herrgard MJ, Thiele I, Reed JL, Palsson BO. Reconstruction of biochemical networks in microorganisms. Nat Rev Microbiol. 2009;7:129–143. doi: 10.1038/nrmicro1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Joyce AR, Palsson BO. The model organism as a system: integrating ‘omics’ data sets. Nat Rev Mol Cell Biol. 2006;7:198–210. doi: 10.1038/nrm1857. [DOI] [PubMed] [Google Scholar]
- 7.Neidhardt FC, Ingraham JL, Schaechter M. Physiology of the bacterial cell: a molecular approach. Sunderland, Mass.: Sinauer Associates; 1990. [Google Scholar]
- 8.Feist AM, Henry CS, Reed JL, Krummenacker M, Joyce AR, Karp PD, Broadbelt LJ, Hatzimanikatis V, Palsson BO. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol Syst Biol. 2007;3 doi: 10.1038/msb4100155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thiele I, Palsson BO. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat Protoc. 2010;5:93–121. doi: 10.1038/nprot.2009.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thiele I, Jamshidi N, Fleming RM, Palsson BO. Genome-scale reconstruction of Escherichia coli's transcriptional and translational machinery: a knowledge base, its mathematical formulation, and its functional characterization. PLoS Comput Biol. 2009;5:e1000312. doi: 10.1371/journal.pcbi.1000312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Savinell JM, Palsson BO. Network analysis of intermediary metabolism using linear optimization. I. Development of mathematical formalism. Journal of Theoretical Biology. 1992;154:421–454. doi: 10.1016/s0022-5193(05)80161-4. [DOI] [PubMed] [Google Scholar]
- 12.Savinell JM, Palsson BO. Network analysis of intermediary metabolism using linear optimization. II. Interpretation of hybridoma cell metabolism. Journal of Theoretical Biology. 1992;154:455–473. doi: 10.1016/s0022-5193(05)80162-6. [DOI] [PubMed] [Google Scholar]
- 13.Pramanik J, Keasling JD. Stoichiometric model of Escherichia coli metabolism: Incorporation of growth-rate dependent biomass composition and mechanistic energy requirements. Biotechnology and Bioengineering. 1997;56:398–421. doi: 10.1002/(SICI)1097-0290(19971120)56:4<398::AID-BIT6>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 14.Burgard AP, Maranas CD. Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnol Bioeng. 2003;82:670–677. doi: 10.1002/bit.10617. [DOI] [PubMed] [Google Scholar]
- 15.Knorr AL, Jain R, Srivastava R. Bayesian-based selection of metabolic objective functions. Bioinformatics. 2007;23:351–357. doi: 10.1093/bioinformatics/btl619. [DOI] [PubMed] [Google Scholar]
- 16.Schuetz R, Kuepfer L, Sauer U. Systematic evaluation of objective functions for predicting intracellular fluxes in. Escherichia coli Mol Syst Biol. 2007:3. doi: 10.1038/msb4100162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gianchandani EP, Oberhardt MA, Burgard AP, Maranas CD, Papin JA. Predicting biological system objectives de novo from internal state measurements. BMC Bioinformatics. 2008;9:43. doi: 10.1186/1471-2105-9-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kumar VS, Maranas CD. GrowMatch: an automated method for reconciling in silico/in vivo growth predictions. PLoS Comput Biol. 2009;5:e1000308. doi: 10.1371/journal.pcbi.1000308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ow DS, Lee DY, Yap MG, Oh SK. Identification of cellular objective for elucidating the physiological state of plasmid-bearing Escherichia coli using genome-scale in silico analysis. Biotechnol Prog. 2009;25:61–67. doi: 10.1002/btpr.51. [DOI] [PubMed] [Google Scholar]
- 20.Ozturk SS, Palsson BO. Growth, Metabolic, and Antibody Production Kinetics of Hybridoma Cell Culture: II. Effects of Serum Concentration, Dissolved Oxygen Concentration, and Medium pH in a Batch Reactor'. Biotechnology Progress. 1991;7:481–494. doi: 10.1021/bp00012a002. [DOI] [PubMed] [Google Scholar]
- 21.Price ND, Reed JL, Palsson BO. Genome-scale models of microbial cells: evaluating the consequences of constraints. Nat Rev Microbiol. 2004;2:886–897. doi: 10.1038/nrmicro1023. [DOI] [PubMed] [Google Scholar]
- 22.Pal C, Papp B, Lercher MJ. Adaptive evolution of bacterial metabolic networks by horizontal gene transfer. Nat Genet. 2005;37:1372–1375. doi: 10.1038/ng1686. [DOI] [PubMed] [Google Scholar]
- 23.Pal C, Papp B, Lercher MJ. Horizontal gene transfer depends on gene content of the host. Bioinformatics. 2005;21 Suppl 2:ii222–ii223. doi: 10.1093/bioinformatics/bti1136. [DOI] [PubMed] [Google Scholar]
- 24.Pal C, Papp B, Lercher MJ, Csermely P, Oliver SG, Hurst LD. Chance and necessity in the evolution of minimal metabolic networks. Nature. 2006;440:667–670. doi: 10.1038/nature04568. [DOI] [PubMed] [Google Scholar]
- 25.Nielsen J. It is all about metabolic fluxes. J Bacteriol. 2003;185:7031–7035. doi: 10.1128/JB.185.24.7031-7035.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Edwards JS, Ibarra RU, Palsson BO. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat Biotechnol. 2001;19:125–130. doi: 10.1038/84379. [DOI] [PubMed] [Google Scholar]
- 27.Ibarra RU, Edwards JS, Palsson BO. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 2002;420:186–189. doi: 10.1038/nature01149. [DOI] [PubMed] [Google Scholar]
- 28.Fong SS, Palsson BO. Metabolic gene-deletion strains of Escherichia coli evolve to computationally predicted growth phenotypes. Nat Genet. 2004;36:1056–1058. doi: 10.1038/ng1432. [DOI] [PubMed] [Google Scholar]
- 29.Teusink B, Wiersma A, Molenaar D, Francke C, de Vos WM, Siezen RJ, Smid EJ. Analysis of growth of Lactobacillus plantarum WCFS1 on a complex medium using a genome-scale metabolic model. J Biol Chem. 2006;281:40041–40048. doi: 10.1074/jbc.M606263200. [DOI] [PubMed] [Google Scholar]
- 30.Teusink B, Wiersma A, Jacobs L, Notebaart RA, Smid EJ. Understanding the adaptive growth strategy of Lactobacillus plantarum by in silico optimisation. PLoS Comput Biol. 2009;5:e1000410. doi: 10.1371/journal.pcbi.1000410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Herring CD, Raghunathan A, Honisch C, Patel T, Applebee MK, Joyce AR, Albert TJ, Blattner FR, van den Boom D, Cantor CR, et al. Comparative genome sequencing of Escherichia coli allows observation of bacterial evolution on a laboratory timescale. Nat Genet. 2006;38:1406–1412. doi: 10.1038/ng1906. [DOI] [PubMed] [Google Scholar]
- 32.Conrad TM, Joyce AR, Applebee MK, Barrett CL, Xie B, Gao Y, Palsson BO. Whole-genome resequencing of Escherichia coli K-12 MG1655 undergoing short-term laboratory evolution in lactate minimal media reveals flexible selection of adaptive mutations. Genome Biol. 2009;10:R118. doi: 10.1186/gb-2009-10-10-r118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Burgard AP, Pharkya P, Maranas CD. Optknock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol Bioeng. 2003;84:647–657. doi: 10.1002/bit.10803. [DOI] [PubMed] [Google Scholar]
- 34.Pharkya P, Burgard AP, Maranas CD. OptStrain: a computational framework for redesign of microbial production systems. Genome Res. 2004;14:2367–2376. doi: 10.1101/gr.2872004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Patil KR, Rocha I, Forster J, Nielsen J. Evolutionary programming as a platform for in silico metabolic engineering. BMC Bioinformatics. 2005;6:308. doi: 10.1186/1471-2105-6-308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Feist AM, Zielinski DC, Orth JD, Schellenberger J, Herrgard MJ, Palsson BO. Model-driven evaluation of the production potential for growth-coupled products of Escherichia coli. Metab Eng. 2009 doi: 10.1016/j.ymben.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fong SS, Burgard AP, Herring CD, Knight EM, Blattner FR, Maranas CD, Palsson BO. In silico design and adaptive evolution of Escherichia coli for production of lactic acid. Biotechnol Bioeng. 2005;91:643–648. doi: 10.1002/bit.20542. [DOI] [PubMed] [Google Scholar]
- 38.Walsh KJ, Koshland DE. Branch point control by the phosphorylation state of isocitrate dehydrogenase. A quantitative examination of fluxes during a regulatory transition. Journal of Biological Chemistry. 1985;260:8430–8437. [PubMed] [Google Scholar]
- 39.Schmidt K, Nielsen J, Villadsen J. Quantitative analysis of metabolic fluxes in Escherichia coli, using two-dimensional NMR spectroscopy and complete isotopomer models. J Biotechnol. 1999;71:175–189. doi: 10.1016/s0168-1656(99)00021-8. [DOI] [PubMed] [Google Scholar]
- 40.Reed JL, Vo TD, Schilling CH, Palsson BO. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR) Genome Biology. 2003;4:R54.51–R54.12. doi: 10.1186/gb-2003-4-9-r54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Perrenoud A, Sauer U. Impact of global transcriptional regulation by ArcA, ArcB, Cra, Crp, Cya, Fnr, and Mlc on glucose catabolism in Escherichia coli. J Bacteriol. 2005;187:3171–3179. doi: 10.1128/JB.187.9.3171-3179.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nanchen A, Schicker A, Sauer U. Nonlinear dependency of intracellular fluxes on growth rate in miniaturized continuous cultures of Escherichia coli. Appl Environ Microbiol. 2006;72:1164–1172. doi: 10.1128/AEM.72.2.1164-1172.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Emmerling M, Dauner M, Ponti A, Fiaux J, Hochuli M, Szyperski T, Wuthrich K, Bailey JE, Sauer U. Metabolic flux responses to pyruvate kinase knockout in Escherichia coli. J Bacteriol. 2002;184:152–164. doi: 10.1128/JB.184.1.152-164.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gombert AK, Moreira dos Santos M, Christensen B, Nielsen J. Network identification and flux quantification in the central metabolism of Saccharomyces cerevisiae under different conditions of glucose repression. Journal of Bacteriology. 2001;183:1441–1451. doi: 10.1128/JB.183.4.1441-1451.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Baba T, Ara T, Hasegawa M, Takai Y, Okumura Y, Baba M, Datsenko KA, Tomita M, Wanner BL, Mori H. Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol Syst Biol. 2006;2:2006.0008. doi: 10.1038/msb4100050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Caspi R, Foerster H, Fulcher CA, Kaipa P, Krummenacker M, Latendresse M, Paley S, Rhee SY, Shearer AG, Tissier C, et al. The MetaCyc Database of metabolic pathways and enzymes and the BioCyc collection of Pathway/Genome Databases. Nucleic Acids Res. 2008;36:D623–631. doi: 10.1093/nar/gkm900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kanehisa M, Araki M, Goto S, Hattori M, Hirakawa M, Itoh M, Katayama T, Kawashima S, Okuda S, Tokimatsu T, et al. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008;36:D480–484. doi: 10.1093/nar/gkm882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wang Z, Xiang L, Shao J, Wegrzyn A, Wegrzyn G. Effects of the presence of ColE1 plasmid DNA in Escherichia coli on the host cell metabolism. Microb Cell Fact. 2006;5:34. doi: 10.1186/1475-2859-5-34. [DOI] [PMC free article] [PubMed] [Google Scholar]