Cellular heterogeneity: when do differences make a difference? (original) (raw)
. Author manuscript; available in PMC: 2010 Nov 1.
Abstract
A central challenge of biology is to understand how individual cells process information and respond to perturbations. Much of our current knowledge is based on ensemble measurements. However, cell-to-cell differences are always present to some degree in any population of cells, and the ensemble behaviors of a population may not represent the behaviors of any individual cell. Here, we discuss examples of when heterogeneity cannot be ignored, and describe practical strategies for analyzing and interpreting cellular heterogeneity; while ensemble measurements may be too simplistic, capturing all variation among cells may be unnecessary. To develop accurate models of individual cell behavior–be they in the form of cartoons, words, or mathematics–it is essential to identify which cell-cell differences are important and which can be ignored.
A hidden world beneath population averages
After decades, of probing, measuring, and analyzing the behaviors of single cells, it has become clear that the challenge is no longer to demonstrate that populations of “seemingly identical” cells are heterogeneous. Indeed, phenotypic differences among cells are always present at a fine-enough resolution of inspection. Rather, the daunting challenge is to determine which–if any–components of observed cellular heterogeneity serve a biological function or contain meaningful information.
Population-averaged assays are powerful tools in biology, enabling the identification of components and interactions within complex metabolic, signaling, and transcriptional networks. Such measurements1 can succinctly capture population state, and readily report how these states change in response to perturbations. An assumption of such assays is that ensemble averages reflect the dominant biological mechanism operating within individual cells within a population.
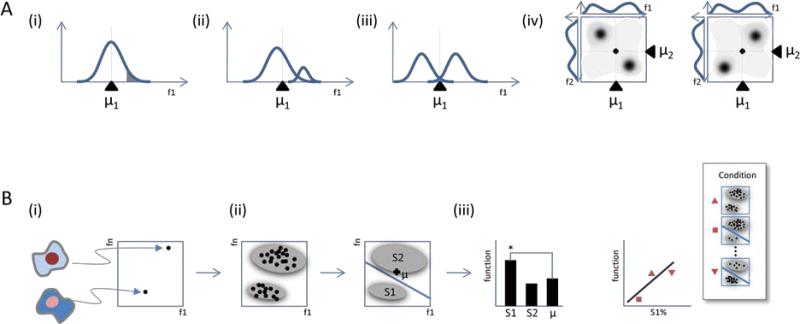
What about cells away from the mean (Figure A(i))? The behavior of such cells may be similar to that of the average behavior of the population, and observed variation summarized by a mean–and perhaps a variance–with no loss of meaningful biological information. Biochemical noise (Elowitz et al., 2002; Newman et al., 2006; Ozbudak et al., 2002; Raser and O'Shea, 2004) may give rise to cellular differences that have no functional significance. So-called “housekeeping” genes are often chosen as references in assays under the assumption that their variation in expression is small and/or biologically unimportant (though, such assumptions are increasingly challenged (Bahar et al., 2006)). As a more specific example, subpopulations of R1-R6 photoreceptor cells in the Drosophila compound eye are considered functionally equivalent with respect to their response and adaptation to light signals (Yau and Hardie, 2009). However, biochemical noise can also lead to important functional differences, such as seen for competence decisions in B. subtilis and selection of color vision photoreceptors in D. maelanogaster (Losick and Desplan, 2008). Recently, it was demonstrated that subpopulations of clonally-derived hematopoietic progenitor cells with low or high expression of the stem cell marker Sca-1 can be in dramatically different transcriptional states and give rise to different lineages (Chang et al., 2008). Therefore, models derived from ensemble averages may not represent individual cell function even for a simple bell-shaped distribution of single-cell measurements.
Figure.
A. Ensemble-averaged measurements can mask information contained in heterogeneity. Behaviors of cells in (i) tail of a distribution (shaded area) or (ii) small subpopulation (at right) may differ from the remainder of the population or from the “mean” behavior (dashed line at μ1). (iii) For bimodal cellular behaviors, a population mean may poorly represent the majority of cells. (iv) Multiple measurements may be required to distinguish different patterns of cellular heterogeneity. Correlated (left) or anticorrelated (right) behaviors of cells may be indistinguishable based on single measurements alone (compare histograms at sides of left and right density plots). Axis labels features f1 and f2 represent single cell measurements (e.g. cell size, division time, or expression of cell surface marker). Dashed lines and triangles indicate population means.
B. Decompositions of heterogeneity may be tested for functionally-important information. (i) Single cell measurements allow cells (left) to be represented as points in a (high-dimensional) feature space (right). (ii) Cell populations can be partitioned into distinct regions of feature space. This partition may be determined manually or automatically. Illustrated is a decomposition into two subpopulations, S1 and S2; μ represents the population mean. (iii) The values of a functional readout for individual subpopulations and population mean can be tested for significant differences within a population (left; * indicates significance). Alternatively, different mixtures of heterogeneity observed from populations in different conditions can be tested for correlation with function (right). “Function” refers to the evaluation of a functional readout over a collection of cells, either at the subpopulation- or whole-population level (e.g. drug sensitivity).
Population distributions can also mask the presence of rare or small subpopulations of cells (Figure A(ii)). In such a case, a population mean may represent the vast majority of cells, yet miss important biology. Recent studies have investigated the presence and dynamics of small subpopulations present within isogenic populations of bacteria. These include the identification of pre-existing subpopulations of slow-growing “persister cells” that have negligible effect on fitness under normal conditions, but enable survival under drug treatment (Balaban et al., 2004). In other studies, variability in the duration of a transiently-differentiated state may increase fitness in fluctuating environments (Cagatay et al., 2009). Similarly, small reservoirs of dormant stem cells have been identified within larger haematopoietic stem cell populations. The rapid reactivation of these subpopulations during times of injury plays a crucial role in re-establishment of homeostasis (Wilson et al., 2008). Finally, cancer is a highly heterogeneous disease (Heppner, 1984; Rubin, 1990). The origins of subpopulations that contribute unequally to disease progression or response to therapeutic intervention are the subject of debate. However, heterogeneity poses practical challenges for building accurate clinical models–particularly ones based on population-averaged measurements–to guide diagnosis and treatment of the disease (Campbell and Polyak, 2007). Even within clonal populations in carefully controlled laboratory conditions, the dynamics and responses of single cancer cells to drugs can vary widely (Cohen et al., 2008; Gascoigne and Taylor, 2008).
An even more problematic situation is when the ensemble-averaged measurement poorly reflects the internal states of the majority of the cells, any subpopulation of cells, or even any single cell (Figure A(iii)). This can occur, for example, when the population contains several dominant, yet phenotypically distinct subpopulations. This situation is observed for populations of immature Xenopus oocytes (Ferrell and Machleder, 1998). Ensemble averages suggest that a graded input of the maturation-inducing hormone progesterone is converted to a graded signaling output, in this case phosphorylation levels of the downstream readout p42 MAPK. Physical models based on these measurements would predict the “average” oocyte would exhibit an intermediate level of commitment for an intermediate level of progesterone stimulation. However, for individual oocytes, commitment is an all-or-nothing response. That is, the population is comprised of two non-overlapping subpopulations–committed and non-committed–with no oocytes at intermediate levels of commitment. Thus, when populations are mixtures of distinct subpopulations, the biological models of relevance are mechanisms operating within each subpopulation.
Signaling networks, even for narrowly-defined biological functions, can be quite complex, and constructing accurate models may require monitoring multiple components (Sachs et al., 2005). New layers of complexity to heterogeneity may be revealed by monitoring multiple readouts simultaneously per cell (Figure A(iv)). At lowest resolution, the state of a population may be approximated by the mean of each readout, such as is routinely performed with western blots or microarrays, though with all of the caveats previously discussed. At an intermediate resolution, the distributions of each readout may be analyzed independently (so-called “univariate” analysis). Though such approaches simplify analysis (Perlman et al., 2004), and may uncover heterogeneity one readout at a time, important relationships among the readouts within individual cells may be missed. At highest resolution, analysis of all cellular readouts from individual cells simultaneously (so-called “multivariate” analysis) may reveal both heterogeneity and important coupling among the readouts. Consider the case of two readouts, whose population distributions are each bimodal (low or high values). In principle, any cell could have one of four possible combinations of (low/high, low/high) values for these two markers. However, analysis of each marker independently would not distinguish, for example, between correlated and anti-correlated expression of the two readouts within individual cells. By contrast, multivariate analysis of the readouts would identify which of the four potential modes were present within any given population. For example, during adipogenesis of the classic 3T3-L1 cell system, readouts such as overall Adiponectin or lipid droplet expression increase from low to high levels suggesting that the “average” cell progresses towards a (high, high) internal state (for (Adiponectin, Lipid droplet)). However, single-cell studies revealed that cells moved from a beginning (low, low) state, to an intermediate (high, low) state, to a final (low, high) state (Loo et al., 2009a). The expected (high, high) cellular state, observed with only small probability, was an illusion of ensemble-averaged measurements. Decomposing heterogeneity was required to develop accurate models of the signaling states of relevance–those occurring in individual adipocytes.
Thus, ensemble measurements can provide accurate descriptions of individual cellular behavior when heterogeneity simply reflects functionally-meaningless fluctuations around a single cellular state. However, when a population is composed of multiple cellular states, ignoring heterogeneity can lead to models that may be accurate at the level of population trends, but do not reflect the signaling states of any individual cell. Hence, the use of ensemble measurements must be justified when moving from descriptive to predictive models.
Interpreting cellular heterogeneity
Heterogeneity is observed for essentially all dimensions of single cell measurements at high resolution. Some well-understood dimensions are routinely used to sort populations into mixtures of cells in distinct and meaningful biological states, such as defined by distinct cell cycle stages or cell types. But what about the multitudes of other dimensions, for which cell-to-cell variation has no obvious or known biological interpretation? In some cases, cellular states can be distinguished by detailed molecular differences. The selection of a specific molecule from a large repertoire of possibilities generates enormous diversity by individual cell variation, such as seen for odorant, cell adhesion, or immune molecules (Coufal et al., 2009; Lomvardas et al., 2006; Morishita and Yagi, 2007; Muotri et al., 2005; Ribich et al., 2006). In other cases, states can be distinguished by large-scale changes, such as signal transduction responses to hormone stimulation (Ferrell and Machleder, 1998), and detailed molecular differences are unimportant–particularly when function is buffered against biochemical fluctuations (Shinar and Feinberg, 2010). A general challenge is to determine which details give rise to biologically-meaningful distinctions within and among populations, and which can be ignored (i.e. when an ensemble average is justified).
Determining whether observed heterogeneity has functional significance requires a framework for quantifying heterogeneity and assessing its information content. An intuitive and tractable approach is to decompose heterogeneous populations into mixtures of simpler, more homogeneous subpopulations, based on the expectation that cells with relatively similar measured states should behave relatively similarly. The biological relevance of such a decomposition could be tested by determining whether different subpopulations, or mixtures of subpopulations, have different functional properties. Decomposition-independent approaches are also possible for testing whether heterogeneity contains information. The assumption is that populations with different distributions have functional differences. For example, mechanisms of drug action can be classified based on comparison of the different distributions of cellular responses that they induce (Perlman et al., 2004). However, informative decompositions can provide useful guides for future studies, including further probing of the molecular states of the subpopulations (Loo et al., 2009a; Loo et al., 2009b). In general, the investigation of heterogeneity requires a combined approach for capturing population statistics from single-cell measurements, identifying patterns of heterogeneity, and testing whether these patterns contain functional information.
Heterogeneity is essentially a statistical properly of cellular populations. A range of cellular behaviors can be estimated from observations of a small number of cells over long times, or a large number of cells at a small number of times. (In theory, if each cell behaved ergodically–allowing averaged behaviors from both observational approaches to be related–these distributions would be equally informative (Brock et al., 2009); however, the ansatz of ergodicity is difficult to test rigorously.) In practice, statistical properties of a cellular population are often estimated from snapshots of large numbers of cells. Single-cell phenotypes be captured by many different measurement technologies (Figure 1B(i)) (Anselmetti, 2009), including flow cytometry, electrophysiology, microscopy, and single cell PCR or sequencing. For some technologies, the choices of cellular features are well defined, while for others the choices are less clear. For example, the total intensity of each labeled biomarker is a standard readout in flow cytometry, while there is virtually no limit to the number of features that can be extracted in microscopy. The desire to extract all relevant information from single-cell assays may require strategies that balance between two, somewhat opposing goals: interpretability and comprehensiveness. Interpretability suggests an intuitive connection between a familiar biological phenotype and the measured values of a feature. Comprehensiveness suggests the ability to capture all important information; large collections of features are measured with the hope that all anticipated (or unanticipated but important) biological variation is captured. In microscopy, strategies striving for interpretability may use expert-selected features, such as cell shape, marker intensity or marker localization, while strategies striving for comprehensiveness may use features derived from general-purpose transformations, such as such as Haralick texture features or Zernike moments that report large numbers of statistical properties of marker staining patterns (Boland and Murphy, 2001). Regardless of the strategy, the outcome is that each individual cell is represented by its collection of extracted features as a point in (high-dimensional) “feature” space, with each axis representing a different measurement. Therefore, populations of cells have been transformed into distributions (of points) in feature space.
The problem of identifying patterns of distinct cellular behaviors in feature space (Figure 2B(ii)) can be reduced to well-studied, analytical and computational problems of decomposing heterogeneous distributions, for which extensive methodology exists and is used in diverse applications ranging from gene function prediction to speech and face recognition (Duda et al., 2001). In supervised approaches, expert knowledge is used to partition the feature space. Approaches range from simple, user-defined thresholds (such as routinely used to separate subpopulations in flow cytometry) to more complex, machine-learning algorithms that iteratively train computers to identify subpopulations based on examples (such as recently developed for high-throughput microscopy screening (Boland and Murphy, 2001; Jones et al., 2009; Ramo et al., 2009; Yin et al., 2008)). In unsupervised approaches, computational algorithms partition distributions in naive, or unbiased, manners. Intuitively, methods such as deterministic _K_-means clustering or probabilistic Gaussian mixture modeling, seek to identify local, high-density regions of phenotype space (Figure 1B(ii)) (Pyne et al., 2009; Slack et al., 2008). There are always questions of whether cellular behaviors can categorized by a finite number of states, and whether a distribution has been partitioned into too few or too many subpopulations. Analytical criteria (Wang et al., 2007), or even visual inspection may be used to provide guidelines for such questions.
However, the ultimate usefulness of a decomposition is the degree to which it reveals biological information for a given functional readout. One can test whether the behaviors of specific subpopulations are significantly different from each other and/or an ensemble average (Figure 1B(iii, left)). As examples, bacterial subpopulations with different growth rates can have different resistances to antibiotics (Balaban et al., 2004), and adherent eukaryotic subpopulations with different microenvironmental properties can have different functional behaviors for viral infection and endocytosis (Snijder et al., 2009). One can also test whether an entire decomposition of heterogeneity is informative (Figure 1B(iii, right)). This case is important when individual subpopulations cannot be physically isolated for functional testing, or interact with one another. As examples, different patterns of heterogeneity for general signaling markers in untreated cancer populations were found to predict differences in drug sensitivities (Singh et al., 2010), and different patterns of heterogeneous signaling responses to drug treatment were used to predict mechanism of drug action (Slack et al., 2008). Further, in tumor samples, different heterogeneous mixtures of isolated tumor infiltrating lymphocytes (TILs) were found to predict tumor reactivity or non-reactivity (Oved et al., 2009). An intriguing possibility is that heterogeneity can serve not only as a passive readout of population state, but also as a predictor of future response to perturbations, or even as a property that can be manipulated to affect a desired population output. Of course, it is not to be expected that every decomposition will contain functional information. Presumably, no significant functional differences should be observed when subpopulations are chosen randomly (i.e. ignoring all feature values), or chosen based on features that are uncorrelated with the functional readout. Taken together, the framework described above serves as starting points for rigorously exploring biological information contained in heterogeneity.
Conclusion
Heterogeneity has been classically observed and speculated to be a fundamental property of cellular systems (Elsasser, 1984; Rubin, 1990). While we focused our discussion on cells, heterogeneity–and the loss of information due to ensemble averages–has been studied at many scales of biology, from single molecules (English et al., 2006) to communities of whole populations (Kimura and Weiss, 1964). Here, we sidestepped difficult and fascinating problems of identifying the origins of cellular heterogeneity (Brock et al., 2009; Muotri et al., 2005; Raj and van Oudenaarden, 2008; Spencer et al., 2009), or understanding its differences between conditions that are physiological and pathophysiological, or in vivo and in vitro. Rather, we focused on the general challenge of characterizing and interpreting information contained within heterogeneity. While well-characterized biological systems may present ready choices for connecting heterogeneity and function, heterogeneity is often observed in experimental settings for which there are no immediate, a priori clues to its meaning or functional relevance. Additionally, interpreting heterogeneity is not solely an analytical challenge of fitting complex, multi-dimensional distributions, as even simple distributions (e.g. observed for the marker Sca-1) can contain subpopulations enriched for biologically-distinct functions. Finally, beyond study of single subpopulations, properties of heterogeneity (e.g. the proportions of subpopulations within an overall population) may serve as informative readouts of population physiology and predictors of responses to perturbations. The ability to transform heterogeneity into a tractable, computable, and bone fide property of cellular populations provides a rigorous starting point for determining which variation is random and which is meaningful, and for building better modeling the behaviors of individual cells.
Acknowledgements
We thank members of the Altschuler and Wu labs, Mike Brown, Nuno Lages, Tom Maniatis, David Mangelsdorf, Rama Ranganathan, and Gürol Süel for critical feedback on this manuscript. This research was supported by National Institute of Health grants R01 GM081549 (L.F.W.) and R01 GM085442 (S.J.A.), the Endowed Scholars program at UT Southwestern Medical Center (L.F.W. and S.J.A.), the Welch Foundation I-1644 (L.F.W.) and I-1619 (S.J.A.), the Rita Allen Foundation (S.J.A.) and the Mary Kay Ash Charitable Foundation (S.J.A.).
Footnotes
1
Here, population-averages can refer to experimental measurements derived from assays that pool analytes from large numbers of cells (e.g. immunoblots or microarrays), or mathematical averages taken over distributions of single-cell measurements (e.g. flow cytometry or microscopy).
References
- Anselmetti D, editor. Single Cell Analysis: Technologies and Applications. VCH; Wiley: 2009. [Google Scholar]
- Bahar R, Hartmann CH, Rodriguez KA, Denny AD, Busuttil RA, Dolle ME, Calder RB, Chisholm GB, Pollock BH, Klein CA, et al. Increased cell-to-cell variation in gene expression in ageing mouse heart. Nature. 2006;441:1011–1014. doi: 10.1038/nature04844. [DOI] [PubMed] [Google Scholar]
- Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. Bacterial persistence as a phenotypic switch. Science. 2004;305:1622–1625. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- Boland MV, Murphy RF. A neural network classifier capable of recognizing the patterns of all major subcellular structures in fluorescence microscope images of HeLa cells. Bioinformatics. 2001;17:1213–1223. doi: 10.1093/bioinformatics/17.12.1213. [DOI] [PubMed] [Google Scholar]
- Brock A, Chang H, Huang S. Non-genetic heterogeneity--a mutation-independent driving force for the somatic evolution of tumours. Nat Rev Genet. 2009;10:336–342. doi: 10.1038/nrg2556. [DOI] [PubMed] [Google Scholar]
- Cagatay T, Turcotte M, Elowitz MB, Garcia-Ojalvo J, Suel GM. Architecture-Dependent Noise Discriminates Functionally Analogous Differentiation Circuits. Cell. 2009 doi: 10.1016/j.cell.2009.07.046. [DOI] [PubMed] [Google Scholar]
- Campbell LL, Polyak K. Breast tumor heterogeneity: cancer stem cells or clonal evolution? Cell Cycle. 2007;6:2332–2338. doi: 10.4161/cc.6.19.4914. [DOI] [PubMed] [Google Scholar]
- Chang HH, Hemberg M, Barahona M, Ingber DE, Huang S. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature. 2008;453:544–547. doi: 10.1038/nature06965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AA, Geva-Zatorsky N, Eden E, Frenkel-Morgenstern M, Issaeva I, Sigal A, Milo R, Cohen-Saidon C, Liron Y, Kam Z, et al. Dynamic proteomics of individual cancer cells in response to a drug. Science. 2008;322:1511–1516. doi: 10.1126/science.1160165. [DOI] [PubMed] [Google Scholar]
- Coufal NG, Garcia-Perez JL, Peng GE, Yeo GW, Mu Y, Lovci MT, Morell M, O'Shea KS, Moran JV, Gage FH. L1 retrotransposition in human neural progenitor cells. Nature. 2009;460:1127–1131. doi: 10.1038/nature08248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. 2 edn Interscience; Wiley: 2001. [Google Scholar]
- Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- Elsasser WM. Outline of a theory of cellular heterogeneity. Proc Natl Acad Sci U S A. 1984;81:5126–5129. doi: 10.1073/pnas.81.16.5126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- English BP, Min W, van Oijen AM, Lee KT, Luo G, Sun H, Cherayil BJ, Kou SC, Xie XS. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat Chem Biol. 2006;2:87–94. doi: 10.1038/nchembio759. [DOI] [PubMed] [Google Scholar]
- Ferrell JE, Jr., Machleder EM. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science. 1998;280:895–898. doi: 10.1126/science.280.5365.895. [DOI] [PubMed] [Google Scholar]
- Gascoigne KE, Taylor SS. Cancer cells display profound intra- and interline variation following prolonged exposure to antimitotic drugs. Cancer Cell. 2008;14:111–122. doi: 10.1016/j.ccr.2008.07.002. [DOI] [PubMed] [Google Scholar]
- Heppner GH. Tumor heterogeneity. Cancer Res. 1984;44:2259–2265. [PubMed] [Google Scholar]
- Jones TR, Carpenter AE, Lamprecht MR, Moffat J, Silver SJ, Grenier JK, Castoreno AB, Eggert US, Root DE, Golland P, et al. Scoring diverse cellular morphologies in image-based screens with iterative feedback and machine learning. Proc Natl Acad Sci U S A. 2009;106:1826–1831. doi: 10.1073/pnas.0808843106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Weiss GH. The Stepping Stone Model of Population Structure and the Decrease of Genetic Correlation with Distance. Genetics. 1964;49:561–576. doi: 10.1093/genetics/49.4.561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomvardas S, Barnea G, Pisapia DJ, Mendelsohn M, Kirkland J, Axel R. Interchromosomal interactions and olfactory receptor choice. Cell. 2006;126:403–413. doi: 10.1016/j.cell.2006.06.035. [DOI] [PubMed] [Google Scholar]
- Loo LH, Lin HJ, Singh DK, Lyons KM, Altschuler SJ, Wu LF. Heterogeneity in the physiological states and pharmacological responses of differentiating 3T3-L1 preadipocytes. The Journal of Cell Biology. 2009a;187:375–384. doi: 10.1083/jcb.200904140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loo LH, Lin HJ, Steininger RJ, 3rd, Wang Y, Wu LF, Altschuler SJ. An approach for extensibly profiling the molecular states of cellular subpopulations. Nat Methods. 2009b;6:759–765. doi: 10.1038/nmeth.1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losick R, Desplan C. Stochasticity and cell fate. Science. 2008;320:65–68. doi: 10.1126/science.1147888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morishita H, Yagi T. Protocadherin family: diversity, structure, and function. Curr Opin Cell Biol. 2007;19:584–592. doi: 10.1016/j.ceb.2007.09.006. [DOI] [PubMed] [Google Scholar]
- Muotri AR, Chu VT, Marchetto MC, Deng W, Moran JV, Gage FH. Somatic mosaicism in neuronal precursor cells mediated by L1 retrotransposition. Nature. 2005;435:903–910. doi: 10.1038/nature03663. [DOI] [PubMed] [Google Scholar]
- Newman JR, Ghaemmaghami S, Ihmels J, Breslow DK, Noble M, DeRisi JL, Weissman JS. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature. 2006;441:840–846. doi: 10.1038/nature04785. [DOI] [PubMed] [Google Scholar]
- Oved K, Eden E, Akerman M, Noy R, Wolchinsky R, Izhaki O, Schallmach E, Kubi A, Zabari N, Schachter J, et al. Predicting and controlling the reactivity of immune cell populations against cancer. Mol Syst Biol. 2009;5:265. doi: 10.1038/msb.2009.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozbudak EM, Thattai M, Kurtser I, Grossman AD, van Oudenaarden A. Regulation of noise in the expression of a single gene. Nat Genet. 2002;31:69–73. doi: 10.1038/ng869. [DOI] [PubMed] [Google Scholar]
- Perlman ZE, Slack MD, Feng Y, Mitchison TJ, Wu LF, Altschuler SJ. Multidimensional drug profiling by automated microscopy. Science. 2004;306:1194–1198. doi: 10.1126/science.1100709. [DOI] [PubMed] [Google Scholar]
- Pyne S, Hu X, Wang K, Rossin E, Lin TI, Maier LM, Baecher-Allan C, McLachlan GJ, Tamayo P, Hafler DA, et al. Automated high-dimensional flow cytometric data analysis. Proc Natl Acad Sci U S A. 2009;106:8519–8524. doi: 10.1073/pnas.0903028106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A, van Oudenaarden A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell. 2008;135:216–226. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramo P, Sacher R, Snijder B, Begemann B, Pelkmans L. CellClassifier: supervised learning of cellular phenotypes. Bioinformatics. 2009;25:3028–3030. doi: 10.1093/bioinformatics/btp524. [DOI] [PubMed] [Google Scholar]
- Raser JM, O'Shea EK. Control of stochasticity in eukaryotic gene expression. Science. 2004;304:1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribich S, Tasic B, Maniatis T. Identification of long-range regulatory elements in the protocadherin-alpha gene cluster. Proc Natl Acad Sci U S A. 2006;103:19719–19724. doi: 10.1073/pnas.0609445104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin H. The significance of biological heterogeneity. Cancer Metastasis Rev. 1990;9:1–20. doi: 10.1007/BF00047585. [DOI] [PubMed] [Google Scholar]
- Sachs K, Perez O, Pe'er D, Lauffenburger DA, Nolan GP. Causal protein-signaling networks derived from multiparameter single-cell data. Science. 2005;308:523–529. doi: 10.1126/science.1105809. [DOI] [PubMed] [Google Scholar]
- Shinar G, Feinberg M. Structural sources of robustness in biochemical reaction networks. Science. 2010;327:1389–1391. doi: 10.1126/science.1183372. [DOI] [PubMed] [Google Scholar]
- Singh DK, Ku CJ, Wichaidit C, Steinenger RJI, Wu LF, Altschuler SJ. Patterns of basal signaling heterogeneity can distinguish cellular populations with different drug sensitivities. Molecular Systems Biology. 2010 doi: 10.1038/msb.2010.22. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slack MD, Martinez ED, Wu LF, Altschuler SJ. Characterizing heterogeneous cellular responses to perturbations. Proc Natl Acad Sci U S A. 2008;105:19306–19311. doi: 10.1073/pnas.0807038105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snijder B, Sacher R, Ramo P, Damm EM, Liberali P, Pelkmans L. Population context determines cell-to-cell variability in endocytosis and virus infection. Nature. 2009;461:520–523. doi: 10.1038/nature08282. [DOI] [PubMed] [Google Scholar]
- Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK. Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature. 2009;459:428–432. doi: 10.1038/nature08012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M, Zhou X, King RW, Wong ST. Context based mixture model for cell phase identification in automated fluorescence microscopy. BMC Bioinformatics. 2007;8:32. doi: 10.1186/1471-2105-8-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson A, Laurenti E, Oser G, van der Wath RC, Blanco-Bose W, Jaworski M, Offner S, Dunant CF, Eshkind L, Bockamp E, et al. Hematopoietic stem cells reversibly switch from dormancy to self-renewal during homeostasis and repair. Cell. 2008;135:1118–1129. doi: 10.1016/j.cell.2008.10.048. [DOI] [PubMed] [Google Scholar]
- Yau KW, Hardie RC. Phototransduction motifs and variations. Cell. 2009;139:246–264. doi: 10.1016/j.cell.2009.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin Z, Zhou X, Bakal C, Li F, Sun Y, Perrimon N, Wong ST. Using iterative cluster merging with improved gap statistics to perform online phenotype discovery in the context of high-throughput RNAi screens. BMC Bioinformatics. 2008;9:264. doi: 10.1186/1471-2105-9-264. [DOI] [PMC free article] [PubMed] [Google Scholar]