Cellular Proteomes Have Broad Distributions of Protein Stability (original) (raw)
Abstract
Biological cells are extremely sensitive to temperature. What is the mechanism? We compute the thermal stabilities of the whole proteomes of Escherichia coli, yeast, and Caenorhabditis elegans using an analytical model and an extensive database of stabilities of individual proteins. Our results support the hypothesis that a cell's thermal sensitivities arise from the collective instability of its proteins. This model shows a denaturation catastrophe at temperatures of 49–55°C, roughly the thermal death point of mesophiles. Cells live on the edge of a proteostasis catastrophe. According to the model, it is not that the average protein is problematic; it is the tail of the distribution. About 650 of E. coli's 4300 proteins are less than 4 kcal mol−1 stable to denaturation. And upshifting by only 4° from 37° to 41°C is estimated to destabilize an average protein by nearly 20%. This model also treats effects of denaturants, osmolytes, and other physical stressors. In addition, it predicts the dependence of cellular growth rates on temperature. This approach may be useful for studying physical forces in biological evolution and the role of climate change on biology.
Introduction
Small changes in temperature can have a large impact on biological cells. Changes of a few degrees can reversibly rescue cancer-prone fibroblast cells from cancer (1), selectively kill pancreatic cancer cells (the Lance Armstrong effect) (2,3), or shift the ratio of males to females in reptile embryos (4,5). Temperature is a key coupler of the biosphere to the geosphere: few-degree changes are believed to have caused major evolutionary marine extinctions and mammalian turnover (6,7). Small differences in temperature can affect rates of genetic divergence and speciation (8) and can be the difference between the optimal and dangerous temperatures for some species (9). Cells have evolved substantial machinery to handle the thermal denaturation of the proteome including stress-responsive signaling pathways that transcriptionally upregulate proteostasis capacity including chaperones, chaperonins, folding enzymes, and coupled disaggregation and degradation activities (10,11). When heat-shock protein HSP90 is impaired, improperly chaperoned proteins are prone to faster evolution and cancer (12,13).
By what mechanism are cells so sensitive to temperature? The breadth of consequences listed above points to a general mechanism rather than to a few specific genes or proteins. Biological thermal sensitivities are not likely due to physical kinetics or diffusion, which are proportional only to RT, or to kinetic activation barriers, which appear to be too high by >400 kJ/mol (14,15). Because proteins are both the least stable and most common biomolecule (Escherichia coli is ∼17% protein and 7% nucleic acids by volume), it is plausible that such high thermal sensitivities are because cellular proteins are poised near their denaturation phase boundaries (14,15). In support of this view, cells undergo sharp death transitions from external physical factors such as high pressure, chemical denaturants, toxic material, and acids or bases—all the types of agents that can sharply denature proteins.
Model
Here, we develop a quantitative model for exploring the hypothesis that cells live near the edge of a proteostasis catastrophe. Our calculations are based on two observations. First, extensive data on the reversible folding stabilities of 63 globular proteins show that the dominant dependence of the thermal properties of proteins is simply on the chain length of the protein (16,17). There is little systematic dependence of a protein's stability on its native fold, its secondary or tertiary structure, or its amino acid composition (17). This data has recently been captured in a model for the free energy of folding, Δ_G_, as a function of temperature, T, and chain length, L (17),
| ΔG(T,L)=ΔH(L)+ΔCp(L)(T−Th)−TΔS(L)−TΔCp(L)lnTTs, | (1) |
|---|
where ΔH(L)=(−5.03L−41.6) kJ/mol is the average enthalpy of folding at Th=373.5 arising due to the formation of amino acid contacts upon folding, ΔCp(L)=(−0.062L+0.53) kJ/(mol-K) is the average heat capacity change upon folding, ΔS(L)=(−16.8L−85) J/(mol-K) is the chain entropy of folding at Ts=385K, the temperature at which the entropy from the hydrophobic effect is zero (16,17), and Th=373.5 K is the average temperature at which the enthalpy of folding from the hydrophobic effect is zero. Because these data show that the key variable determining a protein's thermal stability is its chain length, they open the possibility for studying whole proteomes, since the chain lengths of all the proteins in a proteome are directly available from genomic data. It is known that the distribution of chain lengths over the proteomes from 22 fully sequenced organisms can be approximated by a gamma distribution (18):
| p(L)=Lα−1exp−L/θΓ(α)θα. | (2) |
|---|
The two parameters of the protein chain-length distribution of a proteome, α and θ, are obtained from the measured mean and variance observed for a given proteome, using the expressions
| 〈L〉=αθand〈(ΔL)2〉=αθ2, | (3) |
|---|
where the brackets 〈…〉 indicate averaging over all the proteins in a proteome. For E. coli, for example, the average protein length is 〈L〉≈325, and α=2.33 (18). Using this model, we find the following results.
Results
First, we can compute the average stability of a cell's proteome. For E. coli, at 37°C, the average protein has a folding free energy of 〈ΔG〉=−11.9RT≈−7.1 kcal/mol, where RT is the gas constant multiplied by absolute temperature (for which we used T = 300 K here). For yeast (Saccharomyces cerevisiae (SCE)), for which 〈L〉≈475 and α=1.56, the average stability is 〈ΔG〉=−14.7RT≈−8.8 kcal/mol. For the worm (Caenorhabditis elegans (CEL)), for which 〈L〉≈425 and α=1.23, the average protein stability is 〈ΔG〉=−13.7RT≈−8.2 kcal/mol.
Hundreds of cellular proteins are marginally stable
Second, Figs. 1 and 2 show the distribution of the free energies of folding of all the proteins in the proteome, a key property of proteomes that is not yet accessible by experiments. The model indicates that the distribution of protein stabilities throughout a proteome is very broad. In Fig. 1, we also compare to the ProTherm database of protein stabilities and evolutionary model due to Zeldovich et al (19,20). ProTherm is nonsorted data, from many different organisms, and taken under different conditions, so it is not strictly comparable to the fully temperature-dependent species-specific quantities that we compute here. The value of comparing to ProTherm is that it contains a large number of proteins, and therefore gives some evidence that our predictions would not change much if we had parameterized them on a database bigger than curated set of 63 proteins that we used following Robertson Murphy dataset (16,17).The standard deviations of the stability distributions are 4.3 RT, 7.5 RT, and 7.5 RT for E. coli, yeast, and worm, respectively. A key conclusion from the model is that these variances are not negligible. Nearly 650 proteins, or ∼15% of E. coli's proteome, are <4 kcal/mol stable against denaturation (one in a thousand protein molecules denatured), indicating that cells live on the margins of a proteostasis catastrophe. Small stresses on cells could unfold a significant fraction of a cell's proteome. The smallest proteins are the least stable, on average. Perhaps the temperature sensors for evolutionary change in biology come from the large pool of the cell's smallest proteins.
Figure 1.
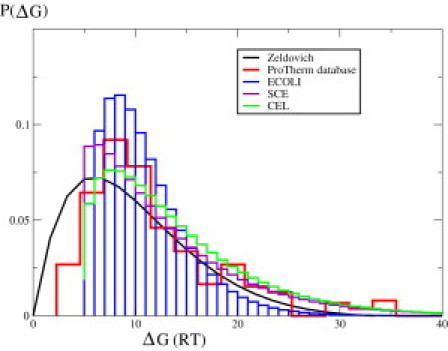
Distribution of free energies of folding of the proteins in the proteomes of E. coli (blue), yeast (SCE; violet), and worm (CEL; green) at 37°C. The free-energy bin size is 1_RT_. Red shows the distribution obtained from the ProTherm database (19,20) for comparison. The black curve represents the infinite-time solution of an evolutionary model (20).
Figure 2.
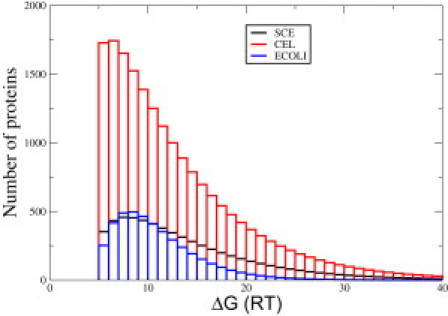
Distribution of free energies of folding of the proteins in the proteomes of E. coli, yeast (SCE), and worm (CEL) at 37°C. The free-energy bin size is 1_RT_. The area under each curve equals the total number of proteins in the proteome (4300 for E. coli, 6000 for SCE, and 19,500 for CEL). Color figure is available online.
What we believe is novel in this model is not the calculation of average stability, but the full distribution. It is well known that the average protein is stable by 5–10 kcal/mol. This could be regarded as implying that proteins are quite stable, and therefore that proteomes should be quite stable, too. However, the conclusion from this model is quite different: it is the tail of the distribution that is problematic, not the average protein. This model says that proteome instability arises because of the shape of the distribution: hundreds of proteins are far less stable than the average protein.
The proteome denatures in a sharp transition
Killing cells by heating them is important for sterilization and pasteurization. Thermal cell death is a sharp transition, like a phase change. Sharp transitions are also observed for the typical denaturation of individual proteins. What is not known, however, is whether the collective denaturations of all cell proteins coincide with each other as a collective sharp transition of the whole proteome. Our model gives quantitative support to this hypothesis (see Fig. 3). Rearranging Eq. 1 gives the fraction, η(L), of proteins of length L that are unfolded at temperature T:
| η(L,T)=11+exp(−ΔG(L,T)/RT) | (4) |
|---|
Figure 3.
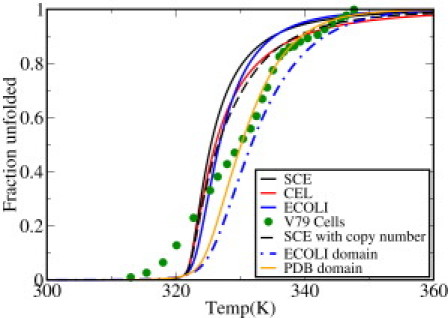
Fraction of proteins unfolded in the proteomes of E. coli, yeast (SCE), and worm (CEL) as a function of temperature. Solid circles show the experimentally measured fraction of denatured proteins as a function of temperature for mammalian V79 cells using differential scanning calorimetry (14). Black dashed line shows the prediction based on the copy-number distribution from yeast. Blue dashed line shows the results based on domain-length distribution (33) in the E. coli genome. Orange line shows the same based on domain-length distribution obtained from Protein Data Bank structures (32). Color figure is available online.
Hence, the average fraction of the whole proteome that is unfolded at temperature T is
| 〈η(T)〉=∫η(L,T)p(L)dL. | (5) |
|---|
Is the equilibrium cell-death temperature of mesophiles universal?
The model predicts a denaturation catastrophe around 49–55°C, consistent with the observed cell-death temperature in E. coli (21). It is interesting to note that the model also predicts that all mesophiles should have essentially the same equilibrium cell-death temperature. This universality is predicted because the denaturation temperature (the point at which Δ_G_ = 0) is approximately independent of the protein chain length. In support of this prediction, Fig. 3 shows the results of recent differential scanning calorimetry experiments on V79 cells (14), indicating a transition midpoint very close to the temperature predicted by the model, with no parameters in the model adjusted for that organism. However, further experiments will be required to establish universality more definitively.
Our model predicts that 1% of the E. coli proteome should denature at T = 47°C and 50% should denature at T = 54°C. Because our model is based only on the physics of protein folding and denaturation, it cannot address the biological question of what fraction of proteins must denature to be lethal to the cell. However, when combined with evidence that the highest survival temperature in E. coli correlates with peaks in differential scanning calorimetry measurements of protein denaturation (14), our model implies that at the thermal-death midpoint, ∼4% of the proteome is denatured.
Small changes in temperature can affect proteostasis
We now compute how a small shift in temperature, a 4°C change from 37° to 41°, affects proteome stability. Such shifts are common in biological experiments. Fig. 4 shows the result that a 4°C increase in temperature destabilizes the proteome significantly. Two measures of this destabilization are that 1), heating decreases the average protein stability in E. coli by 20%, i.e., a shift from 7 kcal/mol to 5.6 kcal/mol; and 2), ∼10% of the proteome (∼400 proteins in E. coli) is destabilized by >2.4 kcal-mol−1. As a metaphor, if you changed the average component in an electronic device, such as a television, by 25%—which would be more than fivefold outside the range of typical electronic component tolerances of 5%—it would likely destroy the function of the device. Animals have thermal regulatory systems and biological cells have thermal buffering machinery, such as chaperone proteins and the unfolded protein response. These calculations just reflect the extra burden that is imposed on cells by applied thermal stresses.
Figure 4.
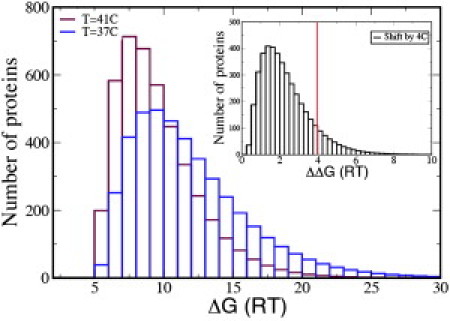
Distribution of free energies at 37°C (blue) and 41°C (maroon) for E. coli. (Inset) Number of proteins with a given free-energy shift due to 4°C change in temperature. The bin size is 0.25_RT_. The line indicates that 10% of the proteome (∼400 proteins) of E. coli are destabilized by >∼4_RT_ ≈ 2.4 kcal/mol. Color figure is available online.
As an approximate single-number measure of the health of the proteome, we define the proteostasis potential, Ψ, as
| Ψ(x,T)=〈ΔG(x,T)〉〈ΔG0〉. | (6) |
|---|
Ψ is the average stability free energy for a proteome, under condition x and temperature T, divided by the average stability free energy of the wild-type version of the proteome at the point of the maximum average free energy. Here, we take Δ_G_(0) to be at 17°C, where the stability of the ideal proteome is maximal. The simplified expression for ψ(x,T) can be computed using Eqs. 6 and 7 for x molar urea:
| 〈ΔG(x,T)〉=〈L〉[−18.127−.0552x+.0452T−.062TlnT385]+239.555−.615T+.53TlnT385, | (7) |
|---|
with 〈ΔG0〉=〈ΔG(0,290)〉. Thus, Ψ is a simple measure of proteome health, ranging from Ψ = 0 at the proteome denaturation midpoint (55°C in this case) to Ψ = 1 for a maximally healthy proteome. Ψ may be useful for quantitating the effects of chemicals, oxidation, disease, or aging on proteostatic health. The premise for this definition, which is only an approximation, is that all proteins are equivalent in terms of their contributions to proteostasis. We find that Ψ changes markedly with small changes in temperature. Fig. 5 shows that heating by 10°C from physiological temperature (37°C) decreases the proteostasis potential from 0.7 to 0.3. We note that the optimal temperature for proteome stability coincides neither with physiological temperature, 37°C, nor with a cell's functionally optimal temperature (22). We also studied cold denaturation of the proteome using Eq. 1. We find a cooperative transition for that process too, with a midpoint around 255 K.
Figure 5.
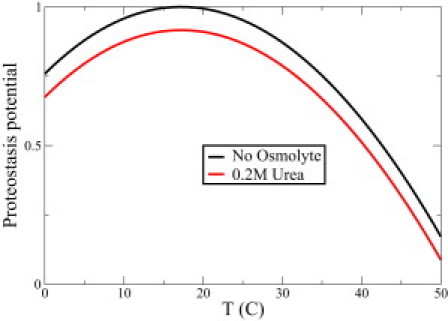
Proteostasis potential Ψ(T) versus temperature for E. coli with no osmolyte (black) and E. coli with 0.2 M urea denaturant (red). Color figure is available online.
Chemicals: denaturants, osmolytes, and salts
With the model presented here, we can also compute how the proteostasis of a cell depends on salts, pH, chemical denaturants and osmolytes, and steric confinement (17). We find, for example, that 0.2 M urea, or some equivalent destabilizer, should denature proteomes of E. coli by about the same amount as heating a cell by ∼10°C from 290 K. We find that osmolytes, which stabilize proteins, should stabilize proteomes, consistent with observations that osmolytes make sick cells healthy under some conditions (23,24) and consistent with the importance of osmolyte balance in cells (25).
Growth-rate calculation and comparison with experiments
In this section, we use the model to compute cellular growth rates, r(T), as a function of temperature T. For a given proteome, we take
| r(T)=r0exp(−ΔH†/RT)∏i=1Γ11+exp(ΔGi/RT), | (8) |
|---|
where _r_0 is an intrinsic rate. ΔH†represents an Arrhenius activation barrier for a metabolic reaction rate (26,27). The product term describes the stabilities of proteins i=1,2,3,…,Γ, where Γ is the number of essential proteins that are important for the growth rate. We assume that the overall growth rate is a product of the fraction folded of all the essential proteins. This captures the fact that compromising the stability of any one of these essential proteins will diminish the overall growth rate. Equation 8 has already been successfully used to model growth rates in different organisms (26,27). Taking the logarithm of the rate, Eq. 8 becomes
| logr(T)=logr0−ΔH†RT−∑i=1Γlog(1+exp(ΔGi/RT)). | (9) |
|---|
We approximate the sum as the integral over the entire proteome free-energy distribution, P(Δ_G_), and express the average rate (26) as
| 〈logr(T)〉=logr0−ΔH†RT−Γ∫log(1+exp(ΔG/RT))P(ΔG)dΔG. | (10) |
|---|
Equation 10 predicts that cellular growth rates increase with temperature at low temperature due to the assumed activated process and that growth rates decrease at high temperatures due to proteome denaturation (see Fig. 6). This equation predicts maximum growth at an optimum growth temperature. These curves are highly asymmetrical near their temperature of maximum growth and our model predicts this well. For this calculation, our model requires two free parameters, ΔH† and Γ, which we determine by fitting the experimental data for E. coli O111:H (28), shown in Fig. 6. The fitted value of ΔH† is 14 kcal/mol, which is in the range of previous estimates (27,26). The value of Γ is ∼236, which is also reasonable, given estimates that the number of essential genes in E. coli is ∼300 (29).
Figure 6.
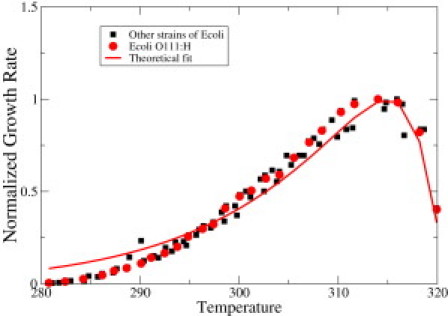
Red circles denote growth rate as a function of temperature for E. coli O111:H (28). In the y axis, we plot growth rate normalized with respect to the maximal growth rate. Solid red line is the fit to this data using Eq. 10. The value of Δ_H_† is 14.2 kcal/mol and Γ is 236. Black squares denote data for other strains of E. coli (28) for comparison purposes. Color figure is available online.
Accounting for multidomains in protein stabilities
Our model described above treats only single domains of proteins. However, many proteins have multiple domains (30). It has been estimated that multidomain proteins constitute more than two-thirds of the genome in prokaryotes (30,31) and possibly an even larger fraction in eukaryotes (30,32). In this section, we describe how we treat multidomains. First, we seek the stabilities of the individual domains. Our estimate above, which is based on the chain lengths of full proteins, is likely to overestimate the stabilities of proteins with multiple domains. Instead, we calculate the stabilities of the domains themselves. We use the domain distribution of Lipman et al. (33), based on a nonredundant set of domains and a domain-identification algorithm (34). An advantage of using this method is that it does not define domains by conserved regions. Our results based on this distribution are shown in Fig. 3 (blue dash-dotted line). Here, we show results for domains only in the E. coli proteome. The results are nearly identical for the other proteomes. This also reflects the fact that ∼50% of the distribution has a stability of ≤4 kcal mol−1 (Fig. 7, red), a number significantly higher than the calculation based on the full protein chain. Based on this analysis, the average stability now becomes 8.3 RT, or ∼5 kcal/mol for E. coli, indicating less stability than predicted based on the calculations described above. We augment this by a separate independent calculation where we use the length distribution of PDB domains (32) only, which is not specific to any organism. That calculation indicates the same trend as shown by the orange line in Figs. 3 and 7. A key result, shown in Fig. 3, is that accounting for domains decreases the stability even further and makes the proteome denaturation curve less cooperative.
Figure 7.
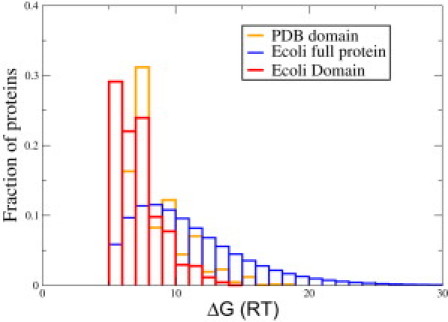
Comparison of free-energy distribution in E. coli at 37°C based on whole-length protein (blue) and domains (red) using data from Lipman (33). We also plot the results based on PDB domain distributions (orange) (32). Inclusion of domains shows that ∼50% of the distribution has stability of <4 kcal/mol. Color figure is available online.
Discussion
There are some caveats to the model presented here. First, this model only applies to mesophilic proteins, which dominate the available database of stabilities. Also, although most of our comparisons are with the limited database of 63 proteins of Robertson and Murphy, we have made another test with the much larger ProTherm database (19) (Fig. 1). Although various limitations of the databases were noted by Zeldovich et al. (20), we see no significant dependence of our predictions on the size of the database. Second, recent work shows that proteins from thermophilic organisms have evolved a different set of thermal parameters (35). It is also possible that evolutionary pressure could stabilize shorter chains, perhaps accounting for the small discrepancy between the evolutionary model and our thermodynamic model. Third, the distributions of protein copy numbers are not known for cells except yeast, so we assumed equal copy numbers. However, to check this, we performed a modified calculation using the copy numbers measured in yeast (36,37) (Fig. 3, dashed line). Accounting for approximate copy numbers shifts the transition midpoint temperature by ∼1% and decreases the cooperativity of the transition (in slightly better agreement with the experimental data on V79). Fourth, it is possible that protein stabilities could be different inside cells than in vitro due to protein-protein interaction and other factors. However, two key experimental studies show that protein stability in cells is approximately the same as in vitro (38,39). As an additional check, we computed the effects of macromolecular crowding using the model of Zhou (40), using a crowding-agent concentration of 400 g/L to mimic cellular conditions. That model predicts that such effects, when combined with copy number calculation mentioned above for SCE, are not significant, shifting the proteostasis edge by <1%. Also, present data are not sufficient to allow us to improve upon our assumption that folding is two-state, which will overestimate the true cooperativity. Fifth, other factors—such as heating rates, protein aggregation, and metabolism—may affect how cell proteomes respond to temperature, but there is insufficient experimental information to address those here. We consider here only slow (equilibrium) heating. Finally, some proteins are intrinsically disordered, with unknown implications for stability; however, evidence for chain-length independence of these proteins in the proteome (41) supports neglecting such effects here.
Summary
We give an equation for computing the distribution of stabilities of the proteins in a cell's proteome. We apply it to the proteomes of E. coli, yeast, and C. elegans. We present three main findings. First, the proteome undergoes a collective denaturation catastrophe, in which all the cell proteins unfold over a narrow temperature range. The agreement of this proteome denaturation point with measured cell-death temperatures supports the view that thermal death in cells can result primarily from large-scale denaturation of its proteome. Second, we find that cellular proteomes are marginally stable: several hundreds of the proteins in E. coli are within a few RT of unfolding under biological conditions. These numbers could be even higher when one considers the domains of the proteome. Third, heating a normal cell by a few degrees Celsius can cause many proteins to become marginally stable. This model may be useful for exploring how cells are affected by stressors, aging, disease, and climate changes.
Acknowledgments
We acknowledge stimulating discussions with Asoke Chandra Ghose, Banu Ozkan, Eugene Shakhnovich, Hue Sun Chan, Hannes Braberg, John Chodera, John Van Drie, Ilya Chorny, Larry Schweitzer, Martin Margittai, Phill Payne, Jurij Lah, Steve Presse, and Sean Shaheen. We also thank the reviewers for helpful comments and motivating the domain calculations.
K.D. appreciates support from National Institutes of Health grant GM34993 and K.G. acknowledges a Faculty Research Fellowship award grant from the University of Denver.
References
- 1.Weinberg R. Garland Science; London: 2007. The Biology of Cancer. [Google Scholar]
- 2.Coffey D.S., Getzenberg R.H., DeWeese T.L. Hyperthermic biology and cancer therapies: a hypothesis for the “Lance Armstrong effect”. JAMA. 2006;296:445–448. doi: 10.1001/jama.296.4.445. [DOI] [PubMed] [Google Scholar]
- 3.Vertrees R.A., Zwischenberger J.B., Pencil S.D. Oncogenic ras results in increased cell kill due to defective thermoprotection in lung cancer cells. Ann. Thorac. Surg. 2000;69:1675–1680. doi: 10.1016/s0003-4975(00)01421-1. [DOI] [PubMed] [Google Scholar]
- 4.Ferguson M.W., Joanen T. Temperature of egg incubation determines sex in Alligator mississippiensis. Nature. 1982;296:850–853. doi: 10.1038/296850a0. [DOI] [PubMed] [Google Scholar]
- 5.Webb G., Cooper-Preston H. Effects of incubation temperature on crocodiles and the evolution of reptilian oviparity. Am. Zool. 1989;29:953–971. [Google Scholar]
- 6.Kennett J., Stott L. Abrupt deep-sea warming, palaeoceanographic changes and benthic extinctions at the end of the Palaeocene. Nature. 1991;353:225–229. [Google Scholar]
- 7.Ivany L.C., Patterson W.P., Lohmann K.C. Cooler winters as a possible cause of mass extinctions at the Eocene/Oligocene boundary. Nature. 2000;407:887–890. doi: 10.1038/35038044. [DOI] [PubMed] [Google Scholar]
- 8.Allen A.P., Gillooly J.F., Brown J.H. Kinetic effects of temperature on rates of genetic divergence and speciation. Proc. Natl. Acad. Sci. USA. 2006;103:9130–9135. doi: 10.1073/pnas.0603587103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brett J. Energetic responses of salmon to temperature-study of some thermal relations in physiology and freshwater ecology of sockeye salmon (Oncorhynchus nerka) Am. Zool. 1971;11:99–113. [Google Scholar]
- 10.Balch W.E., Morimoto R.I., Kelly J.W. Adapting proteostasis for disease intervention. Science. 2008;319:916–919. doi: 10.1126/science.1141448. [DOI] [PubMed] [Google Scholar]
- 11.Dobson C.M. Protein folding and misfolding. Nature. 2003;426:884–890. doi: 10.1038/nature02261. [DOI] [PubMed] [Google Scholar]
- 12.Rutherford S.L., Lindquist S. Hsp90 as a capacitor for morphological evolution. Nature. 1998;396:336–342. doi: 10.1038/24550. [DOI] [PubMed] [Google Scholar]
- 13.Queitsch C., Sangster T.A., Lindquist S. Hsp90 as a capacitor of phenotypic variation. Nature. 2002;417:618–624. doi: 10.1038/nature749. [DOI] [PubMed] [Google Scholar]
- 14.Lepock J.R. Measurement of protein stability and protein denaturation in cells using differential scanning calorimetry. Methods. 2005;35:117–125. doi: 10.1016/j.ymeth.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 15.Westra A., Dewey W.C. Variation in sensitivity to heat shock during the cell-cycle of Chinese hamster cells in vitro. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 1971;19:467–477. doi: 10.1080/09553007114550601. [DOI] [PubMed] [Google Scholar]
- 16.Robertson A.D., Murphy K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1268. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 17.Ghosh K., Dill K.A. Computing protein stabilities from their chain lengths. Proc. Natl. Acad. Sci. USA. 2009;106:10649–10654. doi: 10.1073/pnas.0903995106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang J. Protein-length distributions for the three domains of life. Trends Genet. 2000;16:107–109. doi: 10.1016/s0168-9525(99)01922-8. [DOI] [PubMed] [Google Scholar]
- 19.Kumar M.D., Bava K.A., Sarai A. ProTherm and ProNIT: thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2006;34(Database issue):D204–D206. doi: 10.1093/nar/gkj103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zeldovich K.B., Chen P., Shakhnovich E.I. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc. Natl. Acad. Sci. USA. 2007;104:16152–16157. doi: 10.1073/pnas.0705366104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ratkowsky D.A., Lowry R.K., Chandler R.E. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 1983;154:1222–1226. doi: 10.1128/jb.154.3.1222-1226.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shoichet B.K., Baase W.A., Matthews B.W. A relationship between protein stability and protein function. Proc. Natl. Acad. Sci. USA. 1995;92:452–456. doi: 10.1073/pnas.92.2.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moeckel G.W., Zhang L., Breyer M.D. COX2 activity promotes organic osmolyte accumulation and adaptation of renal medullary interstitial cells to hypertonic stress. J. Biol. Chem. 2003;278:19352–19357. doi: 10.1074/jbc.M302209200. [DOI] [PubMed] [Google Scholar]
- 24.Mulhern M.L., Madson C.J., Shinohara T. Cellular osmolytes reduce lens epithelial cell death and alleviate cataract formation in galactosemic rats. Mol. Vis. 2007;13:1397–1405. [PubMed] [Google Scholar]
- 25.Yancey P.H., Clark M.E., Somero G.N. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 26.Chen P., Shakhnovich E.I. Thermal adaptation of viruses and bacteria. Biophys. J. 2010;98:1109–1118. doi: 10.1016/j.bpj.2009.11.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ratkowsky D.A., Olley J., Ross T. Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 2005;233:351–362. doi: 10.1016/j.jtbi.2004.10.016. [DOI] [PubMed] [Google Scholar]
- 28.Salter M.A., Ross T., McMeekin T.A. Applicability of a model for non-pathogenic Escherichia coli for predicting the growth of pathogenic Escherichia coli. J. Appl. Microbiol. 1998;85:357–364. doi: 10.1046/j.1365-2672.1998.00519.x. [DOI] [PubMed] [Google Scholar]
- 29.Baba T., Ara T., Hasegawa M., Takai Y., Okumura Y., Baba M., Datsenko K., Tomita M., Wanner B., Mori H. Construction of Escherichia coli K–12 in-frame, single-gene knockout mutants: the Keio collection. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100050. 2006.0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vogel C., Bashton M., Teichmann S.A. Structure, function and evolution of multidomain proteins. Curr. Opin. Struct. Biol. 2004;14:208–216. doi: 10.1016/j.sbi.2004.03.011. [DOI] [PubMed] [Google Scholar]
- 31.Teichmann S.A., Park J., Chothia C. Structural assignments to the Mycoplasma genitalium proteins show extensive gene duplications and domain rearrangements. Proc. Natl. Acad. Sci. USA. 1998;95:14658–14663. doi: 10.1073/pnas.95.25.14658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gerstein M. How representative are the known structures of the proteins in a complete genome? A comprehensive structural census. Fold. Des. 1998;3:497–512. doi: 10.1016/S1359-0278(98)00066-2. [DOI] [PubMed] [Google Scholar]
- 33.Lipman D.J., Souvorov A., Tatusova T.A. The relationship of protein conservation and sequence length. BMC Evol. Biol. 2002;2:20. doi: 10.1186/1471-2148-2-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wheelan S.J., Marchler-Bauer A., Bryant S.H. Domain size distributions can predict domain boundaries. Bioinformatics. 2000;16:613–618. doi: 10.1093/bioinformatics/16.7.613. [DOI] [PubMed] [Google Scholar]
- 35.Ku T., Lu P., Hsiao N. Predicting melting temperature directly from protein sequences. Comput. Biol. Chem. 2009;33:445–450. doi: 10.1016/j.compbiolchem.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 36.Warringer J., Blomberg A. Evolutionary constraint on yeast protein size. BMC Evol. Biol. 2006;6:61. doi: 10.1186/1471-2148-6-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ghaemmaghami S., Huh W.K., Weissman J.S. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
- 38.Ghaemmaghami S., Oas T.G. Quantitative protein stability measurement in vivo. Nat. Struct. Biol. 2001;8:879–882. doi: 10.1038/nsb1001-879. [DOI] [PubMed] [Google Scholar]
- 39.Ignatova Z., Gierasch L.M. Monitoring protein stability and aggregation in vivo by real-time fluorescent labeling. Proc. Natl. Acad. Sci. USA. 2004;101:523–528. doi: 10.1073/pnas.0304533101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Batra J., Xu K., Zhou H.X. Nonadditive effects of mixed crowding on protein stability. Proteins. 2009;77:133–138. doi: 10.1002/prot.22425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Paliy O., Gargac S.M., Dunker A.K. Protein disorder is positively correlated with gene expression in Escherichia coli. J. Proteome Res. 2008;7:2234–2245. doi: 10.1021/pr800055r. [DOI] [PMC free article] [PubMed] [Google Scholar]