Defining Network Topologies that Can Achieve Biochemical Adaptation (original) (raw)
. Author manuscript; available in PMC: 2011 Mar 30.
SUMMARY
Many signaling systems show adaptation—the ability to reset themselves after responding to a stimulus. We computationally searched all possible three-node enzyme network topologies to identify those that could perform adaptation. Only two major core topologies emerge as robust solutions: a negative feedback loop with a buffering node and an incoherent feedforward loop with a proportioner node. Minimal circuits containing these topologies are, within proper regions of parameter space, sufficient to achieve adaptation. Morecomplex circuits that robustly performadaptation all contain at least one of these topologies at their core. This analysis yields a design table highlighting a finite set of adaptive circuits. Despite the diversity of possible biochemical networks, it may be common to find that only a finite set of core topologies can execute a particular function. These design rules provide a framework for functionally classifying complex natural networks and a manual for engineering networks.
For a video summary of this article, see the PaperFlick file with the Supplemental Data available online.
INTRODUCTION
The field of systems biology is largely focused on mapping and dissecting cellular networks with the goal of understanding how complex biological behaviors arise. Extracting general design principles—the rules that underlie what networks can achieve particular biological functions—remains a challenging task, given the complexity of cellular networks and the small fraction of existing networks that have been well characterized. Nonetheless, growing evidence suggests the existence of design principles that unify the organization of diverse circuits across all organisms. For example, it has been shown that there are recurrent network motifs linked to particular functions, such as temporal expression programs (Shen-Orr et al., 2002), reliable cell decisions (Brandman et al., 2005), and robust and tunable biological oscillations (Tsai et al., 2008).
These findings suggest an intriguing hypothesis: despite the apparent complexity of cellular networks, there might only be a limited number of network topologies that are capable of robustly executing any particular biological function. Some topologies may be more favorable because of fewer parameter constraints. Other topologies may be incompatible with a particular function. Although the precise implementation could differ dramatically in different biological systems, depending on biochemical details and evolutionary history, the same core set of network topologies might underlie functionally related cellular behaviors (Milo et al., 2002; Wagner, 2005; Ma et al., 2006; Hornung and Barkai, 2008). If this hypothesis is correct, then one may be able to construct a unified function-topology mapping that captures the essential barebones topologies underpinning the function. Such core topologies may otherwise be obscured by the details of any specific pathway and organism. Such a map would help organize our ever-expanding database of biological networks by functionally classifying key motifs in a network. Such a map might also suggest ways to therapeutically modulate a system. A circuit function-topology map would also be invaluable for synthetic biology, providing a manual for how to robustly engineer biological circuits that carry out a target function.
To investigate this hypothesis, we have computationally explored the full range of simple enzyme circuit architectures that are capable of executing one critical and ubiquitous biological behavior—adaptation. We ask if there are finite solutions for achieving adaptation. Adaptation refers to the system’s ability to respond to a change in input stimulus then return to its prestimulated output level, even when the change in input persists. Adaptation is commonly used in sensory and other signaling networks to expand the input range that a circuit is able to sense, to more accurately detect changes in the input, and to maintain homeostasis in the presence of perturbations. A mathematical description of adaptation is diagrammed in Figure 1A, in which two characteristic quantities are defined: the circuit’s sensitivity to input change and the precision of adaptation. If the system’s response returns exactly to the prestimulus level (infinite precision), it is called the perfect adaptation. Examples of perfect or near perfect adaptation range from the chemotaxis of bacteria (Berg and Brown, 1972; Macnab and Koshland, 1972; Kirsch et al., 1993; Barkai and Leibler, 1997; Yi et al., 2000; Mello and Tu, 2003; Rao et al., 2004; Kollmann et al., 2005; Endres and Wingreen, 2006), amoeba (Parent and Devreotes, 1999; Yang and Iglesias, 2006), and neutrophils (Levchenko and Iglesias, 2002), osmo-response in yeast (Mettetal et al., 2008), to the sensor cells in higher organisms (Reisert and Matthews, 2001; Matthews and Reisert, 2003), and calcium homeostasis in mammals (El-Samad et al., 2002).
Figure 1. Searching Topology Space for Adaptation Circuits.
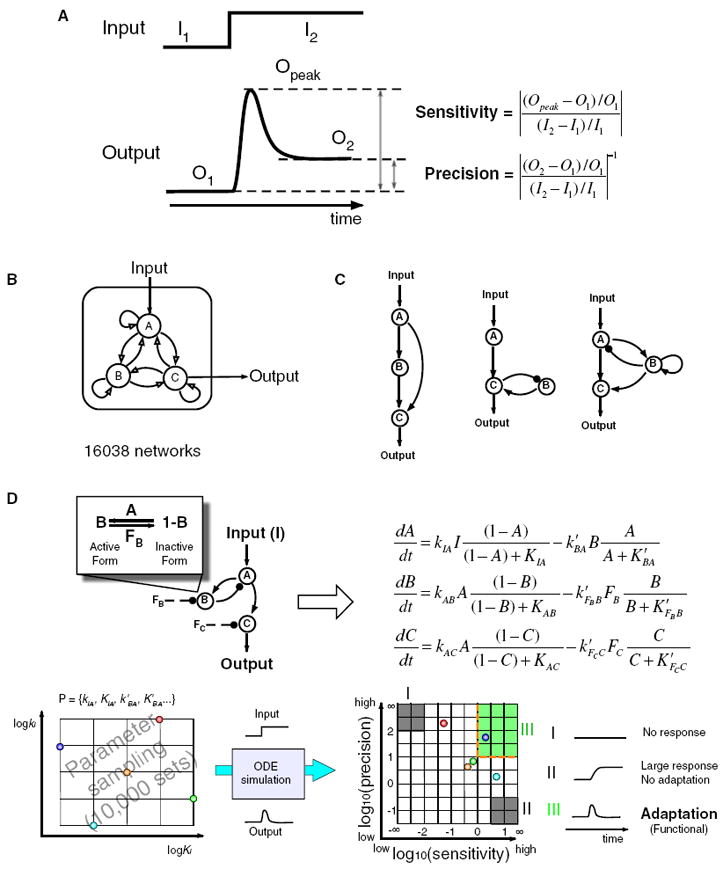
(A) Input-output curve defining adaptation.
(B) Possible directed links among three nodes.
(C) Illustrative examples of three-node circuit topologies.
(D) Illustration of the analysis procedure for a given topology.
Here, instead of focusing on one specific signaling system that shows adaptation, we ask a more general question: What are all network topologies that are capable of robust adaptation? To answer this question, we enumerate all possible three-node network topologies (restricting ourselves to enzymatic nodes) and study their adaptation properties over a range of kinetic parameters (Figure 1B). We use three nodes as a minimal framework: one node that receives input, a second node that transmits output, and a third node that can play diverse regulatory roles. There are a total of 16,038 possible three-node topologies that contain at least one direct or indirect causal link from the input node to the output node. For each topology, we sampled a wide range of parameter space (10,000 sets of network parameters) and characterized the resulting behavior in terms of the circuit’s sensitivity to input change and its ability to adapt. In all we have analyzed a total of 16,038*10,000 ≈ 1.6 × 108 different circuits. This search resulted in an exhaustive circuit-function map, which we have used to extract core topological motifs essential for adaptation. Overall, our analysis suggests that despite the importance of adaptation in diverse biological systems, there are only a finite set of solutions for robustly achieving adaptation. These findings may provide a powerful framework in which to organize our understanding of complex biological networks.
RESULTS
Searching for Circuits Capable of Adaptation
Adaptation is defined by the ability of circuits to respond to input change but to return to the prestimulus output level, even when the input change persists. Therefore, in this study we monitor two functional quantities for each network: the circuit’s sensitivity to input stimulus and its adaptation precision (Figure 1A). Sensitivity is defined as the height of output response relative to the initial steady-state value. Adaptation precision represents the difference between the pre- and poststimulus steady states, defined here as the inverse of the relative error. We have limited ourselves to exploring circuits consisting of three interacting nodes (Figures 1B and 1C): one node that receives inputs (A), one node that transmits output (C), and a third node (B) that can play diverse regulatory roles. Although most biological circuits are likely to have more than three nodes, many of these cases can probably be reduced to these simpler frameworks, given that multiple molecules often function in concert as a single virtual node. By constraining our search to three-node networks, we are in essence performing a coarse-grained network search. This sacrifice in resolution, however, allows us to perform a complete search of the topological space.
For this analysis, we limited ourselves to enzymatic regulatory networks and modeled network linkages using Michaelis-Menten rate equations. As described in Experimental Procedures, each node in our model network has a fixed total concentration that can be interconverted between two forms (active and inactive) by other active enzymes in the network or by basally available enzymes. For example, a positive link from node A to node B indicates that the active state of enzyme A is able to convert enzyme B from its inactive to active state (see Figure 1D). If there is no negative link to node B from the other nodes in the network, we assume that a basal (nonregulated) enzyme would inactivate B. We used ordinary differential equations to model these interactions, characterized by the Michaelis-Menten constants (_K_M’s) and catalytic rate constants (_k_cat’s) of the enzymes. Implicit in our analysis are assumptions that the enzyme nodes operate under Michaelis-Menten kinetics and that they are noncooperative (Hill coefficient = 1). In the Supplemental Experimental Procedures available online, section 10, we show that these assumptions do not significantly alter our results—similar results emerge when using mass action rate equations instead of Michaelis-Menten equations, or when using nodes of higher cooperativity.
Our analysis mainly focused on the characterization of the circuit’s sensitivity and adaptation precision, which can be mapped on the two-dimensional sensitivity versus precision plot (Figure 1D). We define a particular circuit architecture/parameter configuration to be “functional” for adaptation if its behavior falls within the upper-right rectangle in this plot (the green region in Figure 1D)—these are circuits that show a strong initial response (sensitivity > 1) combined with strong adaptation (precision > 10). In most of our simulations we gave a nonzero initial input (I1 = 0.5) and then changed it by 20% (I2 = 0.6). The functional region corresponds to an initial output change of more than 20% and a final output level that is not more than 2% different from the initial output. Nonfunctional circuits fall into other quadrants of this plot, including circuits that show very little response (upper-left quadrant) and circuits that show a strong response but low adaptation (lower-right quadrant). For any particular circuit architecture, we focused on how many parameter sets can perform adaptation—a circuit is considered to be more robust if a larger number of parameter sets yield the behavior defined above.
To identify the network requirements for adaptation, we took two different but complementary approaches. In the first approach, we searched for the simplest networks that are capable of achieving adaptation, limiting ourselves to networks containing three or fewer links. We find that all circuits of this type that can achieve adaptation fall into two architectural classes: _n_egative _f_eed_b_ack _l_oop with a _b_uffering node (NFBLB) and _i_ncoherent _f_eed_f_orward _l_oop with a _p_roportioner node (IFFLP). In the second approach, we searched all possible 16,038 three-node networks (with up to nine links) for architectures that can achieve adaptation over a wide range of parameters. These two approaches converge in their conclusions: the more complex robust architectures that emerge are highly enriched for the minimal NFBLB and IFFLP motifs. In fact all adaptation circuits contain at least one of these two motifs. The convergent results indicate that these two architectural motifs present two classes of solutions that are necessary for adaptation.
Identifying Minimal Adaptation Networks
We started by examining the simplest networks capable of achieving adaptation (defined as sensitivity > 1 and precision > 10) for any of their parameter sets. For networks composed of only two nodes (an input receiving node A and output transmitting node C, with no third regulatory node), there are 4 possible links and 81 possible networks, none of which is capable of achieving adaptation for the parameter space that we scanned (Figure S1).
Next, we examined minimal three-node topologies with only three or fewer links between nodes (maximally complex three-node topologies contain nine links). None of the two-link, three-node networks were capable of adaptation (Figure S2)—the minimal number of links for this to be functional is three. The simplest topologies capable of adaptation, under at least some parameter sets, are eleven three-node, three-link networks. These network architectures are listed in Figure 2 along with examples of the distribution of sensitivity/precision behaviors for the 10,000 parameter sets that were searched (see also Figure S3). An architecture is considered capable of adaptation if this distribution extends into the upper-right quadrant (high sensitivity, high precision). The common features of the networks capable of adaptation are either a single negative feedback loop or a single incoherent feedforward loop. Here, we define a negative feedback loop as a topology whose links, starting from any node in the loop, lead back to the original node with the cumulative sign of regulatory links within the loop being negative. We define an incoherent feedforward loop as a topology in which two different links starting from the input-receiving node both end at the output-transmitting node, with the cumulative sign of the two pathways having different signs (one positive and one negative). The first row of Figure 2 shows several examples of three-link, three-node networks capable of adaptation; the second row shows related counter parts that cannot achieve adaptation. Overall incoherent feedforward loops appear to perform adaptation more robustly than negative feedback loops—they are capable of higher sensitivity and higher precision as indicated by the larger distribution of sampled parameters that lie in the upper-right corner of the sensitivity/precision plot.
Figure 2. Minimal Networks (≤3 Links) Capable of Adaptation.
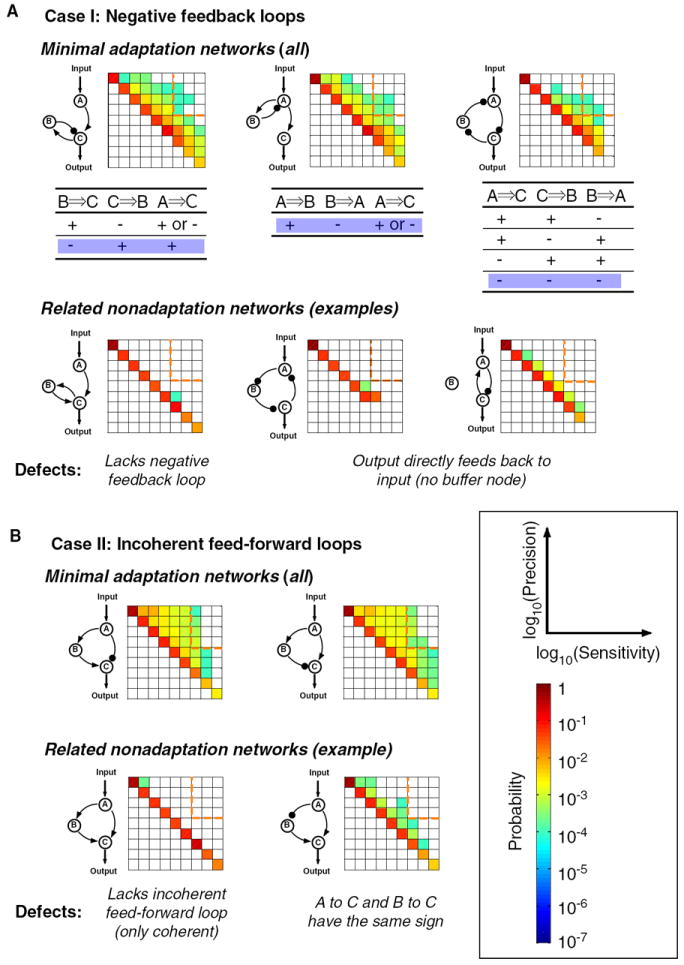
(A) Adaptive networks composed of negative feedback loops. Three examples of adaptation networks are shown in the upper panel. Each is one member (shaded) of a group of similar adaptation networks, whose signs of regulations are listed underneath. For comparison, three examples of nonadaptive networks are shown in the low panel, with their “defects” for adaptation function listed underneath.
(B) Adaptive networks composed of incoherent feedforward loops. The only two minimal adaptation networks in this case are shown in the upper panel. Examples of nonadaptive networks are shown in the lower panel.
While it not surprising that positive feedback loops cannot achieve adaptation (Figure 2A), it is interesting to note that negative feedback loop topologies differ widely in their ability to perform adaptation (Figure 2A, lower panel). Notably, there is only one class of simple negative feedback loops that can robustly achieve adaptation. In this class of circuits, the output node must not directly feedback to the input node. Rather, the feedback must go through an intermediate node (B), which serves as a buffer. The importance of this buffering node will be discussed in detail later.
Among feedforward loops (Figure 2B), coherent feedforward is clearly very poor at adaptation (Figure 2B, lower panel). The three incoherent feedforward loops in Figure 2B also differ drastically in their performance. Of these, only the circuit topology in which the output node C is subject to direct inputs of opposing signs (one positive and one negative) appears to be highly preferred. As will be seen later, the reason this architecture is preferred is because the only way for an incoherent feedforward loop to achieve robust adaptation is for node B to serve as a proportioner for node A—i.e., node B is activated in proportion to the activation of node A and to exert opposing regulation on node C.
Key Parameters in Minimal Adaptation Networks
Two major classes of minimal adaptive networks emerge from the above analysis: one type of negative feedback circuits and one type of incoherent feedforward circuits. Why are these two classes of minimal architectures capable of adaptation? Here we examine their underlying mechanisms, as well as the parameter conditions that must be met for adaptation.
Negative Feedback Loop with a Buffer Node
The NFBLB class of topologies has multiple realizations in three-node networks (Figure 2A), all featuring a dedicated regulation node “B” that functions as a “buffer.” We show how the motif works by analyzing a specific example (Figure 3A), which has a negative feedback loop between regulation node B and output-transmitting node C.
Figure 3. Phase Diagram and Nullcline Analysis of Representative Networks from the Two Classes of Minimal Adaptive Topologies.
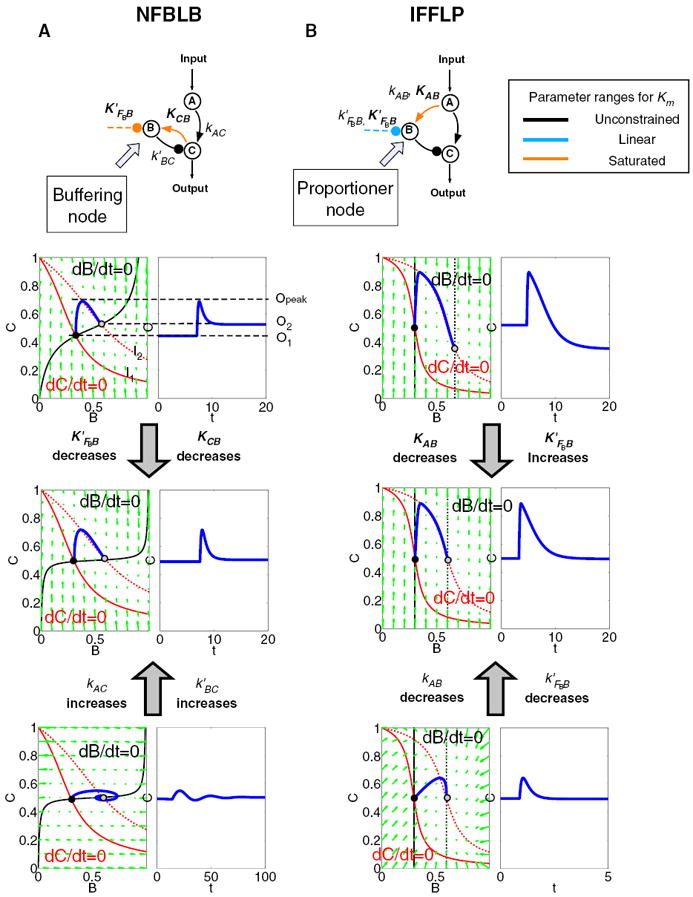
The two networks are shown on the top with the key regulations colored to indicate the parameter constraints for achieving perfect adaptation.
(A) Phase planes of the variables B and C for a NFBLB topology. The B nullclines are drawn in black lines and C nullclines in red (solid red for the initial input _I_1 and dashed red for the changed input _I_2). The steady states with input _I_1 and _I_2 are the intersections of the nullclines and are highlighted by black and gray dots, respectively. When the input is changed from _I_1 to _I_2, the trajectory (blue lines) of the system variables follows the vector field (dB/dt, dC/dt) (with input _I_2), which is denoted by the green arrows. The trajectory’s projection on the C axis is the system’s output and is shown separately right next to the phase plane. (Refer to Figure 1A for the functional meaning of _O_1, _O_2, and_O_peak.) Two sets of key parameters (_K_M’s on B) are used to illustrate their effect on adaptation precision: KF0B′=0.1 and KCB = 0.1 for the top panel and KF0B′=0.01 and KCB = 0.01 for the middle and lower panels. Two sets of rate constants are used to illustrate their effect on sensitivity: kAC = 10 and k′BC = 10 for the top and the middle panels and kAC = 0.1 and k′BC = 0.1 for the lower panel.
(B) Phase planes for an IFFLP topology. KF0B′=1 and KAB = 0.1 for the top panel. KF0B′=100 and KAB = 0.001 for the middle and the lower panels. kAB = 0.5 and kF0B′=10 for the top and the middle panels. kAB = 100 and kF0B′=2000 for the lower panel.
The mechanism by which this NFBLB topology adapts and achieves a high sensitivity can be unraveled by the analysis of the kinetic equations
| dAdt=IkIA(1−A)(1−A)+KIA−FAkFAA′AA+KFAA′dBdt=CkCB(1−B)(1−B)+KCB−FBkFBB′BB+KFBB′dCdt=AkAC(1−C)(1−C)+KAC−BkBC′CC+KBC′ | (1) |
|---|
where FA and FB represent the concentrations of basal enzymes that carry out the reverse reactions on nodes A and B, respectively (they oppose the active network links that activate A and B). In this circuit, node A simply functions as a passive relay of the input to node C; the circuit would work in the same way if the input were directly acting on node C (just replacing A with I in the third equation of Equation 1). Analyzing the parameter sets that enabled this topology to adapt indicates that the two constants KCB and KFBB′ (Michaelis-Menten constants for activation of B by C and inhibition of B by the basal enzyme) tend to be small, suggesting that the two enzymes acting on node B must approach saturation to achieve adaptation. Indeed, it can be shown that in the case of saturation this topology can achieve perfect adaptation. Under saturation conditions, i.e., (1-B) ≫ KCB and B ≫ KFBB′, the rate equation for B can be approximated by the following:
The steady-state solution is
which is independent of the input level I. The output C of the circuit can still transiently respond to changes in the input (see the first and the third equations in Equation 1) but eventually settles to the same steady state determined by Equation 3. Note that Equation 2 can be rewritten as
| dBdt=kCB(C−C∗),B=B∗(I0)+kCB∫0t(C−C∗)dτ. | (4) |
|---|
Thus, the buffer node B integrates the difference between the output activity C and its input-independent steady-state value. Therefore, this NFBLB motif, node C —∣ node B → node C, implements integral control—a common mechanism for perfect adaptation in engineering (Barkai and Leibler, 1997; Yi et al., 2000). All minimal NFBLB topologies use the same integral control mechanism for perfect adaptation.
The parameter conditions required for more accurate adaptation and higher sensitivity can also be visualized in the phase planes of nodes B and C (Figure 3A). The nullclines for nodes B and C (dB/dt = 0 and dC/dt = 0, respectively) are shown for two different input values. For this topology, only the C nullcline (red curve) depends explicitly on the input through A (Equation 1). The B nullcline (black curve) does not depend on A. The steady state of the system is given by the intersection of the B and C nullclines. Thus, the change in steady state for any input change is only determined by the movement of the input-dependent C nullcline (e.g., dashed red curve in Figure 3A). The adaptation precision is therefore directly related to the flatness of the B nullcline near the intersection of the two nullclines. The smaller the dependence of C on B, the smaller the adaptation error. One way to achieve a small dependence of C on B, or equivalently a sharp dependence of B on C, in an enzymatic cycle is through the zeroth order ultrasensitivity (Goldbeter and Koshland, 1984), which requires the two enzymes regulating the node B to work at saturation. This is precisely the condition leading to Equation 2. All NFBLB minimal topologies have similar nullcline structures and their adaptation is related to the zeroth order ultrasensitivity in a similar fashion.
The ability of the network to mount an appropriate transient response to the input change before achieving steady-state adaptation depends on the vector fields (dB/dt, dC/dt) in the phase plane (green arrows, Figure 3). A large response, corresponding to sensitive detection of input changes, is achieved by a large excursion of the trajectory along the C axis. This in turn requires a large initial |dC/dt| and a small initial |dB/dt| near the prestimulus steady state. For this class of topologies, this can be achieved if the response time of node C to the input change is faster than the adaptation time. The response time of node C is set by the first term in the dC/dt equation—faster response would require a larger kAC. The timescale for adaptation is set by the equation for node B and the second term of the equation for node C—slower adaptation time would require a smaller k′ BC/K′ BC and/or a slower timescale for node B. This illustrates an important uncoupling of adaptation precision and sensitivity: once the Michaelis-Menten constants are tuned to achieve operation in the saturated regimes, the timescales of the system can be independently tuned to modulate the sensitivity of the system to input changes.
Incoherent Feedforward Loop with a Proportioner Node
The other minimal topological class sufficient for adaptation is the incoherent feedforward loop with a proportional node (IFFLP) (Figure 2B). In an incoherent FFL, the output node C is subject to two regulations both originating from the input but with opposing cumulative signs in the two pathways. There are two possible classes of incoherent FFL architectures, but only one is able to robustly perform adaptation (Figure 2B, upper panel): the functional architectures all have a “proportioner” (node B) that regulates the output (node C) with the opposite sign as the input to C. We denote this class IFFLP.
The IFFLP topology achieves adaptation by using a different mechanism from that of the NFBLB class. Rather than monitoring the output and feeding back to adjust its level, the feedforward circuit “anticipates” the output from a direct reading of the input. node B monitors the input and exerts an opposing force on node C to cancel the output’s dependence on the input. For the IFFLP topology shown in Figure 3B, the kinetic equations are as follows:
| dAdt=IkIA(1−A)(1−A)+KIA−FAkFAA′AA+KFAA′dBdt=AkAB(1−B)(1−B)+KAB−FBkFBB′BB+KFBB′dCdt=AkAC(1−C)(1−C)+KAC−BkBC′CC+KBC′. | (5) |
|---|
The adaptation mechanism is mathematically captured in the equation for node C: if the steady-state concentration of the negative regulator B is proportional to that of the positive regulator A, the equation determining the steady-state value of C, dC/dt = 0, would be independent of A and hence of the input I. In this case, the equation for node B generates the condition under which the steady-state value B* would be proportional to A*: the first term in dB/dt equation should depend on A only and the second term on B only. The condition can be satisfied if the first term is in the saturated region ((1 − B) ≫ KAB) and the second in the linear region (B≪KFBB′), leading to
| B∗=A∗·kABKFBB′/(FBkFBB′). | (6) |
|---|
This relationship, established by the equation for node B, shows that the steady-state concentration of active B is proportional to the steady-state concentration of active A. Thus B will negatively regulate C in proportion to the degree of pathway input. This effect of B acting as a proportioner node of A can be graphically gleaned from the plot of the B and C nullclines (Figure 3B). In this case, maintaining a constant C* requires the B nullcline to move the same distance as the C nullcline in response to an input change. Here again, the sensitivity of the circuit (the magnitude of the transient response) depends on the ratio of the speeds of the two signal transduction branches: A → C and A → B —∣ C, which can be independently tuned from the adaptation precision.
Analysis of All Possible Three-Node Networks: An NFBLB or IFFLP Architecture Is Necessary for Adaptation
The above analyses focused on minimal (less than or equal to three links) three-node networks and identified simple architectures that are sufficient for adaptation. But are these architectures also necessary for adaptation? In other words, are the identified minimal architectures the foundation of all possible adaptive circuits, or are there more complex higher-order solutions that do not contain these minimal topologies? To investigate this question, we expanded our study to encompass all possible three-node networks, each with combinations of up to nine intra-network links. Again, for each network architecture, we sampled 10,000 possible parameter sets. Figure 4A shows a comprehensive map of the functional space, expressed as the distribution of all topologies and all sampled parameter sets on the sensitivity/precision plot. Only the regions above the diagonal are occupied, since by definition sensitivity cannot be lower than adaptation error (Experimental Procedures). The vast majority of the circuits lie on the diagonal where sensitivity = 1/error. This very common functional behavior is simply a monotonic change of the output in response to the input change, a hallmark of a direct, nonadaptive signal transduction response. The distribution plot quickly drops off away from the diagonal as the number of circuits with increasing sensitivity and/or adaptation precision drops. Overall, only 0.01% of all 1.6 × 108 possible architecture/parameter sets fall within the upper-right corner of the plot in Figure 4A—i.e., those circuits that can achieve both high sensitivity and high adaptation precision. We are interested in topologies that are overrepresented in these regions. By overrepresentation, we require that the topology be mapped to this region more than 10 times when sampled with 10,000 parameter sets. There are 395 out of 16,038 such topologies.
Figure 4. Searching the Full Circuit-Space for All Robust Adaptation Networks.
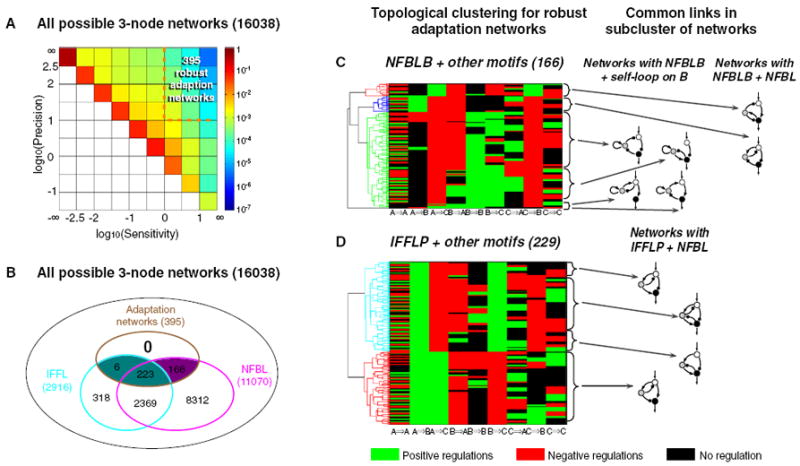
(A) The probability plot for all 16,038 networks with all the parameters sampled. Three hundred and ninety-five networks are overrepresented in the functional region shown by the orange rectangle.
(B) Venn diagram of networks with three characters: adaptive, containing negative FBL, and containing incoherent FFL.
(C) Clustering of the adaptation networks that belong to the NFBLB class. The network motifs associated with each of the subclusters are shown on the right.
(D) Clustering of adaptation networks that belong to the IFFLP class.
Analysis of these 395 robust topologies shows that they are overrepresented with feedback and feedforward loops (Supplemental Experimental Procedures, section 4). Strikingly, all 395 topologies contain at least one NFBLB or IFFLP motif (or both) (Figure 4B). These results indicate that at least one of these motifs is necessary for adaptation.
Motif Combinations that Improve Adaptation
Comparing the sensitivity/precision distribution plot of all networks (Figure 4A) with that of the minimal networks (Figure 2), it is clear that some of the more complex topologies occupy a larger functional space than the minimal topologies. We wanted to investigate what additional features can improve the functional performance in these networks. To address this question, we separated the 395 adaptation networks into the two categories, NFBLB and IFFLP. We then clustered the networks within each category using a pair-wise distance between networks. The results, shown in Figures 4C and 4D, clearly indicate the presence of common structural features (subclusters) in each category, some of which are shown on the righthand side in the figure. One striking feature shared by some of the more complex adaptation networks in the NFBLB category is a positive self-loop on the node B in the case where the other regulation on B is negative. This type of topology, with a saturated positive self-loop on B and linear negative regulation from other nodes, implements a special type of integral control to achieve perfect adaptation—here the Log (B), rather than B itself, is the integrator (Supplemental Experimental Procedures, section 5). Another common feature of the more complex networks, which is present in both categories, is the presence of additional negative feedback loops that go through node B. We found that this feature also enhances the performance—the networks with more such negative feedback loops have larger Q values (defined as the number of sampled parameter sets that yield the target adaptation behavior) than the minimal networks (Supplemental Experimental Procedures, section 12).
Analytic Analysis: Two Classes of Adaptation Mechanisms
In order to elucidate all possible adaptation mechanisms for more complex networks, we analyzed analytically the structure of the steady-state equations for three-node networks. The steady-state equations for any three-node network in our model can be written as dA/dt = f_A_ (A*, B*, C*, I) = 0, dB/dt = f_B_ (A*, B*, C*) = 0 and dC/dt = f_C_ (A*, B*, C*) = 0, where A*, B*, and C* are the steady-state values of the three nodes, and f_A_, f_B_, and f_C_ represent the Michaelis-Menten terms contributing to the production/decay rate of A, B, and C, respectively. In response to a small change in the input: I_→_I+Δ_I_, the steady state changes to A*+Δ_A_*, B*+Δ_B_*, and C*+Δ_C_*, correspondingly. The conditions for perfect adaptation, Δ_C_* = 0, can then be obtained by analyzing the linearized steady-state equations. We refer the reader to Supplemental Experimental Procedures (section 6) for technical details and only summarize the main results below (as schematically illustrated in Figure 5).
Figure 5. General Analysis for Adaptive Circuits.
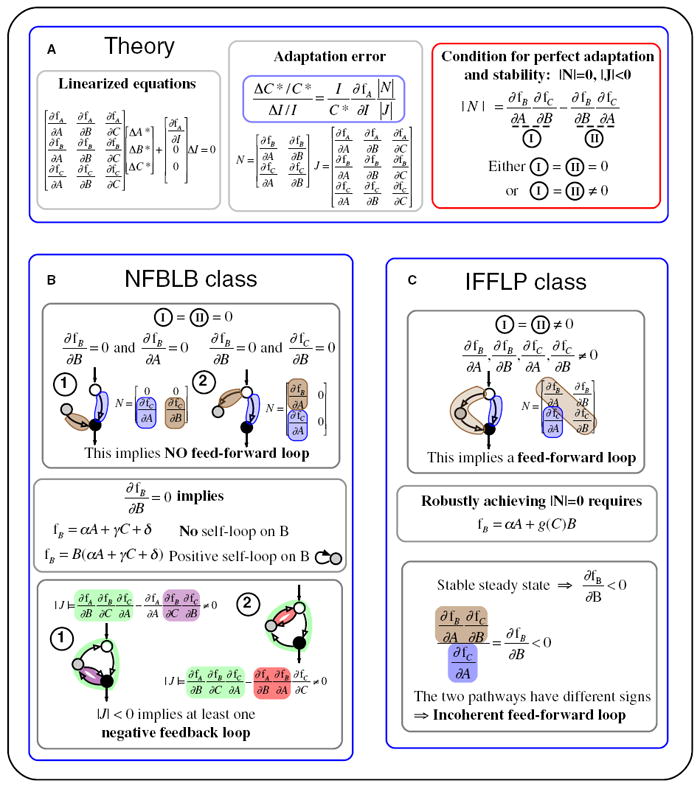
(A) Relevant equations. The steady-state output change Δ_C_* with respect to the input change Δ_I_ can be derived from the linearized steady-state equations. A zero adaptation error around a stable steady state requires a zero minor |N| and a nonzero determinant |J| < 0. There are two terms I and II in |N|, and |N| = 0 implies either both terms are zero or they are equal but nonzero. We are only interested in robust adaptation, i.e., the cases where the condition leading to |N| = 0 holds within a range of parameters and input values.
(B) NFBLB class of adaptive circuits (I = II = 0). In this category ∂f_C_/∂A ≠ 0, which means that there is always a link from node A to node C. (Otherwise, there would be no direct or indirect path from A to C.) Then II = 0 implies that ∂f_B/B_ is always zero. I = 0 implies that at least one of ∂f_B_/∂A and ∂ f_C_/∂B is zero. This condition implies that there is no feedforward loop in this category. In our enzymatic model ∂f_B_/∂B = 0 can be robustly achieved either by saturating the enzymes on the node B so that f_B_ does not depend on B explicitly or by adding a positive self-loop on node B so that the dependence of f_B_ on B can be factored out. An example of the latter is when node B is regulated by itself positively and by C negatively, so thatfB=kBBB(1−B)/(1−B+KBB)−kCB′CB/(B+kCB′)≈kBBB−kCB′CB/kCB′=B(kBB−kCB′/kCB′C), in the limits (1-B) ≫ KBB and B ≪ K_′ CB. The terms in the determinant |J| correspond to different feedback loops as colored in the figure. Thus, there should be at least one, but can be two, negative feedback loops in this category. (C) IFFLP class (I = II ≠ 0). In this category, none of the factors in |N| are zero. This implies the presence of the links colored in the figure and hence a FFL. The condition for |N| = 0 can be robustly satisfied if the FFL exerts two opposing but proportional regulations on C. The proportionality relationship can be established by f_B taking the form shown in the figure.
These analyses again indicate that there are only two ways to achieve robust perfect adaptation without fine-tuning of parameters. The first requires one or more negative feedback loops but occludes the simultaneous presence of feedforward loops in the network (Figure 5B). In this category, the node B is required to function as a feedback “buffer,” i.e., its rate change does not depend directly on itself (∂f_B_/∂B = 0) at steady state. This implies that f_B_ either does not explicitly depend on B (f_B_ = g(A, C)) or takes a form of f_B_ = B × g(A,C) so that the steady-state condition g(A*,C*) = 0 guarantees that ∂f_B_/∂B = 0 at steady state. In either case, within the Michaelis-Menten formulation, the steady-state condition for B, g(A*,C*) = 0, establishes a mathematical constraint αA* + γ_C_* + δ = 0 that is satisfied by A* and/or C*, with α, γ, and δ constant. This equation plays a key role in setting the steady-state value C* to be independent of the input. All the minimal adaptation networks in the NFBLB class discussed before are simple examples of this case. In particular, the minimal network analyzed in Figure 3A is characterized by f_B_ = g(C) when both enzymes on B work in saturation. Hence, the steady-state equation for the node B reduces to γ_C_* + δ = 0 (Equation 3). The case in which f_B_ = B × g(A, C) corresponds to adaptation networks in which node B has a positive self-loop.
The other way to achieve robust perfect adaptation requires an incoherent feedforward loop, but in this case allowing for other feedback loops in the network (Figure 5, panel C). In this category, ∂f_B_/∂B ≠ 0 and the condition for robust perfect adaptation implies a form of f_B_ to be f_B_ = αA + g(C)B. The steady-state condition f_B_ = 0 establishes a proportionality relationship between B and A: B* = G(C*) A*, where G is a nonzero function of C*. Thus, the node B here is required to function as a “proportioner.” All minimal adaptation networks in the IFFLP class are special cases of this category. For example, the network in Figure 3B sets B* = constant × A* (Equation 6).
Therefore, the above analyses indicate that all robust adaptation networks should fall into one of these two categories, which can be viewed as the generalization of the two classes of the minimal topologies for adaptation. Indeed, we found that all 395 robust adaptation networks can be classified based on their membership of the broad NFBLB and IFFLP categories (indicated by the two different colors in Figure 4B).
Design Table of Adaptation Circuits
Our results can be concisely summarized into a design table for adaptation circuits, as exemplified in Figure 6. Overall, there are two architectural classes for adaptation: NFBLB and IFFLP. In each class, the minimal networks are sufficient for perfect adaptation. These minimal networks also form the topological core for the more complex adaptation networks that, with additional characteristic motifs, can exhibit enhanced performance. Figure 6 illustrates three examples in which such motifs can be added to minimal networks to generate networks of increasing complexity and increasing robustness (Q values).
Figure 6. Design Table of Adaptation Networks.
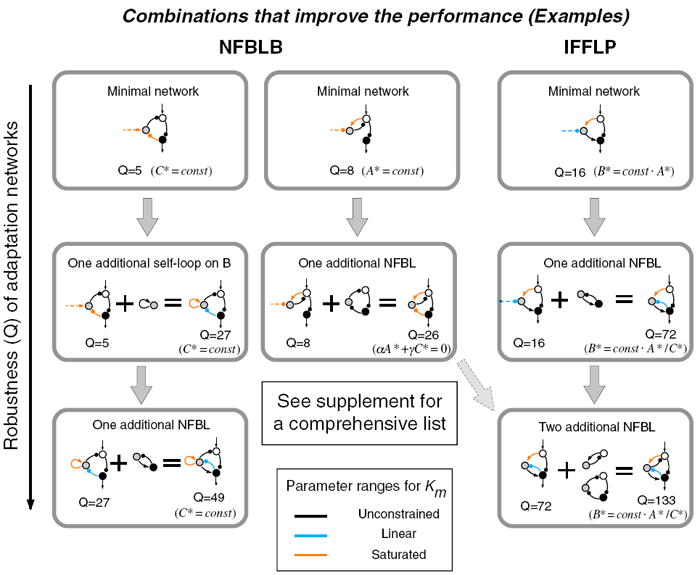
Two examples are shown on the left for the NFBLB class of adaptation networks, which require a core NFBLB motif with the node B functioning as a buffer. One example is shown on the right for the IFFLP class, which require a core IFFLP motif with the node B functioning as a proportioner. The table is constructed by adding more and more beneficial motifs to the minimal adaptation networks. The Q value (Robustness) of each network is shown underneath, along with the mathematical relation the node B establishes.
Let us first focus on the example shown in the middle column of Figure 6. On the top is a minimal network in the NFBLB class. Adding one C—∣B link (or equivalently, adding one more negative feedback loop) to the minimal network results in a network with two negative feedback loops that go through the control node B that has a larger Q value. Note that no more negative feedback loops that go through B can be added to the network without creating an incoherent feedforward loop. Adding a link B→C generates one more negative feedback loop that goes through B but results in an IFFLP motif. This changes the network to the IFFLP class—consequently, the adaptation mechanism and the key regulations on B are changed (C—∣B changed from saturated to linear).
In the example shown in the left column of Figure 6, we start with one of the minimal networks in the NFBLB class that have inter-node negative regulations on B. Adding a positive self-loop on B to this type of network significantly improves the performance. One additional negative feedback loop further increases the performance. When we arrive at the network shown at the bottom of the left column, no negative feedback loops that go through B can be added without resulting in an incoherent feedforward loop.
In the last example (Figure 6, right column), a minimal IFFLP network is layered with more and more negative feedback loops to increase the Q value. A comprehensive design table with all minimal networks and all their extensions that increase the robustness, along with the analysis of their adaptation mechanisms, is provided in Supplemental Experimental Procedures, section 12 and Figure S15. (The readers can simulate and visualize the behavior of these and other networks of their own choice with an online applet at http://tang.ucsf.edu/applets/Adaptation/Adaptation.html.)
DISCUSSION
Design Principles of Adaptation Circuits
Despite the great variety of possible three-node enzyme network topologies, we found that there are only two core solutions that achieve robust adaptation. The main functional feature of the adaptation circuits is to maintain a steady-state output that is independent of the input value. This task is accomplished by a dedicated control node B that functions to establish different mathematical relationships among the steady-state values of the nodes that regulate it (see Supplemental Experimental Procedures, section 7 for a comprehensive analysis) with the goal of setting a constant steady-state output C*. Importantly, these desired relationships necessary for perfect adaptation are not achieved by fine-tuning any of the circuit’s parameters but rather by the key regulations on the control node B approaching the appropriate limits (saturation or linear) (Barkai and Leibler, 1997). This is the reason behind the functional robustness of the adaptation circuits of either major class. Furthermore, the requirements central to perfect adaptation are relatively independent from other properties. In particular, the circuit’s sensitivity to the input change can be separately tuned by changing the relative rates of the control node to those of the other nodes.
Several authors have computationally investigated the circuit architecture for adaptation (Levchenko and Iglesias, 2002; Yang and Iglesias, 2006; Behar et al., 2007). In particular, François and Siggia simulated the evolution of adaptation circuits using fitness functions that combine the two features of adaptation we considered here: sensitivity and precision (François and Siggia, 2008). Starting from random gene networks, they found that certain topologies emerge from evolution independent of the details of the fitness function used. Their model circuits have a mixture of regulations (enzymatic, transcriptional, dimerization, and degradation), and they did not enumerate but focused on only a few adaptation circuits. Nonetheless, it is very interesting to note that the adaptation architectures that emerged in their study seem to also fall into the two general classes we found here. Further studies are needed to systematically investigate the general organization principles for the adaptation circuits made of other (than enzymatic) or mixed regulation types.
Biological Examples of Adaptation
A well-studied biological example of perfect adaptation is in the chemotaxis of E. coli (Barkai and Leibler, 1997; Yi et al., 2000) (Figure 7). Intriguingly, we found that one of the minimal topologies (NFBLB) we identified is equivalent to the Barkai-Leibler model of perfect adaptation (Barkai and Leibler, 1997). In E. coli the binding of the chemo-attractant/repellant to the chemoreceptor R and its methylation level M modulate the activity of the histidine kinase CheA, which forms a complex with the chemoreceptor R. CheA phosphorylates the response regulator CheY, which in turn regulates the motor activity of the flagella. The methylation level M of the receptor/CheA complexes is determined by the activities of the methylase CheR and the demethylase CheB. According to the Barkai-Leibler model, CheR works at saturation with a constant methylation rate for all receptor/CheA complexes, independent of the methylation level M, whereas CheB binds only to the active receptor/CheA complexes, resulting in a demethylation rate that is dependent only on the system’s output (CheA activity). Therefore, the network structure or topology of the E. coli chemotaxis is very similar to one of the topologies we found (Figure 7), with the buffer node B corresponding to the methylation level of the chemoreceptors.
Figure 7. The Network of Perfect Adaptation in E. coli Chemotaxis Belongs to the NFBLB Class of Adaptive Circuits.

Left: the original network in E. coli. Middle: the redrawn network to highlight the role and the control of the key node “Methylation Level.” Right: one of the minimal adaptation networks in our study.
In our theoretical study of adaptation circuits with Michaelis-Menten kinetics, the IFFLP class consistently performs better than the NFBLB class. However, there have so far not been clear cases where IFFLP is implemented in any biological systems to achieve good adaptation. Does IFFLP topology have some intrinsic differences concerning adaptation from NFBLB that are not captured by our study? Is it harder to implement in real biological systems? Or, do we simply have to search more biological systems? A clue might be found when we add cooperativity in the Michaelis-Menten kinetics (replacing ES/(S+K) with ESn/(Sn+Kn) in the equations; see Supplemental Experimental Procedures, section 10.2). A higher Hill coefficient n > 1 would help achieve the two saturation conditions necessary for adaptation in the NFBLB class but would hamper the linearity required to establish the proportionality relationship necessary in the IFFLP class. This requirement for noncooperative nodes in the IFFLP class may effectively reduce its robustness and might be one of the reasons behind the apparent scarceness of the IFFLP architecture in natural adaptation systems. The FFL motifs, both coherent and incoherent, are abundant in the transcriptional networks of E. coli (Shen-Orr et al., 2002) and S. cerevisiae (Milo et al., 2002). These transcriptional FFL circuits can perform a variety of functions (Alon, 2007), including pulse generation—a function rather similar to adaptation. It is difficult to draw conclusions from these findings, however, since preliminary analysis (W.M., unpublished results) suggests that the requirements for transcription-based adaptation networks may differ from those of enzyme-based adaptation networks.
Guiding Principles for Mapping, Modulating, and Designing Biological Circuits
The general approach outlined here—to generate a function-topology map constructed from a purely functional perspective—could be applied to many different functions beyond adaptation. The resulting function-topology maps or design tables could have broad usage. First, an increasing number of biological network maps are being generated by various high-throughput methods. Analyzing these complex networks with the guidance of function-topology maps may help identify the underlying function of the networks or lead to testable functional hypotheses. Second, many biological systems that display a clear function (e.g., adaptation) have an unclear mechanism or incomplete network map. In these cases a function-topology map can provide important information about the possible network structure and its key components, thus helping to design experiments to fully elucidate the underlying network. Finally, there is growing interest in learning how to modify cellular networks to generate new behaviors or optimize existing ones. In medicine, an understanding of how specific changes in architecture can shift a system from one behavior to another could greatly aid in developing more intelligent therapeutic strategies for treatment of complex diseases like cancer. In the emerging field of synthetic biology, this type of function-topology design table could serve as a manual providing different possible solutions to building a biological circuit with a target set of behaviors.
EXPERIMENTAL PROCEDURES
Enumeration of Three-Node Topologies
We considered all possible three-node network topologies (Figure 1B). There are a total of nine directed links among the three nodes. Each link has three possibilities: positive regulation, negative regulation, or no regulation. Thus there are 39 = 19,683 possible topologies. We let the input act on node A and use as the output the active concentration of node C. There are 3,645 topologies that have no direct or indirect links from the input to the output. We use all the remaining 16,038 topologies in our study.
Equations of the Circuit
We assume that each node (labeled as A, B, C) has a fixed concentration (normalized to 1) but has two forms: active and inactive (here “_A_” represents the concentration of active state, and “1-_A_” is the concentration of the inactive state). The enzymatic regulation converts its target node between the two forms. For example, a positive regulation of node B by node A as denoted by a link A→B would mean that the active A converts B from its inactive to its active form and would be modeled by the rate R(_B_inactive→_B_active) = kAB A(1 − B) / [(1 − B) + _KAB_], where A is the normalized concentration of the active form of node A and 1 − B the normalized concentrations of the inactive form of node B. Likewise, A—∣B implies that the active A catalyzes the reverse transition of node B from its active to its inactive form, with a rate R(_B_active→_B_inactive) = k_′_AB AB / (B+_K_′ AB). When there are multiple regulations of the same sign on a node, the effect is additive. For example, if node C is positively regulated by node A and node B, R(_C_inactive → _C_active) = kAC A (1 − C) / [(1 − C) + _KAC_] + kBC B(1 − C) / [(1 − C) + _KBC_]. We assume that the interconversion between active and inactive forms of a node is reversible. Thus if a node i has only positive incoming links, it is assumed that there is a background (constitutive) deactivating enzyme Fi of a constant concentration (set to be 0.5) to catalyze the reverse reaction. Similarly, a background activating enzyme Ei = 0.5 is added for the nodes that have only negative incoming links. The rate equation for a node (e.g., node B) takes the form:
| dBdt=∑iXi·kXiB·(1−B)(1−B)+KXiB−∑iYi⋅kYiB′·BB+kYiB′, | (7) |
|---|
where Xi = A, B, C, EA, EB, or EC are the activating enzymes (positive regulators) of B and Yi = A, B, C, FA, FB, or FC are the deactivating enzymes (negative regulators) of B. In the equation for node A, an input term is added to the right-hand-side of the equation: IkIA(1-A)/((1-A)+KIA). The number of parameters in a network is np = 2_nl_+2, where nl is the number of links in the network (including links from the basal enzymes if present).
Functional Performance
For each network topology, 10,000 parameter sets were sampled uniformly in logarithmic scale in the _np_-dimensional parameter space, using the Latin hypercube sampling method (Iman et al., 1980). The sampling ranges of the parameters are _k_~0.1-10 and _K_~0.001-100. A circuit refers to a network topology with a particular choice of parameters. The typical output curve of an adaptive circuit has two steady-state values _O_1 and _O_2, corresponding to the two input values _I_1 and _I_2, respectively, and, in response to the input change, has a transient pulse with the peak value _O_peak (Figure 1A). III-behaved circuits are excluded from further analysis. They can be circuits with too small steady-state values (<0.001) of the active or inactive enzymes, the ones spending too much time to approach a steady state, or those with persistent or too weakly underdamped oscillations (Supplemental Experimental Procedures, section 1). The remaining circuits were evaluated for their sensitivity to input change and adaptation precision.
- Precision: the inverse of the adaptation error. The error E is defined as the relative difference between the output steady states before and after the input change.
| P=E−1=(|O2−O1|/O1|I2−I1|/I1)−1 | (8) |
| --------------------------------- | --- | - Sensitivity: the largest transient relative change of the output divided by the relative change of the input.
| S=|Opeak−O1|/O1|I2−I1|/I1 | (9) |
| --------------------------- | --- |
It is obvious that S ≥ E since |_O_peak − _O_1| ≥ |_O_2 − _O_1|. This implies that log(S) + log(P) ≥ 0.
The overall performance of a topology is measure by its Robustness or the Q value, defined here as the number of times the topology is mapped to the high-sensitivity/high-precision region of the functional space (the green rectangle in Figure 1D).
Clustering of Networks
There are nine possible links for a network. For every network, we assign a value to each of the nine links: 1 for positive regulation, −1 for negative regulation, and 0 for no regulation. Thus a network is represented by a sequence of length 9. We define the distance between two networks as the Hamming distance between their sequences, that is, the number of regulations that differ in the two networks. The distance matrix is then used for clustering, using the MATLAB function clustergram.
Supplementary Material
Supplementary Data
Acknowledgments
We thank Caleb Bashor, Noah Helman, Morten Kloster, Ilya Nemenman, and Eduardo Sontag for helpful discussions, Angi Chau, Kai-Yeung Lau, Thomas Shimizu, and David Burkhardt for critical reading of the manuscript. W.M. acknowledges the support from the Li Foundation. A.T. acknowledges the support from the Sandler Family Supporting Foundation. This work was supported in part by the National Science Foundation (DMR-0804183) (C.T.), Ministry of Science and Technology of China (C.T.), the National Natural Science Foundation of China (C.T.), the Howard Hughes Medical Institute (W.A.L.), the Packard Foundation (W.A.L.), the NIH (W.A.L.), and the NIH Nano-medicine Development Centers (W.A.L.).
Footnotes
References
- Alon U. Network motifs: theory and experimental approaches. Nat Rev Genet. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- Behar M, Hao N, Dohlman HG, Elston TC. Mathematical and computational analysis of adaptation via feedback inhibition in signal transduction pathways. Biophys J. 2007;93:806–821. doi: 10.1529/biophysj.107.107516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg HC, Brown DA. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972;239:500–504. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- Brandman O, Ferrell JE, Jr, Li R, Meyer T. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science. 2005;310:496–498. doi: 10.1126/science.1113834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Samad H, Goff JP, Khammash M. Calcium homeostasis and parturient hypocalcemia: an integral feedback perspective. J Theor Biol. 2002;214:17–29. doi: 10.1006/jtbi.2001.2422. [DOI] [PubMed] [Google Scholar]
- Endres RG, Wingreen NS. Precise adaptation in bacterial chemotaxis through “assistance neighborhoods”. Proc Natl Acad Sci USA. 2006;103:13040–13044. doi: 10.1073/pnas.0603101103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- François P, Siggia ED. A case study of evolutionary computation of biochemical adaptation. Phys Biol. 2008;5:026009. doi: 10.1088/1478-3975/5/2/026009. [DOI] [PubMed] [Google Scholar]
- Goldbeter A, Koshland DE., Jr Ultrasensitivity in biochemical systems controlled by covalent modification. Interplay between zero-order and multistep effects. J Biol Chem. 1984;259:14441–14447. [PubMed] [Google Scholar]
- Hornung G, Barkai N. Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. PLoS Comput Biol. 2008;4:e8. doi: 10.1371/journal.pcbi.0040008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iman RL, Davenport JM, Zeigler DK. Latin Hypercube Sampling (Program User’s Guide) Albuquerque, NM: Sandia Labs; 1980. p. 77. [Google Scholar]
- Kirsch ML, Peters PD, Hanlon DW, Kirby JR, Ordal GW. Chemotactic methylesterase promotes adaptation to high concentrations of attractant in Bacillus subtilis. J Biol Chem. 1993;268:18610–18616. [PubMed] [Google Scholar]
- Kollmann M, Lovdok L, Bartholome K, Timmer J, Sourjik V. Design principles of a bacterial signalling network. Nature. 2005;438:504–507. doi: 10.1038/nature04228. [DOI] [PubMed] [Google Scholar]
- Levchenko A, Iglesias PA. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma W, Lai L, Ouyang Q, Tang C. Robustness and modular design of the Drosophila segment polarity network. Mol Syst Biol. 2006;2:70. doi: 10.1038/msb4100111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macnab RM, Koshland DE., Jr The gradient-sensing mechanism in bacterial chemotaxis. Proc Natl Acad Sci USA. 1972;69:2509–2512. doi: 10.1073/pnas.69.9.2509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR, Reisert J. Calcium, the two-faced messenger of olfactory transduction and adaptation. Curr Opin Neurobiol. 2003;13:469–475. doi: 10.1016/s0959-4388(03)00097-7. [DOI] [PubMed] [Google Scholar]
- Mello BA, Tu Y. Quantitative modeling of sensitivity in bacterial chemotaxis: the role of coupling among different chemoreceptor species. Proc Natl Acad Sci USA. 2003;100:8223–8228. doi: 10.1073/pnas.1330839100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mettetal JT, Muzzey D, Gomez-Uribe C, van Oudenaarden A. The frequency dependence of osmo-adaptation in Saccharomyces cerevisiae. Science. 2008;319:482–484. doi: 10.1126/science.1151582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- Parent CA, Devreotes PN. A cell’s sense of direction. Science. 1999;284:765–770. doi: 10.1126/science.284.5415.765. [DOI] [PubMed] [Google Scholar]
- Rao CV, Kirby JR, Arkin AP. Design and diversity in bacterial chemotaxis: a comparative study in Escherichia coli and Bacillus subtilis. PLoS Biol. 2004;2:E49. doi: 10.1371/journal.pbio.0020049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisert J, Matthews HR. Response properties of isolated mouse olfactory receptor cells. J Physiol. 2001;530:113–122. doi: 10.1111/j.1469-7793.2001.0113m.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- Tsai TY, Choi YS, Ma W, Pomerening JR, Tang C, Ferrell JE., Jr Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A. Circuit topology and the evolution of robustness in two-gene circadian oscillators. Proc Natl Acad Sci USA. 2005;102:11775–11780. doi: 10.1073/pnas.0501094102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang L, Iglesias PA. Positive feedback may cause the biphasic response observed in the chemoattractant-induced response of Dictyostelium cells. Syst Contr Lett. 2006;55:329–337. doi: 10.1016/j.sysconle.2005.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi TM, Huang Y, Simon MI, Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc Natl Acad Sci USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Data