Evaluation of Different Biological Data and Computational Classification Methods for Use in Protein Interaction Prediction (original) (raw)
. Author manuscript; available in PMC: 2012 Jan 4.
Published in final edited form as: Proteins. 2006 May 15;63(3):490–500. doi: 10.1002/prot.20865
Abstract
Protein–protein interactions play a key role in many biological systems. High-throughput methods can directly detect the set of interacting proteins in yeast, but the results are often incomplete and exhibit high false-positive and false-negative rates. Recently, many different research groups independently suggested using supervised learning methods to integrate direct and indirect biological data sources for the protein interaction prediction task. However, the data sources, approaches, and implementations varied. Furthermore, the protein interaction prediction task itself can be subdivided into prediction of (1) physical interaction, (2) co-complex relationship, and (3) pathway co-membership. To investigate systematically the utility of different data sources and the way the data is encoded as features for predicting each of these types of protein interactions, we assembled a large set of biological features and varied their encoding for use in each of the three prediction tasks. Six different classifiers were used to assess the accuracy in predicting interactions, Random Forest (RF), RF similarity-based k-Nearest-Neighbor, Naïve Bayes, Decision Tree, Logistic Regression, and Support Vector Machine. For all classifiers, the three prediction tasks had different success rates, and co-complex prediction appears to be an easier task than the other two. Independently of prediction task, however, the RF classifier consistently ranked as one of the top two classifiers for all combinations of feature sets. Therefore, we used this classifier to study the importance of different biological datasets. First, we used the splitting function of the RF tree structure, the Gini index, to estimate feature importance. Second, we determined classification accuracy when only the top-ranking features were used as an input in the classifier. We find that the importance of different features depends on the specific prediction task and the way they are encoded. Strikingly, gene expression is consistently the most important feature for all three prediction tasks, while the protein interactions identified using the yeast-2-hybrid system were not among the top-ranking features under any condition.
Keywords: protein–protein, interaction, high-throughput data, joint learning
INTRODUCTION
Protein–protein interactions (PPI) form the physical basis for formation of complexes and pathways that carry out different biological processes. Correctly identifying the set of interacting proteins in an organism is useful for deciphering the molecular mechanisms underlying given biological functions and for assigning functions to unknown proteins based on their interacting partners. It is estimated that there are around 30,000 specific interactions in yeast, with the majority to be discovered.1,2
A number of high-throughput experimental approaches have been applied to determine the set of interacting proteins on a proteome-wide scale in yeast. These include the two-hybrid (Y2H) screens3,4 that detect both transient and stable interactions, and mass spectrometry methods that are used to identify components of protein complexes. 5,6 However, both methods suffer from high false-positive and false-negative rates.2 For the Y2H method, this is due to insufficient depth of screening and misfolding of the fusion proteins. In addition, interaction between “bait” and “prey” proteins has to occur in the nucleus, where many proteins are not in their native compartment. The mass spectrometry methods (tandem affinity purification, TAP,5 and high-throughput mass-spectrometric protein complex identification, HMS-PCI6) may miss complexes that are not present under the given conditions; tagging may disturb complex formation and weakly associated components may dissociate and escape detection. Von Mering et al.2 were among the first to discuss the problem of accurately inferring protein interactions from high-throughput data sources: ~80,000 interactions have been predicted in yeast by various high-throughput methods, but only a small number (~2400) are supported by more than one method.2 The solution proposed by von Mering et al. to use the intersection of direct high-throughput experimental results was able to achieve a very low false-positive rate. However, the coverage was also very low. Less than 3% of known interacting pairs were recovered using this method.
Recently, it was shown that some indirect biological datasets contain information on protein interactions. Integrating such information with direct measurements of protein interactions could improve the quality of protein interaction data. For example, many interacting pairs are coexpressed,2 and proteins in the same complex are in some cases bound by the same transcription factor(s).2,7 Sequence data can also be used to infer protein interactions from interdomain interactions.8 There may be many other characteristics of a gene or protein pair with predictive value.
Based on these observations, a number of researchers have recently suggested that direct data on protein interactions can be combined with indirect data in a supervised learning framework.9–16 Such in silico prediction methods were shown to improve the success of protein interaction prediction when compared to direct data alone, not just from the perspective of predicting novel interactions but also for the purpose of stratifying the many candidate interactions by confidence. Although these approaches are related in that they use a classification algorithm to integrate diverse biological datasets, they differed in three design issues: (1) the gold standard data sets used for training and testing, (2) the set of features used for prediction and the way these features were encoded, and (3) the learning method employed. The previous approaches applied are briefly described below with respect to these three design issues and summarized in Table I.
TABLE I.
Summary of Three Design Issues and the Previous Methods for the Supervised Protein Interaction Prediction Task
| Prediction task/feature encodingtype | Co-complex | Physical interaction | Pathway |
|---|---|---|---|
| Summary | Naïve Bayes,11 Random Forest,13 Logistic Regression13 | Logistic Regression,9 Random Forest similarity-based k-Nearest Neighbor16 | Bayesian Statistics Scoring12 |
| Detailed | Decision Tree15 | Kernel method14 |
The Gold Standard Datasets
Three gold standard datasets were previously used to train and test algorithms for protein protein interaction prediction. These three tasks are the prediction of (1) physical interaction, (2) co-complex relationship, and (3) pathway co-membership. For predicting direct physical interaction between protein pairs, the Database of Interacting Proteins (DIP) (“small-scale” subset16) is used.17–19 A broader definition of protein interaction is the co-complex relationship in which proteins are considered pairs even if they do not directly interact but are connected through other proteins. The Munich Information Center for Protein Sequences (MIPS) complex catalog20 has been used as the gold standard dataset for this prediction task.11,13,15 Finally, the Kyoto Encyclopedia of Genes and Genomes (KEGG) database21 has provided the gold standard for inferring pathway networks.12
Feature Encoding
Two fundamentally different general types of feature encoding were used in the past: a “detailed” encoding style, where every experiment is considered separately [15], and a “summary” style, where similar types of experiments, such as all expression experiments, are grouped together and provide a single value.11,13,17
Classification Methods
Many different classifiers were suggested for the protein interaction prediction task. Logistic regression (LR) has been used to estimate the posterior probability that a pair of proteins interacts9 for predicting direct physical interactions from high-throughput features. We have recently proposed a method (kRF17) that combines Random Forest (RF) and kNN with a summary feature set using DIP (“small-scale” subset16) as our gold standard. To predict co-complex relationships, Jansen et al.11 applied a Naïve Bayes (NB) classifier using a summary feature set including mRNA expression data, data from the Gene Ontology database, essentiality data, and direct high-throughput interaction experiments. Lin et al.13 repeated these experiments using two other classifiers, Random Forest (RF), and Logistic Regression (LR). Within this framework, the MIPS and Gene Ontology functional categories were found to be the most informative. Zhang et al.15 used a decision tree (DT) with a detailed feature set for this co-complex prediction task. To predict pathway protein interactions, Yamanishi et al.14 presented a method using a variant of kernel canonical correlation analysis applied to a detailed feature set. Lee et al.12 integrated diverse functional genomic data encoded in a summary style to provide numerical likelihoods that genes are functionally linked based on KEGG co-pathway membership evidence.
In summary, previous studies differed in terms of classifiers, feature sets, and their encodings and gold-standard datasets used (Table I). These differences make it hard to directly compare approaches and to identify features that perform well on the different types of protein interaction prediction tasks. These are important questions, especially when designing experiments to infer protein interactions in organisms other than yeast. For example, identifying the set of important features can help determine if enough data exists for such a prediction task in a particular organism, and to indicate which type of data is most useful.
In this article we present a systematic analysis of the effect of varying each of the different design issues discussed above. We compared prediction performance by testing on all 36 possible combinations of feature encoding styles (summary and detailed), reference datasets (DIP, MIPS, and KEGG) and classifiers (DT, LR, NB, SVM, RF, and kRF). Because our goal was to systematically compare different features and their encoding for the different subtasks, we did not attempt to reimplement precisely the previously applied strategies. Instead, we used a constant set of features, with two different encodings, constant evaluation strategy, and standard implementation of the above classification algorithms. We then used the classifier that performed the best in this comparison, the RF classifier, to evaluate the information contribution of each feature group for the three protein interaction prediction tasks.
Below, we first provide detailed description about each of the three design issues. We then present a systematic analysis of how these issues affect the final performance in predicting protein interactions and discuss how the contribution of each feature varies with respect to the different tasks.
MATERIALS AND METHODS
Gold Standard Datasets
All methods applied to the protein interaction prediction task in this article use the supervised learning framework and therefore require a training and a test set (or gold standard set).
Positive Examples
To obtain the positive examples, three gold standard datasets were used. (1) For predicting direct (physical) protein–protein interactions, DIP16 was used. DIP provides a set of ~3000 physically interacting protein pairs validated by small-scale experiments. (2) For predicting co-complex protein pairs, the MIPS20 database was used. MIPS was created and hand curated in 1998 based on evidence derived from a variety of experimental techniques and does not include information from high-throughput datasets. It contains ~8000 protein co-complex associations in yeast. (3) For predicting co-pathway relationships, the KEGG pathway database21 was used. KEGG contains graphical representations of cellular processes. The gold standard set we derived from KEGG was similar to the one used in ref. 12. Briefly, if two genes have at least one shared KEGG pathway membership, they are considered to constitute a positive pair.
Data Overlap in Gold Standard Datasets
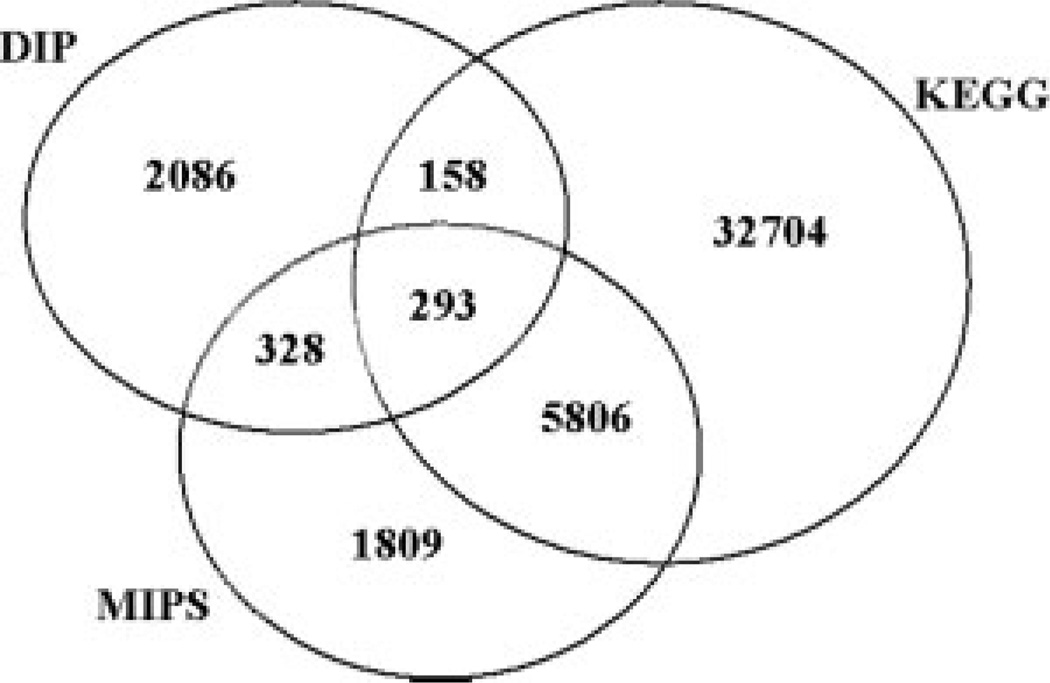
Table II lists the number of protein pairs and the total number of proteins in each of the three positive sets. Note that the DIP derived positive set is smaller than the MIPS data set and the MIPS data set is, in turn, smaller than the KEGG-derived positive set. However, this does not mean that these are subsets of each other. Figure 1 presents the overlap of protein pairs between these three sets. Although the overlap between DIP and MIPS and between DIP and KEGG is small, it is much higher between MIPS and KEGG. Roughly 75% of the entries in MIPS are also present in KEGG.
TABLE II.
Number of Protein Pairs and the Total Number of Related Proteins Contained in the Three Gold Standard Positive Sets
| DIP(physicalinteraction) | MIPS(Cocomplex) | KEGG(Copathway) | |
|---|---|---|---|
| Number of protein pairs | 2865 | 8236 | 38,961 |
| Total number of proteins | 1536 | 870 | 1129 |
Fig. 1.
Venn diagram of the overlap between the three gold standard positive datasets.
Negative Examples
Identification of negative examples for training and testing is difficult. Unlike positive interactions, it is rare to find a confirmed report of noninteracting pairs, especially not on a large scale. Here, we follow the approach described by Zhang et al.,15 and use a random set of protein pairs (after filtering the positive ones) as the negative set. This selection is justified because the fraction of interacting pairs in the total set of potential protein pairs is small. It is estimated that only one in several hundred potential protein pairs actually contain interacting partners. Thus, over 99% of our random data is indeed noninteracting, which is probably better than the accuracy of most training data. Following refs. 10 and 22, our final gold standard set contained one positive interaction for every 600 negative interaction pairs, unless noted otherwise.
Feature Types and Encoding
Features sources
The supervised learning framework investigated here is general, and can be used with any type of biological data. We used a total of 162 features representing 17 distinct groups of biological data sources. Overall, these data sources can be divided into three categories: Direct experimental data sets (two-hybrid screens and mass spectrometry), indirect high throughput data sets (gene expression, protein–DNA binding, biological function, biological process, protein localization, protein class, essentiality, etc.) and sequence based data sources (domain information, gene fusion, etc.). Table III lists the 17 groups of features used in this article. Details about where these features come from and how we process them are in the supplementary material (Table S1).
TABLE III.
Features Used
| Index | Feature category | Number of features | Coverage (percentage) | Reference |
|---|---|---|---|---|
| 1 | Gene expression | 20 | 88.9 | 7 |
| 2 | GO molecular function | 21 | 80.7 | 23 |
| 3 | GO biological process | 33 | 76.1 | 23 |
| 4 | GO component | 23 | 81.5 | 23 |
| 5 | Protein expression | 1 | 42.8 | 32 |
| 6 | Essentiality | 1 | 100.0 | 33 |
| 7 | HMS_PCI mass | 1 | 8.3 | 1, 6a |
| 8 | TAP mass | 1 | 8.8 | 1, 5a |
| 9 | Yeast-2-Hybrid | 1 | 3.9 | 3, 4 |
| 10 | Synthetic lethal | 1 | 7.6 | 2, 22 |
| 11 | Gene neighborhood/gene fusion/gene co-occurrence | 1 | 100.0 | 2 |
| 12 | Sequence similarity | 1 | 100.0 | 34 |
| 13 | Homology-based PPI | 4 | 100.0 | 19, 34 |
| 14 | Domain-domain interaction | 1 | 100.0 | 8 |
| 15 | Protein_DNA TF group binding | 16 | 98.0 | 35 |
| 16 | MIPS protein class | 25 | 4.6 | 20 |
| 17 | MIPS mutant phenotype | 11 | 9.4 | 20 |
Most biological datasets are noisy and contain many missing values. For example, for the Yeast-2-Hybrid (Y2H)-derived feature, the interactions involving membrane proteins go essentially undetected. The fourth column in the table describes the average coverage of each feature category. As can be seen, different features have varying degrees of missing values. The coverage of the 17 groups (Table III) ranges from 3.9% for Y2H to over 88.9% for gene expression and 100% for sequence based features.
Feature encoding
There are two possible ways for encoding these biological datasets: “Summary” and “Detailed.” In “Summary” encoding, each biological source is represented by a single value. In “Detailed” encoding, the same information source is described by multiple values. These two feature encoding methods result in very different sizes of the feature vectors. For example, if we are using 20 different gene expression datasets (each measuring a time series expression profile) we can either compute one global similarity score for each pair of proteins or 20 distinct scores for each pair (one for each dataset).11,15 Similarly, the functional similarity of a protein pair could be encoded by treating the GO23 functional catalog as a hierarchical tree of functional classes. In the “Summary” style, the intersection of the tree positions that two proteins share gives their functional annotation similarity.11 In the “Detailed” style each evidence type was mapped to one or more binary variables (“attributes”). For each functional class, a binary attribute is defined to be present if both proteins are members of this class. Table III lists the numbers of features when using “Detailed” encoding (for “Summary” encoding each value is “1”) for the 17 feature groups used in this study.
Classification Algorithms
We compared six classifiers (DT, LR, NB, SVM, RF, and kRF) in this study. Our goal was to identify which of these classifiers is appropriate to the different prediction tasks listed above. Below we briefly discuss each of these classifiers.
Support Vector Machines
Support Vector Machines (SVM) is a relatively recent but increasingly popular learning approach for solving two-class pattern recognition problems. It is based on the structure risk minimization principle for which error-bound analysis has been theoretically motivated. The method is defined over a vector space where the problem is to find a decision surface that “best” separates the data points in two classes by finding a margin. The SVM problem can be solved using quadratic programming techniques, using an optimization algorithm where the working set selection is based on steepest feasible descent. It can handle several hundred to thousands of training examples. We used the SVMLight tool box provided by Thorsten Joachims,24 which is an implementation of SVMs in C. The types of kernels and related parameters were varied in experiments to find optimal parameters for each task.
Naïve Bayes
Naïve Bayes (NB) probabilistic classifiers use the joint probabilities of features and categories to estimate the probabilities of categories given feature evidence. NB assumes feature independence, that is, the conditional probability of a feature given a category is assumed to be independent from the conditional probabilities of other features given that category. This makes NB classifiers extremely efficient. Despite the inappropriateness of this assumption for most applications, the NB classifier works surprisingly well for many different tasks.25 The NB classifier was obtained from the WEKA machine learning26 tool box.
Logistic Regression
Logistic Regression (LR) is a generalized linear statistical model that can predict a discrete outcome from a set of variables that may be continuous, discrete, dichotomous, or a mixture of these. Generally, the response variable is dichotomous, such as presence/absence or success/failure. It applies maximum likelihood estimation after transforming the dependent into a logit variable (the natural log of the odds of the dependent occurring or not). In this way, logistic regression can be used to estimate the probability of a certain event (here: interaction). The LR classifier was obtained from the WEKA machine learning tool box that uses a ridge estimator for building a binary LR model.26
Decision Tree-J48
A decision tree (DT) is a tree where the nonleaf nodes are labeled with attributes, the arcs out of a node are labeled with each of the possible values of the attribute, and the leaves of the tree are labeled with classifications. DT learns a classification function to predict the value of a dependent response (variable) given the values of the input attributes. We used the J4826 implementation (Java version of C4.5-Quinlan27) because it incorporates numerical (continuous) attributes, allows postpruning after induction of trees, and can handle incomplete information (missing attribute values).
Random Forest
The RF classifier “grows” many DTs simultaneously where each node uses a random subset of the features. To classify a new object from an input vector, each input vector is subjected to analysis by each of the trees in the forest. Each tree provides a classification output, that is, the tree “votes” for that class. The forest chooses the classification based on majority vote (over all the trees in the forest). Because the trees are generated from random subsets of the possible attributes, missing values can be handled by an iterative algorithm. RF was implemented by using the Berkeley Random Forest package.28 We grew 200 trees in each run. For the number of variables randomly selected at each node, we used the default value that was equal to the square root of the feature dimension.
Random Forest-based k-Nearest Neighbor
This method (kRF17) starts by creating a RF to compute similarity between protein interaction pairs. Protein pairs are propagated down the trees and a similarity matrix based on leaf occupancy is calculated for all pairs. Next, a weighted _k_-Nearest Neighbor algorithm, where distances are based on the computed similarity, is used to classify pairs as interacting or not. kRF was implemented by using the Berkeley Random Forest package and weighted _k_-Nearest Neighbor program in C. The parameters related to RF were similar to the ones described above for using RF alone. The parameter k in the weighted kNN part was optimized for each task.
Evaluation of Performance
Training/testing procedures
Performance comparisons were based on the following training and testing procedures. Parameter optimization was carried out in all cases using separate training and test datasets. We randomly sampled a training set containing 30,000 yeast protein pairs to learn the decision model. Then we sampled a test set (another 30,000 pairs) from the remaining protein pairs, and used the trained model to evaluate the performance of the classifier in the context of the data set and feature encoding used. The above random run was repeated 25 times for each case and average values are reported. Due to the small number of true positives expected, we have used a cost sensitive analysis strategy that penalizes more harshly misclassification of true positives. See supplement for more details.
We used two measures to evaluate performance, Precision versus Recall curves and R50 partial area under Receiver Operator Characteristic scores.
Precision versus Recall
In Precision versus Recall29 curves, precision refers to the fraction of interacting pairs predicted by the classifier that are truly interacting (“true positives”). Recall measures how many of the known pairs of interacting proteins have been identified by the learning model. The Precision versus Recall curve is then plotted for different cutoffs on the predicted score.
AUC scores
Receiver Operator Characteristic (ROC) curves30 plot the true positive rate against the false-positive rate for different cutoff values of the predicted score. ROC curves therefore measure the tradeoff between sensitivity and specificity. The area under the ROC curve (AUC) is commonly used as a summary measure of diagnostic accuracy. It can take values from 0.0 to 1.0. AUC values are interpreted as the probability that a randomly selected “event” will be regarded with greater suspicion (in terms of its continuous measurement) than a randomly selected “nonevent.” In some cases, rather than looking at the area under the entire ROC curve, it is more informative to only consider the area under a portion of the curve. Consequently, only part of the area under the curve is relevant.
Partial AUC scores
In our prediction task, we are predominantly concerned with the detection performance of our models under conditions where the false-positive rate is low. Within the high false-positive rate region, for example fp = 0.1, for a testing set of size 30,000, there are roughly 3000 negative examples misclassified as positive interacting pairs. Even if the true positive examples (about 50 examples) are all correctly classified (which is often impossible), the precision of this prediction is just 0.016. We use 50 as a cutoff, that is, R50 is a partial AUC score that measures the area under the ROC curve until reaching 50 negative predictions. This cutoff is reasonable for this task considering the fact that in our random test set, there are approximately 50 positive items (because 1 in 600 pairs are interacting and we selected 30,000 pairs), but the R50 score is also a popular evaluation metric in the machine learning literature in general.
RESULTS AND DISCUSSION
A systematic comparison of prediction performance is pursued on three aspects. First, we compared the six classifiers, DT, LR, NB, SVM, RF, and kRF. Second, for each classifier we used two styles of feature encoding: “Detailed” and “Summary.” Third, for every combination of classifier and feature set, we varied the specific prediction task by predicting (1) protein co-complex relationship (MIPS), (2) direct protein–protein interaction (DIP), and (3) protein co-pathway relationship (KEGG).
Performance Comparison
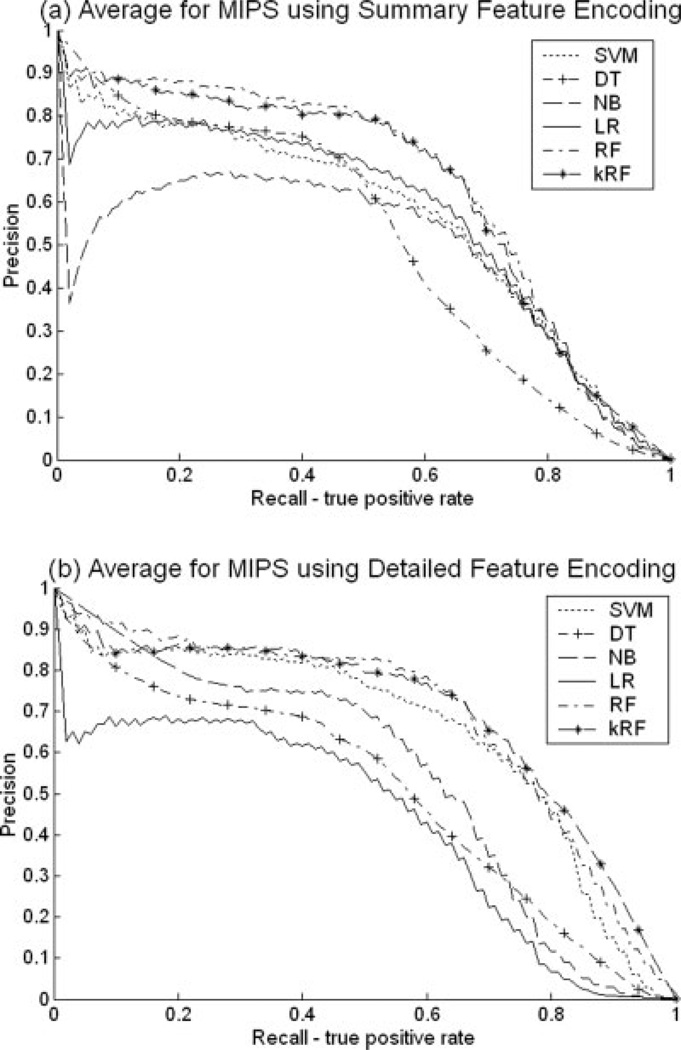
Figure 2 presents a comparison of the six classifiers on the co-complex (MIPS) protein pair prediction task. Figure 2(a) and (b) contain the Precision versus Recall curves using the “Summary” and the “Detailed” encoding feature styles, respectively. In both cases, RF and kRF methods outperform all other methods for this task with SVM a close third. The “Detailed” encoding style improves the performance compared to the “Summary” encoding for this task. Similar results were obtained when using the R50 partial AUC score [see Fig. 1(a)]. Because both Precision versus Recall curves and the R50 scores provide similar conclusions, for the remaining two tasks (direct interaction prediction and co-pathway prediction), we only present the R50 scores. The respective Precision versus Recall curves can be found in the supplementary material.
Fig. 2.
Precision versus Recall curves for the six classifiers, Support Vector Machine (SVM), Decision Tree (DT), Naïve Bayes (NB), Linear Regression (LR), Random Forest (RF), and RF-based kNN approach (kRF) for the co-complex prediction task using the MIPS data set. (a) Features were encoded as “Summary.” (b) Features were encoded as “Detailed.”
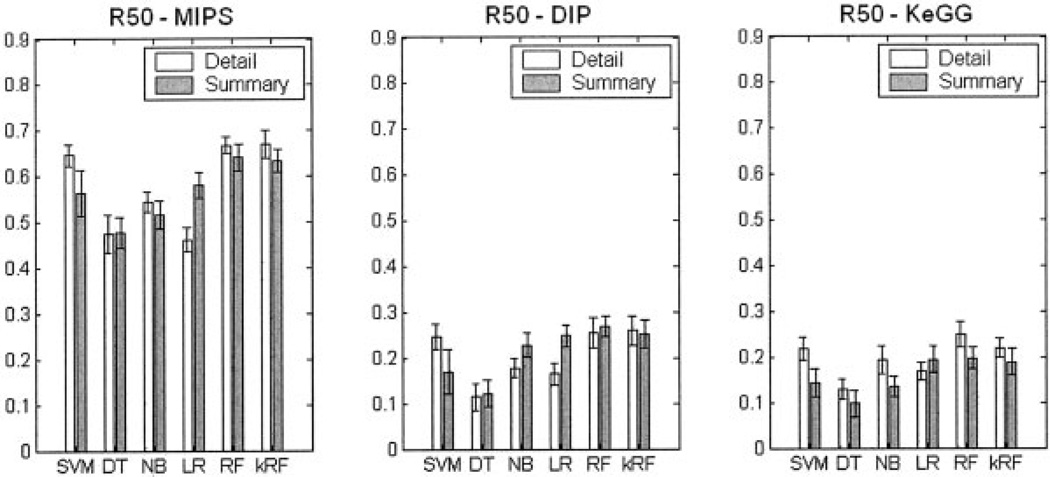
Figure 3 presents the R50 partial AUC scores for the six classification methods on the three prediction tasks. Within each subgraph, “Detailed” encoding and “Summary” encoding styles are compared. As can be seen from Figure 3(b) and (c), for both the physical interaction prediction (DIP) and the co-pathway relationship prediction (KEGG), RF consistently outperforms other methods, closely followed by kRF and SVM.
Fig. 3.
R50 Partial AUC score comparison between the six classification methods for all three prediction tasks. Each subgraph describes one specific prediction task: (a) protein co-complex relationship (MIPS), (b) direct protein–protein interaction (DIP), and (c) protein co-pathway relationship (KEGG). Within each subgraph, the white and gray represent “Detailed” and “Summary” encodings of the features, respectively. Abbreviations of the six classifiers are the same as in Figure 2. The averages of the R50 values are shown as bars. For each bar, the confidence interval of the mean of the estimate R50 are drawn as thin error bar lines.
The results also show that “Detailed” encoding is generally better than “Summary” encoding for the best classifiers. A notable exception is found when comparing performance using the DIP data set. Here, NB and LR, and to a smaller extent RF, perform better with the “Summary” feature encoding. We believe that the reason for this difference is because of the comparatively harder task of predicting physical interaction than co-complex or co-pathway relationships. This is expected, because our features, in particular the indirect features, are less likely to be strongly correlated with physical interaction than with the other two tasks. This may lead to an overfitting effect by the “Detailed” feature set when compared to the “Summary” feature encoding.
Finally, the prediction of co-complex pairs appears to be a much easier task than either physically interacting pair prediction or co-pathway membership. For the MIPS prediction, the worst classification R50 value was 0.47, and the highest R50 value was 0.68, while the worst prediction of both DIP and KEGG was 0.12 and the best was 0.26. The absolute prediction value is also dependent on the ratio between positive and negative pairs using during training and testing procedures. At the current stage it is impossible to know the true ratio of the interaction pairs compared to the noninteraction pairs. Although this ratio is estimated to be 1:600,10,22 it is possible that this ratio needs to be revised. To investigate this possibility, we also tested another ratio of 1 interacting pair for every 100 noninteraction pairs in constructing our gold standard sets for the co-pathway prediction task. This new ratio resulted in an improvement in the absolute values in the Precision–Recall curve position and its R50 value for all classification methods. However, the relative performance difference between the six classifiers and the two different encoding types did not change when using a 1:100 compared to a 1:600 ratio (results not shown). Thus, our conclusions hold regardless of the true positive to negative ratio.
Performance Analysis when Varying Training Set Size
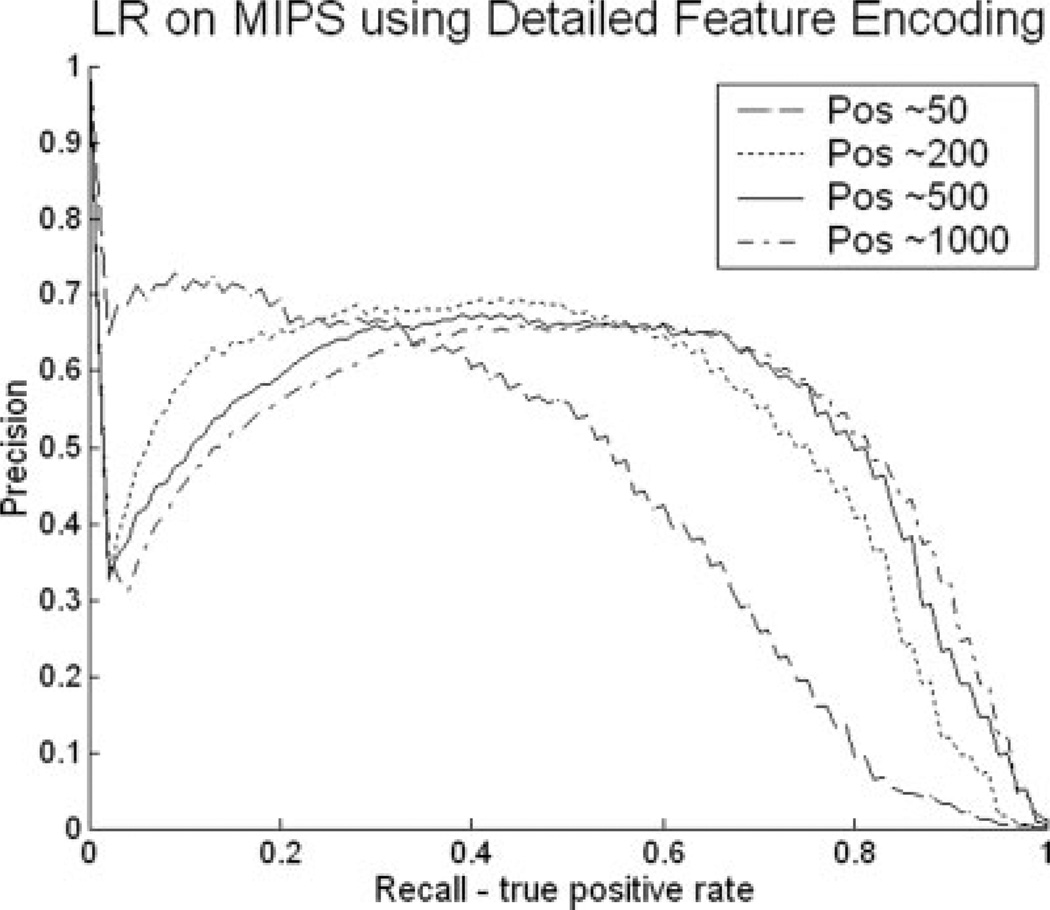
As can be seen in Figures 2 and 3, DT and NB performed the worst among the six classifiers in all cases, while the RF classifier performed consistently among the best two. Although LR performed reasonably well when using the “Summary” encoding, it performed especially poorly with “Detailed” encoding. To ensure that the reason for the poor performance of LR and the high performance of RF was not the way we set up the experiment, we considered whether this relative difference in performance may be an artifact of the high ratio of features to positive examples, especially when using the detailed encoding style, which may lead to overfitting. To test for potential overfitting problems, we varied the number of true positives in our training and test sets. Figure 4 presents the Precision versus Recall curves when varying the training set size for the co-complex prediction task using the detailed feature encoding. Each curve corresponds to a specific training size: (a) 30,000 (with about 50 positive pairs) (b) 120,000 (200 positive pairs) (c) 300,000 (500 positive pairs) (d) 600,000 (1000 positive pairs). As the training size increases, the performance of LR improves. However, when comparing these results with Figure 2, it is clear that the RF classifier still outperforms LR, even when LR is allowed to use a much larger training set. Specifically within the recall range of [0.2, 0.6] in Figure 2(b), RF gives a consistent precision that is better than 0.8, whereas for LR (Fig. 4), all four curves do not rise above a precision of 0.7 within this recall range. Similar results are obtained for the physical interaction task and co-pathway prediction tasks and when comparing the different other classifiers. See supplementary material for more details.
Fig. 4.
Precision versus Recall curves for the co-complex prediction task (MIPS) when varying the training set size to have (a) 50 interaction pairs, (b) 200 interaction pairs, (c) 500 interaction pairs, (d) 1000 interaction pairs. Features were encoded using the “Detailed” encoding style.
There may be several factors that contribute to the success of RF when compared with LR and other classifiers: (a) the currently available direct and indirect protein interaction data is inherently noisy and contains many missing values. The randomization and ensemble strategies within RF make it more robust to noise when compared to LR. (b) Biological datasets are often correlated with each other and thus should not be treated as independent sources. Linear and nonlinear regression models assume independence, and may therefore perform worse than other classifiers in tasks where correlations among features are strong. In contrast, the RF classifier does not make any assumptions about the relationship between the data, which makes it more appropriate for the type of data available for the protein interaction prediction task.
Feature Importance
Biologically, it is of particular interest to identify the extent to which heterogeneous data sources carry information about protein interactions. Considering that most biological datasets have missing values, redundant features are important and can provide complementary information. Thus, an analysis of the contribution of different features can help uncover relationships between different data sources that are not directly apparent. In addition, it can help identify what data sources should be generated for determining interaction in other species (e.g., in humans). Moreover, these evaluations can help determine more parsimonious models with comparable or better prediction accuracy.
One way to determine such feature importance is to use the resulting RF trees. The RF classifier uses a splitting function called the Gini index to determine which attribute to split on during the tree learning phase. The Gini index measures the level of impurity/inequality of the samples assigned to a node based on a split at its parent. In our case, where there are two classes, let p represent the fraction of interacting pairs assigned to node m and 1 – p the fraction of the noninteracting pairs. Then, the Gini index at m is defined as:
The purer a node is, the smaller the Gini value. Every time a split of a node is made using a certain feature attribute, the Gini value for the two descendant nodes is less than the parent node. The sum of these Gini value decreases (from parent to sons) for each feature over all trees in the forest and provides a simple and reliable estimate of the feature importance for this prediction task.28 The RF Gini feature importance selector is generally a popular metric used in a variety of feature selection tasks.31
Table IV contains a ranked list of normalized Gini importance scores for the top six categories for each of the three prediction tasks (using the “Detailed” encoding type). The score for each feature category is the sum over the scores from all the members of the given feature group.
TABLE IV.
The Six Most Important Categories for Each Task Ranked Using the RF Gini Variable Importance Criterion
| Order | Co-complex | Importance | Direct interaction | Importance | Co-pathway | Importance |
|---|---|---|---|---|---|---|
| 1 | Gene expression | 0.4217 | Gene expression | 0.1906 | Gene expression | 0.4766 |
| 2 | GO process | 0.2009 | GO process | 0.1709 | GO process | 0.1729 |
| 3 | GO component | 0.1365 | GO component | 0.1107 | GO function | 0.1297 |
| 4 | GO function | 0.1198 | TAP MS | 0.1035 | GO component | 0.0958 |
| 5 | TAP MS | 0.0731 | GO function | 0.0852 | Mutant phenotype | 0.0488 |
| 6 | Protein class | 0.0109 | Mutant phenotype | 0.0668 | Gene fusion/gene cooccurrence | 0.0207 |
For all three tasks, gene coexpression had the highest score. Following gene expression are the three Gene Ontology based categories: process, component, and function. These are also the features with the highest coverage. Thus, indirect information plays a very important role in the decision process due to the fact that direct experiments only cover less than 20% of all protein pairs. It is particularly encouraging that gene coexpression is such an important category as it supports the notion that large amounts of indirect data are helpful in predicting interaction partners. It should be noted that the gene expression features we used in our prediction came from a large number (20) of different experiments carried out under a diverse set of conditions.7
Although some feature datasets are important for all prediction tasks, others are not. For example, the TAP dataset that directly measures protein complex relationships was found to be useful for co-complex (MIPS) task and physical interaction (DIP) predictions but not for co-pathway (KEGG) task. On the other hand, the knockout mutant phenotype feature, which likely represents genes in the same pathway, was important for KEGG but not for MIPS.
If one considers the difference in feature coverage, direct high-throughput interaction datasets become more important. For example, the mass spectrometry TAP feature only covers 8% of protein pairs, but contributes very significantly to both, the co-complex and the direct PPI prediction tasks. This suggests that the high-throughput experimental PPI datasets significantly contribute to our ability to derive protein network information despite their high false-positive and high false-negative rates. Finally, mass spectrometry data is clearly more significant than Y2H screen data, consistent with the notion that mass spectrometry identification of protein–protein interaction is less prone to artifacts than Y2H experiments.
Performance Analysis Based on Feature Composition
The feature importance analysis above suggests that a small number of features may be sufficient to accurately predict protein interactions. To evaluate this idea we investigated the performance when only using the top ranked feature categories. For this study we used the best classifier, RF, with “Detailed” feature encoding.
We used the ordering of Table IV to add one feature category at a time. Thus, we first chose the most important feature category, gene expression, and trained and tested RF using only this dataset for each of the three prediction tasks. Next we added the second ranked category for each task and so forth until all six top feature categories were included.
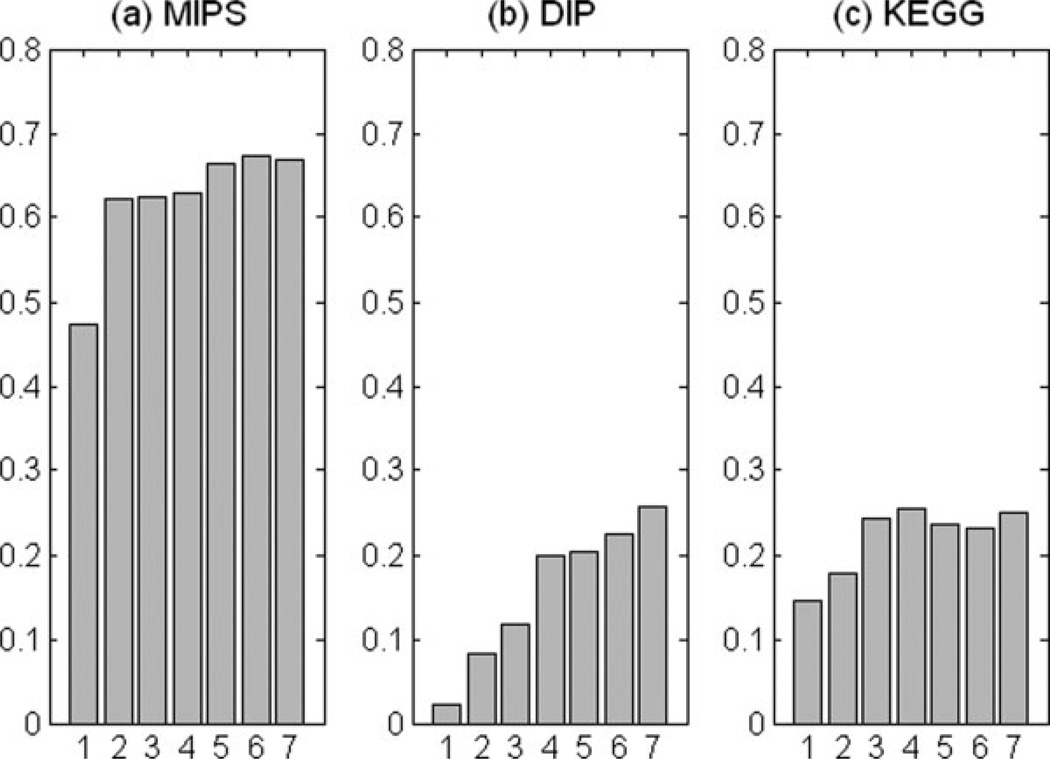
Figure 5 presents the results. Plotted are the R50 partial AUC scores for the three prediction tasks using the features as described above. The seventh bar on each subgraph presents the R50 score when using the full set of features. Overall, the performance gradually increased as we added more categories. For all tasks, the top six feature categories (out of 17) achieve results that are the same, or close to, the R50 value when using the full feature set. The Precision versus Recall curves of corresponding runs are provided in the supplementary material.
Fig. 5.
R50 Partial AUC score comparison when using the top 6 ranked feature categories for each prediction task. The features were added one after the other according to the order in Table IV. The Random Forest classifier with “Detailed” feature encoding was used for this experiment. Each subgraph describes one specific prediction task: (a) protein co-complex relationship (MIPS), (b) direct protein–protein interaction (DIP), and (c) protein co-pathway relationship (KEGG). Each bar represents the score using all features up to that rank (1 to 6). The seventh bar presents the R50 score when using the full set of features.
Some of the features we collected are not useful for the prediction task and some even hurt the performance. For example, in Figure 5(c) the bars at positions 5 and 6 are lower than at 4 and 7, indicating that adding mutant phenotype and gene fusion/co-occurrence data did not help for this prediction task in the absence of the full complement of features. Remarkably, for MIPS and KEGG, more than 60% of the maximum R50 value can already be achieved by using a single feature group, gene expression. However, for DIP, the performance using gene expression alone is poor. Adding top feature groups, in turn, gradually improved performance toward the full feature case. This difference between DIP and the other two data sets is also reflected in the scores of top ranking features in Table IV. For DIP, the top six feature groups are not as important as for MIPS and KEGG.
In Figure 5(a), the R50 value increases upon adding the second feature (from bar-1 to bar-2) much more so than when adding the third or fourth feature (from bar-2 to bar-3 and bar-3 to bar-4). Similar observations are made in the other prediction tasks. This behavior is caused by the randomization strategy of RF. RF builds decision trees from random subsets of the possible attributes. Thus, feature variables having similar predictive power receive a similar Gini ranking from the RF even if they are redundant.
CONCLUSIONS
We presented a systematic study of the protein interaction prediction task when learning from multiple sources, focusing on the following four aspects: (1) we compared six different classifiers to assess the difference in their performance. (2) We used many different features and varied their encoding. (3) We investigated the relative contribution of different features to the prediction accuracy. (4) Finally, we varied the specific prediction task by predicting (a) direct (physical) protein–protein interactions using the DIP dataset, (b) protein co-complex relationships using the MIPS dataset, and (c) protein co-pathway relationship using the KEGG-pathway dataset.
Based on performance evaluations, we find that (1) the co-complex relationship is the easiest to predict. This can be understood intuitively, because co-complex prediction is an intermediate task between the general pathway membership prediction in which protein pairs may be quite different from functional and regulatory points of view, and direct physical interactions which are strongly modulated by variations in environmental factors, cell signaling state, and developmental stages. The biological data sources we used encode this intermediate (co-complex prediction) task better than the other two tasks. We believe that the situation may change when more data becomes available, specifically data that utilizes knowledge about known modulators of interactions such as phosphorylation. (2) Appropriate encoding of the feature attributes contributes to computational performance. In general, the “Detailed” encoding style is preferred. (3) The RF classifier performs robustly and favorably in general among the six methods for the protein–protein interaction prediction task in all three subtasks. This is most likely related to the following three factors. (A) RF like other tree-based methods can easily combine different types of data including discrete, continuous, and categorical data. (B) RF does not assume that the features are independent, like some of the other classifications methods we considered (e.g., NB). This is clearly an advantage in this domain because many of the datasets are expected to be correlated. For example, gene expression is a consequence of protein–DNA binding, and so these two datasets are dependent.7 (C) RF is particularly robust against noise and missing values. RF performs better than a single decision tree because RF can utilize randomization and redundant features. This is important if a pair has values for one redundant feature but not the other. Furthermore, the RF has the additional advantage that it can be used to estimate missing values.28 (4) Different features have different importance when it comes to predicting protein interactions. Interestingly, many of the important features are derived from indirect information sources. Our findings therefore suggest that we should be able to extend this framework for determining interacting pairs in organisms where little direct high-throughput information is available (for example, in humans).
Supplementary Material
Supplement
Acknowledgments
Grant sponsor: a Graduate Fellowship from the Merck Computational Biology and Chemistry Program at Carnegie Mellon University established by the Merck Company Foundation; Grant sponsor: National Science Foundation; Grant numbers: 0225656 and CAREER CC044917; Grant sponsor: National Institutes of Health; Grant number: NLM108730.
Footnotes
REFERENCES
- 1.Bader GD, Hogue CW. Analyzing yeast protein–protein interaction data obtained from different sources. Nat Biotechnol. 2003;20:991–997. doi: 10.1038/nbt1002-991. [DOI] [PubMed] [Google Scholar]
- 2.von Mering C, Krause R, Snel B, Cornell M, Oliver S, Fields S, Bork P. Comparative assessment of large-scale data sets of protein–protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
- 3.Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci USA. 2001;10:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, Qureshi-Emili A, Li Y, Godwin B, Conover D, Kalbfleisch T, Vijayadamodar G, Yang M, Johnston M, Fields S, Rothberg JM. A comprehensive analysis of protein–protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. [DOI] [PubMed] [Google Scholar]
- 5.Gavin AC, Bosche M, Krause R, Grandi P, Marzioch M, Bauer A, Schultz J, Rick JM, Michon AM, Cruciat CM, Remor M, Hofert C, Schelder M, Brajenovic M, Ruffner H, Merino A, Klein K, Hudak M, Dickson D, Rudi T, Gnau V, Bauch A, Bastuck S, Huhse B, Leutwein C, Heurtier MA, Copley RR, Edelmann A, Querfurth E, Rybin V, Drewes G, Raida M, Bouwmeester T, Bork P, Seraphin B, Kuster B, Neubauer G, Superti-Furga G. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature. 2002;415:141–147. doi: 10.1038/415141a. [DOI] [PubMed] [Google Scholar]
- 6.Ho Y, Gruhler A, Heilbut A, Bader GD, Moore L, Adams SL, Millar A, Taylor P, Bennett K, Boutilier K, Yang L, Wolting C, Donaldson I, Schandorff S, Shewnarane J, Vo M, Taggart J, Goudreault M, Muskat B, Alfarano C, Dewar D, Lin Z, Michalickova K, Willems AR, Sassi H, Nielsen PA, Rasmussen KJ, Andersen JR, Johansen LE, Hansen LH, Jespersen H, Podtelejnikov A, Nielsen E, Crawford J, Poulsen V, Sorensen BD, Matthiesen J, Hendrickson RC, Gleeson F, Pawson T, Moran MF, Durocher D, Mann M, Hogue CW, Figeys D, Tyers M. Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature. 2002;415:6868. doi: 10.1038/415180a. [DOI] [PubMed] [Google Scholar]
- 7.Bar-Joseph Z, Gerber G, Lee T, Rinaldi NJ, Yoo JY, Robert F, Gordon DB, Fraenkel E, Jaakkola TS, Young RA, Gifford D. Computational discovery of gene modules and regulatory networks. Nat Biotechnol. 2003;21:1337–1342. doi: 10.1038/nbt890. [DOI] [PubMed] [Google Scholar]
- 8.Deng M, Mehta S, Sun F, Chen T. Inferring domain–domain interactions from protein–protein interactions. Genome Res. 2002;12:1540–1548. doi: 10.1101/gr.153002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bader JS, Chaudhuri A, Rothberg JM, Chant J. Gaining confidence in high-throughput protein interaction networks. Nat Biotechnol. 2004;22::78–85. doi: 10.1038/nbt924. [DOI] [PubMed] [Google Scholar]
- 10.Gilchrist MA, Salter LA, Wagner A. A statistical framework for combining and interpreting proteomic datasets. Bioinformatics. 2004;20:689–700. doi: 10.1093/bioinformatics/btg469. [DOI] [PubMed] [Google Scholar]
- 11.Jansen R, Yu H, Greenbaum D, Kluger Y, Krogan NJ, Chung S, Emili A, Snyder M, Greenblatt JF, Gerstein M. A Bayesian networks approach for predicting protein–protein interactions from genomic data. Science. 2003;302:449–453. doi: 10.1126/science.1087361. [DOI] [PubMed] [Google Scholar]
- 12.Lee I, Date SV, Adai AT, Marcotte EM. A probabilistic functional network of yeast genes. Science. 2004;306:1555–1558. doi: 10.1126/science.1099511. [DOI] [PubMed] [Google Scholar]
- 13.Lin N, Wu B, Jansen R, Gerstein M, Zhao H. Information assessment on predicting protein–protein interactions. BMC Bioinformatics. 2004;5:154. doi: 10.1186/1471-2105-5-154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamanishi Y, Vert JP, Kanehisa M. Protein network inference from multiple genomic data: a supervised approach. Bioinformatics. 2004;20:363–370. doi: 10.1093/bioinformatics/bth910. [DOI] [PubMed] [Google Scholar]
- 15.Zhang L, Wong S, King OD, Roth FP. Predicting co-complexed protein pairs using genomic and proteomic data integration. BMC Bioinformatics. 2004;5:38. doi: 10.1186/1471-2105-5-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xenarios I, Salwinski L, Duan XJ, Higney P, Kim SM, Eisenberg D. DIP, the database of interacting proteins: a research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 2002;30:303–305. doi: 10.1093/nar/30.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qi Y, Klein-Seetharaman J, Bar-Joseph Z. Random forest similarity for protein–protein interaction prediction from multiple sources. Pacific Symp Biocomput. 2005;10:531–542. [PubMed] [Google Scholar]
- 18.Salwinski L, Eisenberg D. Computational methods of analysis of protein–protein interactions. Curr Opin Struct Biol. 2003;13:377–382. doi: 10.1016/s0959-440x(03)00070-8. [DOI] [PubMed] [Google Scholar]
- 19.Sprinzak E, Sattath S, Margalit H. How reliable are experimental protein–protein interaction data. J Mol Biol. 2003;327:919–923. doi: 10.1016/s0022-2836(03)00239-0. [DOI] [PubMed] [Google Scholar]
- 20.Mewes HW, Amid C, Arnold R, Frishman D, Guldener U, Mannhaupt G, Munsterkotter M, Pagel P, Strack N, Stumpflen V, Warfsmann J, Ruepp A. MIPS: analysis and annotation of proteins from whole genomes. Nucleic Acids Res. 2004;32(Database issue):D41–D44. doi: 10.1093/nar/gkh092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kanehisa M, Goto S. KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tong AH, Lesage G, Bader GD, Ding H, Xu H, Xin X, Young J, Berriz GF, Brost RL, Chang M, Chen Y, Cheng X, Chua G, Friesen H, Goldberg DS, Haynes J, Humphries C, He G, Hussein S, Ke L, Krogan N, Li Z, Levinson JN, Lu H, Menard P, Munyana C, Parsons AB, Ryan O, Tonikian R, Roberts T, Sdicu AM, Shapiro J, Sheikh B, Suter B, Wong SL, Zhang LV, Zhu H, Burd CG, Munro S, Sander C, Rine J, Greenblatt J, Peter M, Bretscher A, Bell G, Roth FP, Brown GW, Andrews B, Bussey H, Boone C. Global mapping of the yeast genetic interaction network. Science. 2004;303:808–813. doi: 10.1126/science.1091317. [DOI] [PubMed] [Google Scholar]
- 23.The Gene Ontology Consortium. Gene ontology: tool for the unification of biology. Nat Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Joachims T. Dissertation. New York: Kluwer; 2002. Learning to classify text using support vector machines. [Google Scholar]
- 25.George HJ, Langley P. Estimating continuous distributions in bayesian classifiers; Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence; 1995. pp. 338–345. [Google Scholar]
- 26.Witten IH, Frank E. Data mining: practical machine learning tools with Java implementations. San Francisco, CA: Morgan Kaufmann; 2000. [Google Scholar]
- 27.Quinlan R. C4.5: programs for machine learning. San Francisco, CA: Morgan Kaufmann; 1993. [Google Scholar]
- 28.Breiman L. Random forests. Machine Learn. 2001;45:5–32. [Google Scholar]
- 29.Jones KS. Information retrieval experiment. London: Butterworths; 1981. pp. 213–255. [Google Scholar]
- 30.Flach P. The many faces of ROC analysis in machine learning, ICML-04 Tutorial. 2004 Notes available from http://www.cs.bris.ac.uk/flach/ICML04tutorial/.
- 31.Guyon I, Elisseeff A. An introduction to variable and feature selection. J Machine Learn Res. 2003;5:1157–1182. [Google Scholar]
- 32.Ghaemmaghami S, Huh WK, Bower K, Howson RW, Belle A, Dephoure N, O’Shea EK, Weissman JS. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
- 33.The Saccharomyces Genome Deletion Project. 2004 http://www-sequence.stanford.edu/group/yeast_deletion_project.
- 34.Dolinski K, Balakrishnan R, Christie KR, Costanzo MC, et al. Saccharomyces Genome Database (SGD) 2004 http://www.yeastgenome.org.
- 35.Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, Jennings EG, Zeitlinger J, Pokholok DK, Kellis M, Rolfe PA, Takusagawa KT, Lander ES, Gifford DK, Fraenkel E, Young RA. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplement