A direct characterization of human mutation based on microsatellites (original) (raw)
. Author manuscript; available in PMC: 2013 Apr 1.
Published in final edited form as: Nat Genet. 2012 Aug 23;44(10):1161–1165. doi: 10.1038/ng.2398
Abstract
Mutations are the raw material of evolution, but have been difficult to study directly. We report the largest study of new mutations to date: 2,058 germline changes discovered by analyzing 85,289 Icelanders at 2,477 microsatellites. The paternal-to-maternal mutation rate ratio is 3.3, and the rate in fathers doubles from age 20 to 58 whereas there is no association with age in mothers. Longer microsatellite alleles are more mutagenic and tend to decrease in length, whereas the opposite is seen for shorter alleles. We use these empirical observations to build a model that we apply to individuals for whom we have both genome sequence and microsatellite data, allowing us to estimate key parameters of evolution without calibration to the fossil record. We infer that the sequence mutation rate is 1.4–2.3×10−8 per base pair per generation (90% credible interval), and that human-chimpanzee speciation occurred 3.7–6.6 million years ago.
The largest studies of human germline mutation to date have focused on whole-genome sequencing of nuclear families1–3 and identified more than a hundred new mutations. However, too few mutations were detected and too few families studied to provide a detailed characterization of the mutation process4–7. One outcome of understanding the mutation process would be a direct estimate of the rate of ticking of the molecular clock, which would make it possible to estimate dates from genetic data without relying on the fossil record for calibration.
Here we focus on microsatellites: 1–6 base pair motifs that vary in the number of times they repeat. Due to DNA polymerase slippage during replication, the mutation rate of microsatellites is around 10−4 to 10−3 per locus per generation8–12, far higher than the nucleotide substitution rate of 10−8. We analyzed 2,477 autosomal microsatellites that had been genotyped as part of linkage-based disease gene mapping studies and h were ascertained to be highly polymorphic13. The data set included 85,289 Icelanders from 24,832 father-mother-child trios, after restricting to individuals genotyped for at least half of these loci and without evidence of inaccurate parental assignment (Online Methods, Supplementary Figure 1). The median genotype error rate was 1.8×10−3 per allele (Supplementary Figure 2, Supplementary Note), high compared to the mutation rate, and thus we took additional steps to reduce the error.
To distinguish genuine mutations from genotype errors, we used two approaches (Online Methods, Supplementary Note). In the ‘trio’ approach (Figure 1A), we identified 1,695 mutations in 5,085,672 transmissions by restricting to instances in which each member of the trio was genotyped more than once. In the ‘family’ approach (Figure 1B), we identified 363 mutations in 952,632 transmissions, validating new mutations by requiring them to be seen in at least one of the proband’s children, and validating ancestral alleles by requiring them to be seen in all of the proband’s siblings (in the family approach, we also used haplotypes of nearby microsatellites to determine the parental origin of mutations; Online Methods, Supplementary Note). The trio and family approaches produced indistinguishable inferences about the mutation process (Table 1, Supplementary Figure 3, Supplementary Figure 4), and hence we combined the data for subsequent analysis (62 mutations were counted twice due to overlap).
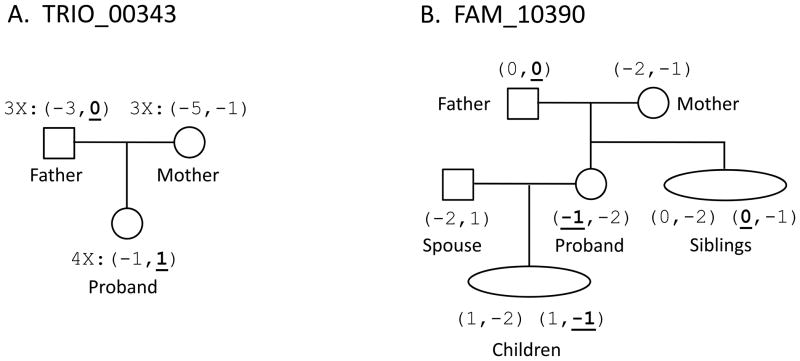
Figure 1. Examples of verified mutations from a trio and a family.
The proband is the individual inheriting a mutation, and all individuals are named relative to the proband. All alleles are given in repeat units and shifted so that the ancestral allele has length 0. The mutating allele is underlined. (A) We show a mutation detected using the trio approach. Confirmation of the mutation is from multiple genotyping of the trio: the father, mother, and proband are genotyped 3×, 3×, and 4×, respectively. (B) We show a mutation detected using the family approach. One sibling verified the ancestral allele, and one child verified the mutant allele. The phasing of alleles from the mutant locus and other loci from the same chromosome shows that the sibling with alleles (0,-2) did not inherit the ancestral ‘0’ but rather the other ‘0’ allele from the father.
Table 1.
Direct estimates of microsatellite mutation rates
| Mutation rate (×10−4)* | ||||
|---|---|---|---|---|
| Mutations | Transmissions | mean | 5th – 95th percentile | |
| di-nucleotide loci† | ||||
| Trio-approach | 1,218 | 4,578,348 | 2.66 | 2.47 – 2.85 |
| Family-approach | 269 | 861,204 | 3.12 | 2.65 – 3.59 |
| Combined | 1,487 | 5,439,552 | 2.73 | 2.56 – 2.91 |
| tetra-nucleotide loci | ||||
| Trio-approach | 380 | 393,072 | 9.67 | 8.44 – 10.89 |
| Family-approach | 86 | 72,516 | 11.86 | 8.70 – 15.02 |
| Combined | 466 | 465,588 | 10.01 | 8.86 – 11.15 |
To estimate the proportion of candidate mutations that are real, we re-genotyped samples of 103 trio mutations and 99 family mutations leading to false-positive rate estimates of 2.9% and 2.6% respectively (Supplementary Table 1, Supplementary Figure 5). We also estimated the false-positive rate due to errors in the allele-calling algorithm to be 4.3% by manually re-scoring the electropherograms of 316 individuals from the family dataset, and declaring a false-positive if there was disagreement. Combining the two modes, we estimate a 7.2% false-positive rate (Supplementary Table 1). We also obtained an entirely independent estimate by analyzing next-generation sequencing data from the proband and the transmitting parent for 14 candidate mutations for which we had such data, allowing us to validate all but one leading to an estimated false positive rate of 7.1% (Supplementary Table 2). The false-negative rate (probability of an undetected real mutation) was estimated to be 9.0% by simulating mutations and recording the fraction that we failed to detect (Online Methods).
The estimated mutation rate of tetra-nucleotides is 10.01×10−4 per locus per generation, 3.7 times higher than the di-nucleotide rate of 2.73×10−4 (Table 1). Estimates are nearly unchanged after correcting for false-positives and false-negatives by (1–0.072)/(1–0.090), and thus we quote unadjusted rates in what follows. Our estimate of the male-to-female mutation rate ratio is α=3.3 (95% CI 2.9–3.7) (Supplementary Table 3), within the range of 2–7 previously inferred for sequence substitutions4,14,3,15. Paternal age is correlated with mutation rate (P=9.3×10−5), whereas maternal age is not (P=0.47; Figure 2A, Supplementary Figure 6), consistent with observations based on disease-causing mutations, and the fact that male germ cells undergo numerous mitoses as a man ages, whereas female oocytes do not undergo postnatal cell division4.
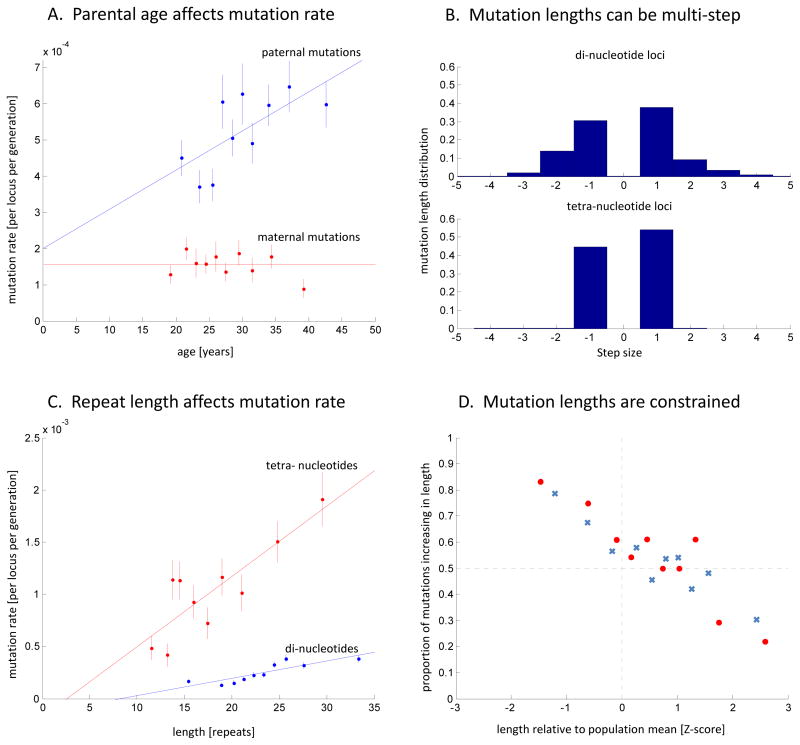
Figure 2. Characteristics of the microsatellite mutation process.
(A) Paternal (blue) and maternal (red) mutation rates. The x-axis shows the parental age at child-birth. The data points are grouped into 10 bins (vertical bars show 1 standard error). The paternal rate shows a positive correlation with age (logistic regression of raw data: P=9.3×10−5; slope = 1.1×10−5/yr), with an estimated doubling of rate from age 20 to 58. The maternal rate shows no evidence of increasing with age (P=0.47). (B) Mutation length distributions differ between di- and tetra-nucleotides (upper and lower histograms), with the x-axis in units of step-size. While the di-nucleotide loci experience multi-step mutations in 32% of instances, tetra-nucleotides mutate almost exclusively by a single-step of 4 bases. (C) Mutation rate increases with allele length: di-nucleotides (blue) have a slope of 1.65×10−5per repeat unit (P=1.3×10−3) and tetra-nucleotides (red) have a slope of 6.73×10−5 per repeat unit (P=1.8×10−3). (D) Constraints on allele lengths: When the parental allele is relatively short, mutations tend to increase in length, and when the parental allele is relatively long, mutations tend to decrease in length. Di- and tetra- nucleotides are shown in blue crosses and red circles, respectively. Probit regression of the combined di- and tetra- data shows highly significant evidence of an effect (P=2.8×10−18).
These data allow the first high resolution direct characterization of the mutation process for the highly polymorphic di- and tetra-nucleotide microsatellites that are typically genotyped8. First, 32% of mutations at di-nucleotide microsatellites are multi-step, compared to 1% in tetra-nucleotides (Figure 2B, Supplementary Figure 3) (this explains why the variance of allele length distribution at the tetra-nucleotides is similar to that of di-nucleotides despite their 3.7-fold higher mutation rate16,17). Second, mutation rate increases with allele length18,19, quadrupling between 30–70 bp for di-nucleotides and 40–120 bp for tetra-nucleotides (both tests significant at P<0.002) (Figure 2C). Third, loci with uniform repeat structures (e.g. CACACACA) have a 40% higher rate (P=3×10−7) than compound repeat structures (e.g. CACATCACA), consistent with less DNA polymerase slippage for interrupted tandem repeats8,20 (Supplementary Figure 7). Fourth, we detect length constraints21,22, with shorter alleles tending to mutate to become longer and vice versa (P=2×10−15) (Figure 2D, Supplementary Figure 8, Supplementary Figure 920,23,24). This pattern contrasts with tri-nucleotide repeat disorders, where long alleles tend to get even longer19. Fifth, mutation rate correlates (P<10−4) with motif length, repeat number, allele-size, distance from exons, gender, and age, but not with recombination rate, distance from telomeres, human-chimpanzee divergence, or parental heterozygosity (Supplementary Table 4; Supplementary Table 5; Supplementary Note).
Microsatellites have been widely used for making inferences about evolutionary history. However, the accuracy of these inferences has been limited by a poor understanding of the mutation process. We developed a new model of microsatellite evolution (Supplementary Note). This model can estimate the time to the most recent common ancestor (TMRCA) between two samples at a microsatellite by taking into account: (1) the dependence of mutation rate on allele length and parental age (Figure 2A,C); (2) the step-size of mutations (Figure 2B); (3) the size constraints on allele length (Figure 2D, Supplementary Figure 8, Supplementary Figure 9); and (4) the variation in generation interval over history. In contrast to the Generalized Stepwise Mutation Model (GSMM), which predicts a linear increase of average squared distance (ASD) between microsatellite alleles over time, the new model predicts a sub-linear increase (Figure 3) and saturation of the molecular clock, due to the constraints on allele lengths. We also extended the model to estimate the sequence mutation rate, using the per-nucleotide diversity flanking each microsatellite as an additional datum. To implement the model, we used a Bayesian hierarchical approach, first generating global parameters common to all loci, followed by locus-specific parameters, and finally the microsatellite alleles at each locus (Online Methods). We used Markov Chain Monte Carlo to infer TMRCA and sequence mutation rate.
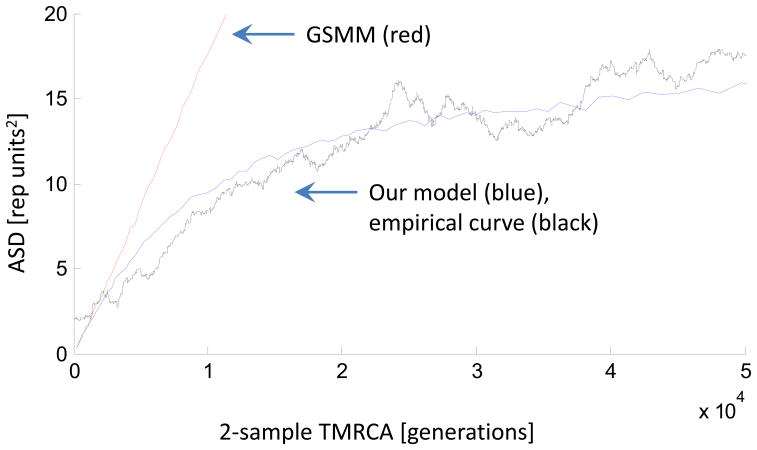
Figure 3. Empirical validation of our model with sequence-based estimates of TMRCA.
In red is the simulation of ASD as a function of TMRCA for the standard random walk (GSMM) model. In blue is the simulation of our model, in which the non-linearity compared to GSMM is primarily due to the length constraint that we empirically observed in microsatellites. In black is the empirically observed ASD at microsatellites in 23 HapMap individuals as a function of sequence-based estimates of TMRCA, which is estimated using θseq2μseq, where θseq is the local sequence diversity surrounding each microsatellite locus, and μseq is 1.82×10−8 (obtained from Table 2). The close match of the empirical curve to our model simulations suggests that our model works, and motivates the analysis in which we use the sequence substitution rate in small windows around the microsatellites to make inferences about evolutionary parameters like the sequence mutation rate.
We validated the model in three ways (Online Methods). First, we simulated datasets in which we know the true sequence mutation rate and TMRCA, and found that our model is unbiased in estimating sequence mutation rate while producing accurate estimates of the standard error (Supplementary Note). Second, we carried out sensitivity analyses by perturbing model parameters and found that our key inferences are robust (Supplementary Note, Supplementary Figure 10). Third, we empirically validated the model by analyzing 23 individuals for whom we had both microsatellite genotypes and whole genome sequence (WGS) data2, and comparing the ASD to the surrounding sequence heterozygosity as a surrogate for TMRCA. The ASD predicted by our model is similar to the empirical curve (Figure 3, Supplementary Figure 11)
Our approach allows inference of evolutionary parameters without calibration to the fossil record. Using the empirical ASD at the di-nucleotide microsatellites in each of the 23 individuals of European, East Asian and sub-Saharan African ancestry for whom we had WGS sequence data (Online Methods), and comparing the ASD to local heterozygosity and human-macaque divergence (as a surrogate for the local mutation rate; Online Methods), we inferred a sequence mutation rate and the TMRCA averaged across the genome (Table 2). We also inferred a 90% credible interval (CI) based on a Bayesian approach integrating over uncertainty in the model parameters (Online Methods; Supplementary Note, Supplementary Table 6). Empirically, mutation rates tend to be more similar within than between populations (Supplementary Table 7; Supplementary Figure 12). The differences across populations are not likely to be due to poor modeling of demographic history, as when we model more realistic histories involving two bottlenecks in non-Africans we obtain the same results (Supplementary Figure 13). The mutation rate differences between populations may be due to shared history, but they are not significant, so we pooled our data across the 23 individuals to produce a sequence mutation rate estimate of 1.82×10−8 per bp per generation (90% CI 1.40–2.28×10−8/bp/generation, Table 2) (the confidence interval takes into account correlations in the 23 peoples’ histories through a jackknife) (Online Methods).
Table 2.
Estimates of mutation rates and human-ape divergence times
| Mean | 5th – 95th percentile* | mean | 5th – 95th percentile | |
|---|---|---|---|---|
| Present-day mutation rates | units: per generation per site | units: per year per site | ||
| di-nucleotide microsatellite rate (per locus) | 2.73 × 10−4 | 2.56 – 2.91 × 10−4 | 9.47 × 10−6 | 8.29 – 10.82 × 10−6 |
| μ̂seq: nucleotide substitution rate (per base) | 1.82 × 10−8 | 1.40 – 2.28 × 10−8 | 6.76 × 10−10 | 5.11 – 8.41 × 10−10 |
| Genetic divergence times | units: thousand generations ago | units: million years ago | ||
| tCEU : Western Europeans | 22.8 | 17.8 – 29.6 | 0.546 | 0.426 – 0.709 |
| tYRI : Yoruba (African) | 30.2 | 23.6 – 39.2 | 0.720 | 0.562 – 0.933 |
| tHC : human-chimpanzee | 352 | 272 – 459 | 7.49 | 5.80 – 9.77 |
| τHO : human-orangutan | 932 | 717 – 1220 | 19.8 | 15.2 – 25.9 |
| τHC : human-chimpanzee speciation time | 233 | 176 – 309 | 4.97 | 3.75 – 6.57 |
Our inference of the sequence mutation rate is consistent with Nachman and Crowell’s estimate of μ̄seq = 1.3–2.7×10−8/bp/generation based on calibration to the fossil record6. It is also consistent with Kondrashov’s direct estimate of μ̂seq = 1.8×10−8/bp/generation25 from studies of disease causing genes. However, the lower bound of our 90% CI is higher than two recent studies based on whole-genome sequencing (WGS): μ̂seq = 1.1×10−8/bp/generation based on 28 sequence mutations detected in a four member family1, and μ̂seq = 1.0×10−8 and 1.2×10−8/bp/generation based on 84 sequence mutations detected in two trios2,3. We considered the possibility that this discrepancy might be due to ascertainment bias, because the microsatellites we analyzed were selected to be highly polymorphic (for disease gene mapping) which could cause a too-high ASD. However, this would overestimate TMRCA at the loci we analyzed and thus underestimate the mutation rate, opposite to what would be necessary to explain the discrepancy (Supplementary Figure 12 and Supplementary Note). We hypothesize that the lower mutation rate estimates from the WGS studies might be due to: (i) the limited number of mutations detected in the WGS studies which explains why their confidence intervals overlap ours, (ii) possible underestimation of the false-negative rate in the WGS studies, or (iii) variability in the mutation rate across individuals so that a few families cannot provide a reliable estimate of the population-wide rate. There is already empirical evidence for variability in the mutation process across individuals: in one trio analyzed in the 1000 Genomes Project study8, the father transmitted 92% of the mutations, while in the other trio the father transmitted 36%. Studies of sequence substitution in many families are important, as they will make it possible to measure population-wide rates and study features of the sequence substitution process not accessible to microsatellite analysis.
Our direct estimation of the microsatellite mutation rate, combined with comparative genomics data, also allows us to estimate the date of human-chimpanzee speciation τHC, which we define as the date of last gene flow between human and chimpanzee ancestors26,27. We estimate a genome-wide average human-chimpanzee genetic divergence time tHC = 5.80–9.77 Mya28 (Online Methods; Table 2). By definition, this must be older than the speciation date τHC. We then inferred the human-chimpanzee speciation to be τHC = 3.75–6.57 Mya by integrating our posterior distribution on tHC with a prior distribution on τHC/tHC of 0.663±0.041 whose mean we obtained by modeling-based estimates of τHC/tHC = 0.61–0.6829,30, and whose 95th percentile upper bound of <0.73 we obtained by analyzing human-chimpanzee sequence data in regions with a reduced divergence compared to the autosomal average due to being (1) on chromosome X, (2) in proximity to genes, and (3) near divergent sites that cluster humans and chimpanzees to the exclusion of gorilla (Supplementary Note). Our upper bound of τ_HC_ < 6.57 Mya is lower than the 6.8–7.2 Mya31 date estimate for Sahelanthropus tchadensis, a fossil interpreted as being on the human lineage after the final separation of human and chimpanzee ancestors32 because it shares derived features with other hominins such as bipedal posture, reduced canines and expanded post-canines with thicker enamel33. In the Supplementary Note, we also obtain an independent upper bound on the human-chimpanzee speciation date of τ_HC_ <6.3 Mya based on calibration to the fossil record of human-orangutan speciation26. A possible explanation for the discrepancy between the genetic and fossil dates is that Sahelanthropus was not a hominin, but instead shared independently-derived similarities (homoplasies)34. Alternatively, populations with hominin traits may have continued to exchange genes with chimpanzee ancestors after Sahelanthropus26. Finally, the age of Sahelanthropus31 may be overestimated.
URL: Complete Genomics data: http://www.completegenomics.com/.
Online Methods
Data sets
Microsatellite genotypes were obtained at deCODE Genetics using DNA extracted from blood, and multiplexed capillary gel electrophoresis with automated allele calling13. We restricted to 2,477 autosomal loci that were genotyped most heavily (all had a minimum repeat length of 5 units). We analyzed 85,289 individuals genotyped for at least half of these loci, from which we identified 25,067 mother-father-offspring trios using the deCODE Genetics genealogical database (Íslendingabók).
To filter out trios with inaccurate parental assignments, we computed the fraction of loci where both alleles differ between a parent and a child. We empirically set the threshold to filter out almost all known uncle-proband and aunt-proband pairs while retaining almost all known parent-proband pairs (Supplementary Figure 1).
To estimate the per-locus genotyping error rate, we used discordance rates in cases of repeated genotypes (Supplementary Note).
Deep whole genome sequencing data was obtained from two sources. We downloaded 9 sequences generated using Illumina technology, mapping reads using BWA35 and calling SNPs with SAMtools36. We also downloaded 20 Complete Genomics sequences, 6 of which overlap the Illumina sequences (Supplementary Table 7, Supplementary Figure 14). To estimate heterozygosity around each microsatellite, we extracted a window of data centered around it (in most cases, 0.001 centimorgans masking out the central 1kb37; Supplementary Figure 15),
Detecting mutations
For the trio approach, we restricted to transmissions in which all members of the trio were genotyped at least twice and searched for Mendelian inheritance incompatibilities. There were some detected mutations in which the parental origin was ambiguous (Supplementary Note), and we included these for analyses of the mutation rate but not for analyses requiring parental origin (Fig 2B). For mutations with unambiguous parental origin, the ancestral allele was defined as the one that was closer in length to the mutant allele (we randomly chose the ancestral allele if both were equally close). We filtered out 49 loci that harbored many more mutations from homozygous parents to homozygous children than expected based on Hardy-Weinberg equilibrium, a phenomenon that affected the trio, but not the family data. We determined that this is a real error mode due to polymorphisms under the PCR primer sites38–40 by sequencing primer sites from 15 mutations and identifying 5 with SNPs in the primer region (Supplementary Note).
For the family approach, we restricted to transmissions where genotyping was available not just for a proband’s two parents, but also for at least one child and one sibling (Figure 1B). We identified putative mutations by searching for Mendelian incompatibilities between the proband and their parents. We used Allegro 2.041 to phase the family masking out the mutant locus, using all available loci from the same chromosome. We then assigned the haplotype carrying the mutation to one of the proband’s parents (Supplementary Note). To validate the mutation, we required at least one sibling to carry the haplotype with the ancestral allele, no sibling to carry the mutant, and at least one child to carry the haplotype with the mutant.
The trio and family approaches provide complementary information. A bias that only affects the trio approach is somatic mutations in the lineage of genotyped cells but not germline cells transmitted to offspring (this is minimized since the DNA we analyzed was extracted from blood, but is still a concern). A bias that only affects the family-based approach is that mutations in progenitor germ cells might cause a mutation to be observed simultaneously in the proband and its siblings, causing us to reject a real mutation. The fact that both approaches produce consistent inferences despite the difference biases increases our confidence in the results.
False-positive and false-negative rates
To estimate the false-positive rate, we re-genotyped candidate mutations. In the trio dataset, we randomly re-genotyped 103 mutations. In the family dataset, we targeted mutations that had a higher a priori chance of being in error (Supplementary Table 1). To provide an entirely independent estimate of the false-positive rate, we identified 14 candidate mutations where we had at least 7-fold whole genome sequencing data from the proband as well as (at least) the transmitting parent. We then manually examined the data, failing to validate only 1 of the 14 mutations (Supplementary Table 2).
To estimate the false-negative rate (the proportion of genuine mutations that were missed), we randomly distributed mutations on the genealogy and then tested whether they gave rise to detectable inheritance errors. As an example, suppose that the father-mother-proband trio has genotypes of allele-lengths (6 10), (8 10), (8 10), respectively. If the mother passed allele 10 to the proband, and the father passed a 6 → 8 mutation, then this mutation would not be detected.
Statistical characterization of the microsatellite mutation process
To infer the standard error of the mutation rate, taking into account rate variation across loci, we used a hierarchical Bayesian model (Supplementary Note). To infer the number of microsatellite repeats, we started with the amplicon size, which includes not just the repeats but all the sequence between the PCR primers. We then subtracted the span of the flanking sequence inferred from the human genome reference (Supplementary Figure 16). To compute the relative length of an allele, we measured the mean and standard deviation over all individuals at that locus, and report the standard deviations from the mean (Z-score). To estimate motif impurity (Supplementary Figure 7), we applied the Tandem Repeat Finder software to the human genome reference (Supplementary Figure 16). To test for association between the microsatellite mutation process and genomic features (Supplementary Table 4), we performed a logistic regression to mutation rate and directionality, and a Poisson regression to step size. To test for interaction, we performed multivariate logistic regression (Supplementary Table 5).
Prior distributions on evolutionary parameters
For our Bayesian modeling of sequence mutation rate and genetic divergence times, we required prior distributions on evolutionary parameters (Supplementary Table 6):
- Generation interval: Based on interviews with experts on chimpanzee and gorilla demographic structure (L Vigilant and K Langergraber), we assume that the ancestral generation time was 22.5±4.2 (mean ± SD) years. Based on the literature42,43 (Supplementary Figure 17), we assume that present-day generation time is 29±2 years. We also assume that the difference between the male and female generation time was 0.5±3.3 years in the ancestral population and 6.0±2.0 today (Supplementary Note). We sample the transition between ancestral to present-day generation time to be a mixture of 3 equally weighted exponential distributions, with means of 50Kya, 200Kya, and 2Mya, corresponding to hypothetical changes around the Upper Paleolithic revolution, evolution of modern humans, and evolution of Homo erectus.
- Human-ape relative genetic divergences: From the literature, we assume that the ratio of human-chimpanzee to European-European genetic divergence per base pair is28 15.400±0.356, and that the ratio of human-orangutan to human-chimpanzee genetic divergence of 2.650±0.075.26,29 We assume that the molecular process of mutation has been constant over great ape history.
- Human-chimpanzee speciation time (τHC): Human-chimpanzee speciation time is by definition less than human-chimpanzee genetic divergence time. Our prior on τHC/tHC has a normal distribution with mean 0.663, within the range of 0.61–0.68 from model-based analyses29,30. We use a standard deviation of 0.041 based on an analysis in the Supplementary Note suggesting showing that an upper bound on the ratio of human-chimpanzee speciation to genetic divergence is 0.73 (our prior distribution is set that 95% of its density is below this).
A model of microsatellite evolution assisted by flanking sequence heterozygosity
As a metric of microsatellite allelic divergence between two samples, we use the Average Squared Distance (ASD). Given allele lengths _x_1, _x_2, …, xn, ASD=1n(n-1)·∑i,j(xi-xj)2.
To model ASD along with flanking sequence heterozygosity, we simulate the evolution of a pair of chromosomes from a common ancestor, over multiple loci and individuals. The model is hierarchical: At the top level, global parameters (Supplementary Table 6) common to all loci are simulated, such as the genome-wide present-day sequence and microsatellite mutation rates, and generation-time effects. One level down, locus-specific mutation rates are computed based on global parameters and locus-specific information. At the third level, for each individual, a two-sample coalescent tree is generated (Supplementary Note).
A potential pitfall in inferring TMRCA with our data is that the microsatellites we analyzed were ascertained to be highly polymorphic in Europeans. This raises two complications. First, the sequence flanking the microsatellites may have a different mutation rate than the genome average, and to correct for this, we compared ASD to the ratio of sequence heterozygosity and human-macaque divergence at each locus (as a surrogate for local mutation rate). Second, ascertainment of highly polymorphic microsatellites can bias toward deeper genealogies than the genome average which in turn can bias average TMRCA to be too high. By studying the sequence flanking the microsatellites, we determined that the trees were on average 1.04 times deeper than the genome average, and we corrected Table 2’s estimate of genome-wide average TMRCA by this factor (Supplementary Note, Supplementary Table 8).
To infer sequence mutation rate and TMRCA using the microsatellite evolution model, we use a Markov Chain Monte Carlo (MCMC) following the method of ref. 44 (Supplementary Note). Combining data across individuals is not trivial because of shared history across individuals. To obtain proper standard errors for the combined mutation rate, we performed a jackknife45, where each locus is removed at a time. This gives the final set of standard errors.
Editorial Summary (AOP and Month, same)
David Reich and colleagues report a direct characterization of the human mutation rate based on analysis of 85,289 Icelandic individuals genotyped at 2,477 autosomal microsatellite loci. They use this to build a model of microsatellite evolution and estimate key evolutionary parameters.
Supplementary Material
1
Figure 4. Human-chimpanzee speciation date inferred without a fossil calibration.
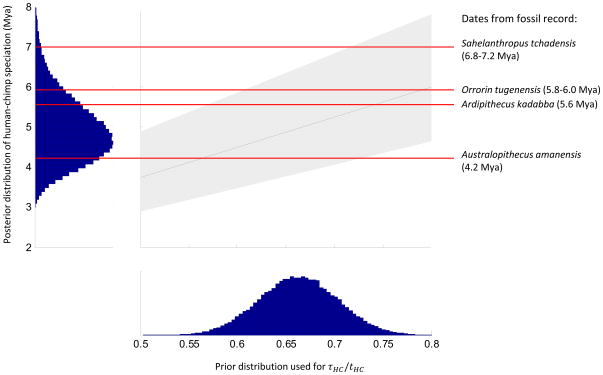
In the square panel, we give the 90% Bayesian credible interval for human-chimpanzee speciation time (gray), for a range of values of the ratio of speciation time to divergence time τHC/tHC. The blue curve shows our prior probability distribution for τHC/tHC, justified in Supplementary Note. The red horizontal lines are the dates of fossils that are candidates for being on the hominin lineage post-dating the speciation of humans and chimpanzees. Australopithecus amanensis, Orrorin tugenensis and Ardipithecus kadabba are within our plausible speciation times, while Sahelanthropus tchadensis pre-dates the inferred speciation time for all plausible values of τHC/tHC. Our prior distribution for τHC/tHC is shown in the bottom histogram, and our posterior distribution of human-chimpanzee speciation time is shown in the left histogram.
Acknowledgments
We thank DF Gudbjartsson for advice on running Allegro 2.0; J Fenner, J Hawks, K Langergraber, D Pilbeam and L Vigilant for discussions that informed the prior distributions on evolutionary parameters; and Y Erlich, M Gymrek, D Lieberman, B Payseur, D Pilbeam, A Siepel, S Sunyaev, and anonymous reviewers for critiques. This work was supported by a Bioinformatics and Integrative Genomics PhD training grant (JXS), a Burroughs Wellcome Travel Grant (JXS), a Burroughs Wellcome Career Development Award in the Biomedical Sciences (DR), a HUSEC seed grant from Harvard University (DR), a SPARC award from the Broad Institute of Harvard and MIT (DR), a National Science Foundation HOMINID grant 1032255 (DR), and a National Institute of Health grant R01HG006399 (DR).
Footnotes
Author Contributions
JXS, AH, GM, and DR conceived and performed the research. AH, GM, AK, DR, and KS jointly supervised the study, with AH being the coordinator at deCODE Genetics and DR at Harvard Medical School. AH and GM prepared the raw microsatellite data. JXS, AH, and SSE designed and analyzed the re-genotyping, re-sequencing, and electropherogram re-checking experiments; AH analyzed next generation sequencing data to independently validate mutations. JXS, AH, NP, AK, and DR designed and analyzed the microsatellite modeling and the statistics. SM, HL, and JXS processed and extracted sequence data for the 23 HapMap individuals. SM, SG, and DR performed the analyses of human-chimpanzee genetic divergence and developed the prior distributions relevant to human-chimpanzee speciation. The paper was written primarily by JXS, AH, and DR. The supplementary information was written by JXS and DR.
Data Access
The informed consents associated with the samples at deCODE Genetics specify that genotypes cannot be shared outside of Iceland. However, researchers who wish to re-analyze the data can visit deCODE Genetics to perform these analyses by arrangement with K. Stefansson.
References
- 1.Roach JC, et al. Analysis of genetic inheritance in a family quartet by whole-genome sequencing. Science. 2010;328:636–9. doi: 10.1126/science.1186802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Durbin RM, et al. A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–73. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Conrad DF, et al. Variation in genome-wide mutation rates within and between human families. Nature genetics. 2011;43:712–714. doi: 10.1038/ng.862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Crow JF. The origins, patterns and implications of human spontaneous mutation. Nat Rev Genet. 2000;1:40–7. doi: 10.1038/35049558. [DOI] [PubMed] [Google Scholar]
- 5.Crow JF. Age and sex effects on human mutation rates: an old problem with new complexities. J Radiat Res (Tokyo) 2006;47 (Suppl B):B75–82. doi: 10.1269/jrr.47.b75. [DOI] [PubMed] [Google Scholar]
- 6.Nachman MW, Crowell SL. Estimate of the mutation rate per nucleotide in humans. Genetics. 2000;156:297–304. doi: 10.1093/genetics/156.1.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arnheim N, Calabrese P. Understanding what determines the frequency and pattern of human germline mutations. Nat Rev Genet. 2009;10:478–88. doi: 10.1038/nrg2529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ellegren H. Microsatellites: simple sequences with complex evolution. Nat Rev Genet. 2004;5:435–45. doi: 10.1038/nrg1348. [DOI] [PubMed] [Google Scholar]
- 9.Weber JL, Wong C. Mutation of human short tandem repeats. Hum Mol Genet. 1993;2:1123–8. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]
- 10.Xu X, Peng M, Fang Z. The direction of microsatellite mutations is dependent upon allele length. Nat Genet. 2000;24:396–9. doi: 10.1038/74238. [DOI] [PubMed] [Google Scholar]
- 11.Whittaker JC, et al. Likelihood-based estimation of microsatellite mutation rates. Genetics. 2003;164:781–7. doi: 10.1093/genetics/164.2.781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang QY, et al. Mutation patterns at dinucleotide microsatellite loci in humans. Am J Hum Genet. 2002;70:625–34. doi: 10.1086/338997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kong A, et al. A high-resolution recombination map of the human genome. Nat Genet. 2002;31:241–7. doi: 10.1038/ng917. [DOI] [PubMed] [Google Scholar]
- 14.Makova KD, Li WH. Strong male-driven evolution of DNA sequences in humans and apes. Nature. 2002;416:624–6. doi: 10.1038/416624a. [DOI] [PubMed] [Google Scholar]
- 15.Lynch M. Rate, molecular spectrum, and consequences of human mutation. Proc Natl Acad Sci U S A. 2010;107:961–8. doi: 10.1073/pnas.0912629107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Slatkin M. A measure of population subdivision based on microsatellite allele frequencies. Genetics. 1995;139:457–62. doi: 10.1093/genetics/139.1.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goldstein DB, Ruiz Linares A, Cavalli-Sforza LL, Feldman MW. An evaluation of genetic distances for use with microsatellite loci. Genetics. 1995;139:463–71. doi: 10.1093/genetics/139.1.463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ballantyne KN, et al. Mutability of Y-chromosomal microsatellites: rates, characteristics, molecular bases, and forensic implications. Am J Hum Genet. 2010;87:341–53. doi: 10.1016/j.ajhg.2010.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cummings CJ, Zoghbi HY. Fourteen and counting: unraveling trinucleotide repeat diseases. Hum Mol Genet. 2000;9:909–16. doi: 10.1093/hmg/9.6.909. [DOI] [PubMed] [Google Scholar]
- 20.Kruglyak S, Durrett RT, Schug MD, Aquadro CF. Equilibrium distributions of microsatellite repeat length resulting from a balance between slippage events and point mutations. Proc Natl Acad Sci U S A. 1998;95:10774–8. doi: 10.1073/pnas.95.18.10774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhivotovsky LA, Feldman MW, Grishechkin SA. Biased mutations and microsatellite variation. Mol Biol Evol. 1997;14:926–33. doi: 10.1093/oxfordjournals.molbev.a025835. [DOI] [PubMed] [Google Scholar]
- 22.Feldman MW, Bergman A, Pollock DD, Goldstein DB. Microsatellite genetic distances with range constraints: analytic description and problems of estimation. Genetics. 1997;145:207–16. doi: 10.1093/genetics/145.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sainudiin R, Durrett RT, Aquadro CF, Nielsen R. Microsatellite mutation models: insights from a comparison of humans and chimpanzees. Genetics. 2004;168:383–95. doi: 10.1534/genetics.103.022665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Garza JC, Slatkin M, Freimer NB. Microsatellite allele frequencies in humans and chimpanzees, with implications for constraints on allele size. Mol Biol Evol. 1995;12:594–603. doi: 10.1093/oxfordjournals.molbev.a040239. [DOI] [PubMed] [Google Scholar]
- 25.Kondrashov AS. Direct estimates of human per nucleotide mutation rates at 20 loci causing Mendelian diseases. Hum Mutat. 2003;21:12–27. doi: 10.1002/humu.10147. [DOI] [PubMed] [Google Scholar]
- 26.Patterson N, Richter DJ, Gnerre S, Lander ES, Reich D. Genetic evidence for complex speciation of humans and chimpanzees. Nature. 2006;441:1103–8. doi: 10.1038/nature04789. [DOI] [PubMed] [Google Scholar]
- 27.Steiper ME, Young NM. Primate molecular divergence dates. Molecular phylogenetics and evolution. 2006;41:384–94. doi: 10.1016/j.ympev.2006.05.021. [DOI] [PubMed] [Google Scholar]
- 28.Green RE, et al. A draft sequence of the Neandertal genome. Science. 2010;328:710–22. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Burgess R, Yang Z. Estimation of hominoid ancestral population sizes under bayesian coalescent models incorporating mutation rate variation and sequencing errors. Mol Biol Evol. 2008;25:1979–94. doi: 10.1093/molbev/msn148. [DOI] [PubMed] [Google Scholar]
- 30.McVicker G, Gordon D, Davis C, Green P. Widespread genomic signatures of natural selection in hominid evolution. PLoS genetics. 2009;5:e1000471. doi: 10.1371/journal.pgen.1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lebatard AE, et al. Cosmogenic nuclide dating of Sahelanthropus tchadensis and Australopithecus bahrelghazali: Mio-Pliocene hominids from Chad. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:3226–31. doi: 10.1073/pnas.0708015105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brunet M, et al. A new hominid from the Upper Miocene of Chad, Central Africa. Nature. 2002;418:145–51. doi: 10.1038/nature00879. [DOI] [PubMed] [Google Scholar]
- 33.Lieberman DE. The Evolution of the Human Head. Belknap Press of Harvard University Press; 2011. [Google Scholar]
- 34.Wood B, Harrison T. The evolutionary context of the first hominins. Nature. 2011;470:347–52. doi: 10.1038/nature09709. [DOI] [PubMed] [Google Scholar]
- 35.Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25:1754–60. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li H, et al. The Sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25:2078–9. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hinch AG, et al. The landscape of recombination in African Americans. Nature. 2011;476:170–5. doi: 10.1038/nature10336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Weber JL, Broman KW. Genotyping for human whole-genome scans: past, present, and future. Adv Genet. 2001;42:77–96. doi: 10.1016/s0065-2660(01)42016-5. [DOI] [PubMed] [Google Scholar]
- 39.Johansson AM, Sall T. The effect of pedigree structure on detection of deletions and other null alleles. Eur J Hum Genet. 2008;16:1225–34. doi: 10.1038/ejhg.2008.75. [DOI] [PubMed] [Google Scholar]
- 40.Callen DF, et al. Incidence and origin of “null” alleles in the (AC)n microsatellite markers. Am J Hum Genet. 1993;52:922–7. [PMC free article] [PubMed] [Google Scholar]
- 41.Gudbjartsson DF, Thorvaldsson T, Kong A, Gunnarsson G, Ingolfsdottir A. Allegro version 2. Nat Genet. 2005;37:1015–6. doi: 10.1038/ng1005-1015. [DOI] [PubMed] [Google Scholar]
- 42.Fenner JN. Cross-cultural estimation of the human generation interval for use in genetics-based population divergence studies. Am J Phys Anthropol. 2005;128:415–23. doi: 10.1002/ajpa.20188. [DOI] [PubMed] [Google Scholar]
- 43.Helgason A, Hrafnkelsson B, Gulcher JR, Ward R, Stefansson K. A populationwide coalescent analysis of Icelandic matrilineal and patrilineal genealogies: evidence for a faster evolutionary rate of mtDNA lineages than Y chromosomes. Am J Hum Genet. 2003;72:1370–88. doi: 10.1086/375453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Marjoram P, Molitor J, Plagnol V, Tavare S. Markov chain Monte Carlo without likelihoods. Proc Natl Acad Sci U S A. 2003;100:15324–8. doi: 10.1073/pnas.0306899100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Efron B, Gong G. A leisurely look at the bootstrap, the jackknife, and cross-validation. The American Statistician. 1983;37:36–48. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
1