Detecting differential usage of exons from RNA-seq data (original) (raw)
Abstract
RNA-seq is a powerful tool for the study of alternative splicing and other forms of alternative isoform expression. Understanding the regulation of these processes requires sensitive and specific detection of differential isoform abundance in comparisons between conditions, cell types, or tissues. We present DEXSeq, a statistical method to test for differential exon usage in RNA-seq data. DEXSeq uses generalized linear models and offers reliable control of false discoveries by taking biological variation into account. DEXSeq detects with high sensitivity genes, and in many cases exons, that are subject to differential exon usage. We demonstrate the versatility of DEXSeq by applying it to several data sets. The method facilitates the study of regulation and function of alternative exon usage on a genome-wide scale. An implementation of DEXSeq is available as an R/Bioconductor package.
In higher eukaryotes, a single gene can give rise to a multitude of different transcripts (isoforms) by varying the usage of splice sites, transcription start sites, and polyadenylation sites. We are only beginning to understand which part of this diversity is functional (for recent reviews, see, e.g., Nilsen and Graveley 2010; Grabowski 2011). High-throughput sequencing of mRNA (RNA-seq) promises to become an important technique for the study of alternative isoform regulation, especially in comparisons between different tissues or cell types, or between cells in different environmental conditions or with different genetic backgrounds.
Shotgun sequencing
The median length of human transcripts is 2186 nt, with the longest transcripts having sizes of up to 101,206 nt. (These numbers are based on UCSC hg19 annotation.) An ideal RNA-seq technology would produce sequence reads that directly correspond to full-length transcripts. Current implementations of RNA-seq, however, use shorter reads and use a shotgun sequencing approach. For instance, Illumina’s HiSeq 2000 produces reads of length 100 nt, which are typically paired so that they cover the two ends of shotgun fragments of lengths between 200 and 500 nt.
Approaches to the analysis of such data may be grouped into three main categories. First, in an approach that is reminiscent of microarray expression profiling, one simply counts the fragments from each gene locus, irrespective of transcript isoform, to measure each gene’s overall expression strength in each experimental sample. Several methods have been published for the detection of statistically significant differences in such count values across conditions, including edgeR (Robinson et al. 2010b), DESeq (Anders and Huber 2010), and baySeq (Hardcastle and Kelly 2010).
Second, one tries to assemble the fragments into full-length transcripts, using the fragment coverage to estimate each transcript’s expression strength in each of the samples. This approach has been pursued by Jiang and Wong (2009), Trapnell et al. (2010), and Turro et al. (2011). Of these, only Trapnell et al. (2010) attempt inference of differential expression by comparing between these estimates. Such inference is challenging, due to uncertainties from the assembly step. In addition, the accumulation of uncertainties might lead to less inferential power for certain types of questions than the third category of approaches, as is shown in the following.
Third, one avoids the assembly step and looks for differences across conditions between quantities that are directly observable from the shotgun data, such as the (relative) usage of each exon. This is the approach that is described in this article.
Transcript inventory versus differential expression
Shotgun RNA-seq data can be used both for identification of transcripts and for differential expression analysis. In the former, one annotates the regions of the genome that can be expressed, i.e., the exons, and how the pre-mRNAs are spliced into transcripts. In differential expression analysis, one aims to study the regulation of these processes across different conditions. For the method described here, we assume that a transcript inventory has already been defined, and focus on differential expression.
Biological variability
If our aim is to make a statement about the regulation of a biological process across different conditions with some generality, rather than only making statements about singular biological samples, then a suitable level of replication in the data is needed. While this may be obvious to a reader unfamiliar with the field, it is noteworthy that most methods suggested so far for the study of alternative isoform regulation (AIR) have evaded this point. Wang et al. (2008) presented a method for inference of differential exon usage based on 2 × 2 contingency tables of read counts and Fisher’s exact test. As we show in the Discussion, this method cannot account for biological variability, and in fact, the data used to demonstrate the method comprised only a single sample per tissue type. In follow-up work, Katz et al. (2010) refined this method (now termed MISO); however, they still compared only a single knockdown sample with a single control sample and made no attempt to address biological variability. Griffith et al. (2010) demonstrate their ALEXA-seq analysis method by comparing a cell line derived from a single colorectal tumor resistant to a drug with a cell line derived from a single tumor sensitive to the drug. This method, too, cannot be applied to replicated samples. Trapnell et al. (2010), when presenting the Cufflinks/Cuffdiff tool chain, compared consecutive time points, using data from one sample for each time point. The Cuffdiff software tool, in the version described in the paper, can only process pairs of samples without replicates. Brooks et al. (2010) used replicates but did not use them to assess biological variability because they used a modified version of the method of Wang et al. (2008). A notable instance in which biological variation was accounted for in the statistical analysis is the work of Blekhman et al. (2010). However, their method relies on the availability of a moderate-to-large number of samples, and no software implementation was provided.
The importance of accounting for biological variation has been pointed out by Baggerly et al. (2003) and recently by Hansen et al. (2011). Methods to do so when inferring differential expression were suggested by Baggerly et al. (2003) and Lu et al. (2005). Subsequently, Robinson and coworkers presented the edgeR method (Robinson and Smyth 2007, 2008; Robinson et al. 2010b), which introduced the use of the negative binomial distribution to RNA-seq analysis. Robinson et al. (2010a) extended edgeR with generalized linear models (GLMs) and the Cox-Reid dispersion estimator, discussed below. The basic approach of using exon–condition interactions in linear or generalized linear models to detect differential exon usage has been explored before by Cline et al. (2005) and Purdom et al. (2008) for exon microarrays and by Blekhman et al. (2010) for RNA-seq data. Our method can be seen as a further development of these approaches that also incorporated ideas from DESeq (Anders and Huber 2010).
In this article, we first explain the proposed statistical inference procedure and then use it to reanalyze published data sets by Brooks et al. (2010), by Brawand et al. (2011), and by The ENCODE Project Consortium (2011). In the Discussion, we elaborate on the observation that most published methods are unable to account for biological variation, focusing on the analysis provided by Brooks et al. (2010) for their data (which is based on the method of Wang et al. 2008), and illustrate how this leads to unreliable results. Finally, we compare DEXSeq with the one competing tool that claims to account for biological variation, namely, the new versions of Cuffdiff.
Method
Preparation: Flattening gene models and counting reads
The initial step of an analysis is the alignment of the sequencing reads to the genome. Here, it is important to use a tool capable of properly handling reads that straddle introns. Then, transcriptome annotation with coordinates of exon boundaries is required. For model organisms, reference gene model databases as provided, e.g., by Ensembl (Flicek et al. 2011), may be used. In addition, such a reference may be augmented by information retrieved from the RNA-seq data set that is being studied. Garber et al. (2011) review tools for the above tasks.
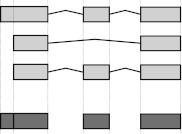
The central data structure for our method is a table that, in the simplest case, contains for each exon of each gene the number of reads in each sample that overlap with the exon. Special attention is needed, however, if an exon’s boundary is not the same in all transcripts. In such cases, we cut the exon in two or more parts (Fig. 1). We use the term “counting bin” to refer to exons or parts of exons derived in this manner. Note that a read that overlaps with several counting bins of the same gene is counted for each of these.
Figure 1.
Flattening of gene models: This (fictional) gene has three annotated transcripts involving three exons (light shading), one of which has alternative boundaries. We form counting bins (dark shaded boxes) from the exons as depicted; the exon of variable length gets split into two bins.
Model and inference
We denote by kijl the number of reads overlapping counting bin l of gene i in sample j. We interpret kijl as a realization of a random variable Kijl. The number of samples is denoted by m, i.e., j = 1, …, m.
We write μ_ijl_ for the expected value of the concentration of cDNA fragments contributing to counting bin l of gene i, and relate the expected read count E(Kijl) to μ_ijl_ via the size factor sj, which accounts for the depth that sample j was sequenced: E(kijl) = sj_μ_ijl. Note that sj depends only on j, i.e., the differences in sequencing depth are assumed to cause a linear scaling of the read counts. We estimate the size factors with the same method as in DESeq (Anders and Huber 2010; for details, please see Supplemental Note S.1).
A generalized linear model
We use generalized linear models (GLMs) (McCullagh and Nelder 1989) to model read counts. Specifically, we assume Kijl to follow a negative binomial (NB) distribution:
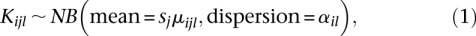
where α_il_ is the dispersion parameter (a measure of the distribution’s spread; see below) for counting bin (i, l), and the mean is predicted via a log-linear model as
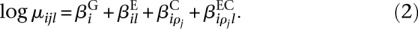
The negative binomial distribution in Equation 1 has been useful in many applications of count data regression (Cameron and Trivedi 1998). It can be seen as a generalization of the Poisson distribution: For a Poisson distribution, the variance v is equal to the mean μ, while for the negative binomial, the variance is v = μ + αμ2, with the dispersion α describing the squared coefficient of variation in excess of the Poisson case. Lu et al. (2005) and Robinson and Smyth (2007) motivated the use of the NB distribution for SAGE and RNA-seq data; we briefly summarize their argument in Supplemental Note S.2.
We fit one model for each gene i, i.e., the index i in Equation 2 is fixed. The linear predictor μ_ijl_ is decomposed into four factors as follows: 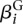 represents the baseline expression strength of gene i.
represents the baseline expression strength of gene i. 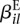 is (up to an additive constant) the logarithm of the expected fraction of the reads mapped to gene i that overlap with counting bin l.
is (up to an additive constant) the logarithm of the expected fraction of the reads mapped to gene i that overlap with counting bin l. 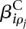 is the logarithm of the fold change in overall expression of gene i under condition ρ_j_ (the experimental condition of sample j). Finally,
is the logarithm of the fold change in overall expression of gene i under condition ρ_j_ (the experimental condition of sample j). Finally, 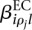 is the effect that condition ρ_j_ has on the fraction of reads falling into bin l.
is the effect that condition ρ_j_ has on the fraction of reads falling into bin l.
To make the model identifiable, constraints on the coefficients are needed; see Supplemental Note S.3.
Of interest in this model are the effects 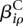 and
and 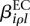 . If one of the
. If one of the 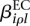 is different from zero, this indicates that the counting bin it refers to is differentially used. A value of
is different from zero, this indicates that the counting bin it refers to is differentially used. A value of 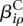 different from zero indicates an overall differential abundance that equally affects all counting bins, i.e., overall differential expression of the gene. Before we describe the analysis-of-deviance (ANODEV) procedure to test for these effects, we need to discuss the aspect of dispersion.
different from zero indicates an overall differential abundance that equally affects all counting bins, i.e., overall differential expression of the gene. Before we describe the analysis-of-deviance (ANODEV) procedure to test for these effects, we need to discuss the aspect of dispersion.
Parameter fitting
For a fixed choice of the dispersion parameter, the NB distribution is a member of the exponential family with respect to the mean. Hence, the iteratively reweighted least square (IRLS) algorithm, which is commonly used to fit GLMs (McCullagh and Nelder 1989), allows fitting of the model (1, 2) if the dispersion α_il_ is given.
Ordinary maximum likelihood estimation of the dispersion is not suitable, because it has a strong negative bias when the number of samples is small. The bias is caused by not accounting for the loss of degrees of freedom that arises when estimating the coefficients. Robinson and Smyth (2008) reviewed alternatives and derived an estimator based on the work of Cox and Reid (1987) and Smyth and Verbyla (1996). Cox and Reid suggested modifying the profile likelihood for the parameter of interest (here, the dispersion) by dividing out a term containing the Fisher information for the other parameters as an approximation to conditioning on the profiled-out parameters. This works if the parameter of interest is approximately independent from the other parameters with respect to Fisher information, which is the case for the NB likelihood with respect to its parameters mean and dispersion. However, calculating the Cox-Reid correction term for dispersion estimation in GLMs is not straightforward. The (to our knowledge) best method has been proposed by McCarthy et al. (2012). The authors have been using it in their edgeR package (Robinson et al. 2010a) since September 2010 (version 1.7.18). We make use of this approach to estimate the dispersion for each counting bin; details are provided in Supplemental Note S.4.
Two noise components
It is helpful to decompose the extra-Poisson variation of Kijl into two components: variability in gene expression and variability in exon usage. If the expression of a gene i (i.e., the total number of transcripts) in sample j differs from the expected value for experimental condition ρ_j_, the values μijl for all of the counting bins l of gene i will deviate from the values expected for condition ρ_j_ by the same factor. We denote this the variability in gene expression. By variability in exon usage, we refer to variability in the usage of particular exons or counting bins. The dispersion parameter α_il_ in Equation 1 with respect to the model of Equation 2 contains both of these parts. However, if we replace Equation 2 with
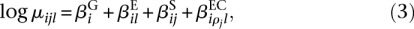
i.e., instead of fitting one parameter 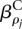 for the effect of each condition ρ on the expression, we fit one parameter
for the effect of each condition ρ on the expression, we fit one parameter 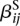 for each sample j, the gene expression variability is absorbed by the model parameters and we are only left with the exon usage variability. Hence, we use model (3) to increase power in our test for differential exon usage. This is possible because we test for an interaction effect. If the aim were to test for a main effect such as differential expression, dispersion estimation would need to be based on model (2).
for each sample j, the gene expression variability is absorbed by the model parameters and we are only left with the exon usage variability. Hence, we use model (3) to increase power in our test for differential exon usage. This is possible because we test for an interaction effect. If the aim were to test for a main effect such as differential expression, dispersion estimation would need to be based on model (2).
We fit the model (3) for each gene i separately and use the Cox-Reid dispersion estimator of McCarthy et al. (2012), as described above, to obtain a dispersion value 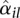 for each counting bin l in the gene.
for each counting bin l in the gene.
Information sharing across genes
If only a few replicates are available, as is often the case in high-throughput sequencing experiments, we need to be able to deal with the fact that the dispersion estimator for a single counting bin has a large sampling variance. A commonly used solution is to share information across estimators (Tusher et al. 2001; Lönnstedt and Speed 2002). We noted that there is a systematic trend of dispersions as a function of the mean, and consider the relationship

This relation appears to fit many data sets we have encountered in practice. (See also Di et al. 2011 for a comparison of approaches to model mean-variance relations in RNA-seq data.) To obtain the coefficients _a_0 and _a_1, we regress the dispersion estimates 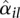 for all counting bins from all genes on their average normalized count values
for all counting bins from all genes on their average normalized count values 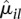 with a gamma-family GLM. To ensure robustness of the fit, we iteratively leave out bins with large residuals until convergence is achieved (Huber 1981).
with a gamma-family GLM. To ensure robustness of the fit, we iteratively leave out bins with large residuals until convergence is achieved (Huber 1981).
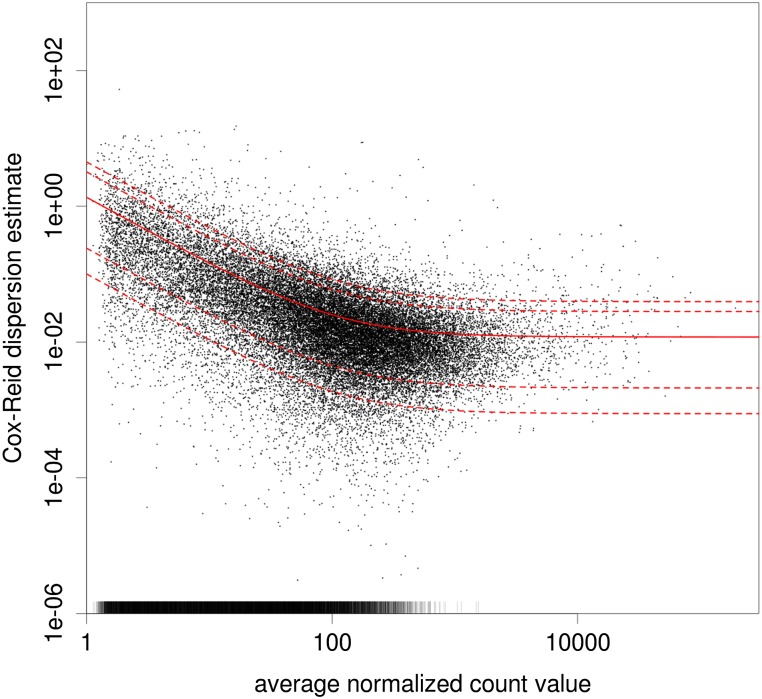
Figure 2 shows a scatterplot of dispersion estimates 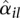 against average normalized count values
against average normalized count values 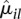 , together with the fit α(μ). For many counting bins, the difference between the sample estimate
, together with the fit α(μ). For many counting bins, the difference between the sample estimate 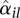 and the fitted value
and the fitted value 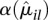 is compatible with a χ2 sampling distribution (indicated by the dashed lines). Nevertheless, there are sufficiently many bins with a sample estimate
is compatible with a χ2 sampling distribution (indicated by the dashed lines). Nevertheless, there are sufficiently many bins with a sample estimate 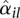 so much larger than the fitted value
so much larger than the fitted value 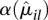 that it would not be justified to only rely on the fitted values. Hence, for the ANODEV (see below), we use as dispersion value α_il_ the maximum of the per-bin estimate
that it would not be justified to only rely on the fitted values. Hence, for the ANODEV (see below), we use as dispersion value α_il_ the maximum of the per-bin estimate 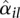 and the fitted value
and the fitted value 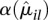 . On average, this overestimates the true dispersion and costs power, but we consider this preferable to using either only the fitted values or the sample estimates, both of which carry the risk of producing many undesirable false positives. More sophisticated alternatives for this step, which usefully interpolate between the two extremes, and perhaps incorporate further covariates besides μ, might become available in the future.
. On average, this overestimates the true dispersion and costs power, but we consider this preferable to using either only the fitted values or the sample estimates, both of which carry the risk of producing many undesirable false positives. More sophisticated alternatives for this step, which usefully interpolate between the two extremes, and perhaps incorporate further covariates besides μ, might become available in the future.
Figure 2.
Dependence of dispersion on the mean. Each dot corresponds to one counting bin in the data of Brooks et al. (2010) (discussed in detail in the Results section); (_x_-axis) normalized count, averaged over all samples; (_y_-axis) estimate of the dispersion. The bars at the bottom denote dispersion values outside the plotting range (in particular, those cases in which the sample dispersion is close to zero). (Solid red line) The regression line; (dashed lines) the 1-, 5-, 95-, and 99-percentiles of the χ2 distribution with 4 degrees of freedom scaled such that it has the fitted mean.
Analysis of deviance
We test for each counting bin whether it is differentially used between conditions. More precisely, we test against the null hypothesis that the fraction of reads overlapping with a counting bin l, of all the reads overlapping with the gene, does not change between conditions. To this end, we fit for each gene i a reduced model with no counting-bin–condition interaction:
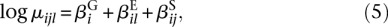
and, separately for each bin _l_′ of gene i, a model with an interaction coefficient for only this bin, but as in Equation 5, main effects for all bins l,
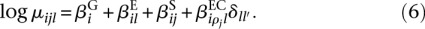
Here, δ_ll_′ is the Kronecker delta symbol, which is 1 if l = l_′ and 0 otherwise. We compute the likelihood of these models using the dispersion values α_il as estimated from model (3), with the information-sharing scheme presented earlier. Comparing the fit (6) for counting bin _l_′ of gene i with the fit (5) for gene i, we get an analysis-of-deviance _P_-value _pil_′ for each counting bin by means of a χ2 likelihood-ratio test. Note that we test against the null hypothesis that none of the conditions influences exon usage, and hence, if there are more than two different conditions ρ, we aim to reject the null hypothesis already if any one of the conditions causes differential exon usage.
Differential exon usage, as treated here, cannot be distinguished from overall differential expression of a gene if the gene only consists of a single counting bin or if all but one of its counting bins have zero counts. Hence, we mark all counting bins with zero counts in all samples, and all bins in genes with less than two nonzero bins, as not testable. Furthermore, we skip counting bins with a count sum across all samples below a threshold chosen low enough that a significant result would be unlikely, to speed up computation. Such filtering can also improve power (see Bourgon et al. 2010).
Note that we perform one test for each counting bin, always fitting an interaction coefficient only for the single bin _l_′ under test. Therefore, it is valid that a read that overlaps with several exons is counted for each of these exons: In each test, for the purpose of estimating and testing the interaction coefficient, any given read is only considered at most once.
Additional covariates
The flexibility of GLMs makes it easy to account for further covariates. For example, if in addition to the experimental condition ρ_j_ we wish to account for a further covariate τj, we extend model (3) as follows:
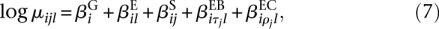
When testing for differential exon usage, the extra term 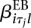 is added to both the reduced model (5) and the full model (6).
is added to both the reduced model (5) and the full model (6).
An example is provided in the next section with Equation 9.
Visualization
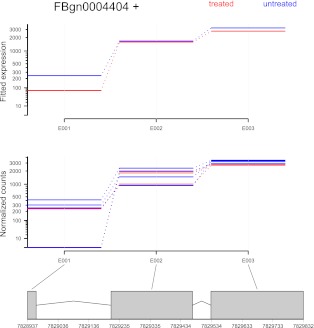
The DEXSeq package offers facilities to visualize data and fits. An example is shown in Figure 3, using the data discussed in the next section. Data and results for a gene are presented in three panels. The top panel depicts the fitted values from the GLM fit. For this plot, the data are fitted according to model (2), with the y coordinates showing the exponentiated sums:
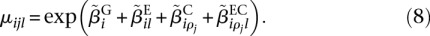
The tildes indicate that a decomposition of the linear predictors has been used that separates the effects of expression and isoform regulation, as described in Supplemental Note S.3.
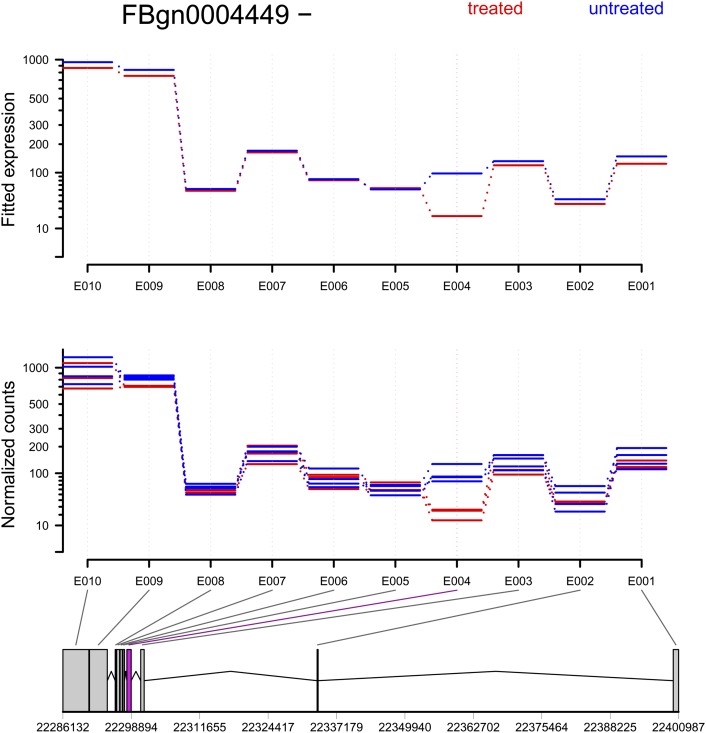
Figure 3.
The treatment of knocking down the splicing factor pasilla affects the fourth exon (counting bin E004) of the gene Ten-m (CG5723). (Top panel) Fitted values according to the linear model; (middle panel) normalized counts for each sample; (bottom panel) flattened gene model. (Red) Data for knockdown samples; (blue) control.
For genes with differential overall expression, it can be difficult to see the evidence for differential exon usage in a plot based on Equation 8. For these cases, the software offers the option to average over the expression effects. Supplemental Figure S1 shows this for the pasilla gene.
Variance stabilizing transformation
In Figure 3, a special axis scaling is used, because neither a linear nor a logarithmic scale seems appropriate. Instead, the software “warps” the axis scale such that, for data that follow the fitted mean-dispersion relation, the standard deviation corresponds to approximately the same scatter in the y direction throughout the dynamic range. See Supplemental Note S.5 for details.
Results
Analysis of the data set of Brooks et al.
We considered the data by Brooks et al. (2010), who used Drosophila melanogaster cell lines and studied the effect of knocking down pasilla with RNA-seq. The gene pasilla and its mammalian homologs NOVA1 and NOVA2 are well-studied splicing factors.
Brooks et al. (2010) prepared libraries from RNA extracted from seven biologically independent samples: three control samples and four knockdown samples. They sequenced the libraries on an Illumina Genome Analyzer II, partly using single-end and partly paired-end sequencing and using various read lengths. We obtained the read sequences from the NCBI Gene Expression Omnibus (accession numbers GSM461176–GSM461181), trimmed them to a common length of 37 nt, and aligned them against the D. melanogaster reference genome (assembly BDGP5/dm3, without heterochromatic sequences) (Hoskins et al. 2007) with TopHat 1.2 (Trapnell et al. 2009). We defined counting bins, as described above, based on the annotation from FlyBase 5.25 (Tweedie et al. 2009) as provided by Ensembl 62 (Flicek et al. 2011).
After counting read coverage for the counting bins, we estimated dispersion values for each bin by fitting, for each gene, a model based on Equations 2 and 3. Here, since we have a mixture of single-end and paired-end libraries, we extended Equation 3 to account for this additional covariate:
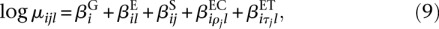
where τ_j_ = 1, 2 is the library type of sample j, single-end or paired-end.
The estimated dispersions are shown in Figure 2. The fitted line is given by α(μ) = 1.3/μ + 0.012, which has the form of Equation 4. The parameter _a_0 = 0.012 represents the amount of biological variation: Taking the square root, we can see that the exon usage typically differs with a coefficient of variation of ∼11% between biological replicates for strongly expressed exons.
Here, we can also see the advantage of absorbing expression variability in a sample coefficient. Had we used Equation 2 instead of Equation 3, we would have had to work with a higher dispersion, namely, α′(μ) = 1.6/μ + 0.018, and so would have lost power.
We performed the test for differential exon usage described in the context of Equations 5 and 6 for all counting bins that had at least 10 counts summed over all seven samples. We controlled the false discovery rate (FDR) with the Benjamini-Hochberg method and found, at 10% FDR, significant differential exon usage for 259 counting bins, affecting 159 genes.
Figure 3 shows the gene Ten-m, which exhibited a clear signal for differential usage of counting bin E004 (p = 2.1 × 10−11; after Benjamini-Hochberg adjustment padj = 1.2 × 10−8). Similar plots can be found, for all genes in this study, at http://www-huber.embl.de/pub/DEXSeq/psfb/testForDEU.html.
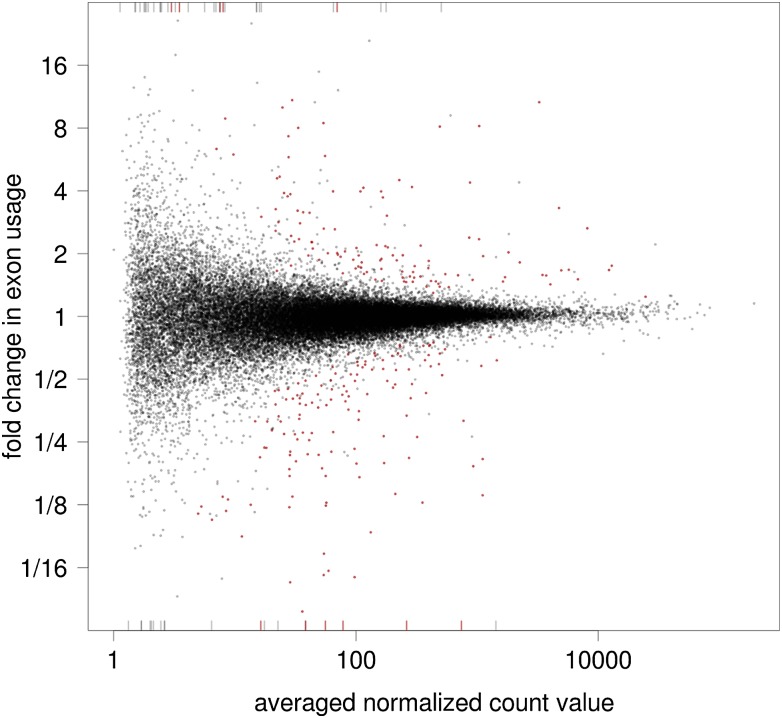
Figure 4 gives an overview of the test results and shows how the detection power depends on the mean: For strongly expressed exons, log2 fold changes around 0.5 (corresponding to fold changes around 40%) can be significant, while for weakly expressed exons with around 30 counts, fold changes above twofold are required. This is a consequence of the fact that the coefficient of variation (CV) of the count values decreases with their mean, as explained in more detail in Supplemental Note S.2.
Figure 4.
Fold changes of exon usage versus averaged normalized count value for all tested counting bins for the Brooks and coworkers data. (Red) Significance at 10% FDR. Bars at the margin represent bins with fold changes outside the plotting range.
Analysis of the chimpanzee data of Brawand et al.
While the preceding application was on a controlled experiment with a cell culture under sharp treatment, in this section, we analyze data from an observational study with complex subject-to-subject variation (Brawand et al. 2011). This data set includes RNA-seq from prefrontal cortex samples from six chimpanzees and cerebellum samples from two further chimpanzees. We used DEXSeq to test for exon usage differences between these two brain tissue types.
We aligned the RNA-seq reads (GEO accessions GSM752664–GSM752671) from these samples to the chimpanzee genome (CHIMP2.1.4 from Ensembl 64) using GSNAP 2012-01-11 (Wu and Nacu 2010). Prior to alignment, we trimmed all reads to a common length of 76 nt, single-ended. The trimming was necessary to make the data comparable across samples; DEXSeq itself has no length limitation and can deal with any read length.
At 10% FDR, DEXSeq found significant differential exon usage for 866 counting bins in 650 genes. The result table, with plots for all genes with significant differential exon usage, can be found at http://www-huber.embl.de/pub/DEXSeq/chimp/testForDEU.html.
Exploration of this hit list reveals interesting differences between the tissues. For example, one of the top hits, the gene PRKCZ (protein kinase C zeta; ENSPTRG00000000042) expresses its first four exons only in cerebellum but not in the prefrontal cortex (Supplemental Fig. S4). Inspecting the Pfam (Finn et al. 2010) and SMART (Letunic et al. 2012) databases of protein domains reveals that these four exons encode the heterodimerization domain PB1. This suggests the hypothesis that the gene product loses its ability to bind to its partner protein in the prefrontal cortex. Indeed, these two isoforms are well studied (for review, see Hirai and Chida 2003). The long isoform protein product PKZζ is widely expressed and is activated by a second messenger, PARD6A, which removes the protein’s auto-inhibition by binding to the PB1 domain. The truncated protein, denoted PKMζ, is specific to the brain and, due to the lack of the PB1 domain, constitutively active. It plays a major role in long-term potentiation and memory formation. In this context, it is noteworthy that, as our analysis shows, its expression is confined to certain brain regions.
Another example is provided by the gene PLCH2 (phospholipase C eta 2; ENSPTRG00000000051), for which DEXSeq indicated differential usage of counting bin E011 (fourth exon). According to SMART and Pfam, this exon contains an EF hand, a calcium binding helix–loop–helix motif. Here, we are not aware of prior work on the isoform(s) lacking this exon. We can speculate that the shorter isoform’s activity might no longer depend on calcium concentration, on which PLCH2’s enzymatic activity normally depends strongly (Nakahara et al. 2005). Furthermore, Zhou et al. (2008) studied the activation of PLCH2 by Gβγ complexes and found that the EF hand domain of PLCH2 is required for this interaction. Another hypothesis might hence be that the observed tissue-specific usage of the fourth exon serves to modulate the regulation of PLCH2 by G-proteins.
For the gene ENSPTRG00000000130, DEXSeq reports increased usage of the second exon in the cerebellum and of the second-to-last exon in the prefrontal cortex. This gene codes for precortistatin, a protein that gets cleaved to give rise to the neuropeptide cortistatin, which (in human) comprises the last 17 amino acids of the full protein’s C terminus (de Lecea et al. 1997), which are contained in the last exon. While the overall expression differences seen in the data agree with the known main location of cortistatin—the cortex, the observed differential exon usage is intriguing and more difficult to interpret: The affected parts of the protein are not part of the final product. Nevertheless, the presence or absence of these parts could affect the efficiency of the cleavage process or the stability of the mRNA, to coregulate the tissue-specific expression.
These three examples illustrate how a DEXSeq analysis can serve as a starting point for hypothesis formation. We picked these three genes by inspecting the first 10 genes with significant differential exon usage, as sorted by numerical Ensembl gene ID (not by _P_-value); that is, in essence we inspected a mere 10 randomly chosen hits. The richness of the biology seen indicates that many novel insights into gene function and regulation may be expected from the analysis of tissue-specific exon usage patterns.
Comparison of human cell lines
As a third application, we briefly present a comparison between two human cell lines. The ENCODE Project Consortium (2011) performed RNA-seq experiments for several human cell lines, of which we chose H1 human embryonic stem cells (h1-hESC) and human umbilical vein endothelial cells (HUVEC) (Laboratory of B. Wold; sequenced with 76-nt paired-end reads; GEO accession numbers GSM758573 and GSM767856), because they were performed in biological duplicates. Such a comparison offers high detection power because of the typically small within-group variability that one may expect for untreated cells and the many differences between these two cell lines. In fact, we find 7795 genes to be affected by differential exon usage, which can be seen in the report generated by DEXSeq, available at http://www-huber.embl.de/pub/DEXSeq/encode/testForDEU.html. For a plot of exon usage fold change, see Supplemental Figure F5, and for an example of a differentially spliced gene, see Supplemental Figure S6. Since the cell lines were derived from different subjects, the many observed differences could be due both to the difference in cell type and to differences in their genetic background.
Discussion
Importance of modeling overdispersion
The method presented here differs from previous work by using an error model that accounts for sample-to-sample variation in excess of Poisson variation. In the following, we investigate whether this extra variation is important enough to influence results in practice.
To address this question for our inference procedure, we recomputed the tests for differential exon usage for the Brooks and coworkers data after setting the dispersion values α_il_ in Equations 1, 5, and 6 to zero. This corresponds to assuming that the variation in the data follows a Poisson distribution. Cutting again the Benjamini-Hochberg–adjusted _P_-values at 10%, we obtained 36 times as many hits: Significant differential exon usage was reported for 9432 counting bins in 3610 genes (see Supplemental Fig. S2; cf. Fig. 4). For these extra hits, however, the treatment effect was not large compared with the variation seen between replicates, i.e., the data do not provide evidence for them being true positives.
The assumption that variability is limited to Poisson noise is implicit in analysis methods based on a Fisher’s test, which we discuss next.
Analyses based on Fisher’s test
To test for differential isoform regulation, Wang et al. (2008) and Brooks et al. (2010) used 2 × 2 contingency tables and a Fisher’s exact test. In this approach, the contingency table’s rows corresponded to control and treatment, the cells in one column contained the numbers of reads supporting inclusion of an exon (i.e., reads overlapping the exon), and the cells in the other column gave the numbers of reads supporting exclusion (e.g., in the case of cassette exons, reads straddling the exon). In the study of Wang et al. (2008), each row corresponded to a single sample, while Brooks et al. (2010) summed up the number of reads from their replicates. The MISO method (Katz et al. 2010) proposed a different way of setting up the contingency table. In all cases, the contingency tables did not contain information on sample-to-sample variability (Baggerly et al. 2003), and, therefore, one should expect the results to contain an inflated number of false positives.
As an example, Supplemental Figure S3 shows the gene Lk6, for which Brooks et al. (2010) reported differential use of its alternative first exons, while our analysis did not call a significant differential use. Clearly, the average expression strength of exon E002 is different between the conditions. However, examining the counts from the individual biological replicates reveals that the variance within the treatment groups is large compared with this difference, and hence, the data do not support the claim of a significant effect of the treatment.
Heterogeneity of dispersions
In our model, we allow the counting bins of a gene to have different dispersion values. The gene RpS14b (Fig. 5) exhibits very different variability for its three exons and thus illustrates the need for this modeling choice.
Figure 5.
Ribosomal protein gene RpS14b (from the Brooks and coworkers data) is shown here as an example for a gene with heterogeneous dispersion. The first exon has zero count in the paired-end samples untreated 2, in the single-end sample treated 2, and in the paired-end sample treated 3, and large nonzero counts in the four other samples. Colors are as in Figure 3.
The first exon also illustrates the value of replicates and the importance of making use of their information. This exon had between 252 and 416 (normalized) counts in four of the samples and no counts in three. However, this difference cannot be attributed to the treatment because both the control and the treatment group contained samples with zero counts as well as samples with several hundreds of counts. Hence, the reason for the difference in read counts for this exon cannot be the knockdown of pasilla and is likely some other difference between the samples’ treatment that was not under the experimenters’ control.
If one just adds up or averages the samples in a treatment group, as done in the contingency table method, one would only see a sizeable difference, as in the upper panel of the figure, and might call a significant effect. It is also crucial that the test for differential exon usage does not rely on the fitted dispersion (solid line in Fig. 2) only, because the effect size would seem significant if one did not take note that the actual observed within-group variance is so much larger that the fitted value is implausible. The maximum rule discussed in the section on information sharing ensures this.
Comparison with Cuffdiff
Cufflinks (Trapnell et al. 2010) is a tool to infer gene models from RNA-seq data and to quantify the abundance of transcript isoforms in an RNA-seq sample. In addition to this, the Cuffdiff module allows testing for differences in isoform abundance. Cuffdiff, as described in Trapnell et al. (2010), compares a single sample with another one and does not attempt to account for sample-to-sample variability. The latter is also true for the version described by Roberts et al. (2011), which allows processing of replicate samples, but uses this for the assessment only of bias, not of variability. Hence, the same drawbacks may be expected as discussed earlier for the Fisher-test-based methods. More recently, starting with version 1.0.0, Cufflinks attempts to assess overdispersion and account for it.
We compared the three knockdown samples of the Brooks and coworkers data set against the four control samples with version 1.3.0 of Cuffdiff. With nominal FDR control at 10%, Cuffdiff reported differential splicing for only 50 genes, and thus showed less power than our approach.
To test the control of false-positive rates, we made use of the fact that there were four replicates for the untreated condition. We formed one group from samples 1 and 3 and another group from samples 2 and 4. We tasked both DEXSeq and Cuffdiff with comparing between the two groups at a nominal FDR of 10%. Because this is a comparison between replicates, ideally no significant calls should be made. Note that each group contained one single-end and one paired-end sample, i.e., the blocking caused by the library type was balanced between the groups. In this mock comparison, DEXSeq found eight genes significant, compared with 159 in the comparison of treatment versus control. Surprisingly, Cufflinks found 639 genes in the mock comparison, many more than the 37 genes that it found in the proper between-groups comparison. Supplemental Note S.6 describes further tests, which confirmed Cufflinks’ difficulty with providing type I error control in this data set.
We also performed the same type of comparison on a data set with quite different characteristics and experimental design, the chimpanzee data of Brawand et al. (2011). In a comparison of the six chimpanzee prefrontal cortex (PFC) samples with the two cerebellum samples, Cuffdiff 1.3.0 reported 114 genes at 10% FDR, again showing less power then DEXSeq (650 genes; see above).
We then used the five PFC samples from male chimpanzees to assess type I error rates. Both tools were tasked to compare any combination of two samples versus two other samples. DEXSeq in each case found substantially fewer genes in these mock comparisons than in the proper comparison (with one exception, always less than 1/65). Cuffdiff, however, always found more than twice as many genes in the mock comparisons than in the true one. For details, see Supplemental Note S.6. Also see Supplemental Note II, which contains the exact commands used for all computations performed for this article.
Comparing exon or isoform usage
The interpretation of the results of our method is straightforward when a single exon of a gene with many exons is called differentially used. However, if many exons within a gene are affected, the interpretation is more complex. For instance, consider a gene with two isoforms, a long one with n exons and a short one consisting of only the first n/2 exons. If an experimental condition increased the number of long transcripts at the expense of the short ones, without changing the total number, one might expect an analysis to indicate differential usage for the last n/2 exons. However, our method cannot distinguish this situation from one in which the gene is overall down-regulated, while the first n/2 exons are more strongly used.
Hence, if differential exon usage is detected within a gene, we can safely conclude that this gene is affected by alternative isoform regulation. However, the test’s output with regard to which of the counting bins are affected can be unreliable if the isoform regulation affects a large fraction of the exons. In practice, the assignment to counting bins is reliable as long as only a small fraction of counting bins in the gene is called significant.
Methods that attempt to estimate not just the abundance of exons but of isoforms, such as the method of Jiang and Wong (2009), Cufflinks (Trapnell et al. 2010) and MMSeq (Turro et al. 2011), may be able to circumvent this issue. Of these, only Cufflinks/Cuffdiff offers the functionality of comparing between samples. We commented on Cuffdiff in the preceding section. (Note added after revision: Recently, Glaus et al. 2012 published BitSeq, another method to identify differential expression of isoforms.)
Apart from the lack of tools for inferring differential expression at the transcript level, there can be concrete advantages in per-exon analysis. If, for example, several transcripts have most exons in common and differ by only a few exons, their abundance estimates will contain substantial correlated uncertainties that reduce the power for inference of differential expression. The remedy would be to disregard the reads that inform about the shared parts of the transcripts and to focus on those reads in which they differ. Hence, an exon-centric analysis might be a crucial component even of a transcript-level method.
In addition, it is not clear that inference about transcripts is always more useful for biological interpretation than inference at the per-exon level. After all, we have knowledge about the functional differences of multiple translated isoforms of a gene for only a small number of proteins. If currently a researcher finds that a gene of interest expresses different transcripts in different conditions, her further analysis will typically start with assessing the difference between the two transcripts. She might find, for example, that they differ in the presence of certain exons and ask which regulatory signals or functional domains these exons may contain. Therefore, we expect that a method such as ours that pinpoints the location of the differences by focusing on specific exons will be valuable for biological interpretation, and sometimes perhaps more valuable than a transcript-centric approach. This expectation is supported by the three examples discussed in the analysis of the chimpanzee data. The next step will be to leverage, in a systematic and automated way, databases with annotation for parts of gene products, e.g., information on protein domains provided by resources such as Pfam (Finn et al. 2010), SMART (Letunic et al. 2012), and PROSITE (Sigrist et al. 2010), or predicted miRNA target sites.
Junction reads
Junction reads are reads whose genomic alignment contains a gap because they start in one exon, end in another exon, and “jump” over the intron in between and possibly over skipped exons. In DEXSeq, such reads are counted for each counting bin with which they overlap, i.e., they appear multiple times in the count table. However, because we test for each exon separately, this does not affect the validity of the test.
Junction reads contain additional information that is especially valuable when inferring gene models and the positions of splice junctions. Unless one works with a very well annotated model system, this information should be used when defining the counting bins, by parsing the spliced alignments with appropriate tools.
Furthermore, junction reads give evidence for connections between counting bins and thus are crucial for isoform deconvolution tools such as Cufflinks and MMSeq. For our exon-by-exon test, however, leveraging this information is not essential, and also not straightforward. In the method presented, we essentially consider for each sample the ratio of the number of reads overlapping with an exon to the number of reads falling onto the whole gene. Alternatively, one could consider the ratio of the number of reads skipping over the exon under consideration to the total count. We anticipate that the latter would offer a moderate increase in power in cases in which the counting bin is much shorter than the typical read length. It may be an interesting future extension to the DEXSeq method to switch to this scheme for bins that are short compared with the read length.
Implementation
We implemented DEXSeq as a package for the statistical programming language R (R Development Core Team 2009) and have made it available as open source software via the Bioconductor project (Gentleman et al. 2004). See the Bioconductor web page for downloading instructions. DEXSeq can be used on MacOS, Linux, and Windows.
For the preparation steps, namely, the “flattening” of the transcriptome annotation to counting bins and the counting of the reads overlapping each counting bin, two Python scripts are provided, which are built on the HTSeq framework (Anders 2011). The first script takes a GTF file with gene models and transforms it into a GFF file listing counting bins, and the second takes such a GFF file and an alignment file in the SAM format and produces a list of counts. The R package is used to read these counts, estimate the size factors and dispersions, fit the dispersion-mean relation, and test for differential exon usage. After the analysis has been performed, all the results are available, together with the input data, in an object derived from the ExpressionSet class, Bioconductor’s standard container type for data from high-throughput assays. The results provided include for each counting bin the following data: the conditional-maximum-likelihood estimate for the dispersion, the dispersion value actually used in the test (which may be different, due to the information sharing across genes), the _P_-value from the test for differential exon usage, the Benjamini-Hochberg-adjusted _P_-value, and the fit coefficients describing the fitted log2 fold change between treatment controls (or, if there are more than two conditions, for pairs of conditions as chosen by the user). Other R or Bioconductor functionality can be used for downstream analyses of these results. If required, the other coefficients as described in Supplemental Note S.3 are also available.
Furthermore, DEXSeq can create a set of HTML pages that contains the results of the tests, and, for each gene, plots like Figures 3 and 5 and Supplemental Figures S1 and S3. The HTML output allows interactive browsing of the results and facilitates sharing of the results with colleagues by uploading the files to a web server.
The DEXSeq package provides functions on different levels. In the simplest case, a single function is called that runs all the steps of a standard analysis. To give experienced users the possibility to interfere with the workflow, functions are also provided to run each step separately, to run some steps only for single genes, and to inspect intermediate and final results.
The use of the package is explained in the vignette (a manual with a worked example) and documentation pages for all functions.
Because the DEXSeq method relies on fitting GLMs of the NB family, a reliable IRLS fitting function is required. We use the function nbglm.fit (McCarthy et al. 2012) from the statmod package, which offers better performance and convergence than older implementations.
Fitting GLMs for many genes and counting bins is a computationally expensive process. When running on a single core of a current desktop computer, the analysis of the Brooks and coworkers data presented here takes several hours. However, the method lends itself easily to parallelization: We use the multicore package (Urbanek 2011) to distribute the computation on several CPU cores.
The complete workflow used to perform all calculations for this article is documented in Supplement II.
Conclusion
We have presented a method, called DEXSeq, to test for evidence of differential usage of exons and hence of isoforms in RNA-seq samples from different experimental conditions using generalized linear models. DEXSeq achieves reliable control of false discovery rates by estimating variability (dispersion) for each exon or counting bin and good power by sharing dispersion estimation across features. The method is implemented as an open source Bioconductor package, which also facilitates data visualization and exploration. We have demonstrated DEXSeq on three data sets of different type and illustrated how the results of a DEXSeq analysis, combined with metadata on parts of transcripts, such as protein domains, form the basis for exploring a biological phenomenon, differential exon usage, that is currently not well understood and whose study may reveal many surprises.
Footnotes
[Supplemental material is available for this article.]
References
- Anders S. 2011. http://www-huber.embl.de/users/anders/HTSeq/ HTSeq: Analysing high-throughput sequencing data with Python.
- Anders S, Huber W 2010. Differential expression analysis for sequence count data. Genome Biol 11: R106 doi: 10.1186/gb-2010-11-10-r106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baggerly KA, Deng L, Morris JS, Aldaz CM 2003. Differential expression in SAGE: Accounting for normal between-library variation. Bioinformatics 19: 1477–1483 [DOI] [PubMed] [Google Scholar]
- Blekhman R, Marioni JC, Zumbo P, Stephens M, Gilad Y 2010. Sex-specific and lineage-specific alternative splicing in primates. Genome Res 20: 180–189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourgon R, Gentleman R, Huber W 2010. Independent filtering increases detection power for high-throughput experiments. Proc Natl Acad Sci 107: 9546–9551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brawand D, Soumillon M, Necsulea A, Julien P, Csárdi G, Harrigan P, Weier M, Liechti A, Aximu-Petri A, Kircher M, et al. 2011. The evolution of gene expression levels in mammalian organs. Nature 478: 343–348 [DOI] [PubMed] [Google Scholar]
- Brooks AN, Yang L, Duff MO, Hansen KD, Park JW, Dudoit S, Brenner SE, Graveley BR 2010. Conservation of an RNA regulatory map between Drosophila and mammals. Genome Res 21: 193–202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron AC, Trivedi PK 1998. Regression analysis of count data. Cambridge University Press, Cambridge, UK [Google Scholar]
- Cline MS, Blume J, Cawley S, Clark TA, Hu J-S, Lu G, Salomonis N, Wang H, Williams A 2005. ANOSVA: A statistical method for detecting splice variation from expression data. Bioinformatics (Suppl 1) 21: i107–i115 [DOI] [PubMed] [Google Scholar]
- Cox DR, Reid N 1987. Parameter orthogonality and approximate conditional inference. J R Stat Soc Ser B Methodol 49: 1–39 [Google Scholar]
- de Lecea L, Ruiz-Lozano P, Danielson PE, Peelle-Kirley J, Foye PE, Frankel WN, Sutcliffe JG 1997. Cloning, mRNA expression, and chromosomal mapping of mouse and human preprocortistatin. Genomics 42: 499–506 [DOI] [PubMed] [Google Scholar]
- Di Y, Schafer DW, Cumbie JS, Chang JH 2011. The NBP negative binomial model for assessing differential gene expression from RNA-Seq. Stat Appl Genet Mol Biol 10 doi: 10.2202/1544-6115.1637 [Google Scholar]
- The ENCODE Project Consortium 2011. A user’s guide to the encyclopedia of DNA elements (ENCODE). PLoS Biol 9: e1001046 doi: 10.1371/journal.pbio.1001046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn RD, Mistry J, Tate J, Coggill P, Heger A, Pollington JE, Gavin OL, Gunasekaran P, Ceric G, Forslund K, et al. 2010. The Pfam protein families database. Nucleic Acids Res 38: D211–D222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flicek P, Amode MR, Barrell D, Beal K, Brent S, Chen Y, Clapham P, Coates G, Fairley S, Fitzgerald S, et al. 2011. Ensembl 2011. Nucleic Acids Res 39: D800–D806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garber M, Grabherr MG, Guttman M, Trapnell C 2011. Computational methods for transcriptome annotation and quantification using RNA-seq. Nat Methods 8: 469–477 [DOI] [PubMed] [Google Scholar]
- Gentleman RC, Carey VJ, Bates DM, Bolstad B, Dettling M, Dudoit S, Ellis B, Gautier L, Ge Y, Gentry J, et al. 2004. Bioconductor: Open software development for computational biology and bioinformatics. Genome Biol 5: R80 doi: 10.1186/gb-2004-5-10-r80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaus P, Honkela A, Rattray M 2012. Identifying differentially expressed transcripts from RNA-seq data with biological variation. Bioinformatics 28: 1721–1728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabowski P 2011. Alternative splicing takes shape during neuronal development. Curr Opin Genet Dev 21: 388–394 [DOI] [PubMed] [Google Scholar]
- Griffith M, Griffith OL, Mwenifumbo J, Goya R, Morrissy AS, Morin RD, Corbett R, Tang MJ, Hou Y-C, Pugh TJ, et al. 2010. Alternative expression analysis by RNA sequencing. Nat Methods 7: 843–847 [DOI] [PubMed] [Google Scholar]
- Hansen KD, Wu Z, Irizarry RA, Leek JT 2011. Sequencing technology does not eliminate biological variability. Nat Biotechnol 29: 572–573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardcastle TJ, Kelly KA 2010. BaySeq: Empirical Bayesian methods for identifying differential expression in sequence count data. BMC Bioinformatics 11: 422 doi: 10.1186/1471-2105-11-422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirai T, Chida K 2003. Protein kinase Cζ (PKCζ): Activation mechanisms and cellular functions. J Biochem 133: 1–7 [DOI] [PubMed] [Google Scholar]
- Hoskins RA, Carlson JW, Kennedy C, Acevedo D, Evans-Holm M, Frise E, Wan KH, Park S, Mendez-Lago M, Rossi F, et al. 2007. Sequence finishing and mapping of Drosophila melanogaster heterochromatin. Science 316: 1625–1628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber PJ. 1981 Robust statistics. Wiley, New York. [Google Scholar]
- Jiang H, Wong WH 2009. Statistical inferences for isoform expression in RNA-seq. Bioinformatics 25: 1026–1032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz Y, Wang ET, Airoldi EM, Burge CB 2010. Analysis and design of RNA sequencing experiments for identifying isoform regulation. Nat Methods 7: 1009–1015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letunic I, Doerks T, Bork P 2012. SMART 7: Recent updates to the protein domain annotation resource. Nucleic Acids Res 40: D302–D305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lönnstedt I, Speed T 2002. Replicated microarray data. Statist Sinica 12: 31–46 [Google Scholar]
- Lu J, Tomfohr JK, Kepler TB 2005. Identifying differential expression in multiple SAGE libraries: An overdispersed log-linear model approach. BMC Bioinformatics 6: 165 doi: 10.1186/1471-2105-6-165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy DJ, Chen Y, Smyth GK 2012. Differential expression analysis of multifactor RNA-seq experiments with respect to biological variation. Nucleic Acids Res 40: 4288–4297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA 1989. Generalized linear models, 2nd ed. Chapman & Hall/CRC, Boca Raton, FL [Google Scholar]
- Nakahara M, Shimozawa M, Nakamura Y, Irino Y, Morita M, Kudo Y, Fukami K 2005. A novel phospholipase C, PLCη2, is a neuron-specific isozyme. J Biol Chem 280: 128–134 [DOI] [PubMed] [Google Scholar]
- Nilsen TW, Graveley BR 2010. Expansion of the eukaryotic proteome by alternative splicing. Nature 463: 457–463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purdom E, Simpson KM, Robinson MD, Conboy JG, Lapuk AV, Speed TP 2008. FIRMA: A method for detection of alternative splicing from exon array data. Bioinformatics 24: 1707–1714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. 2009 R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org. [Google Scholar]
- Roberts A, Trapnell C, Donaghey J, Rinn JL, Pachter L 2011. Improving RNA-seq expression estimates by correcting for fragment bias. Genome Biol 12: R22 doi: 10.1186/gb-2011-12-3-r22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MD, Smyth GK 2007. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics 23: 2881–2887 doi: 10.1093/bioinformatics/btm453 [DOI] [PubMed] [Google Scholar]
- Robinson MD, Smyth GK 2008. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics 9: 321–332 doi: 10.1093/biostatistics/kxm030 [DOI] [PubMed] [Google Scholar]
- Robinson M, McCarthy D, Chen Y, Smyth G 2010a. edgeR: Empirical analysis of digital gene expression data in R. Bioconductor. http://www.bioconductor.org [Google Scholar]
- Robinson MD, McCarthy DJ, Smyth GK 2010b. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26: 139–140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigrist CJA, Cerutti L, de Castro E, Langendijk-Genevaux PS, Bulliard V, Bairoch A, Hulo N 2010. PROSITE, a protein domain database for functional characterization and annotation. Nucleic Acids Res 38: D161–D166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth GK, Verbyla AP 1996. A conditional likelihood approach to residual maximum likelihood estimation in generalized linear models. J R Stat Soc Ser B Methodol 58: 565–572 [Google Scholar]
- Trapnell C, Pachter L, Salzberg SL 2009. TopHat: Discovering splice junctions with RNA-seq. Bioinformatics 25: 1105–1111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Williams BA, Pertea G, Mortazavi A, Kwan G, van Baren MJ, Salzberg SL, Wold BJ, Pachter L 2010. Transcript assembly and quantification by RNA-seq reveals unannotated transcripts and isoform switching during cell differentiation. Nat Biotechnol 28: 511–515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turro E, Su S-Y, Goncalves A, Coin LJM, Richardson S, Lewin A 2011. Haplotype and isoform specific expression estimation using multi-mapping RNA-seq reads. Genome Biol 12: R13 doi: 10.1186/gb-2011-12-2-r13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusher V, Tibshirani R, Chu C 2001. Significance analysis of microarrays applied to ionizing radiation response. Proc Natl Acad Sci 98: 5116–5121 doi: 10.1073/pnas.091062498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tweedie S, Ashburner M, Falls K, Leyland P, McQuilton P, Marygold S, Millburn G, Osumi-Sutherland D, Schroeder A, Seal R, et al. 2009. FlyBase: Enhancing Drosophila Gene Ontology annotations. Nucleic Acids Res 37: D555–D559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urbanek S. 2011 multicore: Parallel processing of R code on machines with multiple cores or CPUs. R package, version 0.1-7. http://cran.r-project.org. [Google Scholar]
- Wang ET, Sandberg R, Luo S, Khrebtukova I, Zhang L, Mayr C, Kingsmore SF, Schroth GP, Burge CB 2008. Alternative isoform regulation in human tissue transcriptomes. Nature 456: 470–476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu TD, Nacu S 2010. Fast and SNP-tolerant detection of complex variants and splicing in short reads. Bioinformatics 26: 873–881 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Sondek J, Harden TK 2008. Activation of human phospholipase C-η2 by Gβγ. Biochemistry 47: 4410–4417 [DOI] [PMC free article] [PubMed] [Google Scholar]