Assessing experimentally derived interactions in a small world (original) (raw)

Abstract

Experimentally determined networks are susceptible to errors, yet important inferences can still be drawn from them. Many real networks have also been shown to have the small-world network properties of cohesive neighborhoods and short average distances between vertices. Although much analysis has been done on small-world networks, small-world properties have not previously been used to improve our understanding of individual edges in experimentally derived graphs. Here we focus on a small-world network derived from high-throughput (and error-prone) protein–protein interaction experiments. We exploit the neighborhood cohesiveness property of small-world networks to assess confidence for individual protein–protein interactions. By ascertaining how well each protein–protein interaction (edge) fits the pattern of a small-world network, we stratify even those edges with identical experimental evidence. This result promises to improve the quality of inference from protein–protein interaction networks in particular and small-world networks in general.

Until recently, network modeling often assumed the topology was either a random graph or a regular lattice. In recent years it has been shown that neither of these options capture the properties of most real networks well, and new graph models have been proposed. One such model, the small-world networks of Watts and Strogatz (1), has inspired a plethora of new research directions (2). A small-world network is one in which the length of the shortest path between any pair of vertices tends to be small (short characteristic path length), but also with densely connected local neighborhoods (high clustering coefficient) (1). The former property is held by random graphs but not regular lattices, whereas the latter property is held by regular lattices but not random graphs, placing small-world networks between these two extremes. Real networks shown to be small-world networks include the Internet (3), scientific collaboration networks (4), neural connections in Caenorhabditis elegans (1), the English lexicon (5), metabolic networks (6), and protein–protein interaction networks (7, 8). It is not surprising that so many real networks are small world, because Watts and Strogatz (1) showed that as you interpolate from either extreme (random or lattice), the graph quickly becomes small world, so that real graphs that are neither completely ordered nor completely random will often be small-world graphs. Properties of small-world networks have been investigated (9–12), various models for their origin have been formulated (13–16), and methods for separating cohesive regions have been devised (17, 18). Other network properties studied in recent years that are also common in real networks include scale-free (or power-law) degree distribution (3, 19–22), community structure (18), and hierarchy (23). Although much analysis has been done on these new network topologies, topological network properties have not previously been used to assess reliability of individual edges in an experimentally derived network.

Biological networks such as protein–protein interaction networks, metabolic networks, and gene regulatory networks are experimentally derived with substantial false-positive and false-negative errors (24, 25). Here we consider in detail a network of protein–protein interactions derived from high-throughput, error-prone yeast two-hybrid (Y2H) studies (26, 27). These data can be depicted graphically with vertices representing proteins and edges (connecting lines) representing interactions between them. Estimates of error rates in Y2H studies range from 50% to 80% (24, 25, 27, 28). Although protein interaction networks have been used to predict protein function (26, 27, 29–32), experimental errors necessarily affect the quality of such inference.

Others have assessed edges in protein–protein interaction networks by using homology (25), gene expression (33), and network topology (considering the number of neighbors with only one neighbor) (34). Each of these methods used threshold values for their assessment, essentially classifying edges as either high or low confidence. We want to estimate the probability that each edge in the network represents a real interaction, or “true edge.” In addition to direct evidence about the veracity of each edge, we want to see whether a property of the overall topology of the true graph can be exploited to locally assess edges in the experimental graph. The neighborhood cohesiveness of a network is an average of a local measure, so it is a natural first choice of a network property to use. We incorporate a measure of neighborhood cohesiveness around the edge as an indication of how well the edge fits the expected topology of protein–protein interaction networks.

Our strategy is as follows. First, we define four variants of a mutual clustering coefficient, Cvw, to measure the neighborhood cohesiveness around an edge in a graph. Second, we show that for our network of protein–protein interactions, true edges (interactions) have distinctly higher Cvw than false-positive edges, as expected if true edges form a small-world network whereas false-positive edges form a more random network. Third, we examine the degree to which the neighborhood cohesiveness of each edge is consistent with a small-world network and show that this measure provides a way to score individual edges according to their likelihood of being true. Fourth, we rank protein interactions according to each variant of Cvw and determine the best definition of Cvw for protein–protein interaction networks. Fifth, we provide a probabilistic framework for integrating diverse types of evidence to better assess confidence for observed high-throughput interactions. Finally, we predict interactions for which we have no experimental evidence and show that upon further investigation a remarkable number of these predictions have already been noted in the biomedical literature.

Mutual Clustering Coefficient

Watts and Strogatz (1) defined a clustering coefficient to give a global measure of the cohesiveness or “cliquishness” of a graph. Small-world networks have high clustering coefficients (1). The cliquishness of the neighborhood around an individual edge should therefore be an indication of how well this edge fits the pattern of a small-world network. Quantifying this seems straightforward. Indeed, the clustering coefficient of a graph was originally defined as the average of a local measurement: The clustering coefficient of a graph defined by Watts and Strogatz used the average value of Cv, a measure of the neighborhood cohesiveness around each vertex v. However, we want to quantify neighborhood cohesiveness around individual edges rather than vertices.

The high clustering coefficients of small-world networks indicate that neighbors of a given vertex are more likely to have edges between them than would be expected in a random graph. Such edges between neighbors of a vertex form triangles cornered at that vertex. This preponderance of triangles in a small-world network means that an edge is likely to be a side of more triangles than would be expected in a random graph. Therefore, for an edge vw between vertices v and w, a neighbor of vertex v is more likely to have an edge to w if the edge is from a small-world graph (illustrated in Fig. 1) than if it is from a random graph. Such “mutual neighbors” of the two endpoints serve to corroborate the edge.

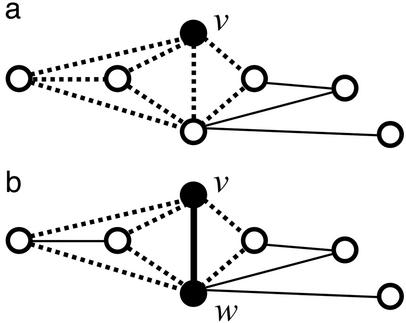
Fig 1.

Fig 1.

Cohesive neighborhoods in a small-world network. (a) The neighbors of a vertex are more likely to be neighbors of each other (forming triangles, shown with dotted lines) in a small-world network than in a random graph. (b) Equivalently, the two vertices of an edge are more likely to have neighbors in common (also forming triangles).

We want to define a mutual clustering coefficient Cvw for a pair of vertices v and w to give a measure of such corroboration. We want this measure to be independent of the existence of an edge between v and w for a leave-one-out approach, so that direct experimental evidence about an interaction between two proteins does not influence our assessment of the neighborhood of the two proteins. We apply this measure not only to edges (vertex pairs with supporting evidence) but to any pair of vertices so we can form hypotheses about missing edges. In defining such a measure, we want to count the number of triangles in which this pair of vertices might be included, but the proper normalization factor (to account for the number of neighbors of the two proteins) is uncertain. Optimal normalization may depend on other aspects of the network topology, such as whether the small-world network also exhibits a scale-free topology, i.e., has a distribution of degree (number of edges to each vertex) that follows a power law (19, 21).

We consider four alternative definitions of Cvw. In each of these definitions, N(x) represents the neighborhood of a vertex x, and Total represents the total number of proteins in the organism. Given fixed neighborhood sizes |N(v)| and |N(w)|, these coefficients all increase with increasing overlap between the neighborhoods. For two vertices v and w, we define these measures of mutual clustering coefficient:

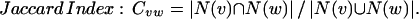
graphic file with name M1.gif

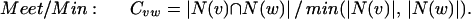
graphic file with name M2.gif

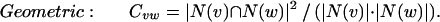
graphic file with name M3.gif

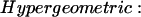
graphic file with name M4.gif

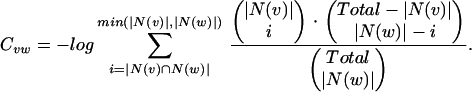
graphic file with name M5.gif

The first three definitions all have as their numerator the number of triangles that contain the edge, although each definition uses a different normalization factor. The Jaccard index (35) is a natural and common graph-theoretic measure that has been used for hierarchical clustering (36), but it is inappropriate if one of the two endpoints of the edge we are considering has a large neighborhood. For example, if the two endpoints of an edge share 10 common neighbors, we might desire more significance if one endpoint has only these 10 neighbors and the other endpoint has 200 neighbors than if each endpoint has 105 neighbors (the union of the two neighborhoods is of size 200 in either case). Such situations can be expected in scale-free networks such as that of protein–protein interactions (21, 22). The meet/min coefficient removes this bias at the expense of discarding information about the larger neighborhood size. This measure is similar to the topological overlap defined by Ravasz et al. (23). The principal difference is that our measure is independent of any evidence of an edge between the two nodes measured (see below). The geometric coefficient is a compromise between the Jaccard and meet/min coefficients and is similar to the measure of signature overlap used by Ihmels et al. (37).

The cumulative hypergeometric distribution is frequently used to measure cluster enrichment (38) and significance of co-occurrence (39). The summation in the hypergeometric coefficient can be interpreted as a p value, the probability of obtaining a number of mutual neighbors between vertices v and w at or above the observed number by chance, under the null hypothesis that the neighborhoods are independent, and given both the neighborhood sizes of the two vertices and the total number of proteins in the organism. The hypergeometric coefficient is then defined to be the negative log of this p value.

To avoid zero denominators in the first three coefficients, we included the edge vw in computation of C_vw_, regardless of direct experimental evidence for that edge. For the hypergeometric coefficient, we excluded the edge vw. This makes C_vw_ (for all definitions) independent of the direct experimental evidence for the edge we are assessing. To expedite computation of the hypergeometric coefficient, a numerical approximation of the Gamma function was used to calculate factorials (40) so that computation time was not an issue.

Protein–Protein Interaction Data

We derived our protein–protein interaction network from high-throughput, error-prone Y2H studies (26, 27) obtained from CuraGen's PathCalling Yeast Interaction Database (ref. 26; http://portal.curagen.com). Such interactions between proteins are known to form a small-world network (7, 8). We chose to focus on data from Y2H studies because they are particularly error-prone and thus stand to maximally benefit from a better assessment of individual interactions. For validation, we used the more reliable conventional evidence (e.g., coimmunoprecipitation) also obtained from the PathCalling database. A total of 6,000 known and hypothetical Saccharomyces cerevisiae proteins were used, of which 1,658 have some type of evidence of interactions with another protein.

To validate predictions of interacting pairs of proteins for which there is no evidence in the PathCalling database, we used Incyte Genomics' Yeast Proteome Database (ref. 41; www.incyte.com/proteome), which is a more comprehensive, biomedical literature-derived database.

Correlation Between Cvw and Validity of Interactions

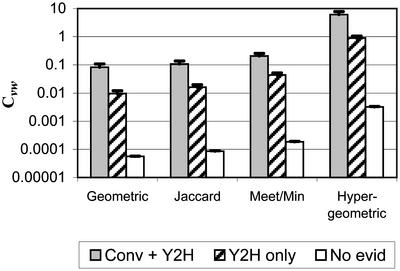
To determine whether there is a correlation between each definition of Cvw and true edges, we examined the Y2H network described above. As shown in Fig. 2, for each of these definitions, the average Cvw of interactions found by high-confidence conventional studies was an order of magnitude higher than the average Cvw of interactions found only in Y2H studies, which in turn was several orders of magnitude higher than the Cvw for pairs of proteins with no evidence of interaction. This finding implies that biologically relevant edges in our Y2H network have a distinct distribution of neighborhood cohesiveness that might be useful in separating true-positive from false-positive edges. This general pattern was observed for each specification of Cvw, so that high neighborhood cohesiveness appears to be independent of our choice of measures and a property of the true protein interaction network. The standard errors shown in Fig. 2 suggest that these differences are significant enough to justify testing the value of Cvw in adjusting our confidence in the veracity of individual edges.

Fig 2.

Fig 2.

Average mutual clustering coefficient (C vw) of interactions found in both conventional studies and Y2H studies (Conv + Y2H), those found in Y2H (Y2H only), and all pairs of proteins with neither conventional nor Y2H evidence supporting their interaction (No evid), for each of four definitions of C vw (see text for definitions). Each bar shows the average C vw minus one standard error and extends up to the average C vw plus one standard error.

Ranking Individual Interactions by Cvw

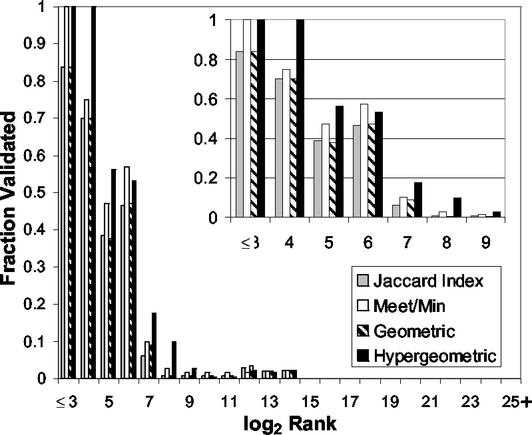
The four definitions of mutual clustering coefficient Cvw were used to rank protein–protein interactions observed in Y2H studies. Fig. 3 describes these results. The fraction of interactions validated by high-confidence conventional evidence is shown for groups of protein pairs ranked in decreasing order by Cvw.

Fig 3.

Fig 3.

Fraction validated by C vw. For each specification of C vw, all pairs of proteins were ranked by C vw and logarithmically binned. The first bin contains the 23 = 8 protein pairs with highest C vw, and subsequent bins contain protein pairs ranked from (2_i_−1 + 1) to 2_i_, inclusive, where i is the label of the bin. The height of each bin indicates the fraction of interactions validated by conventional evidence. In the case of tied ranks that span bins, the number of validated interactions within the tied rank is distributed appropriately. (Inset) A magnification of the bins containing the highest ranked protein pairs. See text for definitions.

If Cvw were unrelated to confidence, the expected fraction would be constant across all bins with height near zero (<10−4). The fraction of validated interactions dominates (is higher than) this line of expectation and is nearly monotonically decreasing for all specifications of Cvw, providing evidence that all specifications of Cvw contain information about the validity of edges in the graph. The hypergeometric curve generally dominates the others, indicating that for a given rank a larger fraction is validated. This finding justified our choice to proceed by using only the hypergeometric specification for Cvw.

Integrating Cvw with Direct Experimental Evidence

Frequently, there is other evidence that bears on confidence in a particular edge. Such integration of diverse evidence can be accomplished by using a Bayesian probabilistic framework. In this case we consider two types of evidence: observed Cvw and the presence of supporting Y2H evidence. Although we are considering two types of evidence, the framework we use can be used for any number of evidence types.

We want to compute the probability of an interaction being true given the experimental (Y2H) evidence and local network topology (Cvw). Because we do not know precisely which interactions are true, we use the existence of evidence from high-confidence conventional experiments as an indication of the truth of an interaction. Rather than compute the probability that two proteins truly interact, we instead estimate the probability that there is high-confidence evidence that the two proteins interact, having concealed the known status of conventional evidence for that pair of proteins. This probability should be correlated with the actual veracity of the protein–protein interaction, although it is likely an underestimate given the sparsity of high-confidence evidence currently available. For simplicity, we call this a posterior probability score of confidence in the interaction of two proteins.

We can compute this score (P+) by using Bayes' rule and the naïve assumption of independence between evidence types as follows:

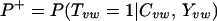
graphic file with name M6.gif

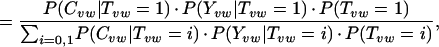
graphic file with name M7.gif

or, by using Bayes' rule to introduce the term P(Tvw = 1|Yvw) and some algebraic manipulation,

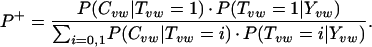
graphic file with name M8.gif

Here Tvw is an indicator variable for the truth of the interaction according to high-confidence evidence; Yvw is an indicator variable for the existence of experimental Y2H data; and Cvw represents the hypergeometric coefficient. The assumption of independence between evidence types was used to limit overfitting the data.

To estimate P(Cvw|Tvw), the likelihood of observing a particular value of Cvw for true or false edges, we “bin” edges by Cvw, initially binning Cvw in equal intervals and then merging bins containing <10 protein pairs. We then count the proportion of known true edges in each bin, using the existence of high-confidence conventional evidence as an indicator for true edges. P(Tvw|Yvw), the prior probability of the truth of an interaction given the Y2H evidence Yvw, is estimated by the proportion of all pairs of proteins with that value of Yvw that have been observed in an independent (higher reliability) conventional experiment. The resulting estimate of P(Tvw = 1|Yvw) is almost certainly an underestimate because many true interactions have not had confirmation by conventional methods.

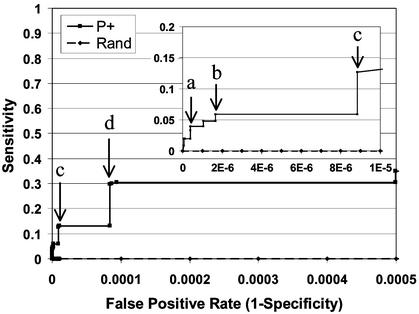
We used a leave-one-out approach to compute P+ for each pair of proteins, wherein the likelihoods and priors were obtained by using all edges except the edge of interest. An indication of our method's ability to discriminate true interactions from false ones is shown in the receiver operating characteristic (ROC) curve in Fig. 4. Fig. 4 graphically depicts tradeoffs between true-positive rates and false-positive rates for different possible thresholds in P+. A curve for a random classifier would be expected to extend from the origin with a slope of 1. Our method substantially dominates this expectation. For example, to achieve a false-positive rate (1-specificity) of 10−5, we have a sensitivity of 0.117, far above the expected sensitivity of 10−5. It is also worth noting that the set of edges exceeding the threshold indicated in Fig. 4 by point d is essentially that set of edges supported by Y2H data. The ROC curve illustrates the ability of our method to stratify interactions, i.e., to allow a researcher to trade lower sensitivity for a lower false-positive rate or vice versa.

Fig 4.

Fig 4.

ROC curve. The trade-off between sensitivity and specificity for different cutoffs of posterior probability score (P+) and the expected performance of a random classifier (Rand) is shown for useful ranges of false-positive rate (1-Specificity). (Inset) A magnification of the region of low false-positive rate most likely to be useful for inference. Note that the curve for a random classifier is not omitted, but lies very close to the _x_-axis. Annotated points are as follows: a, P+ cutoff of 0.999 yields 42 true-positives and seven false-positives; b, P+ cutoff of 0.983 yields 63 true-positives and 30 false-positives; c, P+ cutoff of 0.979 yields 135 true-positives and 159 false-positives; d, P+ cutoff of 0.14 yields 317 true-positives and 1,506 false-positives. False-positives are defined here as protein pairs not observed to interact by high-confidence experiment in our reference set. Many such protein pairs may, in fact, interact.

Predicting Protein–Protein Interactions Without Direct Experimental Evidence

The current experimentally derived protein interaction network is incomplete; that is, many true interactions have not yet been seen in any study (24, 42). Although our original motivation was to assess the quality of protein interactions found in high-throughput studies so that future inferences (such as protein function prediction) could be improved, we would also like to predict protein interactions for which we currently have no evidence. Pairs of proteins with high P+ score and no direct supporting evidence represent predicted interactions.

We view these predicted interactions as a further test of the validity of our method. Many real edges (interactions) were not in our training set because not all true edges have been found (or even tested) and because our training set is based on summaries of the literature that are unlikely to be complete. These edges have essentially been deleted from our training graph of protein–protein interactions, and we would like to learn the lower limit of how well our method can recover these deleted edges by more exhaustively searching the literature for our top predictions.

In Table 1 we show the pairs of proteins with P+ > 0.25 for which we had no evidence of interaction (Y2H or conventional). We examined these interactions further by using the Yeast Proteome Database. Taken together, there are four known physical interactions included in our 13 predictions (p < 10−7). This _p_ value was calculated by using a cumulative hypergeometric distribution with the expected probability of success according to a (conservatively high) estimate of 16 for the global average number of physical interactions per protein (42). The fraction of predictions verified by the literature is likely to be an underestimate of the fraction of predictions that are true, because not all interactions have been tested. Interestingly, four known genetic interactions were observed among the 13 predictions. This result is surprising, given the scarcity of known genetic interactions in yeast (<1,200 such interactions are known among >107 potential interactions) and suggests the possibility of predicting one interaction type from another. Furthermore, according to the Saccharomyces Genome Database (ref. 43; http://genome-www.stanford.edu/Saccharomyces/), in eight of the nine predicted interactions that did not involve a hypothetical ORF, the two proteins share a common molecular function or are known to be involved in the same biological pathway (all except Lsm1p–Lsm8p).

Table 1.

Predictions of protein–protein interactions

Protein 1 Protein 2 Cvw _P_+ Phys Gen
Fus3p (YBL016W) Kss1p (YGR040W) 35.7 1.00 X
Spa2p (YLL021W) Sph1p (YLR313C) 33.8 0.50 X
Ste7p (YDL159W) Ste11p (YLR362W) 32.0 0.50 X X
Mkk1p (YOR231W) Mkk2p (YPL140C) 31.6 0.50 X
Lsm1p (YJL124C) Lsm8p (YJR022W) 30.8 0.50 X
Rps28bp (YLR264W) Rps28ap (YOR167C) 28.9 0.50
Sno3p (YFL060C) Sno1p (YMR095C) 24.3 0.47
Sno3p (YFL060C) YMR322C 24.3 0.47
Sno1p (YMR095C) YMR322C 24.3 0.47
Ktr3p (YBR205W) YPL246C 22.9 0.47
Vam7p (YGL212W) YHR105W 22.8 0.47
Snz1p (YMR096W) Snz2p (YNL333W) 21.3 0.47 X
Snz3p (YFL059W) Snz1p (YMR096W) 21.3 0.47 X

Conclusion

We have described an approach that exploits the local topology of small-world networks to assess confidence in networks derived from data containing errors. Such an approach can be used to improve predictions of protein function that have previously relied on an “all-or-nothing” view of interactions (26, 27, 29–32) or to determine the proteins most likely to be members of particular protein complexes (S. Asthana and F.P.R., unpublished work). This approach is applicable to other small-world networks that are defined experimentally or by heuristic measures, e.g., measures of topic similarity between documents that are used in the field of information retrieval (44). The Bayesian framework we use here for combining local topology measures with Y2H evidence will allow integration of diverse measures of confidence, such as other informative measures of local topology (e.g., “interaction generality”) and other sources of interaction evidence (31, 32, 34).

The uncertain nature of experimentally or heuristically derived networks necessarily impacts network-derived inference. We expect that the measures of confidence in network edges described here will improve inference for protein interaction networks in particular and small-world networks in general.

Acknowledgments

We are grateful to S. Asthana, G. Berriz, D. Miller, and P. D'haeseleer for computational advice and helpful comments. We thank S. Asthana, J. Kleinberg, S. Komili, and S. Wong for critical reading of the manuscript. We gratefully acknowledge the helpful remarks of E. Harlow and the anonymous referees. This research was supported in part by an institutional grant from the Howard Hughes Medical Institute Biomedical Research Support Program for Medical Schools.

Abbreviations

This paper was submitted directly (Track II) to the PNAS office.

References