Efficient de novo assembly of highly heterozygous genomes from whole-genome shotgun short reads (original) (raw)
Abstract
Although many de novo genome assembly projects have recently been conducted using high-throughput sequencers, assembling highly heterozygous diploid genomes is a substantial challenge due to the increased complexity of the de Bruijn graph structure predominantly used. To address the increasing demand for sequencing of nonmodel and/or wild-type samples, in most cases inbred lines or fosmid-based hierarchical sequencing methods are used to overcome such problems. However, these methods are costly and time consuming, forfeiting the advantages of massive parallel sequencing. Here, we describe a novel de novo assembler, Platanus, that can effectively manage high-throughput data from heterozygous samples. Platanus assembles DNA fragments (reads) into contigs by constructing de Bruijn graphs with automatically optimized _k_-mer sizes followed by the scaffolding of contigs based on paired-end information. The complicated graph structures that result from the heterozygosity are simplified during not only the contig assembly step but also the scaffolding step. We evaluated the assembly results on eukaryotic samples with various levels of heterozygosity. Compared with other assemblers, Platanus yields assembly results that have a larger scaffold NG50 length without any accompanying loss of accuracy in both simulated and real data. In addition, Platanus recorded the largest scaffold NG50 values for two of the three low-heterozygosity species used in the de novo assembly contest, Assemblathon 2. Platanus therefore provides a novel and efficient approach for the assembly of gigabase-sized highly heterozygous genomes and is an attractive alternative to the existing assemblers designed for genomes of lower heterozygosity.
With the rapid progress in sequencing technologies, the throughput of sequencers has approached hundreds of billions of base pairs per run. Despite the drawbacks of short read lengths, a number of draft genomes have been constructed solely from these short-read data at an increasingly accelerated pace (Li et al. 2009b; Al-Dous et al. 2011; Jex et al. 2011; Kim et al. 2011; The Potato Genome Sequencing Consortium 2011; Murchison et al. 2012). The draft genome assemblies from high-throughput short reads primarily use de Bruijn-graph-based algorithms (Pevzner et al. 2001; Vinson et al. 2005; Zerbino and Birney 2008; Gnerre et al. 2011). During de novo assembly, the nodes of the de Bruijn graphs represent _k-_mers in the reads, and the edges represent (k − 1) overlaps between the _k_-mers. The graph can be simplified in a variety of ways; and as a consequence, assembled contigs or scaffolds are constructed from subgraphs lacking junctions. The most distinctive advantage of this approach is the computational efficiency that results from omitting the costly pairwise alignment steps that are required in traditional overlap-layout-consensus algorithms (Kurtz et al. 2004). The de Bruijn graph is constructed from information derived from precise _k_-mer overlaps; therefore, its calculation cost is relatively low. Although mismatches between _k_-mers caused by sequencing errors may occur, their distributions are expected to be random, such that sufficient sequence coverage would resolve the sequence error by removing the short, thin tips. Therefore, this approach is suitable for the assembly of a huge number of short reads from a massively parallel sequencer.
Despite its strong functionality, several obstacles remain in applying de Bruijn-graph-based assembly to the data from massively parallel sequencers. One of the primary difficulties to overcome is the existence of heterozygosity between diploid chromosomes (Vinson et al. 2005; Velasco et al. 2007; The Potato Genome Sequencing Consortium 2011; Star et al. 2011; Takeuchi et al. 2012; Zhang et al. 2012; Nystedt et al. 2013; You et al. 2013; Zheng et al. 2013). In cases in which a de Bruijn graph is built up from a diploid sample, different _k_-mers derived from the heterozygous regions corresponding to each homologous chromosome are created and used in the graph structures. As a result, junctions are created in the graph, which represent the borders between homozygous and heterozygous regions. This phenomenon leads to bubble structures in the graph, and most of the existing de Bruijn-graph-based assemblers attempt to simplify such structures by cutting the edge surrounding the junctions and splitting them into multiple straight graphs (Pevzner et al. 2001; Zerbino and Birney 2008; Li et al. 2010; Gnerre et al. 2011). To overcome this problem, many assemblers have developed a common solution by removing one of the similar sequences in a bubble structure with a pairwise alignment. This approach is effective for genome sequences with lower rates of nonstructural variations; however, the assembly of highly heterozygous organisms may encounter more serious problems caused by a high density of single nucleotide variants (SNVs) and structural variations (e.g., repeat sequences and coverage gaps). Algorithms to simply remove bubbles, which are used by the existing de Bruijn-graph-based assemblers, may not be sufficient to resolve these problems.
Thus, several advanced techniques have been used to sequence highly heterozygous genomes. The establishment of inbred lines is the most popular method for targeting highly heterozygous genomes, but this method is both time consuming and costly. Inconveniently, in some cases inbreeding methods can fail to eliminate high levels of heterozygosity; thus, these inbred samples can be unsuitable for use with existing whole-genome shotgun assembly methods (Zhang et al. 2012; You et al. 2013). In contrast, in the Potato Genome Project (The Potato Genome Sequencing Consortium 2011) a homozygous doubled-monoploid clone was first generated using classical tissue culture techniques and then sequenced. However, this method can also be fairly costly and is not always technically possible. Consequently, the fosmid-based hierarchical sequencing method has been increasingly used for sequencing highly heterozygous samples, such as oyster (Zhang et al. 2012), diamondback moth (You et al. 2013), and Norway spruce (Nystedt et al. 2013). Although these approaches have been successful in meeting the functional goals of each sequencing project, all are costly compared with a simple whole-genome shotgun sequencing strategy. Model organisms whose lineages have been maintained in laboratories have long been the main targets of genome sequencing. However, various wild-type organisms that may have highly heterozygous genomes are now targets; thus, a more efficient method to assemble such genomes is needed to further accelerate the genome sequencing of a wide range of organisms.
Here we describe a novel de novo sequence assembler, called Platanus, that can reconstruct genomic sequences of highly heterozygous diploids from massively parallel shotgun sequencing data. Similarly to other de Bruijn-graph-based assemblers, Platanus first constructs contigs from a de Bruijn graph and then builds up scaffolds from the contigs using paired-end or mate-pair libraries. However, various improvements (e.g., _k_-mer auto-extension) have been implemented to allow Platanus to efficiently handle giga-order and relatively repetitive genomes. In addition, Platanus efficiently captures heterozygous regions containing structural variations, repeats, and/or low-coverage sites; it can merge haplotypes during not only the contig assembly step but also the scaffolding step to overcome the challenge of heterozygosity. Key algorithms of Platanus and the results of the intensive evaluation of Platanas using both simulated data and real data, including those from highly heterozygous genomes and those used in the de novo assembly contest Assemblathon 2 (Bradnam et al. 2013), are described here.
Results
Algorithm overview
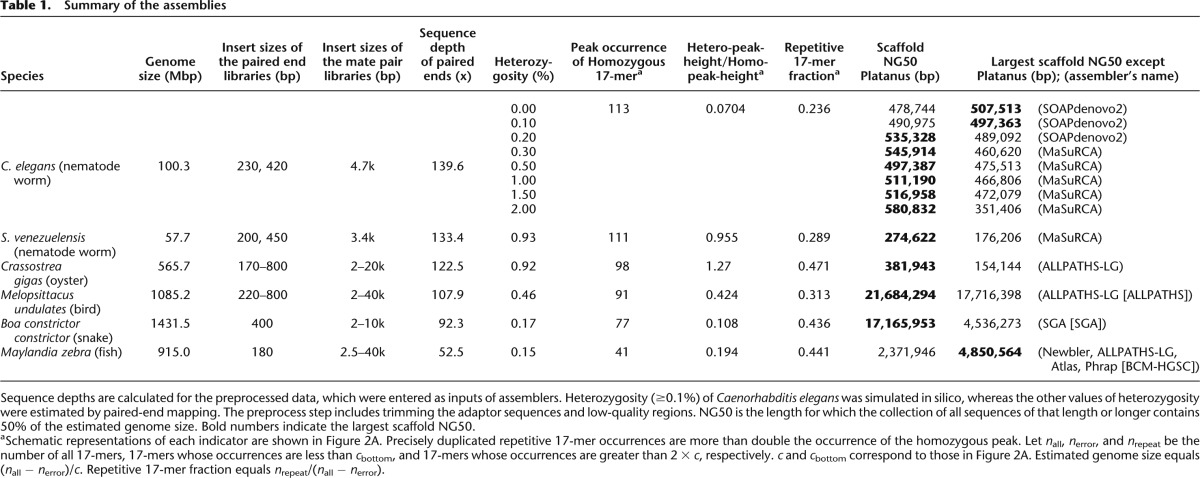
Platanus is divided into three subprograms—Contig-assembly (Fig. 1A), Scaffolding (Fig. 1B), and Gap-close (Fig. 1C)—similar to existing de Bruijn-graph-based assemblers (e.g., SOAPdenovo [Li et al. 2010] and Velvet [Zerbino and Birney 2008]) (see Supplemental Methods for details).
Figure 1.
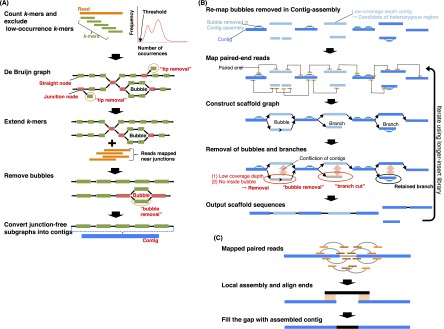
Schematic overview of the Platanus algorithm. (A) In Contig-assembly, a de Bruijn graph is constructed from the read set. Short branches caused by errors are removed by “tip removal.” Short repeats are resolved by _k_-mer extension, in which previous graphs and reads are mapped to nearby _k_-mers at the junctions. Finally, bubble structures caused by heterozygosity or errors are removed. Subgraphs without any junctions represent contigs. (B) In Scaffolding, links between contigs are detected using paired reads. The relationship between contigs is represented by the graph. Bubbles removed in Contig-assembly are remapped on contigs and utilized for mapping of paired-end reads and detection of heterozygous contigs. Heterozygous regions are removed as bubble or branch structures on the graph by the “bubble removal” or “branch cut” step. These simplification steps are characteristic of Platanus and especially effective for assembling complex heterozygous regions. (C) In Gap-close, paired reads are mapped on scaffolds, and reads mapped at nearby gaps are collected for each gap. If a contig is expected to cover the gap and is constructed from collected reads, the gap is closed by the contig.
Contig-assembly
The Contig-assembly subprogram constructs de Bruijn graphs from reads, modifies the graphs, and displays the output sequences of contigs from the graph. Initially, all _k_0-mers (default, _k_0 = 32) in the reads are counted, and the de Bruijn graph is constructed from the _k_0-mers. In this case, the _k_0-mer and (_k_0 – 1) overlaps correspond to the nodes and edges, respectively. Short branches with relatively low coverage are eliminated in the so-called “tip removal” step (Supplemental Fig. 3).
To simplify the graph, Platanus increases the value of k by the step size _k_step and iteratively reconstructs the graphs. _k_pre is the previous k of a certain reconstruction step. When a graph of _k_-mer is constructed based on a graph of _k_pre-mer (_k_pre < k), _k_-mers (nodes) within a distance of _k_step from the junctions are marked. Next, the _k_-mers are extracted from both the contigs of the _k_pre-mer graph and reads containing marked _k_pre-mers. In this way, repeats shorter than k can typically be resolved, and Platanus effectively excludes junctions caused by heterozygosity, short repeats, and errors. However, if k is too long, it will be difficult to ensure sufficient coverage distinguishing correct _k_-mers from _k_-mers derived from sequence errors. Using multiple _k_-mer sizes, Platanus uses the advantages of each k. Platanus also has unique functions to automatically determine both the maximum _k_-mer size and the coverage cutoff (Supplemental Figs. 4–7). This function can efficiently omit the need for manual optimization of its parameters.
Bubble removal in Contig-assembly
After the reconstruction and tip removal of the _k_max-mer graph, the “bubbles” in the graph are removed. Bubble structures are caused by both the heterozygosity of the diploid samples and errors (Supplemental Fig. 8). A bubble is defined as a set of two straight nodes and two junction nodes at which the straight nodes are connected to the same junction in both directions. Platanus requires the following two conditions to split the straight paths surrounding a bubble structure: (1) a high identity between the two straight nodes; and (2) a low coverage depth of _k_-mers in the two straight nodes. The second condition is helpful to distinguish heterozygous regions from repetitive regions. The removed bubble structures are saved and utilized in the Scaffolding step. Lastly, as a result of Contig-assembly, the junction-free subgraphs constructed by these procedures correspond to the contigs.
Scaffolding
In the Scaffolding step, the orders of the contigs are determined using paired-end (mate-pair) information. Initially, Platanus maps reads to contigs based on a hash table (keys are unique _k_-mers on contigs; values are positions). Importantly, the bubbles removed in Contig-assembly are also considered in this step, as they are reallocated to the contigs (Supplemental Fig. 11) prior to read mapping, making it possible to detect the heterozygous contigs. The mapping method of Platanus is designed to maximize the number of accurately mapped paired-ends in highly heterozygous genomes. The mapped positions of the reads on bubbles are converted into corresponding contig positions (Supplemental Fig. 11). The insert size of each library is estimated from pairs mapped to the same contig, and links between the contigs are detected using pairs that are situated in different contigs. Links between contigs are represented as a graph in which the contigs and links correspond to the nodes and edges, respectively. In this case, two contigs are considered to be linked if the number of read pairs bridging the contigs exceeds the threshold n. The contigs are finally combined into scaffolds to the extent that conflicts occur. Scaffolding then continues using each library, ranging from short- to long-insert libraries.
“Bubble removal” and “branch cut” in scaffold graph
The procedures for the removal of bubbles (“bubble removal”) and short branches (“branch cut”) are applied in Scaffolding (Supplemental Figs. 15, 16). Compared with other assemblers, these graph simplification steps in Scaffolding are unique to Platanus and are especially effective in assembling complex heterozygous regions. In these steps, bubbles and branches are primarily derived from highly heterozygous regions (i.e., regions with high SNV densities and/or structural variations), and Platanus constructs each haplotype as separate contigs. Platanus recognizes bubbles or branches derived from the heterozygous regions based on the following information: (1) coverage depth; (2) identity with other contigs; and (3) bubble structures constructed in Contig-assembly. The first and second conditions are similar to the conditions of bubble removal in Contig-assembly. The third condition means that Platanus assumes that the target genome is diploid and therefore does not allow for triple or higher-ordered heterozygote alleles. In the following section describing the assembly of the real data from heterozygous samples, we provide an example of a highly heterozygous region assembled by these algorithms.
Gap-close
Finally, in the Gap-close step, reads are mapped on scaffolds to collect those covering each gap. Each set of reads is assembled locally, and the resulting contigs are used to close the gaps (Supplemental Figs. 18, 19). Both the de Bruijn graphs from multiple _k-_mer sizes and the overlap-layout-consensus algorithm are used in the Gap-close step.
Benchmarks overview
A summary of the assemblies of all species targeted in this study is provided in Table 1. In all benchmarks, the contiguity of the assembly result was measured using the NG50 value, which represents the length at which the collection of all sequences of that length or longer contains 50% of the genome size. NG50 values were calculated for both the scaffolds and contigs. According to the GAGE study (Salzberg et al. 2012), we define a gap as Ns ≥ 3 bp, and contigs are derived from splitting the scaffolds by defined gaps. For species for which reference genomes have not been sequenced, we performed assembly validation using fosmids or BACs. In this validation, we first constructed one-to-one relationships between the fosmids/BACs and the scaffolds and then summed the alignment lengths. The resulting sum is called the “top-hits-length” and is used as the validation score (see Methods for details). In addition, we counted the number of “contained” fosmids/BACs, 90% of the lengths of which were at least covered by one scaffold. The other evaluation criteria are described in each section of Results.
Table 1.
Summary of the assemblies
First, we generated simulated heterozygous data from the Illumina HiSeq 2000 sequence reads for the nematode (Caenorhabditis elegans) and investigated the effect of heterozygosity on the de novo genome assembly. Second, we applied the assemblers to the real-world data from a heterozygous nematode worm (Strongyloides venezuelensis). Third, we performed a test using the data from the oyster (Crassostrea gigas) genome (Zhang et al. 2012), which is heterozygous, large, and highly repetitive. Finally, we assembled the data of a bird (Melopsittacus undulatus), a snake (Boa constrictor constrictor), and a fish (Maylandia zebra), which were produced for Assemblathon 2.
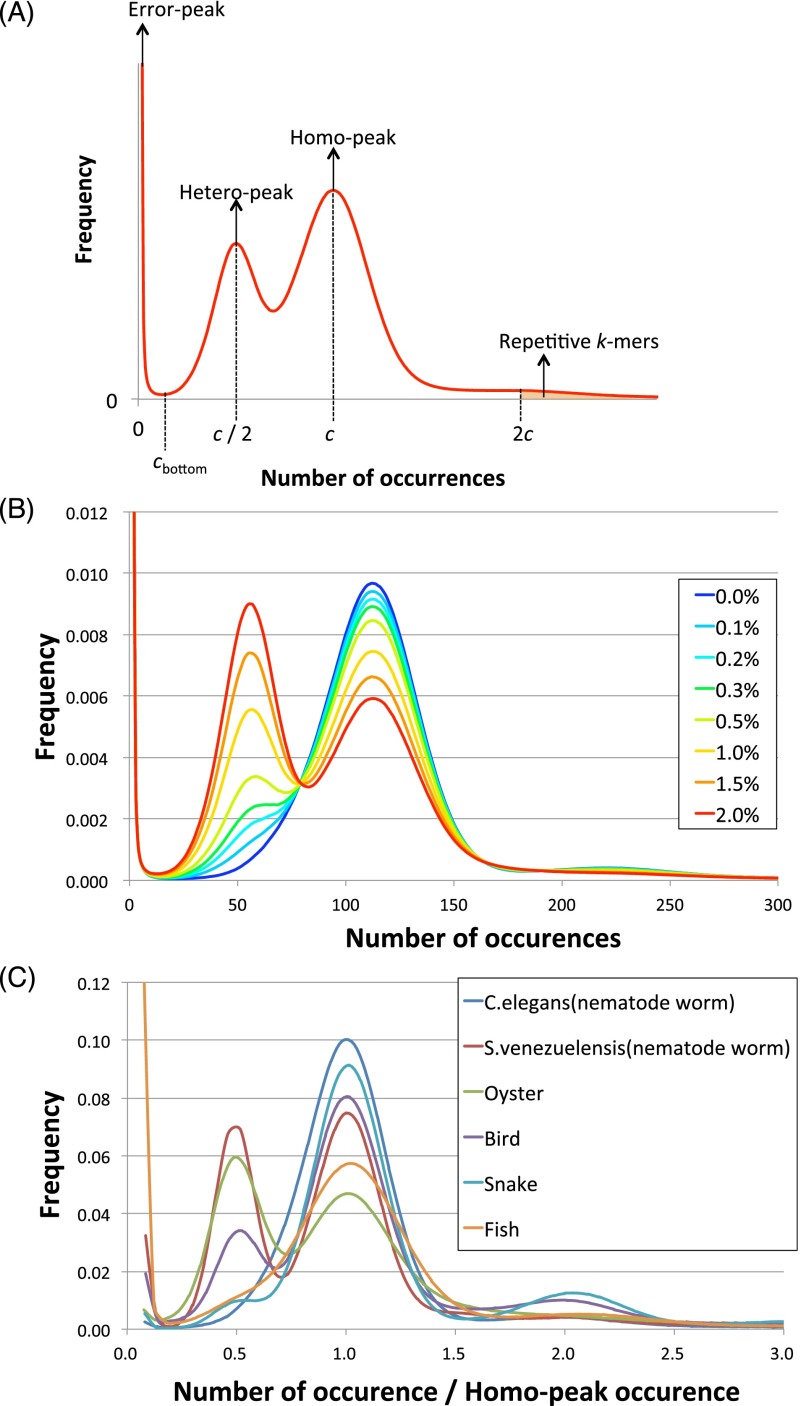
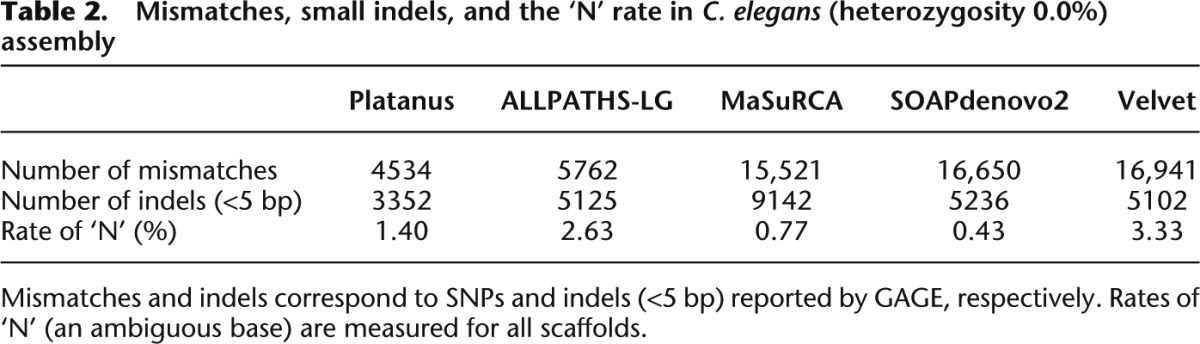
To investigate the characteristics of each genome, we performed 17-mer frequency analysis using paired-end reads. In this analysis, the level of heterozygosity is represented by the height difference of two peaks, with left- and right-hand peaks denoting heterozygous and homozygous regions, respectively (Fig. 2A). Essentially, the greater the degree of heterozygosity, the greater the size of the left-hand peak; thus, our data demonstrate that S. venezuelensis and the oyster are highly heterozygous species compared with other organisms tested here (Fig. 2B,C; Table 1). In addition, the genome size of each species and proportions of precisely duplicated repetitive regions were estimated (Table 1). In short, we observed that (1) the genome sizes and repeat contents of nematode worms are low; (2) the oyster genome is the most repetitive among those investigated; and (3) the three Assemblathon 2 samples have relatively large genome sizes, ranging from 0.9 to 1.5 Gbp, and low or intermediate levels of heterozygosity.
Figure 2.
Distribution of the number of 17-mer occurrences. (A) Schematic model of the distribution of _k_-mer occurrences. This distribution is related to that shown in Table 1. (B) Simulated heterozygous data from C. elegans. (C) Distributions of normalized 17-mer occurrences for all species.
Assemblers for comparisons
We compared Platanus (version 1.2.1) with other major assemblers, including ALLPATHS-LG (Gnerre et al. 2011) (version 44837), MaSuRCA (Zimin et al. 2013) (version 2.0.4), Velvet (Zerbino and Birney 2008) (version 1.2.07), and SOAPdenovo2 (Luo et al. 2012) (version 2.04). When the assembly test of human chromosome 14 was performed in the GAGE study (Salzberg et al. 2012), these assemblers recorded the largest scaffold NG50 values and were ranked first through fourth, respectively.
ALLPATHS-LG, Velvet, and SOAPdenovo2 all use de Bruijn-graph-based algorithms. Velvet was first developed for the assembly of small genomes, whereas ALLPATHS-LG and SOAPdenovo2 were customized for large eukaryotic genomes. In the benchmarks, we optimized SOAPdenovo2 and Velvet for _k-_mer length, the most important parameter. ALLPATHS-LG was implemented with a default _k-_mer length of 96 in accordance with the manual instructions. We also optimized other options of these assemblers relating to the resolution of the heterozygous regions. SOAPdenovo2 possesses a parameter termed “mergeLevel” (-M) that was tested in two ways: the “-M 1” (default) and “-M 3” modes. ALLPATHS-LG was run in the diploid mode (see Supplemental Methods for details).
MaSuRCA was developed based on the Celera assembler (Myers et al. 2000) and uses an overlap-layout-consensus approach. Although this approach is time consuming, it can overcome the repeat sequences, errors, low-coverage regions, and small structural differences caused by heterozygosity. Certain improvements in MaSuRCA have been implemented to handle high-throughput data from such platforms as Illumina. MaSuRCA was run with the default settings except that the option related to memory usage was changed.
Simulations of heterozygosity using C. elegans data
We performed the assembly benchmark against the simulated heterozygous data. We resequenced the genomic DNA of the nematode C. elegans (with a genome size of 100 Mbp), using Illumina HiSeq 2000. Next, the data were processed in silico, and simulated Illumina read sets were generated with various levels of heterozygosity (0.1%–2.0%) (see Methods). By mapping original paired-end reads onto the reference genome (The C. elegans Sequencing Consortium 1998), the raw heterozygosity of C. elegans was estimated to be 1.85 × 10−3% (see Methods). Therefore, the effects of the intrinsic heterozygosity were expected to be low enough to use these simulated data sets to investigate how different levels of heterozygosity affect the assembly.
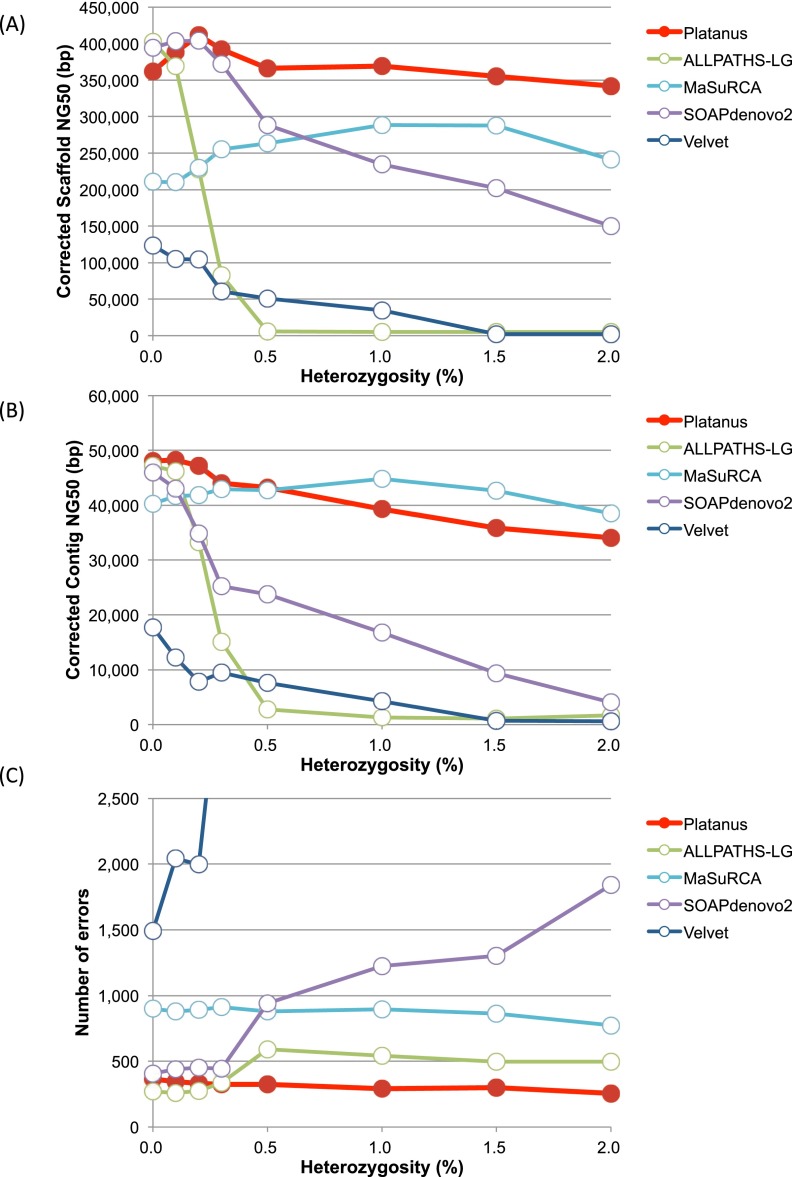
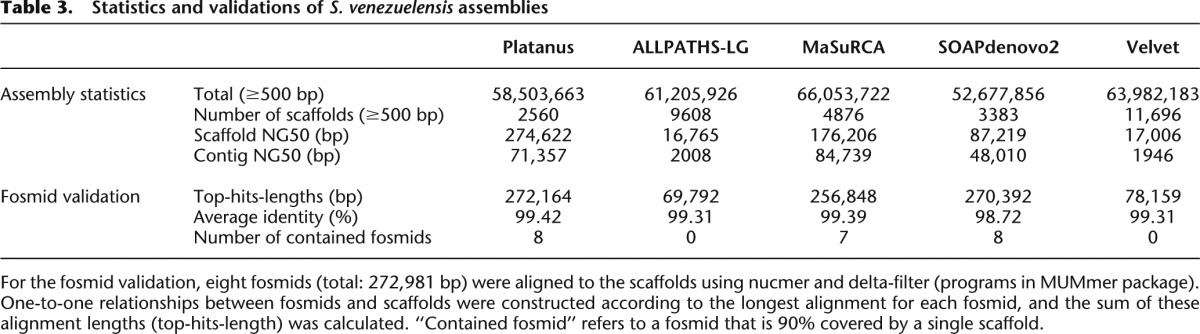
In Figure 3, Supplemental Figure 22, and Supplemental Table 2, the corrected scaffold NG50, the corrected contig NG50, the numbers of errors, and other statistical information of scaffolds (≥500 bp) obtained by each assembler tested are shown. The corrected scaffold NG50 was computed after breaking assembled sequences at each misassembled (structural difference) point detected by the GAGE benchmark program by comparison with the reference genome. According to these benchmarks, heterozygosity has a strong impact on both the corrected scaffold and the contig NG50 of the existing de Bruijn-graph-based assemblers (SOAPdenovo2, ALLPATHS-LG, and Velvet) (Fig. 3A,B). These values sharply decreased in the interval of 0.0%–0.5% compared to the decrease in the interval 0.5%–2.0%. We therefore hypothesize that 0.5% marks the critical point of heterozygosity that determines the seriousness of the effects on these three de Bruijn-graph-based assemblers. For SOAPdenovo2 and Velvet, the numbers of identified errors also increased relative to the level of heterozygosity (Fig. 3C; Supplemental Table 2F). In contrast, only a slight reduction in the corrected scaffold NG50 values from Platanus was observed. No significant reduction was observed in the corrected scaffold NG50 values from MaSuRCA, but the number of errors was approximately twofold greater in MaSuRCA than in Platanus for all heterozygosity levels.
Figure 3.
Results of the benchmarks of heterozygosity simulations (C. elegans). (A) Corrected scaffold-NG50 calculated by GAGE. (B) Corrected contig-NG50. (C) Number of errors reported by GAGE. Errors are defined as inversion, relocation, or translocation.
When the heterozygosity values were 0.0% and 2.0%, the scaffold NG50 values of the initial Platanus contigs (the outputs of Contig-assembly step) were 12,345 bp and 3840 bp, respectively, illustrating that the Contig-assembly step of Platanus was strongly influenced by the heterozygosity. Indeed, the bubble-removal algorithms in the de Bruijn graphs have been implemented in other assemblers; thus, it would appear that Platanus does not possess an advantage in this step. However, the NG50 values of the final scaffolds of Platanus were significantly greater than those from the other assemblers (478,744 bp [heterozygosity: 0.0%] and 580,832 bp [heterozygosity: 2.0%]), indicating that Platanus was able to effectively overcome the high heterozygosity in the scaffolding step.
Next, we investigated the per-base accuracy of the scaffolds according to the numbers of mismatches (SNPs) and indels (<5 bp) reported in the GAGE evaluations of the C. elegans data in the absence of simulated heterozygosity (Table 2). The raw heterozygosity of the C. elegans genome was estimated to be 1.85 × 10−3%, and the expected number of variants was estimated to be less than 1850. The higher-than-predicted numbers obtained are likely due to errors in the assemblies. For both the numbers of mismatches and indels, the number generated by Platanus displayed the lowest value (thereby indicating the fewest errors), from which we infer that the scaffolds had the best per-base accuracy. There may be a tradeoff between the per-base accuracy and the ‘N’ rate because the number of mismatches and indels is reduced when an assembler has the tendency to report less confidential regions as ‘N’s. The ‘N’ rate of Platanus was the middle value (third) among the five assemblers assessed, and Platanus did not decrease the number of mismatches and indels at the cost of its ‘N’ rate. In contrast, MaSuRCA and SOAPdenovo2 recorded lower ‘N’ rates but considerably higher numbers of mismatches (more than three times the number reported by Platanus). In contrast to the scaffold NG50 values, the contig NG50 values of Platanus were not much greater than those of the other assemblers. However, Platanus produced the fewest mismatches and small indels, implying that it constructs highly accurate contigs using a relatively conservative approach in contig assembly.
Table 2.
Mismatches, small indels, and the ‘N’ rate in C. elegans (heterozygosity 0.0%) assembly
Assembly of real data from the highly heterozygous nematode S. venezuelensis
The heterozygosity of S. venezuelensis was estimated to be 0.927% by mapping paired-end reads on fosmid sequences. According to 17-mer frequency analysis (Table 1), the number of precisely duplicated repeats in S. venezuelensis (0.289) is comparable to that of C. elegans (0.236). This similarity indicates that S. venezuelensis is useful for investigating the effect of real heterozygosity on de novo assemblies.
We measured scaffold NG50 values using the estimated genome size of 57.7 Mbp derived from the 17-mer analysis (Table 3). Platanus produced the largest scaffold NG50, confirming its effectiveness for real heterozygous data. Compared with the 1.0%-heterozygous C. elegans data (Fig. 3; Supplemental Table 2), the obtained scaffold-NG50/Platanus-scaffold-NG50 ratios were smaller for all other assemblers (Supplemental Table 5). This observation implies that true heterozygous data consist of complex variations that were not simulated in the C. elegans tests and that Platanus was able to successfully resolve such variants. We provide an example of complex variant resolution in the following paragraph. Next, we performed assembly validation by aligning eight fosmid sequences (a total of 272,981 bp) to the scaffolds (Table 3). Platanus displayed the largest top-hits-lengths, and all fosmids were contained within the relevant scaffolds, confirming that no large misassembly occurred at least in these fosmid regions. If there is an inaccurate sequence or a gap in regions covered by fosmids, a top-hits-lengths value may decrease because an unaligned region appears. Although fosmids covered the genome partially, this result implies that Platanus’ scaffolds possess higher accuracy and/or fewer gaps compared with those produced by the other assemblers.
Table 3.
Statistics and validations of S. venezuelensis assemblies
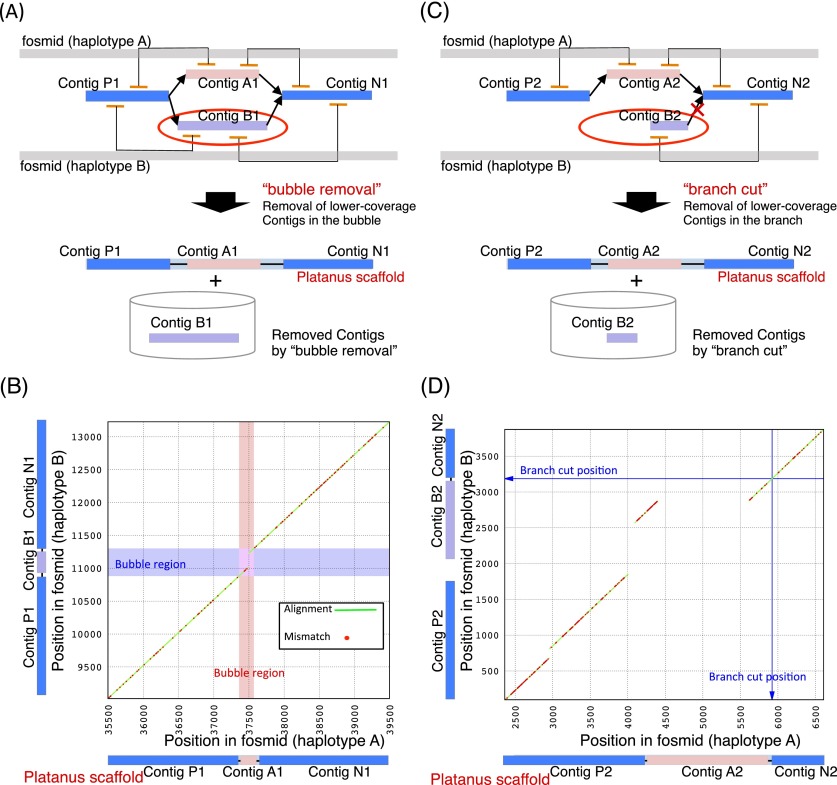
We further performed a fine evaluation of Platanus’ scaffolds using two fosmid pairs, each representing the two haplotypes at a single locus. As noted in the section describing the algorithm overview, we anticipated that Platanus predominantly extends the assembly using a characteristic simplification of the scaffold graph. In the Platanus Scaffolding step, the bubble and branch structures from the heterozygous regions were removed by “bubble removal” and “branch cut” functions, respectively. Platanus should also execute these procedures in the two regions covered by the fosmid pairs.
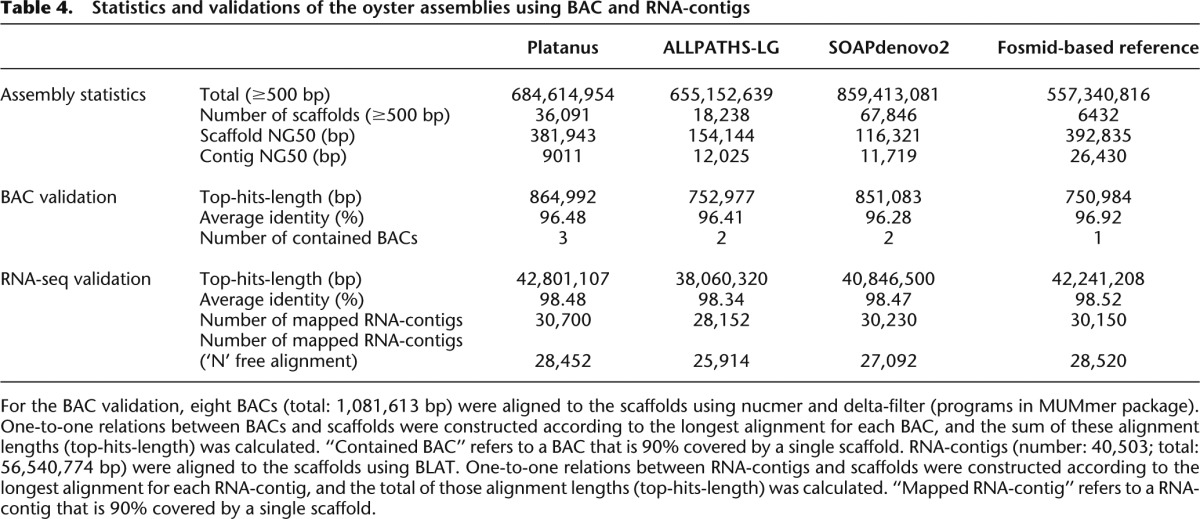
First, we provide an example of “bubble removal” in Scaffolding (Fig. 4A,B) using a dot plot analysis within the nucmer alignment program. For the alignment of two fosmids covering the region where the bubble was removed (Fig. 4B), a 209-bp indel was present with 2.09% heterozygosity level. The scaffold generated by Platanus (ContigP1–ContigA1–ContigN1) was correctly aligned to one of the fosmids, corresponding to the diagonal line shown in Supplemental Figure 24A. We replaced the bubble region contig (ContigA1) in the scaffold with the removed contig sequence (ContigB1), and the resulting scaffold (ContigP1–ContigB1–ContigN1) was aligned to the fosmid of another haplotype with no gap (Supplemental Fig. 24B). These results indicate that Platanus correctly resolved the region containing a relatively large indel, many SNVs, and several small indels that existed simultaneously using the bubble-removal routine. Second, we provide an example of “branch cut” (Fig. 4C,D). As in the “bubble removal” example, we aligned the two fosmids covering the position of the branch cut (Fig. 4D). This algorithm was designed to resolve heterozygous regions in which the bubble structures do not appear in graphs due to complex variants, repeats, or low coverage depth. Three indels were apparent, with sizes of 126 bp, 715 bp, and 1206 bp and with a high heterozygosity (1.93%). The scaffold sequence (ContigP2–ContigA2–ContigN2) could be aligned to one fosmid of the pair (Supplemental Fig. 25), and the removed branch (size: 1217 bp; ContigB2) matched the other fosmid, confirming the correctness of Platanus’ resolution. Platanus may derive its advantage by using the improved scaffolding algorithms typified by the preceding examples to assemble such complex regions, resulting in higher scaffold NG50 numbers in the simulated data from C. elegans, in which only SNVs and small indels were simulated.
Figure 4.
Example of a heterozygous region resolved by “bubble removal” and “branch cut.” (A) Schematic model of “bubble removal” in Platanus scaffolding. (B) Alignment dot plot between two fosmids. Green lines and red dots indicate alignments and mismatches, respectively. Red and blue boxes indicate the regions corresponding to the bubbles. (C) Schematic model of “branch cut” in Platanus scaffolding. (D) Alignment dot plot between two fosmids. Green lines and red dots indicate alignments and mismatches, respectively. The blue arrow indicates the position corresponding to the root of the branch.
Because the fosmids only partially covered the genome, we also investigated the distribution of heterozygosity across the entire genome. As a complete or draft genome of S. venezuelensis has not yet been published, we used the Platanus’ assembly, which demonstrated the largest scaffold NG50 in the reference sequences. SNVs and small indels on the scaffolds were detected by mapping paired-end reads (see Methods), and heterozygosity was calculated for every 1-kbp nonoverlapping window. The average heterozygosity was 0.950%, and the resulting distribution of heterozygosity is shown in Supplemental Figure 26. Compared with the 1.0%-heterozygous C. elegans data, the S. venezuelensis data had an uneven distribution of heterozygosity. This uneven distribution may be another cause of the observed different statistics between the real data and the simulated data. The fact that the proportion of low heterozygosity regions is greater in S. venezuelensis than in the 1.0%-heterozygous C. elegans might make assemblies easier, but small scaffold NG50 rates were actually produced by other assemblers. To investigate the reason for this observation, we measured the intervals of 1-kbp windows with high levels of heterozygosity (≥1.0%), and our results suggest that the average length of these intervals was not very long (1930 bp). Consequently, regions of low heterozygosity were bordered by highly heterozygous regions, creating a mosaic structure of both high and low heterozygosity. This mosaic structure may have contributed to the small scaffold NG50 produced by the other assemblers.
Real data from the highly heterozygous and repetitive oyster genome
We input whole-genome shotgun data sequenced in the Oyster Genome Project into the assemblers. The heterozygosity of the oyster genome was estimated to be 0.923% by mapping paired-ends to eight BACs a total of 1,081,613 bp in length. The 17-mer frequency analysis (Table 1) indicated that both the genome size and repeat content of the oyster genome are larger than those of the nematodes. In addition to being highly heterozygous, the oyster is also a suitable model organism for testing the scalabilities and performances of the repetitive sequences. Similar to the process for S. venezuelensis, the scaffold NG50 values for the oyster were measured based on the estimated genome size, and validations were performed using the eight BAC sequences (Table 4). For the scaffold NG50 and BAC validation, Platanus’ scaffold NG50 and top-hits-length exceeded those of the other assemblers. Velvet and MaSuRCA crashed during the execution of the runs (RAM: 512 GB; CPU: 32). Velvet is not scalable for use with large eukaryotic genomes in the GAGE benchmark (Bombus impatiens). MaSuRCA ran for more than 1 mo in real time (using 32 threads) but stopped as a result of an error. Although this assembler is customized for Illumina data, this result is indicative of the time-consuming nature of the overlap-layout-consensus algorithm, which is unsuitable for organisms with a large-sized genome such as the oyster. We also compared the assembling result in this study with sequences assembled by the fosmid-based hierarchal methods produced in the Oyster Genome Project. Remarkably, the values from Platanus were comparable to these fosmid-based reference sequences.
Table 4.
Statistics and validations of the oyster assemblies using BAC and RNA-contigs
We also investigated whether Platanus’ scaffolds could substitute reference sequences during post-assembly analysis. Thus, we investigated the coverage of the transcript sequences. Reads from all the RNA-seq data in the Oyster Genome Project were assembled into contigs (RNA-contigs) using Trinity (Supplemental Methods; Grabherr et al. 2011). We then mapped RNA-contigs whose lengths exceeded 500 bp. Using BLAT (Kent 2002), “top-hits-lengths” were calculated in the same manner as in the BAC validation, and the number of mapped RNA contigs with alignments of the top hit showed ≥90% coverage and ≥90% identity (Table 4). The average identities of top-hit alignments were also calculated. The top-hits-length, mapped RNA-contig numbers, and average identities produced by Platanus were the best of the three whole-genome-based assembly results and were comparable to the results from the fosmid-based reference sequence. These findings demonstrate that Platanus’ assembly results are sufficient for practical usage in gene annotation for highly heterozygous genomes. In addition, we counted the number of mapped RNA-seq contigs without any ‘N’-bases in the alignment between the RNA-contigs and assembled genome sequences. The result is shown in Table 4 as the “Number of mapped RNA-contigs (‘N’ free alignment).” Even in this benchmark, Platanus showed results that were nearly identical to the fosmid-based results, although its contig NG50 was the smallest. This result suggests that Platanus’ contigs are sufficient for gene annotation.
Assembly of the Assemblathon 2 data
Finally, we applied Platanus to larger genomes and compared its assembly with additional methods to confirm its versatility. We demonstrated the assemblies of three species (bird, snake, and fish) during Assemblathon 2. In this contest, sequence reads were opened and each team freely chose their methods, including the preprocess steps, assemblers, and machines. By mapping the reads to genomic sequences (bird and snake: fosmids; fish: Platanus’ scaffolds), we estimated the heterozygosity of the bird, snake, and fish genomes to be 0.463%, 0.165%, and 0.147%, respectively. Consequently, these species are not suitable for testing the assembly of highly heterozygous (>0.5%) samples. Nevertheless, the Assemblathon 2 benchmark has several benefits. First, the assembly protocols of other teams were assumed to be highly optimized. For many teams, the participants were themselves the authors of the assembly tools, decreasing the likelihood that their optimization methods would be insufficient. Second, these three species all have relatively large genome sizes (0.9–1.4 Gbp in length), making it possible to test Platanus’ capacity to assemble giga-order-size genomes.
A summary of the results for this section is provided in Table 1, and detailed results are provided in Supplemental Table 7. For the bird and snake, fosmid data (a total of 1,035,129 bp and 378,186 bp, respectively) are available, and we validated the resulting assemblies in the same manner as for the S. venezuelensis and oyster assemblies. Platanus recorded the highest values for both the scaffold NG50 (bird: 21,684,294 bp; snake: 17,165,953 bp) and “top-hits-length” of fosmid validation. For the snake assembly in particular, the scaffold NG50 of Platanus was unexpectedly large, more than three times the size of the second largest value. According to the 17-mer frequency analysis (Fig. 2; Table 1), the snake genome is rich in repetitive 17-mers and has sufficient coverage depth compared to that of the fish genome. In the fish assemblies, the scaffold NG50 of Platanus (2,371,946 bp) was the fifth largest of 17 entries. When limited to a single program’s results, the scaffold NG50 of Platanus was second, behind that of ALLPATHS-LG. One important feature of the fish data is the low coverage depth (52.5×) of their paired-end reads, which most likely reduced Platanus’ scaffold NG50 value.
Time and peak memory usage
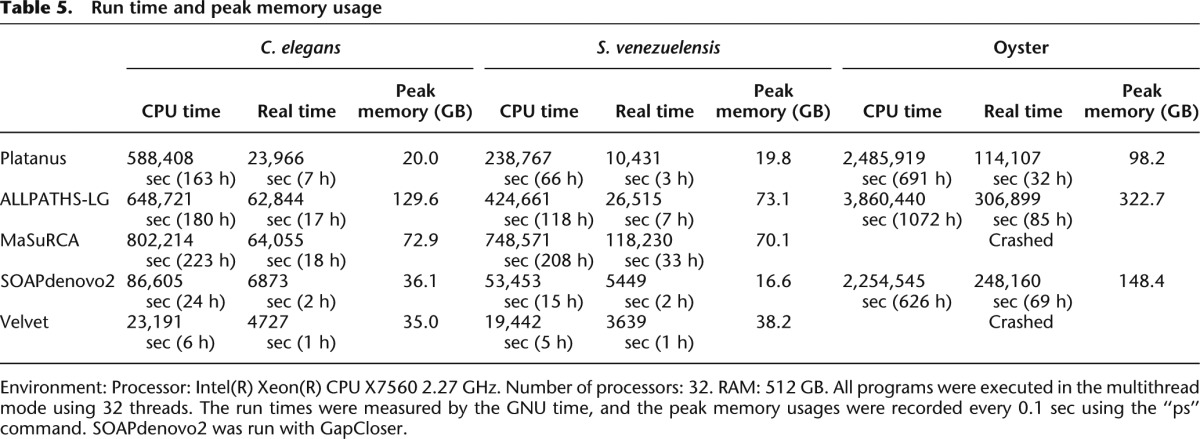
The execution times (real and CPU) and peak memory usages are shown in Table 5. The execution environment is conducted with 32 threads of an Intel Xeon 2.27 GHz CPU with 512 GB RAM. SOAPdenovo2 exhibited the fastest performance in real time for nematodes, whereas Platanus exhibited the fastest performance for the oyster, which has a larger genome size and a greater number of repeats. Notably, MaSuRCA, which is based on the overlap-layout-consensus algorithm, had a considerably longer run time than the de Bruijn-graph-based assemblers. Although SOAPdenovo2 and Velvet were optimized for certain parameters, their execution times did not include the iteration for optimizations and therefore consumed more time for the benchmarks.
Table 5.
Run time and peak memory usage
Discussion
Although heterozygosity poses a challenge to genome assembly, its effects on genome assembly have never been systematically evaluated. To our knowledge, our simulation of heterozygosity (0.0%–2.0%) using C. elegans data is the first attempt to address this issue. All of the de Bruijn-graph-based assemblers tested, except for Platanus, showed dramatically reduced scaffold NG50 values when the heterozygosity was >0.5%. MaSuRCA, the overlap-layout-consensus–based assembler, did not undergo a sharp decrease in its scaffold NG50 in our simulation. However, in assembling real data from various organisms, Platanus was superior, as shown by its scaffold NG50 values that were much larger than those from MaSuRCA, possibly due to the presence of more complex variants in the actual data set. Furthermore, MaSuRCA required excessive execution time for assembly; for example, more than 1 mo in real time (using 32 threads) was required to assemble the oyster data. The oyster genome is ∼0.5 Gbp, and de Bruijn-graph-based methods, such as Platanus, can efficiently handle the data from much larger genomes. ALLPATHS-LG exhibited the best performance with overlapping paired-ends (insert size: 180 bp) and a long-jump library (insert size: ∼10 kbp), which is consistent with the results of the present study. ALLPATHS-LG’s scaffold NG50 was relatively large in the oyster test, for which library insert sizes ranged from 180 to 20 kbp; however, its scaffold NG50 was inferior to that of Platanus. An additional advantage of Platanus is that it does not require the manual optimization of any parameters. In fact, Platanus was executed using the default parameters in all tests performed in this study. In contrast, we needed to iteratively execute SOAPdenovo2 and Velvet with various _k-_mer sizes (21–91), as both substantially depend on this parameter. For example, dependent on the _k-_mer sizes used, SOAPdenovo2’s scaffold NG50 for S. venezuelensis varied from 4479 to 87,219 bp.
Platanus merges haplotype sequences into a single contig/scaffold, resulting in mosaic sequences of both haplotypes. By adopting this approach, Platanus can achieve remarkably longer scaffolds. An alternative strategy for addressing highly heterozygous data involves the separate construction of each haplotype (haplotype assembly method), which has been applied to Ciona intestinalis (Kim et al. 2007) (heterozygosity: 1.2%; scaffold N50: 37.9 kbp) and Ciona savignyi (Vinson et al. 2005; Small et al. 2007) (heterozygosity: 4.6%; scaffold N50: 496 kbp) (note that both projects used the Sanger sequencing method). These results suggest that longer haplotype sequences are constructed for higher variant densities. Why should heterozygosity be high for the construction of longer haplotype assemblies? The explanation is simple: To construct a haplotype assembly, the linkage information between neighboring SNVs or indels should be resolved. This linkage information requires neighboring SNVs or indels to be almost covered with one read or pair of reads by one DNA fragment. If the linkage information is broken by a long nonheterozygous region, the haplotype assembly will be disrupted at that point. As described for the assembly of the S. venezuelensis genome, the regions in which no sequence variation was observed within a 1-kbp window encompass 11.8% of the entire genome. This observation suggests that if haplotype assembly is adapted to S. venezuelensis, the results will be very poor. The C. savignyi haplotype assembly may represent a rather exceptional case of a successful run of a genome with extremely high heterozygosity and the use of long Sanger reads. We thus propose that the merging method is suitable for the assembly of most heterozygous samples.
Although Illumina reads are often described as “short reads,” they have advantages regarding their throughput and accuracy. In the bird assembly for Assemblathon 2, Platanus’ scaffold NG50 was the highest, exceeding those of other strategies that utilize other types of sequence data (Roche 454 and/or PacBio). It should be noted that the conditions are not equivalent regarding the cost and coverage depths for each data type, and thus, it cannot be conclusively stated that Illumina data are the most suitable for de novo assembly. Therefore, whole-genome shotgun short-read (Illumina) data remain a strong candidate for the strategy of de novo assembly, particularly for the assembly of large and highly heterozygous genomes. In this study, all data except the fish have >90× sequence coverage depths of paired-ends reads (Table 1). There is the possibility that each assembler has optimal coverage depth, and we performed the benchmark test using reduced amount of sequence data for C. elegans (heterozygosity: 0%, 1%, 2%) (Supplemental Fig. 28; Supplemental Table 14). In summary, Platanus indicated the largest corrected scaffold NG50 for heterozygous data whose coverage depth >100× but was sensitive to the downsampling effect. This result corresponds to the small scaffold NG50 of Platanus in the test of the fish. Consequently, the optimal coverage depth for Platanus is probably >100×, which may be suitable for the increasing throughput of sequencers.
Fosmid-based assembly has recently been introduced as an effective and economic method for highly heterozygous genomes (Zhang et al. 2012). However, this method may require many more sequence reads compared to the whole-genome shotgun strategy. For instance, if the fosmid library is constructed to have a depth of 10× against the genome size and each fosmid is sequenced to a depth of 100×, the total required reads may be as much as 1000× the genome size. In the Diamondback Moth Genome Project (You et al. 2013) and Oyster Genome Project (Zhang et al. 2012), paired-end reads with a coverage depth of 2170× (total reads: 855 Gbp) and 690× (total reads: 390 Gbp) against the genome size were produced to assemble the fosmids, respectively. In addition, whole-genome shotgun reads were separately produced, and these data were also used in those projects. Therefore, if highly heterozygous genomes could be assembled from whole-genome shotgun data alone, the cost would be expected to decrease significantly. When a project targets many genomes of nonmodel and/or wild-type samples, such as the Genome 10K Project (Genome 10K Community of Scientists 2009), Platanus is especially helpful because it does not require inbreeding, which is often the bottleneck of the project.
Finally, it should be noted that even in samples with a heterozygosity of <0.5%, such as the C. elegans data (0.0%–0.3% heterozygosity) and the Assemblathon 2 data, Platanus produced the largest scaffold NG50 and/or the best validation results. This result indicates the great versatility of Platanus; its effectiveness is not restricted to highly heterozygous samples.
Methods
Data for benchmarks
- C. elegans reference sequences: NC_001328.1, NC_003279.6, NC_003280.8, NC_003281.8, NC_003282.6, NC_003283.9, and NC_003284.7
- Oyster genomic reads: SRA040229
- Oyster reference sequences: AFTI01000000
- Oyster BACs: GU207451.1, GU207446.1, GU207415.1, GU207462.1, GU207436.1, GU207459.1, GU207449.1, and GU207460.1
- Oyster RNA-seq: GSE31012 (Gene Expression Omnibus)
- Bird (Assemblathon 2) genomic reads: ERA200248, ERA201590, and ERA250291
- Snake (Assemblathon 2) genomic reads: ERA198728, ERA199152, and ERA250292
- Fish (Assemblathon 2) genomic reads: SRA026860
- Fosmid sequences (VFR) and assembly results related to Assemblathon 2:
- Downloaded from the website of Assemblathon 2 (http://assemblathon.org/assemblathon2)
Construction of simulated sequencing data sets with various rates of heterozygosity
Simulated heterozygous diploid chromosome sequences were constructed from the reference genome sequences by randomly introducing substitutions and indels (with a substitution:indel ratio of 9:1). The reads from HiSeq 2000 were mapped to the reference genome of C. elegans using Bowtie 2 (Langmead and Salzberg 2012), and the positions of the reads were determined. Approximately 50% of the mapped reads were transformed into the sequence of the simulated heterozygous chromosome. For each simulated heterozygous site, the rate of the transformed reads followed a normal distribution. Linkages between variants were simulated because the transformations were performed as a unit of paired reads.
Variant calling and estimations of heterozygosity
We called variants using Bowtie 2 and SAMtools (Li et al. 2009a). Paired ends were mapped on the C. elegans reference genome using Bowtie 2. Mapping was initially performed using a single-end mode. A read was excluded if it had multiple best hits or if the edit distance of the best hit was greater than 5. The insert sizes were counted for each of the pairs whose reads were mapped on the same scaffold with a reasonable direction. Pairs whose insert sizes were within the mean (±2 × standard deviation) were used for the analysis, and the remainders were excluded. The mapping results were merged using SAMtools. In this case, PCR-duplicate reads were removed (samtools rmdup).
When the mapping results were merged, base-quality filtering was performed (minimum: 30, set in the –Q option of “samtools mpileup”). For variant calling, the minimum coverage was 20 and the maximum coverage was twice the average. Sites closer than 100 bp to either the gaps (‘N’) or ends were also excluded. Finally, we searched the remaining regions. The variants were counted if rates of variant reads were in the range of 0.25 to 0.75.
To ensure that this method correctly computes heterozygosity, we applied it to simulated heterozygous data (Supplemental Table 3). Because we filtered out reads with a minimum edit distance of 5, over-filtering occurred in 2% of the heterozygous data and the rates were underestimated, whereas data with heterozygosity rates ≤1.5% were successfully analyzed. Therefore, we assumed that the low heterozygosity calculated for the C. elegans genome was reliable. For data on S. venezuelensis, oyster, bird, and snake, we applied the same methods to estimate heterozygosity, mapping the reads on fosmids or BACs. For the fish, reads were mapped on the scaffolds of Platanus because neither a fosmid nor a BAC was available.
Validation of assemblies using fosmid or BAC
We used three programs (nucmer, delta-filter, and show-coords) in the MUMmer package (Kurtz et al. 2004). First, each fosmid (BAC) was aligned (queried) to scaffolds using nucmer. Second, the results from nucmer (out.delta) were filtered using delta-filter with the –g switch (one-to-one global alignment, not allowing for rearrangements). Third, the filtered results were entered as input to show-coords, and the coordinates of the resulting alignments were determined. Finally, we picked up alignments that represented the longest length (top-hit) for each fosmid (BAC) and summed those lengths. This sum was referred to as the “top-hits-length.” The one-to-one relations can be used to exclude overestimations of the alignment length from the redundant scaffolds. The top-hits-length decreases when the scaffolds contain errors and gaps. Note that ‘N’ regions were not counted as ‘hit.’ Thus, this value summarizes the quality of the scaffolds. Fosmids (BACs) with top-hits-lengths of at least 0.9 times their length were defined as “contained.”
Data access
The newly sequenced C. elegans and S. venezuelensis genomic reads for this study were submitted to the DDBJ Sequence Read Archive (DRA; http://trace.ddbj.nig.ac.jp/dra/index_e.html) under accession numbers DRA000967 and DRA000971, respectively. Platanus is freely available at http://platanus.bio.titech.ac.jp/. All of the benchmark data sets are available from http://platanus.bio.titech.ac.jp/platanus_benchmark.
Acknowledgments
We thank all the members of the laboratories involved in this project for their helpful discussions. This work was supported by KAKENHI (Grant-in-Aid for Scientific Research on Innovative Areas, No. 22125008), KAKENHI (Grant-in-Aid for Scientific Research [B], No. 24310142), and KAKENHI for Innovative Areas “Genome Science” (No. 221S0002) from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Author contributions: Project design and coordination: T.I., F.A., Y.K., and T.H. Algorithm development: R.K., H.N., and T.I. Program development: R.K. and K.T. Benchmark: R.K., M.O., K.T., and T.I. Genome sequencing: E.N., Y.O., H.M., T.H., A.T., A.F., Y.K., M.Y., M.H., and T.I. Management and dissection: A.F., T.H., Y.K., and T.I. Imaging: R.K. and T.I. Writing: R.K., T.H., and T.I.
Footnotes
[Supplemental material is available for this article.]
References
- Al-Dous EK, George B, Al-Mahmoud ME, Al-Jaber MY, Wang H, Salameh YM, Al-Azwani EK, Chaluvadi S, Pontaroli AC, DeBarry J, et al. 2011. De novo genome sequencing and comparative genomics of date palm (Phoenix dactylifera). Nat Biotechnol 29: 521–527 [DOI] [PubMed] [Google Scholar]
- Bradnam KR, Fass JN, Alexandrov A, Baranay P, Bechner M, Birol I, Boisvert S, Chapman JA, Chapuis G, Chikhi R, et al. 2013. Assemblathon 2: evaluating de novo methods of genome assembly in three vertebrate species. Gigascience 2: 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The C. elegans Sequencing Consortium 1998. Genome sequence of the nematode C. elegans: a platform for investigating biology. Science 282: 2012–2018 [DOI] [PubMed] [Google Scholar]
- Genome 10K Community of Scientists 2009. Genome 10K: a proposal to obtain whole-genome sequence for 10,000 vertebrate species. J Hered 100: 659–674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gnerre S, Maccallum I, Przybylski D, Ribeiro FJ, Burton JN, Walker BJ, Sharpe T, Hall G, Shea TP, Sykes S, et al. 2011. High-quality draft assemblies of mammalian genomes from massively parallel sequence data. Proc Natl Acad Sci 108: 1513–1518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabherr MG, Haas BJ, Yassour M, Levin JZ, Thompson DA, Amit I, Adiconis X, Fan L, Raychowdhury R, Zeng Q, et al. 2011. Full-length transcriptome assembly from RNA-Seq data without a reference genome. Nat Biotechnol 29: 644–652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jex AR, Liu S, Li B, Young ND, Hall RS, Li Y, Yang L, Zeng N, Xu X, Xiong Z, et al. 2011. Ascaris suum draft genome. Nature 479: 529–533 [DOI] [PubMed] [Google Scholar]
- Kent WJ 2002. Blat—the BLAST-like alignment tool. Genome Res 12: 656–664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JH, Waterman MS, Li LM. 2007. Diploid genome reconstruction of Ciona intestinalis and comparative analysis with Ciona savignyi. Genome Res 17: 1101–1110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim EB, Fang X, Fushan AA, Huang Z, Lobanov AV, Han L, Marino SM, Sun X, Turanov AA, Yang P, et al. 2011. Genome sequencing reveals insights into physiology and longevity of the naked mole rat. Nature 479: 223–227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz S, Phillippy A, Delcher AL, Smoot M, Shumway M, Antonescu C, Salzberg SL. 2004. Versatile and open software for comparing large genomes. Genome Biol 5: R12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Salzberg SL. 2012. Fast gapped-read alignment with Bowtie 2. Nat Methods 9: 357–359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R, 1000 Genome Project Data Processing Subgroup . 2009a. The Sequence Alignment/Map format and SAMtools. Bioinformatics 25: 2078–2079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Fan W, Tian G, Zhu H, He L, Cai J, Huang Q, Cai Q, Li B, Bai Y, et al. 2009b. The sequence and de novo assembly of the giant panda genome. Nature 463: 311–317 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Zhu H, Ruan J, Qian W, Fang X, Shi Z, Li Y, Li S, Shan G, Kristiansen K, et al. 2010. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res 20: 265–272 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo R, Liu B, Xie Y, Li Z, Huang W, Yuan J, He G, Chen Y, Pan Q, Liu Y, et al. 2012. SOAPdenovo2: an empirically improved memory-efficient short-read de novo assembler. Gigascience 1: 1–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murchison EP, Schulz-Trieglaff OB, Ning Z, Alexandrov LB, Bauer MJ, Fu B, Hims M, Ding Z, Ivakhno S, Stewart C, et al. 2012. Genome sequencing and analysis of the Tasmanian devil and its transmissible cancer. Cell 148: 780–791 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers EW, Sutton GG, Delcher AL, Dew IM, Fasulo DP, Flanigan MJ, Kravitz SA, Mobarry CM, Reinert KH, Remington KA, et al. 2000. A whole-genome assembly of Drosophila. Science 287: 2196–2204 [DOI] [PubMed] [Google Scholar]
- Nystedt B, Street NR, Wetterbom A, Zuccolo A, Lin YC, Scofield DG, Vezzi F, Delhomme N, Giacomello S, Alexeyenko A, et al. 2013. The Norway spruce genome sequence and conifer genome evolution. Nature 497: 579–584 [DOI] [PubMed] [Google Scholar]
- Pevzner PA, Tang H, Waterman MS. 2001. An Eulerian path approach to DNA fragment assembly. Proc Natl Acad Sci 98: 9748–9753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Potato Genome Sequencing Consortium 2011. Genome sequence and analysis of the tuber crop potato. Nature 475: 189–195 [DOI] [PubMed] [Google Scholar]
- Salzberg SL, Phillippy AM, Zimin A, Puiu D, Magoc T, Koren S, Treangen TJ, Schatz MC, Delcher AL, Roberts M, et al. 2012. GAGE: a critical evaluation of genome assemblies and assembly algorithms. Genome Res 22: 557–567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Small KS, Brudno M, Hill MM, Sidow A. 2007. Extreme genomic variation in a natural population. Proc Natl Acad Sci 104: 5698–5703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Star B, Nederbragt AJ, Jentoft S, Grimholt U, Malmstrøm M, Gregers TF, Rounge TB, Paulsen J, Solbakken MH, Sharma A, et al. 2011. The genome sequence of Atlantic cod reveals a unique immune system. Nature 477: 207–210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeuchi T, Kawashima T, Koyanagi R, Gyoja F, Tanaka M, Ikuta T, Shoguchi E, Fujiwara M, Shinzato C, Hisata K, et al. 2012. Draft genome of the pearl oyster Pinctada fucata: a platform for understanding bivalve biology. DNA Res 19: 117–130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velasco R, Zharkikh A, Troggio M, Cartwright DA, Cestaro A, Pruss D, Pindo M, Fitzgerald LM, Vezzulli S, Reid J, et al. 2007. A high quality draft consensus sequence of the genome of a heterozygous grapevine variety. PLoS ONE 2: e1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinson JP, Jaffe DB, O’Neill K, Karlsson EK, Stange-Thomann N, Anderson S, Mesirov JP, Satoh N, Satou Y, Nusbaum C, et al. 2005. Assembly of polymorphic genomes: algorithms and application to Ciona savignyi. Genome Res 15: 1127–1135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- You M, Yue Z, He W, Yang X, Yang G, Xie M, Zhan D, Baxter SW, Vasseur L, Gurr GM, et al. 2013. A heterozygous moth genome provides insights into herbivory and detoxification. Nat Genet 45: 220–225 [DOI] [PubMed] [Google Scholar]
- Zerbino DR, Birney E. 2008. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res 18: 821–829 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang G, Fang X, Guo X, Li L, Luo R, Xu F, Yang P, Zhang L, Wang X, Qi H, et al. 2012. The oyster genome reveals stress adaptation and complexity of shell formation. Nature 490: 49–54 [DOI] [PubMed] [Google Scholar]
- Zheng W, Huang L, Huang J, Wang X, Chen X, Zhao J, Guo J, Zhuang H, Qiu C, Liu J, et al. 2013. High genome heterozygosity and endemic genetic recombination in the wheat stripe rust fungus. Nat Commun 4: 2678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimin AV, Marçais G, Puiu D, Roberts M, Salzberg SL, Yorke JA. 2013. The MaSuRCA assembler. Bioinformatics 29: 2669–2677 [DOI] [PMC free article] [PubMed] [Google Scholar]