Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape (original) (raw)

Significance

Characterization of cellular heterogeneity and hierarchy are important tasks in developmental biology and may help overcome drug resistance in treatment of cancer and other diseases. Single-cell technologies provide a powerful tool for detecting rare cell types and cell-fate transition events, whereas traditional gene expression profiling methods can be used only to measure the average behavior of a cell population. However, the lack of suitable computational methods for single-cell data analysis has become a bottleneck. Here we present a method with the focuses on automatically detecting multilineage transitions and on modeling the associated changes in gene expression patterns. We show that our method is generally applicable and that its applications provide biological insights into developmental processes.

Keywords: single cell, gene expression, bifurcation, differentiation

Abstract

We present single-cell clustering using bifurcation analysis (SCUBA), a novel computational method for extracting lineage relationships from single-cell gene expression data and modeling the dynamic changes associated with cell differentiation. SCUBA draws techniques from nonlinear dynamics and stochastic differential equation theories, providing a systematic framework for modeling complex processes involving multilineage specifications. By applying SCUBA to analyze two complementary, publicly available datasets we successfully reconstructed the cellular hierarchy during early development of mouse embryos, modeled the dynamic changes in gene expression patterns, and predicted the effects of perturbing key transcriptional regulators on inducing lineage biases. The results were robust with respect to experimental platform differences between RT-PCR and RNA sequencing. We selectively tested our predictions in Nanog mutants and found good agreement between SCUBA predictions and the experimental data. We further extended the utility of SCUBA by developing a method to reconstruct missing temporal-order information from a typical single-cell dataset. Analysis of a hematopoietic dataset suggests that our method is effective for reconstructing gene expression dynamics during human B-cell development. In summary, SCUBA provides a useful single-cell data analysis tool that is well-suited for the investigation of developmental processes.

Stem and progenitor cells constantly face critical choices between different cell-fate events, such as self-renewal, differentiation, and cell death (1), leading to significant cellular heterogeneity. Although the molecular mechanisms involved in these processes are not yet completely understood, it is generally accepted that transcriptional regulators, such as DNA-binding transcription factors and chromatin regulators, play an important role in cell-fate decisions. In certain cases, the activity of a small number of transcription factors, also known as master regulators, may initiate cell-fate transitions by activating a large number of cell-type-specific genes. Well-known examples include GATA1 for erythropoiesis (2), Pu.1 for myelopoiesis (3), and MyoD for skeletal muscle formation (4). Conversely, pluripotency can be reestablished by forced expression of a small number of selected transcription factors in differentiated cells (5). Another important process contributing to cellular heterogeneity is biological noise, caused by, for example, random environmental fluctuations or stochastic effects in transcriptional networks. Sufficient noise can enable cells to reach dynamically unstable states (6, 7). Despite these important studies, it remains difficult to reconstitute the sequence of events generating cell-fate transitions and cellular heterogeneity.

A major challenge for the characterization of the source of cellular heterogeneity is that stem and progenitor cells are underrepresented in the total cell population. Owing to their low abundances, they are difficult to detect using traditional approaches, which only measure averages over large populations of cells. Even more difficult is the task of capturing the precise time when a cell undergoes a cell-fate transition. Recently, new technologies are being rapidly developed to quantify gene expression at the single-cell resolution (7–23), providing an unprecedented opportunity for the detection of such rare events. Nonetheless, interpretation of these novel kinds of data remains a difficult task owing to the lack of suitable computational methods.

In some previous studies the generation of cellular heterogeneity has been described using dynamical system approaches. In the simplest scenario, a dynamical system is an autonomous system that evolves in time according to a set of deterministic rules (24). Although the exact trajectory depends on the initial point, in time, most trajectories will converge to an attractor, which may be characterized as an equilibrium state, an oscillation, or a more complex behavior. Rigorous studies of catastrophic phenotypic changes were pioneered by René Thom, who showed that a surprisingly small number of prototypic scenarios can explain a wide variety of phenomena (25).

Different cell types can be modeled as attractors of the dynamic gene regulatory networks (26, 27), and catastrophic changes of the attractors may lead to significant cellular heterogeneity (28). To date, the dynamical systems approach has been applied to the study of a number of biological systems (28–32), but most of these systems are relatively simple, in the sense that the underlying regulatory network is well understood. To overcome this limitation, here we have developed an approach, called single-cell clustering using bifurcation analysis (SCUBA), to systematically identify bifurcation events directly from single-cell data without prior biological knowledge.

We have successfully applied SCUBA to three distinct data-types: RT-PCR (9), RNA sequencing (RNA-seq) (19), and mass cytometry data (33). Using single-cell RT-PCR data (9), we have correctly identified two bifurcation events during early development of mouse embryos, reconstructed the dynamic landscape of changes in gene expression patterns, and experimentally validated our model by testing its prediction for the effect of Nanog perturbation on cell lineage biases. Analysis of RNA-seq data gave similar results, indicating that our method is robust with respect to experimental platform differences. We have further developed an approach based on principal curve analysis (34) to infer temporal order, thereby extending the applicability of SCUBA to datasets with no temporal information. Taken together, SCUBA provides a useful and robust tool for characterizing cellular heterogeneity and gene expression dynamics from single-cell gene expression data.

Results and Discussion

General Framework of SCUBA.

Consider an experimental study in which, to investigate cell differentiation events during development, multiple cells are subjected to single-cell measurements and grouped according to developmental time (Fig. 1, Top), which might be either known a priori or inferred indirectly. Our goal is to automatically identify gene expression patterns associated with cell differentiation from single-cell data. We model the developmental process using a stochastic dynamical system that has the following properties: First, at each developmental time, single-cell gene expression changes are determined by a stochastic dynamical system, containing both deterministic and stochastic components; second, each cell is randomly sampled from the equilibrium distribution of the stochastic dynamical system; and third, the changes of the stochastic dynamical system across time can be parameterized. An immediate consequence is that most cells reside in states that are close to the attractors, whereas only a small number of cells may undergo transitions from one attractor to another. The appearance of multiple new cell types is modeled as a bifurcation process, corresponding to the emergence of new attractors. The major goals of SCUBA are to recover the cellular hierarchy and to quantify the dynamics along the bifurcation events.

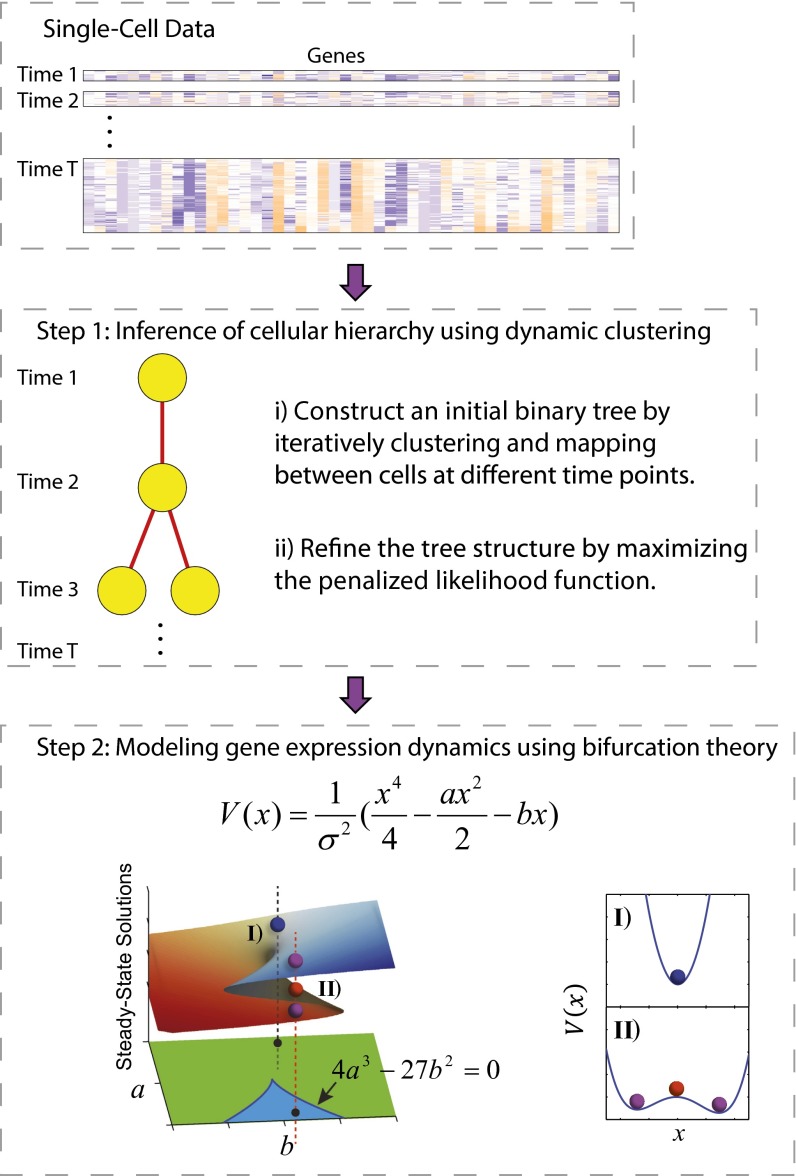
Fig. 1.

Fig. 1.

Overview of the SCUBA method. (Top) Structure of single-cell data. Individual cell samples are ordered by their corresponding developmental time. (Middle and Bottom) Schematic of the two main steps of SCUBA. In the bottom panel, the parameter space is divided into two regions, corresponding to one (green region and I) or two attractor states (blue region and II**)**, respectively. The surface on top of parameter space shows the steady-state solutions corresponding to each parameter setting. Stable and unstable steady states are colored differently.

Specifically, our method uses a two-step approach, as illustrated in Fig. 1. In the first step, we estimate the locations of the stage-specific attractors and their relationships, using a binary tree model. For simplicity, we only consider steady-state attractors. In the second step, we quantitatively model the dynamics in the reduced state space along each bifurcation direction, using a potential V(x) to characterize gene expression dynamics associated with each bifurcation event (Fig. 1, Bottom). Of note, the parameter space is divided into two regions, corresponding to one or two attractor states, respectively, and their boundary is given by 4_a_3 − 27_b_2 = 0. The details are explained in Materials and Methods.

Bifurcation Events During Mouse Early Embryonic Development.

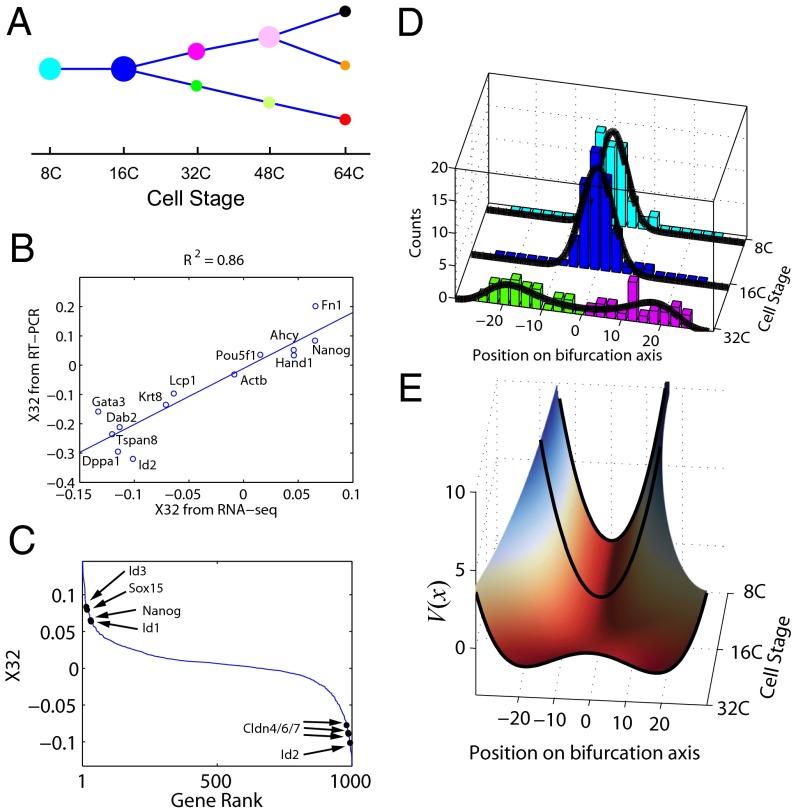
We first applied SCUBA to analyze a published dataset (9) where the developmental stage for each cell is known. In that study, the authors used high-throughput RT-PCR to quantify the expression levels of 48 selected genes, including 27 key developmental transcription factors, in 438 individual cells isolated from early-stage mouse embryos. Cells were extracted at seven distinct time points, each corresponding to a cell-doubling event, from the 1-cell zygote to the 64-cell blastocyst. There are two well-characterized cell differentiation events during this process (35). The first one occurs at the 32-cell stage, where totipotent cells differentiate into trophectoderm (TE) and inner cell mass (ICM), whereas the second event occurs at the 64-cell stage, where ICM further differentiates into primitive endoderm (PE) and epiblast (EPI). At the end of this period, the embryo contains three distinct cell types: TE, PE, and EPI.

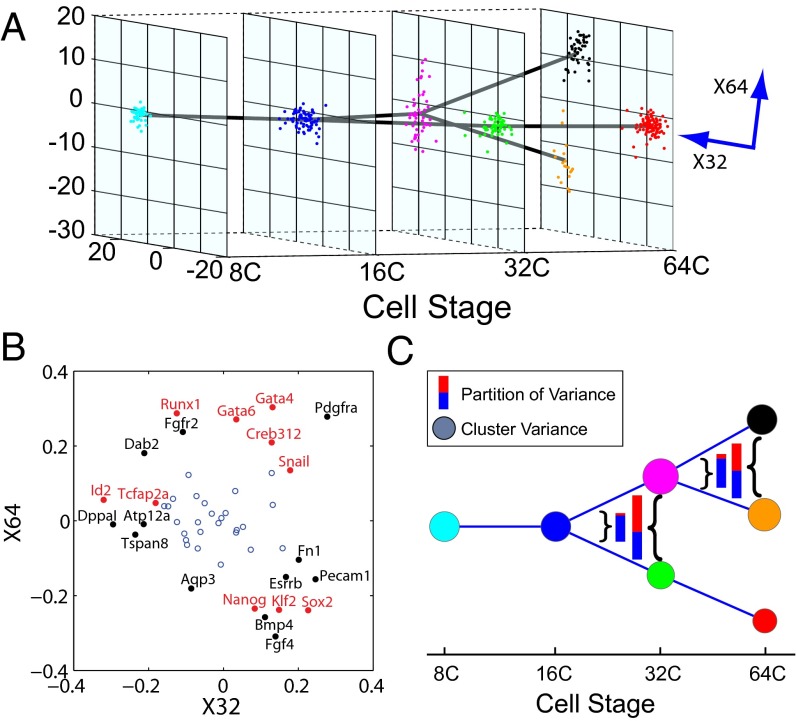
By applying the first step of SCUBA we identified two bifurcation events, at the 32-cell and 64-cell stages, respectively (Fig. 2_A_). The timing of these events matched exactly the occurrence of the aforementioned cell-differentiation events. To test whether our clustering results indeed reflected true lineage differences, we used our results as the basis to predict cell lineages in an independent fluorescently labeled cell population studied in ref. 9. Out of the 37 cells that could be compared in this manner, we found only one misclassification error, indicating that our predictions were highly accurate (Fig. S1) (see SI Materials and Methods for details). To further test the robustness of our clustering results, we simulated and analyzed 1,000 datasets by resampling the data using bootstrap (36) (see SI Materials and Methods for details). Cells were assigned to the same clusters with high frequencies (Fig. S2), indicating the stability of our method. Furthermore, we subsampled the data to test how many cells were needed to reliably detect bifurcations. Whereas the 32-cell bifurcation was detected with as few as 20 cells (Fig. S3_A_), at least 50 cells were required to detect the 64-cell stage with 70% sensitivity (Fig. S3_B_). Therefore, the number of cells that need to be assayed at a certain developmental stage depends not only on the differences between the cell clusters but also on the complexity of the tree structure at that stage.

Fig. 2.

Fig. 2.

Lineage tree reconstructed based on single-cell RT-PCR data in mouse embryos. (A) Overall structure of the dynamic clustering and projection of the clustering pattern onto the plane spanned by the two bifurcation directions. Note that these two directions, X32 and X64, are not exactly orthogonal. Each color represents a different cluster. Parent–progeny cluster pairs are connected by straight lines. (B) Relative weight of all genes on the two bifurcation directions. Genes with the biggest and smallest weights along X32 and X64 are labeled. Transcription factor labels are in red. (C) Change of gene expression variance associated with dynamic clustering. Node size represents total variance for each cluster, color-coded as in A. Inset color bars compare the total variance before and after each bifurcation event, as indicated by the curly brackets. The total variance is further decomposed into two portions, corresponding to the bifurcation direction (red) and all other directions (blue).

Despite the complexity of the 48-dimensional gene expression pattern, each bifurcation direction clearly separated cells into two distinct populations. In comparison, the traditional principal component analysis method applied independently at each stage can also separate the different cell types (Fig. S4). However, because different principal components are derived at different stages, it is difficult to compare the patterns across time and to infer lineage relationships between different developmental stages.

The weight of each gene along a bifurcation direction revealed its relative contribution to the differentiation process (Fig. 2_B_ and Dataset S1). Many known important developmental regulators (red labels in Fig. 2_B_) had large weights that were consistent with their functional role (37–39). For example, at the 32-cell stage, the bottom-ranked transcription factors were Id2 (inhibitor of DNA binding 2) and Tcfap2a and the top-ranked transcription factors Sox2 [SRY (sex determining region Y)-box 2] and Snai1. At the 64-cell stage, the bottom-ranked transcription factors were Sox2 and Klf2 and the top-ranked transcription factors Gata4 (GATA binding protein 4) and Runx1.

For comparison, we applied SPADE (spanning-tree progression analysis of density-normalized events), a popular method that does not take temporal information into account (10, 40), to the same dataset. We found that SPADE could not effectively distinguish cells from different time points and cell lineages (Fig. S5), suggesting the utility of temporal information in accurate reconstruction of the cellular hierarchy (see SI Materials and Methods for details).

We then focused on the local dynamic change of gene expression patterns associated with each bifurcation event. As expected, the overall variance of gene expression increased dramatically during both bifurcation events (see total bar lengths in Fig. 2_C_). Interestingly, the increase was almost entirely contributed by the bifurcation direction (red portion in bars in Fig. 2_C_), suggesting that insights can be gained by focusing on the reduced dynamics along the bifurcation directions.

Modeling Dynamic Changes in Gene Expression Patterns Associated with Bifurcations.

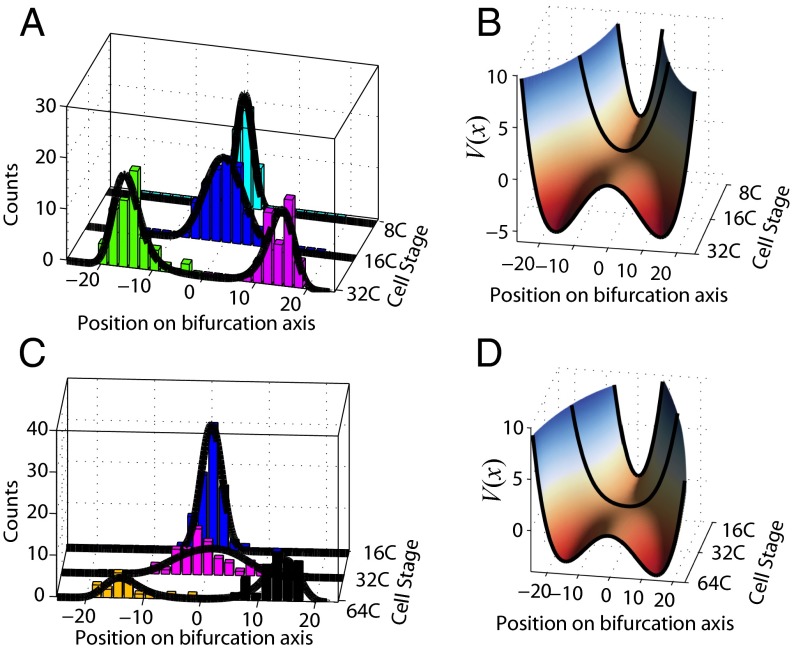
Next we investigated the gene expression dynamics associated with each bifurcation event by using step 2 of SCUBA. Specifically, we projected the high-dimensional gene expression pattern on the bifurcation direction and then inferred the potential function V(x) by fitting the projected data (see Eq. 3 in Materials and Methods). The fitted parameters values are shown in Table 1. As expected, the potential changed from single-well to double-well for both bifurcations (Fig. 3). Such catastrophic changes are characteristic of multilineage cell-fate transitions.

Table 1.

Fitted model parameters for the 32- and 64-cell bifurcations of the RT-PCR dataset

Bifurcation σ b aT0 aT1 aTb
32-cell 75.6 −18.0 −1,156.9 −204.0 232.7
64-cell 81.8 84.8 −1,003.3 −68.5 205.7

Fig. 3.

Fig. 3.

Reconstructed gene expression dynamics associated with the 32-cell (A and B) and 64-cell (C and D) bifurcations. (A and C) Histograms of cell populations along the bifurcation axis and fitted equilibrium distributions (dark curves). (B and D) The potential function V(x) inferred from the equilibrium distribution. The smooth surface is obtained by interpolation.

Prediction of the Effect of Biological Noise on the Maintenance of Lineage Diversity.

Our analysis provides a systematic way to evaluate the contributions of deterministic and stochastic forces in establishing cell-fate selection. It is important to note that 4a3−27b2>0 does not guarantee that the two states after the bifurcation will be clearly distinguishable in the data, because stochastic noise may mask the difference between these two states. Similarly, 4a3−27b2<0 may not be sufficient to maintain the stability of a cell type, if its stabilizing effect can be countered by noise. Eq. 3 (Materials and Methods) provides a guide to quantitatively assess the balance between the deterministic and stochastic forces. In particular, for cases with small b and approximately symmetric attractors, differences between the two attractors after bifurcation can only be detected when a>σ2. For both bifurcations, b is small and the estimated value of a is so that a>σ2, providing a theoretical explanation for why distinct cell types can be observed at these time points. However, the existence of noise provides a window of opportunity for manipulating cell fates, which may have interesting applications.

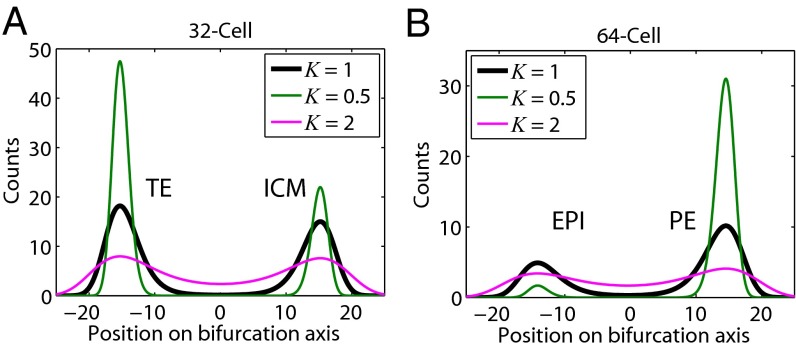
To investigate the effect of gene expression noise on the choice of cell fates during differentiation, we compared results from changing the noise level σ (see Eq. 3 and Eq. S4 in SI Materials and Methods) to Kσ. The steady-state distribution ψS now becomes ψS(x)=C e−2V(x)/K2. Fig. 4_A_ shows that the peaks corresponding to the two attractors at the 32-cell stage become broader as K increases, indicating each attractor state becomes less stable. Also, the areas under the peaks are more similar, indicating that the bias between these two states is reduced. For example, doubling the noise (K=2) would result in an almost even distribution between the two states, whereas reducing the noise by a factor of 2 (K=1/2) would lead to a stronger bias toward the TE lineage. The effect of noise is more dramatic at the 64-cell stage (Fig. 4_B_), where the potential V(x) is more asymmetric. It is important to note that our calculations represent an upper-bound estimate of the effects of biological noise, because they do not take into account the technical variation in single-cell gene expression measurements. These results point out that noise may play an important role in the maintenance of cell-type diversity.

Fig. 4.

Fig. 4.

Prediction of the effect of biological noise on the maintenance of lineage diversity. (A and B) Equilibrium distributions for the (A) 32- and (B) 64-cell population when noise levels were changed by a factor K. Black line, cell counts as in our fits to the data in the last stages in Fig. 3 A and C. Increasing the noise by a factor of 2 (K = 2, red line) broadens the distributions. Reducing the noise levels by a factor of 2 (K = 1/2, green line) leads to an increase of the TE population at the 32-cell stage and a very significant increase of the PE population at the 64-cell stage, with a near disappearance of the EPI population.

Prediction and Experimental Validation of the Effects of Transcription Factor Expression Level Perturbations on Lineage Bias.

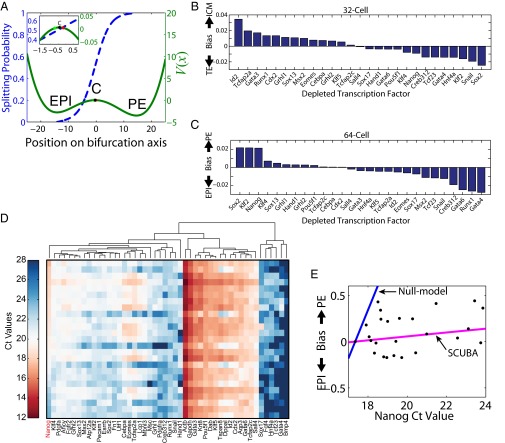
SCUBA provides a venue to predict the effect of perturbing the expression level of a certain transcription factor on the differentiation process leading to two new cell types. We reasoned that if the perturbation size is sufficiently small its effect could be approximated by the change in the initial conditions without modifying the underlying epigenetic landscape. In a system that contains multiple attractor cell states, changes in initial conditions may alter the final population composition into different cell types. We defined the lineage bias introduced by a transcription factor perturbation as the change induced in the probability of reaching each attractor cell state. To predict the bias resulting from perturbing each transcription factor, we first calculated its effect in changing the initial conditions (away from C in Fig. 5_A_) and then made use of the splitting probability functions (41) (Fig. 5_A_ and SI Materials and Methods). For example, our model predicts that a twofold reduction of Id2 would result in an ∼0.035 (∼7%) increase in the splitting probability of falling into the ICM attractor at the 32-cell stage (Fig. 5_B_), and a twofold reduction of Sox2 (red dot in Fig. 5_A_) would result in an ∼0.02 (∼4%) increase in the splitting probability of falling into the PE attractor at the 64-cell stage (Fig. 5_C_). It is important to note that our model predicts a relatively small effect of a single factor on the differentiation bias, suggesting that the combination of multiple regulators is required to control cell-fate transitions.

Fig. 5.

Fig. 5.

Prediction and validation of the effect of perturbing transcription factors on lineage bias. (A) Predicted splitting probabilities for the 64-cell bifurcation (left axis) overlaid with the potential function V(x) (right axis). EPI and PE correspond to the local minima of the potential and C (black dot) is the local maximum of the potential, located at approximately −0.5. The predicted effect of a twofold depletion of the transcription factors Gata4 (green dot) or Sox2 (red dot) is highlighted. (B and C) Predicted lineage bias at the (B) 32- and (C) 64-cell stage after a twofold depletion of each profiled transcription factor. (D) Heat map shows Ct values for 48 genes (columns) in 25 different whole embryos (rows sorted by Nanog Ct values). Coexpressed genes are grouped together by hierarchical clustering. (E) Lineage bias introduced by decreasing Nanog expression values. Experimentally determined values are shown as black dots and model predictions as colored lines.

We then focused on a specific transcription factor Nanog (Nanog homeobox protein) and carried out experimental validation. Nanog is known to be an important regulator in mouse embryo development, with a role in epiblast lineage specification (42), and whose transient fluctuations mark commitment (43). Consistent with the literature, our model predicted that altering the levels of Nanog would change the balance between the different cell lineages (Fig. 5 B and C). Specifically, decreasing the level of Nanog would lead to a bias away from EPI and toward PE at the 64-cell bifurcation (Fig. 5_C_).

To test this prediction, we generated Nanog mutant mouse embryos by heterozygous crosses and quantified the expression level of the 48 genes in each embryo using the same RT-PCR assay as in ref. 9 (see SI Materials and Methods for details). A total of 25 embryos were profiled at approximately the 64-cell stage, and some of their genetic differences were reflected by their Nanog expression levels (Fig. 5_D_). Although each embryo was profiled as a whole, we were able to estimate its cell-type composition by decomposing its gene expression pattern as a weighted sum of the three cell-type-specific signatures and then estimating the lineage bias associated with the 64-cell bifurcation (see SI Materials and Methods for details). As expected, decreasing Nanog expression values (higher Ct) led to a bias toward PE in mutant embryos (Fig. 5_E_). However, looking at Nanog values provides only a partial explanation, because predictions of a null model based on the Nanog expression levels alone drastically overestimated the effect of the perturbation (Fig. 5_E_). A likely explanation is that the loss of Nanog was counterbalanced by other factors. To test whether such coordinated effects can be correctly predicted by our SCUBA analysis, we predicted the bias introduced by Nanog perturbation based on the perturbed gene expression dynamics as discussed above (also see Fig. 5_C_ and SI Materials and Methods). This provides a much more accurate prediction (Fig. 5_E_). The remarkable agreement between our predictions and the experimental results strongly validates our method.

Analysis of Single-Cell RNA-seq Data Shows Robustness of SCUBA.

Recent developments in single-cell RNA-seq technologies have enabled whole-transcriptome profiling. To test whether SCUBA is useful for analyzing RNA-seq data we reanalyzed a recently published dataset (19) covering the same time span in early mouse embryo development as the RT-PCR dataset analyzed here (9). The RNA-seq experiments detected a total of 22,958 genes in 294 single cells, but many genes were expressed at a low level and subject to considerable technical variation (19, 44). Therefore, we focused on a subset of genes that were likely to be discriminative, selecting the 1,000 most variable genes that were expressed (>1 reads per kilobase of transcript per million reads mapped) in at least 30% of the cells. SCUBA analysis of this filtered RNA-seq gene signature resulted in a binary tree structure similar to that for the RT-PCR data (Figs. 2_C_ and 6_A_), both having two bifurcations at the same developmental stages. The slight difference of the timing of the second bifurcation is likely because the RNA-seq dataset also includes some 48-cell embryos, which were not profiled in the RT-PCR dataset.

Fig. 6.

Fig. 6.

SCUBA analysis of the single-cell RNA-seq data in mouse embryo. (A) Lineage tree reconstructed by SCUBA. Node sizes are proportional to number of cells. (B) Comparison of the 32-cell bifurcation directions derived from the RNA-seq vs. RT-PCR datasets. Scatter plot shows the gene weights associated with each of the 13 common genes between the two datasets. (C) Distribution of gene weights for the 1,000 most variable genes. Some well-characterized regulators are indicated. (D) Equilibrium distribution and (E) potential function V(x) corresponding to the 32-cell bifurcation.

To do a quantitative comparison we focused on the 32-cell bifurcation, because the other bifurcation was only supported by a small number of cells in the RNA-seq dataset. Among the 1,000 most variable genes, 13 were also present in the RT-PCR dataset. Of note, the contributions of these genes to the bifurcation axis were remarkably reproducible despite the platform differences (_R_2 = 0.86; Fig. 6_B_). In addition, the RNA-seq analysis uncovered additional genes known to be important for either embryonic development [such as Sox15 (45) or Id2/Id3 (46, 47)] or the establishment of tight junctions to form the placenta [such as claudins (48, 49)] that were also associated with high weights (Fig. 6_C_). We projected the expression profile of the 1,000 genes onto the bifurcation direction and fitted the potential landscape based on Eq. 3 (Materials and Methods and Fig. 6 D and E). The resulting landscape had a shape similar to the one obtained for the RT-PCR dataset (Fig. 3_B_). Taken together, these analyses strongly suggest that SCUBA is also useful for RNA-seq data analysis and the results are robust with respect to experimental platform differences.

Analysis of Human B-cell Differentiation and Comparison with Other Methods.

Whereas the bifurcation analysis in SCUBA requires temporal information, it has not escaped our notice that such information may be difficult to obtain experimentally. In some cases, it is feasible to infer the temporal order between the cells by inspecting the expression pattern of known lineage markers. More generally, computational methods [Wanderlust (33) and Monocle (50)] have been recently developed to infer “pseudotime” in silico. Therefore, one strategy is to combine these methods with SCUBA to analyze datasets with no temporal information. In addition, here we present an alternative strategy to infer pseudotime and compare its performance with existing methods.

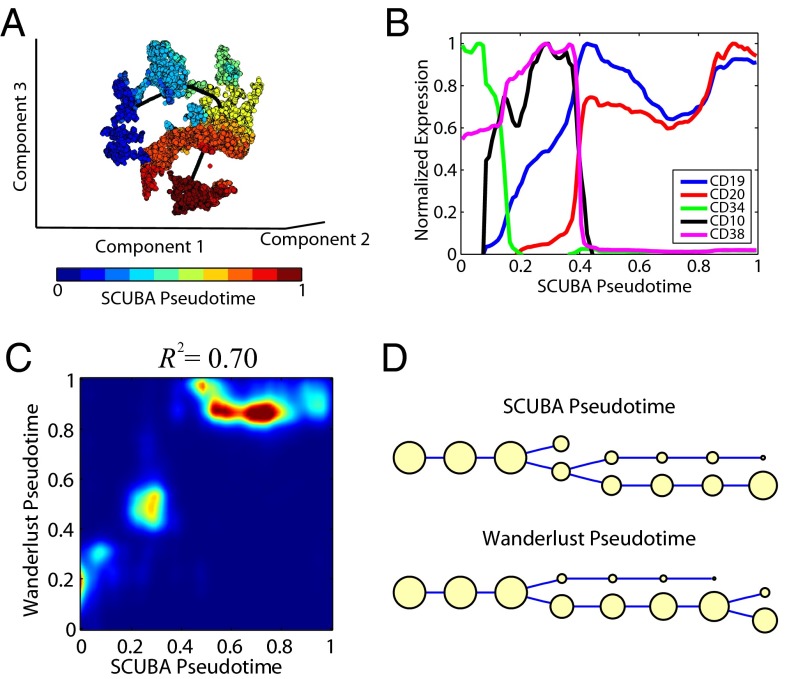
As an example, we obtained a publicly available single-cell mass cytometry dataset, measuring 18 markers in ∼20,000 cells at different stages of human B-cell development (33). Cells were extracted from a snapshot of the bone marrow, therefore bearing no temporal information. The B-cell development is primarily a monolineage differentiation process, serving as a new test for SCUBA. We inferred the pseudotime in two steps. First, we used t-SNE (51) to reduce the data into a 3D space. Second, we fitted a smooth curve passing through the reduced data using the principal curved analysis (34) (see SI Materials and Methods for details). Although the resulting curve had no direction, we were able to further distinguish the start and end positions based on the expected change of CD34 expression during hematopoiesis. For each cell, its corresponding pseudotime, called SCUBA pseudotime, was quantified by its relatively mapped position along the principal curve and the values were normalized between 0 and 1 (Fig. 7_A_). After sorting the cells based on pseudotime, we reconstructed the temporal gene expression profiles during B-cell development (Fig. 7_B_) and found that the pattern was in good agreement with the literature (52). Specifically, cells had initially high values of CD34, followed by CD38 and CD10, and finally high levels of CD19 and CD20, which are known landmarks of B-cell development.

Fig. 7.

Fig. 7.

SCUBA analysis of human B-cell development data. (A) Inference of SCUBA pseudotime based on t-SNE and principal curve analysis. The dataset was reduced to a 3D space by using t-SNE (colored dots). Black line is the principal curve fitted to the data. Cells are color-coded by pseudotime. (B) Selected normalized gene expression profiles for cells sorted using SCUBA pseudotime. (C) Density plot for the distribution of SCUBA pseudotimes (x axis) against Wanderlust pseudotimes (y axis). (D) Lineage tree inferred by applying SCUBA to the pseudotime estimated by our principal curve analysis (Top) or Wanderlust (Bottom).

Compared with two recently published methods, Wanderlust (33) and Monocle (50), our pseudotime inference strategy is conceptually simpler. Also, unlike Wanderlust, it is unnecessary to select an initialization cell, but the principal curve analysis automatically detects the start and end as part of the curve fitting procedure. Of note, the inferred pseudotime was highly correlated with Wanderlust (_R_2 = 0.70; Fig. 7_C_). The temporal gene expression patterns inferred from SCUBA and Wanderlust were also similar (compare Fig. 7_B_ and Fig. S6). In contrast, Monocle (50) seemed to have problems analyzing a large number of cells because it failed to run whenever we included more than ∼900 cells in the analysis. We tried to overcome this limitation by random subsampling but found the results were highly sensitive to the sampling differences (see Fig. S7 and SI Materials and Methods for details).

Using the pseudotime inferred from SCUBA (or Wanderlust, respectively), we divided the cells into eight equally sized groups ordered by pseudotime and then applied our bifurcation analysis to infer cellular hierarchy. Most of the cells were aligned along a single branch of the binary tree, largely consistent with a monolineage differentiation process view of B-cell development. However, analyses of the data ordered with both methods detected a bifurcation event, separating cells into two branches with about one-third and two-thirds of the population, respectively, for the SCUBA analysis (Fig. 7_D_). Comparison of the signatures of the two branches revealed that cells in the smaller subpopulation had higher IgM (intracellular and especially on the surface) and Kappa (Fig. S8), indicating that a fraction of the cells formed a more mature B-cell subpopulation. These results highlight the utility of SCUBA to detect cell populations with distinct gene signatures.

Discussion

We have presented a method, SCUBA, for analyzing single-cell gene expression data. Our method is suitable for the analysis of time-course data sampled with sufficient temporal resolution, and it can detect bifurcations reliably with as few as 20 cells. We have shown that SCUBA is applicable to RT-PCR, RNA-seq, and mass cytometry data and its results are robust with respect to experimental platform differences. SCUBA uses bifurcation theory to focally investigate the dynamic changes of gene expression patterns during development. The major strengths are to automatically detect critical multilineage cell-fate transitions without using prior biological knowledge and to model the gene expression dynamics associated with bifurcation events. SCUBA may also be used to test whether the progression of a developmental process is along a monolineage trajectory; however, in that case the second step of SCUBA is not applicable. We have applied SCUBA to analyze three different datasets and shown that it provides a useful tool for reconstructing cellular hierarchy and dynamics in complex systems.

Through analysis of public datasets we correctly identified two bifurcation events during early development of mouse embryos and quantified the major initiation events during cell differentiation. Our model exquisitely explained the gene expression dynamics around each bifurcation event and predicted the effect of perturbing key regulators in inducing lineage bias. We experimentally tested these predictions by gene expression profiling of Nanog mutant embryos and found excellent agreement between our predictions and the experimental data. Although it requires additional experimental validation, our method also provides a promising framework to systematically evaluation the function of stochastic noise in development. The agreement between RT-PCR and RNA-seq analysis suggests that our method is robust with respect to the experimental platform differences.

One of the limitations of SCUBA is its requirement of data with temporal information for bifurcation analysis. Such information may be difficult to obtain experimentally owing to technical challenges. In certain situations one might be able to infer missing temporal information by applying existing computational methods (33, 50, 53) or the principal curve analysis approach presented here. However, it remains difficult to infer temporal information in general, especially if the cellular hierarchy is complex.

During the preparation of this paper we were aware of a recent study (54) that also used Fokker–Planck equations as a model to study the epigenetic landscape during cell reprogramming. In their model, a constant energy function was used to model the entire epigenetic landscape, and cell-fate transition was modeled as moving from one local minimum to another. This is very different from our current approach, where we use a series of energy functions to model the epigenetic landscape. Our strategy is essential here to identify the bifurcation events, where a local change of energy function leads to the emergence of new minima. Comparing these two approaches, SCUBA provides a more natural framework for modeling multilineage differentiations.

A major goal of systematic characterization of cellular heterogeneity is to provide insights into disease processes, which in turn may lead to novel disease-treatment methods. For example, it is well known that each cancer constitutes a highly heterogeneous set of cells and tissues. A fundamental task is to understand the role of each cell type in tumor genesis and maintenance. In particular, increasing experimental evidence suggests the dominant role of a small set of specialized cells known as cancer stem cells (55, 56). Single-cell gene expression analysis, powered by both technological and computational advances, will likely play an important role in addressing these issues.

Materials and Methods

SCUBA uses a two-step approach, as illustrated in Fig. 1. The mathematical details of the two steps are explained below.

Step 1: Inference of Cellular Hierarchy Using Dynamic Clustering.

We infer the cellular hierarchy by iteratively clustering and mapping between cells at the different developmental time points. We assume that the gene expression patterns change smoothly in time, so that a parental cell and its immediate progeny have similar gene expression profiles. During development, a cell may differentiate in a monolineage manner or may differentiate into multiple cell lineages, which we refer to as a bifurcation event. In such an event, we assume that it only gives rise to two new lineages and that the temporal resolution of the data is sufficiently high to capture every bifurcation. Although these assumptions are not universally applicable, they are likely to be valid in many situations and in practice may not be a severe limitation.

At the initial time point we divide cells into clusters with similar a gene expression pattern using _k_-means clustering and use the gap statistic (57) to determine the number of clusters. At each of the following time points, each cell is assigned to a parental cluster based on its gene expression profile. To determine whether a bifurcation event occurs, the progeny of each parental cluster is further divided into two distinct clusters by _k_-means, and the gap statistic is used to select either the single-cluster or two-cluster model. This procedure is repeated until the final time point. In this way we create a binary tree (Fig. 1, Middle) as an initial estimate of the cellular hierarchy. Of note, if the process only involves monolineage differentiation, then the resulting tree simply has no bifurcations.

Next, we refine the binary tree structure to optimally describe the global gene expression pattern. To this end, we evaluate the performance of each parameterization by using the following penalized likelihood function:

L(θ)=log⁡P(x|θ)−λ∑c‖μc−μa(c)‖2, [1]

where θ indicates all of the parameters involved in defining the tree structure, x is the observed data, μc and μa(c) are the centers of clusters c and a(c), respectively, a(c) is the parent cluster of c, and λ is a predefined constant, set to λ=1 in this paper. During this refinement process, the overall tree structure might change as some clusters become empty, but it may not create additional bifurcations. Further details and certain generalizations are described in SI Materials and Methods.

Step 2: Modeling Gene Expression Dynamics Using Bifurcation Theory.

Our next goal is to model the dynamic changes of gene expression patterns along the cellular hierarchy reconstructed in step 1. We focus on the bifurcation events identified in step 1 and simplify the dynamics to one dimension by projecting the high-dimensional gene expression patterns onto the bifurcation direction, which is defined as the line connecting the centers of the two clusters obtained from a common parental cluster. In the applications discussed in the main text we found that such a dramatic reduction of dimensionality still preserved significant information, allowing us to gain key mechanistic insights about the developmental process.

We begin by considering an idealized scenario where the underlying dynamics is deterministic. In this case, for all initial conditions the system will eventually approach one of the attractor states. Therefore, each observable cell state should correspond to an attractor, and two new cell types arise as a result of a change in the attractor landscape, namely, one attractor loses stability and is replaced by two new attractors. The general bifurcation that can describe the appearance of new attractors in one-dimensional dynamical systems is the two-parameter cusp bifurcation (see the equation in Fig. 1, Bottom and ref. 58), one of the seven irreducible unfoldings according to Thom’s Classification Theorem (25).

Mathematically, a cusp bifurcation is represented by the following first-order ordinary differential equation (ODE) (24, 58):

with control parameters a and b. Depending on the values of these parameters, Eq. 2 may have either one or two attractor states (Fig. 1, Bottom). To further take into account the intrinsic stochasticity of gene expression (30, 31, 59), we modify Eq. 2 by addition of a stochastic term and model the ensemble distribution of differentiation trajectories by the Fokker–Planck equation (see details in SI Materials and Methods). The equilibrium distribution is given by ref. 41:

with C a normalization constant and V(x) our potential (see step 2 in Fig. 1). In this form, this potential V(x) is analogous to the epigenetic landscape schematically described by Waddington (60), represented by a marble rolling down a hill with rugged topology. By fitting Eq. 3 to single-cell gene expression data, the model parameters can be estimated (see details in SI Materials and Methods). Of note, in this step we do not make any assumption about the mechanisms controlling the potential landscape.

Supplementary Material

Supplementary File

Supplementary File

Acknowledgments

We thank Drs. Kimberly Glass, Sidinh Luc, and Junhyong Kim for helpful discussions. G.-C.Y.’s research was supported by National Institutes of Health Grant R21HG006778 and grants from Harvard Stem Cell Institute and the Army Research Office.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File

Supplementary File