A community effort to assess and improve drug sensitivity prediction algorithms (original) (raw)
. Author manuscript; available in PMC: 2015 Aug 24.
Published in final edited form as: Nat Biotechnol. 2014 Jun 1;32(12):1202–1212. doi: 10.1038/nbt.2877
Abstract
Predicting the best treatment strategy from genomic information is a core goal of precision medicine. Here we focus on predicting drug response based on a cohort of genomic, epigenomic and proteomic profiling data sets measured in human breast cancer cell lines. Through a collaborative effort between the National Cancer Institute (NCI) and the Dialogue on Reverse Engineering Assessment and Methods (DREAM) project, we analyzed a total of 44 drug sensitivity prediction algorithms. The top-performing approaches modeled nonlinear relationships and incorporated biological pathway information. We found that gene expression microarrays consistently provided the best predictive power of the individual profiling data sets; however, performance was increased by including multiple, independent data sets. We discuss the innovations underlying the top-performing methodology, Bayesian multitask MKL, and we provide detailed descriptions of all methods. This study establishes benchmarks for drug sensitivity prediction and identifies approaches that can be leveraged for the development of new methods.
The success of precision medicine hinges on our ability to effectively translate genomic data into actionable, customized prognosis and treatment regimens for individual patients. This requires identifying a genomic disease signature from a patient, then matching it with the most effective therapeutic intervention. As a scientific community, we are moving toward this goal, but many questions still remain, including, what data are needed to develop these genomic signatures and what methods are needed to extract the appropriate information from high-dimensional genomic data sets? The first step in addressing these challenges is to generate comprehensive drug sensitivity profiling measurements across many drugs, many disease (sub)types, and many genomic profiling technologies. Several of these data sets have been generated with a focus on cancer biology1–9, and in particular breast cancer4,5,10–14. From these data, the bottleneck then becomes identifying robust computational approaches that connect genomic profiles to drug and disease response.
In the past 20 years, there has been measurable improvement in breast cancer outcomes with a steady decrease in mortality15. The identification of HER2 amplification and subsequent discovery of HER2-targeted therapies (e.g., trastuzumab (Herceptin), lapatinib (Tykerb)) demonstrates that the identification of genomic biomarkers can be used to effectively guide treatment decisions and improve outcomes. However, identification of such biomarkers is complicated by substantial genomic and epigenomic heterogeneity in breast cancer2,10,16,17, indicating that multiple ‘drivers’ may serve as targets for breast cancer treatment. Effective personalized treatments will require matching therapeutic interventions to the complex genomic context of each patient.
The ideal data set(s) to build predictive models linking genomic context to treatment would be systematically characterized drug sensitivities across a large cohort of patients, but these data are time-intensive to generate, prohibitively expensive, and limited in the scope of drugs that can be tested. Performing such assays in cell culture and focusing on breast cancer affords the opportunity to learn the factors that contribute to building effective predictive models in a tractable biological system; these factors can then be used for the design of marker-based clinical trials. Comparisons have shown that cell lines mirror many aspects of the ‘omic’ diversity found in primary tumors4,18,19, suggesting that they can be used as a proxy for characterizing the response to therapeutic interventions. Previous work has characterized relationships between genomic profiles and drug response1,3,6,7,20 and several drug sensitivity prediction algorithms have been proposed1,3,20,21,22; however, a thorough and unbiased comparison of such methods has not been reported.
The Dialogue for Reverse Engineering Assessment and Methods (DREAM) project (http://www.the-dream-project.org/) is the ideal framework to assess predictive models from researchers across the world. The DREAM project is organized around a community of data scientists, where high-impact data along with challenges are presented annually, participants submit their best models, and unbiased assessment is performed using standardized metrics and blinded gold standards. This effort results in a rigorous assessment and performance ranking of methods, and cultivates a community of scientists interested in biomedical research problems.
In collaboration with the NCI, we developed the NCI-DREAM drug sensitivity prediction challenge with the goal of identifying and benchmarking top-performing methods for predicting therapeutic response from genomic, proteomic, and epigenomic profiling data (hereafter referred to as profiling data sets) in breast cancer cell lines. The scientific community submitted 44 sets of predictions, providing a rich sampling of state-of-the-art algorithms. The submissions were rigorously scored against an unpublished and hidden gold-standard data set. We identify the top-performing methods and discuss the details of the top two performers. We relate trends in methodologies to overall performance, in particular, modeling nonlinearities in the data and the benefit of using prior knowledge, often in the form of biological pathways. Finally, we provide an analysis of the tested therapeutic compounds and cell line profiling data sets.
RESULTS
Summary of data sets and challenge
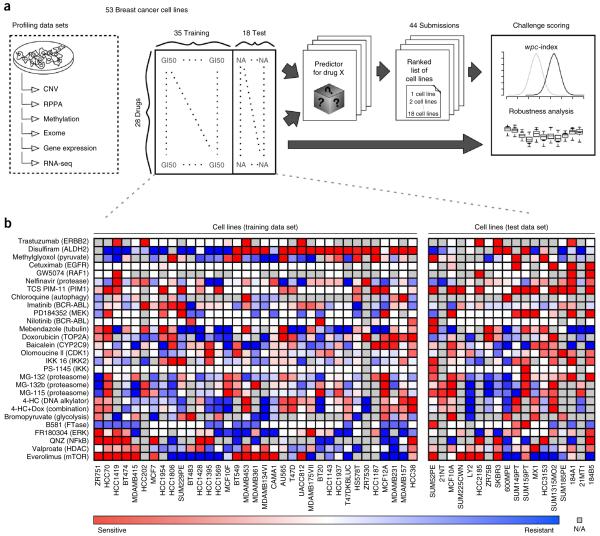
We assembled a panel of 53 breast cancer cell lines, which have been previously profiled for DNA copy-number variation, transcript expression, mutations, DNA methylation and protein abundance23. In addition, dose-response values of growth inhibition were compiled for each cell line exposed to 28 therapeutic compounds (Fig. 1). (See Online Methods for a detailed description of the profiling data sets.)
Figure 1.
The NCI-DREAM drug sensitivity challenge. (a) Six genomic, epigenomic, and proteomic profiling data sets were generated for 53 breast cancer cell lines, which were previously described23. Drug responses as measured by growth inhibition were assessed after treating the 53 cell lines with 28 drugs. Participants were supplied with all six profiling data sets and dose-response data for 35 cell lines and all 28 compounds (training set). Cell line names were released, but drug names were anonymized. The challenge was to predict the response (ranking from most sensitive to most resistant) for the 18 held-out cell lines (test set). The training and test cell lines were balanced for cancer subtype, dynamic range and missing values (Supplementary Fig. 11). Submissions were scored on their weighted average performance on ranking the 18 cell lines for 28 compounds. (b) Dose-response values for the training and test cell lines displayed as heatmaps.
Outlined in Figure 1, participants were supplied with the full set of profiling data for all 53 cell lines, and drug response data for 35 cell lines for the 28 compounds. The gold-standard evaluation data set, which was hidden from the participants, consisted of drug-response data for the remaining 18 cell lines. Cell lines were assigned to the training and test data sets to ensure a balance of breast cancer subtypes.
Participants were challenged to predict a ranked list of the most sensitive (to be ranked first) to most resistant (to be ranked last) cell lines for each individual drug across all the 18 test cell lines. Assessment of predictions was based on participant’s ranking of all 28 therapeutic compounds across all 18 test cell lines.
Characterizing methods to predict drug sensitivity
Participants submitted 44 sets of predictions that cover a range of methodologies. We assigned submissions to one of six categories: (i) kernel methods, (ii) nonlinear regression (regression trees), (iii) sparse linear regression, (iv) PLS (partial least-squares) or PC (principal component) regression, (v) ensemble/model selection and (vi) other (those methods not falling cleanly into the previous five categories). All methods are listed in Table 1 with a short description that covers pre- and postprocessing, along with the underlying methodology (expanded team summarizations can be found in Supplementary Table 1).
Table 1.
NCI-DREAM drug sensitivity prediction methods
| Team | Synopsis | _wpc_-index (scaled) | FDR | Data |
|---|---|---|---|---|
| Kernel method | ||||
| 1 | Bayesian multitask MKL (see main text). | 0.583(0.629) | 2.6 × 105 | exnmrc OI |
| 2 | A predefined number of features were selected using Pearson correlation, training and prediction was done using support vector regression (SVR; radial basis). | 0.559(0.592) | 1.0 × 103 | enmrc |
| 3 | Separate normalizations were applied to each dataset, several support vector machine (SVM) classifiers were independently trained (varying kernels and input data), final predictions were made using a weighted average of all SVM outputs. | 0.553(0.582) | 2.7 × 103 | exnmrc |
| 4 | Bidirectional search was used to select features, training and prediction was done using a SVM (radial basis). | 0.549(0.575) | 4.8 × 103 | enmrc |
| Nonlinear regression (regression trees) | ||||
| 1 | Features were randomly selected to built an ensemble of unpruned regression trees for each dataset, missing values were imputed, weights for the models were calculated, final predictions were made using a weighted sum of the individual models. | 0.577(0.620) | 7.2 × 105 | enm |
| 2 | Features were filtered based on their correlation to dose-response values, random forests were trained for each dataset, missing values were imputed, final rankings were based on a composite score from four individual dataset models (enrc). | 0.569(0.607) | 2.9 × 104 | enrc OI |
| 3 | Features were filtered based on their correlation to dose-response values, random forests were trained for each dataset, missing values were imputed, final rankings were based on a composite score from five individual dataset models (enmrc). | 0.565(0.601) | 5.1 × 104 | enmrc OI |
| 4 | Features were filtered based on their correlation to dose-response values, random forests were trained for each dataset, missing values were imputed, final rankings were based on a composite score from five individual dataset models (exnrc). | 0.564(0.599) | 5.1 × 104 | exnrc OI |
| 5 | Features were filtered based on their correlation to dose-response values, random forests were trained for each dataset, missing values were imputed, final rankings were based on a composite score from individual dataset models (exnmrc). | 0.559(0.591) | 1.0 × 103 | exnmrc OI |
| 6 | Gene features were selected using linear regression and maximal information coefficient, pathway information was also used to derive features, training and prediction was done using a random forest model. | 0.551(0.579) | 3.3 × 103 | exnmrc |
| 7 | Random forests were constructed in a stacked approach, an ensemble of regression trees was constructed for all drug/dataset pairs, missing values were imputed, predictions were made for individual models and another random forest was used to combine the different predictions for the drugs to a final prediction. | 0.548(0.575) | 5.0 × 103 | exnmrc |
| 8 | Features were ranked according to the absolute value of Spearman’s correlation, the average rank of all cell lines was calculated according to the top features. | 0.548(0.574) | 5.0 × 103 | exnmrc |
| 9 | Features were selected using Pearson correlation and a combination of bagging and gradient boosting, prediction was made using selected features and a regression tree. | 0.544(0.568) | 1.0 × 102 | exnmrc |
| 10 | Features were selected using matrix approximation methods leveraging SVD, training and prediction were done using a regression tree models using gradient boosting. | 0.538(0.560) | 1.9 × 102 | en |
| 11 | Features were selected for individual cell lines by constructing random forests and pruning (recursive feature elimination), missing values were imputed, final predictions were made by training a random forest using features from all cell lines. In addition to cell line features, bioactivity spectra of the individual compounds were included as compound features. | 0.524(0.538) | 9.2 × 102 | exnmrc |
| Sparse linear regression | ||||
| 1 | Features were simultaneously selected and a ranking model built for each drug by lasso regression. | 0.564(0.600) | 5.1 × 104 | en |
| 2 | Features were initially filtered based on linear regression to drug response, training and prediction were done using elastic nets. | 0.564(0.600) | 5.1 × 104 | exnmrc |
| 3 | Gene and pathway features were determined using a one-dimensional factor analysis, training and predictions were made with spike and slab multitask regression, drug dose-response values were recalculated from raw growth curves. | 0.564(0.598) | 5.1 × 104 | exnmrc OI |
| 4 | Missing features were imputed, combinations of datasets were enumerated and used to train elastic net regression models, for each drug, final predictions were made using the best-performing model. | 0.551(0.579) | 3.3 × 103 | exmrc |
| 5 | Gene and pathway features were determined using a one-dimension factor analysis, training and predictions were made with spike and slab multitask regression, drug dose-response values were recalculated from raw growth curves, Heiser et al. data were used to train the model. | 0.539(0.560) | 1.9 × 102 | exnmrc OI |
| 6 | Features were removed with low dynamic range, missing feature values were imputed, training and predictions were made using lasso regression on individual datasets, final predictions were made using the weighted sum of regression models. | 0.539(0.560) | 1.9 × 102 | exnmrc |
| 7 | Statistically significant features were selected using Spearman correlation, training and prediction were done using an elastic net. | 0.532(0.549) | 4.7 × 102 | e |
| 8 | Features were constructed by grouping genes according to GO terms, training and prediction were done using relaxed lasso regression. | 0.531(0.548) | 4.7 × 102 | en OI |
| 9 | Gene and pathway features were determined using a one-dimension factor analysis, training and predictions were made with spike and slab multitask regression, GI50 values were used. | 0.531(0.547) | 4.9 × 102 | exnmrc OI |
| 10 | Features were selected using a regression with log penalty, which bridges the L0 and L1 penalty, missing values were imputed, penalized regression models were trained on individual datasets, final predictions were made using a weighted average. | 0.531(0.547) | 4.9 × 102 | exnrc |
| 11 | Features were selected based on elastic nets, missing values were imputed, training and predictions were done using ridge regression. | 0.527(0.543) | 6.7 × 102 | exnmrc |
| 12 | Features were filtered on dataset-specific criteria, missing values were set to random numbers, training and predictions were made using the interior point method for L1-regularization. | 0.519(0.529) | 1.5 × 101 | enmrc |
| 13 | Features were selected using a Gompertz growth model, predictions were made using a lasso regression model. | 0.517(0.526) | 1.8 × 101 | exnmrc |
| 14 | Putative gene set expression values were calculated from constituent genes, training and predictions were made using linear regression. | 0.485(0.477) | 8.0 × 101 | e |
| PLS or PC regression | ||||
| 1 | Removed lowly expressed and/or low variance features, features were selected based on correlation to drug response, multiple partial least squares regression models were trained and consensus determined for final prediction. | 0.562(0.597) | 5.5 × 104 | en OI |
| 2 | Features were selected by using lasso regression and groups of genes predefined by core signaling pathways, predictions were made by linear regression of the reduced feature set to drug response, predictor datasets were merged in advance of drug response prediction, and responses were predicted simultaneously sharing information among drugs. | 0.543(0.567) | 1.0 × 102 | exnmrc OI |
| 3 | Training and prediction were done using principal component regression for individual drugs. | 0.535(0.554) | 3.1 × 102 | exnmrc |
| 4 | Statistically significant features were selected using correlation, models were fit using principal component regression, final predictions were made using a weighted average of models. | 0.524(0.538) | 9.2 × 102 | en |
| Ensemble/model selection | ||||
| 1 | Features were selected using correlation, dimensionality reduced using principal component analysis, lasso and ridge method, several regression models were trained for individual drugs and the top cross-validated model was selected to make final predictions for each drug. | 0.562(0.597) | 5.5 × 104 | exnmrc |
| 2 | Features were selected on outside information, missing values were imputed, predictions were made by aggregating results from an ensemble of machine-learning methods. | 0.556(0.587) | 1.6 × 103 | exnmrc |
| 3 | Features were selected using Spearman’s rank correlation, missing values were imputed, predictions were made using the best-performance method (determined by cross-validation on the training set) among an ensemble of methods (random forest, support vector machine and linear regression). | 0.554(0.583) | 2.6 × 103 | exnmrc |
| 4 | Gene and pathway features were compiled using outside data, an ensemble of prediction models were trained, final predictions were based on a rank-aggregation of combined prediction models. | 0.517(0.527) | 1.7 × 101 | exnmrc OI |
| 5 | Features were selected using outside pathway and interaction data, missing values were imputed, individual drug predictions were made using the best model selected from an ensemble of methods. | 0.506(0.509) | 3.7 × 101 | e OI |
| Other | ||||
| 1 | Features were weighted based on Pearson’s correlation to drug response, predictions were made using the correlation of the weighted features. | 0.570(0.608) | 2.9 × 104 | enr |
| 2 | Gene features showing strong survival from the METABRIC dataset were selected, then hierarchically clustered, a linear model was built to fit gene clusters to drug response, predictions were made using a regression model. | 0.553(0.582) | 2.6 × 103 | e OI |
| 3 | Missing features were imputed, signatures were extracted for each dataset, predictions were made using 1-nearest-neighbor to training cell lines via Pearson’s correlation between signatures for each data type, final predictions are the weighted sum of the individual datasets. | 0.553(0.581) | 2.7 × 103 | exnmrc |
| 4 | Features were selected using dataset-specific criteria, missing values were imputed, predictions were made using KNN. | 0.531(0.549) | 4.7 × 102 | exnmrc |
| 5 | Features were filtered using dataset-specific criteria, an ensemble of Cox regression models were constructed using random sampling from top-performing features, final prediction is the average of all models. | 0.528(0.543) | 6.5 × 102 | nmc |
| 6 | Features were selected using the concordance index, predictions were made using an integrated voting strategy based on each feature’s ability to predict the order of pairs of cell lines. | 0.521(0.532) | 1.3 × 101 | enmrc |
Preprocessing and feature selection are core components of building a predictor. In this challenge, features in the profiling data sets (P) far outnumber the total samples (N), increasing the risk of overfitting. To address this, teams often reduced the number of features modeled by correlating the features in the profiling data set to the dose-response data. Other preprocessing steps included principal component analysis, regularized regression (e.g., lasso, ridge or elastic nets) and mapping gene-level measurements to biological pathways.
Postprocessing includes summarizing or integrating predictions from individual algorithms or data sets into a final set of predictions. For instance, many participants built models for each of the six profiling data sets individually, and then integrated these models to derive the final cell line response predictions for submission. Most frequently, teams computed a weighted average across individual profiling data set predictions. Detailed descriptions of team methods can be found in Supplementary Note 1.
Evaluating drug sensitivity predictions
Team predictions were scored using a modified version of the concordance index (_c_-index)24, the probabilistic _c_-index (_pc_-index), where variation in the experimentally determined dose-response measurements was directly incorporated into the calculation. We present all dose-response values as −log10(GI50), where GI50 is the concentration that inhibited cell growth by 50% after 72 hours of treatment. Raw dose-response measurements can be found in Supplementary Table 2. A team’s final score was calculated as the weighted average of the _pc_-index for all 28 tested compounds, which we termed the weighted, probabilistic _c_-index (_wpc_-index, see Online Methods and Supplementary Note 3). Drug weights reflect the statistical significance of the gold-standard cell-line ranking compared to a distribution of randomly generated predictions. We note that the range of the _wpc_-index will change according to experimental variation in the dose-response measurements, thus we also report a scaled version of the _wpc_-index to map the values to the range [0,1]. To verify scoring consistency, we also evaluated teams using a resampled Spearman correlation approach (Online Methods). Results from both scoring methods were consistent (ρ = 0.89; Supplementary Fig. 1); we present the _wpc_-index results in Table 1 and the resampled Spearman correlation results in Supplementary Table 3. Additionally, we explored a team’s accuracy in predicting sensitive and resistant cell lines irrespective of predicted rank order (Supplementary Table 4 and Supplementary Fig. 2) and found a tight relationship between this measure of accuracy and the _wpc_-index (ρ = 0.78; Supplementary Fig. 3). For the top-performing method, _wpc_-index = 0.583, which corresponds to a balanced accuracy = 0.78. Details of this analysis can be found in Supplementary Note 2 with a mapping of the _wpc_-index to the sensitive and resistant balanced accuracy in Supplementary Table 5.
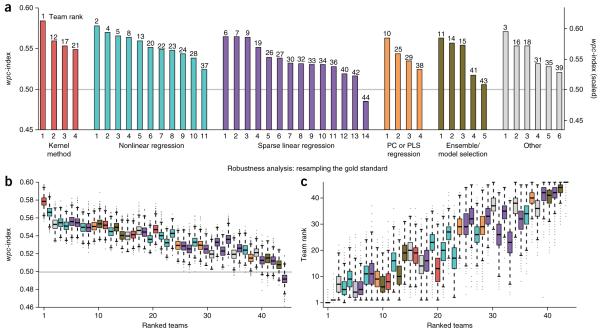
To evaluate the significance of an individual team score, we compared the _wpc_-index to a null model of randomly predicted dose-response values. For 34 of the 44 teams, the null model of randomly generated predictions could be rejected (two-sided, _t_-test, false-discovery rate (FDR) < 0.05) (Fig. 2a). These results indicate that many diverse methods can be implemented to make drug sensitivity predictions from pretreatment profiling data sets. Consistent with previous DREAM challenge results25, we observed that no single method category consistently outperformed the others (Fig. 2a and Table 1). This suggests that the separation in performance is heavily based on factors such as feature selection and method-specific implementations. Examples of innovative approaches from the two top-performing teams are presented in the following section.
Figure 2.
Evaluation of individual drug sensitivity prediction algorithms. Prediction algorithms (n = 44) are indexed according to Table 1. (a) Team performance was evaluated using the weighted, probabilistic concordance index (_wpc_-index), which accounts for the experimental variation measured across cell lines and between compounds. Overall team ranks are listed on top of each bar. The gray line represents the mean random prediction score. (b,c) Robustness analysis was performed by randomly masking 10% of the test data set for 10,000 iterations. Performing this procedure repeatedly generates a distribution of _wpc_-index scores for each team (b). Additionally, after each iteration, teams were re-ranked to create a distribution of rank orders (c). The top two teams were reliably ranked the best and second-best performers (one-sided, Wilcoxon signed-rank test for b and c, FDR « 10−10).
All submissions were subjected to a robustness (resampling) analysis by randomly masking 10% of the gold-standard data set, then recalculating team scores (Fig. 2b,c). From this analysis, the top two teams were reliably ranked the best and second best, both when comparing team scores (one-sided, Wilcoxon signed-rank test, FDR < 10−10; Fig. 2b) and team ranks (one-sided, Wilcoxon signed-rank test, FDR < 10−10; Fig. 2c). When directly compared, the top-ranked team outperformed the second-best team for 91%, and the remaining teams, for over 99% of the resampled iterations. The second-best team outperformed the remaining teams for over 95% of the resampled iterations (Supplementary Fig. 4 and Supplementary Table 6); however, the third through fourteenth ranked teams were not statistically different (Supplementary Tables 6 and 7).
Of the 44 submissions, 23 used all six profiling data sets to make their predictions, 8 used five data sets, 4 used three data sets, 5 used two data sets and 4 used one data set. We compared the average rank performance of teams that used all six profiling data sets to teams using five or fewer data sets, but did not find a significant difference in their performance (average rank 22.7 versus 22.3). We explored several additional variables (missing values being imputed, outside information being used, method category) and found that only the inclusion of outside information in the form of annotated biological pathways26,27 or published drug response data sets1,3,4 improved the average team rank (17.4 versus 24.9; one-sided, Wilcoxon rank-sum test, p = 0.03).
The observation that integrating predictions across multiple, independent teams produces the most robust score has been previously made25. For such a ‘wisdom of crowds’ phenomenon to hold, individual predictions must provide complementary information derived from independent methods. We tested this phenomenon and found that the wisdom of crowds resulted in better performance (Supplementary Fig. 5a), along with increasingly robust predictions (i.e., greater mean, lower variance), by integrating greater numbers of teams (Supplementary Fig. 5b). Furthermore, predictions from the aggregation of a random subset of methods were very often better than the best of the individual methods in that subset (Supplementary Fig. 5c). These results indicate that individual team methods do provide complementary sets of predictions.
Top-performing methods exploit nonlinear modeling
The top-performing team from Aalto University and the University of Helsinki (co-authors on this manuscript) developed a machine-learning method that integrates multiple profiling data sets and knowledge-enhanced data representations into a nonlinear, probabilistic regression model to learn and predict drug sensitivities for all drugs simultaneously (Fig. 3 and Supplementary Note 1; source code provided as Supplementary Software). Their Bayesian multitask multiple kernel learning (MKL) method leveraged four machine-learning principles: kernelized regression, multiview learning, multitask learning, and Bayesian inference.
Figure 3.
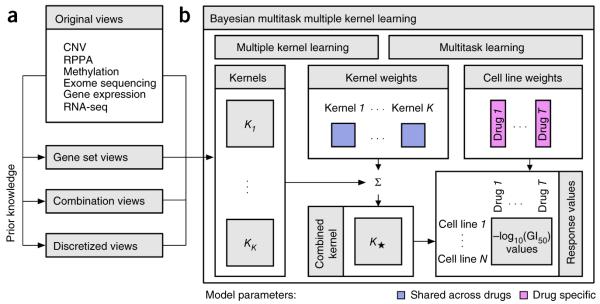
The method implemented by the best performing team. (a) In addition to the six profiling data sets, three different categories of data views were compiled using prior biological knowledge, yielding in total 22 genomic views of each cell line. (b) Bayesian multitask MKL combines nonlinear regression, multiview learning, multitask learning and Bayesian inference. Nonlinear regression: response values were computed not directly from the input features but from kernels, which define similarity measures between cell lines. Each of the K data views was converted into an N_×_N kernel matrix Kk (k = 1,…_,K_), where N is the number of training cell lines. Specifically, the Gaussian kernel was used for real-valued data, and the Jaccard similarity coefficient for binary-valued data. Multiview learning: a combined kernel matrix K* was constructed as a weighted sum of the view-specific kernel matrices Kk, k = 1,…,K. The kernel weights were obtained by multiple kernel learning. Multitask learning: training was performed for all drugs simultaneously, sharing the kernel weights across drugs but allowing for drug-specific regression parameters, which for each drug consisted of a weight vector for the training cell lines and an intercept term. Bayesian inference: the model parameters were assumed to be random variables that follow specific probability distributions. Instead of learning point estimates for model parameters, the parameters of these distributions were learned using a variational approximation scheme.
The underlying model was kernelized regression, a regression approach that computes outputs from similarities between cell lines, which is analogous to the usage of kernel methods in classification tasks (e.g., support vector machines). In contrast, other regression approaches compute outputs directly from the input features. The kernel formulation28,29 has two advantages. First, it reduces the number of model parameters to match the number of samples (training cell lines) and not the number of features. Second, it captures nonlinear relationships between genomic and epigenomic features, and cell-line drug sensitivities.
In multiview learning, heterogeneous input data (views) are integrated into a single model. This makes it possible to include not only different profiling data sets but also various representations of the same data set. For example, gene expression values can be summarized at the pathway level. We use the term ‘view’ to describe these representations (analogous to views in a database). Besides the original profiling data sets, three types of computed data views were considered, including gene set summaries, data combinations, and data discretization (Fig. 3a). Sets of related genes, defined in the MSigDB27,30 collections C2 (curated gene sets) and CP (canonical pathways), were used to calculate aggregated gene set views (average value for expression data, otherwise maximum). Data combination views were calculated as the product of individual data sets or according to the PARADIGM algorithm31. Finally, discretized views were compiled by binarizing continuous measures. A total of 22 views were generated. For the kernelized regression, each of the views was converted into a kernel matrix containing pair-wise similarities between all cell lines. Gaussian kernels were used for real-valued views and Jaccard similarity coefficients for binary-valued views. To integrate the views, the team modeled a global similarity matrix as a weighted sum of the view-specific kernel matrices. This approach is known as multiple kernel learning or MKL32 (Fig. 3b, left). The kernel weights reflect the relevance of each view for predicting drug sensitivities; the corresponding model parameters are shared across drugs.
The sharing of information between drugs, implying simultaneous modeling of drug sensitivities across all the drugs, is called multitask learning33 (Fig. 3b, right). Here, the kernel weight parameters were shared, providing robustness to the overall model. The second set of model parameters comprises the core parameters of kernelized regression, which were drug-specific: for each drug, there was a vector of weights for the training cell lines and an individual intercept term. To handle the uncertainty resulting from the small sample size, all model parameters were learned by Bayesian inference, assuming for each model parameter a specific probability distribution, where parameters were learned using a computationally efficient variational approximation scheme (Supplementary Note 1).
After being benchmarked against the Genomics of Drug Sensitivity in Cancer (GDSC) data set3, the Bayesian multitask MKL method was applied to the NCI-DREAM test cell lines. By training the model with all 22 views, predictive performance was improved by 9% over using only the six profiling data sets, yielding a final _wpc_-index = 0.583 (one-sided, _t-_test from random predictions, FDR = 2.5 × 10−5; scaled _wpc_-index = 0.629).
The second-best performing team of Qian Wan and Ranadip Pal from Texas Tech University leveraged the strengths of random forest regression34 to account for nonlinearities in the NCI-DREAM data (Supplementary Note 1). First, an ensemble of unpruned regression trees with random feature selection was compiled based on a bootstrapped sampling of a given profiling data set. For each profiling data set, a final model based on averaging of predictions over the collection of trees was generated. Each model was then weighted according to its least-squares fit to the training drug sensitivity data. The final predictions were calculated as the weighted sum of all six profiling data set models, yielding a final _wpc_-index = 0.577 (one-sided, _t_-test, FDR = 7.2 × 10−5; scaled _wpc_-index = 0.620). For this approach, the most informative profiling data sets were gene expression followed by methylation.
Profiling data sets provide nonredundant predictive signals
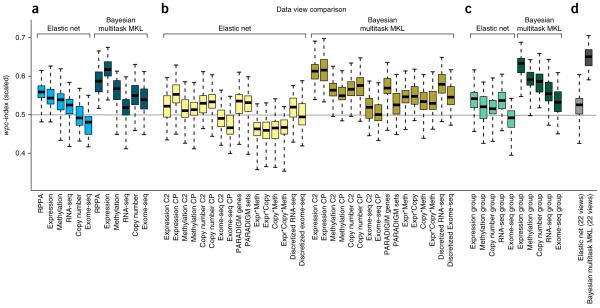
We used the insights provided by participating teams in a post-challenge comparative analysis between the Bayesian multitask MKL method (kernel 1) and an elastic net to characterize the predictive power of the original six profiling data sets. Teams most often reported that gene expression microarrays carried the greatest weight in their models (Supplementary Note 1). We tested this observation by performing 50 independent simulations of the NCI-DREAM challenge, randomly splitting all data sets into 35 training and 18 test cell lines, balanced for breast cancer subtype. To establish a baseline performance, we chose an elastic net model because it had been used previously1, was widely used by teams (Supplementary Note 1), and could be easily applied off-the-shelf (glmnet R package35). Averaged across all tested drugs, we found that the RPPA data showed the highest performance for the elastic net, followed closely by gene expression data (Fig. 4a). The Bayesian multitask MKL performed better than the elastic net using the RPPA data (one-sided, Wilcoxon signed-rank test, FDR = 1.3 × 10−6), and Bayesian multitask MKL using gene expression data significantly outperformed the use of RPPA data (two-sided, Wilcoxon signed-rank test, FDR = 1.3 × 10−6). For both methods, the performance varied across individual drugs (Supplementary Fig. 6). We also examined the effect of profiling data sets on drug classes (as defined in Supplementary Table 8) and found that for Bayesian multitask MKL, the ‘Signaling growth’ drugs had higher predictive scores in general, with gene expression and RPPA data being the data sets with the most predictive power (Supplementary Fig. 6).
Figure 4.
Performance comparison of data set views. The top-performing method, Bayesian multitask MKL, and an elastic net predictor were trained on (a) the original profiling data sets, (b) computed views, (c) groups of data views, and (d) the fully integrated set of all data views. Boxplots represent the distribution of 50 random simulations matching the NCI-DREAM challenge parameters, where whiskers indicate the upper and lower range limit, and the black line, the median. (b) The computed views were derived from gene sets, combined data sets, calculated as the product of values between data sets, and discretizing continuous measures into binary values. (c) Data view groups were defined as all views derived from one profiling data set. (d) For Bayesian multitask MKL, the integration of all data views achieves the best performance. Gene expression is the most predictive profiling data set, slightly outperformed by gene set views of expression data and the integration of original and gene set expression data.
Between the six profiling data sets, we explored the issue of data complementarity and redundancy, specifically, which data set combinations provide performance gains over single data sets. For the Bayesian multitask MKL method, we found that exome sequencing data best complemented gene expression data, whereas for the elastic net, methylation data best complemented gene expression data. For both methods, all other data sets were best complemented by gene expression, to varying degrees (Supplementary Fig. 7). Additionally, by evaluating methods trained with five instead of the full six profiling data sets, we identified methylation as the most independent, non-redundant profiling data set because removing methylation showed the largest average drop in performance (Supplementary Figs. 7 and 8).
In addition to the original data sets, we explored the performance of computed data views, as defined in the previous section. For both methods, gene set views (CP and C2) showed improved performance for copy number variation (CNV) data compared to the original data. In contrast, discretization of RNA-seq data improved the performance only with Bayesian multitask MKL and not with the elastic net. Comparing all computed views, the gene set view (CP) of gene expression data achieved the best performance for both methods (Fig. 4b). Finally, we tested whether all views for a single profiling data set (original data set plus computed views) could be integrated to improve performance. For the elastic net, we only found a slight gain in performance for the RNA-seq and CNV groups, whereas the Bayesian multitask MKL method showed performance gains for all groups except for exome sequencing (Fig. 4c), with the top-performing group coming from gene expression data. Notably, the fully integrated model of all 22 data views improved performance against the gene expression group (one-sided, Wilcoxon signed-rank test, FDR = 7.3 × 10−7; Fig. 4d). Taken together, these results suggest that gene expression data provides the most predictive power for any individual profiling data set. Also, predictive power can be gained within a data set by generating new computational views that integrate across profiling data sets and incorporate prior knowledge. Notably, this improvement comes with no additional experimental cost (Supplementary Figs. 9 and 10).
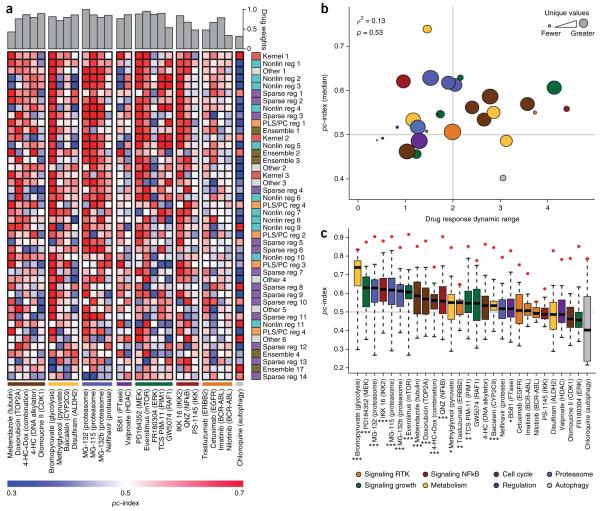
A predictive signal can be identified for most drugs
Teams were scored according to their ability to rank cell lines across all 28 tested therapeutic compounds. Here, we explored teams’ abilities to predict individual drug response. Inhibition of cell growth was predicted well for some compounds (e.g., bromopyruvate (glycolysis), PD184352 (MEK)), whereas for other compounds, teams generally performed poorly (e.g., chloroquinine (autophagy), FR180304 (ERK)) (Fig. 5a). To characterize factors that influence compound predictability, we measured the Pearson correlation between the _pc_-index and a compound’s dynamic range (minimum to maximum −log10(GI50) values). A mild positive trend exists (ρ = 0.14), though it is not statistically significant (p = 0.49) (Fig. 5b). We found that proteasome inhibitors tend to be predicted more accurately than other drug classes (as defined in Supplementary Table 8), though with a relatively small number of compounds in each class, this analysis is not well-powered. One factor that did confound our assessment of individual drug performance was the number of −log10(GI50) values measured for a drug (Fig. 5b). That is, missing values and multiple cell lines with the same measured response resulted in underpowered, drug-specific statistics. This observation is the basis for weighting drugs to calculate the _wpc_-index score.
Figure 5.
Prediction performance on individual drugs. Prediction algorithms are indexed and colored according to Table 1. (a) The heatplot illustrates participant performance on individual drugs, grouped by drug class (values can be found in Supplementary Table 9). Drug weights, which take into account the number of missing values and the noise in the −log10(GI50) measurements, are displayed at the top of the heatplot. Team submissions are ordered according to their overall performance from best performer at the top of the list. (b) The dynamic range of drugs across all cell lines was compared to the median team score. The node size reflects the number of distinct −log10(GI50) values for each drug across all 53 cell lines. The node colors reflect mode-of-action classes. The gray horizontal line is the mean score of random predictions and the vertical gray line separates low dynamic range (<2) from high dynamic range (>2), where dynamic range for a drug is the maximum −log10(GI50) − minimum −log10(GI50). (c) The distribution of team scores (n = 44) for individual drugs was compared to the null model of random predictions (gray line where _pc_-index = 0.5). The red points correspond to the maximum possible pc index (pc index of gold standard in the test data). On average, 21/28 drugs performed better than the null model; using the Kolmogorov-Smirnov test, 16/28 drugs were significantly better than the null model (*FDR < 0.05; **FDR < 0.01; ***FDR < 0.001).
We further assessed the predictability of individual drugs by comparing the distribution of team predictions to a random model and found that 21/28 drugs performed better than the average null model, and 16/28 drugs were significantly better (Kolmogorov-Smirnov test, FDR < 0.05; Fig. 5c). This strongly indicates that a predictive signal is being identified by a majority of teams for more than half of the tested compounds. Further, these observations demonstrate that it is possible to identify predictive features for compounds representing diverse modes of action. We also quantified the gap in performance between team predictions and the best possible ranking (as defined by the rank order of the test cell lines). Across 28 compounds, the Bayesian multitask MKL method accounted for 73% of the maximum possible score, with the second-best performing team accounting for 71% of the maximum possible signal. Although promising, this indicates that these drug sensitivity predictions could benefit from further refinement.
DISCUSSION
Over a period of 5 months, 127 researchers focused their time and efforts on addressing the challenge of drug sensitivity prediction. To our knowledge, no previous studies have assessed a comprehensive benchmarked set of algorithms for predicting therapeutic response based on genomic, epigenomic, and proteomic profiles of untreated cells. The Bayesian multitask MKL method provides an excellent example of how the NCI-DREAM challenge drove innovation in algorithm development. Considering all 44 submitted methods, the insights gained provide a valuable resource for future algorithm development (Supplementary Note 1).
In particular, our analysis of this collection of algorithms revealed several insights about predicting drug sensitivity. First, we found that modeling nonlinearities in the data was a common component of top-performing methods. Second, the Bayesian multitask MKL method showed improved performance by learning weights for the input data sets. Sharing the weights across drugs provided greater robustness of the prediction model and resulted in an increased overall performance, particularly for the drugs with many missing values. Finally, the application of prior knowledge, particularly in the form of biological pathways, improved drug sensitivity predictions. This was demonstrated in the Bayesian multitask MKL method through data views, though many top-performing teams implemented similar approaches to leverage pathway information.
We observed that gene expression was the most informative data set in many approaches, which may partly reflect the fact that analysis tools for this data type are more abundant and advanced. That is, we do not yet know the best approaches to extract predictive information from the other large profiling data sets; in particular the sparsity of exome sequencing data requires novel analysis methods36. However, when combined with expression data, these other data sets can enhance prediction performance.
The analysis of individual compounds showed that predictors of response could be robustly identified for the majority of compounds tested. This suggests a prioritization scheme for identifying compounds and their associated signatures with the most promise for validation in patient populations. Both targeted and nontargeted compounds, as well as those with both high and low dynamic ranges of response could be predicted, indicating that predictive features are present in the profiling data sets for a diverse array of drug mechanisms.
The −log10(GI50) drug response measurement used in this study represents one available metric to quantify drug response. Recent studies have demonstrated that dose-response curves can be parameterized in many meaningful ways1,37. It is possible that applying the algorithms assessed here to other parameters of the curves would yield more robust predictions for some of the compounds for which predictions were poor. In addition, the −log10(GI50) reflects the combined effect of growth inhibition and apoptosis, two related but distinct processes that can be modeled separately, and even targeted separately as a cancer treatment strategy38. Expanding the measurements to include endpoints that mediate oncogenic behavior of cells39 would allow for improved model construction and has recently been shown to be experimentally and technologically feasible40.
A limitation of this work is the small number of cell lines and compounds tested. The efforts by NCI-DREAM participants have laid the groundwork for the development of improved drug sensitivity models that can be applied to newly generated data sets1,3. Another consideration is that preclinical work is only a very early step in the translation to clinical samples. Now that genomic, epigenomic and/or proteomic profiles are frequently a component of clinical trials (e.g., I-SPY 2 Trial: http://www.ispy2.org/), these data will be available to test and refine models developed from this challenge in human trials. Moreover, participants were not given any information about the mode of action, target or chemical structure of the compounds, which could be included as additional features for the models22.
The success of precision medicine will depend on our ability to translate large compendia of genomic, epigenomic, and proteomic data into clinically actionable predictions. Examples such as the recent Sage Bionetworks-DREAM breast cancer prognosis challenge41 and this NCI-DREAM drug sensitivity challenge demonstrate the evolution of challenge-based competitions, resulting in rapid advancement of robust algorithms and establishment of benchmarked models. Equally important, challenge-based competitions build the critical mass of collaborative scientists necessary to address fundamental biomedical questions42. The evolution of the DREAM project will continue as the challenges in biomedical research expand to the genome scale.
ONLINE METHODS
Challenge data and gold standard
The NCI-DREAM drug sensitivity prediction challenge is outlined in Figure 1. A total of seven data sets were provided for 53 breast cancer cell lines, as discussed in detail in two recent publications: Heiser et al.4 and Daemen et al.23. The cell lines were selected to represent the major, clinically relevant subtypes of breast cancer, including luminal, basal, claudin-low, ERBB2-amplified, and nonmalignant. The drugs were selected based on data availability (on average, drugs were tested on 80% of the 53 cell lines) and novelty (drug response data were unpublished, not distributed throughout the community of participants, and not available from other sources (Supplementary Note 4)). Most of the included drugs have not been tested clinically in breast cancer, and therefore have the potential to serve as novel therapeutics.
A total of six genomic, epigenomic and proteomic profiling data sets were collected from untreated cells in growth conditions. Descriptions of each profiling data set can be found in the annotation files associated with each data set supplied through the DREAM website (http://www.the-dream-project.org/). Not all profiling data were collected for every cell line, and drugs were not equally sampled across all of the cell lines.
- (1) DNA copy-number variation (CNV). Affymetrix Genome-Wide Human SNP6.0 Array. Copy number ratios were estimated relative to a set of 20 normal samples, and data were segmented using circular binary segmentation (CBS)43;
- (2) Transcript expression values. Affymetrix GeneChip Human Gene 1.0 ST microarrays were processed using the R package aroma.affymetrix44 (over 18,000 expression values);
- (3) Whole exome sequencing (exome seq). Mutation status was obtained from exome-capture sequencing (Agilent Sure Select system). Mutations across all cell lines were filtered as follows: (i) average sum of the base quality scores of all mismatches in the reads containing the mutant allele ≤ 20; (ii) average number of other mismatches in the reads ≤ 1.5; (iii) average distance of the mutant alleles to the 3′ end of their respective reads between 0.2 and 0.8; (iv) mutant allele read support ≥ 4; (v) number of reads per variant supporting either the reference or mutant allele < 400 (over 33,000 reported mutations);
- (4) RNA sequencing data (RNA-seq). RNA-seq libraries were prepared using the TruSeq RNA Sample Preparation Kit (Illumina) and Agilent Automation NGS system per manufacturers’ instructions. Expression analysis was performed with the ALEXA-seq software package45 (just under 37,000 RNAs);
- (5) DNA methylation data. The Illumina Infinium Human Methylation27 BeadChip Kit was used for the genome-wide detection of 27,578 CpG loci, spanning 14,495 genes46. GenomeStudio Methylation Module v1.0 was used to express the methylation for each CpG locus as a value between 0 (completely unmethylated) and to 1 (completely methylated) (over 27,000 CpGs);
- (6) RPPA. An antibody-based method to quantitatively measure protein abundance. RPPA data were generated and preprocessed as previously described47 (131 proteins assayed).
In addition to the profiling data, drug response for each of the 53 cell lines to 28 drugs was tested. Dose-response curves were generated and the GI50[M] was calculated. To estimate the GI50, a series of assays were done, as previously described48. Briefly, cells were treated for 72 h with a set of nine doses of each compound in 1:5 serial dilution. Cell viability was determined using the Cell Titer Glo assay. We used nonlinear least-squares to fit the data with a Gompertz curve. The fitted curve was transformed into a GI curve using the method (http://dtp.nci.nih.gov/branches/btb/ivclsp.html) described in Monks, et al.49. In cases where the underlying growth data were of high quality, but the GI50 was not reached, the values were set to the highest concentration tested. The drug response data were filtered according to previously described criteria4. All reported drug response values and calculations for scoring were done using −log10(GI50). The complete set of unfiltered raw drug response data is in Supplementary Table 2.
Participants were supplied with the full set of profiling data for all of the cell lines and drug response data for 35 (of the 53) cell lines for all 28 drugs. The gold-standard evaluation data set consisted of drug response data for the remaining 18 cell lines, which were hidden from the participants. Cell lines were assigned to the training and test data sets to ensure a balanced set of breast cancer subtypes.
Participants were challenged to predict a ranked list of the most sensitive (to be ranked first) to most resistant (to be ranked last) cell lines for each individual drug across all the 18 test cell lines. We note that the drug response values, −log10(GI50), ranked from highest to lowest values, correspond to a ranking of the most-sensitive to the most-resistant cell lines. Assessment of predictions was based on participant’s ranking of the 18 test cell lines. Participants supplied their final submission as a comma-separated text file with the drugs listed as columns and cell lines listed as rows. The cells in the matrix represent ranks of each cell line for a given drug.
Team scoring
Drug response measurements, −log10(GI50), are subject to noise. To account for these uncertainties, a pooled variance,
sd2=Σi=1n(ri−1)si2Σi=1n(ri−1),
was calculated for each tested drug individually, d, over n = 53 cell lines, where ri and si2 are the replicate number and variance of the ith cell lines, respectively. There were several drugs (bromopyruvate (glycolysis), chloroquine (autophagy), GW5074 (RAF1), and QNZ (NFκB)) with low replicate numbers; in these instances, the global pooled variance across all drugs and cell lines was used. Values used to calculate the pooled variance can be found in Supplementary Table 10. The pooled variance was then taken into account when scoring team submissions as described in the following section.
The final team submissions were evaluated using two independent scoring methods. The first scoring method, a weighted, probabilistic concordance-index (_wpc_-index), was used to report the final team rankings of the challenge. The second method, a resampled Spearman correlation, was used to verify the consistency between team rankings based on a separate scoring method and implementation. Team scores were then subjected to a resampled, robustness analysis to ensure team rankings were not affected by perturbations to the gold-standard test cell lines. Team scores were based on the set of 18 test cell lines.
Weighted probabilistic concordance-index (_wpc_-index)
The concordance index (_c_-index) is a nonparametric scoring method that provides a measure of similarity between two lists of measurements or ranks24. For a detailed description of the scoring methodology, see Supplementary Note 3.
Resampled Spearman correlation
The key idea motivating this scoring metric is to compare the predicted ranked list for each drug, d, and n cell lines (n = 18 for the set of test cell lines), Rd = (_r_1, _r_2,…, rn) against an ensemble of t different possible realizations of the gold standard, Ĝ d,t = (G d,1,G d,2, …,G d,t), for the same drug and cell lines, where each realization Gd is defined as Gd = (_g_1, _g_2,…, gn). Each of the possible t realizations of the gold-standard samples a drug’s −log10(GI50) dose in a cell line from the normal distribution, N(xd,n, sd) where xd,n is the sample mean of the drug response for d and cell line n, and sd is the pooled s.d. for d over all tested cell lines. The ensemble of gold standards, Ĝd,t, is then converted into ranked gold-standard cell lines, Rd∗. Afterwards we compared these rank gold-standard cell lines to the predicted ranks, Rd:
Spearmancorrelationρ(Rd∗,Rd)=Σt=1n(Rd,t−R‒d)(Rd,t∗−R‒d∗)Σt=1n(Rd,t−R‒d)2Σt=1n(Rd,t∗R‒d∗)2,
where R‒d∗ and R̄d are the mean gold standard ranks and predicted rank, respectively.
Robustness analysis
To ensure team rankings are robust to perturbations in the gold-standard data set, a subsampling analysis was performed. A set of t = 10,000 evaluation data sets, E=(G1′,G2′…Gt′), was generated where 10% of the gold-standard data set, G, was randomly masked to create _G_′. All predictions in E were scored to create an empirical null distribution of _wpc_-index scores. Individual teams were rescored using _G_′ and compared to the null distributions using a single-sample, two-sided, Student’s _t_-test. FDRs were calculated using the Benjamini-Hochberg correction. In addition to the _wpc_-index, on each iteration, submissions were re-ranked to create a distribution of team ranks, which were compared using the Wilcoxon signed-rank test.
Data view analysis
Besides the six profiling data sets supplied in the challenge, additional views were constructed by challenge organizers (discretized RNA-seq) and by the top-performing team (discretized exome sequencing, gene set summaries for individual data types and genewise combination of two or more data sets). The analysis of individual and grouped data views was done using the Bayesian multitask MKL method from the top-performing team and an elastic net linear regression implemented in the R package, glmnet35. A total of 50 simulations of the challenge were run by randomly selecting 35 training and 18 test cell lines, keeping the subtypes of cell lines balanced.
At each iteration of the challenge simulations, the Bayesian multitask MKL method was applied using a single view or a group of views as input data. The elastic net was learned using the same training and test cell lines as the Bayesian multitask MKL method and modeling each drug separately. For each selection of input views and each drug, an elastic net regression model was learned, where regularization parameters were selected by fivefold cross-validation on the training data, using α values from 0 to 1 in increments of 0.1 and the default λ sequence. The final prediction model was trained on all training cell lines, using the parameters with minimal cross-validation error. Elastic net models were first trained using all features in a data set, but performance was poor due to the high dimensionality compared to low sample size. Thus, for data sets with more than 5,000 features, only the top 10% most-variable features were used. For the analysis of multiple grouped views, a simple data concatenation approach was first tried, but resulted in decreased performance due to an increase in the number of input features. Therefore, a fraction of 12 top-varying features was kept for each view when integrating K views. Statistical significance was calculated using the Wilcoxon signed-rank test and FDR corrected.
Data deposition
The NCI-DREAM data set is a subset of the data reported in Daemen et al.23 Genome copy number data has been deposited at the European Genome-Phenome Archive (http://www.ebi.ac.uk/ega/), hosted at the EBI (accession numbers EGAS00000000059 and EGAS00001000585). Gene expression data for the cell lines were derived from Affymetrix GeneChip Human Genome U133A and Affymetrix GeneChip Human Exon 1.0 ST arrays. Raw data are available in ArrayExpress (http://www.ebi.ac.uk/arrayexpress), hosted at the EBI (accession number E-TABM-157 and E-MTAB-181). RNA-seq and exome-sequencing data can be accessed at the Gene Expression Omnibus (GEO) (http://www.ncbi.nlm.nih.gov/geo/), accession number GSE48216. Genome-wide methylation data for the cell lines are also available through GEO, accession number GSE42944. Scripts to perform the _wpc_-index and resampled Spearman scoring can be found on the DREAM website (http://www.the-dream-project.org/). Source code for the Bayesian multitask MKL method can be found as Supplementary Software.
Supplementary Material
Supplemental analysis
Supplementary Software - Top performing team code
Supplementary figures 1-11 and Supplementary notes 1-4
Supplementary tables 1-10
ACKNOWLEDGMENTS
The data were kindly provided before publication for this challenge by J.W.G. We acknowledge the contributions of all participants in the co-organized NCI and DREAM Summit held on April 23, 2012, for the development of the challenge (http://www.the-dream-project.org/sites/the-dream-project.org/files/documents/dream7/dream_participant_list.docx). This work is supported in part by the following: MaGNeT grant (5U54CA121852-08); National Institutes of Health, National Cancer Institute grant U54 CA 112970; Stand Up To Cancer-American Association for Cancer Research Dream Team Translational Cancer Research grant SU2C-AACR-DT0409; Prospect Creek Foundation; Howard Hughes Medical Institute (HHMI); and The Academy of Finland (Finnish Center of Excellence in Computational Inference Research COIN, grant nos. 251170 and 140057).
We acknowledge the computational resources provided by Aalto Science-IT project.
9. NCI-DREAM Community
Jean-Paul Abbuehl15, Tero Aittokallio7, Jeffrey Allen16, Russ B Altman17, Muhammad Ammad-ud-din4, Shawn Balcome18, Mukesh Bansal6, Alexis Battle19, Andreas Bender20, Bonnie Berger21, Jonathan Bernard15, Madhuchhanda Bhattacharjee22,23, Krithika Bhuvaneshwar24, Andrew A Bieberich25, Fred Boehm26,27, Andrea Califano6, Christina Chan28–30, Beibei Chen16, Ting-Huei Chen31, Jaejoon Choi32, Luis Pedro Coelho33, Thomas Cokelaer5, James C Collins1,2,10, James C Costello1,2,13, Chad J Creighton34, Jike Cui35, Will Dampier36, V Jo Davisson25, Bernard De Baets37, Raamesh Deshpande18, Barbara DiCamillo38, Murat Dundar39, Zhana Duren40, Adam Ertel41, Haoyang Fan26,27, Hongbin Fang42, Dan Gallahan11, Robinder Gauba24, Elisabeth Georgii4, Mehmet Gönen4, Assaf Gottlieb17, Michael Grau43, Joe W Gray3, Yuriy Gusev24, Min Jin Ha31, Leng Han44, Michael Harris24, Laura M Heiser3, Nicholas Henderson26,27, Hussein A Hejase45, Petteri Hintsanen7, Krisztian Homicsko15, Antti Honkela8, Jack P Hou46, Woochang Hwang32, Adriaan P IJzerman47, Olli Kallioniemi7, Bilge Karacali48, Samuel Kaski4,8, Sunduz Keles26,27, Christina Kendziorski26,27, Suleiman A Khan4, Junho Kim32, Min Kim16, Youngchul Kim49, David A Knowles19, Daphne Koller19, Junehawk Lee32,50, Jae K Lee49, Eelke B Lenselink47, Biao Li51, Bin Li35, Jun Li44,52, Han Liang44,53, Jian Ma46, Subha Madhavan24,54, Michael P Menden5, Sean Mooney51, John-Patrick Mpindi7, Chad L Myers18, Michael A Newton26,27, John P Overington55, Ranadip Pal56, Jian Peng57, Richard Pestell36, Robert J Prill58, Peng Qiu59, Bartek Rajwa60, Anguraj Sadanandam15, Julio Saez-Rodriguez5, Francesco Sambo38, Hyunjin Shin35, Dinah Singer11, Jiuzhou Song61, Lei Song24, Arvind Sridhar62, Michiel Stock37, Gustavo Stolovitzky12, Wei Sun31, Tram Ta26,27, Mahlet Tadesse63, Ming Tan42, Hao Tang16, Dan Theodorescu64, Gianna Maria Toffolo38, Aydin Tozeren36, William Trepicchio35, Nelle Varoquaux65–67, Jean-Philippe Vert65–67, Willem Waegeman37, Thomas Walter65–67, Qian Wan56, Difei Wang24,54, Nicholas J Wang3, Wen Wang18, Yong Wang40, Zhishi Wang26,27, Joerg K Wegner68, Krister Wennerberg7, Tongtong Wu69, Tian Xia18, Guanghua Xiao16, Yang Xie16, Yanxun Xu44,70, Jichen Yang16, Yuan Yuan44,53, Shihua Zhang40, Xiang-Sun Zhang40, Junfei Zhao40, Chandler Zuo26,27, Herman W T van Vlijmen68 & Gerard J P van Westen55
15Swiss Institute for Experimental Cancer Research (ISREC), Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, Switzerland. 16Quantitative Biomedical Research Center, University of Texas Southwestern Medical Center, Dallas, Texas, USA. 17Departments of Genetics and Bioengineering, Stanford University, Stanford, California, USA. 18Department of Computer Science and Engineering, University of Minnesota, Minneapolis, Minnesota, USA. 19Department of Computer Science, Stanford University, Palo Alto, California, USA. 20Unilever Centre, Cambridge University, Cambridge, UK. 21Computer Science and Artificial Intelligence Laboratory, MIT, Cambridge, Massachusetts, USA. 22Department of Statistics, University of Pune, Pune, India. 23School of Mathematics and Statistics, University of Hyderabad, Hyderabad, India. 24Innovation Center for Biomedical Informatics, Georgetown University Medical Center, Washington, DC, USA. 25Department of Medicinal Chemistry and Molecular Pharmacology, Purdue University, W. Lafayette, Indiana, USA. 26Department of Statistics, University of Wisconsin, Madison, Wisconsin, USA. 27Department of Biostatistics and Medical Informatics, University of Wisconsin, Madison, Wisconsin, USA. 28Department of Computer Science and Engineering, Michigan State University, East Lansing, Michigan, USA. 29Department of Chemical Engineering and Materials Science, Michigan State University, East Lansing, Michigan, USA. 30Department of Biochemistry and Molecular Biology, Michigan State University, East Lansing, Michigan, USA. 31Department of Biostatistics, University of North Carolina, Chapel Hill, North Carolina, USA. 32Korea Advanced Institute of Science and Technology, Daejeon, Korea. 33Instituto de Medicina Molecular, Faculdade de Medicina da Universidade de Lisboa, Lisbon, Portugal. 34Department of Medicine, Dan L. Duncan Center Division of Biostatistics, Baylor College of Medicine, Houston, Texas, USA. 35Translational Medicine, Millennium Pharmaceuticals, Cambridge, Massachusetts, USA. 36Center for Integrated Bioinformatics, Drexel University, Philadelphia, Pennsylvania, USA. 37Department of Mathematical Modelling, Statistics and Bioinformatics, Ghent University, Ghent, Belgium. 38Department of Information Engineering, University of Padova, Padova, Italy. 39Computer and Information Science Department, IUPUI, Indianapolis, Indiana, USA. 40National Center for Mathematics and Interdisciplinary Sciences, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, China. 41Jefferson Kimmel Cancer Center, Drexel University, Philadelphia, Pennsylvania, USA. 42Department of Biostatistics, Bioinformatics and Biomathematics, Georgetown University Medical Center, Washington, DC, USA. 43Department of Physics, University of Marburg, Marburg, Germany. 44Department of Bioinformatics and Computational Biology, The University of Texas MD Anderson Cancer Center, Houston, Texas, USA. 45Department of Computer Science and Engineering, Michigan State University, East Lansing, Michigan, USA. 46Department of Bioengineering and Institute for Genomic Biology, University of Illinois, Champaign-Urbana, Illinois, USA. 47Leiden Academic Center for Drug Research, University of Leiden, Leiden, Netherlands. 48Izmir Institute of Technology, Izmir, Turkey. 49Division of Biostatistics, University of Virginia School of Medicine, Charlottesville, Virginia, USA. 50Korea Institute of Science and Technology Information, Daejeon, Korea. 51Buck Institute, Novato, California, USA. 52CAS-MPG Partner Institute for Computational Biology, Key Laboratory of Computational Biology, Shanghai Institute for Biological Sciences, Chinese Academy of Sciences, Shanghai, P.R. China. 53Graduate Program in Structural and Computational Biology and Molecular Biophysics, Baylor College of Medicine, Houston, Texas, USA. 54Department of Oncology, Lombardi Comprehensive Cancer Center, Georgetown University Medical Center, Washington, DC, USA. 55ChEMBL Group, The EMBL-European Bioinformatics Institute, Cambridge, UK. 56Electrical and Computer Engineering, Texas Tech University, Lubbock, Texas, USA. 57Computer Science and Artificial Intelligence Laboratory, MIT, Cambridge, Massachusetts, USA. 58IBM Almaden Research Center, IBM Almaden Research Center, San Jose, California, USA. 59Department of Bioinformatics and Computational Biology, University of Texas MD Anderson Cancer Center, Houston, Texas, USA. 60Bindley Bioscience Center, Purdue University, W. Lafayette, Indiana, USA. 61Department of Animal and Avian Science, University of Maryland, College Park, Maryland, USA. 62Embedded Systems Laboratory (ESL), Institute of Electrical Engineering, Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, Switzerland. 63Department of Mathematics and Statistics, Georgetown University, Washington, DC, USA. 64The University of Colorado Cancer Center, University of Colorado School of Medicine, Aurora, Colorado, USA. 65Centre for Computational Biology, Mines ParisTech, Fontainebleau, France. 66Institut Curie, Paris, France. 67INSERM U900, Paris, France. 68Janssen Pharmaceutica, Beerse, Belgium. 69Department of Biostatistics and Computational Biology, Rochester University Medical Center, Rochester, New York, USA. 70Department of Statistics, Rice University, Houston, Texas, USA.
Footnotes
Accession codes. EBI: EGAS00000000059 and EGAS00001000585, E-TABM-157 and E-MTAB-181. GEO: GSE48216 and GSE42944.
Note: Any Supplementary Information and Source Data files are available in the online version of the paper.
AUTHOR CONTRIBUTIONS
J.C.C., M.P.M., L.M.H., M.B., D.G., D.S., J.S.-R., J.J.C., J.W.G. and G.S. designed the challenge. The top-performing approach was designed by E.G., M.G., M.A., P.H., S.A.K., J.-P.M., O.K., A.H., T.A., K.W. and S.K. Data analysis for the top-performing approach was conducted by E.G., M.G., M.A., P.H., S.A.K. and S.K. M.G. and S.K. designed the Bayesian model and M.G. implemented the inference algorithm for the top-performing approach. The NCI-DREAM Community provided drug sensitivity predictions and Supplementary Note 1. descriptions. J.C.C., L.M.H. and M.P.M. performed analysis of challenge predictions. J.C.C., L.M.H., E.G., M.P.M., J.S.-R., S.K. and G.S. interpreted the results of the challenge and performed follow-up analyses for the manuscript. L.M.H., N.J.W. and J.W.G. generated experimental data. J.C.C., L.M.H., E.G., M.G., M.P.M., J.J.C., J.S.-R., S.K., J.W.G. and G.S. wrote the paper.
COMPETING FINANCIAL INTERESTS
The authors declare no competing financial interests.
References
- 1.Barretina J, et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature. 2012;483:603–607. doi: 10.1038/nature11003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cancer Genome Atlas Network Comprehensive molecular portraits of human breast tumours. Nature. 2012;490:61–70. doi: 10.1038/nature11412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Garnett MJ, et al. Systematic identification of genomic markers of drug sensitivity in cancer cells. Nature. 2012;483:570–575. doi: 10.1038/nature11005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Heiser LM, et al. Subtype and pathway specific responses to anticancer compounds in breast cancer. Proc. Natl. Acad. Sci. USA. 2012;109:2724–2729. doi: 10.1073/pnas.1018854108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.International Cancer Genome Consortium et al. International network of cancer genome projects. Nature. 2010;464:993–998. doi: 10.1038/nature08987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lamb J, et al. The Connectivity Map: using gene-expression signatures to connect small molecules, genes, and disease. Science. 2006;313:1929–1935. doi: 10.1126/science.1132939. [DOI] [PubMed] [Google Scholar]
- 7.Yang W, et al. Genomics of Drug Sensitivity in Cancer (GDSC): a resource for therapeutic biomarker discovery in cancer cells. Nucleic Acids Res. 2013;41:D955–D961. doi: 10.1093/nar/gks1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shoemaker RH. The NCI60 human tumour cell line anticancer drug screen. Nat. Rev. Cancer. 2006;6:813–823. doi: 10.1038/nrc1951. [DOI] [PubMed] [Google Scholar]
- 9.Wilson TR, et al. Widespread potential for growth-factor-driven resistance to anticancer kinase inhibitors. Nature. 2012;487:505–509. doi: 10.1038/nature11249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Curtis C, et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature. 2012;486:346–352. doi: 10.1038/nature10983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reis-Filho JS, Pusztai L. Gene expression profiling in breast cancer: classification, prognostication, and prediction. Lancet. 2011;378:1812–1823. doi: 10.1016/S0140-6736(11)61539-0. [DOI] [PubMed] [Google Scholar]
- 12.Sorlie T, et al. Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proc. Natl. Acad. Sci. USA. 2001;98:10869–10874. doi: 10.1073/pnas.191367098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van ‘t Veer LJ, et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- 14.Wu J, et al. Identification and functional analysis of 9p24 amplified genes in human breast cancer. Oncogene. 2012;31:333–341. doi: 10.1038/onc.2011.227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Howlader N, et al. SEER Cancer Statistics Review, 1975–2010. National Cancer Insitute; Bethesda, MD: 2013. [Google Scholar]
- 16.Stephens PJ, et al. The landscape of cancer genes and mutational processes in breast cancer. Nature. 2012;486:400–404. doi: 10.1038/nature11017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wood LD, et al. The genomic landscapes of human breast and colorectal cancers. Science. 2007;318:1108–1113. doi: 10.1126/science.1145720. [DOI] [PubMed] [Google Scholar]
- 18.Kao J, et al. Molecular profiling of breast cancer cell lines defines relevant tumor models and provides a resource for cancer gene discovery. PLoS ONE. 2009;4:e6146. doi: 10.1371/journal.pone.0006146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Neve RM, et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell. 2006;10:515–527. doi: 10.1016/j.ccr.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Daemen A, et al. Modeling precision treatment in breast cancer. Genome Biol. 2013;14:R110. doi: 10.1186/gb-2013-14-10-r110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bussey KJ, et al. Integrating data on DNA copy number with gene expression levels and drug sensitivities in the NCI-60 cell line panel. Mol. Cancer Ther. 2006;5:853–867. doi: 10.1158/1535-7163.MCT-05-0155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Masica DL, Karchin R. Collections of simultaneously altered genes as biomarkers of cancer cell drug response. Cancer Res. 2013;73:1699–1708. doi: 10.1158/0008-5472.CAN-12-3122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Menden MP, et al. Machine learning prediction of cancer cell sensitivity to drugs based on genomic and chemical properties. PLoS ONE. 2013;8:e61318. doi: 10.1371/journal.pone.0061318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harrell FE. Regression Modeling Strategies. Springer; New York: 2001. [Google Scholar]
- 25.Marbach D, et al. Wisdom of crowds for robust gene network inference. Nat. Methods. 2012;9:796–804. doi: 10.1038/nmeth.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kanehisa M, Goto S. KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schölkopf B, Smola AJ. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press; 2001. [Google Scholar]
- 29.Shawe-Taylor J, Cristianni N. Kernel Methods for Pattern Analysis. Cambridge University Press; New York, NY: 2004. [Google Scholar]
- 30.Liberzon A, et al. Molecular signatures database (MSigDB) 3.0. Bioinformatics. 2011;27:1739–1740. doi: 10.1093/bioinformatics/btr260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vaske CJ, et al. Inference of patient-specific pathway activities from multi-dimensional cancer genomics data using PARADIGM. Bioinformatics. 2010;26:i237–i245. doi: 10.1093/bioinformatics/btq182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gönen M, Alpaydin E. Multiple kernel learning algorithms. J. Mach. Learn. Res. 2011;12:2211–2268. [Google Scholar]
- 33.Caruana R. Multitask learning. Mach. Learn. 1997;28:41–75. [Google Scholar]
- 34.Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
- 35.Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010;33:1–22. [PMC free article] [PubMed] [Google Scholar]
- 36.Leiserson MD, Blokh D, Sharan R, Raphael BJ. Simultaneous identification of multiple driver pathways in cancer. PLoS Comput. Biol. 2013;9:e1003054. doi: 10.1371/journal.pcbi.1003054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fallahi-Sichani M, Honarnejad S, Heiser LM, Gray JW, Sorger PK. Comparing drug activity across cell line banks reveals systematic variation in properties other than potency. Nat. Chem. Biol. 2013;9:708–714. doi: 10.1038/nchembio.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kwong LN, et al. Oncogenic NRAS signaling differentially regulates survival and proliferation in melanoma. Nat. Med. 2012;18:1503–1510. doi: 10.1038/nm.2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 40.Rantala LM, Kwon S, Korkola JE, Gray JW. Expanding the diversity of image-based RNAi screen applications using cell spot microarrays. Microarrays. 2013;2:97–114. doi: 10.3390/microarrays2020097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Margolin AA, et al. Systematic analysis of challenge-driven improvements in molecular prognostic models for breast cancer. Sci. Transl. Med. 2013;5:181re1. doi: 10.1126/scitranslmed.3006112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Costello JC, Stolovitzky G. Seeking the wisdom of crowds through challenge-based competitions in biomedical research. Clin. Pharmacol. Ther. 2013;93:396–398. doi: 10.1038/clpt.2013.36. [DOI] [PubMed] [Google Scholar]
- 43.Venkatraman ES, Olshen AB. A faster circular binary segmentation algorithm for the analysis of array CGH data. Bioinformatics. 2007;23:657–663. doi: 10.1093/bioinformatics/btl646. [DOI] [PubMed] [Google Scholar]
- 44.Bengtsson H, Wirapati P, Speed TP. A single-array preprocessing method for estimating full-resolution raw copy numbers from all Affymetrix genotyping arrays including GenomeWideSNP 5 & 6. Bioinformatics. 2009;25:2149–2156. doi: 10.1093/bioinformatics/btp371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Griffith M, et al. Alternative expression analysis by RNA sequencing. Nat. Methods. 2010;7:843–847. doi: 10.1038/nmeth.1503. [DOI] [PubMed] [Google Scholar]
- 46.Fackler MJ, et al. Genome-wide methylation analysis identifies genes specific to breast cancer hormone receptor status and risk of recurrence. Cancer Res. 2011;71:6195–6207. doi: 10.1158/0008-5472.CAN-11-1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tibes R, et al. Reverse phase protein array: validation of a novel proteomic technology and utility for analysis of primary leukemia specimens and hematopoietic stem cells. Mol. Cancer Ther. 2006;5:2512–2521. doi: 10.1158/1535-7163.MCT-06-0334. [DOI] [PubMed] [Google Scholar]
- 48.Kuo WL, et al. A systems analysis of the chemosensitivity of breast cancer cells to the polyamine analogue PG-11047. BMC Med. 2009;7:77. doi: 10.1186/1741-7015-7-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Monks A, et al. Feasibility of a high-flux anticancer drug screen using a diverse panel of cultured human tumor cell lines. J. Natl. Cancer Inst. 1991;83:757–766. doi: 10.1093/jnci/83.11.757. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental analysis
Supplementary Software - Top performing team code
Supplementary figures 1-11 and Supplementary notes 1-4
Supplementary tables 1-10