Wishbone identifies bifurcating developmental trajectories from single-cell data (original) (raw)
. Author manuscript; available in PMC: 2016 Nov 2.
Published in final edited form as: Nat Biotechnol. 2016 May 2;34(6):637–645. doi: 10.1038/nbt.3569
Abstract
Recent single-cell analysis technologies offer an unprecedented opportunity to elucidate developmental pathways. Here we present Wishbone, an algorithm for positioning single cells along bifurcating developmental trajectories with high resolution. Wishbone uses multi-dimensional single-cell data, such as mass cytometry or RNA-seq data, as input and orders cells according to their developmental progression by pinpointing bifurcation points and labeling each cell as pre-bifurcation or as one of two post-bifurcation cell fates. Using 30-channel mass cytometry data, we show that Wishbone accurately recovers the known stages of T cell development in the mouse thymus, including the bifurcation point. We also apply the algorithm to mouse myeloid differentiation and demonstrate its generalization to additional lineages. A comparison of Wishbone to diffusion maps, SCUBA and Monocle shows that it outperforms these methods both in the accuracy of ordering cells and in the correct identification of branch points.
Introduction
Multi-cellular organisms develop from a single cell that undergoes many stages of proliferation and differentiation, resulting in a vast array of progenitor and terminal cell types. Although many of the key stages and cell populations in these processes have been characterized using fluorescence-activated cell sorting and genetic perturbations, much of development remains uncharted. Emerging high-throughput technologies such as single-cell RNA-seq [1] and mass cytometry [2] can measure a large number of parameters simultaneously in single cells and interrogate an entire tissue without perturbation. As many tissues maintain homeostasis through continuous and asynchronous development, this presents an opportunity to measure cells at almost all stages of maturity at high resolution. The challenge is to devise computational algorithms capable of exploiting this resolution to order cells based on their maturity and to identify the branch points that give rise to the full complement of functionally distinct cells.
Recently, several reports have demonstrated approaches to order single cells based on their maturity [3, 4]. However, these approaches assume non-branching trajectories and thus are poorly suited to model multiple cell fates. Two key challenges to constructing branching trajectories are ordering cells based on their developmental maturity, and associating cells to their respective developmental trajectories and identifying the branch point. Methods such as SCUBA [5] can identify branches in data, along with pseudo-temporal ordering of cells, but with considerable loss in temporal resolution and accuracy.
Here we present Wishbone, a trajectory detection algorithm for bifurcating systems. We use mass cytometry data measuring T cell development in mouse thymus, where lymphoid progenitors differentiate to either CD8+ cytotoxic or CD4+ helper T cells, to demonstrate the accuracy and robustness of Wishbone. The wishbone algorithm recovers the known stages in T cell development with high accuracy and developmental resolution. We order DN (1–4), DP, CD4+ and CD8+ cells from a single snapshot along a unified bifurcating trajectory. We show that Wishbone de novo recovers the known stages in T cell development with increased accuracy and resolution compared with competing methods. The resulting trajectory and branches match the prevailing model of T cell differentiation with the full complement of cell types.
We determine that a substantial part of heterogeneity in expression of developmental markers is explained by developmental maturity, rather than stochasticity in expression. Additionally, we apply Wishbone to early and late human myeloid differentiation data generated using mass cytometry [2] and mouse myeloid differentiation data generated using single-cell RNA-seq [6]. Wishbone successfully identifies maturation and branch-points in myeloid development de novo, demonstrating its broad applicability to systems with bifurcating trajectories across diverse single cell technologies.
Results
Learning bifurcating developmental trajectories
To infer a branching trajectory directly from data Wishbone makes the following assumptions about the data: (a) differentiation is a continuous process, (b) a snapshot of primary tissue represents the entire differentiation process and (c) the trajectory of a cell bifurcates to one of two fates. Differentiation is punctuated by the rise and fall of phenotypic markers, and thus standard distance metrics such as Euclidean metrics do not adequately capture the difference in maturity between two cells (Figure 1A). Similarly to our previous non-branching trajectory detection algorithm, Wanderlust [3], we use nearest-neighbor graphs to capture developmental distance and identify an initial ordering of cells using shortest paths (Online methods). Each node in the graph represents a cell, and edges connect each cell to its most similar cells based on expression (Figure 1A). Distances between cells can be computed using shortest paths, i.e., a series of short steps through the neighbors in the graph, where each step between closely related cells is likely to represent similarity in degree of maturity.
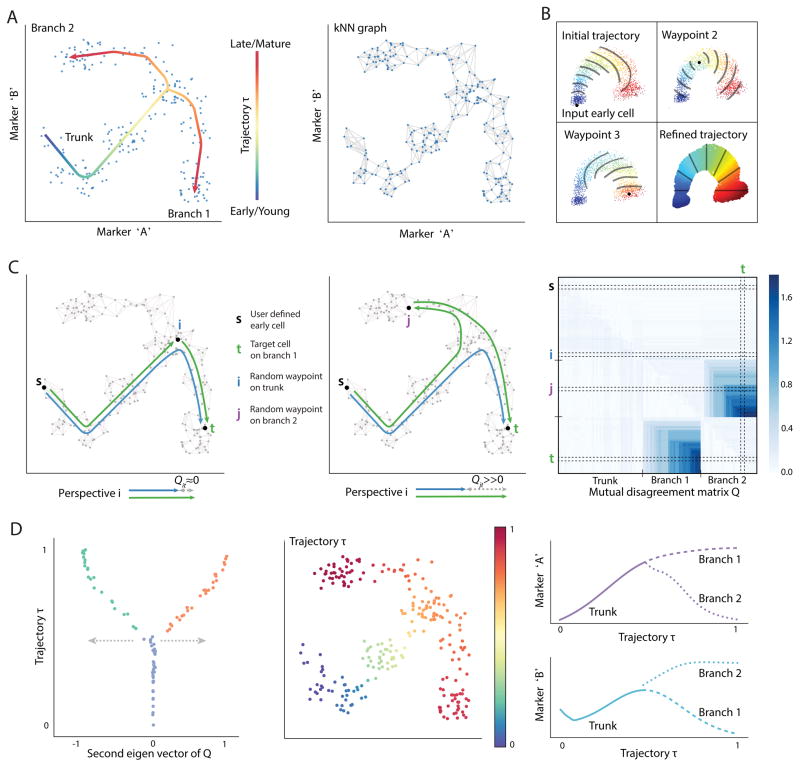
Figure 1. Alignment of cells along bifurcating trajectories.
(A) Wishbone aims to achieve high resolution ordering and branching of cells along bifurcating developmental trajectories. The data is represented as a _k_-nearest neighbor graph where each cell is a node and edges connect each cell to its most phenotypically similar cells. A cartoon depiction of a kNN graph is illustrated. The data depicted in this figure is simulated.
(B) Wishbone uses a set of cells called “waypoints” to guide the ordering of cells. An initial ordering is derived using the shortest path distances from the input early cell (top left panel). The distances from waypoints are aligned to the initial ordering to derive waypoint perspectives and the refined trajectory is determined as a weighted average of these perspectives (bottom right panel). The contour lines illustrate bands of cells that are at a similar distance from the corresponding waypoint.
(C) Waypoints are also used for branch point identification and branch associations. The difference between the shortest path of waypoint t from early cell and a path that goes through another waypoint i is ≈ 0 if i and t are on the same trajectory (left panel) and ≫ 0 if they are on different branches (middle panel). These disagreements accumulate in the presence of a true branch to create a mutual disagreement matrix Q: observed are two sets of waypoints that agree within the set and disagree between sets (right panel).
(D) The second Eigen vector of the Q matrix provides a summary of the disagreements with values ≈ 0 for waypoints on the trunk, > 0 for waypoints on one branch and < 0 for waypoints on the other branch. The branch point and branch associations are used to further refine the trajectory. The resulting trajectory and branches are used to study marker dynamics along differentiation.
Wishbone uses shortest paths from an input ‘early cell’ to build an initial ordering of cells, which is subsequently refined using a selected set of cells, called waypoints. Finally, the inconsistencies in distances between waypoints are used to identify the branch point and branch associations for all cells. The quality of the nearest-neighbor graph is critical for accurate ordering, and major source of noise is the presence of “short-circuits” – spurious edges between cells that are farther apart in maturity [3]. Notably, a single short-circuit is sufficient to route all shortest paths between developmentally distant cells leading to incorrect ordering. Short-circuits are particularly prevalent in branching datasets, since cells following the bifurcation point might not be sufficiently distinct in their phenotypic characteristics (Supplementary Fig. 3). Wishbone overcomes these short-circuits by reconstructing the graph in projected space of reduced dimensions generated using diffusion maps [7] (Online Methods). Diffusion maps consider all possible paths between any pair of cells to dramatically reduce short-circuits. Wishbone uses the top diffusion components to construct the graph, capturing the major geometric structures in the data, while removing small fluctuations likely resulting from measurement noise.
The algorithm uses a select set of cells, called waypoints, to act as guides at different regions of the graph. Waypoints are randomly sampled cells, selected to represent regions along the entire trajectory and its branches (Online Methods). Each waypoint contributes a perspective, based on its computed distance to all other cells (Figure 1B). The placement of a cell in the trajectory is determined by averaging the perspectives of all waypoints, with closer waypoints getting a higher weighting. Thus closer, more reliable waypoints predominantly determine a cell’s position, while retaining a degree of influence of the distal waypoints to derive a consistent global structure (Figure 1B, bottom right panel). These waypoints are key to accurately identifying branch points.
Waypoints are also the key to identifying branch points: If two waypoints i and t are along the same trajectory, the difference between the shortest path from the early cell to t and a path that goes through i is close to zero (Figure 1C, left panel). On the other hand, if the two waypoints are on different branches, this difference is significantly greater than zero (Figure 1C, middle panel). In the presence of a true branch, the disagreements between waypoints of the two branches accumulate to create two sets of waypoints that agree within each set and disagree between sets. These disagreements create a structured matrix (Figure 1C, right panel): waypoints on the trunk have low disagreements with all waypoints, waypoints on one branch agree with other waypoints on the same branch and have high disagreements with all waypoints on the different branch (Online Methods). This structure can be identified with clustering approaches.
Specifically, from spectral clustering techniques, the second Eigen vector of this matrix summarizes all the disagreements for a given waypoint and provides a quantitative measure of branch association for the waypoints (Figure 1D, left panel, Online Methods). The extent of deviation from zero is a function of the maturity of the cell creating a Wishbone-like structure and giving the algorithm its name (Figure 1D, left panel). Wishbone recovers the ordering of cells along their developmental trajectory, finds the branch point, and assigns cells following this point to one of the two branches (Figure 1D).
Analysis of mouse thymus mass cytometry dataset
During T cell development in the mouse thymus, CD4+ helper T cells and CD8+ cytotoxic T cells bifurcate from lymphoid progenitors (Figure 2A) [8, 9]. We applied Wishbone to mass cytometry data from mouse thymus, with surface markers and transcription factors chosen based on their broad functionality in T cell development (Supplementary Table 1, Online Methods). We collected data for 5 independent thymuses from Black6 mice with an average of 230k cells were collected per sample.
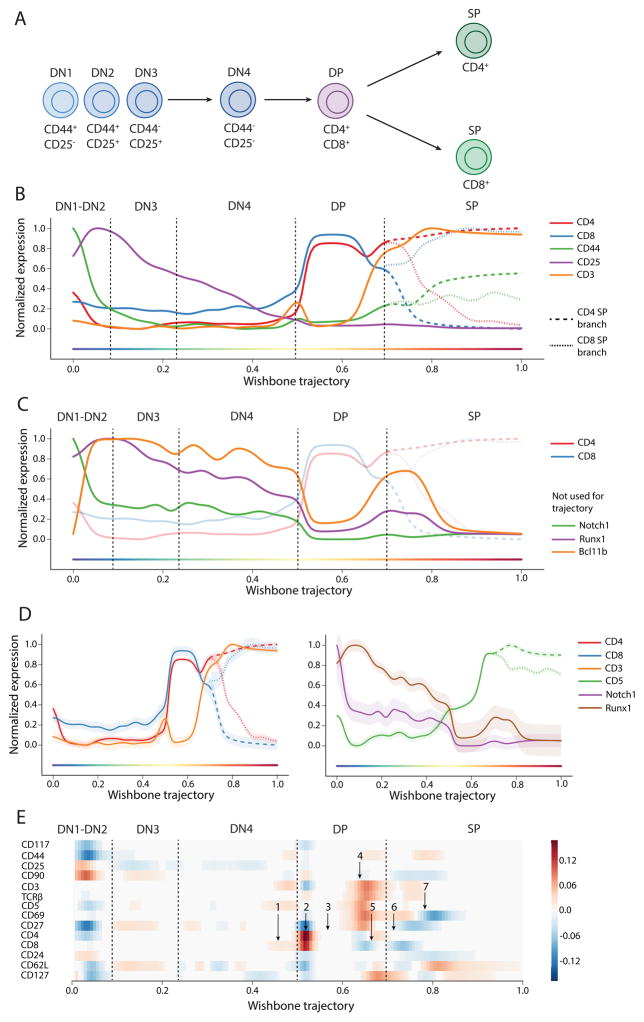
Figure 2. Wishbone robustly recovers hallmarks of T cell differentiation.
(A) T cell development in the mouse thymus is characterized by progression of DN cells to two SP populations through different stages.
(B) Marker trends for DN markers CD44, CD25, CD117 and lineage markers CD4, CD8 and CD3 are consistent with known stages of T cell differentiation. Cells were first binned along Wishbone trajectory and weighted averages were calculated for each bin to determine marker traces (see supplement for computational details). Following bifurcation, markers with different expression patterns in the two SP populations are shown in a dashed line for CD4 lineage and a dotted line for the CD8 lineage.
(C) Bcl11b, Runx1 and Notch1 were not used for learning but the dynamics of these markers are consistent with their roles in specific developmental stages.
(D) The variance of markers along the trajectory is tight further highlighting the robustness of Wishbone results.
(E) Derivative plot, showing the changes in expression of markers in successive bins, is used to time key events along the trajectory: (1) CD8+CD4− Intermediate Single Positive stage in DN to DP transition, (2) Upregulation of CD4 and CD8 establishing DP cells, (3) Stable expression of lineage markers during DP, (4) Downregulation of both CD4 and CD8 accompanied by coordinated upregulation of CD3, TCRβ, CD5, CD69 and CD27 during positive selection, (5) Specific downregulation of CD8 alongside up-regulation of CD4 indicating intermediate thymocytes, (6) Lineage commitment to two SP population and finally (7) Successful completion of negative selection identified by downregulation of CD69 and upregulation of CD62L indicating successful maturation. The branch with the highest expression is shown for markers with different expression patterns in the two SP branches.
Wishbone was independently applied to each thymus, using only the surface markers for computing cell similarities (Supplementary Table 1) and defining the DN cell population as the starting point [8]. Marker trends along the resulting trajectory are depicted in Figure 2B (Online Methods). Wishbone accurately recovered the known stages in T cell development (Figures 2B, Supplementary Fig. 4), including the bifurcation into two single positive lineages (CD4+ and CD8+). Specifically, the trajectory begins at the Double negative (DN) stage (CD4−CD8−), transitions to the double positive (DP) stage (CD4+CD8+) and finally branches to the two single positive (SP) populations [8]. We note that Wishbone correctly ordered the DN populations: DN2 (CD44+CD25+), DN3 (CD44−CD25+), and DN4 (CD44−CD25−), even though these cells are rare and constitute <1% of the cells in the thymus. DN1 (CD44+CD25−) cells are extremely rare and we do observe a signature resembling these cells at the beginning of the trajectory (Figure 2B). To further test Wishbone’s accuracy, we evaluated the expression trends of markers not used while learning the trajectory: TFs Runx1 and Bcl11b and signal molecule Notch1 (Figure 2C). The abundance of all these markers is consistent with their known roles and timing in DN stages of T cell development (Supplementary Note 1).
Additional evidence of Wishbone’s accuracy is the tightness of marker variation over the course of the trajectory (Figure 2D). Not only do the median marker levels follow expected trends, but almost every single cell is correctly placed in the trajectory, as indicated by low variance of markers across most of the trajectory. The variance is low for markers irrespective of whether the marker was used for learning the trajectory (Figure 2D, Supplementary Fig. 5), reinforcing the robustness of Wishbone results.
Previous studies characterizing thymic development have largely relied on genetic perturbations and subsequent cell sorting that invariably eliminate specific developmental compartments. With 30 channels simultaneously measured, we could place DN, DP, CD4+ and CD8+ cells from a single thymus along a unified bifurcating trajectory and precisely order the course of multiple events along the trajectory measured directly from thymic tissue in an unbiased manner. We used derivative analysis to time key events along the trajectory (Figure 2E) in a single frame of reference and found that Wishbone recovers a precise temporal ordering and branching of cells along with high resolution and accuracy using cells collected from a complex primary tissue (Supplementary Note 1) (Figures 2B, 2E).
Wishbone results are consistent across replicates and are robust to parameter choices
To test robustness, we applied Wishbone to three independent mouse thymuses and recovered consistent trajectories and branching behavior across all replicates. We used cross correlation to align the expression of individual markers, providing a quantitative measure for consistency across replicates (Figure 3A). We find that the dynamics of marker expression and order of events along the trajectories are consistent across the replicates (Supplementary Fig. 6).
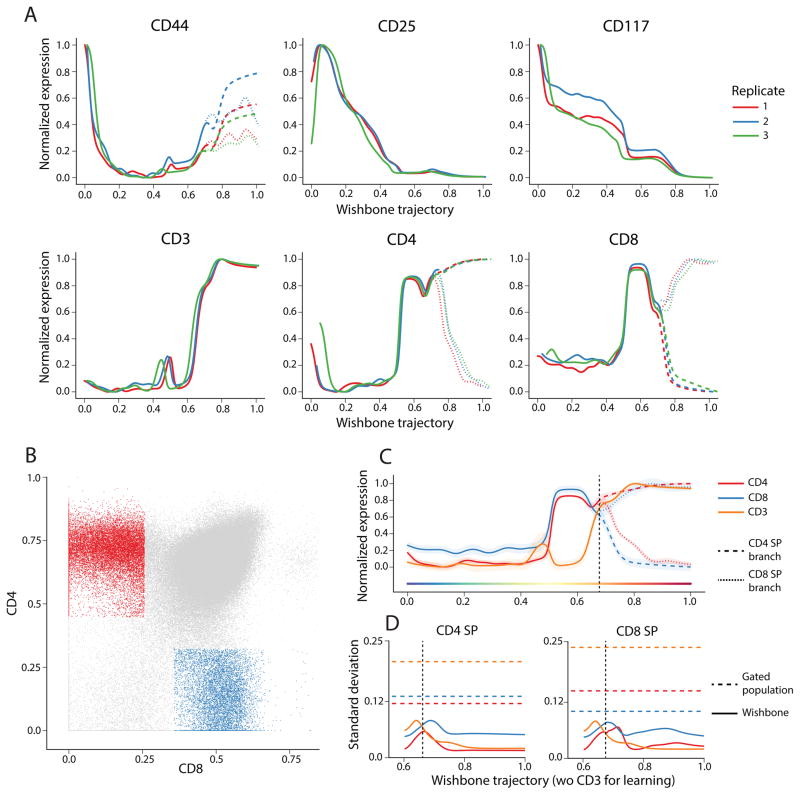
Figure 3. Heterogeneity in gated populations is explained in part by variance along trajectory.
(A) Plots comparing the dynamics of CD44, CD25, CD117, CD3, CD4 and CD8 across thymses from three independent replicates. Cross correlation was used to align expression dynamics of each marker across the replicates.
(B) Gating scheme for identifying CD4+ and CD8+ SP populations to compare variance of gated populations to variance along the differentiation trajectory.
(C) Wishbone results after excluding CD3 from the learning are similar to results obtained when CD3 was included.
(D) The variance of CD3 and lineage markers CD4 and CD8 along the trajectory (solid line) are substantially lower than the population variance (dotted line) in both branches indicating that heterogeneity in gated populations is a result of comparing cells at different stages along their developmental maturity.
We investigated the sensitivity of the trajectory and branching to the various free parameters: Number of neighbors k, for the graph construction, Number of waypoints nW, the sampling of waypoints from the cells and number of diffusion components used. The ordering of cells and their branch point are remarkably robust to these different parameter choices across replicates. (Supplementary Figs. 7 and 8, Supplementary Note 3). Wishbone results are also largely robust to exclusion of individual markers used for learning (Supplementary Fig. 9). Moreover, the branches identified by Wishbone remain consistent irrespective of whether cells of DN or SP population are used as the input early cell (Supplementary Fig. 10).
Maturity controls for marker levels within individual cell types
We observe considerable heterogeneity in canonical surface markers. We hypothesized that at least part of this variation might be a result of developmental maturity, where cells from varied developmental stages are pooled into a single gated population. Using the fine temporal resolution of Wishbone’s trajectory, we compared the marker variance, conditioned on the developmental progression of the cells, to that observed in gated populations. To make this comparison, we first identified the two SP populations using the standard gating scheme on the expression of the two lineage markers: CD4 and CD8 (Figure 3B) [8]. We next compared the variance in these gated populations to the variance of the corresponding markers, conditioned on the Wishbone trajectory. In both SP populations, the variance of the lineage markers CD4 and CD8 and the co-receptor CD3, when controlled for maturity along the trajectory, is substantially low compared to population variance in the gated populations (Figure 3D, Supplementary Fig. 11A).
As an additional test, we ran Wishbone without using CD3 as one of the markers while learning the trajectory. The identified trajectory and branches are similar to results obtained including CD3 and is accompanied with only a minor increase in variance of CD3 all along the trajectory (Figure 3C). However, the variance of all receptor and co-receptor molecules, CD4, CD8 and CD3, continue to be substantially lower along the trajectory compared to variance in the gated populations (Figure 3D). These results similarly hold when either of CD4 or CD8 are excluded from learning (Supplementary Fig. 11B–C). Collectively, these results suggest that a substantial part of the heterogeneity of marker expression in gated populations are a result of comparing cells at different stages along their developmental maturity, rather than stochasticity in marker expression.
Transcription factor dynamics along SP trajectories
Next we set out to explore the dynamics of key transcription factors along the two SP trajectories, using revised panel including the transcription factors ThPOK, Gata3 and Runx3. ThPOK and Gata3 have been shown to be critical for the CD4 SP population [10] and Runx3 has been demonstrated to be key for CD8 SP commitment [10]. The dynamics of these factors along the trajectory is shown in Figure 4A, B.
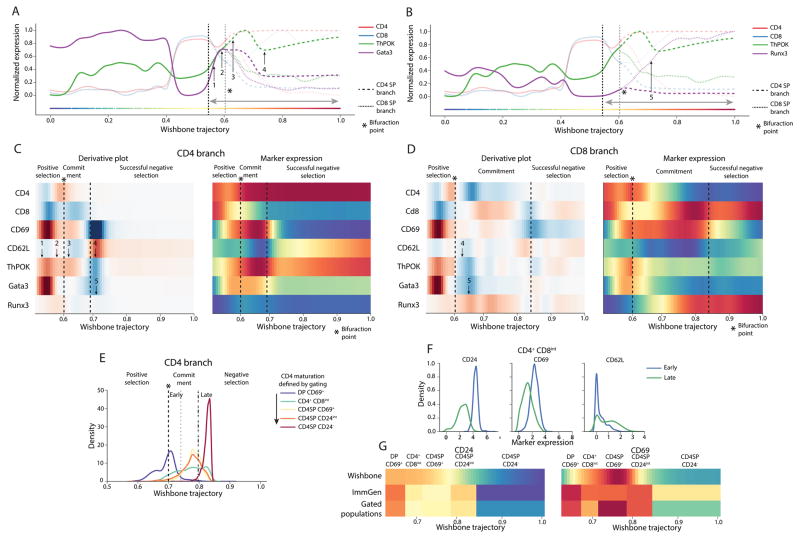
Figure 4. Transcription factors show distinct dynamics in SP populations.
(A–B) Plots comparing the dynamics of CD4 lineage commitment factors ThPOK and Gata3 with dynamics of CD8 lineage commitment factor Runx3.
(C–D) Derivative plots (left panels) and expression trends (right panels) of key markers in the two SP populations along the trajectory following positive selection (The highlighted region is indicated in A–B) showing the distinct dynamics of lineage commitment factors. CD69 and CD62L were used to identify the landmarks of SP commitment and maturation: CD69hi and CD62Llow for successful commitment and CD69 low and CD62L high for negative selection. (1) ThPOK and Gata3 are both upregulated during positive selection with ThPOK showing a slower upregulation (2). ThPOK shows a marginal upregulation specifically in the CD4 branch following commitment (3). ThPOK and Gata3 show a marginal downregulation in the CD4 branch during negative selection (C(4)). On the other hand, these factors are downregulated in the CD8 branch following commitment (D(4)). This downregulation is accompanied with a CD8 specific upregulation of Runx3 (5).
(E) Cells were gated using the scheme defined in Supplementary Fig. 13 and were expected to be placed in the following order indicating CD4 maturity: DP CD69+, CD4+CD8int, CD4SP CD69+, CD4SP CD24int and CD4SP CD24−. Instead cells of the three intermediate gates are placed all along the CD4 Wishbone trajectory. These cells were divided into “Early” and “Late” populations based on their position in the Wishbone trajectory.
(F) The “Early” cells in the CD4+CD8int gate show significantly higher expression of CD69 and CD24 and lower expression of CD62L compared to “Late” cells (p < 1e-6, Kolmogorov-Smirnov test). This indicates that “Late” cells are more mature than the “Early” cells.
(G) mRNA expression of CD69 and CD24 in ImmGen sorted populations are correlated with mean expression in the gated populations demonstrating that the discrepancy between Wishbone and gating is not dataset specific.
To place the dynamics of these transcription factors in context, we used CD69 and CD62L to identify landmarks of maturation such as lineage commitment and successful negative selection (Figure 4C–D). Our results suggest that these factors follow distinct dynamic patterns in achieving commitment: ThPOK and Gata3 are upregulated during positive selection but Runx3 appears to only be upregulated following the detected branch point (Supplementary Note 4, Supplementary Fig. 12). Gata3 has been shown to regulate ThPOK expression [11] and might offer an explanation as to why ThPOK trails Gata3 in expression changes (Figure 4C). The different dynamics can potentially be indicative of distinct regulatory mechanisms through which these factors achieve linage commitment. Further experiments are necessary to elucidate these mechanisms.
We compared marker dynamics along the Wishbone trajectory to the dynamics derived from gating of developing SP cells [12–14] (Supplementary Fig. 13, Online Methods) and compared the ordering of cells within each population along the Wishbone trajectory.
We observe that cells within most gated populations are spread out along the trajectory (Figure 4E, Supplementary Fig. 14B), particularly cells of the CD4+CD8int population, where the lineage decision is thought to occur [15]. To address this discrepancy between Wishbone and gating, we divided the CD4+CD8int cells into “Early” and “Late” groups based on their positions in the Wishbone trajectory (Figure 4E, Online Methods) and compared the expression of known maturation markers CD69, CD24 and CD62L in the two groups. The “Early” cells show significantly higher expression of CD69, CD24 and lower expression of CD62L compared to “Late” cells (Figure 4F, p < 1e-6, Kolmogorov-Smirnov test) demonstrating that the cells in “Early” and “Late” are groups immature and mature respectively. Similar results for additional gated populations in CD4 and CD8 branch (Supplementary Fig. 14) indicate that the conventional gating scheme leads to inclusion of cells at different stages of maturation in each gate. We conclude that Wishbone provides more reliable estimates of cell maturation and hence marker dynamics along SP maturation.
We next compared the mean gene expression of markers in ImmGen sorted populations [16] to Wishbone marker dynamics and note discrepancies between the datasets. To understand the source of this discrepancy, we compared gated populations from our data and indeed mean protein expression in our gated populations and mean mRNA expression in ImmGen populations is correlated. Thus the discrepancy between dynamics observed along the Wishbone trajectory and gating is not a dataset specific observation (Figure 4G). The mixing of developmentally distinct cells in each gate can lead to confounding effects on expression change patterns along maturation: While CD24 shows a continuous decrease along Wishbone trajectory, the expression is more variable in the gated and ImmGen populations (Figure 4G left panel). Sustained upregulation of CD69 following positive selection is not observed in gated populations since CD69 itself is used for gating (Figure 4G right panel). Finally, Gata3 expression changes in gated populations do not show the dynamics observed in Wishbone (Figure 4C (1, 5)) even though Gata3 was not used for gating (Supplementary Figure 14G), further demonstrating the ability of Wishbone to recover marker dynamics at higher resolution.
Application of Wishbone to human myeloid development
We evaluated the performance of Wishbone on two human myeloid development datasets. We used previously published mass cytometry data [2] consisting of markers that are suitable to recover early and late Myeloid bifurcations [17] but not amenable for fine-grained profiling of transitional myeloid populations (Supplementary Fig. 15, Online Methods).
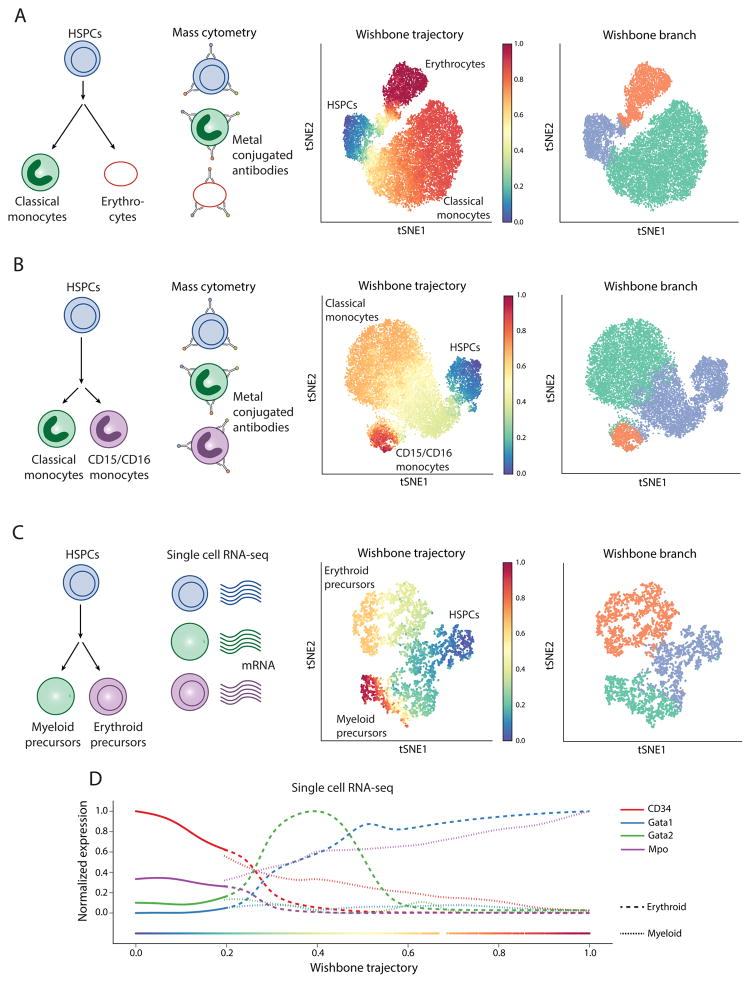
Wishbone was able to track the differentiation of monocytes (CD14+CD11b+CD11c+) and erythroid cells (CD235ab+) from hematopoietic stem and progenitor cells (HSPCs) (Figure 5A, Supplementary Fig. 16A) and accurately recover the monocyte and erythroid branches (Figure 5A). More over, expression of markers along the trajectory was consistent with known literature [18] (Supplementary Fig. 16C).
Figure 5. Generalization of Wishbone to branches in human and mouse myeloid development spanning mass cytometry and single-cell RNA-seq.
(A) Wishbone was applied to an early step in human myeloid development to track the differentiation of classical monocytes (CD14+CD11b+CD11c+) and erythrocytes (CD235ab+) from hematopoietic stem and progenitor cells (HSPCs). See also Supplementary Fig. 16.
(B) tSNE map of the data with each cell colored by the trajectory (left panel) and the branch associations (right panel). Wishbone accurately orders the cells with HSPCs at the start and the differentiated cells towards the end. The inferred branch associations are also consistent with the annotated cell types (Supplementary Fig. 16).
(C – D) same as in A–B for tracking differentiation of classical monocytes and CD15+ monocytes, a late step in human myeloid development.
(C – D) Wishbone was applied to single-cell RNA-seq data from the hematopoietic precursors from the mouse and accurately recovered the trajectory and branches to track differentiation of myeloid and erythroid precursors from HSPCs.
Wishbone accurately recovered the trajectory starting from HSPCs and the branching of the two-monocyte classes, classical monocytes and CD16 monocytes (CD16+CD15+) (Figure 5B). This is a harder problem since most of the markers show identical distributions between the two populations except for the characteristic markers, CD15 and CD16 (Supplementary Fig. 16D). The expression of markers along the trajectory is consistent with known literature (Supplementary Fig. 16E), with the detected bifurcation point coinciding with significant downregulation of CD38.
Extension of Wishbone to single-cell RNA-seq data
Single-cell RNA-seq technologies can profile thousands of single cells and enable genome wide characterization of developing systems [6, 19]. However such data poses a challenge in that the behavior of many genes is related not to developmental maturity but to processes such as cell cycle and stress. Thus, the success of trajectory and branch detection relies on removing unrelated factors and retaining those that track with differentiation.
We used recently published single cell RNA-seq data [6] to select cells involved in differentiation of myeloid and erythroid progenitors from HSPCs (Figure 5C, Supplementary Fig. 17A). We devised an extension of Wishbone, adapted to single-cell RNA-seq that uses diffusion maps to help focus on components related to development and maturation. Diffusion maps capture the major structures and trends in the data and, in the case of mass cytometry, different diffusion components track the differences among constituent cell types (Supplementary Fig. 8A). We project genes down onto each diffusion component, rank genes based on how well their expression tracks along this component and then use this ranking to perform gene set enrichment analysis (GSEA) [20] (Online methods). Some diffusion components are enriched for immune related functions (e.g. defense response, antigen processing and phagocytosis), whereas other components are enriched for other biological processes (e.g. Cell cycle, Ribosome biogenesis and metabolic processes) (Supplementary Fig. 17C, Online methods). This provides a natural way to retain the components that are most relevant to the differentiation processes. With similar reasoning, Buettner et.al. use latent variable models to remove the contribution of cell cycle in single cell RNA-seq [21].
We constructed Wishbone’s neighbor graph based on a projection of the data onto only the differentiation related components and once this graph is constructed we proceed with wishbone as described for mass cytometry. Wishbone accurately recovered the trajectory starting from HSPCs and terminating at the two precursor cell types and the branch associations (Figure 5C). The marker trends show a consistent decrease of HSPC marker CD34 along the trajectory with an increase in expression of myeloid marker Mpo [22] along the myeloid branch (Supplementary Fig. 17C). Consistent with known biology, Gata2 is upregulated before Gata1 along the erythroid lineage [23] (Figure 5D).
Wishbone outperforms competing methods in both trajectory and branch identification
We compared the performance of Wishbone to Diffusion maps [7], SCUBA [5] and Monocle [24] (Figure 6). While we use diffusion maps to build the kNN graph, we tested whether diffusion maps on their own can recapitulate developmental trajectories [25, 26]. Note that diffusion maps do not explicitly provide bifurcations and we can only evaluate their ability to recapitulate an accurate ordering. Diffusion maps correctly recover the various known stages in T cell development (Supplementary Fig. 18B), especially in the early DN states, but suffer from a considerable lack of resolution in DP and SP populations (Supplementary Fig. 18A–B). Moreover, while diffusion maps recover the right order in the two myeloid datasets (Supplementary Fig. 18C, E), in the monocyte dataset, diffusion maps order precursors after the mature cells (Supplementary Fig. 18D). Thus, while diffusion maps significantly reduce the noise in the data (Supplementary Fig. 3, Online Methods), the additional steps taken by Wishbone to refine ordering of cells are critical to derive robust, high-resolution trajectories.
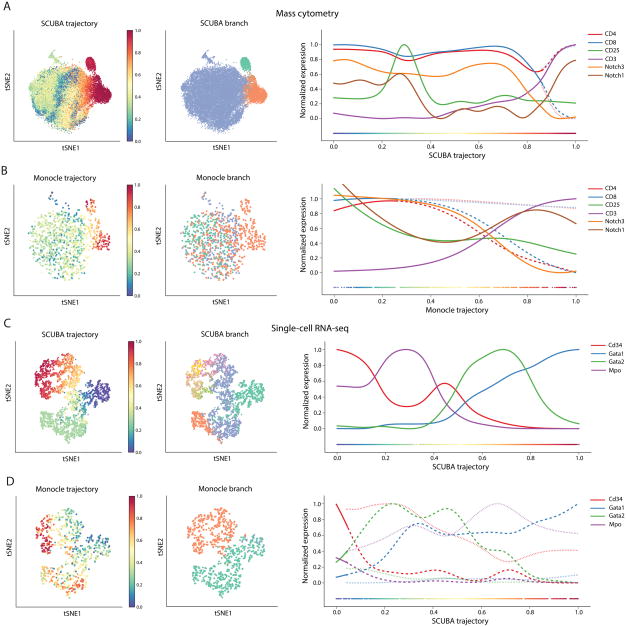
Figure 6. Wishbone outperforms competing methods in both ordering of cells and branch associations.
(A) tSNE maps showing SCUBA results for a random sample of 20000 mouse thymic cells (left and middle panels). SCUBA trajectory does not distinguish between the DN and DP stages. While SCUBA recovers the SP branches, it suffers from a loss of resolution in the SP stage (right panel).
(B) Plots showing Monocle results for a random sample of 1000 mouse thymus cells. Monocle fails to correctly order the cells and the branches do not correspond to the SP populations.
(C) SCUBA accurately recovers the ordering of mouse myeloid cells and the marker dynamics are largely consistent with known biology. SCUBA however results in a large number of incoherent branches.
(D) Monocle fails to accurately order the myeloid precursors correctly and also fails to detect a coherent HSPC branch.
Next we compared Wishbone to SCUBA [5]. SCUBA has a large memory footprint and therefore could only be run by subsampling 20,000 cells from the thymus dataset. The SCUBA trajectory of the thymus does not order the stages correctly and we observe the different DN cells interspersed among the DP cells (Figure 6A). SCUBA does identify the two SP populations as the two branches, but with reduced resolution at the bifurcation point compared to Wishbone (Figure 6A). Moreover, different random sample of cells leads to largely inconsistent results (Supplementary Fig. 19A–C) in both trajectory and branching. SCUBA trajectory in the mass cytometry monocyte and the single cell RNA-seq myeloid datasets is consistent with known biology, but yields a large number of incoherent branches (Figure 6C, Supplementary Fig. 19D). Moreover, SCUBA fails to correctly recover the order and branching in the monocyte-erythroid dataset (Supplementary Fig. 19E).
Finally we compared Wishbone to Monocle [24], which was specifically developed for application to single-cell RNA-seq data. Monocle could not be run with more than 1000 cells and we therefore subsampled 1000 cells from each dataset. Monocle does not recover the correct ordering in the thymus data with DN and DP cells interspersed (Figure 6B). While the trajectory does end at the two SP populations, the branching identified by Monocle does not correspond to any specific stages in T cell development, and both the SP populations are identified to be part of the same branch (Figure 6B). Repeated subsampling of the data resulted in largely inconsistent results with the two SP populations repeatedly assigned to the same branch (Supplementary Fig. 20A–C). Monocle also failed to recover the trajectory and branches in the single-cell RNA-seq myeloid dataset with incorrect ordering of cells and lack of detection of a coherent branch (Figure 6D). Monocle does recover ordering in the monocyte dataset, but the branching results in all the myeloid datasets do not correspond to the correct mature cell populations (Supplementary Fig. 20D–E).
Thus, Wishbone outperforms competing methods in fine ordering of cells, identification of branch point and branch associations and consistent robustness across replicates.
Discussion
We have developed an algorithm that enables accurate and high resolution ordering of cells along branched developmental trajectories (Supplementary Fig. 21). We first demonstrated Wishbone on T-cell development in the mouse thymus, using the throughput of mass cytometry to collect ≥200,000 cells per sample. Wishbone constructed a bifurcating trajectory starting from DN stages through maturation of the two SP lineages, providing an order and timing of events that closely recapitulated previous studies of this system [15]. The high resolution of Wishbone enabled us to identify subtle but key dynamics of lineage markers such as detection of the rare CD8+CD4− intermediate single positive cells during transition of DN to DP cells and the intermediate CD4+/CD8low state towards the end of DP.
The selection of a good marker set was key to the resolution we achieved. Marker choice can be guided by a combination of prior knowledge and preliminary screens. However, in the myeloid branching we demonstrated that even with a limited panel that included only a small number of distinguishing myeloid markers, Wishbone correctly ordered cells, identified the bifurcation and associated cells to the proper branch. While an explicit ground truth is not necessarily available, both SCUBA and Monocle fail to recover the expression trends and bifurcations that are consistent with known biology in these more challenging datasets. Wishbone only requires a few canonical markers to properly identify bifurcation, and achieves increasingly finer resolution in transitional populations, as additional markers are included.
Single cell RNA-seq is an attractive alternative to mass cytometry as its unbiased, genome-wide nature provides measurements for thousands of genes and circumvents the need for a-priori selection of a limited marker set. However, transcriptional changes un-related to development can confound the analysis, and even data for developmentally related genes has substantial noise, including drop-out effects [27]. We use diffusion maps to consolidate the key biological trends and remove unrelated biological processes. We demonstrated that Wishbone substantially outperforms methods developed specifically for single cell RNA-seq data [28].
Even with the increasing throughput of single cell RNA-seq, current datasets include thousands of cells, as compared to hundreds of thousands available in mass cytometry. Since transitional populations have been shown to be as rare as 1/10,00 cells [3], the throughput of mass cytometry is better suited to achieve finer temporal resolution. In our view, the two technologies are complementary. For example, single-cell RNA-seq can be used for unbiased marker selection in less-studied developmental systems, and finer temporal resolution can then be achieved with mass cytometry using the identified panel.
Data availability and software
The mouse thymus mass cytometry data can be downloaded from Cytobank (https://www.cytobank.org/cytobank/experiments/52942). The cleaned data along with the Wishbone results for different replicates is available through the supplementary website (http://www.c2b2.columbia.edu/danapeerlab/html/wishbone.html). Myeloid mass cytometry data was downloaded from Cytobank (http://reports.cytobank.org/1/v1). Mouse myeloid single cell RNA-seq was downloaded from GEO (accession number: GSE72857). Wishbone results for all the myeloid datasets is available through the supplementary website http://www.c2b2.columbia.edu/danapeerlab/html/wishbone.html). Wishbone has been integrated into our single analysis suite cyt and can be downloaded from (http://www.c2b2.columbia.edu/danapeerlab/html/cyt-download.html) and from Supplementary software. A python package for Wishbone algorithm is available through github (https://github.com/ManuSetty/wishbone).
Online methods
Mouse thymus data and mass cytometry
Female C57BL/6 mice were obtained from Harlan Laboratories. All mice were housed at the Weizmann Institute in compliance with national and international regulations.
Thymocytes were isolated from the thymus of 6-week-old C57Bl mice. Cells were stained with metal-conjugated antibodies according to manufacturer’s protocol (Supplementary Table 1). Briefly around 200k cells were stained with cell-ID TM Cisplatin (Fluidigm) (5min RT). Next cells were stained with surface antibodies (30 min RT), and fixed with 1.6% PFA (10 min RT). After permeabilization with 100% ice-cold Methanol (15 min, 4C), the cells were stained with intracellular antibodies (30 min, RT). Finally the cells were labeled with Iridium DNA intercalator for DNA content and analyzed by CyTOF mass cytometry using CyTOF2. Data was normalized using bead normalized with bead standards [1].
We collected data for 5 independent thymuses from Black6 mice using two different marker panels. The first predominantly contains cell surface markers and the second combines the most informative of these surface markers with known regulators of lineage commitment (Supplementary Table 1).
Data preprocessing and choice of parameters for Wishbone
Mass cytometry data channels were first arcsinh transformed with a cofactor of 5 [2]. Cell doublets, barcodes, dead cells and debris were removed from the data using the gating scheme shown in Supplementary Fig. 1. Next, the cells were clustered using Phenograph [29].
For the mouse thymus dataset, the clusters corresponding to myeloid cells (expression of CD11b, CD11c), B cells (CD19), NK cells (CD161), regulatory T cells (CD25) and TCRγδ cells were filtered out from the analysis (Supplementary Fig. 2). The remaining clusters correspond to the DN, DP and SP populations. Finally, for each thymus a start cell was sampled from the DN population and the same start cell was used for all the analyses of that thymus. The results presented in the paper were generated using number of nearest neighbors _k_=15 and number of waypoints _nW_=250.
Human bone marrow mass cytometry data was downloaded from [2]. Doublets, cell debris and dead cells were removed as described above. Phenograph was used to identify the clusters of cells and all the lymphoid clusters were removed (Supplementary Fig. 15) and clusters for generating the datasets used in Figures 5–6 were identified by expression of characteristic markers (Supplementary Fig. 16 A and D).
Overview of the Wishbone algorithm
Introduction
Differentiation is a complex process involving multiple decision points to decide cell fate. This process can be seen as hierarchical tree with the multipotent stem and progenitor cells at the root and the mature differentiated cell types at the bottom with various precursor cells as intermediate cell types [15, 17, 30]. Emerging high throughput technologies such as single cell RNA-seq [1, 19, 31] and mass cytometry [2] are enabling generation of data with unprecedented resolution and require computational algorithms capable of exploiting this resolution. Wishbone uses multi-dimensional single-cell data to align cells along bifurcating trajectories. Wishbone was developed to study systems where the developmental trajectory of cell bifurcates to one of two cell fates (Figure 1A).
There are two key challenges involved in studying trajectories with branches: (1) Ordering of cells within the trunk and in each of the branches, (2) Identification of bifurcation or branch point and assignment of cells to either the trunk or one of the branches. Previous studies attempting to study differentiation have largely relied on sorted populations. While these have led to important advances, the dynamics of marker behavior along the maturation trajectory cannot be characterized without an accurate high resolution ordering of cells, capable of characterizing the order and timing of key molecular events during development. The second challenge is to assign the cells to their respective branches. Given a right set of markers, it is relatively straightforward to classify the mature cells into the correct branches. However, there are many uncharacterized bifurcations where such markers are not well defined. Moreover, a precise identification of branch point is central to achieve a high resolution into bifurcating trajectories to understand the series of events leading up to and following cell fate decisions. Furthermore, cells can be thought of as being in a state of flux at the branch point necessitating a soft assignment of branches.
Wishbone addresses these challenges by taking a graph-based approach to measure distances between cells, similar to the approach used by Wanderlust [3], our previously published algorithm for detecting non-branching trajectories. Wishbone first constructs a nearest neighbor graph of cells and estimates distances between them using the shortest path algorithm. The greedy nature of shortest path algorithms makes them susceptible to short circuits i.e., connections between developmentally distal cells. Wishbone overcomes this problem by use of diffusion maps [7], a dimensionality reduction technique, to reduce noise and eliminate short circuits. The initial ordering of cells as determined by shortest path distances from an input early cell are increasingly prone to noise as distance increases. Wishbone uses a series of cells called waypoints, sampled all along the entire trajectory to locally refine the ordering of cells and overcome this noise. Finally, the disagreements between waypoint’s and the early cell’s distances to other cells are used to detect the branch point and branch assignments. The ordering and branch assignments are iteratively repeated until convergence. These randomly sampled waypoints provide a sparse approximation for the entire dataset. Randomly sampled subsets have previously been used to achieve more computationally efficient dimensionality reduction [32]. A key distinction between Wishbone’s waypoints to other such sparse approximation schemes is that the waypoints are themselves the driving force underlying the algorithm. Thus Wishbone recovers an accurate high resolution ordering and branching of cells in bifurcation trajectories.
Wishbone makes the following assumptions about the data: (1) The maturation process along differentiation is continuous and (2) the snapshot of primary tissue any given point is representative of the entire differentiation process with various intermediate and rare populations represented and (3) the developmental trajectory of a cell bifurcates to one of only two cell fates.
Nearest neighbor graph and shortest paths
Differentiation is characterized by a series of increases and decreases in expression of specific markers [3]. Furthermore, the rise and fall of the markers involved in development create non-linear relations between the markers and their relation to maturity (Figure 1) [3]. Therefore, distance metrics such as Euclidean distance fail to accurately capture the similarity between cells that are at distinct stages of development. As previously demonstrated [3], nearest neighbor graphs are a powerful alternative to capture developmental distances. Here, each cell is a node and is connected to its nearest neighbors i.e., the cells that are most similar in the phenotypic profiles. The underlying assumption being that for very short distances, marker similarity represents a similar developmental maturity. The edge weights are set to the similarity between the connected cells.
Given the graph, a path can be defined from one cell to another through a series of short steps represented by edges, since each of these edges represent a more confident developmental proximity. While there are many possible paths through the graph between any given pair of cells, an efficient choice is to take a path such that the total weight of edges is minimized. This minimal sum of weights also referred to as the shortest path distance between two cells and can be used a distance metric between cells [3]. Thus the shortest path distances to all cells from the viewpoint of a cell early in development, denoted s, can be used as a starting point to build the trajectory.
Short circuits and diffusion maps
Key to the success of the algorithm is construction of a good graph, where edges in the graph connect cells that are indeed close in their developmental progression. One of the problems affecting the construction of a good graph is presence of short circuits: spurious edges between cells that are farther apart in development but are identified as neighbors due to measurement noise. A single short circuit is sufficient to route all the shortest paths between distant cells through this anomalous edge resulting in incorrect ordering of cells. Since short circuits are relatively rare in non-branching trajectories, Wanderlust proposed the use of ensemble of graphs where trajectories were determined by repeatedly sampling a subset of edges from the graph [3].
Short circuits however, are considerably more prevalent in branching datasets particularly close to the bifurcation point since the markers that characterize the branches might not be sufficiently distinct in this region. Furthermore, depending on extent of separation of the branch and noise in the characteristic markers, short circuits might also be present all along maturation trajectory. An illustrative example is shown in Supplementary Fig. 22A. The ensemble of graph methods fails to sufficiently remove these short circuits since it assumes the number of short circuits to be significantly fewer in number (Supplementary Fig. 22B – each panel was derived by sampling a subset of edges).
Wishbone therefore uses diffusion maps [7] to remove short circuits in the data and construct a graph that is more faithful to the developmental trajectory. Diffusion maps are a non-linear dimensionality reduction technique to derive a low-dimensional description of high dimensional data by exploiting local similarities [7]. Rather than rely solely on the shortest paths in the phenotypic marker space, diffusion maps generate a low-dimensional embedding by approximating all possible paths through the graph, avoiding the harmful effect of short circuits. One can view diffusion maps as a non-linear version of Principle Component Analysis (PCA). Often data is de-noised by projecting data onto the top principle components, assuming the smaller components represent noise [33]. Similarly, by projecting the data onto the top diffusion components, we capture the major structures in the graph and remove small fluctuations, providing a non-linear data clean up step.
While diffusion maps often generate a first order approximation of the developmental trajectory, the resulting resolution is not sufficiently fine as shown in Figure 6. Therefore Wishbone constructs a nearest neighbor graph in the embedded space to bring together advantages of graph-based methods for trajectory building and de noising nature of diffusion maps. The graphs constructed in the embedded space tend to be free of most short circuits (Supplementary Fig. 22C) and therefore shortest paths can be used for computing distances between cells.
Graph construction and initial ordering of cells
Formally, given a dataset with N cells and M markers, Wishbone starts by transforming the high dimensional phenotypic data into low-dimensional data using diffusion maps. The embedding is computed by using the diffusion geometry code (http://www.math.duke.edu/~mauro/diffusiongeometries.html) with default parameters. This embedded space is used to construct a _k_-nearest-neighbor graph (k - NNG), G, spanning all the cells. Each cell i is connected to its k nearest cells via Euclidean distance in the embedded space and edges connecting cells to their nearest neighbors are weighted by the Euclidean distance between them.
An early cell s, provided as user input, is then used to compute an initial alignment of cells by computing shortest path distances from s to all cells. The distance from s to any given cell i is calculated using Dijkstra’s algorithm:
where P is a path between s and i, and G e_1,e_2 is the weight of edge e. Note that the graph is undirected and therefore Dis = Dsi.
The trajectory or ordering of cells is initialized to the shortest path distance from s i.e., τi(0)=Dis. This initial ordering encapsulates this early cell’s perspective of the other cells’ progression, based on their computed shortest-path distance from s (Figure 1B, top right panel).
Waypoints and perspectives
Shortest path distances are robust at short distances but become less reliable with increasing distance from the source cell. Supplementary Fig. 23A shows the loss in reliability of shortest path distances. The additive nature of noise leads to accumulation of mistakes with distance and becomes the dominant factor with greater distances (Supplementary Fig. 23A, Figure 1B).
Wishbone, like Wanderlust, overcomes this issue by sampling a series of cells throughout the trajectory termed “waypoints” to act as guides in ordering the cells [34]. The ordering of cells is then averaged across the waypoints with closer waypoints giving a bigger “vote”. This improves the robustness by taking advantage of reliability of shortest path distances over short distances. As described later, waypoints are also used for branch associations and due to the importance of waypoints for both the ordering of the cells and branch identification, a key difference between Wanderlust and Wishbone is how waypoints are selected and weighted.
A random sample of cells can potentially select outliers as waypoints. Wishbone therefore refines the choice of waypoints by using a median filter [34]. For each randomly selected waypoint, its k nearest neighbors are identified and is replaced by the cell closest to the median profile generated using these neighbors. This refinement step has been shown to be effective in preventing the outlier cells from being chosen as waypoints for learning trajectories [34].
Next, shortest path distances are computed for each of the waypoints to obtain the distance matrix, D ∈ ℝ**n**W_×_N, where nW is the number of waypoints including the early cell s. Individually, the distances from each waypoint are still affected by the same issues of increasing noise with distance from the waypoint (Supplementary Fig. 23A). But collectively, each cell is close to a number of waypoints that can reliably estimate the ordering along developmental axis.
Waypoints are introduced to robustly order the cells by computing a weighted average but the distances from different waypoints in D are not aligned and therefore are not directly comparable (Supplementary Fig. 23A). Thus, Wishbone computes the positioning or ordering of cells from the perspective of each waypoint using the initial trajectory τ(0) as the reference. The perspective of a cell i with respect to waypoint w is the distance of i from the s from the viewpoint of w and is computed as
| Pwi:={τw(0)+Dwiifτi(0)>τw(0)τw(0)-Dwiotherwise | (2) |
|---|
This ensures that cells beyond the waypoint in the initial ordering have a higher perspective than cells that lie before the waypoint (Supplementary Fig. 23B, Figure 1B). Thus the unaligned distance matrix D is converted to an aligned perspective matrix P ∈ ℝ**n**W_×_N where each entry represents the position of a cell along the trajectory from the viewpoint of the corresponding waypoint yielding nW proposed orderings for each cell. Note that the perspective of the early cell s is the initial ordering τ(0) itself.
These perspectives can now be used increase the accuracy of the ordering by computing a weighted average across the proposed orderings. The weighting scheme should increase the vote for closer waypoints to take advantage of reliability of shortest paths over shortest distances. However, it is important to also include a degree of influence from the distal waypoints to derive a consistent global structure. This requirement is satisfied by weights that are inversely proportional to the distance from waypoint. Thus the weights are calculated by a Gaussian kernel applied to the distances, as defined by
| Wwi=exp(-Dwi2σ)/∑k=1:Nexp(-Dwk2σ) | (3) |
|---|
where σ is the standard deviation of distance matrix D. The denominator is the summation of inverted distances over all cells and used for normalization. This defines the weight matrix W ∈ ℝ**n**W_×_N. The weighted average is then calculated by
| τi(1)=∑w∈WaypointsetPwi∗Wwi | (4) |
|---|
The vector τ(1) is the refined trajectory of all cells (Figure 1B, Bottom right panel). Note that the W matrix is adjusted to ensure waypoints on one branch have reduced influence on ordering of cells in the other branch by a muting scheme described in the section “Refining the ordering using branch association scores”.
Branch point identification
Inconsistencies between waypoints are used to identify a branching point and the branch associations of each cell. Consider a waypoint t and a second waypoint i, with t being further along the trajectory. If i and t lie along the same trajectory (either both lie in the trunk, or i lies on the trunk and t on of one of the branches, or i and t are both on the same branch), the path from s to t will lie roughly along the path used for calculating perspective of t relative to i (Figure 1C, left panel). Therefore the perspective relative to t will be in agreement with (i.e. be similar) the perspective of early cell s. Now consider another waypoint j such that j and t lie on different branches. In this case, there will be a disagreement between the perspective of s and t regarding the placement of j. The path from s to t will be significantly shorter than the path to determine the perspective of t with respect to j (Figure 1C, middle panel). That path first involves a traversal to j from s and another traversal back through j’s branch and then back out on _t_’s branch to reach t. Therefore for any two waypoints, the mutual disagreement between the perspective of one waypoint relative to other and the early cell’s perspective provides a quantitative measure of whether the two waypoints lie on same or different branches.
However, mutual disagreement between a single pair of waypoints alone does not suggest a branch point, as such a disagreement could be caused by noise accumulated during longer walks. However, when a true branch exists, there will be a disagreement between a considerable number of waypoints (those on different branches), which will cue the existence of a branching. In the case of branching a clear structure emerges, where two groups of branch points A and B all disagree between waypoints across A and B and agree with waypoints within the same branch.
To identify this structure, Wishbone computes disagreements for all pairs of waypoints to construct the matrix Q ∈ ℝ**n**W_×n_W, where
In particular, Qij ≫ 0 if the two waypoints, i and j are on different branches and Qij ≈ 0 if one or both are on the trunk, or both are on the same branch. In summary, the distance matrix D is used to determine a perspective matrix P, which in turn is used to both refine the order and calculate the disagreement matrix Q used to determine branch associations as described below.
Figure 1C (right panel) shows an example of the Q matrix. This matrix captures similarities and differences between waypoints that belong to the same or different branch respectively. In particular, in the case of a branching trajectory, Q is effectively composed of three blocks. The first block consists of the waypoints in the trunk with Qij ≈ 0 for trunk waypoint i and any other waypoint j. The remaining two blocks represent the two branches with Qij ≈ 0 if i and j are on the same branch and Qij ≫ 0 if they are on different branches. A natural way to identify these blocks or clusters is by use of unsupervised clustering methods.
Spectral clustering methods are a family of clustering algorithms designed to work on adjacency matrices representing graphs. Specifically, spectral methods are based on Eigen decomposition of the graph adjacency matrix and connections between the resulting Eigen vectors and properties of the graph structure. The Q matrix can itself be seen as an adjacency matrix with the disagreement representing the weight of the edge between waypoints and as such spectral clustering can be used to classify the waypoints into trunk and the two branches. For a real symmetric matrix, the second highest Eigen value, v2, approximates the optimal graph partition [35]. Specifically, if v_2_i is the projection of the node i onto the second Eigen vector, the graph partition divides the nodes into two clusters whose elements can be identified by the sign of. v_2_i.
The Q matrix is real because all the perspectives and distances are real. It is also symmetric: Consider any two waypoints, i and j and assume i follows j without loss of generality. Then, Qij=|Pij-τj(0)|=|τi(0)+Dij-τj(0)| and Qji=|Pji-τi(0)|=|τj(0)-Dji-τi(0)|=|-(-τj(0)+Dji+τi(0))|=|τi(0)+Dij-τj(0)|, since Dji = Dij. Therefore Q matrix is symmetric. Thus the second highest Eigen values of Q can be used to identify branch associations of waypoints. Wishbone uses the Matlab eigs function for Eigen value decomposition.
The second Eigen vector, v2of Q matrix in Figure 1C, right panel is shown in Figure 1D. If waypoint w is on of the branches then v_2_w > 0 or v_2_w < 0 and v_2_w ≈ 0 if w is on the trunk, since Qij ≈ 0 for all pairs of waypoints on the trunk. Moreover, |v_2_w|increases as waypoints progress further along the trajectory away from the branch point. This creates a Wishbone-like structure, giving the algorithm its name (Figure 1D).
The v_2_w values provide a reliable partitioning of waypoints that lie towards the end of developmental trajectory on either branch. However the values of v_2_w are noisy during transition from trunk to the two branches and care must be taken to pinpoint the branching point (Figure 1D). Any path from a waypoint in a particular branch to a waypoint in the other branch will first traverse towards the trunk and then away from it. By definition, the point on path with minimum trajectory value τ(0), represents the point at which the path will be closest be to the early cell. This also represents the point where the path changes direction to enter the other branch, or in other words an estimated branch point (Supplementary Fig. 24A). For increased robustness, Wishbone uses multiple paths between branch waypoints to estimate the branch point. Specifically, all the paths between the five furthest waypoints along the trajectory τ(0), from each side of the v2 spectrum are determined. The position with shortest distance to s from each path is selected and the median position over all paths is an estimate of the branching point, bp (Supplementary Fig. 24B). Formally, let BrA and BrB be the set of five furthest waypoints of the two branches.
| BrA={i∣highestfiveτi(0)withsign(v2i)>0}BrB={i∣highestfiveτi(0)withsign(v2i)<0} | (6) |
|---|
These waypoints are then used to determined the branch point by
| bp=median{τk(0):k=minp{τp(0):p∈path(i,j)}}i∈BrAandj∈BrB | (7) |
|---|
Branch assignment to cells
The v_2_w values provide a partition of the waypoints that help determine branch assignments to all cells. Cells towards the end of the trajectory would have acquired most of the characteristics of the differentiated cell types and thus are relatively easy to classify. However, cells undergoing fate decision near the branch point do not always have a clear identity. This necessitates the use of a soft score of branch association for cells close to the branch point rather than hard branch assignments.
Wishbone uses the v_2_w values to estimate a branch association score or BAS for each cell. The estimated BAS has the following properties: for all cells on the trunk, BAS ≈ 0, whereas BAS < 0 _or BAS_ > 0 for cells on either branches. The v_2_w deviation from zero is a measure of confidence for branch association. Note that the values already satisfy these properties. Therefore BAS for each cell is determined by a weighted average of the v_2_w values, with closer waypoints getting higher votes. First, the v_2_w values also normalized for each branch to account for any trajectory value differences between the two branches:
| v2wnrom=sign(v2w)∗abs(v2w)max(v2k∣sign(v2k)==sign(v2w)) | (8) |
|---|
The weight matrix defined in Equation (3) and v2 norm are then used to calculate BAS for each cell i
An example of scores for all cells is shown in Supplementary Fig. 25A. These scores satisfy the properties outlined above and represent a soft association of branches to cells. For any downstream analyses, BAS scores and the branch point bp can be used to determine branch assignments for all cells. Cells before the branch point are considered part of the trunk and cells beyond the branch point are assigned to one of the two branches based on sign of BAS. Formally, branch assignment for cell i is determined as
| ci={1(Trunk)if,τi(0)≤bp2if,τi(0)>bpandBASi>03if,τi(0)>bpandBASi≤0 | (10) |
|---|
The branch assignments for the illustrative dataset are shown in Supplementary Fig. 24B.
Refining the ordering using branch association scores
Following a branching point, waypoints that are part of one branch should not significantly influence the ordering of cells in the other branch. Wishbone achieves this by a cross branch-muting scheme that adjusts the weights defined in section “Waypoints and Perspectives” to ensure waypoints of a branch predominantly influence the ordering of cells in the respective branch. An example of weights before adjustment is shown in Supplementary Fig. 25A. The left panel shows a waypoint in branch B that can influence the ordering of the mature cells in branch A.
The BAS scores described in the previous section can also be used for cross branch muting. Recall that weights that define the influence of waypoints on ordering cells is determined by a Gaussian kernel on the distance matrix D (Equation 3):
Wwi=exp(-Dwi2σ)/∑k=1:Nexp(-Dwk2σ)
For any cell i, the sign of BASi defines branch membership. Therefore for a given waypoint w, if the sign of BASw is not the same as the sign of BASi, the weight Wwi must be muted to reduce the influence of w in ordering the cell i. The extent of muting is directly proportional to the deviation of BASi from 0 and ensures that the influence of waypoints on one branch for ordering cells on the other branch progressively reduces along the developmental trajectory.
For each cell i, the weights of waypoints that belong to a different branch are muted as below
| Mutb=max(exp(-∣BASk∣∣sign(BASk)≠sign(BASi))),waypointkWmutwi={Wwi,ifsign(BASw)==sign(BASi)Wwi∗max(exp(-∣BASi∣),Mutb),otherwise | (11) |
|---|
This muting scheme exponentially reduces the influence of waypoints that do not belong to same branch. The weights after muting are shown in Supplementary Fig. 25B. The waypoint in branch B no longer influences the ordering of mature cells in branch A (Supplementary Fig. 25B, left panel). The muting does not affect the weights of waypoints outside branches (Supplementary Fig. 25B, right panel).
Finally, as mentioned before, the refined trajectory is calculated by the weighted average over all the perspectives using the muted weights as:
| τi(1)=∑w∈WaypointsetPwi∗Wmutwi | (12) |
|---|
Iterative refinement of trajectory and branching
The waypoints are themselves cells. Therefore, their position often changes following the refinement step. Since all cell positions depend on waypoint positioning, the shift in waypoints might obsolete the newly calculated ordering. Therefore, the refinement step is repeated with the new waypoint positions until the ordering of all cells converges.
As defined earlier, τi(0)=Dis. At any iteration t the perspective and Q matrix are calculated by
| Piw={τi(t-1)+Diwifτi(t-1)<τw(t-1)τi(t-1)-DiwotherwiseQij=|Pij-τj(t-1)| | (13) | | -------------------------------------------------------------------------------- | ---- |
The Q matrix is then used to determine the branch point bp and the BAS scores. These scores are then used for cross branch muting and a refined ordering or trajectory at iteration t is determined by
| τi(t)=∑w∈WPiw∗Wmutiw | (14) |
|---|
This procedure is repeated until convergence: corr(τ(t),τ(t−1)) > 0.9999. Finally, the branch assignments are calculated using the branch point bp and BAS scores. Note that the most time consuming parts of Wishbone are the construction of nearest neighbor graph G and computation of the shortest path distances to all cells from waypoints to build the distance matrix D. These are both one-time steps and are not repeated during the iterations. Moreover, besides from graph construction, computation of D matrix is the most computationally intensive task and is performed only once. On the other hand, P and Q matrices, determined at each iteration, are not computationally intensive.
In summary, Wishbone aligns cells along bifurcating developmental trajectories in high resolution with accurate detection of the bifurcation point. The graph-based approach used by Wishbone is central is achieving the high resolution. Diffusion maps help overcome short circuits, a key hurdle of the graph-based approaches for constructing trajectories. Waypoints and their perspectives not only help alleviate the additive noise of shortest path distances but also provide the basis for identifying branch associations by means of disagreements between waypoint and early cell perspectives. Finally, spectral clustering methods are used on these disagreements to determine branch association scores and refine the ordering. The trajectory detection and branch associations are repeated until convergence. Supplementary Note 2 shows the pseudocode of the Wishbone algorithm.
Selection of diffusion components
Diffusion maps decompose the data along the major axes of variation and capture the major structures in the data [7]. In mass cytometry, this is reflected by the first few components capturing the differences among constituent cell types provided that the markers were chosen appropriately. The subsequent eigen vectors typically capture noise and/or outliers. As an example, the top diffusion components for mouse thymus replicate 1 is shown in Supplementary Fig. 8A. The first component is trivial with same value for all the cells and is associated with eigen value of 1. Components 2,3 and 4 identify the differences among the constituent DN, DP and two SP cell types. The fifth component and beyond do not explain major structure in the data and encode for outliers and/or noise. Thus Wishbone was run using components 2,3 and 4.
While this procedure does require manual selection of components, the first two to four non-trivial components typically explain the differences between cell types in datasets with trajectories with two branches (Supplementary Fig. 8A, 16B, 16E, 17B), making the selection feasible. Moreover, Wishbone is robust to the inclusion of a number of noisy in the higher order components (Supplementary Fig. 8B), with very similar results achieved when including any number between 3 to 9 of the top components. A degree of automation can be achieved by examining the distribution of eigen values of the diffusion components, and selecting the eigen vector with biggest eigen gap (difference between successive eigen values) among first few components. The eigen value distribution of the mouse thymus replicate 1 is shown in Supplementary Fig. 8C and shows that there is a large eigen gap between the 4th and 5th eigen values. This is consistent with the observation of fifth and higher components encoding outliers and noise, there by justifying the use of the components 2, 3 and 4 for learning trajectories.
In single-cell RNA-seq, diffusion components not only explain the differences between cell types, but also identify the variation along various biological processes like metabolism, cell cycle etc. See section “Application of Wishbone to single-cell RNA-seq data” for component selection procedure for single-cell RNA-seq.
Marker expression along trajectory and derivative plots
The trajectory was first divided into 150 equally spaced bins. A Gaussian filter centered at each bin was used to estimate the weighted average expression of individual markers in each bin. The density of cells is non-uniform along the trajectory and binning the trajectory for estimating average expression rather than moving average captures the density differences. The weight matrix K ∈ ℝ150×N is determined as follows:
| Kbj=12πσ2exp(-(τj(t)-bτ)2σ2) | (15) |
|---|
where bτ is the mean trajectory value in bin b and σ is the standard deviation of the trajectory. The weighted average expression of a marker in each bin is then calculated as
where Mi is the marker expression in cell i. The weighted standard deviation for each bin is also calculated along similar lines.
For bins past the branch point, the weighted expression on a particular branch is determined by muting the weights of cells on the other branch. Markers with a weighted average difference of at least 0.1 in any bin beyond the branch point are plotted with dotted lines representing the expression in the two branches.
After calculating of the weighted averages, the derivatives were calculated as the difference in weighted average in successive bins.
Cross correlation of trajectories
For a given marker, cross correlation of expression along trajectories of different replicates were determined. The trajectory was shifted to maximize the mean of all cross correlations.
Variance analysis
The two SP populations were identified by the gating scheme defined in Figure 3B. Population level standard deviation was calculated for each marker in these gated populations. The calculation of standard deviations along trajectory is described in “Marker expression along trajectory and derivative plots”.
For running Wishbone after exclusion of a particular marker, diffusion maps were first used to determine low dimensional embedding of the phenotypic space without the marker. Wishbone was then run on the embedded space with the same parameters used for the runs with all markers.
Trajectories in gated populations and comparison to Immgen
Gating of SP cells was performed using the scheme recommended by the Immunological Genome Project (Immgen) [13]. While Immgen used Forward and Side Scatter channels to remove non-lymphoid cells, we used mass channels, which measure non-lymphoid cell surface markers and removed these cells using the clustering method Phenograph (See section “Data preprocessing and choice of parameters for Wishbone”).
Raw mRNA expression data was downloaded from the Immunological Genome Project website (GEO accession number: GSE15907). This data was background corrected using RMA and quantile normalized using the affy R Bioconductor package [36]. The expression of each gene was then scaled to be between 0–1 among the different sorted T cell populations: T.DP69+, T.4+8int, T.4SP69+, T.4SP24int, T.4SP24−, T.4int8+, T.8SP69+, T.8SP24int, T.8SP24−.
The results in this section were derived using the thymus dataset that did not profile the TFs (Figs 2–3). The dataset with TFs did not have strong staining for CD24 and as such gating could be performed accurately.
Adaptation of Wishbone to single-cell RNA-seq data
Data processing
The count matrix was downloaded from GEO (GSE72857) [6]. As a first step, cells with less than 250 molecules were discarded. Library size correction was performed by dividing the molecule counts of each cell by the library size [37]. The corrected molecule counts were then multiplied by the median of the library size across cells [37]. To address gene drop-out [27], the data was transformed using PCA to identify “meta-genes”. We note that while phenotypic space defined by cells is non-linear in its nature, the relationships between genes are largely collinear, making PCA appropriate on the gene dimension. These meta-genes were then used to cluster cells using Phenograph [29] and the clusters corresponding to HSPCs, erythroid precursors and myeloid precursors were identified by expression of characteristic genes: HSPCs - Cd34, Erythroid precursors - Gata1, Gata2, Myeloid precursors - Mpo, Csf1r, Irf8 (Supplementary Fig. 17A).
Selection of diffusion components
Diffusion maps decompose the data along the major axes of variation and capture the major structures in the data [7]. In mass cytometry data with a relevant marker set, this amounts to accounting for differences in the constituent cell types (Supplementary Fig. 8A). In genome-wide data, many of the components reflect additional biological processes such as cell cycle, stress and metabolism that would confound building trajectories. Therefore, we identify the biological processes associated with each diffusion component and keep only those that are related to development and maturation.
To identify the biology associated with each component, we sought to find genes whose expression pattern was correlated with the component. Mean expression in sliding windows of 10 cells along the component was used to determine the correlation between each gene and component. Gene Set Enrichment Analysis (GSEA) [20] was performed using the correlation based ranking to annotate each component. Gene sets from Gene Ontology Biological Process [38] database were used for annotations. Once the diffusion components are annotated, we can take one of two approaches, in sufficiently studied systems we can positively select the relevant components. In less studied systems, we can simply remove confounding components such as cell cycle, ribosomes and metabolism.
In the application here, the top 15 principal components were used for constructing the diffusion maps and the resulting enrichments for the top diffusion components of the single-cell RNA-seq dataset are shown in Supplementary Fig. 17C. Components 2 and 3 are enriched for ontologies related to immune cell differentiation. Wishbone was run using the components 2 and 3 with a randomly selected cell from the HSPC cluster as the input early cell. We note that both trajectory and branches are robust to the number of principal components used (Supplementary Fig. 17D)
Diffusion maps, Monocle and SCUBA
Diffusion maps provide low dimensional projections of the phenotypic space. Euclidean distance between the points in their low dimensional embedding onto the diffusion map is equivalent to their diffusion distance [7]. Therefore we used the Euclidean distance from the start cell in the space spanned by the first three non trivial diffusion map eigen vectors to construct the developmental trajectories in mouse thymus and human myeloid mass cytometry datasets (Figure 6, Supplementary Fig. 18). Diffusion components used for Wishbone were also used to estimate the distances from the start cell in the mouse myeloid single-cell RNA-seq dataset (Figure 6).
Monocle was downloaded from Bioconductor [24]. 1000 cells were randomly sampled from each of the datasets and Monocle was run with default parameters apart from number of branches, which was set to two and the root cell was set to the start cell used for Wishbone. The results in Supplementary Fig. 20A–C were obtained by repeatedly sampling 1000 cells from replicate 1 with the number of branches set to 2. The start cell was set to the same start cell used for Wishbone. Different runs were compared using the procedure described in section “Cross correlation analysis”.
SCUBA was downloaded from the supplementary website [5]. 25000 cells were randomly sampled from the mouse thymus and SCUBA was run with default parameters. The MassCytometry_preprocess.m script was used. The expected input, processDataMat Matlab data matrix was created and the ordering and branches were determined using the function EstimatePseudotime. As with Monocle, the results in Supplementary Fig. 19A–C were obtained by repeatedly sampling 25000 cells from replicate 1 and the different runs were compared using the procedure in “Cross correlation analysis”. SCUBA was run using all cells for the human and mouse myeloid datasets.
The resulting trajectory and branches from both Monocle and SCUBA were visualized using tSNE projections of the full dataset. Marker expression along the Monocle trajectories was determined using the procedure described in “Marker expression along trajectory and derivative plots”. A similar procedure was used for SCUBA with muting turned off since SCUBA resulted in more than 2 branches.
Supplementary Material
1
2
Acknowledgments
We would like to thank Alex Bloemendal, Zina Good, Nir HaCohen, Smita Krishnaswamy, Jacob Levine and Ambrose J Carr for their helpful comments. MDT is supported by an NSF graduate fellowship. This work was supported by NSF MCB-1149728, NIH DP1- HD084071, NIH R01CA164729 to DP. DP holds a Packard Fellowship for Science and Engineering. This work was also supported by David and Fela Shapell Family Foundation INCPM Fund, the WIS staff scientists grant from the Nissim Center, for the Development of Scientific Resources, and ISF 1184/15 to NF.
Footnotes
Contributions
SCB, DP conceived the study. MS, MDT, OA, DP designed and developed Wishbone. MS, DP performed statistical analysis and comparison of Wishbone. SRZ, TMS, NF performed all bench experiments and data acquisition. MS, SRZ, NF, DP performed the biological analysis and interpretation. MDT, MS, PK, KC, AJC programmed the software tools. MS, SRZ, NF and DP wrote the manuscript.
Competing financial interests
The authors declare no competing financial interests.
References
- 1.Tang F, et al. mRNA-Seq whole-transcriptome analysis of a single cell. Nat Methods. 2009;6(5):377–82. doi: 10.1038/nmeth.1315. [DOI] [PubMed] [Google Scholar]
- 2.Bendall SC, et al. Single-cell mass cytometry of differential immune and drug responses across a human hematopoietic continuum. Science. 2011;332(6030):687–96. doi: 10.1126/science.1198704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bendall SC, et al. Single-cell trajectory detection uncovers progression and regulatory coordination in human B cell development. Cell. 2014;157(3):714–25. doi: 10.1016/j.cell.2014.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shin J, et al. Single-Cell RNA-Seq with Waterfall Reveals Molecular Cascades underlying Adult Neurogenesis. Cell Stem Cell. 2015;17(3):360–72. doi: 10.1016/j.stem.2015.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Marco E, et al. Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape. 2014;111(52):E5643–50. doi: 10.1073/pnas.1408993111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Paul F, et al. Transcriptional Heterogeneity and Lineage Commitment in Myeloid Progenitors. Cell. 2015;163(7):1663–77. doi: 10.1016/j.cell.2015.11.013. [DOI] [PubMed] [Google Scholar]
- 7.Coifman RR, et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc Natl Acad Sci U S A. 2005;102(21):7426–31. doi: 10.1073/pnas.0500334102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Koch U, Radtke F. Mechanisms of T cell development and transformation. Annu Rev Cell Dev Biol. 2011;27:539–62. doi: 10.1146/annurev-cellbio-092910-154008. [DOI] [PubMed] [Google Scholar]
- 9.Yui MA, Rothenberg EV. Developmental gene networks: a triathlon on the course to T cell identity. Nat Rev Immunol. 2014;14(8):529–45. doi: 10.1038/nri3702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Egawa T. Regulation of CD4 and CD8 coreceptor expression and CD4 versus CD8 lineage decisions. Adv Immunol. 2015;125:1–40. doi: 10.1016/bs.ai.2014.09.001. [DOI] [PubMed] [Google Scholar]
- 11.Wang L, et al. Distinct functions for the transcription factors GATA-3 and ThPOK during intrathymic differentiation of CD4(+) T cells. Nat Immunol. 2008;9(10):1122–30. doi: 10.1038/ni.1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Love PE, Bhandoola A. Signal integration and crosstalk during thymocyte migration and emigration. Nat Rev Immunol. 2011;11(7):469–77. doi: 10.1038/nri2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mingueneau M, et al. The transcriptional landscape of alphabeta T cell differentiation. Nat Methods. 2013;14(6):619–32. doi: 10.1038/ni.2590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamashita I, et al. CD69 cell surface expression identifies developing thymocytes which audition for T cell antigen receptor-mediated positive selection. Int Immunol. 1993;5(9):1139–50. doi: 10.1093/intimm/5.9.1139. [DOI] [PubMed] [Google Scholar]
- 15.Singer A, Adoro S, Park JH. Lineage fate and intense debate: myths, models and mechanisms of CD4- versus CD8-lineage choice. Nat Rev Immunol. 2008;8(10):788–801. doi: 10.1038/nri2416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Heng TS, Painter MW. The Immunological Genome Project: networks of gene expression in immune cells. Nat Immunol. 2008;9(10):1091–4. doi: 10.1038/ni1008-1091. [DOI] [PubMed] [Google Scholar]
- 17.Rosenbauer F, Tenen DG. Transcription factors in myeloid development: balancing differentiation with transformation. Nat Rev Immunol. 2007;7(2):105–17. doi: 10.1038/nri2024. [DOI] [PubMed] [Google Scholar]
- 18.Doulatov S, et al. Revised map of the human progenitor hierarchy shows the origin of macrophages and dendritic cells in early lymphoid development. Nat Immunol. 2010;11(7):585–93. doi: 10.1038/ni.1889. [DOI] [PubMed] [Google Scholar]
- 19.Klein AM, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161(5):1187–201. doi: 10.1016/j.cell.2015.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci U S A. 2005;102(43):15545–50. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Buettner F, et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. 2015;33(2):155–60. doi: 10.1038/nbt.3102. [DOI] [PubMed] [Google Scholar]
- 22.Pinkus GS, Pinkus JL. Myeloperoxidase: a specific marker for myeloid cells in paraffin sections. Mod Pathol. 1991;4(6):733–41. [PubMed] [Google Scholar]
- 23.Kaneko H, Shimizu R, Yamamoto M. GATA factor switching during erythroid differentiation. Curr Opin Hematol. 2010;17(3):163–8. doi: 10.1097/MOH.0b013e32833800b8. [DOI] [PubMed] [Google Scholar]
- 24.Trapnell C, et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. 2014;32(4):381–6. doi: 10.1038/nbt.2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Haghverdi L, Buettner F, Theis FJ. Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics. 2015;31(18):2989–98. doi: 10.1093/bioinformatics/btv325. [DOI] [PubMed] [Google Scholar]
- 26.Moignard V, et al. Decoding the regulatory network of early blood development from single-cell gene expression measurements. 2015;33(3):269–76. doi: 10.1038/nbt.3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stegle O, Teichmann SA, Marioni JC. Computational and analytical challenges in single-cell transcriptomics. Nat Rev Genet. 2015;16(3):133–45. doi: 10.1038/nrg3833. [DOI] [PubMed] [Google Scholar]
- 28.Rinn JL, et al. Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape. Nat Biotechnol. 2014;111(52):E5643–50. doi: 10.1073/pnas.1408993111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levine JH, et al. Data-Driven Phenotypic Dissection of AML Reveals Progenitor-like Cells that Correlate with Prognosis. Cell. 2015;162(1):184–97. doi: 10.1016/j.cell.2015.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Waddington CH. An introduction to modern genetics. London: George Allen & Unwin; 1939. [Google Scholar]
- 31.Macosko EZ, et al. Highly Parallel Genome-wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell. 2015;161(5):1202–14. doi: 10.1016/j.cell.2015.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.de Silva V, Tenenbaum JB. Sparse multidimensional scaling using landmark points. 2004 [Google Scholar]
- 33.Amir el AD, et al. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat Biotechnol. 2013;31(6):545–52. doi: 10.1038/nbt.2594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gut G, et al. Trajectories of cell-cycle progression from fixed cell populations. 2015;12(10):951–4. doi: 10.1038/nmeth.3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.von Luxburg U. A tutorial on spectral clustering. Statistics and Computing. 2007;17(4):395–416. [Google Scholar]
- 36.Gautier L, et al. affy--analysis of Affymetrix GeneChip data at the probe level. Bioinformatics. 2004;20(3):307–15. doi: 10.1093/bioinformatics/btg405. [DOI] [PubMed] [Google Scholar]
- 37.Grun D, et al. Single-cell messenger RNA sequencing reveals rare intestinal cell types. Nat Biotechnol. 2015;525(7568):251–5. doi: 10.1038/nature14966. [DOI] [PubMed] [Google Scholar]
- 38.Huang da W, Sherman BT, Lempicki RA. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat Protoc. 2009;4(1):44–57. doi: 10.1038/nprot.2008.211. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
1
2
Data Availability Statement
The mouse thymus mass cytometry data can be downloaded from Cytobank (https://www.cytobank.org/cytobank/experiments/52942). The cleaned data along with the Wishbone results for different replicates is available through the supplementary website (http://www.c2b2.columbia.edu/danapeerlab/html/wishbone.html). Myeloid mass cytometry data was downloaded from Cytobank (http://reports.cytobank.org/1/v1). Mouse myeloid single cell RNA-seq was downloaded from GEO (accession number: GSE72857). Wishbone results for all the myeloid datasets is available through the supplementary website http://www.c2b2.columbia.edu/danapeerlab/html/wishbone.html). Wishbone has been integrated into our single analysis suite cyt and can be downloaded from (http://www.c2b2.columbia.edu/danapeerlab/html/cyt-download.html) and from Supplementary software. A python package for Wishbone algorithm is available through github (https://github.com/ManuSetty/wishbone).