Single Particle Refinement and Variability Analysis in EMAN2.1 (original) (raw)
. Author manuscript; available in PMC: 2017 Jul 1.
Published in final edited form as: Methods Enzymol. 2016 Jul 1;579:159–189. doi: 10.1016/bs.mie.2016.05.001
Abstract
CryoEM single particle reconstruction has been growing rapidly over the last three years largely due to the development of direct electron detectors, which have provided data with dramatic improvements in image quality. It is now possible in many cases to produce near-atomic resolution structures, and yet 2/3 of published structures remain at substantially lower resolutions. One important cause for this is compositional and conformational heterogeneity, which is both a resolution limiting factor as well as presenting a unique opportunity to better relate structure to function. This manuscript discusses the canonical methods for high-resolution refinement in EMAN2.12, and then considers the wide range of available methods within this package for resolving structural variability, targeting both improved resolution as well as additional knowledge about particle dynamics.
1 Introduction
1.1 History
The first version of EMAN (Ludtke, Baldwin & Chiu,1999) was developed in 1998. At that time SPIDER (Frank, Radermacher, Penczek, Zhu, Li, Ladjadj & Leith,1996; Shaikh, Gao, Baxter, Asturias, Boisset, Leith & Frank,2008) and IMAGIC (van Heel, Harauz, Orlova, Schmidt & Schatz,1996) were the primary non-icosahedral single particle reconstruction packages in use, both of which had a steep learning curve, and required substantial manual effort. EMAN was the first of these packages to offer a substantial graphical interface (GUI), and gave the end-user a straightforward path to follow towards 3-D reconstruction. It is important to note that at this time subnanometer resolution was just emerging, and near-atomic resolution, while theorized as possible (Henderson,1995), was still in the distant future. EMAN’s contributions at the time, in addition to its ease of use, was its integrated CTF correction strategy (Ludtke, Jakana, Song, Chuang & Chiu,2001), and a single integrated refinement program which automated all of the steps in the reconstruction process. The combination of supervised classification and iterative class-averaging to reduce model bias and speed convergence were also key features leading to its popularity.
The first version of EMAN2 (Tang, Peng, Baldwin, Mann, Jiang, Rees & Ludtke,2007) was developed in the mid 2000’s, and was a complete refactoring of EMAN1 into a hybrid C++/Python environment with a modern object oriented design. One of the motivations in this development was a collaborative effort to make EMAN2 work with the PHENIX X-ray crystallography package, under an effort led by Dr. Robert Glaeser. This same effort brought Dr. Pawel Penczek into the collaborative effort, which allowed EMAN2 and SPARX (Hohn, Tang, Goodyear, Baldwin, Huang, Penczek, Yang, Glaeser, Adams & Ludtke,2007) to share a common C++ image processing core and Python library, which continues to this day. While the collaboration with PHENIX proved to be a bit premature at that time, since few CryoEM projects were achieving resolutions where X-ray tools were useful, it was an accurate predictor of the future, as PHENIX is now a frequently used tool for performing real-space refinement of Cryo-EM derived models and other tasks. SPARX was then ceded to Penczek’s group, which continues active development.
The development of EMAN2.1, first released in 2013, transitioned from the unpopular BDB database storage system used in EMAN2.0 to the interdisciplinary HDF5 image format. In addition, EMAN2.1 included automatic resolution estimation during each refinement iteration using the “gold standard” FSC, automatic refinements using a system of heuristics, which could provide virtually all of the refinement parameters automatically, a new optimized orientation determination system an order of magnitude faster than the methods in EMAN1, as well as many other improvements.
The EMDatabank (Lawson, Patwardhan, Baker, Hryc, Garcia, Hudson, Lagerstedt, Ludtke, Pintilie, Sala, Westbrook, Berman, Kleywegt & Chiu,2015) now identifies over 50 software packages which have some use in CryoEM reconstruction. The seven most-used of these packages: EMAN, RELION (Scheres,2012), SPIDER (Shaikh, Gao, Baxter, Asturias, Boisset, Leith & Frank,2008), SPARX (Hohn, Tang, Goodyear, Baldwin, Huang, Penczek, Yang, Glaeser, Adams & Ludtke,2007), IMAGIC (van Heel, Harauz, Orlova, Schmidt & Schatz,1996), FREALIGN (Grigorieff,2007a) and XMIPP (de la Rosa-Trevín, Otón, Marabini, Zaldívar, Vargas, Carazo & Sorzano,2013), account for over 97% of the published single particle reconstructions in 2015.
1.2 The Scope of the Problem
Direct detectors and current generation microscopes are producing data of unprecedented quality, and indeed over 20% of the maps published in 2015 were at a resolution of 4 Å or better, with another 14% at 6 Å or better. Given the state of the art, one might ask why 2/3 of structures are still published when they are at comparatively low resolution. One theory for this phenomenon might be insufficient access to current generation hardware, however, while the statistics for improved microscopes and detectors are skewed slightly towards high resolution, only half of the structures published using an FEI Krios in 2016 surpassed 6 Å resolution. Similar statistics apply for use of Gatan K2 Summit detectors. So, even with current generation hardware it seems near-atomic resolution is not assured. While there may be specimen preparation issues, such as ice thickness or low contrast due to buffer constituents (detergent being a particular problem), it is hoped that these problems are largely being resolved on far less expensive equipment, similar to the use of tabletop crystallography machines to verify crystal quality prior to using time on a beamline. The most likely remaining resolution limiting factor is conformational and compositional variability in the specimen.
An assumption fostered by the long success of crystallography over recent decades is the implicit assumption that structures are rigid, or at least fairly rigid, such that a single structure exists to determine. Even with the recognition of many examples where large scale motion is an integral part of the function, it is still common to refer to the structure of a macromolecule, and deal with local motion in terms of B-factors describing Gaussian deviations from the true location of each atom, though use of the more extensive TLS analysis (Chaudhry, Horwich, Brunger & Adams,2004) is becoming more common. Since the vitreous state used in CryoEM mimics a native aqueous environment, and lacks the crystal packing forces in crystallography, it is not surprising that substantial flexibility is observed. Characterizing this motion is not just a mechanism for improving resolution, but can reveal fundamental insights into the structure-function relationship.
Even if a user’s first experience with CryoEM turns out to be straightforward and rapidly achieves high resolution, it is important to remember that this is relatively uncommon, and it will frequently be necessary to invoke a variety of experimental methods and software tools. In the case of a specimen which is extremely rigid in solution, and data has been collected on high-end equipment, in our experience the various algorithms and software packages used in CryoEM tend to produce equivalent structures, in terms of both measured resolution and visible features. However, if the specimen has either compositional or conformational variability then it is very common for various algorithms to explore the variability in different ways, and produce visibly different structures. Understanding the nature of the variability through the differences among software packages, algorithms or even additional experiments is frequently required to obtain a complete and correct understanding of the system.
1.3 EMAN2.1 Philosophy
The overall philosophy of processing in EMAN2 would be best termed “guided flexibility”. EMAN2 offers tools at every level ranging from graphical interfaces to low level image processing algorithms to encourage and support detailed exploration of experimental CryoEM and CryoET data. There is a simple to use workflow interface (e2projectmanager) to guide users through a range of different tasks from evaluation of micrograph quality through high resolution 3-D reconstruction and heterogeneity analysis. Tools like e2refine_easy (Bell, Chen, Baldwin & Ludtke,2016) and e2refine2d, provide quick and automatic processing of single particle data (in 3-D and 2-D), similar in function to the refinement programs offered in packages focusing on a single algorithm, such as RELION (Scheres,2012) (and chapter by Scheres) and FREALIGN (Grigorieff,2007b) (and chapter by Grigorieff). e2refine_easy has an extensive set of heuristics, such that for well-behaved projects, almost no options need be specified by the user. However, when projects prove to be more complicated than initially anticipated, it also offers a diverse set of options and alternative workflows, which can be used to gain more insight into the behavior of the specimen. Since there can be considerable value in comparative refinements, there is also an extensive set of interoperability tools making it straightforward to interoperate/interconvert among EMAN, RELION, FREALIGN and CTFFIND3/4 (Mindell & Grigorieff,2003; Rohou & Grigorieff,2015). Since its inception, EMAN2 and SPARX have been jointly distributed, and while they have evolved different philosophies, different end-user programs, and different pipelines, they share a common core image processing system, Python programming environment and image access. It is also possible to seamlessly exchange image data between EMAN2 and the popular NumPy/SciPy environments. Finally, EMAN2 has committed to supporting EMX (Marabini, Ludtke, Murray, Chiu, Jose, Patwardhan, Heymann & Carazo,2016), the new Electron Microscopy Exchange format for metadata interchange among CryoEM software packages.
At the highest level the graphical user interface e2projectmanager can guide the user through a canonical single particle refinement starting with micrographs, particle locations, particles or even particles with predetermined CTF information. This pipeline includes several 2-D analysis steps including identification of bad particles and de-novo initial model generation. These pipelines are designed such that each step in the process should be straightforward, and in most cases alternative algorithms can be trivially substituted into the workflow. If a user believes CTFFIND3/4 will compute more accurate astigmatism values than the built-in particle based approach, there is a tool for importing these values and automatically computing the additional particle-based values EMAN2 requires, while retaining defocus and astigmatism from the external software. If a user finds they prefer RELION’s 2-D class averages to EMAN2’s, they can easily take that diversion. In short, EMAN2 offers its own complete pipeline, but also endeavors to make it simple to compare tools among multiple packages.
When tasks are initiated in the graphical workflow interface, in reality the interface is simply building commands then executing them on the local machine. Any of these commands can, instead, be copied from the GUI for execution on a Linux cluster or other high-performance computer, as desired. The majority of the processing in EMAN2.1 can be completed on a mid-range or high-end workstation, with the exception of final high-resolution refinements for large projects. The current EMAN2.1 tutorial makes use of a subset of ~4200 beta-galactosidase particles drawn from the 2015 EMDatabank Map Challenge (http://challenges.emdatabank.org), which can be processed to ~4 Å resolution on a workstation in a few hours. Clearly there are larger projects which require clusters for high resolution refinement, particularly in cases of variability, where very large data sets must be divided into several subpopulations. For such uses, the system supports both MPI and threaded parallelism. All executed EMAN2 commands are logged when executed, and processes like e2refine_easy further produce an output report with resolution plots as well as a detailed description of the methodologies employed during the refinement, and often suggestions for proceeding.
While there is a complex system of heuristics in place for many of the high level tasks in the system, all of these can be overridden by the user, should the need arise. For example, a canonical e2refine_easy refinement run requires only: starting model, input particle stack, particle mass, target resolution, symmetry, number of iterations, “speed” and parallelism settings. All other settings can be determined automatically based on the properties of the particle. However if desired, this command offers ~40 additional documented options which can be specified should the user elect to do so. It must also be noted that the automatic system records all of the options selected by the heuristics, so one can easily see which options were selected automatically as a starting point for manual adjustments. For the majority of structures, this detailed option setting will not be useful, and should the user find it necessary to do so to achieve optimal results, they are encouraged to report what they changed and why, for use in improving future versions of the heuristics.
The system has a highly modular core, with methods for specific tasks organized by name and categorized by task (Tang, Peng, Baldwin, Mann, Jiang, Rees & Ludtke,2007). If someone were to design, for example, a new 3-D reconstruction algorithm, it would be added to the system as a new named option, and would immediately be usable in any program within the system, with no additional reprogramming required. The built in e2help command provides documentation for each method of each type, as does the built-in help system in e2projectmanager.
2 Single Particle Reconstruction
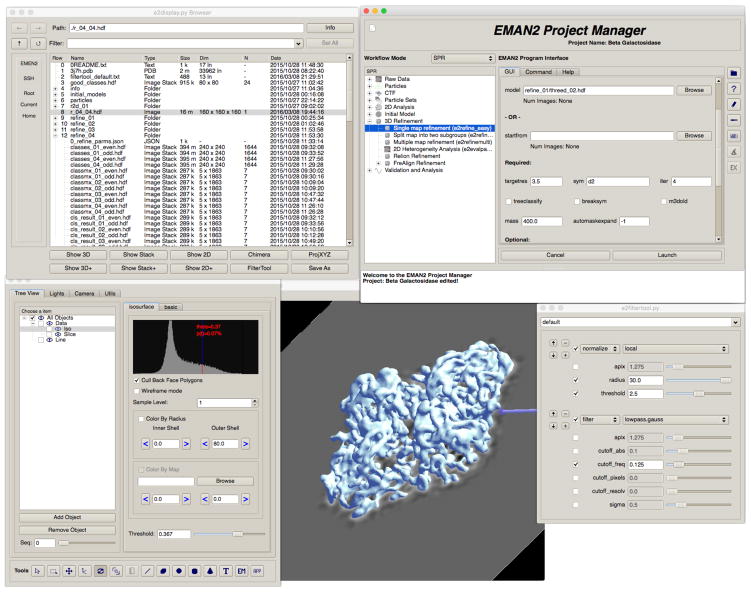
We begin with a brief summary of EMAN2.1’s approach to a typical single particle reconstruction, then move on to assessing the structure, and finally, what to do when structures prove to be less tractable than hoped. Details on the internal workings of the processes invoked in this workflow can be found in other sources (Bell, Chen, Baldwin & Ludtke,2016). Here we consider the broader perspective of the diverse set of situations which may be encountered in single particle analysis. Normally the most convenient way to complete a standard refinement is to use the e2projectmanager interface (shown later in Figure 4). This interface is useful for both beginners as well as experienced users, but exposes only the commonly used options in each program. Exactly the same process can be followed via a sequence of command-line programs. Detailed tutorials, both textual and video, are available online and are updated regularly (http://wiki.eman2.org).
Figure 4.
A panel showing just a few of EMAN2.1’s many graphical tools. The main project manager is shown in the upper right, with a portion of the dialog for a run of e2refine_easy shown. On the upper left is the file browser, note the metadata displayed in the columns of the browser, as well as the actions available at the bottom of the window specific to the selected file type. The bottom three windows show e2filtertool operating on a 3-D volume. The 3-D display in the center shows an isosurface with a slice through the middle and a 3-D arrow annotation. The control panel, which permits modifying this display, is shown on the left. On the right is the e2filtertool dialog, where a sequence of two image processing operations have been added: first, a “local normalization” operation, which helps compensate for low resolution noise and ice gradients; second, a Gaussian low-pass filter set to 8 Å resolution. The parameters of these operations can be adjusted in real-time with corresponding updates in the 3-D display. 2-D images and stacks can also be processed using this program. Any of over 200 image processing operations can be used from this interface, and command-line parameters are provided mimicking the final adjusted parameters.
The general sequence of steps in a simple single particle refinement is:
- Movie alignment (if applicable) – If the data were collected on a direct detector in movie-mode, whole-frame movie alignment is the first step. Tools for optimal alignment remain an active area of research in the community (see chapter by Rubinstein). EMAN2.1 has e2ddd_movie and e2ddd_particles, but any other alignment tool can also be used for this task.
- Micrograph assessment – This includes determining defocus and (optionally) astigmatism as well as assessing the suitability of the image. EMAN2.1 has e2evalimage and e2rawdata for interactive or noninteractive processing. CTFFIND or EMX files can also be imported.
- Particle picking – Many tools exist for this. EMAN2.1 includes e2boxer for both manual and semi-automatic picking. SPARX has a module for fully automatic picking. Any other tool can be used as well. EMAN1 .box files and EMX files can be imported, as can already extracted particle stacks. Note that it is absolutely critical for EMAN2.1 that box-size recommendations be followed. If not, results are guaranteed to be suboptimal (http://www.eman2.org/emanwiki/EMAN2/BoxSize).
- Particle based CTF and SSNR – If the defocus and astigmatism have not already been determined in a previous step, EMAN2.1 uses particle-based determination for this process. If existing values are provided, they may be used without modification, in which case this step determines the radial SSNR per-micrograph and an estimated radial structure factor. This step must be performed in EMAN2.1, using e2ctf, and is performed automatically by several of the particle import procedures.
- Set building – In EMAN2.1, a set is a text file containing references to an arbitrary fraction of the particles the project. Conceptually this is somewhat similar to the STAR files used in some of the other CryoEM packages, but a major difference is that the .lst files can be used directly as if they were an image stacks by any EMAN2.1 program. This mechanism can be also used to coordinate multiple versions of particles, for example one set of particles based on only the first few movie frames for reconstruction and another set using all frames (high dose) for orientation determination. Implemented in e2buildsets.
- 2-D unsupervised class-averaging – This process, implemented in e2refine2d, is used for two purposes. First, it can identify specific types of bad particles, and mark them as such so they are excluded from future sets. Second, it can be used to assess the amount of compositional and conformational variability in the specimen. Since this process does not require the 2-D averages to be based on a consistent 3-D map, they are free to express the full range of variations present among the particles.
- Initial model generation – The programs e2initialmodel and e2initialmodel_hisym normally serve this purpose, but a starting model can be drawn from any other source as well. See below for a discussion of model bias.
- 3-D refinement – As described above, e2refine_easy is the canonical program for this, assuming a highly homogeneous data set. This is also a possible branch point for running comparative refinements in other packages.
- Evaluate 3-D reconstruction – Validation and considering possible compositional or conformational variability are critical. These issues are discussed in the remainder of this chapter.
It is important to note that EMAN2.1 uses a standard directory structure for all projects (http://www.eman2.org/emanwiki/EMAN2/DirectoryStructure), and the user has limited freedom to deviate from this during canonical workflows. This is not as onerous as it sounds. It is simply a standard naming convention for files and folders. Each macromolecular system should have its own project directory, and all e2* programs should normally be run from this directory, not from any of the subdirectories. However, when using EMAN2.1 as a utility, rather than following a workflow, programs can be run from any location on the hard drive. Utilities such as e2display, e2proc2d, e2proc3d, e2procpdb, e2proclst, e2procxml, e2filtertool and e2iminfo can be useful even if using another software package for 3-D refinement.
Internally, EMAN2.1 uses the HDF5 file format as a standard for all images and volumes. This format supports stacks of 1-3D images with arbitrary tagged metadata in the header of each image. It is also compatible with UCSF Chimera, so no conversion is required before visualization. EMAN2.1 still supports all documented file formats in CryoEM, and any program can transparently read/write any format. However, specific programs often require specific metadata, such as CTF information, to be stored in the image header, so running e2refine_easy directly on an MRCS stack, for example, will result in disabling CTF correction.
Non-header metadata is now stored in JSON format, which is a human-readable format popular for web programming. Note that some JSON files may contain binary image data encoded as text, which makes these files difficult to read with a text editor. The “Info” button in the EMAN2.1 file browser can be used in these cases to interactively browse JSON files.
3 Assessing a Refinement and Identifying Variability
3.1 Resolution
In recent years, the “gold standard” FSC (Henderson, Sali, Baker, Carragher, Devkota, Downing, Egelman, Feng, Frank, Grigorieff, Jiang, Ludtke, Medalia, Penczek, Rosenthal, Rossmann, Schmid, Schröder, Steven, Stokes, Westbrook, Wriggers, Yang, Young, Berman, Chiu, Kleywegt & Lawson,2012; Scheres,2012) has become a fairly universal standard in the cryo-EM field, though it is not without its detractors. The concept is quite simple, the particle data is split into two sets at the very beginning of processing, and different starting models are generated for each half of the data. Refinement then proceeds completely independently for the two halves, and only at the end of refinement are the two independent maps compared and averaged. In EMAN 2.1, the independent starting models are generated by randomizing phases beyond a resolution 1.5–2x worse than the target resolution, insuring that any model bias will be completely different in the two independent maps. This methodology is an intrinsic part of e2refine_easy to the extent that it is no longer possible to run a refinement without following these practices.
The primary objections to the “gold standard”, as far as we are aware, is that it does not prevent model bias (Stewart & Grigorieff,2004) from occurring and is not immune to algorithmic bias. What the “gold standard” does do is to prevent resolution exaggeration due to model bias. In addition, since the FSC is also used to filter the map between iterations, it may help to retard the actual noise bias. e2refine_easy also has an independent strategy for minimizing bias through iterative 2-D class-averaging integrated into the 3-D refinement loop (Ludtke, Baldwin & Chiu,1999). The “gold standard” also does nothing to prevent resolution exaggeration due to mask correlation, algorithmic bias, or a range of other effects, which can cause resolution to be overestimated. Unfortunately, achieving near-atomic resolution has done little to minimize problems with resolution exaggeration. While there are landmarks at specific resolutions to validate claimed results, such as helix separation at 7–9 Å resolution and strand separation at 4–5 Å resolution. It does nothing to validate that apparent sidechains appearing at 3–5 Å resolution range are real. It is unreasonable to expect that people will not try to claim the best resolution they believe they can justify for their reconstructions, so it remains critical that the field develop strong validators and mandate their use to counter this tendency towards exaggeration. The “gold standard” represents one critical step in this direction, which is mandatory in EMAN2.1 refinements, but is clearly an incomplete solution.
3.2 Map Accuracy, Variability and Symmetry
While a structure may be a homo-multimer, it should be clear that no real molecule or assembly will have perfect geometric symmetry at infinitely high resolution. At some resolution the symmetry will be broken. As we approach true atomic resolution this symmetry breaking will begin being observed even for the most rigid structures. In X-ray crystallography, the crystal packing forces act to restrain this variability somewhat, and what remains is typically expressed as B-factors. Since prior to vitrification, CryoEM molecules are in solution, typically at near room-temperature, much larger scale variability should be expected. To assess the reliability of high resolution maps, we must consider a variety of methods.
One powerful test which is necessary, but not sufficient, to demonstrate a correct structure, is agreement among projections, projection-based class-averages, unsupervised class-averages and the particles themselves (Murray, Flanagan, Popova, Chiu, Ludtke & Serysheva,2013). Clearly there are limits to comparisons with individual particles due to their low information content. However, both types of class-averages should agree with a corresponding projection to the limits of the variation between two angular steps. These comparisons can be made in EMAN2.1 using e2classvsproj and e2ptclvsmap. When any significant disagreement exists, even locally, this is an indication of imperfect agreement of the data and the 3-D map, which should be investigated further.
While largely an issue of low, not high, resolution reconstruction, if there is a question of the accuracy of the quaternary structure in a reconstruction, e2RCTboxer and e2tiltvalidate can be used together to validate the reliability of the map (Murray, Flanagan, Popova, Chiu, Ludtke & Serysheva,2013; Rosenthal & Henderson,2003). As also discussed below, there is an extensive set of subtomogram averaging tools, which can also be applied for validation of quaternary structure (Galaz-Montoya, Flanagan, Schmid & Ludtke,2015; Shahmoradian, Galaz-Montoya, Schmid, Cong, Ma, Spiess, Frydman, Ludtke & Chiu,2013).
Another potential difficulty is preferred orientation. Particularly in cases where a continuous carbon substrate is used, but even in some cases where particles are frozen over holes, macromolecules may exhibit preferred orientation on the grid. The extent to which this causes a problem for the reconstruction is highly dependent on both the shape and symmetry of the structure as well as the nature of the preferred orientation. Let us consider two examples. First, GroEL (Braig, Otwinowski, Hegde, Boisvert, Joachimiak, Horwich & Sigler,1994), a homo 14-mer, consisting of 2 back-to-back rings forming a cylindrical shape. GroEL on the grid, even in the absence of continuous carbon, is found predominantly in end-on views, with projection direction near parallel to the 7-fold symmetry axis, and in side-views within a few degrees of the set of 2-fold symmetries relating the two rings (Ludtke, Jakana, Song, Chuang & Chiu,2001). Very few particles are found in orientations between these extremes. While this might seem to be a very poor distribution, in fact, this represents precisely the minimum information required for a complete reconstruction in Fourier space. While the preferred orientation does cause some resolution anisotropy, this occurs in a pattern difficult to even track by eye, and generally speaking reconstructions are excellent to near-atomic resolution.
The second case we consider is the ribosome (either 70S or 80S). Ribosomes are almost always frozen on a continuous carbon substrate, and in this environment tend to sit with one of two specific points on the surface stuck to the carbon. While there is some angular variation near these specific orientations, and there is a fraction of particles present in truly random orientations, this preferred orientation leads to some severe artifacts visible in many published ribosome structures. Specifically, this causes a highly anisotropic resolution in the CryoEM reconstruction, forcing a choice. The entire map could be filtered to a resolution achievable isotropically. However, this is unsatisfying since clearly the isotropic resolution is substantially worse than the achievable resolution over much of the unit sphere. Failing to do this, however, can lead to a pattern of semi-localized ‘streaking’ visible in the structure, which is clearly an artifact. For the ribosome, this problem is further complicated by the presence of multiple ratcheting states, which can lead to additional local streaking/blurring artifacts.
While anisotropic resolution poses the major problem caused by preferred orientation, there are also two other potential problems. First, if one particular orientation is massively overpopulated, for example with 10–100x more particles than typical orientations, then the very small fraction of particles which are inevitably assigned to the incorrect orientation may wind up contaminating the less populated orientations, and cause significant structural distortions. The main solution to this problem is to eliminate some of the excess particles in the preferred orientation such that there are no more than ~10x as many particles in these orientations than in the typical orientation. Second, to achieve a complete (but not isotropic) reconstruction, it is necessary to have all orientations along a great-circle around the unit sphere populated with number of particles. Otherwise the preferred orientation may lead to an artifact similar to the missing cone from random-conical tilt reconstructions. If information is completely absent in some directions in Fourier space, then the reconstruction algorithm may fill these missing areas with anything that is otherwise difficult to fit into the structure, such as contamination or particles in a different conformation, which again may lead to significant artifacts. There is no satisfactory computational solution to this problem, meaning alterations to surface chemistry should be considered to try and eliminate or reduce the preferred orientation experimentally. One common trick is to include a very tiny amount of a weak detergent to block the air-water interface and to exclude the continuous carbon substrate (Zhang, Baker, Schröder, Douglas, Reissmann, Jakana, Dougherty, Fu, Levitt, Ludtke, Frydman & Chiu,2010), but many other such tricks also exist (Glaeser, Han, Csencsits, Killilea, Pulk & Cate,2016).
The problem of broken symmetry or pseudosymmetry can be more difficult to address quantitatively. The first question to address is whether a pseudosymmetry is broken in a consistent way, such as with the unique vertex present in many icosahedral viruses, or whether it is broken by independent motion among the subunits. If the former, then the correct solution is to refine the structure with no symmetry imposed at all, or potentially, with symmetry imposed only among subunits expected to be identical. The difficulty is that there must be sufficient information present in each individual particle to discriminate among the possible symmetry-related orientations unambiguously. In the case of a large portal on a virus particle, this is unlikely to be an impediment. However, in a case like CCT, a chaperonin with two copies of 8 different proteins arranged in two back to back rings, the question can become intractable (Cong, Baker, Jakana, Woolford, Miller, Reissmann, Kumar, Redding-Johanson, Batth, Mukhopadhyay, Ludtke, Frydman & Chiu,2010; Leitner, Joachimiak, Bracher, Mönkemeyer, Walzthoeni, Chen, Pechmann, Holmes, Cong, Ma, Ludtke, Chiu, Hartl, Aebersold & Frydman,2012). In CCT the 8 subunits are so highly homologous, that differences among them only become significant at near-atomic resolution, where relatively little signal is present in the image data. In these cases, counting-mode direct detectors, which provide a significant contrast boost at high resolution, may be the difference between success and failure, as they increase the information available about each individual particle.
If the symmetry is broken due to independent Brownian-like motion among the subunits, then this problem is similar to the general issue of structures with conformational variability discussed in 4.5 below. The problem of self-consistent pseudosymmetric structures is discussed in 4.6.
3.3 Model-based Refinement
As atomistic models based solely on CryoEM maps are now becoming more commonplace, it is natural for our field to consider adaptations of refinement methods long-used in X-ray crystallography (see chapter by Murschadov). In this case, specifically, using models as a tool to improve the CryoEM maps themselves. The basic concept is to refine a structure to high resolution, build a model for that map, then use that model to generate a starting map for another round of refinement.
Naturally there is a significant risk of producing a self-fulfilling prophecy via this approach. That is, side-chains are modeled, then model bias amplifies the modeled sidechains during refinement, whether they are accurate or not. To avoid this trap, we need a mechanism for validating any improved results. The simplest approach, which represents a trade-off between validation and potential structure improvement, is to strip the sidechains from the model-based starting map. Then if side-chains reappear, particularly if they agree among the even/odd halves of the data, clearly they must have resulted from the data itself, and not the side-chain free model. However, this also means side-chains aren’t present to help anchor the orientation of the structure. A slightly more aggressive method would be to, for example, remove all of the even numbered side-chains from the initial map used for the even particles, and the odd numbered side-chains from the initial map used for the odd particles. Then, once again, any correlations among the side-chains between the two maps clearly could not have resulted from model bias. Alternatively, we can require two completely independent reconstructions with independent modeling, akin to a suggested method for model validation (DiMaio, Zhang, Chiu & Baker,2013), but this requires that only half of the data be available for the modeling/remodeling process, which may be a limiting factor in this method.
These tasks can easily be experimented with using the e2pdb2mrc program to convert models to maps. Further, we have developed a new version of e2pathwalker, which can generate acceptably accurate backbone traces of high resolution CryoEM maps fully automatically. This eliminates the need for a human to be involved in the model building process after each refinement cycle, and paves the way for possible iterative model-dependent refinement in the future.
4 Conformational and Compositional Variability
It should not be surprising that a large fraction of large macromolecules undergo some amount of motion in solution, or that even for ligands with measured high affinity, a significant amount of compositional variability is frequently observed. The underlying assumption in all single model CryoEM refinements is that the particles being reconstructed are identical at some target resolution. When this is not the case, the impact on the structure may be modest or severe depending on quaternary structure and the nature of the variability. At present we do not believe there is any single strategy to unambiguously treat all of these situations. Indeed, resolving certain types of structural variability may be a mathematically ill-posed problem, and require specialized data collection to resolve. EMAN2.12 offers several different strategies oriented at resolving these issues in different specific situations.
4.1 Variance Analysis
Before proceeding with the more detailed analyses below, it is useful to assess the variance of the map, and locate any hotspots that indicate variability in the underlying structure. EMAN2.1 includes e2refinevariance, a slightly modified implementation of the bootstrapping method described in (Penczek, Yang, Frank & Spahn,2006). In the original published method the entire population of particles is resampled with replacement to build a set of N maps from which the variance could be computed. It was later determined that there were weaknesses in this approach for systems with non-uniform particle orientations, and that this effect should be compensated for when resampling (Zhang, Kimmel, Spahn & Penczek,2008). Since e2refine_easy makes use of reference-based class-averages, these already roughly account for orientation anisotropy, so rather than resampling the particle population directly, e2refinevariance performs resampling with replacement on each class-average independently, then reconstructs the class-averages as usual (Chen, Luke, Zhang, Chiu & Wittung-Stafshede,2008).
This procedure works well, but one important caveat for all variance maps, regardless of source, is that a low-pass filtered variance map is not equivalent to a variance map computed from a low-pass filtered data set. That is, to observe low-resolution variances in the structure, it is necessary to filter the original independent reconstructions prior to computing the variance. It is not equivalent to low-pass filter the variance computed from the full resolution data. Most interesting variances are low-resolution features associated with large scale motion or variability. For this reason, and for speed, it is typical to low-pass filter and downsample the class-averages (or alternatively the particles), an option provided directly within the program.
Once computed, variance maps are typically displayed as a color pattern overlaid on an isosurface. While _e2display_’s 3-D widget does have support for ‘color by map’, UCSF Chimera (Goddard, Huang & Ferrin,2007) has a much more complete interface, and is recommended for this purpose. It is important to note that due to differences in sampling, higher variance will always be observed on and near symmetry axes. While real, this is a mathematical effect, and does not actually indicate a higher level of variability along the axis.
4.2 Multi Model Refinement
This general method, implemented as e2refinemulti, is widely used in multiple software packages, and has been in common use for well over a decade (Brink, Ludtke, Kong, Wakil, Ma & Chiu,2004; Chen, Song, Chuang, Chiu & Ludtke,2006). The concept is straightforward. Normal refinement uses projections of an initial model to determine individual particle orientations. In multi-model refinement, N sets of projections from N different initial models are used to determine which of the models each particle matches the best in addition to orientation. After reconstructing N new models, the process is iterated in the same way as normal single-model refinement. Procedurally, the only change is that multiple initial models must be provided. These N models can come from any source. They must not be perfectly identical, or the refinement will fail. However, perturbing the same starting model N times by adding a small amount of noise is a perfectly acceptable and unbiased strategy, though convergence could take as many as 15–20 iterations if the starting models are nearly identical. Alternatively, with some knowledge about the system, such as a ligand which may be present or absent, two starting models could be the single model refined map and the same map with the ligand manually masked out. In this case, convergence will normally be achieved much more rapidly (3–5 iterations).
This algorithm is guaranteed to converge to produce N final maps, and it will tend to converge to maps as different as possible given the provided data. If the data are completely homogeneous apart from noise, N different maps will still emerge, and the observed differences will then be due to model bias. When structural variability is present in the data, providing that the variability is detectable in individual particles, this real variability will tend to dominate the classification process, rather than any sort of model bias. Nonetheless, it is important to follow this multi-model refinement with additional validations to insure the results are reliable.
The first recommended step is to perform a cross-validation. The particles associated with each of the N models are automatically split into N new .lst files at the end of the e2refinemulti job. During the job, particles are free to migrate among the N maps during each iteration. The final particle separation is static, and should be used as input for a new e2refine_easy refinement to achieve better convergence. As one validation, the starting model for each of these single map refinements should be the final map from one of the other N-1 results, rather than the final result associated with the same particle set. If the refinement converges back to the e2refinemulti result associated with the particle set (away from the starting model), then it implies that this map is truly discriminated from the other N-1 maps by the particles. This, in itself does not prove that the results are meaningful, just that the particle sets are sufficiently well discriminated to overcome initial model bias.
The other obvious validation would be to re-run e2refinemulti using a different set of N starting models. If noise was used to discriminate among starting models in the first run, then this could be repeated with different noise. If deterministic starting models were used initially, then some strategy for perturbing them significantly could be applied, such as randomizing high-resolution phases using the filter.lowpass.randomphase processor.
It is critical to realize that in all least-squares classification methods, including methods such as maximum likelihood, while the N, 3-D maps produced by the method may be quite representative of the actual specimen variability, the accuracy of the classification of individual particles may be quite low. This is true for basically the same reason that in statistics the standard deviation of the mean is much smaller than the standard deviation of the distribution that formed it. Individual particles are noisy and difficult to classify, so, while we speak of the particles associated with a particular map, this subset is often highly contaminated with particles which should be in other subsets. Some of the methods described below strive to address this problem by stepping outside the least-squares framework, through use of masks, thresholds, exact subtraction and other methods, to help improve the statistical accuracy of the classification of each individual particle.
4.3 Splitting 3-D Refinements using 2-D PCA
Based on the above discussion it would be desirable to have a more accurate mechanism for accurate classification of particles and/or for identifying important structural variabilities. EMAN2.1 includes e2refine_split, for unbiased binary separation of a single-model 3-D refinement. This method divides the data into two subsets, and produces a new 3-D reconstruction for each state.
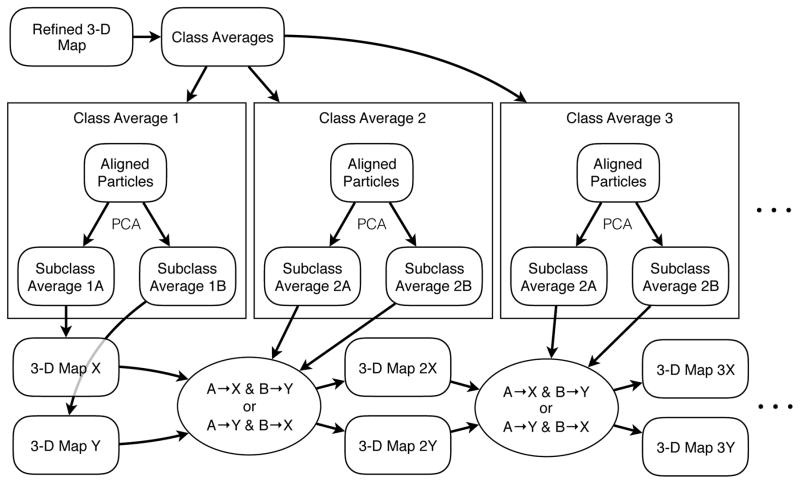
Consider the set of particles going into a single class-average. Principal component analysis (PCA) can be applied to the aligned particles to identify the most prominent differences, and split the particles into two sets, thus producing two class-averages from one. Applying this to an entire data set leads to two class-averages for each orientation, but does not identify whether each average should be associated with map A or map B.
The approach used by e2refine_split to perform this assignment (Fig. 1) is to begin with the class-average with the largest number of particles, and arbitrarily assign average A to map X and B to map Y. Next, the next most populous class-average is compared to the 3-D Fourier volume after the first assignment. The two possibilities, A->X, B->Y or A->Y, B->X are compared, the best match is selected and the class averages inserted into the corresponding Fourier volumes. The process is then repeated for each pair of averages in particle count order, with Fourier space gradually becoming more and more complete, thus providing more information for each subsequent decision. That is, at the beginning of the process, there are few overlaps in Fourier space, but each inserted class-average has a comparatively large number of particles, and thus provides a high SSNR for A/B classification. Later in the process, where the tested class-averages are noisier due to low particle counts, Fourier space is more completely filled providing more existing information to make the decision. At the end of the process, two 3-D maps and two sets of particles are produced where only one existed before.
Figure 1.
A diagram showing how e2refine_split separates a single 3-D refinement into two distinct maps, by subclassifying the particles within each class-average.
There are several advantages of this algorithm over e2refinemulti. First, it is unbiased, requiring no starting models. Second, it is very fast, since no additional 3-D orientation determination is required, and class-averaging is a fast process. Third, the effective noise reduction provided by PCA leads to more accurate classification.
There are also some weakness of the method: First, if the data includes a wide range of defocus values and the structural variability is modest, then the first PCA component may represent defocus variation rather than a structural difference. Second, if there are multiple independent motions present in a 3-D map, this method may identify a different variation as being the most prominent in one orientation than the variation identified for another orientation. In this situation, the algorithm will simply do the best it can, and it is hoped that a second round of binary splitting, applied to each of the maps in the first round, will identify the next strongest remaining inhomogeneity among the data, and thus effectively separate the two motions. The user also has the option to select which PCA vector is used in the classification, though, so it may be possible to combat problems such as defocus dominating the result.
While in principle it would be possible to develop a method which splits each class-average into N groups rather than only 2 groups, this would increase the number of permutations to consider exponentially as well as increase sensitivity to misassignment of class averages, so at present we limit the method to 2 states at a time. A related technique (Zhang, Minary & Levitt,2012) proposes to use individual class-averages in conjunction with simulation methods to derive more continuous dynamics information. It is possible that a future algorithm could hybridize these approaches and yield a data-based solution for rigorous separation of states.
4.4 Model Based Binary Separation in 3-D
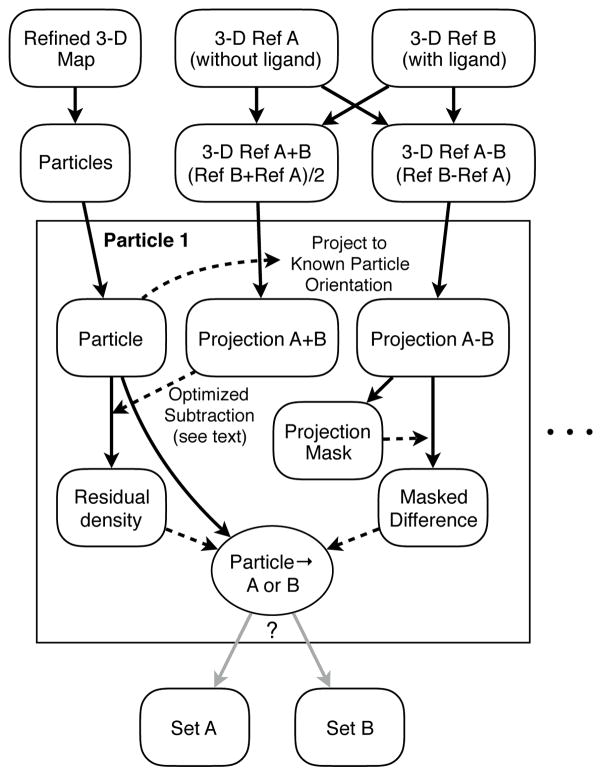
In the approach above, classification is performed in 2-D and is bias-free. However, if more information about the specific variation is available, this can be used to improve per-particle classification accuracy (Fig. 2). For example with ligand binding, or with a localized discrete motion, the voxels which vary the most in 3-D between the two states can be identified, then the voxels which don’t profitably contribute to classification can be excluded or aggressively downweighted. This method is implemented in e2classifyligand (Park, Ménétret, Gumbart, Ludtke, Li, Whynot, Rapoport & Akey,2014).
Figure 2.
A diagram showing how particles can be accurately classified between two 3-D reference maps. The classification performed using this process provides demonstrably better statistical separation than standard multimodel refinement (4.2), provided the major differences between the two references are fairly localized.
This algorithm requires two starting maps representative of the two states to be separated. The average of the two maps is computed to serve as a neutral standard, and the difference of the two maps is computed to construct a mask and a classification vector. For each particle a projection of the sum and difference maps is generated in the already known orientation. A mask, identifying the most important pixels for classification, is constructed, and applied to the difference projection. The neutral standard projection is used to eliminate as much irrelevant information from the particle as possible. This subtraction includes appropriate CTF imposition, filtration and density matching, similar to the method described below in 4.5. Ideally, this remaining density would include only noise and the information relevant for classification. This residual density is then used in conjunction with the masked classifier to separate the particles. In addition to A<->B separation, ambiguous particles can also optionally be split into a separate class, retaining only the particles most clearly representative of each state. In addition, the per particle classification values are stored, and can be used to assess the statistics of the separation.
4.5 Robust Extraction of Particle Fragments
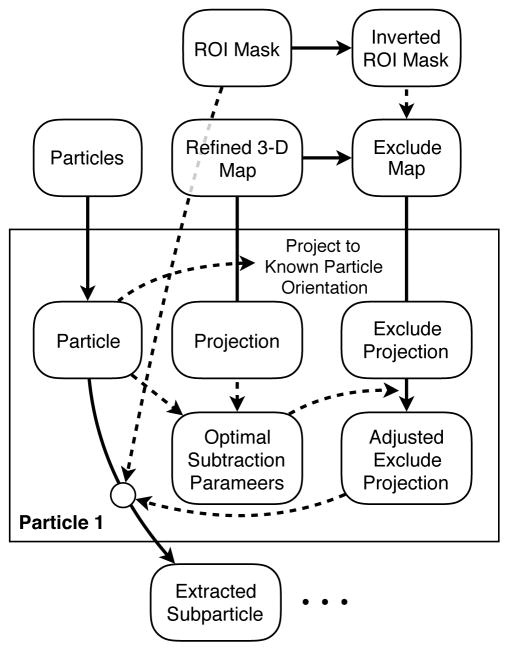
In some instances one particular domain of a particle may undergo some motion independent from any other structural variability in the particle. In such situations, it is desirable to focus classification and in some cases, alignment, on only this region of interest (ROI). However, to isolate only one portion of the particle from a projection image, the remaining ‘constant’ portion of the particle must be very accurately subtracted from the image (Fig. 3). This process is very similar to the process used in 4.4 above for 2-D classification. After completion of a standard 3-D refinement of the data, the final 3-D reconstruction is masked, such that the region being targeted for variability analysis is excluded from the volume, creating an exclusion map, which contains only the density we are not interested in. For each particle a projection of this masked map is generated in the same orientation as the particle, modified for CTF, filtered to match and with densities rescaled to best match the projection for optimal subtraction. After subtracting the masked projection, what is left behind is ostensibly only the ROI, still in the same orientation with respect to the refined map. While there may also be some structural variability present outside the ROI making the subtraction imperfect, this operation still isolates the region of interest far better than would, say, a simple mask.
Figure 3.
A diagram showing how local fragments can be accurately isolated from 2-D images of individual particles based on a 3-D mask and a refinement of the complete data set.
If the particle possesses symmetry or pseudosymmetry, it may be possible to impose this symmetry during the masking process to extract individual monomers as independent particles, each in a different orientation. For example, if a homo-tetramer is believed to undergo independent motion in each subunit within a specific domain, that domain could be extracted from each of the four subunits, providing four times as many extracted particle fragments.
If the extracted particle fragments are very small, it may not be feasible to perform any further alignment on them, and simply classifying into subsets based on their already known orientations with respect to the rest of the structure may be appropriate. If the extracted fragments are sufficiently large, they may be treated as single particles in their own right, and be refined using a process like e2refine_easy.
This approach was actually the precursor to the classification methodology described in 4.4, and has been available in EMAN1 (as extractmonomers) and EMAN2 (as e2extractsubparticles) for over a decade. While it has been used for preliminary analysis of data frequently over that time, until the development of direct detectors, the lower size limit for particles (or fragments) in CryoEM was generally regarded to be ~200 kDa. This limit put practical constraints on the use of this methodology, since the extracted fragments needed to be large enough to be processed somewhat independently as particles. With the dramatic improvement in DQE extending to high resolution provided by direct electron detectors, this and similar (Nguyen, Galej, Bai, Savva, Newman, Scheres & Nagai,2015) (and see chapter by Scheres) methods have become practical for a wide range of purposes.
4.6 Breaking symmetry
The previously described approach is appropriate for symmetric particles in which each symmetry-related copy is undergoing some form of variability independently. However, if this is not the case, and the particle possesses some form of self-consistent symmetry breaking, then alternative methods are required. The standard example is an icosahedral virus particle with a portal at one or more vertices (Chang, Schmid, Rixon & Chiu,2007; Xiang, Morais, Battisti, Grimes, Jardine, Anderson & Rossmann,2006). Such portals not only break the icosahedral symmetry, but also generally possess a symmetry mismatch with the underlying pentagonal vertex they are positioned over. Initial reconstructions are typically performed assuming full 60-fold symmetry, since this effectively provides 60 (or at least 55) times more information about each subunit, and can produce high resolution structures with small numbers of particles. The 11 near-identical vertices dominate the average in such cases, and only residual hints of the unique vertex remain.
To gain information about the unique vertex in such situations, the particles could simply be treated as asymmetric objects in a standard refinement. However, there are several problems with this approach. When generating uniformly distributed projections on the unit sphere, the pattern of projections would be different within each pseudosymmetric unit. If the symmetry-breaking differences in the structure are subtle, the symmetry may potentially be broken by this angular inconsistency rather than by the true symmetry breaking features in the object. Second, this method is far less efficient than it should be. Assuming an underlying near-symmetry, particle orientations can be determined much more efficiently.
An option in e2refine_easy, called –breaksym is the preferred way to respond to this situation in EMAN2.1. When the pseudosymmetry is specified with –breaksym, projections are generated identically among the asymmetric units, maximizing the chance of detecting a true difference. The orientation determination strategy in EMAN2.1 always occurs in two stages for improved efficiency. In the first stage, coarse orientation is determined, among the least-similar projections, and in the second stage the orientation is refined among a subset of similar particles. Projections are not grouped together for this first stage based on their relative orientations, but rather based on mutual similarity among projections. So, in the case of a pseudosymmetry, the symmetry-related copies are averaged together and the first stage classification becomes orientation determination within one asymmetric unit, followed by the second stage classification to determine which of the N symmetry-related orientations is the best match.
4.7 Subtomogram averaging
The situations discussed so far have focused on discrete variability, or continuous variability largely localized to a specific region of a larger assembly. However, a significant fraction of large biomolecules and assemblies make use of flexibility as a critical aspect of their function. In 4.2 we assumed that it was possible to unambiguously discriminate between changes of particle orientation and changes of conformation. For example, addition or subtraction of a ligand (Roseman, Chen, White, Braig & Saibil,1996) or large scale discrete motions such as ribosome ratcheting (Frank & Agrawal,2000) do not create an orientation ambiguity as long as the appropriate number of models are being refined. However, macromolecules such as mammalian fatty acid synthase (Brignole, Smith & Asturias,2009; Brink, Ludtke, Kong, Wakil, Ma & Chiu,2004), undergo multiple independent large scale continuous motions. In such a situation, without a large set of accurate starting models, there can be ambiguity over whether a small difference observed in 2-D is due to a change in orientation or conformation. Even with human intuition involved in the process to eliminate physically unreasonable models, results are frequently still ambiguous. We have generally observed that once a set of accurate starting models for valid states of the system have been obtained, e2refinemulti will successfully refine normal single particle data to produce better structures, and accurately classify particles. However, this statement cannot be proven to be true for all conceivable situations, so caution is still required.
When the motions involved in a system are significant, perhaps ~15 Å, one viable approach is subtomogram averaging, also known as single particle tomography (see chapter by Briggs). This is a powerful technique with a range of applications, including in-situ structural biology, but in the present context this method simply provides a tool for disambiguating complex macromolecular motion. The reason ambiguity exists in traditional single particle analysis is each particle is imaged only in a single orientation. When comparing particles in two different orientations to look for self-consistency, these two projections share only a single common-line of shared information in Fourier space, and this line simply may not possess sufficient information to discriminate among multiple functional states. If multiple putative orientations are considered simultaneously, the number of required simultaneous projections to resolve ambiguities rapidly becomes intractable, and even then, the necessary information may simply not be present in the data.
By collecting a tomographic tilt series on a traditional single particle cryo specimen, the multiple views of each particle provide sufficient information to unambiguously disambiguate orientation vs. conformational change. This is, of course, complicated by the presence of the missing wedge and the low dose in each tilt. Further, there are many intricacies involved in performing this analysis, which are too detailed for this manuscript. Several existing manuscripts document EMAN2’s capabilities for subtomogram alignment, averaging and classification (Galaz-Montoya, Flanagan, Schmid & Ludtke,2015; Schmid & Booth,2008; Shahmoradian, Galaz-Montoya, Schmid, Cong, Ma, Spiess, Frydman, Ludtke & Chiu,2013). The general convention is for these programs to be named e2spt_*, and at present there are over 30 such programs covering a wide range of situations.
The goal of these methods in the present context is to determine multiple structures for a given system. This process always begins with tomographic reconstruction, followed by e2spt_boxer or e2spt_autoboxer to identify and extract particle volumes. All of the subsequent algorithms compensate for the missing wedge artifact present in all CryoET data. The stacks of subvolumes must then be aligned and classified. One approach is to use e2spt_hac, which performs all-vs-all comparison and hierarchical ascendant classification (Frank, Bretaudiere, Carazo, Verschoor & Wagenknecht,1988), in 3-D, to group together and average similar structures. Alternatively, e2spt_refinemulti is the tomographic equivalent of e2refinemulti, for situations where N putative starting models are available.
It is also possible to perform PCA-based classification of subtomograms using a sequence of programs. A detailed description of this workflow is available via the online tutorials, but briefly, e2spt_align is used to align all particles to a common reference, and e2spt_average is used to produce a single overall average volume for all of the particles. Next, this average volume is used to fill the missing wedge of the individual subtomograms using e2spt_wedgefill. This prevents the PCA analysis from focusing on the missing wedge instead of actual particle variations. e2msa, which works on both 2-D and 3-D data is then used to perform PCA. This information is then combined using e2basis, and e2classify classifies the results. The classified particles can then be realigned and averaged using any of the available methods for this.
Once any of these methods have been applied to produce a set of characteristic maps, these can be used as initial models for e2refinemulti, targeting higher resolution from traditional single particle refinement. While subtomogram averaging with CTF correction has successfully achieved subnanometer resolution (Bharat, Russo, Löwe, Passmore & Scheres,2015; Schur, Hagen, de Marco & Briggs,2013), this is a difficult and time-consuming process, and it is clear that high resolution is far easier to achieve using single particle methods once the heterogeneity can be dealt with. Indeed, the presence of significant motion may remain the resolution limiting factor in many cases. Consider a molecule undergoing a single mode of motion, moving ~20 Å. Achieving 4 Å resolution on this specimen would require subdividing the data into at least 5 subsets, requiring at least 5x the number of particles as compared to a rigid structure to achieve comparable resolution. If an additional independent motion were present, the number of required subsets could easily rise to 50 or 100. Further, as discussed above, for this to be successful, it must be possible to at least partially discriminate among all of these possibilities for each individual particle. Again, the improved per-particle contrast provided by direct electron detectors has made many previously impossible problems feasible.
4.8 Tilt validation
When performing single particle reconstruction in a new system, initial reconstructions may be low resolution, and largely provide information about quaternary or possibly tertiary structure. Lacking landmarks such as alpha helices or strands in beta sheets to clearly show a “protein-like” structure, it is often difficult to tell whether such structures are accurate interpretations of the single particle data. As discussed above, roughly half of published single particle reconstructions still fail to achieve the subnanometer resolution required to resolve alpha helices, so this problem is far from uncommon. If subtomogram averaging has been performed, then the use of tilt information implicit in this process already serves as a strong validation for structure. However, if only traditional single particle analysis is being used, some additional validations may be required to demonstrate reliability of low resolution maps. One strong validation is tilt validation (Rosenthal & Henderson,2003) (and chapter by Rosenthal). In this method a few tilt-pairs are collected from the single particle specimen, with one image having the specimen typically tilted to 10–20 degrees. Matching pairs of particles are selected, and the orientation of all of all tilted and untilted particles is determined using projections of a 3-D structure requiring validation. We can then ask whether the orientation relationship among these pairs of particles matches the known experimental tilt. If it matches consistently for a majority of the particles, then this demonstrates that the 3-D map is consistent with the data. EMAN2.1 implements this methodology through e2RCTboxer and e2tiltvalidate (Murray, Flanagan, Popova, Chiu, Ludtke & Serysheva,2013). There are a number of potential difficulties in this methodology, and even for very good specimens, the results are often not perfect. Nonetheless, it is generally possible to distinguish between valid and invalid quaternary structures using this methodology.
5 Interactive Tools
In addition to its workflows and utility programs, EMAN2.1 contains a range of graphical tools (Fig. 4) which may be useful as utilities regardless of what software is used to perform high resolution reconstructions. Most, but not all of these tools are also available from the main e2projectmanager GUI, but all can also be launched directly from the command-line. A few of these tools are summarized here.
- e2display – This is a general-purpose CryoEM-aware file browser and display program. In addition to displaying data and metadata about all supported CryoEM image filetypes in the browser, this interface provides access to: 3-D display including multi-volume isosurfaces, arbitrary slices, volume rendering, and annotations; 2-D single-image display including measurement and image manipulation capabilities; 2-D tiled image display for looking at image stacks all together, including capabilities for deleting images from stacks and forming new sets; X-Y plotting, including the ability to easily switch axes among multi-column text files to explore multi-dimensional spaces.
- e2filtertool – This versatile tool can process 3-D volumes, 2-D stacks or individual 2-D images. This tool permits chains of image processing operations (filters, masks, transformations,…) to be constructed, and parameters to be adjusted interactively with real-time update of the image/volume being processed.
- e2evalimage – A tool for assessment of whole micrographs. Provides a variety of tools for generating power spectra and other features, and performing automatic CTF fitting with manual adjustment. This includes keyboard shortcuts for rapidly traversing lists of thousands of micrographs, and interactively marking those to in/exclude from a project.
- e2boxer, e2helixboxer, e2RCTboxer and e2spt_boxer – Tools for interactive or semi-automatic particle picking in 2-D and 3-D. Can be used with EMAN2.1 reconstructions or as independent extraction tools.
- e2evalparticles – Primarily useful with EMAN2.1 results. This permits extraction of selected particles associated with user-selected class-averages. For instance, if e2refine2d is used to generate reference-free class-averages, and the user wishes to mark particles associated with bad class-averages as bad particles, this program provides that capability.
- e2eulerxplor – Primarily useful with EMAN2.1 refinements. This program permits visualization of the Euler angle distribution for a standard 3-D refinement. It also has some generic asymmetric unit visualization capabilities in 3-D which may be useful in other situations.
6 Conclusion
In this manuscript we have discussed the broad philosophy adopted by EMAN2.12 for single particle reconstruction, targeting the highest possible resolution for each molecular system. We extensively discussed various methods for working with compositional and conformational variability both to extract information about the variability itself as well as to achieve higher resolutions. While many structures now being produced in this field are now achieving near-atomic resolution, it is still critical for the field to remain grounded and develop a strong culture of validation of results. EMAN2.12’s interoperability capabilities and implementations of standard validation methods can play a very strong role in this process, and we strongly encourage other developers to embrace the interoperability concept. The algorithms described in this manuscript continue to evolve, and new methods in single particle analysis, subtomogram averaging and cellular tomography segmentation are being developed. We believe that significant room for improvement still exists in single particle analysis software, and reiterate that our aim is to produce the best structures possible from a given set of data.
EMAN2.12 remains a highly dynamic project, which has recently completed a transition to GitHub, becoming truly public open-source, and we welcome direct contributions from other developers. A number of important developments are planned for EMAN2/SPARX in the near future. Anaconda is an open-source Python distribution, which incorporates many useful packages, including SciPy, an expansive library for mathematical computation in Python. In the near future, our binary distribution mechanism will switch to use Anaconda as its base. This will permit easy interoperability between EMAN2 and a range of scientific libraries available through this system. EMAN2 is also beginning the transition from Python2 to Python3, which represents a significant shift in the Python development community. In short, we are working to maintain EMAN2/SPARX as a cutting-edge development platform for the next generation of image processing scientists, while maintaining its easy-to-use and user-friendly nature.
Acknowledgments
We would like to gratefully acknowledge the support of NIH grants R01GM080139 and P41GM103832. We would like to thank Dr. Pawel Penczek and developers of the SPARX package whose contributions to the shared EMAN2/SPARX C++ library have helped make it into a flexible and robust image processing platform.
References
- Bell JM, Chen M, Baldwin PR, Ludtke SJ. High resolution single particle refinement in EMAN2.1. Methods. 2016 doi: 10.1016/j.ymeth.2016.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharat TA, Russo CJ, Löwe J, Passmore LA, Scheres SH. Advances in single-particle electron cryomicroscopy structure determination applied to sub-tomogram averaging. Structure (London, England : 1993) 2015;23(9):1743–53. doi: 10.1016/j.str.2015.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braig K, Otwinowski Z, Hegde R, Boisvert DC, Joachimiak A, Horwich AL, et al. The crystal structure of the bacterial chaperonin groel at 2.8 Å. Nature. 1994;371(6498):578–86. doi: 10.1038/371578a0. [DOI] [PubMed] [Google Scholar]
- Brignole EJ, Smith S, Asturias FJ. Conformational flexibility of metazoan fatty acid synthase enables catalysis. Nature Structural & Molecular Biology. 2009;16(2):190–7. doi: 10.1038/nsmb.1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brink J, Ludtke SJ, Kong Y, Wakil SJ, Ma J, Chiu W. Experimental verification of conformational variation of human fatty acid synthase as predicted by normal mode analysis. Structure (London, England : 1993) 2004;12(2):185–91. doi: 10.1016/j.str.2004.01.015. [DOI] [PubMed] [Google Scholar]
- Chang JT, Schmid MF, Rixon FJ, Chiu W. Electron cryotomography reveals the portal in the herpesvirus capsid. Journal of Virology. 2007;81(4):2065–8. doi: 10.1128/JVI.02053-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhry C, Horwich AL, Brunger AT, Adams PD. Exploring the structural dynamics of the E.Coli chaperonin groel using translation-libration-screw crystallographic refinement of intermediate states. Journal of Molecular Biology. 2004;342(1):229–45. doi: 10.1016/j.jmb.2004.07.015. [DOI] [PubMed] [Google Scholar]
- Chen DH, Luke K, Zhang J, Chiu W, Wittung-Stafshede P. Location and flexibility of the unique c-terminal tail of aquifex aeolicus co-chaperonin protein 10 as derived by cryo-electron microscopy and biophysical techniques. Journal of Molecular Biology. 2008;381(3):707–17. doi: 10.1016/j.jmb.2008.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen DH, Song JL, Chuang DT, Chiu W, Ludtke SJ. An expanded conformation of single-ring groel-groes complex encapsulates an 86 kda substrate. Structure (London, England : 1993) 2006;14(11):1711–22. doi: 10.1016/j.str.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Cong Y, Baker ML, Jakana J, Woolford D, Miller EJ, Reissmann S, et al. 4.0-A resolution cryo-em structure of the mammalian chaperonin tric/CCT reveals its unique subunit arrangement. Proceedings of the National Academy of Sciences of the United States of America. 2010;107(11):4967–72. doi: 10.1073/pnas.0913774107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiMaio F, Zhang J, Chiu W, Baker D. Cryo-EM model validation using independent map reconstructions. Protein Science : A Publication of the Protein Society. 2013;22(6):865–8. doi: 10.1002/pro.2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank J, Agrawal RK. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 2000;406(6793):318–22. doi: 10.1038/35018597. [DOI] [PubMed] [Google Scholar]
- Frank J, Bretaudiere JP, Carazo JM, Verschoor A, Wagenknecht T. Classification of images of biomolecular assemblies: A study of ribosomes and ribosomal subunits of escherichia coli. Journal of Microscopy. 1988;150(Pt 2):99–115. doi: 10.1111/j.1365-2818.1988.tb04602.x. [DOI] [PubMed] [Google Scholar]
- Frank J, Radermacher M, Penczek P, Zhu J, Li Y, Ladjadj M, et al. SPIDER and WEB: Processing and visualization of images in 3D electron microscopy and related fields. Journal of Structural Biology. 1996;116(1):190–9. doi: 10.1006/jsbi.1996.0030. [DOI] [PubMed] [Google Scholar]
- Galaz-Montoya JG, Flanagan J, Schmid MF, Ludtke SJ. Single particle tomography in EMAN2. Journal of Structural Biology. 2015;190(3):279–90. doi: 10.1016/j.jsb.2015.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaeser RM, Han BG, Csencsits R, Killilea A, Pulk A, Cate JH. Factors that influence the formation and stability of thin, cryo-em specimens. Biophysical Journal. 2016;110(4):749–55. doi: 10.1016/j.bpj.2015.07.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goddard TD, Huang CC, Ferrin TE. Visualizing density maps with UCSF chimera. Journal of Structural Biology. 2007;157(1):281–7. doi: 10.1016/j.jsb.2006.06.010. [DOI] [PubMed] [Google Scholar]
- Grigorieff N. FREALIGN: High-resolution refinement of single particle structures. Journal of Structural Biology. 2007a;157(1):117–25. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Grigorieff N. FREALIGN: High-resolution refinement of single particle structures. Journal of Structural Biology. 2007b;157(1):117–25. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Henderson R. The potential and limitations of neutrons, electrons and x-rays for atomic resolution microscopy of unstained biological molecules. Quarterly Reviews of Biophysics. 1995;28(2):171–93. doi: 10.1017/s003358350000305x. [DOI] [PubMed] [Google Scholar]
- Henderson R, Sali A, Baker ML, Carragher B, Devkota B, Downing KH, et al. Outcome of the first electron microscopy validation task force meeting. Structure (London, England : 1993) 2012;20(2):205–14. doi: 10.1016/j.str.2011.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohn M, Tang G, Goodyear G, Baldwin PR, Huang Z, Penczek PA, et al. SPARX, a new environment for cryo-em image processing. Journal of Structural Biology. 2007;157(1):47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- de la Rosa-Trevín JM, Otón J, Marabini R, Zaldívar A, Vargas J, Carazo JM, et al. Xmipp 3.0: An improved software suite for image processing in electron microscopy. Journal of Structural Biology. 2013;184(2):321–8. doi: 10.1016/j.jsb.2013.09.015. [DOI] [PubMed] [Google Scholar]
- Lawson CL, Patwardhan A, Baker ML, Hryc C, Garcia ES, Hudson BP, et al. EMDataBank unified data resource for 3DEM. Nucleic Acids Research. 2015 doi: 10.1093/nar/gkv1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner A, Joachimiak LA, Bracher A, Mönkemeyer L, Walzthoeni T, Chen B, et al. The molecular architecture of the eukaryotic chaperonin tric/CCT. Structure (London, England : 1993) 2012;20(5):814–825. doi: 10.1016/j.str.2012.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, Baldwin PR, Chiu W. EMAN: Semiautomated software for high-resolution single-particle reconstructions. Journal of Structural Biology. 1999;128(1):82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Jakana J, Song JL, Chuang DT, Chiu W. A 11.5 A single particle reconstruction of groel using EMAN. Journal of Molecular Biology. 2001;314(2):253–62. doi: 10.1006/jmbi.2001.5133. [DOI] [PubMed] [Google Scholar]
- Marabini R, Ludtke SJ, Murray SC, Chiu W, Jose M, Patwardhan A, et al. The electron microscopy exchange (EMX) initiative. Journal of Structural Biology. 2016 doi: 10.1016/j.jsb.2016.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mindell JA, Grigorieff N. Accurate determination of local defocus and specimen tilt in electron microscopy. Journal of Structural Biology. 2003;142(3):334–47. doi: 10.1016/s1047-8477(03)00069-8. [DOI] [PubMed] [Google Scholar]
- Murray SC, Flanagan J, Popova OB, Chiu W, Ludtke SJ, Serysheva II. Validation of cryo-em structure of IP3R1 channel. Structure (London, England : 1993) 2013;21(6):900–9. doi: 10.1016/j.str.2013.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TH, Galej WP, Bai XC, Savva CG, Newman AJ, Scheres SH, et al. The architecture of the spliceosomal U4/U6.U5 tri-snrnp. Nature. 2015;523(7558):47–52. doi: 10.1038/nature14548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park E, Ménétret JF, Gumbart JC, Ludtke SJ, Li W, Whynot A, et al. Structure of the secy channel during initiation of protein translocation. Nature. 2014;506(7486):102–6. doi: 10.1038/nature12720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penczek PA, Yang C, Frank J, Spahn CM. Estimation of variance in single-particle reconstruction using the bootstrap technique. J Struct Biol. 2006;154(2):168–83. doi: 10.1016/j.jsb.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Rohou A, Grigorieff N. CTFFIND4: Fast and accurate defocus estimation from electron micrographs. Journal of Structural Biology. 2015;192(2):216–21. doi: 10.1016/j.jsb.2015.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roseman AM, Chen S, White H, Braig K, Saibil HR. The chaperonin atpase cycle: Mechanism of allosteric switching and movements of substrate-binding domains in groel. Cell. 1996;87(2):241–51. doi: 10.1016/s0092-8674(00)81342-2. [DOI] [PubMed] [Google Scholar]
- Rosenthal PB, Henderson R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. Journal of Molecular Biology. 2003;333(4):721–45. doi: 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
- Scheres SH. RELION: Implementation of a bayesian approach to cryo-em structure determination. Journal of Structural Biology. 2012;180(3):519–30. doi: 10.1016/j.jsb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid MF, Booth CR. Methods for aligning and for averaging 3D volumes with missing data. Journal of Structural Biology. 2008;161(3):243–8. doi: 10.1016/j.jsb.2007.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schur FK, Hagen WJ, de Marco A, Briggs JA. Determination of protein structure at 8.5Å resolution using cryo-electron tomography and sub-tomogram averaging. Journal of Structural Biology. 2013;184(3):394–400. doi: 10.1016/j.jsb.2013.10.015. [DOI] [PubMed] [Google Scholar]
- Shahmoradian SH, Galaz-Montoya JG, Schmid MF, Cong Y, Ma B, Spiess C, et al. TRiC’s tricks inhibit huntingtin aggregation. ELife. 2013;2:e00710. doi: 10.7554/eLife.00710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaikh TR, Gao H, Baxter WT, Asturias FJ, Boisset N, Leith A, et al. SPIDER image processing for single-particle reconstruction of biological macromolecules from electron micrographs. Nature Protocols. 2008;3(12):1941–74. doi: 10.1038/nprot.2008.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart A, Grigorieff N. Noise bias in the refinement of structures derived from single particles. Ultramicroscopy. 2004;102(1):67–84. doi: 10.1016/j.ultramic.2004.08.008. [DOI] [PubMed] [Google Scholar]
- Tang G, Peng L, Baldwin PR, Mann DS, Jiang W, Rees I, et al. EMAN2: An extensible image processing suite for electron microscopy. Journal of Structural Biology. 2007;157(1):38–46. doi: 10.1016/j.jsb.2006.05.009. [DOI] [PubMed] [Google Scholar]
- van Heel M, Harauz G, Orlova EV, Schmidt R, Schatz M. A new generation of the IMAGIC image processing system. Journal of Structural Biology. 1996;116(1):17–24. doi: 10.1006/jsbi.1996.0004. [DOI] [PubMed] [Google Scholar]
- Xiang Y, Morais MC, Battisti AJ, Grimes S, Jardine PJ, Anderson DL, et al. Structural changes of bacteriophage φ29 upon DNA packaging and release. The EMBO Journal. 2006;25(21):5229–5239. doi: 10.1038/sj.emboj.7601386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Baker ML, Schröder GF, Douglas NR, Reissmann S, Jakana J, et al. Mechanism of folding chamber closure in a group II chaperonin. Nature. 2010;463(7279):379–83. doi: 10.1038/nature08701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Minary P, Levitt M. Multiscale natural moves refine macromolecules using single-particle electron microscopy projection images. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(25):9845–50. doi: 10.1073/pnas.1205945109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Kimmel M, Spahn CM, Penczek PA. Heterogeneity of large macromolecular complexes revealed by 3D cryo-em variance analysis. Structure (London, England : 1993) 2008;16(12):1770–6. doi: 10.1016/j.str.2008.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]