Genotype–environment interactions in mouse behavior: A way out of the problem (original) (raw)

Abstract

In behavior genetics, behavioral patterns of mouse genotypes, such as inbred strains, crosses, and knockouts, are characterized and compared to associate them with particular gene loci. Such genotype differences, however, are usually established in single-laboratory experiments, and questions have been raised regarding the replicability of the results in other laboratories. A recent multilaboratory experiment found significant laboratory effects and genotype × laboratory interactions even after rigorous standardization, raising the concern that results are idiosyncratic to a particular laboratory. This finding may be regarded by some critics as a serious shortcoming in behavior genetics. A different strategy is offered here: (i) recognize that even after investing much effort in identifying and eliminating causes for laboratory differences, genotype × laboratory interaction is an unavoidable fact of life. (ii) Incorporate this understanding into the statistical analysis of multilaboratory experiments using the mixed model. Such a statistical approach sets a higher benchmark for finding significant genotype differences. (iii) Develop behavioral assays and endpoints that are able to discriminate genetic differences even over the background of the interaction. (iv) Use the publicly available multilaboratory results in single-laboratory experiments. We use software-based strategy for exploring exploration (see) to analyze the open-field behavior in eight genotypes across three laboratories. Our results demonstrate that replicable behavioral measures can be practically established. Even though we address the replicability problem in behavioral genetics, our strategy is also applicable in other areas where concern about replicability has been raised.

Keywords: across-laboratory replicability, mixed-model ANOVA, open-field behavior

In behavior genetics, behavior patterns of standardized mouse genotypes, such as inbred strains or knockouts, are characterized to associate them with particular gene loci. The need for such characterization, referred to as behavioral phenotyping, has prompted the design of behavioral test batteries for mice (1–3). A practical problem well known to most experimenters in the field, however, is that it can be difficult to replicate behavioral phenotyping results in a different laboratory. This replicability problem was largely ignored until brought to light in 1999 by Crabbe, Wahlsten, and Dudek (3). In this pioneering study they conducted an experiment concurrently in three laboratories, comparing eight genotypes by using seven standard behavioral characteristics (endpoints) in a well coordinated study closely following identical protocols. Their main positive finding was that large genotype differences were demonstrated in all studied endpoints. On the negative side they found significant differences between laboratories across all genotypes in many endpoints. Although the difficulties raised by such significant laboratory effects can be overcome by running a common genotype as a local control, they reported yet another critical problem: even the genotype differences frequently did not remain constant across laboratories. As a typical example of this phenomenon in our data (to be discussed below), the measured distance traveled by the BALB/cByJ strain of mice is higher than that of the A/J strain in two laboratories, whereas it is lower in the third (see Fig. 2). Such a genotype × laboratory interaction (GxL) might arise if a particular genotype reacts differently than another genotype, for no identifiable cause, to the peculiarities of a specific laboratory, and therefore cannot be eliminated by using a common genotype as a local control. Crabbe et al. (3) thus concluded: “experiments characterizing mutants may yield results that are idiosyncratic to a particular laboratory.” The lack of across-laboratory replicability demonstrated in their study might be interpreted by some critics as a serious shortcoming in behavior genetics at large (4) because currently almost all experiments are conducted within a single laboratory.

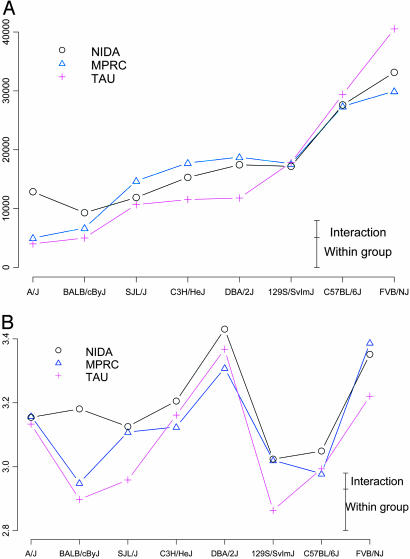
Fig. 2.

Fig. 2.

Group means of distance traveled (Upper in cm) and segment acceleration (Lower, in cm/s per s, log-transformed). Each genotype was measured in three laboratories: National Institute of Drug Abuse (NIDA), Maryland Psychiatric Research Center (MPRC), and Tel Aviv University (TAU). Small vertical bars on the right represent the SD of GxL interaction and the within-group (individual animal) variability.

When analysis reveals a substantial GxL effect, this effect might be caused by some methodological artifact in the test or the laboratory environment, which is in no way edifying and in every way misleading. It would be seen as bad science, once the artifact is traced to its origins. Successful correction of this artifact will be reflected by a great reduction in the size of the interaction.

The main remedy advocated to date for the GxL problem is thus a more careful standardization of test protocol, housing procedures, and laboratory environment (refs. 5–8, but see refs. 9 and 10 for an opposing view). Such standardization, however, would require a vast coordinated community effort, because currently each laboratory typically has its own housing conditions, protocols, hardware, and technical limitations (3, 8). The level of standardization and coordination in the Crabbe et al. study (3) was much higher than is currently practiced in the field, yet not enough to render most laboratory and GxL effects insignificant. Moreover, it has been suggested that although standardization efforts are important, they can rarely eliminate all interaction (8, 11–13). We refer to this remaining interaction variability simply as the GxL variability and propose a dual approach for handling it: a measurement model where the size of the interaction can be estimated from multilaboratory experiments (see The Proposed Measurement Model) and an endpoint design that reduces the interaction size (see The Open-Field Test with see). Note, however, that the two arms of this approach may be used independently of each other.

The Proposed Measurement Model

The Mixed-Model (MM) Approach. We model the value of a measured endpoint in a specific mouse as the sum of four effects: a genotype effect (G), a laboratory effect (L), an effect of the interaction between the genotype and the laboratory in which it is measured (GxL), and an individual animal effect (within group). In behavior genetics G is a precisely replicable factor, because of the availability of inbred strains and genetic monitoring. Furthermore, our interest is in the value of an endpoint for the particular phenotype(s). These reasons allow us to treat G as a fixed factor across all experiments. A laboratory is a well defined location with particular measurement procedures, which might have a typical effect on the measured endpoint for all genotypes. However, the scientific interest is usually not in the value at the particular participating laboratory, but ideally in the “true” value, one that could be derived in principle by measuring the phenotype at all possible laboratories and averaging out laboratory variation. Having no access to measured values from nonparticipating laboratories, we just assume that the effects vary randomly and independently from one laboratory to the other, and treat L as a random factor. The GxL effect, which is the way the specific laboratory affects each measured genotype differently, is similarly assumed to vary randomly across all laboratories and genotype combinations. Finally, L and GxL are assumed to be independent of each other and the within-group effect.

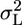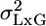Although we do not know the values of L and GxL effects at an additional laboratory, treating them as random allows us at least to assess their likely size by estimating their variability, Inline graphic and Inline graphic, respectively, by using multilaboratory experiments. Such situations are not unique to behavior genetics, and a well established statistical model is available for the purpose: the MM (e.g., ref. 14). It is called mixed because one factor is fixed, whereas the other is random. Procedures for MM ANOVA are available in most statistical software. However, we make a unique use of the MM to address the replicability problem in single-laboratory experiments as well (see below).

The MM in Multilaboratory Experiments. The currently used fixed model (FM) approach for analyzing multilaboratory experiments considers G, L, and GxL as having fixed effects (3). Only the individual's (within group) effect is treated as random. It is widely accepted that this within-group variability σ2 is not likely to ever be eliminated completely, even though animals within each group are genetically identical and the experimental conditions are standardized as much as possible within the laboratory. FM takes this variability as unavoidable fact of life and uses it as the yardstick against which genotype differences are tested. 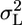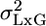MM merely extends this approach to L and GxL, by treating them as random, taking their variability as unavoidable as well, and incorporating Inline graphic and Inline graphic into the yardstick (see below).

Under both models, the average genotype difference over the participating laboratories is used to estimate the “ideal” genotype difference, that average value “over all possible laboratories” that can never be precisely known. Thus the distinction between the models lies not in the estimated difference, but in the estimated variability of the difference. Introducing L and GxL variabilities, the MM sets a higher benchmark for showing a significant genotype difference. To decrease the benchmark both the group size and the number of laboratories has to be increased.

The MM in Single-Laboratory Experiments. It is possible to use the MM to analyze results from a single-laboratory experiment, but first the variabilities of L and GxL must be estimated from some multilaboratory experiment using MM analysis. Consider a single-laboratory experiment in which a group of n same-genotype mice are phenotyped. The expected variance of their mean according to the usual FM is the within-group variability divided by the group size, i.e., σ2/n. According to the MM, however, one needs to add the previously reported laboratory and interaction variances to get 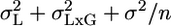Inline graphic. Ignoring them, as is currently done in single-laboratory analysis, involves the hidden assumption that they are 0. Suppose that one further phenotypes in the same laboratory an independent group of m “knockouts” derived from the above genotype. The difference between the knockout and the original genotype is estimated by the difference between the two group means. Laboratory effect is identical for both genotypes, and hence drops out (as it also does in the multilaboratory analysis). In contrast, the interaction effects of the two genotypes with the laboratory are not identical but vary independently, so their difference does not disappear. Because the variance of the difference is the sum of the variances, the benchmark for reporting a significant knockout difference is 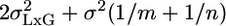Inline graphic, which is larger than the usual (FM) benchmark σ2(1/m + 1/n). Moreover, increasing m and n, while useful for reducing the contribution from within-group variability, cannot decrease the interaction variability.

Thus, for both types of experiment, MM analysis is more conservative, and weak genotype differences, which are less likely to stand the scrutiny of replicability in additional laboratories, will be weeded out (see Supporting Text, which is published as supporting information on the PNAS web site). The negative side of this protection is that fewer endpoints will show genotype differences. Hence an obvious concern is that students of quantitative behavior will be left with few phenotyping measures to use. We have focused on one commonly used behavioral test, the open-field test, to demonstrate an approach for developing a behavioral assay and endpoints that are able to discriminate genetic differences even over the higher yardstick of the MM.

The Open-Field Test with see

We demonstrate the premise of our thesis by using see (software-backed strategy for exploring exploration, ref. 15, available at www.tau.ac.il/~ilan99/see/help) in eight genotypes across three laboratories.

The see open-field test (Fig. 1) is based on ethological-oriented studies of rats and mice exploration of an unfamiliar environment (15–20). These studies found that, in contrast to a common view of this behavior as an essentially stochastic phenomenon, it is structured and consists of typical behavior patterns: progression segments separated by lingering episodes, which in turn may be further grouped into excursions from a preferred place (home base) established by the animal. Quantitative properties of these behavior patterns can be measured, and we report here the results for 17 previously established endpoints (13). Moreover, see has an open-ended approach, so new endpoints can be designed by using its visualization, exploratory data analysis, and programming capabilities to analyze the dynamic properties of the animal's path (15). Identifying aspects of behavior that are more replicable across laboratories than others can guide the design of such endpoints (21–23). Although our statistical approach and behavioral approach are in principle independent, we show in Discussion how they complement each other to create a powerful and robust strategy of phenotyping.

Fig. 1.

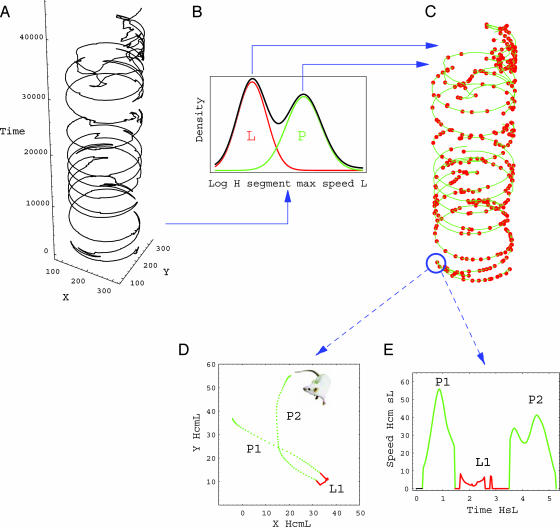
Fig. 1.

Principles of see analysis: the time series of the animal's location in the arena is automatically tracked and smoothed. (A) The path in a 3D representation of X, Y, and time (in data points) is shown. (B) The distribution of speed peaks (dark line) is used to parse the data into segments: slow local movements (lingering, L, in red) and progression (P, in green). (C) The data can be treated as a string of these discrete units. (D and E) The path plot and speed profile of two progression segments (P1 and P2) are separated by one lingering episode (L1). The typical properties of these units are used to quantify the behavior. For example, the segment acceleration endpoint (Fig. 2 Lower) is estimated by dividing the segment's speed peak by its duration, i.e., the aspect ratio of a segment in the speed profile.

Methods

Animals, Testing, and Path Analysis. The eight genotypes were the inbred strains A/J, BALB/cByJ, C3H/HeJ, C57BL/6J, DBA/2J, FVB/NJ, SJL/J, and 129S1/SvImJ, all included in the first priority group recommended for phenotyping by the Mouse Phenome Database (a community repository for strain characteristics data and protocols, www.jax.org/phenome) of The Jackson Laboratory. The experiment was conducted in three laboratories: the National Institute of Drug Abuse–Intramural Research Program in Baltimore, the Maryland Psychiatric Research Center, and the Department of Zoology at Tel Aviv University. In each laboratory two batches of mice were designated, each including six animals from each strain (see Table 1, which is published as supporting information on the PNAS web site). The batches were shipped and tested 1 month apart.

Mice were 65- to 75-day-old males transported from The Jackson Laboratory and housed in the specific laboratory for at least 14 days before being tested. They were kept in standard conditions of 12:12 light cycle, 22°C room temperature, with water and food ad libitum, and housed two to four per cage except for the SJL/J mice that were singly housed because of their aggressiveness. The experimental protocols followed the Principles of Laboratory Animal Care (National Institutes of Health publication no. 86-23, 1996). The animals were maintained in facilities fully accredited by the American Association for the Accreditation of Laboratory Animal Care at the Maryland Psychiatric Research Center and the National Institute of Drug Abuse or by National Institutes of Health Animal Welfare Assurance no. A5010-01 at Tel Aviv University. Open-field testing, tracking procedures, and path analysis with see (Fig. 1) were conducted as detailed (13) with some slight changes that were needed because of the different behavior displayed by some of the new strains (Table 2, which is published as supporting information on the PNAS web site). Behavior was quantified with 17 endpoints (see Fig. 3), most of them simple properties of lingering or progression segments, such as their number, length, maximal speed, etc. (see Table 2 and ref. 13).

Fig. 3.

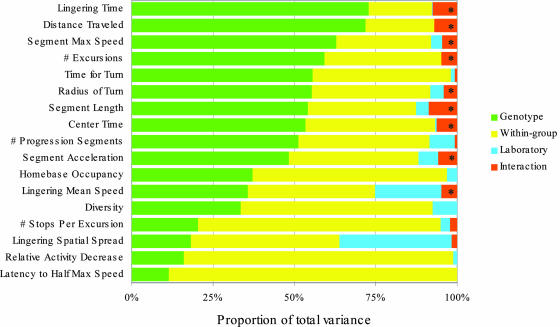
Fig. 3.

The proportion of variance attributed to each factor for all endpoints by using MM is shown. Endpoints are sorted by their proportion of genotypic variance. Genotypic differences for all endpoints are significant when using MM. Asterisks indicate interaction effects that were found to be significant according to the traditionally used FM at a level of 5%.

Statistical Analysis. For all endpoints the appropriate transformations were chosen so that the residuals distribution is close to normal, and the variances were homogeneous across genotypes and laboratories.

The formal MM: let Y_lgi be the value of an endpoint for laboratory l and genotype g. Index i represents the repetition within each group, μg is the genotype effect which is considered fixed, a_l is the laboratory random effect, which is assumed to have 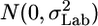Inline graphic distribution, and _c_Gxl is the interaction random effect, which is assumed to have 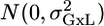Inline graphic. Finally, εlgi is the individual noise, assumed to have 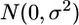Inline graphic. With these notations the model is _Y_lgi = μg + al + cGxL + εl_g_i.

The restricted maximum likelihood (REML) approach was used to estimate the MM variabilities (see Supporting Text). When the data are balanced, with an equal number of mice from each genotype at each laboratory, REML is equivalent to the regular mixed ANOVA F test, where the mean square error (MSE) between genotypes is divided by the MSE of interaction in the ANOVA table and compared with the appropriate quantile of the F distribution. In such a case the expected value of the MSE of the interaction is a weighted sum of σ2 and 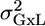Inline graphic.

To investigate whether within-laboratory replications could be used as a surrogate for across-laboratory replications the experiment was split within each laboratory into two separately tested batches. For all but one endpoint the batch effect was not significant when using false discovery rate (FDR) (see Table 3, which is published as supporting information on the PNAS web site). For relative activity decrease, the SD of the batch within-laboratory was small relative to the individual noise. Hence batch effect was ignored throughout. For comparison, the ordinary FM ANOVA was fitted, with both laboratory and genotype as fixed factors (see Table 4, which is published as supporting information on the PNAS web site).

Tests of significance increase type I error when conducted on many endpoints, as is the case here. We address this multiplicity problem by using the FDR, the expected proportion of the falsely rejected hypotheses among the rejected ones (24), which we control at level 5% as in ref. 13.

Results

Means, SD, and Interactions. Group means and SDs for all strains in all laboratories with the 17 endpoints are given in Table 5, which is published as supporting information on the PNAS web site, and were submitted to the Mouse Phenome Database (25). Fig. 2 displays results in two of the endpoints, distance traveled and segment acceleration. Some GxL interaction is apparent, as the laboratory lines are not parallel and sometimes even cross each other. As noted the MM allows us to estimate the likely size of the interaction random effect through its variability. The square root of the GxL variability, together with that of the within-group variability, are displayed in Fig. 2. It is evident from Fig. 2 that many genotype differences are large enough to be seen over the background of this interaction. The pattern of genotype differences in segment acceleration is different from that displayed by the traditional distance traveled endpoint. That is, the former contributes information about genotype differences not available in the latter.

Genotypic Differences. The genotype differences in all 17 endpoints were highly statistically significant when using the MM (see Table 3). They remain significant even after using FDR (FDR-adjusted P ≤ 0.001).

Proportions of Variance. For each endpoint, the total variance between the mice in a multilaboratory experiment can be decomposed into the between-genotype variability, between-laboratory variability, interaction variability, and within–group variability. Fig. 3 displays the proportion of variance attributable to the above four sources in all endpoints by using MM (see Supporting Text and Table 6, which is published as supporting information on the PNAS web site). The proportion of variance attributed to genotype is a relatively conservative estimator of the broad-sense heritability (13), the latter being the proportion of total phenotypic variance that can be attributed to the genotypic variance. In 9 of 17 endpoints it was >50%, which is considered high broad-sense heritability even in experiments conducted in a single laboratory (e.g., ref. 26). Although some endpoints captured genotype-specific properties much better than others, the contribution of GxL to the overall variance was consistently small.

The traditional FM analysis sets a lower benchmark for showing significant genotype effects, so it is no surprise that the genotype differences were even more significant (FDR adjusted P < 0.0001). Fig. 3 also demonstrates a disturbing observation about the FM analysis: most of the best-performing endpoints (in terms of high broad-sense heritability) also had statistically significant interaction (asterisks in Fig. 3). That is, according to the traditional statistical analysis these endpoints should have been discarded as nonreplicable across laboratories. On the other hand, most of the low-performing endpoints had, according to the FM, nonsignificant interactions. This paradoxical result is not limited to our data, but stems from the mathematics of the FM. Because all differences are compared with the yardstick of within-groups variability, more powerful tests and endpoints, associated with smaller within-group variability, do better detecting genotypic differences, but also detecting laboratory differences and GxL. Thus the better the behavioral test is, the more likely it is to be deemed nonreplicable across laboratories in FM.

Discussion

We have shown that, although the MM presents a higher benchmark than the traditionally used FM for showing genotypic differences, this benchmark is not too high for practical behavioral phenotyping. The MM is a more appropriate model to assess the replicability of a behavioral test and coincides better with the intuitive notion of replicability across laboratories. Notably, within-laboratory repetitions did not differ significantly, and thus cannot be used as a substitute for the role of multilaboratory experiments to estimate the variabilities used in the MM. The utility of the approach outlined herein and its implications for behavioral phenotyping was illustrated in the phenotyping conducted by using see. Several see endpoints were found to have high broad-sense heritability and are useful for high-throughput, replicable phenotyping.

The MM approach, together with the results presented here, suggests a more realistic approach for behavioral phenotyping: developing endpoints that are able to detect genotypic differences over the background of the interaction. Such development may take place at the level of the hardware (e.g., refs. 11–13) and/or the level of behavioral analysis (e.g., refs. 22 and 23). It should be the responsibility of developers of new endpoints to test them in a multilaboratory study and report the estimated SD of L and GxL. This procedure will require cooperation between laboratories at a level much easier to achieve than was previously anticipated, as strict coordination is no longer a critical issue. In the experiment reported here the protocol was the same, but no unusual measures were taken to standardize housing and testing and coordinate timing. This choice perhaps increased the measured interaction, but it also means our three laboratories better represent the population of all laboratories in which phenotyping might take place.

The MM approach to replicability may seem strange to statistically oriented researchers because many statistical books warn not to use MM unless the levels in the experiment are a true random sample of the possible levels, implying that the laboratories participating in a multilaboratory study should be chosen randomly from the pool of possible phenotyping laboratories. This is quite impossible to assure, first because the population of such laboratories is unknown, and more importantly because laboratories cannot be forced to participate in a study. However, this difficulty merely means that our estimates of L and GxL variabilties will not be of the best possible quality. Jones, Lewis, and Tukey (27), addressing a similar problem, suggest that experimenters may subjectively decide whether their sample of convenience is representative enough to use it as is in the MM analysis. They add that if the available sample is judged to reflect extreme variation in the prevailing conditions in the levels, or judged as too similar, the estimates could be shrunk toward the FM values or expanded. Either way, one should not trash the MM approach in favor of the FM when having a nonrandom sample, because the latter is equivalent to making the idealistic and unreal assumption that L and GxL variabilties are in fact 0.

It is also possible that certain genes have inherently large interaction even with extremely small environment variations, and thus even developing better tests will not decrease this interaction. In such a case the existence and size of the interaction might be an interesting topic of research by itself, even when the average genotype difference across several laboratories is 0. In behavioral phenotyping, however, investigators are usually interested in genotype differences that can be replicated in other laboratories. Many replicable behavioral endpoints already exist outside of the see open-field test. For example, our reanalysis of the eight endpoints studied by Crabbe et al. (3) reveals that most genotype differences remain significant even when taking the MM approach (using results from www.albany.edu/psy/obssr3 collapsed over shipment and sex). The single endpoint that does not pass MM analysis is time spent in open arms in the elevated plus maze. Moreover, although we argue that the interaction cannot be completely eliminated, it can still be decreased by better-designed tests and endpoints. We believe that the search for more replicable behavioral endpoints will continue productively by using a wide array of phenotyping assays, as today's interaction is the field of tomorrow's improvements.

Our call for multilaboratory experiments need not eliminate single-laboratory experiments. The user of an endpoint that has been already developed as outlined above can conduct an experiment, e.g., screening for mutations or quantitative trait loci analysis, in a single laboratory, as long as the previously reported variances of laboratory interaction are taken into account. For a well designed endpoint that enjoys small interaction variability, such an extra burden on the proof would not be harmful. In the few important enough cases where a single-laboratory experiment did not give a clear answer, resorting to multilaboratory experiments would help.

As a general scientific strategy, MM analysis is a viable alternative to traditional analyses when facing replicability problems. It can be especially efficient when used with public databases to which many laboratories contribute results on mice and rats, such as the Mouse Phenome Database (25), because the number of laboratories is an important factor in enhancing MM analysis, while strict coordination is less critical. Using such databases is also a way for achieving results from samples of laboratories that are more representative and better approximate random samples.

Taking this strategy to phenotyping open-field behavior, the exploratory data analysis capabilities of see make it especially suitable for in silico extraction of behavioral measures with ever-increasing replicability in this and other spatial behavior tests (22, 23). This capacity promotes a unique approach to behavioral phenotyping, where the path traced by the animal (Fig. 1 A) is considered as a structured and information-rich string of meaningful units (Fig. 1_C_) that can be stored in a public database and reanalyzed (13, 21–22). Although phenotyping databases (e.g., Mouse Phenome Database) store endpoint results, from which variances of laboratory interaction can be calculated as outlined here, the see database also stores the behavior raw data. Researchers from many laboratories can contribute to such a database, while many data analysis specialists can use it to develop more replicable endpoints without the need to conduct their own experiments. Any progress in the design of new endpoints can be immediately used by the experimenters to reevaluate old experiments and design new experiments. This approach is suitable for tackling the inherent complexity of behavioral phenotypes and may lead to the algorithmic identification of behavioral traits that are highly heritable and highly replicable, and thus more valuable for any analysis aiming to understand the link between genes and behavior.

Supplementary Material

Supporting Information

Acknowledgments

We thank Noldus Information Technology (Wageningen, The Netherlands) for the loan of its EthoVision tracking system to Tel-Aviv University. This study is part of the project “Phenotyping Mouse Exploratory Behavior” supported by National Institutes of Health Grant R01 NS40234. Generous funds from AstraZeneca were used to defray the cost of mice through the Mouse Phenome Project Collaborations Program.

Author contributions: N.K., Y.B., G.I.E., and I.G. designed research; N.K., Y.B., G.I.E., and I.G. performed research; N.K., Y.B., and A.S. analyzed data; Y.B. and A.S. contributed new reagents/analytic tools; and N.K., Y.B., A.S., G.I.E., and I.G. wrote the paper.

Abbreviations: GxL, genotype × laboratory interaction; MM, mixed model; FM, fixed model; FDR, false discovery rate.

Data deposition: Data have been submitted to the Mouse Phenome Database, www.jax.org/phenome (Project MPD: 109).

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information