Meta-analysis of genome-wide association studies for height and body mass index in ∼700000 individuals of European ancestry (original) (raw)
Abstract
Recent genome-wide association studies (GWAS) of height and body mass index (BMI) in ∼250000 European participants have led to the discovery of ∼700 and ∼100 nearly independent single nucleotide polymorphisms (SNPs) associated with these traits, respectively. Here we combine summary statistics from those two studies with GWAS of height and BMI performed in ∼450000 UK Biobank participants of European ancestry. Overall, our combined GWAS meta-analysis reaches N ∼700000 individuals and substantially increases the number of GWAS signals associated with these traits. We identified 3290 and 941 near-independent SNPs associated with height and BMI, respectively (at a revised genome-wide significance threshold of P < 1 × 10−8), including 1185 height-associated SNPs and 751 BMI-associated SNPs located within loci not previously identified by these two GWAS. The near-independent genome-wide significant SNPs explain ∼24.6% of the variance of height and ∼6.0% of the variance of BMI in an independent sample from the Health and Retirement Study (HRS). Correlations between polygenic scores based upon these SNPs with actual height and BMI in HRS participants were ∼0.44 and ∼0.22, respectively. From analyses of integrating GWAS and expression quantitative trait loci (eQTL) data by summary-data-based Mendelian randomization, we identified an enrichment of eQTLs among lead height and BMI signals, prioritizing 610 and 138 genes, respectively. Our study demonstrates that, as previously predicted, increasing GWAS sample sizes continues to deliver, by the discovery of new loci, increasing prediction accuracy and providing additional data to achieve deeper insight into complex trait biology. All summary statistics are made available for follow-up studies.
Introduction
Over the past 15 years, genome-wide association studies (GWAS) have been increasingly successful in unveiling many aspects of the genetic architectures of complex traits and diseases (1–6). GWAS have led to the discovery of tens of thousands of polymorphisms [single nucleotide polymorphisms (SNPs) in general] associated with interindividual differences in quantitative traits or disease susceptibility. They have also been used to generate experimentally testable hypotheses and predict traits and disease risk (7,8). One of the early challenges faced by GWAS has been to bridge the gap between the amount of trait variance explained by genome-wide significant (GWS) loci (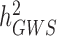 ) compared to estimates of heritabilities from pedigree-based studies (
) compared to estimates of heritabilities from pedigree-based studies (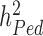 ). The reasons explaining the gap between
). The reasons explaining the gap between 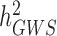 and
and 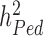 , also termed as missing heritability, are now better understood. Contributions from Yang et al. (9–11) and others (12) have helped clarifying the distinction between what can potentially be explained by all SNPs (aka SNP heritability,
, also termed as missing heritability, are now better understood. Contributions from Yang et al. (9–11) and others (12) have helped clarifying the distinction between what can potentially be explained by all SNPs (aka SNP heritability, 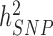 ) and what remains out of the reach of SNP array-based GWAS, for instance causal variants that are not tagged by genotyped or imputed SNPs. It is worth noting that untagged variants are often rare or even unique to single nuclear families. Therefore, their effects might remain statistically undetectable, despite still contributing to the difference between
) and what remains out of the reach of SNP array-based GWAS, for instance causal variants that are not tagged by genotyped or imputed SNPs. It is worth noting that untagged variants are often rare or even unique to single nuclear families. Therefore, their effects might remain statistically undetectable, despite still contributing to the difference between 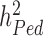 and
and 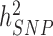 . Overall, clarifying the differences between
. Overall, clarifying the differences between 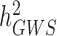 ,
, 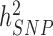 and
and 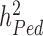 has been a major advance in the field and has helped providing theoretical guarantees that increasing GWAS sample sizes would continue to yield more discoveries, as long as the difference between
has been a major advance in the field and has helped providing theoretical guarantees that increasing GWAS sample sizes would continue to yield more discoveries, as long as the difference between 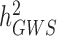 and
and 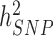 persists.
persists.
To date, the largest published GWAS of height (5) and body mass index (BMI) (6) in ∼250000 participants on average have uncovered 697 and 97 near-independent SNPs associated with these traits and explaining ∼15% and ∼3% of trait variance, respectively. Compared to 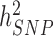 estimates of height and BMI, i.e. ∼50% and ∼30%, respectively (9–11), this indicates an enormous potential for discoveries expected simply from increasing sample sizes. However, the required sample size to explain all SNP heritability by identified individual GWS loci is not known because it depends on the joint distribution of allele frequency and effect size at causal variants. Here we perform a meta-analysis of previous GWAS of the Genetic Investigation of ANthropometric Traits (GIANT) consortium studies with new GWAS of height and BMI in ∼450000 participants of the UK Biobank (UKB). In total, our sample size reaches ∼700000, which is unprecedented for GWAS of these traits. The present study is part of a larger effort led by the GIANT consortium, expected in the near future to yield one the largest GWAS ever conducted (N between 1.5 and 2 million). We describe below our findings in terms of number of GWAS signals, variance explained and prediction accuracy and also conduct analyses to prioritize genes for follow-up investigations. The summary statistics of these two meta-analyses (height and BMI) are made available (URLs).
estimates of height and BMI, i.e. ∼50% and ∼30%, respectively (9–11), this indicates an enormous potential for discoveries expected simply from increasing sample sizes. However, the required sample size to explain all SNP heritability by identified individual GWS loci is not known because it depends on the joint distribution of allele frequency and effect size at causal variants. Here we perform a meta-analysis of previous GWAS of the Genetic Investigation of ANthropometric Traits (GIANT) consortium studies with new GWAS of height and BMI in ∼450000 participants of the UK Biobank (UKB). In total, our sample size reaches ∼700000, which is unprecedented for GWAS of these traits. The present study is part of a larger effort led by the GIANT consortium, expected in the near future to yield one the largest GWAS ever conducted (N between 1.5 and 2 million). We describe below our findings in terms of number of GWAS signals, variance explained and prediction accuracy and also conduct analyses to prioritize genes for follow-up investigations. The summary statistics of these two meta-analyses (height and BMI) are made available (URLs).
Results
GWAS of height and BMI identify 3290 and 941 associated SNPs, respectively
We first performed a GWAS of height and BMI in 456426 UKB participants of European ancestry (Materials and Methods). We tested associations of 16652994 genotyped and imputed SNPs (Materials and Methods) with both traits using a linear mixed model to account for relatedness between participants and population stratification. Analyses were performed with BOLT-LMM v2.3 (13,14) using a set of 711933 HapMap 3 (HM3) SNPs to model the polygenic component to control for relatedness and population stratification (Materials and Methods). After fitting age, sex (inferred from SNP data) (15), 10 genotypic principal components (PCs), recruitment centre and genotyping batches as fixed effects, phenotypes were residualized (separately for males and females) and inverse-normally transformed before analysis. A parallel analysis of 451 099 individuals and using a slightly different set of parameters for sample selection and adjustment revealed very similar results (Materials and Methods), and so we proceeded with the larger sample of 456426 UKB participants. We then performed fixed-effect inverse-variance weighted meta-analysis of UKB results with publicly available GWAS summary statistics of height (5) (GIANTheight) and BMI (6) (GIANTBMI) using the software METAL (16). In total, our meta-analysis involves ∼2.4 million HapMap 2 (HM2) SNPs with available summary statistics in GIANTheight or GIANTBMI, N = 693 529 participants on average for height and N = 681 275 participants on average for BMI. Figure 1 shows Manhattan plots for both meta-analyses. We found in both traits a marked deviation of the distribution of _P_-values from the uniform null distribution (height: λGC = 3.6; BMI: λGC = 2.7), suggesting polygenicity and possibly population stratification. The mean of association chi-square statistics is ∼8.8 for height and ∼3.9 for BMI, consistent with a randomly chosen SNP, on average, being associated with height at P < 0.003 and with BMI at P < 0.047. We performed linkage disequilibrium (LD) score regression (LDSC) (17,18) to quantify the contribution of population stratification to our results. We found that LDSC intercept (ILDSC) was inflated for both height (ILDSC = 1.48, Standard Error (s.e.) 0.1) and BMI (ILDSC = 1.03, s.e. 0.02), suggesting a significant contribution of population stratification. However, although classically used, this statistic may not accurately reflect the contribution of population stratification as it can rise above 1 with increased sample size and heritability (14). In contrast, the attenuation ratio statistic RPS = (ILDSC − 1)/(mean of association chi-square statistics − 1), which does not have these limitations, was shown to yield a better quantification of population stratification14. We found for height and BMI that RPS equals 0.06 (s.e. 0.01) and 0.01 (s.e. 0.01), respectively, which implies that polygenicity is the main driver of the observed inflation of test statistics. We also used the LDSC methodology to estimate the genetic correlation between summary statistics from GIANTheight and that from UKB, as well as between summary statistics from GIANTBMI and that from UKB. We found a genetic correlation (rg) of 0.96 (s.e. 0.01) for height and of 0.95 (s.e. 0.01) for BMI, highlighting a strong genetic homogeneity between UKB and previous meta-analyses, and thus confirming the validity of using a fixed-effect meta-analysis. Also, this analysis implied significant overlap of ∼59000 participants between UKB and GIANTheight (bivariate LDSC intercept: 0.17; s.e. 0.05), but not between UKB and GIANTBMI (bivariate LDSC intercept: 0.01; s.e. 0.01). The latter observation is surprising given that the vast majority of cohorts included in GIANTheight are also included in GIANTBMI. Analogous to the univariate case, we show through theory and simulations that large sample sizes and heritabilities can inflate the bivariate LDSC intercept, even in the absence of sample overlap (Supplementary Note 1; Figs. S1–S2). Although sample overlap between UKB and GIANT’s cohorts from the UK (∼14 cohorts, with a maximum sample size of ∼27000) remains likely, UK studies were recruited over many decades and ages and the number of individuals overlapping is more likely to be in the 100s, given our bivariate LDSC analysis that also suggests that it is small and likely has minimal effect on our inference. We therefore conclude that sample overlap is negligible between UKB and GIANTheight, as it is between UKB and GIANTBMI.
Figure 1.
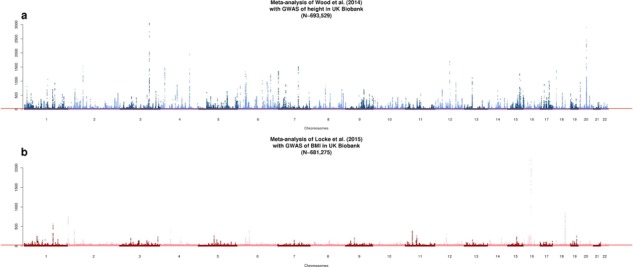
Manhattan plot showing association 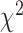 statistics of association between SNPs and height (A) or BMI (B).
statistics of association between SNPs and height (A) or BMI (B).
Using an approximate conditional and joint multiple-SNP (COJO) analysis implemented in Genome-wide Complex Traits Analysis software (GCTA) (19) that takes into account LD between SNPs at a given locus, we identified 3290 and 941 SNPs (COJO P < 1 × 10−8; Table 1) associated with height and BMI, respectively. This more conservative significance threshold was chosen from the recommendations of a previous study (20) that showed that type I error was not properly controlled at the classical 5 × 10−8 threshold when using SNPs imputed to the Haplotype Reference Consortium (HRC) or 1000 genomes imputation reference panels. In theory, given that our study focused on ∼2.4 million HM2 SNPs, the classical 5 × 10−8 threshold would still be valid. However, to ensure comparability with other studies based on 1000 genomes or HRC imputed SNPs, we believe that the latter significance threshold is justified in our study. Compared to GIANTheight and GIANTBMI, our findings represent a ∼5 and ∼10-fold increase of the number of GWAS signals associated with height and BMI, respectively. Note that the latter comparison is based upon numbers of GWS detected using the same 1 × 10−8 significance threshold. The 3290 height-associated SNPs consist of 2388 primary associations and 902 secondary signals, i.e. GWS in GCTA-COJO analysis only. These 3290 SNPs clustered in 712 genomic loci [locus is defined as in (5) as one or multiple jointly associated SNPs located within a 1-Mb window], including 512 loci not previously detected in GIANTheight. For BMI, the 941 SNPs identified consist of 656 primary associations and 285 secondary signals, clustered in 536 genomic loci including 484 loci not previously detected in GIANTBMI. We found that the average number of height and BMI associated SNPs per locus is 4.6 and 1.7, respectively, but also observed a large variability of that number (standard deviation: ∼6 SNPs/locus for height loci and ∼2 SNPs/locus for BMI loci). We found one locus on chromosome 12q23.2 (chr12:102 229 631–103 278 745; genome build hg19) that concentrates up to 19 jointly significant signals for height within ∼1.05 Mb. That locus contains the IGF1 gene that was previously identified in GIANTheight. Note however that only two independent associations within that locus were reported at that time, indicating that larger GWAS improves the characterization of the allelic heterogeneity of genomic loci.
Table 1.
Summary of results from the meta-analysis of GWAS of height and BMI in N ∼700000 individuals of European ancestry and from downstream analyses such as gene-based association tests or SMR
| Summary of results | Meta-analysis of height (mean N ∼693529) | Meta-analysis of BMI (mean N ∼681275) |
|---|---|---|
| Number of near-independent genome-wide significant SNPs (GWS; COJO P < 10−8) | 3290 | 941 |
| Number of main/secondary associations | 2388/902 | 656/285 |
| Number of loci identified | 712 | 536 |
| Number of new loci* | 512 | 484 |
| Number of genes identified through SMR analysis | 610 | 138 |
| Number of methylation sites identified through SMR analysis | 775 | 276 |
| Prediction accuracy (r2) in HRS from GWS SNPs | 19.7% | 5.0% |
| Prediction accuracy (r2) in HRS from SNPs at P < 0.001 | 24.4% | 10.2% |
| Variance explained in HRS from GWS SNPs | 24.6% | 6.0% |
| Variance explained in HRS from SNPs at P < 0.001 | 34.7% | 13.8% |
We assessed the replicability of these associations by estimating the regression slope (RS) of SNP effect size estimated in an independent sample onto the SNP effect sizes (corrected for winner’s curse effects) (21,22) from our meta-analyses, using 8552 unrelated individuals from the Health and Retirement Study (HRS). A similar approach to quantify replicability has been applied in (23). We found significant RS estimates for height (0.90; jackknife s.e. 0.02) and BMI (0.91; jackknife s.e. 0.04), both close to one and therefore suggesting a high level of replicability of our findings (Fig. 2). We note however that the RS estimates for height were significantly (P < 0.05) smaller than 1. Beyond lack of replication, many reasons can explain why this slope can be smaller than 1. One of these reasons is ‘winner’s curse’ effects, which we already accounted for here using (21) correction (Materials and Methods). More generally, under an infinitesimal genetic architecture, the expectation of RS, hereafter denoted E[RS], is a function of the discovery sample size (N), the heritability of the trait (h2) and the number of variants underlying the trait (M): E[RS] = h2/( h2 + M/N), as derived in Supplementary Note 2. We show in that note that it is only when N is infinite that a slope of 1 is to be expected. Another reason, although less likely given the strict significance threshold used in this study, would be the presence of false positive associations in our list of GWS SNPs. We show in Supplementary Note 2 that if a slope of ∼1 is to be expected, therefore ∼10% (i.e. hundreds) of false positive associations within our lists of GWS SNPs would have created the observed slope of ∼0.9. The latter assumption is highly unlikely given the chosen significant threshold.
Figure 2.
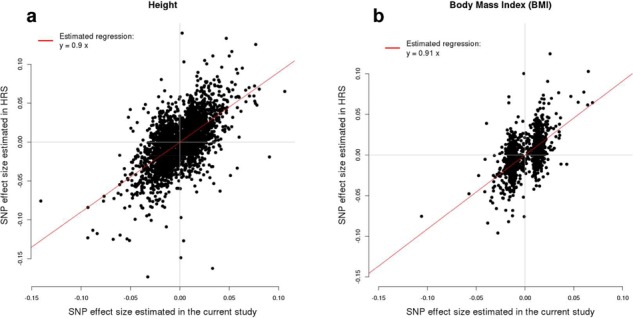
Regression of SNPs effect estimated from the meta-analysis of GWAS of height in UKB and GWAS of height from (5) (A) and GWAS of BMI in UKB and GWAS of BMI from (6) (B) onto SNP effects on height and BMI estimated in HRS.
In addition, we used another method by Qi et al. (24) to quantify the correlation rb of true SNP effects between two studies, while correcting for estimation errors in both studies (Materials and Methods). We underline here one difference with the previous method, which is that estimation errors in the replication study are also corrected. When applying this method to our discovery and replication studies, we found a correlation rb ∼ 0.99 (jackknife s.e. 0.03) for height and rb ∼ 1.00 (jackknife s.e. 0.06) for BMI (Fig. S3). The latter result therefore reinforces the replicability of our findings.
Predictive power of polygenic scores
We estimated in HRS participants using the Genetic relationship based REstricted Maximum Likelihood (GREML) approach implemented in GCTA (9,10,19) that near-independent GWS SNPs explain 24.6% (s.e. 1.3%) and 6.0% (s.e. 0.8%) of the variance of height and BMI, respectively, adjusting for 20 PCs for both traits. This represents a ∼1.9- and ∼3.2-fold improvement in comparison with previous meta-analyses (Fig. 3A and B) and ∼1/2nd and ∼1/4th of the SNP-based heritability of height (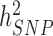 = 48.3%; s.e. 3.7%) and BMI (
= 48.3%; s.e. 3.7%) and BMI (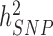 = 22.4%; s.e. 3.7%) estimated in 10 000 randomly sampled UKB participants. The latter
= 22.4%; s.e. 3.7%) estimated in 10 000 randomly sampled UKB participants. The latter 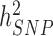 estimates, which are fairly consistent with previous studies (9–11), were calculated using common HM3 SNPs (minor allele frequency >1%). Note also that, to ensure a fair comparison, the improvement folds reported here are obtained after re-analysing summary statistics from GIANTheight and GIANTBMI using the same P < 10−8 revised significance threshold. Therefore, the numbers and proportions of trait variance explained by GWS from these studies are smaller than previously reported (GIANTheight: ∼12.8% in this study versus ∼15% previously reported; GIANTBMI:∼1.8% in this study versus ∼3% previously reported). For each HRS participant, we also calculated genetic predictors of height and BMI from near-independent GWS SNPs as the sum of trait increasing alleles at these loci, weighted by their estimated effect sizes. We found the squared correlation (r2) between predicted height and actual height (corrected for mean and variance sex differences) to be ∼19.7% and between predicted BMI and actual BMI (corrected for mean and variance sex differences) to be ∼5.0% (Fig. 3C and D). We performed additional prediction analyses using SNPs with significance _P_-values larger than 10−8. We performed GCTA-COJO analyses for height and BMI and analysed SNPs with significance _P_-value below 10−3, 10−4, 10−5, 10−6, 10−7 and 10−8. We therefore calculated six genetic predictors for each trait and quantified in HRS participants the fraction of trait variance explained by SNPs contributing to these predictors as well as their predictive capacity (Fig. 3). As reported in Wood et al. (5), we found that including SNPs beyond GWS increases prediction accuracy and variance explained (Fig. 3) in both traits. For height, the variance explained increased from ∼24.6% using 3290 near-independent GWS SNPs to ∼34.7% (s.e. 1.9%) using ∼15 000 near-independent SNPs with P < 0.001. The prediction _r_2 (squared-correlation) also increased from ∼19.7% to ∼24.4%. For BMI, the variance explained using 6781 SNPs selected in the COJO analysis at P < 0.001 is ∼13.9% (s.e. 1.5%) and the corresponding prediction _r_2 is ∼10.2% which is twice the prediction accuracy obtained using GWS loci only.
estimates, which are fairly consistent with previous studies (9–11), were calculated using common HM3 SNPs (minor allele frequency >1%). Note also that, to ensure a fair comparison, the improvement folds reported here are obtained after re-analysing summary statistics from GIANTheight and GIANTBMI using the same P < 10−8 revised significance threshold. Therefore, the numbers and proportions of trait variance explained by GWS from these studies are smaller than previously reported (GIANTheight: ∼12.8% in this study versus ∼15% previously reported; GIANTBMI:∼1.8% in this study versus ∼3% previously reported). For each HRS participant, we also calculated genetic predictors of height and BMI from near-independent GWS SNPs as the sum of trait increasing alleles at these loci, weighted by their estimated effect sizes. We found the squared correlation (r2) between predicted height and actual height (corrected for mean and variance sex differences) to be ∼19.7% and between predicted BMI and actual BMI (corrected for mean and variance sex differences) to be ∼5.0% (Fig. 3C and D). We performed additional prediction analyses using SNPs with significance _P_-values larger than 10−8. We performed GCTA-COJO analyses for height and BMI and analysed SNPs with significance _P_-value below 10−3, 10−4, 10−5, 10−6, 10−7 and 10−8. We therefore calculated six genetic predictors for each trait and quantified in HRS participants the fraction of trait variance explained by SNPs contributing to these predictors as well as their predictive capacity (Fig. 3). As reported in Wood et al. (5), we found that including SNPs beyond GWS increases prediction accuracy and variance explained (Fig. 3) in both traits. For height, the variance explained increased from ∼24.6% using 3290 near-independent GWS SNPs to ∼34.7% (s.e. 1.9%) using ∼15 000 near-independent SNPs with P < 0.001. The prediction _r_2 (squared-correlation) also increased from ∼19.7% to ∼24.4%. For BMI, the variance explained using 6781 SNPs selected in the COJO analysis at P < 0.001 is ∼13.9% (s.e. 1.5%) and the corresponding prediction _r_2 is ∼10.2% which is twice the prediction accuracy obtained using GWS loci only.
Figure 3.
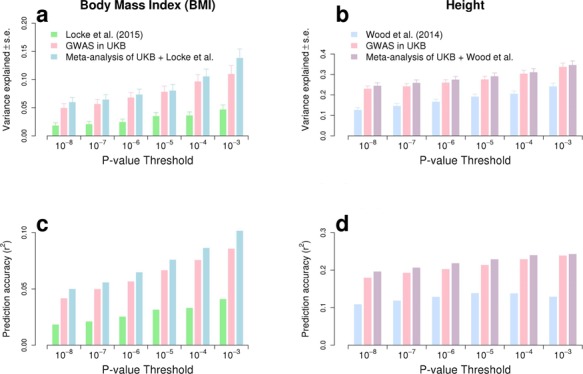
Variance explained and prediction accuracy (squared correlation between trait value and its predictor from SNPs) calculated from six nested sets of near-independent SNPs selected at different significance threshold. Variance explained and prediction accuracy is calculated in 8552 unrelated participants of the HRS cohort.
Gene prioritization
We next attempted to identify genes whose expression levels could potentially mediate the association between SNPs and height or between SNPs and BMI. For this purpose, we performed a summary-data-based Mendelian randomization (SMR) analysis (25). This method aims at testing the association between gene expression (in a particular tissue) and a trait using the top associated expression quantitative trait loci (eQTL) as a genetic instrument. For this analysis, which only requires GWAS summary statistics, we used the publicly available GTEx-v7 database containing eQTLs for multiple genes in multiple tissues (26). We identified 610 and 138 (Table 1) unique genes that genetic control suggestively overlaps (_P_SMR < 5 × 10−8) that of height or BMI, respectively. Significant SMR test indicates evidence of pleiotropy (i.e. the expression of a gene and that of a trait are influenced by the same causal variant at the gene locus) but also the possibility that SNPs controlling gene expression are in LD with those associated with the traits. These two situations can be disentangled using the HEterogeneity In Dependent Instrument (HEIDI) test implemented in the SMR software. The number of genes reported above corresponds to genes already filtered on statistical evidence supporting pleiotropy rather than linkage between variants controlling gene expression and variants controlling height or BMI (_P_HEIDI > 0.05). We found that >95% (597/610 = ∼98% for height and 133/138 = ∼96% for BMI) of height- and BMI-associated genes identified via the SMR analysis show consistent direction of effects across multiple tissues. As an example, we found that higher expression of PIGP across 23 tissues is associated with increased height and that higher expression of HSD17B12 across 22 tissues is associated with decreased BMI. Similarly, we found that higher expression of STAG3L1 in 33 tissues is associated with decreased BMI. We then quantified the enrichment of genes identified via SMR and HEIDI tests into biological pathways. Altogether, we found that height-associated genes are significantly enriched among genes contributing to skeletal growth, cartilage and connective tissue development, while BMI-associated genes are mostly enriched among genes involved in neurogenesis and more generally involved in the development of the central nervous system. These last results therefore confirm findings from (5) and (6), which previously implicated the same pathways and highlighted their connections with height and BMI.
Mediation through epigenetic mechanisms
We performed another SMR and HEIDI analysis to now prioritize CpG dinucleotides at which methylation levels might mediate the association between SNPs and height or BMI. For this analysis, we used publicly available methylation QTL from the study (27) in peripheral blood. We identified 775 and 276 (Table 1) deoxyribonucleic acid (DNA) methylation sites showing pleiotropic associations with height and BMI, respectively. Among all CpG sites identified, we found that increased DNA methylation at cg19825988 (within the ZBTB38 gene) shows the strongest positive association with height (∼0.4 SD for 100% methylation; _p_SMR = 3.5 × 10−9). The ZBTB38 gene, located within a previously identified GWAS locus (GIANTheight), encodes a zinc finger transcriptional activator that binds methylated DNA. This gene was also detected in our first SMR analysis (using gene expression) described above. For BMI, the largest effect of DNA methylation was observed at cg03755535 (within the first exon of the CAMKV gene); where increased DNA methylation correlates with decreased BMI (−0.12 SD for 100% methylation; _p_SMR = 4.8 × 10−8). This gene was not detected in our first SMR analysis but is located within a previously identified GWAS locus.
As mentioned above, one possible interpretation of SMR results is that gene expression or methylation could act as mediators of SNPs effects. Beyond statistical evidence, such an interpretation may not be intuitive for a trait like height, which is measured in mature participants often many decades after their body height had stabilized. We emphasize however that interindividual differences in adult height result from cumulative effects occurring at different stages of the development. Therefore, although our study uses stabilized height, the SNP effects that we estimated would represent a combination of early developmental and post-pubertal effects. We acknowledge nonetheless that additional data supporting the stability over time of the genetic control on these genes and epigenetic marks would be required to strengthen our interpretation, although previous studies (18) have shown a significant genetic correlation between birth length and weight and adult height.
Discussion
We have presented here the results of the meta-analysis of a single large study, the UKB, with previously published GWAS of height and BMI. We found that the number of genomic loci associated with height and BMI is disproportionately increased compared to previously published GWAS and that this increase correlates with increased trait variance explained and improved accuracy of genetic predictors from SNPs at these loci. In addition, we have shown that large GWAS enhance the power of integrative analyses such as pathway enrichment and SMR to unveil relevant genes to be prioritized for further functional studies.
Our analyses revealed a number of challenges to address when dealing with very large GWAS. One of these challenges relates to conclusions from LDSC, a method now routinely used for quality control (detection of confounding effects) and inference of genetic parameters like heritability and genetic correlation. Following the recent study by (14), which pointed out a number of caveats relative to the interpretation of the univariate LDSC intercept as an indicator of confounding due to population stratification or other artefacts, we have shown here that caution must also be applied when interpreting the intercept of the bivariate LDSC. These two problems, which are directly related to each other, both illustrate how the effect of very subtle population stratification can be dramatically magnified when sample sizes are large. We recall here the surprising observation that, despite considering the same sets of cohorts, the conclusions about sample overlap from bivariate LDSC intercept were radically different between GWAS of height and GWAS of BMI. Similar to the univariate case, we recommend the use of an attenuation ratio statistic to measure how much of the inflation in the bivariate LDSC intercept is explained by correlated population stratification or sample overlap.
Another challenge faced in this study relates to the overcorrection of population stratification. In general, setting up expectations with respect to how many GWAS signals can be reasonably detected or how much variance can be explained from SNPs identified in a GWAS of a given sample has always been a difficult question. In particular, the detection of ‘too many’ GWAS signals has often been a concern in the GWAS literature and seen as an indication of potentially uncorrected population stratification. With very large datasets like UKB, some of these questions can be now addressed. We observed that the number of variants and fraction of variance explained by GWAS hits identified from random subsets of UKB of the same size as GIANTheight or GIANTBMI was larger than that discovered in those studies (Table 2). Multiple reasons could explain these differences, as for example genetic and phenotypic heterogeneity between cohorts included in these two meta-analyses (28). Nonetheless, we argue that methods classically used to correct for the effects of population stratification may have removed a substantial amount of the signal to be detected. To further illustrate this point, we re-analysed the data from (6). Our new analysis consisted of deflating the genomic control (GC) corrected standard errors of estimated SNP effects with a factor equal to the square root of the LDSC intercept. This transformation constrains the LDSC intercept to be 1 but is less conservative than the double GC correction (i.e. GC correction in each cohort included in the meta-analys is, and GC correction applied to the outcome of the meta-analysis) used in (6). We found in this secondary analysis that the number of GWAS signals (at P < 10−8) increased from 77 to 210 (∼3-fold increase), the variance explained increased from ∼1.8% to ∼2.8% and the prediction accuracy of genetic predictors using those SNPs from ∼1.8% to ∼2.4% (Fig. S4). This observation demonstrates that a correction based on LDSC intercept performs better than GC correction but still remains imperfect, since we know that LDSC intercept also increases with sample size. Overall, although we acknowledge that GC and LDSC corrections are effective in controlling the inflation of false positives induced by population structure, our study highlights that these methods tend to overcorrect population stratification when sample size is large, which subsequently reduces statistical power to detect associations. New methods must therefore be developed in order to maximize the potential of discovery of forthcoming GWAS of ever-larger sample sizes.
Table 2.
Number, percentage of variance explained and accuracy of genetic predictors from SNPs found associated (P < 10−8) with height or BMI in a random sample of 250 000 unrelated participants of the UKB
| Height | BMI | |||
|---|---|---|---|---|
| Random samplefrom UKB | Wood et al. (5) | Random samplefrom UKB | Locke et al. (6) | |
| Number of near-independent genome-wide significant SNPs (GWS; COJO P < 10−8) | 850 | 594 | 160 | 82 |
| Variance explained by GWS | 14.0% | 12.8% | 2.3% | 1.8% |
| Prediction accuracy (r2) | 14.0% | 10.9% | 2.5% | 1.8% |
In summary, our study confirms the potential for new discoveries of large GWAS, highlights critical methodological issues emerging at such a large scale and announces a gargantuan number of new discoveries for the next iteration of meta-analyses of the GIANT consortium based on sample sizes in the order of 1 million and more.
Materials and Methods
UKB analyses
Sample selection
We analysed data from 488 377 genotyped participants of the UKB. We restricted the analysis to 456 426 participants of European ancestry. Ancestry was inferred using a two-stage approach. The first step consisted of projecting each study participant onto the first two genotypic PCs calculated from HM3 SNPs genotyped in 2504 participants of 1000 genomes project (29). We then used five superpopulations (European, African, East-Asian, South-Asian and Admixed) as reference and assigned each participant to the closest population. Distance was defined as the posterior probability under a bivariate Gaussian distribution of each participant to belong to one of the five superpopulations. This method generalizes the _k_-means method and takes into account the orientation of the reference cluster to improve the clustering. Vectors of means and 2 × 2 variance–covariance matrices were calculated for each superpopulation, using a uniform prior.
SNP selection
We analysed SNPs imputed to the HRC imputation reference panel (30) with an imputation quality score above 0.3. For each UKB participant, we hard-called genotypes with posterior probability larger than 0.9 and kept SNPs with call rate >0.95, minor allele frequency >0.0001 and _P_-value for Hardy–Weinberg test larger than 10−6. In total, we analysed 16 653 239 SNPs. For the meta-analysis, we considered a subset of ∼2.3 millions (out of 16 653 239) SNPs showing consistent alleles with UKB and HRS (used as LD reference) as well as consistent allele frequency (maximum difference <0.15 for minor and major allele).
Association testing
We ran a GWAS of height and BMI in 456 426 UKB participants using linear mixed model association testing implemented in BOLT-LMM v2.3 (13,14) software assuming an infinitesimal model. We used 711 933 HM3 SNPs (LD pruned for SNPs with r2 > 0.9) as model SNPs in our analysis. Height and BMI were adjusted for age, sex, recruitment centre, genotyping batches and 10 PCs calculated from 132 102 out of the 147 604 genotyped SNPs pre-selected by the UKB quality control team (15) for PC analysis. The difference is explained by the quality control of SNPs (minor allele frequency >0.01, genotype call rate >95% and Hardy–Weinberg test _P_-value > 10−6) applied to a different set of samples as compared to (15). PCs were calculated using the flashPCA software (31). In a parallel effort, to provide a sensitivity analysis, using slightly different parameters for sample selection and adjustment, we selected 451 099 individuals of European genetic ancestry as described in (32). This parallel analysis used dosage and not hard-called genotypes. Analyses performed on this second set of UKB participants revealed highly concordant findings compared to the set of 456 426 participants. We therefore reported here results from the larger set of individuals.
Replication
We used genotypes imputed to the 1000 genomes reference panel and phenotypes (height and BMI) from 8552 unrelated (Genetic Relationship Matrix (GRM)<0.05) participants of the HRS to assess the replicability of SNPs found to be associated with height and BMI. We also used these data to assess the variance explained by different sets of SNPs as well as the out-of-sample prediction accuracy of genetic predictors using these sets of SNPs. Analyses were restricted to 2 484 330 HM2 SNPs with an imputation quality score >0.3, a minor allele frequency >0.01 and a _P_-value from Hardy–Weinberg equilibrium test >10−6.
Given that replication of individual SNP is not feasible because of the limited sample size of our replication cohort, we assessed the overall replicability of SNP-traits associations using the regression slope of estimated SNP effects from the replication study onto estimated SNP effect sizes from the discovery study. Values of the replication slope of ∼1 indicate good replicability of GWAS findings, although we show in Supplementary Note 2 that the expectation of the replication slope depends on the discovery sample size, the heritability of the trait and the number of variants underlying the trait. SNPs brought forward for replication are subjected to the winner’s curse effect, and their effect sizes are biased (21,22). We therefore used the correction proposed by Zhong and Prentice (2010) before estimating the replication slope. We also used another method by Qi et al. (24) to quantify the consistency between estimated SNP effect sizes in discovery versus replication study. Assuming that each estimate can be discomposed as the sum of a true effect + an estimation error term, this method attempts to quantify the correlation rb of true effects between two studies, while correcting for estimation errors in both studies. In this study, we estimated rb using the following equation [similar to Eq. (3) in (24), assuming no overlap between discovery and replication study]:
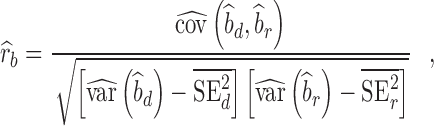 |
(1) |
|---|
where 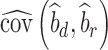 is the observed sample covariance between estimates of SNP effects from discovery (
is the observed sample covariance between estimates of SNP effects from discovery (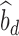 ) and replication (
) and replication (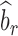 ) studies,
) studies, 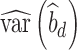 and
and 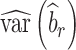 are the observed sample variances of estimates of SNPs effects in discovery and replication study, respectively, and
are the observed sample variances of estimates of SNPs effects in discovery and replication study, respectively, and 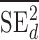 and
and 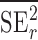 are average squared estimated standard errors of estimates of SNPs effects in discovery and replication study, respectively. We derived a more detailed version of Eq. (1) in Supplementary Note 3. We estimated standard errors of
are average squared estimated standard errors of estimates of SNPs effects in discovery and replication study, respectively. We derived a more detailed version of Eq. (1) in Supplementary Note 3. We estimated standard errors of 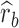 using leave-one-SNP-out jackknife.
using leave-one-SNP-out jackknife.
Summary statistics QC and meta-analyses
Summary statistics of GWAS of height and BMI from Wood et al. (5) and Locke et al. (6) studies were downloaded from the following website: https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files. Before meta-analysis with UKB, we filtered out SNPs which reported pairs of alleles did not match the pairs of alleles in the HRS and UKB and also which had reported allele frequency too different (absolute difference >0.15) from that calculated using unrelated participants of HRS. Fixed-effect inverse variance weighted meta-analysis was performed using the software METAL (16).
LDSC
We performed LDSC to quantify the level of confounding in GWAS due to population stratification as well as quantifying the sample overlap between cohorts involved in previous meta-analyses and the UKB. Analyses were performed using the LDSC software v1.0.0 (https://github.com/bulik/ldsc). We used default parameters but did not apply any threshold on the maximum association chi-square statistics of SNPs included in the analyses. We used LD scores from European participants of the 1000 genomes project that can be downloaded from the LDSC website.
SMR and HEIDI analyses
SMR and HEIDI tests were implemented in the SMR software (http://cnsgenomics.com/software/smr/). SMR analyses were performed using default parameters but specifying a window of 2 Mb up- and downstream genes (expression probes) to include relevant cis-eQTL (instrument) for those genes. The same approach was applied for detecting CpG methylation sites associated with height or BMI. SMR analyses were based on eQTLs from publicly available databases from GTEx-v7 (26) and McRae et al. (2017) (27). Both sets of eQTL in SMR format can be downloaded from the SMR website: http://cnsgenomics.com/software/smr/.
Data download
GWAS summary statistics can be downloaded from the GIANT consortium website: https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files and from the Program in Complex Trait Genomics website: http://cnsgenomics.com/data.html.
Supplementary Material
Supplementary Data
Acknowledgements
Authors are grateful to Dr Sara L. Pullit, Dr Cecilia Lindgren and Dr Ting Qi for insightful comments and discussions. We used genotypic genotypic and phenotypic data from the HRS (HRS: dbGaP phs000428.v1.p1), as well as genotypic and phenotypic data from the UKB under project 12514. We also used eQTL data from The Genotype-Tissue Expression (GTEx) Project, which was supported by the Common Fund of the Office of the Director of the National Institutes of Health, and by NCI, NHGRI, NHLBI, NIDA, NIMH and NINDS. The GTEX data used for the analyses described in this manuscript were obtained on dbGaP accession number phs000424.v6.p1.
Conflict of Interest statement. None declared.
Funding
Australian Research Council (DP130102666, DP160103860, DP160102400); Australian National Health and Medical Research Council (1078037, 1078901, 1103418, 1107258, 1127440 and 1113400); National Institute of Health (NIH grants R01AG042568, P01GM099568 and R01MH100141); Sylvia & Charles Viertel Charitable Foundation.
References
- 1.Visscher P.M., Brown M.A., McCarthy M.I. and Yang J. (2012) Five years of GWAS discovery. Am. J. Hum. Genet., 90, 7–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Visscher P.M., Wray N.R., Zhang Q., Sklar P., McCarthy M.I., Brown M.A. and Yang J. (2017) 10 years of GWAS discovery: biology, function, and translation. Am. J. Hum. Genet., 101, 5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lango Allen H., Estrada K., Lettre G., Berndt S.I., Weedon M.N., Rivadeneira F., Willer C.J., Jackson A.U., Vedantam S., Raychaudhuri S. et al. (2010) Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature, 467, 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Speliotes E.K., Willer C.J., Berndt S.I., Monda K.L.,Thorleifsson G., Jackson A.U., Lango Allen H., Lindgren C.M., Luan J., Mägi R. et al. (2010) Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat. Genet., 42, 937–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wood A.R., Esko T., Yang J., Vedantam S., Pers T.H., Gustafsson S., Chu A.Y., Estrada K., Luan J., Kutalik Z. et al. (2014) Defining the role of common variation in the genomic and biological architecture of adult human height. Nat. Genet., 46, 1173–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Locke A.E., Kahali B., Berndt S.I., Justice A.E., Pers T.H., Day F.R., Powell C., Vedantam S., Buchkovich M.L., Yang J. et al. (2015) Genetic studies of body mass index yield new insights for obesity biology. Nature, 518, 197–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Claussnitzer M., Dankel S.N., Kim K.-H., Quon G., Meuleman W., Haugen C., Glunk V., Sousa I.S., Beaudry J.L., Puviindran V. et al. (2015) FTO obesity variant circuitry and adipocyte browning in humans. N. Engl. J. Med., 373, 895–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sekar A., Bialas A.R., Rivera H., Davis A., Hammond T.R., Kamitaki N., Tooley K., Presumey J., Baum M., Van Doren V. et al. (2016) Schizophrenia risk from complex variation of complement component 4. Nature, 530, 177–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W. et al. (2010) Common SNPs explain a large proportion of heritability for human height. Nat. Genet., 42, 565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang J., Bakshi A., Zhu Z., Hemani G., Vinkhuyzen A.A.E., Lee S.H., Robinson M.R., Perry J.R.B., Nolte I.M., Vliet-Ostaptchouk J.V. et al. (2015) Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet., 47, 1114–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yang J., Zeng J., Goddard M.E., Wray N.R. and Visscher P.M. (2017) Concepts, estimation and interpretation of SNP-based heritability. Nat. Genet., 49, 1304–1310. [DOI] [PubMed] [Google Scholar]
- 12.Wray N.R., Yang J., Hayes B.J., Price A.L., Goddard M.E. and Visscher P.M. (2013) Pitfalls of predicting complex traits from SNPs. Nat. Rev. Genet., 14, 507–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Loh P.-R., Tucker G., Bulik-Sullivan B.K., Vilhjálmsson B.J., Finucane H.K., Salem R.M., Chasman D.I., Ridker P.M., Neale B.M., Berger B. et al. (2015) Efficient Bayesian mixed model analysis increases association power in large cohorts. Nat. Genet., 47, 284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Loh P.-R., Kichaev G., Gazal S., Schoech A.P. and Price A.L. (2018) Mixed-model association for biobank-scale datasets. Nat. Genet., 50, 906–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bycroft C., Freeman C., Petkova D., Band G., Elliott L.T., Sharp K., Motyer A., Vukcevic D., Delaneau O., O’Connell J. et al. (2017) Genome-wide genetic data on ∼500000 UK Biobank participants., bioRxiV, 10.1101/166298.
- 16.Willer C.J., Li Y. and Abecasis G.R. (2010) METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics, 26, 2190–2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bulik-Sullivan B.K., Loh P.-R., Finucane H.K., Ripke S., Yang J., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Patterson N., Daly M.J., Price A.L. and Neale B.M. (2015) LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet., 47, 291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bulik-Sullivan B., Finucane H.K., Anttila V., Gusev A., Day F.R., Loh P.-R., Duncan L., Perry J.R.B., Patterson N., Robinson E.B. et al. (2015) An atlas of genetic correlations across human diseases and traits. Nat. Genet., 47, 1236–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang J., Lee S.H., Goddard M.E. and Visscher P.M. (2011) GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet., 88, 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wu Y., Zheng Z., Visscher P.M. and Yang J. (2017) Quantifying the mapping precision of genome-wide association studies using whole-genome sequencing data. Genome Biol., 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhong H. and Prentice R.L. (2008) Bias-reduced estimators and confidence intervals for odds ratios in genome-wide association studies. Biostatistics, 9, 621–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Palmer C. and Pe’er I. (2017) Statistical correction of the Winner’s Curse explains replication variability in quantitative trait genome-wide association studies. PLoS Genet., 13, e1006916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Turley P., Walters R.K., Maghzian O., Okbay A., Lee J.J., Fontana M.A., Nguyen-Viet T.A., Wedow R., Zacher M., Furlotte N.A. et al. (2018) Multi-trait analysis of genome-wide association summary statistics using MTAG. Nat. Genet., 50, 229–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qi T., Wu Y., Zeng J., Zhang F., Xue A., Jiang L., Zhu Z., Kemper K., Yengo L., Zheng Z. et al. (2018) Identifying gene targets for brain-related traits using transcriptomic and methylomic data from blood. Nat. Commun., 9, 2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhu Z., Zhang F., Hu H., Bakshi A., Robinson M.R., Powell J.E., Montgomery G.W., Goddard M.E., Wray N.R., Visscher P.M. et al. (2016) Integration of summary data from GWAS and eQTL studies predicts complex trait gene targets. Nat. Genet., 48, 481–487. [DOI] [PubMed] [Google Scholar]
- 26.GTEx Consortium (2017) Genetic effects on gene expression across human tissues. Nature, 550, 204–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.McRae A., Marioni R.E., Shah S., Yang J., Powell J.E., Harris S.E., Gibson J., Henders A.K., Bowdler L., Painter J.N. et al. (2017) Identification of 55,000 replicated DNA methylation QTL. bioRxiv, 10.1101/166710. [DOI] [PMC free article] [PubMed]
- 28.Vlaming R., Okbay A., Rietveld C.A., Johannesson M., Magnusson P.K.E., Uitterlinden A.G., Rooij F.J.A., Hofman A., Groenen P.J.F., Thurik A.R. et al. (2017) Meta-GWAS accuracy and power (MetaGAP) calculator shows that hiding heritability is partially due to imperfect genetic correlations across studies. PLoS Genet., 13, e1006495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Genomes Project Consortium, Auton A., Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A. et al. (2015) A global reference for human genetic variation. Nature, 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Haplotype Reference Consortium, McCarthy S., Das S., Kretzschmar W., Delaneau O., Wood A.R., Teumer A., Kang H.M., Fuchsberger C., Danecek P. et al. (2016) A reference panel of 64,976 haplotypes for genotype imputation. Nat. Genet., 48, 1279–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Abraham G. and Inouye M. (2014) Fast principal component analysis of large-scale genome-wide data. PloS One, 9, e93766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tuke M.A., Ruth K.S., Wood A.R., Beaumont R.N., Tyrrell J., Jones S.E., Yaghootkar H., Turner C.L.S., Donohoe M.E., Brooke A.M. et al. (2017) Phenotypes associated with female X chromosome aneuploidy in UK Biobank: an unselected, adult, population-based cohort. bioRxiV, 10.1101/177659.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Data