Molecular interactions underlying liquid-liquid phase separation of the FUS low complexity domain (original) (raw)

. Author manuscript; available in PMC: 2020 Jan 1.

Published in final edited form as: Nat Struct Mol Biol. 2019 Jul 1;26(7):637–648. doi: 10.1038/s41594-019-0250-x

Abstract

The low complexity domain of the RNA-binding protein FUS (FUS LC) mediates liquid-liquid phase separation (LLPS), but interactions between the repetitive SYGQ-rich sequence of FUS LC that stabilize the liquid phase are not known in detail. By combining NMR and Raman spectroscopy, mutagenesis, and molecular simulation, we demonstrate that heterogeneous interactions involving all residue types underlie LLPS of human FUS LC. We find no evidence that FUS LC adopts conformations with traditional secondary structure elements in the condensed phase, rather it maintains conformational heterogeneity. We show that hydrogen bonding, π/sp2 and hydrophobic interactions all contribute to stabilizing LLPS of FUS LC. In addition to contributions from tyrosine residues, we find that glutamine residues participate in contacts leading to LLPS of FUS LC. These results support a model in which FUS LC forms dynamic, multivalent interactions via multiple residue types and remains disordered in the densely packed liquid phase.

Introduction

Macromolecules are organized into organellar compartments that allow the cell to simultaneously carry out tightly-regulated, complex reactions. Besides organelles enclosed by lipid bilayers, proteins and nucleic acids can phase separate into membraneless liquid-like puncta such as the nucleolus, processing-bodies, and stress granules1–3. Given their roles in RNA processing, many membraneless organelles are enriched in proteins that contain both RNA-binding domains and phase-separation prone intrinsically disordered regions4.

The RNA-binding protein FUS (Fused in Sarcoma) is involved in RNA transcription, splicing, and transport. FUS undergoes in vitro and in cell liquid-liquid phase separation (LLPS) mediated by the low complexity domain (FUS LC) and RGG-rich domains5–7. FUS LC is enriched in serine, tyrosine, glycine, and glutamine residues and is sufficient for partitioning into liquid and gel phases in vitro and in cells5–8. Furthermore, self-association into aggregates has been implicated in neurodegenerative diseases amyotrophic lateral sclerosis and frontotemporal dementia9,10. FUS LC is required for cytoplasmic aggregation and works in concert with the RNA-binding and RGG domains to promote cytotoxicity11–15. In addition, chromosomal translocations fusing FUS LC to several DNA-binding domains cause several sarcomas and leukemias via aberrant transcriptional activation possibly by recruiting the C-terminal tail of RNA pol II into a phase separated body5,16–18. As a model protein for LLPS, the importance of FUS LC in FUS function and disease motivates investigation into the molecular interactions that govern its self-assembly.

Efforts have been made to structurally characterize FUS LC in the solid and liquid phases. In solid phases, portions of FUS LC have been shown to form amyloid fibrils (i.e. polymerizing into linear structures with ordered “cross-β” structure) that may be associated with protein function and disease19–21. Conversely, macroscopic condensed phase of FUS LC formed by LLPS remain predominantly disordered5. However, it remains unclear whether secondary structure found in FUS LC fibrils also contributes to stabilizing the liquid states of FUS LC. Similarly, other proteins such as Ddx4, FMRP and elastin-like polypeptides are predominantly disordered in their respective condensed phases22–24. Unlike FUS LC, the Ddx4 condensed phase is stabilized by electrostatic interactions between oppositely charged patches and π-interactions formed by sp2-hydridized groups, which we refer to here as π/sp223,25,26. Conversely, the interactions that drive phase separation of a model elastin-like polypeptide are likely primarily hydrophobic24. Because FUS LC and its paralogs have distinct polar and aromatic-rich sequences (i.e. yeast “prion-like”)4, it remains unclear which interactions – hydrophobic, electrostatic, and/or π/sp2 interactions – are the driving forces for phase separation of this class of domains.

Here, we probe the structural details of the condensed phase of FUS LC using a combination of NMR and Raman spectroscopy to characterize the interactions within the liquid phase. We demonstrate that the condensed phase is devoid of detectable static structures and that amorphous aggregates of FUS LC are structurally different from the liquid phase. We find that the condensed phase is densely packed with dynamic interactions involving all of the major residue types represented in the sequence. Using all-atom molecular simulations, we provide evidence that the interaction network that we observe by NMR is produced by a conformationally heterogeneous ensemble and that hydrogen bonding, hydrophobic and π/sp2 interactions are important for FUS LC LLPS.

Results

Identical structural features in FUS LC droplets and macroscopic condensed phases

We previously developed a method for collapsing spontaneously formed, protein-dense droplets formed through LLPS into a single macroscopic phase5. To test if this macroscopic phase is comparable to microscopic droplets, we conducted two-dimensional 1H-15N heteronuclear single quantum coherence (HSQC) experiments on a biphasic sample of 15N labeled FUS LC. This sample contains FUS LC droplets suspended in a dispersed phase of FUS LC. As shown for biphasic samples of an elastin-like polypeptide, the spectrum of biphasic FUS LC showed two sets of resonances of differing intensities24, corresponding to the dispersed (strong resonances) and condensed (weak, broad resonances) phases (Fig. 1A). The broader set of resonances were most apparent for certain residues (i.e. G80, Q153, S163) that have different chemical shifts in the dispersed and condensed phases5 (Fig. 1A, Supplementary Fig. 1A). Importantly, these broad resonances overlay with resonances from the macroscopic condensed phase of FUS LC, suggesting that they arise from the condensed phase. Hence, FUS LC in spontaneously formed droplets experiences a similar chemical environment to that in the macroscopic phase. To confirm that these broad resonances are not due to an artifact, the biphasic sample was centrifuged to separate dispersed and condensed phases and the spectrum of the supernatant was acquired. Since this spectrum did not contain the second, broad set of resonances present in the biphasic sample (Fig. 1A), we conclude that samples of a single macroscopic phase are a viable proxy for micron-sized droplets.

Figure 1. NMR characterization of condensed FUS LC.

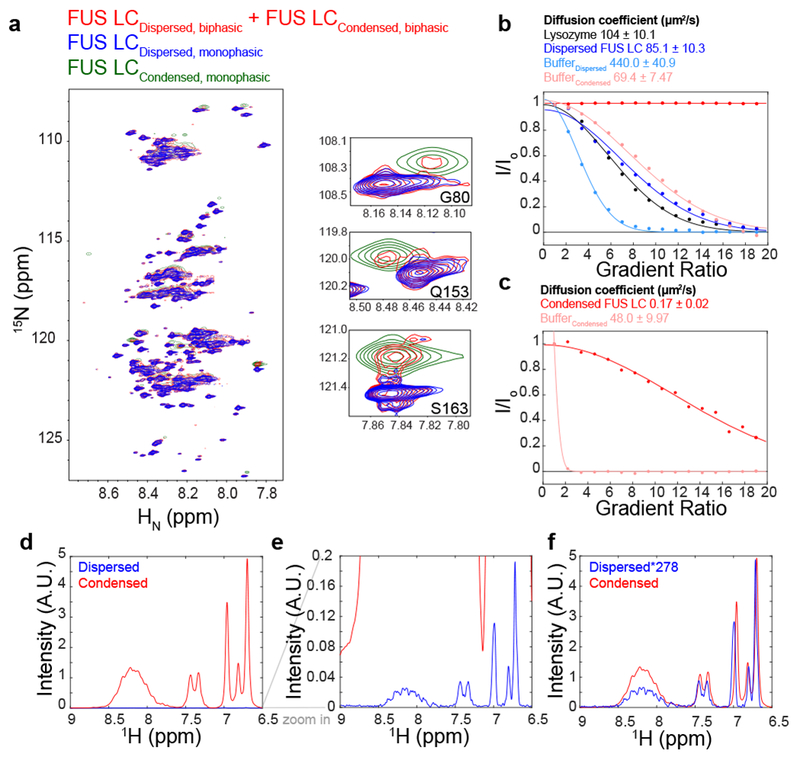
Figure 1.

A) 1H-15N heteronuclear quantum coherence spectrum of FUS LC in the phase separated state. A 1 mM biphasic sample (red), containing both dilute and condensed phases, generates two sets of peaks corresponding to the dilute phase (blue) and to a condensed macroscopic phase (green). B,C) PFG diffusion of the dispersed and condensed phase relative to lysozyme. B) was recorded with a diffusion time of 300 ms and gradient length of 1.2 ms, while C) was recorded with a diffusion time of 1.5 s and gradient length of 7 ms. Solid lines are best-fit solution to I/I0 = _Aedx_2 , where d is proportional to the diffusion coefficient, and the x axis is the gradient ratio. Mean and uncertainty in diffusion coefficient represents confidence interval equal to 1 s.d. in the one dataset shown. (D, E, F) Estimation of the concentration inside of the condensed phase using 1D 1H NMR spectroscopy. Unscaled intensities of condensed FUS LC were compared with 100 μM FUS LC (D,E). The relative intensity of the glutamine side chain residue NMR resonances in the condensed phase compared to a standard concentration (100 μM) dispersed phase FUS LC suggests a concentration of 27.8 mM = 477 mg/mL in the condensed phase (F).

Condensed FUS LC has slow diffusion and high protein density

Previous studies on liquid-like condensates suggest that motions within the condensed phase are slowed due to high protein concentration resulting in a densely packed network of interactions23. To characterize the diffusivity of FUS LC within the dispersed and macroscopic condensed phases, we used pulsed field gradient (PFG) NMR27,28. Diffusion of dispersed FUS LC is comparable to globular reference protein lysozyme in solution (Fig. 1B). Using the same diffusion time and gradient pulse length, FUS LC in the condensed phase does not significantly diffuse (red line, Fig. 1B). However, repeating the experiment with a longer diffusion time and gradient length, we observe that condensed FUS LC diffuses about 500 times slower than in the dispersed phase (Fig. 1C). The diffusion coefficient for condensed FUS LC (0.17 ± 0.02 μm2/s) is similar to the value we estimated for in vitro droplets using fluorescence recovery after photobleaching (FRAP) experiments, further suggesting that the macroscopic phase examined here retains the features of the spontaneous droplets extensively characterized by microscopy5. Interestingly, molecules corresponding to the buffer diffuse six times slower in the condensed phase compared to the dispersed phase, suggesting that diffusion is slowed due to the solvent volume excluded by the high protein density29.

To estimate the concentration in the condensed phase, we compared the 1H NMR signal intensity of dispersed FUS LC of known concentration to the signal intensity of the macroscopic condensed phase (Fig. 1D, E, F). To ensure that the signal intensity was not affected by water resonance pre-saturation and differences in the longitudinal spin relaxation times between the samples, experiments were conducted such that several fold changes in the values of pre-saturation power and repetition rates had no measurable effect on signal intensities. The minimal concentration inside of the macroscopic condensed phase was 477 mg/mL (27.8 mM) with an estimated water content of ~65% by volume, based on both integrated water signal intensity and calculation of the expected partial specific volume of protein using the measured protein concentration24. The FUS LC condensed phase concentration is similar to what has been reported for other RNA-binding proteins that undergo LLPS23,28. Furthermore, the observed concentration is greater than the overlap concentration, where random coil polymers come into contact, calculated to be 285 mg/mL (16.6 mM) based on the radius of hydration measured for dispersed FUS LC30. Taken together, the higher concentration in the condensed phase suggests that FUS LC forms a dynamic network of contacts, as expected for a polymer forming multivalent interactions at many sites along the chain.

No evidence for FUS LC structure in equilibrium with the disordered LLPS state

The NMR-visible conformations in condensed FUS LC are predominantly disordered based on backbone chemical shifts. However, it is possible that phase separated FUS LC takes on minor populations of structured states that are invisible to the previous NMR approach5. To directly probe for the interaction of the disordered state with amyloid-like fibrils or other large assemblies within the macroscopic condensed phase, we used dark-state exchange saturation transfer (DEST)31,32. This technique detects millisecond-second exchange timescale interactions between a low molecular weight major species (here, the disordered, NMR-visible major species) and large protofibrillar and fibrillar assemblies based on large differences in NMR transverse relaxation rates. Unlike the prominent DEST effects observed for the interaction of the disordered C-terminal domain of RNA polymerase II with TAF15 fibrils18, the width of the DEST profiles for all residues in condensed FUS LC can be explained by the measured transverse relaxation rate of the disordered state (Fig. 2A; Supplementary Fig. 1B). Therefore, the profiles show no evidence for transient interactions between the disordered, major state and potential fibril assemblies.

Figure 2. Lack of evidence for structured conformations in condensed phase FUS LC.

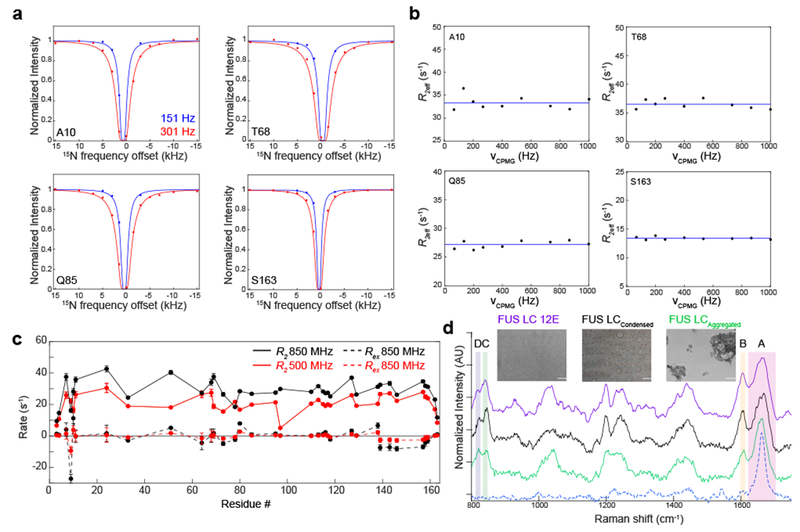
Figure 2.

A) Experimental dark-state exchange saturation transfer profiles (points) for condensed FUS LC as a function of the offset from the 15N carrier frequency and applied saturation field show no deviations from the profiles calculated for a single state (lines) with _R_2 values measured directly on the major, disordered state. Data are plotted as mean ± s.d. (approximately the size of the circles) propagated from best-fit parameter confidence interval equal to 1 s.d. in one representative data set out of two independent experiments. B) 15N CPMG profiles of condensed FUS LC are flat, providing no evidence for significant minor populations of structured states in μs-ms timescale conformational exchange with the primary, disordered state. The blue line is the average R _2_eff at each residue position. C) The fitted R ex component, derived from reduced spectral density mapping at two fields. Data are plotted as mean ± propagated best-fit parameter confidence interval equal to 1 s.d. in one representative data set of two independent experiments. D) The Raman spectral features of FUS LC 12E (dispersed control) and condensed droplets of FUS LC. Hen egg white lysozyme fibrils (dashed blue line) serve as a fibril control. The spectra are stacked for clarity. The amide I region and tyrosine side chain region are indicated by boxes A and B, respectively, while the tyrosine doublet modes are indicated by boxes C and D. Insets are brightfield micrographs of the samples used for vibrational spectroscopy. FUS LC 12E does not assemble into condensates as previously characterized and was used as a high concentration solution control 34. Scale bars are 10 μm.

To probe for the transient formation of structured, intermediate-sized species within the macroscopic condensed phase, we conducted 15N Carr Purcell Meiboom Gill (CPMG) relaxation dispersion experiments. These experiments probe exchange on the microsecond-millisecond timescale between states with different NMR chemical shifts (i.e. different structures). Residues undergoing conformational exchange on this timescale would produce sloping CPMG profiles, showing differences in the effective transverse relaxation rates, R 2eff, as a function of the CPMG field, νCPMG. However, relaxation dispersion profiles for individual residues and over the amide envelope do not show evidence of apparent conformational exchange with structured states within the condensed phase (Fig. 2B, Supplementary Fig. 1C). To probe for exchange with structured states that exists on a faster timescale, we performed spectral density analysis. These data indicate that the overall contribution of exchange to the transverse relaxation rate (R ex) observed for the major state itself is minimal (Fig. 2C; Supplementary Fig. 1D). In other words, we do not find evidence for transient populations of structured states in the condensed phase with exchange rates faster than can be probed by CPMG experiments. The lack of evidence for structured states within the condensed phase of FUS LC is consistent with the disordered nature of the polypeptide and the liquid-like nature of the assemblies.

Evidence for order in amorphous aggregates but not in liquid condensed FUS LC

We find no NMR evidence for significant conformational exchange occurring between the NMR-visible disordered state and structurally-ordered states within the condensed phase. However, it is possible that minor structured states exist but are not in exchange with the major state, making them potentially invisible to direct visualization by NMR due to slow molecular tumbling. To probe for oligomeric or fibrillar states that are present in the condensed phase using an orthogonal technique unaffected by molecular motion, we conducted coherent anti-Stokes Raman spectroscopy (CARS33). We probed the structural features across several material states – a dispersed FUS LC control, condensed FUS LC, aggregated FUS LC, and fibrillar hen egg white lysozyme (HEWL). As a dispersed, high concentration reference, we used a FUS LC variant containing 12 serine or threonine to glutamate mutations, FUS LC 12E, which is disordered but does not undergo LLPS or aggregation due to electrostatic repulsion between negatively-charged glutamate residues34. Representing solid states, we used amorphous aggregates formed by FUS LC after incubation (Fig. 2D). The CARS spectra of all three states showed prominent features at several regions corresponding to molecular vibrations of the side chain of tyrosine residues (830, 850 and 1603, 1616 cm−1) that we used for further analysis. We find that the intensity ratios of the tyrosine side chain peaks are similar for the dispersed and condensed phases but different from aggregated FUS LC (Fig. 2D). The intensity ratio of the tyrosine doublet located at 830 and 850 Raman shifts has been shown to be correlated with tyrosine ring interactions (Table 1)35. The intensity ratio (850 cm−1/830 cm−1) is nearly identical in the dispersed (FUS LC 12E) and condensed phases (1.32±0.08 and 1.25±0.07, respectively), but decreases to 0.96±0.09 for the aggregate, consistent with enhanced hydrophobic/π-π stacking and increased conformational restriction of the tyrosine rings36. Another tyrosine markers, two overlapping side chain peaks (1603 and 1616 cm−1), also follow the trend of becoming conformationally restricted in the aggregate form. Further, the width of the amide I peak, which reports on the carbonyl stretch of the peptide backbone, is narrower for FUS LC aggregates and HEWL fibrils, suggesting a narrower distribution of backbone vibrational modes. Conversely, the amide I peak is broadened for dispersed and condensed FUS LC, suggesting a broad distribution of vibrational modes and hence structural conformations, further suggesting that condensed FUS LC is predominantly disordered. Interestingly, the amide I peak for FUS LC aggregates is not as sharp as for HEWL fibrils which are almost crystalline, supporting the view that FUS LC aggregates contain regions that are disordered19. Overall, the CARS data demonstrate that the condensed phase is structurally similar to the disordered, dispersed phase but different from amorphous aggregates.

Table 1.

Raman intensity ratios for the amide I region and tyrosine doublet region.

Sample (mean ± s.d. derived from baseline noise rmsd in representative samples of at least 2 samples tested.) Tyrosine doublet ratio (850 cm−1/830 cm−1) Tyrosine side chain and amide I (1603 cm−1/1663 cm−1) ratio Amide I peak width(FWHM cm−1)
FUS LC 12E (dispersed control) 1.32 ± 0.08 0.52 ± 0.04 59.1 ± 1.7
FUS LCCondensed 1.25 ± 0.07 0.50 ± 0.03 54.2 ± 2.1
FUS LCAggregated 0.96 ± 0.09 0.36 ± 0.03 39.4 ± 0.5
HEWL amyloid fibril (crystalline control) NA NA 23.4 ± 0.8

Interactions within the liquid phase are promiscuous

Finding no evidence for structured conformations, we focused on characterizing the intermolecular contacts between disordered FUS LC molecules that stabilize the condensed phase. We performed doubly-edited nuclear Overhauser effect (NOE) experiments to directly probe interactions between amide hydrogens (HN) on one molecule and hydrogens attached to carbon atoms on another molecule. To this end, we made a macroscopic condensed FUS LC containing equimolar amounts of 15N12C-enriched and 13C14N enriched protein (Fig. 3A). A NOE mixing time of 250 ms was used; shorter or longer mixing times did not impact the number and relative intensity of the NOE cross peaks observed for tests of 2D planes (data not shown). Though spin diffusion may contribute to the observed NOE cross peaks and limit quantitative interpretation, the fast reorientational motions preserved within the condensed phase should limit its effect5. Due to the overlap of resonances within the 1H-13C-HSQC, interactions between different residue types but not specific residues are resolved. Two dimensional strips that correspond to serine 1H13Cα, tyrosine 1H13Cδ, glycine 1H13Cα, and glutamine 1H13Cγ are shown as examples (Fig. 3B). The NOEs arising from glutamine 1H15Nε side chain positions and glutamine 1H13Cγ are the strongest, likely due to favorable relaxation properties and high glutamine content. Aside from these intensity differences, the strips are all similar except glycine 1H13Cα which shows a slightly different NOE pattern and weakest signal intensity (Fig 3C–F). Further quantitative analysis of the relative intensities of the NOEs is precluded due to other factors contributing to the NOE cross peak intensity such as differential relaxation. Importantly, signals observed here do not arise from intramolecular NOEs due to natural isotopic abundance artifacts (i.e. ~1% 13C in the 15N12C protein fraction), as a control sample lacking 13C FUS LC showed minimal NOE signals (Supplementary Fig. 2A). To probe for interactions at other side-chain positions, we conducted 12C-filtered, 13C edited NOESY-HSQC experiments. Strips for serine 1H13Cβ, tyrosine 1H13Cδ, glycine 1H13Cα, and glutamine 1H13Cγ showed NOEs with a similar interaction network (Supplementary Fig. 2B). As opposed to a model where only particular residue types mediate contacts and generate specific NOEs, the data suggest that all the major residue types present within the sequence participate in interactions.

Figure 3. Non-specific intermolecular contacts between all residue types underlie FUS LC LLPS.

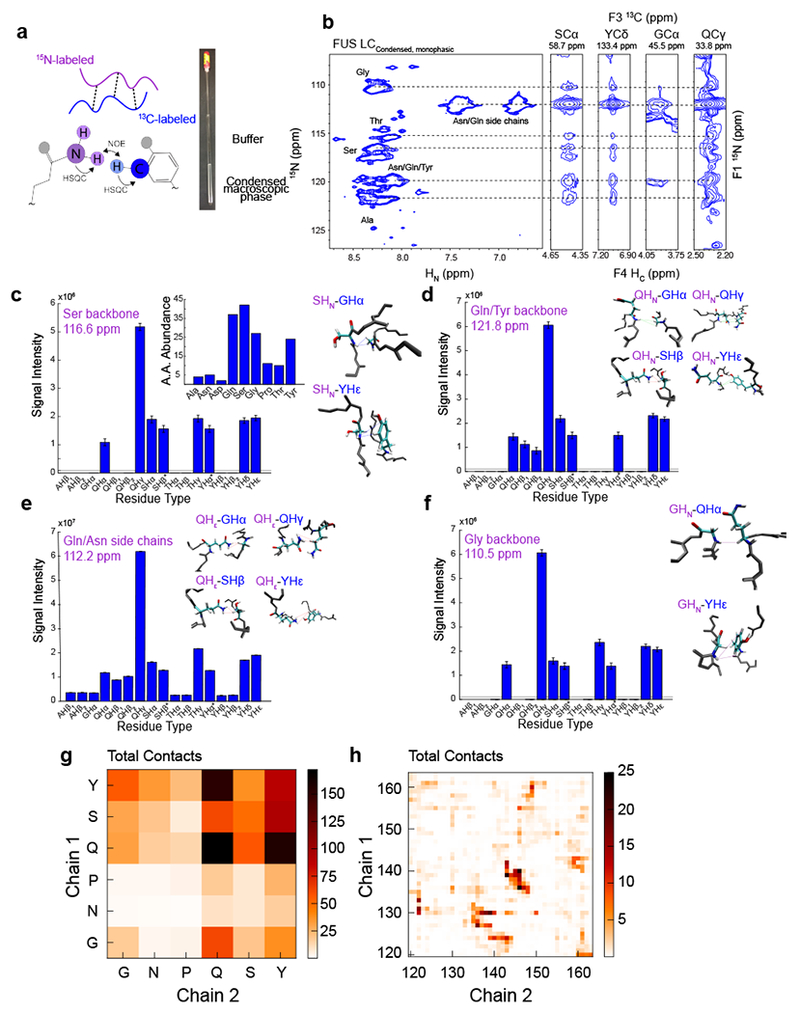
Figure 3.

A) Equimolar amounts of 15N-labeled and 13C-label FUS LC were used to create a condensed macroscopic phase in order to conduct HSQC-NOESY-HSQC experiments. B) NOE strips (left) from SCα, YCδ, GCα, and QCγ show NOEs from 15N regions (right) corresponding to the dashed lines. C, D, E, F) Quantification of NOEs from 15N labeled residues to 13C labeled residues from the serine and threonine backbone regions (C), glutamine/tyrosine backbone regions (D), glutamine/asparagine side-chain regions (E), and glycine backbone regions (F) with corresponding NOE snapshots from a two-chain simulation of FUS LC. The simulated structures were not calculated from the experimental data but are provided to show examples of the types of contacts that would generate the observed NOE profiles. Small contributions from intramolecular interactions were eliminated by subtracting the peak intensity from a control experiment on an equimolar 15N-labeled and natural abundance sample. Gray lines indicate the noise level of the two-dimensional plane. Data are plotted as peak height mean ± uncertainty equal to r.m.s.d. of baseline noise in one representative data set out of two experiments. G) Intermolecular interaction profiles calculated from a two-chain simulation of FUS120-163 binned by residue type. H) Intermolecular interaction profiles calculated from a two-chain simulation of FUS120-163 binned by residue position.

To provide a molecular picture for the interactions that give rise to these NOE profiles, we performed molecular simulations using modern forcefields tested for intrinsically disordered proteins and established advanced sampling approaches. We determined the equilibrium interaction configurations for a system of two chains of FUS120-163, a representative segment of the LC domain that enables effective sampling (Supplementary Fig. 3)28,34. These simulations demonstrate close approach of different residue types engaging in high probability interactions (Fig. 3C–F insets). Glutamine and tyrosine make large contributions to the intermolecular interactions in the simulations, consistent with the observed NOEs (Fig. 3G–H). To demonstrate that disordered contacts could give rise to the observed NOEs, we calculated the intermolecular NOE profile based on r−6 averaged distances and summed over residue type and found that profiles are qualitatively similar to the experimental NOEs (Supplementary Fig. 2C). The higher relative magnitude predicted for tyrosine may be due to enhanced interaction in simulation or the absence of dynamical information in the calculation. To test if the observed NOE profile could arise from a structured state, we predicted NOEs from the fibril structure of FUS 37-9719. We find that the overall predicted NOE profile and ΔCα-Cβ chemical shifts calculated from the fibril structure are different from condensed FUS LC, further suggesting that the primary contacts formed in the condensed phase are between disordered regions (Supplementary Fig. 2D,E). Taken together, these data suggest that the intermolecular interactions that stabilize the liquid phase are promiscuous.

Condensed phase interactions are not confined to a particular sequence region

Previously, we used paramagnetic relaxation enhancement (PRE) NMR experiments to show that transient intra- and intermolecular interactions of dispersed FUS LC are distributed throughout the entire domain34. To visualize the positional distribution of intermolecular interactions within the condensed phase, we prepared natural isotopic abundance FUS LC with paramagnetic spin-label (MTSL) or diamagnetic analog conjugated at single engineered cysteine sites (A16C, S86C, and S142C), added these in a 1:100 molar ratio to 15N-labeled FUS LC, and condensed the mixtures into macroscopic phases (Fig. 4A). Close approach of the paramagnetic labeled region to any 1H nuclei results in enhanced spin relaxation and resonance intensity attenuation (Supplementary Fig. 4). Enhancements in 1H relaxation rates, calculated by _R_2para- _R_2dia = Γ2, across all residues indicate that the interactions underlying LLPS are distributed along the polypeptide and not localized to a specific region (Fig. 4B). This is consistent with the repetitive sequence and disordered nature of FUS LC in both the dispersed and condensed phases.

Figure 4. Interactions in the condensed phase are dispersed throughout the entire sequence.

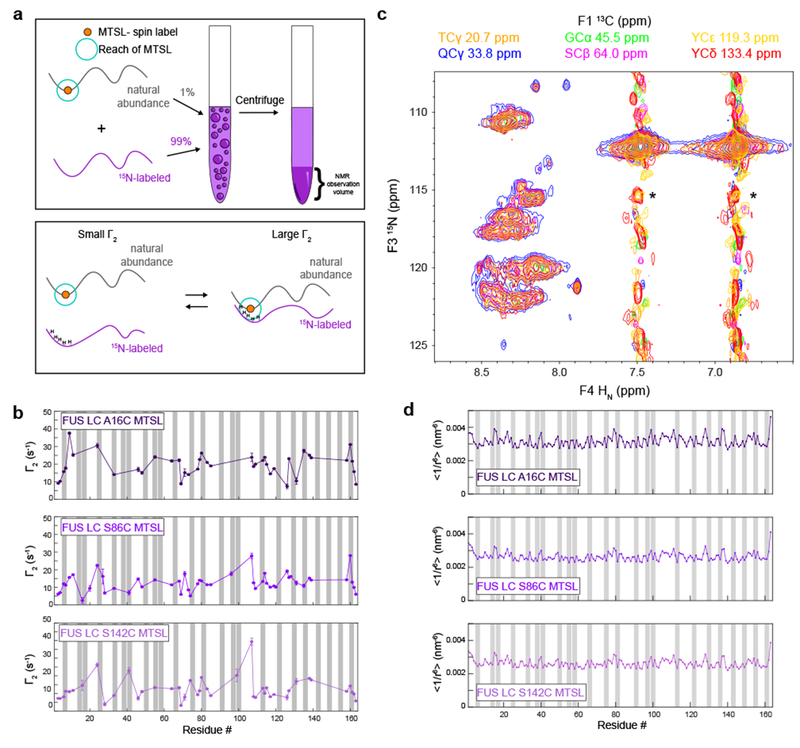
Figure 4.

A) Schematic of the experimental design for the paramagnetic relaxation enhancement experiments. B) Intermolecular paramagnetic relaxation enhancements of condensed 15N FUS LC in the presence of minor amounts of FUS LC labeled at positions A16C, S86C, and S142C. Gray bars correspond to all tyrosines residues. Data are plotted as mean ± best-fit parameter confidence interval equal to 1 s.d. in one data set. C) Observation of NOEs to all observable backbone positions (15N) from all sidechain 13C positions TCγ, QCγ, SCβ, GCα, YCε, and YCδ in 13C-HSQC-NOESY-15N-HSQC planes. Spectral intensity in all planes contoured to the same level. Asterisks indicate incomplete filtering of unlabeled (14N) positions in 13C14N component of sample. D) Predicted intermolecular PRE profiles calculated from FUS LC slab simulations at 300K.

While PRE experiments were useful in determining the distribution of the interactions in the condensed phase, we are not able to determine if the spin label alters the extent of partitioning into the liquid phase of each labeled cysteine variant or has non-specific interactions with the protein, which may explain differences in the 1H transverse relaxation rates observed for the diamagnetic samples labeled at different positions (Supplementary Fig. 4A). To further test if the intermolecular interactions are distributed across the sequence, we performed (1H)13C HSQC-NOESY-1H15N HSQC experiments, which give sequence-specific information. We observe NOEs to each resolved backbone amide position arising from each carbon-attached 1H position (e.g. glutamine Cγ, glycine Cα, tyrosine Cδ) (Fig. 4C). To the limit of the resolution of the spectra, these data indicate that all positions within the FUS LC sequence are interacting with all residue types.

To help determine if the local variations in the observed PREs arise due to slight regional interaction preferences, we performed coarse grained molecular dynamics simulations of condensed FUS LC. Simulated PRE profiles, generated by calculating the r−6 averaged distance of each residue from the spin-labeled positions at A16, S86, and S142, show small local fluctuations (Fig. 4D). The magnitude of interaction is higher for A16C position in both the experimental and simulated datasets, indicating that the N-terminus of FUS LC may interact with other positions with higher probability than the C-terminus. However, the simulated PRE profiles are more uniform than the experimental data, suggesting that the true system may favor interactions between certain regions more than others due to specific atomic interactions not captured by the coarse-grained model. In the future, it will be useful to simulate a condensed phase with an all-atom model to further understand the role of specific atomistic interactions governing the observed experimental behavior, but such simulations are currently infeasible with available hardware resources. Altogether, the intermolecular interactions that contribute to LLPS do not appear uniquely registered nor position specific.

Transient hydrogen bonding interactions and glutamines play a role in LLPS

Because our data directly suggest a network of interactions that involves all residue types, we sought to understand the molecular forces stabilizing these interactions. FUS LC is particularly enriched in polar amino acids containing hydrogen bonding acceptors and donors (Supplementary Fig. 5A). Because glutamine, tyrosine, and serine sidechain resonances showed the largest NOEs, we reasoned that these residues may be important for stabilizing the liquid phase separated state of FUS LC through transient hydrogen bonding interactions. To test this hypothesis, we calculated the average number of hydrogen bonds from an all-atom two-chain simulation of FUS120-163 and found that glutamine residues are more prone to form intermolecular hydrogen bonds than tyrosine or serine (Fig. 5A, B; Supplementary Fig. 5B). Intramolecular hydrogen bonds were observed in single chain simulations, displaying a similar hydrogen bonding pattern (Supplementary Fig. 5C). Interestingly, regions that contain glycine are more prone to forming backbone hydrogen bonds because of the exposed backbone (Fig. 5A). On average, glutamine-glutamine interchain hydrogen bonds were abundant, suggesting that glutamine-glutamine interactions contribute to FUS LC LLPS (Fig. 5C; Supplementary Fig. 5B, E, F), consistent with large experimental NOEs observed from glutamine side-chain positions (Figure 3B).

Figure 5. Hydrogen bonding interactions and glutamines contribute to stabilizing FUS LC LLPS.

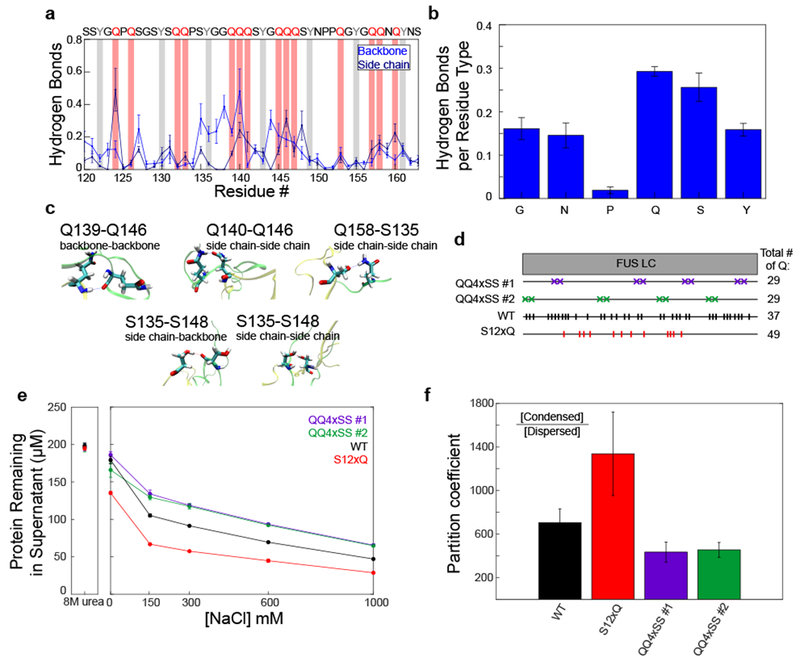
Figure 5.

A) Average number of hydrogen bonds from the backbone and side chain for each residue calculated from a two-chain simulation of FUS120-163. Hydrogen bonds between backbone/side chain and all atoms of the other molecules are considered. Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. Tyrosine and glutamine residues are highlighted with gray and red bars, respectively. B) Average number of intermolecular hydrogen bonds formed by each residue type. Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. C) Example of hydrogen-bonding interactions from the two-chain simulation of FUS120-163. D) Schematic of different FUS LC variants used. QQ4SS #1 and QQ4SS #2 are variants in which eight glutamine residues have been mutated to serine. S12xQ is a variant in which twelve serines have been mutated to glutamine. E) Phase separation assay and F) quantification of the partition coefficient of the glutamine and serine variants in 1M NaCl at 4°C. Data are plotted as mean ± s.d. of n=3 technical replicates.

To experimentally evaluate the importance of glutamine to FUS LC LLPS, we mutated FUS LC to increase or decrease glutamine content (SITable 1). We created two variants where eight glutamine residues were mutated to serine, which lacks side chain hydrogen bonding acceptor sites and contains fewer hydrogen bond donor sites than glutamine (QQ4×SS1, QQ4×SS2; Fig. 5D). As a comparison, we created a variant in which twelve serine residues (not adjacent to tyrosine) were mutated to glutamine (S12×Q). To test the hypothesis that glutamines contribute to stabilizing FUS LC LLPS, we assayed the extent of phase separation of the variants by measuring the remaining FUS LC concentration in the dispersed phase. Reduced glutamine content (QQ4×SS1, QQ4×SS2) resulted in higher concentration of protein remaining in the supernatant compared to WT, suggesting that removal of glutamine reduced phase separation (Fig. 5D, E, F). Increased glutamine content (S12×Q) decreased protein concentration in the supernatant compared to the WT, suggesting that increasing glutamine content promotes phase separation. To quantify differences in partition coefficients for the variants, we induced phase separation at similar conditions resulting in larger volumes of condensed phase: 300 μM FUS LC in the presence of 1 M NaCl and at 4°C. Relative to that of WT, the partition coefficient of S12×Q variant showed increased partitioning into the condensed phase, while the QQ4×SS variants showed decreased partitioning (Fig. 5F). Thus, glutamine contributes to FUS LC LLPS potentially through hydrogen bonding interactions via its side chain and backbone.

Hydrophobic interactions and π/sp2 contacts play a role in phase separation

Hydrophobic interactions play a role in stabilizing the liquid phase of elastin-like peptides and yeast polyA-binding protein Pab124,37. The contribution of hydrophobic interactions is also invoked to explain the ability of hexanediols, aliphatic alcohols, to dissolve the FG-repeats of the nuclear pore, stress granules and in vitro phase separated protein assemblies38,39. Like other phase separating domains from TDP-43, hnRNPA2 and elastin, FUS LC LLPS is enhanced by increased sodium chloride concentration24,28,40, suggesting that FUS LC “salts out” of solution, consistent with hydrophobic contribution to the interactions5. To further characterize the contribution of hydrophobic interactions, we quantified the number and location of intermolecular hydrophobic contacts formed in the all-atom two-chain simulation of FUS120-163. Tyrosine, making up 15% of FUS LC, is the most hydrophobic residue within the sequence and is important for LLPS of FUS17,41,42. From simulations, we find that the majority of inter- and intramolecular hydrophobic contacts within the sequence involve tyrosine (Fig. 6A–C; Supplementary Fig. 5D–F). Interestingly, we find that tyrosine residues have the tendency to form intermolecular hydrophobic contacts both with other tyrosines and with glutamine (Fig. 6C; Supplementary Fig. 5D–F), consistent with total contact analysis where tyrosine and glutamine have a high propensity for participating in contacts (Fig. 3G, H).

Figure 6. Hydrophobic and π/sp2 contacts contribute to FUS LC LLPS.

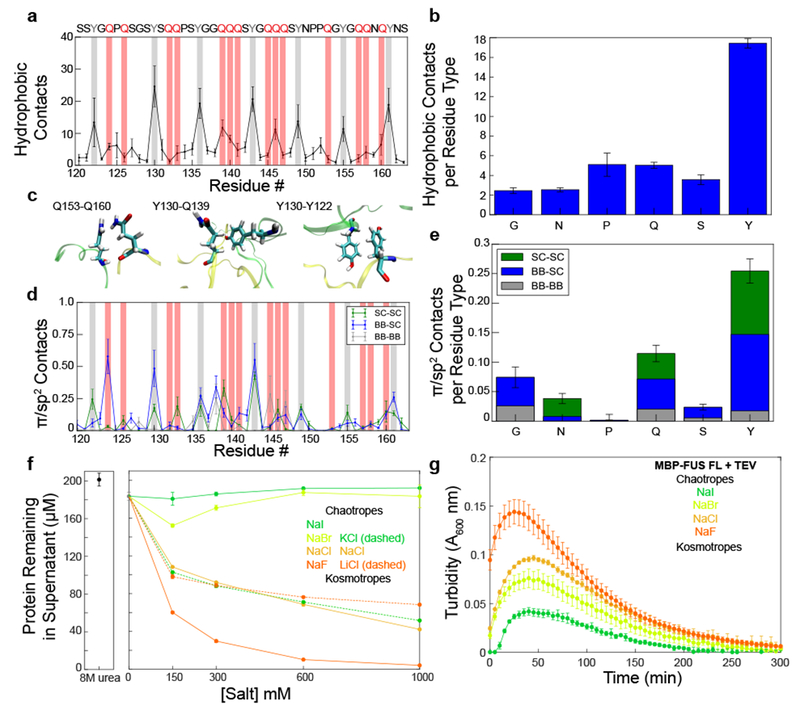
Figure 6.

A) Average number of hydrophobic contacts for any two heavy hydrophobic atoms within 6 Å of each other from a two-chain simulation of FUS120-163. Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. B) Average number of intermolecular hydrophobic contacts formed by each residue type. Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. C) Example of hydrophobic interactions from the two-chain simulation of FUS120-163. D) Average number of π/sp2 contacts from the backbone and side chain for each residue calculated from a two-chain simulation of FUS120-163 Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. Tyrosine and glutamine residues are highlighted with gray and red bars, respectively. E) Average number of π/sp2 contacts formed by each residue type. Data are plotted as mean ± s.e.m of n=5 equal divisions of the total data set. F,G) The Hofmeister salt series changes the amount of protein left in the dispersed phase according to their chaotropic or kosmotropic qualities for both FUS LC (F) and full-length FUS (G). Data are plotted as mean ± s.d. of n=3 technical replicates.

We note that both tyrosine and glutamine side chains also include sp2-hybridized groups. Several studies have suggested that π-interactions involving sp2 groups, including but not limited to aromatic π-π stacking, play a role in LLPS of various protein systems25,43. Thus, π-interactions between the tyrosine side chain and other sp2-hybridized groups may be included in the calculation of hydrophobic contacts. To study the contribution of such π/sp2 contacts to FUS phase separation, we analyzed the two-chain simulation of FUS120-163 to determine which residues are involved in planar π/sp2 interactions using the definition presented by Forman-Kay and colleagues 43. Indeed, both tyrosine and glutamine residues participate in π/sp2 interactions with contributions from backbone peptide bonds and side chains (Fig 6D,E; Supplementary Fig. 5E,F). Following closer examination of the sp2-hybridized atoms of each amino acid, we include the caveat that hydrogen bonds and hydrophobic contacts may be formed by the same atoms involved in π/sp2 interactions43. Furthermore, there may be some degree of cooperativity between the different interaction modes, since both glutamine and tyrosine side chains are capable of all three interaction modes. We also note that the fraction of each amino acid forming intermolecular π/sp2 contacts is in qualitative agreement with results from Vernon et al. (Fig 6E). Our calculations produce quantitatively smaller values because we analyzed intermolecular contacts only and used a disordered domain as opposed to the folded proteins analyzed in the previous bioinformatics study.

To experimentally evaluate the contribution of hydrophobic interactions to FUS LC LLPS, we utilized salts from the Hofmeister series which have been shown to stabilize or destabilize hydrophobic interactions based on their differential ability to remove water from protein surfaces44–46. We measured the extent of phase separation of FUS LC in varying concentrations of monovalent Hofmeister cations and anions. The Hofmeister cations had little effect on LLPS of FUS LC, likely due to their similar interactions with water (Fig. 6F)47; however, phase separation of FUS LC in the presence of the monovalent anions of the same ionic strength follows the expected Hofmeister trend. Relative to sodium chloride, phase separation was nearly completely abrogated in the chaotropic salts sodium iodide and bromide, while phase separation in the kosmotropic salt sodium fluoride was enhanced. The effect on phase separation was not due to a change in FUS LC secondary structure of the dispersed phase (Supplementary Fig. 6). Interestingly, the extent of phase separation of full length FUS once liberated from a maltose binding protein tag by TEV protease also follows the Hofmeister trend, suggesting that the hydrophobic contributions to phase separation are also important in full-length FUS, which contains the RNA- binding and RGG sequence motif domains in addition to the LC (Fig. 6G). Therefore, hydrophobic interactions, particularly from tyrosine residues, contribute to and help stabilize FUS LLPS. We wanted to further test which residues contribute to hydrophobic interactions; however, it is difficult to use mutagenesis to alter only the hydrophobic interactions without disrupting the other contributions to phase separation. We did attempt to evaluate the effect of increasing hydrophobicity by changing all twenty-four FUS LC tyrosines to phenylalanine. However, this resulted in a dramatically more aggregation-prone FUS LC and full-length FUS, consistent with enhanced self-assembly, whose phase separation could not be quantified (Supplementary Fig. 7).

Discussion

Together, these data demonstrate that FUS LC LLPS is governed by non-specific hydrogen bonding, hydrophobic and π/sp2 interactions that involve all of the residue types within the sequence. To illustrate the interactions that stabilize the liquid phase of FUS LC, we used all-atom molecular simulations to generate configurational ensembles for intermolecular contacts between a subregion of FUS LC. The heterogeneity of interactions is highlighted by the array of conformations that each residue type can adopt while interacting with its partner (Fig. 7). The combination of spectroscopy and molecular simulation approaches provides fuller atomic details of the contacts contributing to FUS LC LLPS than previously available.

Figure 7. Interactions between FUS LC molecules that stabilize LLPS are structurally heterogeneous.

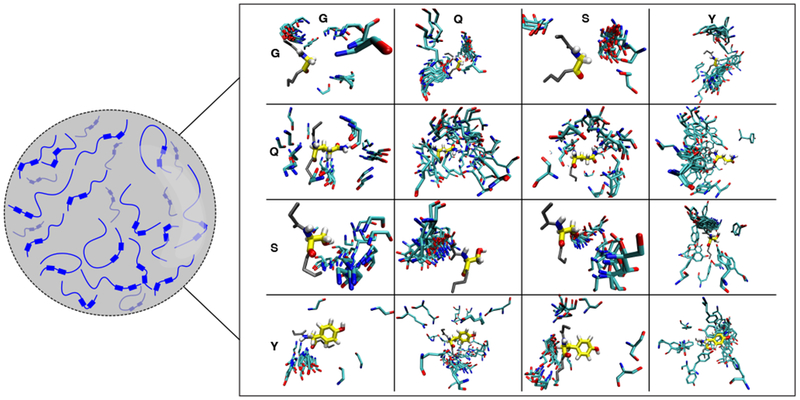
Figure 7.

FUS LC is predominately disordered in the condensed phase. The interactions that stabilize the condensed phase involve all of the residue types that are represented in the sequence. Due to the disordered nature of FUS LC, there is not one structural ensemble that fully represents the interactions that stabilize the condensed phase. Here we provide a model for the dynamic and structurally heterogeneous intermolecular contacts that may stabilize FUS LC phase separation, based on snapshots of intermolecular contacts from two-chain simulations. Example configurations derived from the structural ensemble are aligned to the residue named along the vertical axis (yellow) and the diversity of contact poses with the residue named along the horizontal axis (cyan) are displayed.

Though several studies have solved the structure of FUS LC in β-sheet structures19–21, our multiple spectroscopic approaches do not find evidence that structured states are present in significant quantities within the liquid phase separated state. These data are consistent with our previous findings that FUS LC in the liquid phase appears predominantly disordered5. As in studies probing structural details of other proteins within liquid phases, retention of disorder and non-specific intermolecular interactions are a common theme22–24. However, the conformations of FUS LC within in vivo granules remain to be visualized directly and could contain β-sheet structure. Future work elucidating the conversion of the “fuzzy” interactions that govern the liquid phase to more persistent interactions that stabilize more static aggregate states is needed6,7,48.

Several different types of interactions including electrostatic and hydrophobic interactions are hypothesized to be important for FUS LLPS. Studies have previously shown that removal of tyrosine disrupts LLPS of FUS, which was attributed to disruption of π-interactions41. Our study suggests that hydrogen bonding, hydrophobic, and π/sp2 contacts from many residue types contribute to stabilizing the FUS LC LLPS (Fig. 5,6). Using all-atom simulations and mutagenesis, we found that glutamine and tyrosine significantly contribute to the transient hydrogen bonds formed in the condensed phase. By analyzing contacts formed in simulations and testing salts that alter the hydrophobic effect, we provide evidence that hydrophobicity contributes to FUS LC LLPS. Finally, substitution of all twenty-four tyrosines in FUS LC to phenylalanine produces a protein that is more aggregation-prone, suggesting that increased hydrophobicity and π-interactions and removal of side chain hydrogen bonds pushes the protein further towards forming a solid (Supplementary Fig. 7). Thus, we hypothesize that the protein sequence composition must be balanced to produce liquid-like behavior.

In addition to tyrosine, we find that other residue types contribute to LLPS. Previously, glutamine has been shown to promote hardening of FUS droplets, suggesting that aggregation may stem from strengthening interactions between glutamine residues42. Indeed, many proteins that are associated with LLPS and aggregation contain an abundance of glutamine residues such as Sup35, huntingtin, and Whi349–51. We find that glutamine residues are major contributors to FUS LC intermolecular contacts, have a high propensity for forming hydrogen bond interactions, and modulate partitioning. Interestingly, increased glutamine content in huntingtin promotes phase separation and aggregation, suggesting that glutamine may be an important residue for LLPS due to its propensity for self-association 50,52.

While this study was limited to investigating phase separation of the low complexity domain of FUS, future biophysical studies probing the structural details of interactions outside of the low complexity domain and in a cellular context are needed to fully understand how FUS-containing membraneless organelles function.

Methods

Protein Expression and Purification

Expression and insoluble purification of untagged human FUS LC and his-tagged human FUS LC was carried out as previously reported 5,34. Expression plasmids used in this study are available from AddGene (https://www.addgene.org/Nicolas_Fawzi/). FUS LC variants were purified similarly to wild-type. Isotopically labeled protein was generated by growing E. coli in M9 media (27 mM NaCl, 22 mM KH2PO4, 51 mM Na2HPO4·7H2O, 1 mM MgSO4, 112 μM CaCl2·2H2O, 40 μM Biotin, 38 μM Thiamine) supplemented with 15N-ammonium chloride or 13C-glucose as the sole nitrogen and carbon sources, respectively.

For PRE measurements, FUS LC containing engineered cysteine mutations at A16, S86, and S142 were conjugated to either paramagnetic (1-Oxyl-2,2,5,5-tetramethyl-∆3-pyrroline-3-methyl) or diamagnetic (control) (1-Acetoxy-2,2,5,5-tetramethyl-δ−3-pyrroline-3-methyl) MTSL compounds (Toronto Research Chemicals).

NMR Sample Preparation and NMR Spectroscopy

NMR experiments were recorded on a Bruker Avance 850 MHz 1H Larmor frequency spectrometer with HCN TCl z-gradient cryoprobes. All experiments were carried out at 25°C in 50 mM MES, 150 mM NaCl pH 5.5. All experiments were processed using NMRPipe software package 53 and then visualized using NMRFAM-Sparky 54.

The condensed FUS LC sample was generated as previously described (i.e. with untagged FUS LC purified via anion exchange and size exclusion chromatography) except the sample was centrifuged into a 3 mm NMR tube at 3310 rpm for 10 min at a time at 0-2°C5.

A biphasic sample was generated by diluting FUS LC to 1 mM in 50 mM MES 150 mM NaCl pH 3.6 in a 3mm NMR tube. After the experiment, the sample was then removed from tube, centrifuged at 13000g for 10 min, and the supernatant placed back into the NMR tube to acquire data on dispersed FUS LC.

1H-15N HSQCs for the biphasic and dispersed sample were acquired with 600 and 3072 total points in the indirect 15N and direct 1H dimensions with acquisition times of 174 and 172 ms, and sweep widths of 20 ppm and 10.5 ppm centered at 4.695 ppm and 117 ppm, respectively.

Pulsed field gradient NMR diffusion experiments on condensed FUS LC, 100 μM FUS LC (dispersed), and 60 μM lysozyme (reference) were performed as 2D experiments using the standard Bruker ledbpgppr2s pulse sequence with a gradient strength from 5-98%. The experiment was conducted optimized for dispersed and viscous condensed phases, with diffusion time and gradient time of 300 ms and 1.2 ms or 1500 ms and 7 ms, respectively. Data were analyzed by integrating resonances corresponding to regions including asparagine/glutamine and tyrosine side chains in FUS LC (regions from 6.945-7.065 ppm for dispersed FUS LC and 6.673-6.786 for condensed FUS LC) and the aliphatic region (1.547-1.602 ppm) for lysozyme. Data was analyzed for buffer signals from dispersed and condensed FUS LC for regions 1.959-2.085 and 3.22-3.30 ppm, respectively.

The concentration in the condensed phase was estimated using 1D spectra (zgpr) with 2048 total points, ultra-weak presaturation power of 69 dB weaker than the calibrated hard pulse, and relaxation delay of 12 s. The signal intensity of the asparagine/glutamine and tyrosine side chains of 100 μM FUS LC was compared with condensed FUS LC. The water content of the condensed phase was calculated using a partial specific volume of 0.73 cm3/g for FUS LC or by comparing the integrated intensity of the water peak between the 100 μM FUS LC and condensed FUS LC samples.

Dark-state exchange saturation transfer (DEST) experiments were used to interrogate ms-s conformational exchange of FUS LC in the condensed phase and were acquired with 200 and 4096 total points for each interleaved experiment in the indirect 15N and direct 1H dimensions with sweep widths of 20 and 10.5 ppm centered at 117 and 4.693 ppm, respectively. 900 ms 15N radiofrequency (RF) continuous wave pulses were applied at powers of either 151 or 301 Hz and 15N carrier frequency offsets between 15 and −15 kHz (for 301 Hz: 15, 10, 7, 5, 3, 1.5, −1.5, −3, −5, −7, −10, −15 kHz offsets, and for 151 Hz: 5, 3, 1.5, −3 kHz offsets) and reference experiments which had no applied RF field. To test the hypothesis that observed DEST profiles could be explained by the single state, the DEST data were analyzed using DESTfit31 using the values of the transverse relaxation rate _R_2 at each position and a two-state model assuming Δ_R_2 equal to zero (i.e. no exchange to second state) for all residues.

15N Carr Purcell Meiboom Gill (CPMG) relaxation dispersion experiments55 were used to interrogate μs-ms timescale conformational exchange of FUS LC in the condensed phase and were acquired with 128 and 3072 total points in the indirect 15N and direct 1H dimensions with acquisition times of 22.5 and 157 ms, and sweep widths of 33 ppm and 11.5 ppm centered at 4.7 ppm and 117 ppm, respectively. Each 15N CPMG relaxation dispersion experiment comprises of 10 interleaved 15N _B_1 fields: 0, 67, 133, 200, 267, 400, 533, 733, 866, and 1000 Hz, with a total CPMG relaxation delay of 60 ms.

Motions of the backbone of condensed FUS LC were measured at both 850 MHz and 500 MHz 1H frequencies using standard pulse sequences (hsqct1etf3gpsitc3d, hsqct2etf3gpsitc3d, hsqcnoef3gpsi). Experiments were recorded where the sample was placed within a 5mm tube containing 100% D2O due to trouble with locking on 10% D2O. 15N _R_2 experiments at 850 MHz were recorded with 256 and 2048 total points with acquisition times of 74 ms and 115 ms and a sweep width of 20 and 10.5 ppm centered at 117 and 4.7 ppm in the indirect 15N and direct 1H dimensions, respectively. 15N _R_2 experiments at 500 MHz were recorded with 256 and 2048 total points with acquisition times of 126 ms and 263 ms with a sweep width of 20 and 10.5 ppm centered at 117 and 4.7 ppm in the indirect 15N and direct 1H dimensions, respectively. Each 15N _R_2 is made up of six interleaved relaxation delays with an interscan delay of 2.5 s, a CPMG field of 556 Hz, and total R2 relaxation CPMG loop-lengths of 16.5, 264.4, 33.1, 132.2, 66.1, 198.3 ms at 1H 850 MHz frequency and 16.5, 264.4, 33.1, 132.2, 66.1, and 231.4 ms at 1H 500 MHz frequency.15N _R_1 experiments at 850 MHz were recorded with 256 and 3072 total points with acquisition times of 74 ms and 115 ms and a sweep width of 20 and 10.5 ppm centered at 117 and 4.7 ppm in the indirect 15N and direct 1H dimensions, respectively. 15N _R_1 experiments at 500 MHz were recorded with 256 and 3072 total points with acquisition times of 126 ms and 178 ms and a sweep width of 20 and 10.5 ppm centered at 117 and 4.7 ppm. Each 15N _R_1 experiment is made up of six interleaved 15N _R_1 relaxation delays of 5, 1000, 100, 800, 500, and 300 ms. (1H) 15N heteronuclear NOE experiments are made up of interleaved sequences with and without proton saturation with a recycle delay of 5 s. (1H) 15N hetNOE experiments were recorded with 256 and 4096 total points with a sweep width of 20 and 10.5 ppm centered at 117 and 4.7 ppm in the indirect 15N and direct 1H dimensions, respectively.

Intermolecular NOE-based experiments were recorded on condensed FUS LC containing a 1:1 mixture of 15N/12C and 14N/13C FUS LC or a 1:1 mixture of 15N/12C and 14N/12C FUS LC as a control. 3D 13C/15N edited 1H-15N-HSQC-NOESY-1H-13C-HSQC (based on 4D hsqcnoesyhsqcncgp4d but omitting incrementing the indirect 1H dimension) experiments were recorded with a mixing time of 250 ms and with 58, 2, 58 and 2048 total points with sweep widths of 20, 10.5, 56, and 10.5 ppm centered at 117, 4.7, 42, and 4.7 ppm for aliphatic regions in the F3 dimension or sweep widths of 20, 10.5, 26, and 10.5 ppm centered at 17, 4.7, 123, and 4.7 ppm for aromatic regions in the F3 dimension, for indirect 15N, indirect 1H, indirect 13C, and direct 1H dimensions, respectively. 3D 13C/15N edited 1H-13C-HSQC-NOESY-1H-15N-HSQC (based on hsqcnoesyhsqccngp4d but omitting incrementing the indirect 1H dimension) experiments were recorded with a mixing time of 250 ms and with 58, 2, 58 and 2048 total points with sweep widths of 56, 10.5, 20, and 10.5 ppm centered at 42, 4.7, 117, and 4.7 ppm for aliphatic regions in the F1 dimension or sweep widths of 150, 10.5, 20, and 10.5 ppm centered at 75, 4.7, 117, and 4.7 ppm for aromatic regions in the F1 dimension, for indirect 13C, indirect 1H, indirect 15N, and direct 1H dimensions, respectively. 3D 13C,15N-filtered/edited NOESY-1H-13C-HSQC (noesyhsqcgpwgx13d) experiments were recorded with a mixing time of 100 ms and with 128, 60, and 3072 total points with sweep widths of 9, 56, and 10.5 ppm centered at 4.7, 42, and 4.7 ppm for aliphatic regions in the F2 dimension or sweep widths of 9, 56, and 10.5 ppm centered at 4.7, 110, and 4.7 ppm for aromatic regions in the F2 dimension, for the indirect 1H, indirect 13C, and direct 1H dimensions, respectively.

Intermolecular PREs were recorded on condensates containing 100:1 15N FUS LC and natural abundance MTSL or Ac-MTSL labeled FUS LC. Values of the backbone amide proton transverse relaxation rate constant, 1HN _R_2, were measured as described56 at 850 MHz for paramagnetic and diamagnetic samples, with 256 and 3072 total points and sweep widths of 20 and 10.5 ppm centered at 117 and 4.7 ppm, for the indirect 15N and direct 1H dimensions, respectively. Each 1HN _R_2 experiment is made up of six 1HN _R_2 relaxation delays of 0.2, 40.2, 10.2, 16.2, 20.2, and 4.2 ms. PREs (Γ2) were obtained from the difference in 1H _R_2 values for the paramagnetic and diamagnetic samples.

Coherent anti-Stoke Raman microspectroscopy

Phase separated FUS LC samples were created by diluting 1.2 mM FUS LC stored in 20 mM CAPS pH 11 to 250 μM in 20 mM MES 150 mM NaCl pH 5.5. For the B-CARS measurement 2 μL samples were sandwiched between two glass cover slips in a narrow channel (~2 mm wide) between two double-sided tape strips. Aggregated FUS LC sample was created by dialyzing 1.2 mM FUS LC (20 mM CAPS pH 11) with 8 M guanidine hydrochloride solution (Sigma Aldrich) and exchanging to 20 mM MES 150 mM NaCl buffer, For the measurements for amorphous aggregates only, ~1 μL samples were spread on glass coverslips and left to dry over 1 hour.

For BCARS measurements an analogous home-built system was described in detail previously33. Light from a Millenia green cw laser (Spectra-Physics, Newport Corporation) pumps Tsunami Ti:Sapphire oscillator (Spectra-Physics, Newport Corporation) that generates picosecond pulse train at 800nm (19 nJ/pulse, 80 MHz). This oscillator pulse is then split into two paths by a polarization beam splitter (Thorlabs): one for generating a broadband continuum in a photonic crystal fiber (FemtoWHITE, NKT Photonics) for the Stokes pulse (850-1200 nm), and the other to pass through an acousto-optical modulator connected to CCD camera to produce 1st order beam of a narrowband probe pulse (_λ_c = 800 nm) during the measurement. The continuum pulse is collimated with a parabolic mirror (MPD00M9; ThorLabs) and the two beams are combined by a long-pass filter (FF01-834/LP; Semrock) before injection into the inverted microscope (Eclipse Ti, Nicon). The excitation objective (60×, 1.2 NA, UplanApo; Olympus) tightly focuses both beams into the sample plane and the sample is raster scanned with a computerized x,y,z positioning system (Nano-View Series, Mad City ). The BCARS signal is collected in forward direction and collimated with another objective (10×, 0.25 NA, Newport), spectrally isolated from the excitation light beams by a short-pass filter (FES775, Thorlabs). Timing between the Stokes and probe pulses is controlled by a delay stage in the Stokes beam path such that BCARS intensity is maximized. The B-CARS signal is directed into a spectrograph (Shamrock SR303i; 600 lines mm−1, 300 nm blaze, Andor) that dispersed the light onto a cooled (−70°C) deep depletion CCD (iVac 316, Andor). The spectral resolution of the B-CARS instrument, as determined from HeNe spectrum measurement is 13 cm−1 ± 1 cm−1 and the calibration uncertainty is 11.8 cm−1 ± 1 cm−1. Measurement acquisition and synchronization control is performed by custom software in LabView 2013 (National Instruments).

Hyperspectral data from B-CARS measurements were analyzed with custom routines in IgorPro (v.6.37, WaveMetrics) and MATLAB (R2016a, MathWorks). Since CARS spectrum represents the sum of a resonant and a nonresonant components, a time-domain Kramers-Kronig transform algorithm57 was used to retrieve the resonant imaginary component which represents the underlying Raman-like lineshapes and is usable for further quantitative analysis. The error phase correction was performed by Savitzky-Golay filter of second polynomial order over 151 spectral points (~424 cm-1).

Diffusion coefficient calculation

The data were fit using the equation IIo=Ae-dx2, were I/I0 is the ratio of the integrated peak intensity, A is a constant, d is the diffusion decay rate, and x is the gradient strength percentage. The diffusion decay rate was used to obtain the radius of hydration using the equation Rh=dlysozymed(2.05nm), where dlysozyme is the observed diffusion decay rate of lysozyme and 2.05 nm is the radius of hydration of lysozyme27. The diffusion coefficient, D, was calculated from the Stokes-Einstein equation D=kBT6πηRH where kB is Boltzmann’s constant, T is equal to 298 K, η is equal to 8.9E-4 Pa·s (the viscosity of water at 298 K)58, and RH is the radius of hydration of that molecule. The diffusion coefficient of lysozyme was calculated using the reported RH which was obtained at 293 K.

Reduced spectral density mapping

Discrete spectral density function values at frequencies 0, ωN, and 0.87ωH were evaluated for 15N relaxation data acquired at 850 MHz and 500 MHz 1H Larmor frequencies using reduced spectral density mapping with the assumption that J(0.870ωH)= J(0.921ωH)= J(0.955ωH)59.

Phase separation quantification

The extent of phase separation of FUS LC was assessed by diluting the protein to a concentration of 200 μM from 20 mM CAPS pH 11.0 into 50 mM Tris pH 7.4 containing the appropriate salt concentration. Samples were spun down at 14,000 × g for ten minutes at room temperature. All samples were done in triplicate. The protein concentration of the remaining supernatant was determined with a NanoDrop spectrophotometer.

The partition coefficient for the FUS LC variants was quantified by diluting the protein to a concentration of 300 μΜ from 20 mM CAPS pH 11.0 into 50 mM Tris 1M NaCl pH 7.4 at 4οC. Samples were spun down at 14,000 × g for twenty minutes at 4°C. The dilute phase was transferred to a separate tube and the protein concentration remaining in the supernatant was determined. 5 μL of the condensed phase was diluted 250× or 500× in 8M urea 50 mM Tris pH 7.4, and the concentration in the condensed phase was determined. The partition coefficient was calculated by dividing the concentration in the condensed phase by the concentration in the dispersed phase.

Turbidity Measurements

Turbidity was used to evaluate phase separation of 5 μΜ MBP-FUS FL in the presence of TEV protease in 50 mM Tris pH 7.4 with the appropriate salt concentration. Turbidity experiments were performed in a 96 well clear plate (Costar) with 100 μL samples sealed with clear optical adhesive film to prevent evaporation (MicroAmp, ThermoFisher). The absorbance at 600 nm was monitored over time using a Cytation 3 Cell Imaging Multi-Mode Reader (BioTek) at 5 min time intervals for up to 12 hr with mixing. To normalize the data, the turbidity of a no TEV control for each condition was subtracted from the turbidity of the experimental conditions. Experiments were conducted in triplicate and averaged.

Simulation Details

All atom simulations were conducted using the GROMACS software package60 and the Amber03ws force field61. Single chain simulations were conducted using parallel tempering in the well-tempered ensemble (PT-WTE) with 16 replicas at a range of temperatures spanning 300-514K. Two chain simulations were conducted using a similar PT-WTE setup coupled with a well-tempered metadynamics (WT-MetaD) bias on the intermolecular contacts in order to aid in sampling binding and unbinding events62–64. Initial configurations were generated by conducting 5 ns serial simulations at each temperature used in the parallel tempering. For the two-chain simulation, starting configurations include both bound and unbound states (Supplementary Fig. 2C). Production simulations were carried out for 200 ns (single-chain) or 300 ns (two-chain), with the first 50 ns discarded as equilibration time. For the two-chain simulation, we ascertained convergence of the intermolecular contacts by calculating the free energy surface from the WT-MetaD bias and show that there is little change within the last 20 ns. An additional serial simulation of FUS120-163 was shown to reproduce NMR secondary shifts and relaxation parameters in excellent agreement with experiment (Supplementary Fig. 2A,B ). Convergence of simulations were ascertained by calculating the free energy profile along the collective variables used for well-tempered metadynamics at different time points and determining after which time it no longer develops significantly.

Coarse-grained simulations were conducted using HOOMD-blue65 with a system of 100 full-length FUS chains using our recently developed HPS model which treats amino acid interactions based on a common hydrophobicity scale66 at 300K using the slab geometry as we have previously to sample phase coexistence66,67.

Simulation Analysis

All-atom simulations were analyzed at 300K to match temperatures of experiment. For dimer simulations, all analyses are reweighted based on the converged free energy profile generated from WT-MetaD. Contacts are considered as two groups having at least one heavy atom from each group within 6 Å of each other. Similarly, hydrophobic contacts are considered as having two nonpolar atoms (those with less than an absolute net charge less than 0.25) within 6Å of each other. Hydrogen bonds are considered using the donor-acceptor convention implemented in GROMACS. π/sp2 contacts, calculated for intermolecular contacts, were computed as described previously43. Effective NOEs were calculated from simulation by determining the distance between hydrogen atoms from each location on residues of interest. The combined pseudo-amplitude, ANOE was calculated for each pairing of hydrogen atoms as:

ANOEX,Y=∑iX∑jY1rij6+∑iY∑jX1rij6

where,

X∈GHN,SHN,THN,QHN,YHN,NHδ,QHε

Y∈AHβ,GHα,QHα,QHβ2,QHβ3,QHγ,SHα,SHβ,THα,THβ,THγ,YHα,YHβ2,YHβ3,YHδ,YHε

From coarse-grained simulations, we compare with the PRE shifts calculated from experiment by calculating the ensemble averaged distance from the different probes used (A16, S86 and S142) from all amino acids in neighboring chains as:

Γ2calci=1N(N-1)∑jN∑k≠jN1ri,probe6j,k

where,

to loop over all chain pairs in the coarse-grained simulation box.

Data Availability

Chemical shift assignments and relaxation parameters for the condensed phase can be accessed using the BMRB accession 27887. All other data are available from the corresponding author upon reasonable request.

Code Availability

Simulation software described in Methods section are publicly available and can be found at http://www.gromacs.org/ for the atomistic resolution simulations and (http://glotzerlab.engin.umich.edu/hoomd-blue/) for coarse-grained simulations HOOMD.

Supplementary Material

1

2

Acknowledgements

We thank Mandar Naik for helpful advice and assistance with NMR spectroscopy and Wai Shing Tang for assistance with NOE calculations from simulated ensembles. Research was supported in part by NIGMS R01GM118530 (to N.L.F.) and Human Frontier Science Program RGP0045/2018 (to S.H.P and N.L.F), and NSF 1845734 (to N.L.F.). A.C.M. was supported in part by NIGMS training grant to the MCB graduate program at Brown University (T32GM007601) and NSF graduate fellowship (1644760, to A.C.M.). G.L.D., G.H.Z., and J.M. are supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), Division of Material Sciences and Engineering under Award DESC0013979 (to J.M.). Y.K. and S.H.P are supported by the Deutsche Forschungsgemeinschaft (DFG) PA-252611-1 and Marie Curie Foundation CIG322284 (to S.H.P.). Use of the high-performance computing capabilities of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the NSF grant TG-MCB-120014, is gratefully acknowledged in addition to resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract DE-AC02-05CH11231. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.

Footnotes

Competing Interests Statement

The authors declare no competing interests.

References

Methods-only References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1

2

Data Availability Statement

Chemical shift assignments and relaxation parameters for the condensed phase can be accessed using the BMRB accession 27887. All other data are available from the corresponding author upon reasonable request.