Euclid's Elements, Book I, Proposition 30 (original) (raw)
Straight lines parallel to the same straight line are also parallel to one another.
Let each of the straight lines AB and CD be parallel to EF.
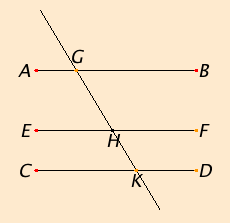
I say that AB is also parallel to CD.
Let the straight line GK fall upon them. Since the straight line GK falls on the parallel straight lines AB and EF, therefore the angle AGK equals the angle GHF.
Again, since the straight line GK falls on the parallel straight lines EF and CD, therefore the angle GHF equals the angle GKD.
But the angle AGK was also proved equal to the angle GHF. Therefore the angle AGK also equals the angle GKD, and they are alternate.
Therefore AB is parallel to CD.
Therefore straight lines parallel to the same straight line are also parallel to one another.
Q.E.D.
Guide
For this proposition it is supposed that the three lines lie in one plane. Proposition XI.9 applies to the case where the three lines do not lie in a plane.
Playfair’s axiom
A number of the propositions in the Elements are equivalent to the parallel postulate Post.5 in the sense that if the rest of the postulates are assumed and any one of these propositions is assumed, then the parallel postulate can be proved as a proposition. This one I.30, the last I.29, either part of I.32, and almost any later one. Thus, Euclid had many statements to choose from to take as a postulate.
In many modern expositions of synthetic geometry, Playfair’s axiom (John Playfair, 1748–1819) is chosen as that postulate instead of Euclid’s parallel postulate Post.5. Playfair’s axiom states that there is at most one line parallel to a given line passing through a given point. (That there is at least one follows from the next proposition I.31, which doesn’t depend on the parallel postulate.)
Two advantages of Playfair’s axiom over Euclid’s parallel postulate are that it is a simpler statement, and it emphasizes the distinction between Euclidean and hyperbolic geometry.
Two disadvantages are that it does not have the historical importance of Euclid’s parallel postulate, and the proof of the parallel postulate from Playfair’s axiom is nonconstructive. That proof is a proof by contradiction that begins assuming that a point does not exist, deriving a contradiction, and concluding that the point must exist, but does not construct it. It may well be that Euclid chose to make the construction an assumption of his parallel postulate rather rather than choosing some other equivalent statement for his postulate.
Elegance in mathematics
Euclid’s Elements form one of the most beautiful works of science in the history of humankind. This beauty lies more in the logical development of geometry rather than in geometry itself. It is not the diagrams that excite our interest; rather it is the concepts, the way the concepts interconnect, and the way Euclid selected and presented these concepts and their interconnections. The Elements are elegant. Elegance in mathematics is characterized by simplicity and clarity. An elegant presentation is easy for the reader to follow. But elegance is not only in the presentation, it is in the selection of definitions and proofs. The elegant definition is the one that makes the rest of the theory easy. The elegant proof is the one that is easiest to follow, one that is designed just right to fit the goal. Extraneous concepts should not be involved. Even the goals need to be adjusted to the right level of generality to cover the concepts, but not so abstract that the abstraction itself obscures the goal.
One of the criticisms of Euclid’s parallel postulate was that it isn’t simple.The statement of this proposition, I.30, is much simpler, and Playfair’s axiom is much simpler. As they’re each logically equivalent to Euclid’s parallel postulate, if elegance were the primary goal, then Euclid would have chosen one of them in place of his postulate. Perhaps the reasons mentioned above explain why Euclid used Post.5 instead.