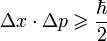Приближение Борна — Оппенгеймера | это... Что такое Приближение Борна — Оппенгеймера? (original) (raw)

Приближение Борна — Оппенгеймера

Квантовая механика
$\Delta x\cdot\Delta p \geqslant \frac{\hbar}{2}$
Принцип неопределённости
Введение ... Математическая формулировка ... Основа Классическая механика · Интерференция · Бра и кет · Гамильтониан Фундаментальные понятия Квантовое состояние · Квантовая наблюдаемая · Волновая функция · Суперпозиция · Запутанность ·Измерение · Неопределённость · Запрет Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннелирование Эксперименты Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга ·Проверка неравенств Белла · Фотоэффект · Эффект Комптона Формулировки Картина Шрёдингера · Картина Гейзенберга · Картина взаимодействия · Матричная квантовая механика · Интегралы по траекториям · Диаграммы Фейнмана Уравнения Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака · Уравнение фон Неймана Интерпретации Копенгагенская интерпретация · Теория скрытых параметров · Многомировая Продвинутые теории Квантовая теория поля · Квантовая электродинамика · Квантовая хромодинамика· Квантовая гравитация Сложные темы Квантовая теория поля · Квантовая гравитация · Теория всего Известные учёные Планк · Эйнштейн · Шрёдингер · Гейзенберг· Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт

Приближение Борна — Оппенгеймера — вариация адиабатического приближения в квантовой механике, метод анализа молекулярных систем, заключающийся в том, что в системе выделяют и раздельно описывают ядра и электроны, для которых характерные времена изменения состояния сильно различаются.

Масса ядра значительно превышает массу электрона, соответственно скорость движения ядра мала по отношению к скорости движения электронов. В результате медленно движущиеся ядра образуют электростатическое поле, в котором с намного большей скоростью движутся электроны, успевающие мгновенно подстроится к любому изменению координат ядер. Поэтому в приближении считают ядра фиксированными и рассматривают только движение электронов. На языке квантовой механики это эквивалентно допущению, что полная волновая функция молекулы может быть выражена в виде произведения электронной и ядерной функций:

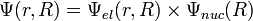$\Psi(r,R) = \Psi_{ el}(r,R) \times \Psi_{ nuc}(R)$	(1)

Приближение Борна-Оппенгеймера является существенным для квантовой химии. В этом приближении полная энергия молекулы представляет собой сумму электронной энергии, вычисленной при фиксированной конфигурации ядер, и колебательно-вращательной энергии ядер:

Обоснование применимости

Уравнение Шрёдингера для молекулы с N ядрами и n электронами и волновой функцией приближения имеет вид

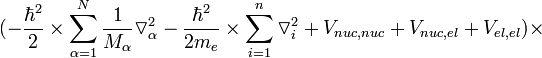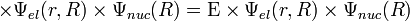$( - \frac{\hbar^2}{2} \times \sum^{N}_{\alpha=1} {\frac{1}{M_{\alpha}} {\triangledown^{2}_{\alpha}}} - \frac{\hbar^2}{2m_{e}} \times \sum^{n}_{i=1} {\triangledown^{2}_{i}} + {V_{nuc,nuc}} + {V_{nuc,el}} + {V_{el,el}}) \times$ $\ \times \Psi_{ el}(r,R) \times \Psi_{ nuc}(R) = \Epsilon \times \Psi_{ el}(r,R) \times \Psi_{ nuc}(R)$	(3)

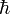$\hbar$ — постоянная Дирака (h / 2π); V n u c,n u c — энергия отталкивания ядер; V n u c,e l — энергия притяжения электронов к ядрам; V e l,e l — энергия отталкивания электронов.

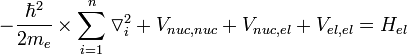
$- \frac{\hbar^2}{2m_{e}} \times \sum^{n}_{i=1} {\triangledown^{2}_{i}} + {V_{nuc,nuc}} + {V_{nuc,el}} + {V_{el,el}} = H_{el}$

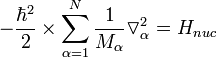
$- \frac{\hbar^2}{2} \times \sum^{N}_{\alpha=1} {\frac{1}{M_{\alpha}} {\triangledown^{2}_{\alpha}}} = H_{nuc}$

Электронная функция Ψ_e_ l(r,R) определяется как собственная функция оператора H e l:

H e l_Ψ_e l(r,R) = E e l_Ψ_e l(r,R),	(4)

где E e l — электронная энергия, обусловленная движением n электронов в поле N ядер молекулы, плюс энергия взаимодействия между ядрами V n u c,n u c. Величину E e l называют адиабатическим электронным термом молекулы или адиабатическим потенциалом.

Учитывая что

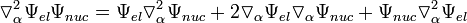$\triangledown^{2}_{\alpha} \Psi_{ el} \Psi_{ nuc} = \Psi_{ el} \triangledown^{2}_{\alpha} \Psi_{ nuc} + 2 \triangledown_{\alpha} \Psi_{ el} \triangledown_{\alpha} \Psi_{ nuc} + \Psi_{ nuc} \triangledown^{2}_{\alpha} \Psi_{ el}$ ;

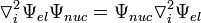$\triangledown^{2}_{i} \Psi_{ el} \Psi_{ nuc} = \Psi_{ nuc} \triangledown^{2}_{i} \Psi_{ el}$ ,

уравнение (3) приобретает вид:

Пренебрегая выражением в первых круглых скобках получаем уравнение:

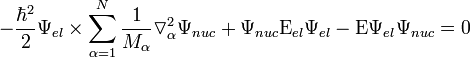
$- \frac{\hbar^2}{2} \Psi_{ el} \times \sum^{N}_{\alpha=1} {\frac{1}{M_{\alpha}} \triangledown^{2}_{\alpha} \Psi_{ nuc}} + \Psi_{ nuc} \Epsilon_{el} \Psi_{ el} - \Epsilon \Psi_{ el} \Psi_{ nuc} = 0$

Разделив все члены этого уравнения на Ψ_e_ l и принимая во внимание (4) получается уравнение для определения Ψ_n_ u c:

(H n u c + Ε_e_ l)Ψ_n_ u c = ΕΨ_n_ u c.

Пренебрежение скобками в уравнении (5) означает, что электронная волновая функция Ψ_e_ l должна быть настолько медленно меняющейся функцией ядерных координат R, что можно пренебречь ее первой и второй производными по этим координатам. М. Борн и Р. Оппенгеймер в 1927 году впервые показали, что электронные волновые функции обычно подчиняются этому условию с требуемой степенью точности.

Для случая устойчивых многоатомных молекул существует простой критерий применимости приближения Б.-О.

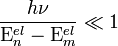$\frac{h \nu}{\Epsilon^{el}_{n} - \Epsilon^{el}_{m}} \ll 1$ ,	(6)

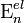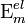где ν — наибольшая из частот малых колебаний ядер вблизи точки равновесия, $\Epsilon^{el}_{n}$ и $\Epsilon^{el}_{m}$ — энергии двух соседних электронных состояний. Критерий (6) обычно выполняется для многих молекул, вследствие этого расчеты физических характеристик молекул, основанные на приближении Б.-О., позволяют получить данные, хорошо согласующиеся с экспериментальными результатами. Ошибка, вносимая при использовании такого приближения, намного меньше ошибок, вносимых другими приближениями. Это позволяет ограничиваться решением только одного электронного уравнения (4). Поправки для возбужденных электронных состояний значительнее, но обычно ими также можно пренебречь по сравнению с неточностями, обусловленными приближенным решением электронного уравнения Шрёдингера (4).

Источники

Минкин В. И., Симкин Б. Я., Миняев Р. М. Строение молекул.
Энциклопедия на сайте [1].

Wikimedia Foundation.2010.