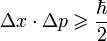Квантовое туннелирование | это... Что такое Квантовое туннелирование? (original) (raw)
Туннельный эффект, туннелирование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике; аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.

Отражение и туннелирование электронного пучка, направленного на потенциальный барьер. Слабое пятно справа от барьера - электроны, прошедшие сквозь барьер. Обратите внимание на интерференцию между падающими и отражающимися волнами.
Содержание
- 1 Краткое квантовомеханическое описание
- 2 Упрощённое объяснение
- 3 Макроскопические проявления туннельного эффекта
- 4 См. также
- 5 История и исследователи
- 6 Примечания
- 7 Ссылки
- 8 Литература
Краткое квантовомеханическое описание
Согласно классической механике, частица может находиться лишь в тех точках пространства, в которых ее потенциальная энергия меньше полной. Это следует из того обстоятельства, что кинетическая энергия частицы 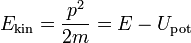 не может (в классич. физике) быть отрицательной, т.к. в таком случае импульс будет мнимой величиной. То есть если две области пространства разделены потенциальным барьером, таким, что
не может (в классич. физике) быть отрицательной, т.к. в таком случае импульс будет мнимой величиной. То есть если две области пространства разделены потенциальным барьером, таким, что 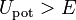 , просачивание частицы сквозь него в рамках классической теории оказывается невозможным. В квантовой же механике мнимое значение импульса лишь соответствует экспоненциальной зависимости волновой функции от координаты. Это видно из уравнения Шредингера с постоянным потенциалом (для простоты возьмем одномерный случай):
, просачивание частицы сквозь него в рамках классической теории оказывается невозможным. В квантовой же механике мнимое значение импульса лишь соответствует экспоненциальной зависимости волновой функции от координаты. Это видно из уравнения Шредингера с постоянным потенциалом (для простоты возьмем одномерный случай):
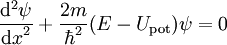
(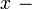 координата;
координата; 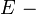 полная энергия,
полная энергия, 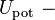 потенциальная энергия,
потенциальная энергия, 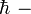 редуцированная постоянная Планка,
редуцированная постоянная Планка, 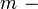 масса частицы), решением которого является функция
масса частицы), решением которого является функция
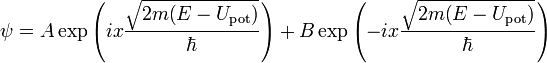
Пусть имеется движущаяся частица, на пути которой встречается потенциальный барьер высотой 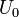 , а потенциал частицы до и после прохождения равен нулю.
, а потенциал частицы до и после прохождения равен нулю.
Для областей 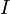 (до прохождения),
(до прохождения), 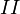 (во время прохождения внутри потенциального барьера) и
(во время прохождения внутри потенциального барьера) и 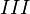 (после прохождения барьера) (начало барьера совпадает с началом координат; его "ширина" равна
(после прохождения барьера) (начало барьера совпадает с началом координат; его "ширина" равна 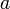 ) получаем соответственно функции
) получаем соответственно функции
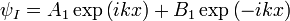
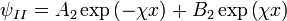
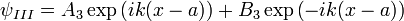
Так как слагаемое 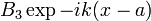 характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить
характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить 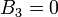 . Для характеристики величины туннельного эффекта введем коэффициент прозрачности барьера, равный модулю отношения плотности потока прошедших частиц к плотности потока упавших:
. Для характеристики величины туннельного эффекта введем коэффициент прозрачности барьера, равный модулю отношения плотности потока прошедших частиц к плотности потока упавших:
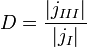
Для определения потока частиц воспользуемся формулой
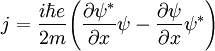
где знак звездочки обозначает комплексное сопряжение.
Подставляя в эту формулу волновые функции, указанные выше, получим
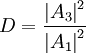
Теперь, воспользовавшись граничными условиями, выразим сначала 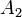 и
и 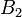 через
через 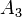 (с учетом, что
(с учетом, что 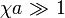 :
:
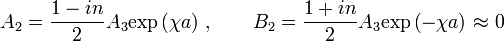
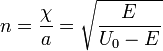
а затем 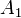 через
через 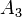 :
:
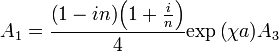
Введем величину
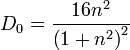
которая будет порядка единицы. Тогда:
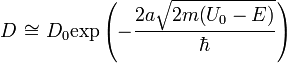
Для потенциального барьера произвольной формы делаем замену
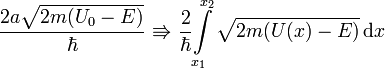
где 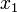 и
и 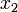 находятся из условия
находятся из условия
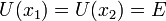
Тогда для коэффициента прохождения через барьер получаем выражение
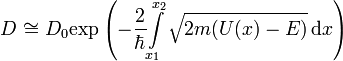
Упрощённое объяснение
Туннельный эффект можно объяснить соотношением неопределённостей.[1] Записанное в виде:
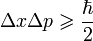 ,
,
оно показывает, что при ограничении квантовой частицы по координате, т.е. увеличении её определённости по x, её импульс p становится менее определённым. Случайным образом неопределённость импульса Δ_p_ может добавить частице энергии для преодоления барьера. Таким образом, с некоторой вероятностью квантовая частица может проникнуть через барьер, а средняя энергия частицы останется неизменной.
Макроскопические проявления туннельного эффекта

Туннельный эффект имеет ряд проявлений в макроскопических системах:
- Туннелирование носителей зарядов через потенциальный барьер p-n перехода, получившее практическое применение в туннельном диоде.
- Туннелирование носителей зарядов через тонкую оксидную пленку, имеющую диэлектрические свойства, покрывающую ряд металлов (в частности, алюминия) и обеспечивающее проводимость точек механического соединения проводников (скрутки проводов, зажимы, джамперы). Применительно к сверхпроводникам это явление получило название эффект Джозефсона.
См. также
- Квантовая механика
- Корпускулярно-волновой дуализм
- Туннельный диод
- Эффект Джозефсона
- Твёрдое тело
- Бета-распад
- Альфа-распад
- К-захват
История и исследователи
В 1928 Георгий Гамов разработал теорию альфа-распада, основанную на туннельном эффекте. Автоэлектронная эмиссия из металла в вакуум (туннелирование электрона сквозь поверхностный барьер) описывается законом Фаулера — Нордгейма, также выведенном в 1928 г.
Примечания
- ↑ Статья "Туннельный эффект" в БСЭ, 2 абзац
Ссылки
- Туннельная эмиссия
- Туннельный эффект, БСЭ на slovari.yandex.ru (2009-06-05). Проверено 2009-06-05.
Литература
- Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963;
- Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 3-е, переработанное и дополненное. — М.: Наука, 1974. — 752 с. — («Теоретическая физика», том III).
Wikimedia Foundation.2010.