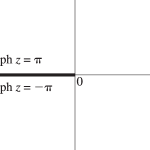§4.2 Definitions ‣ Logarithm, Exponential, Powers ‣ Chapter 4 Elementary Functions (original) (raw)
Contents
- §4.2(i) The Logarithm
- §4.2(ii) Logarithms to a General Base a
- §4.2(iii) The Exponential Function
- §4.2(iv) Powers
§4.2(i) The Logarithm
The principal value, or principal branch, is defined by
where the path does not intersect (−∞,0]; see Figure4.2.1.lnz is a single-valued analytic function onℂ∖(−∞,0] and real-valued when z ranges over the positive real numbers.
Figure 4.2.1: z-plane: Branch cut for lnz and zα.Magnify
The only zero of lnz is at z=1.
Most texts extend the definition of the principal value to include the_branch cut_
| 4.2.4 | z=x, |
|---|---|
| −∞<x<0, | |
| ⓘ Symbols: x: real variable andz: complex variable Permalink: http://dlmf.nist.gov/4.2.E4 Encodings: TeX, pMML, png See also: Annotations for §4.2(i),§4.2 andCh.4 |
by replacing (4.2.3) with
| 4.2.5 | lnz=ln|z|+iphz, | | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------- | | −π<phz≤π. | | | ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,i: imaginary unit,lnz: principal branch of logarithm function,ph: phase andz: complex variable Referenced by: §4.2(i) Permalink: http://dlmf.nist.gov/4.2.E5 Encodings: TeX, pMML, png See also: Annotations for §4.2(i),§4.2 andCh.4 | |
With this definition the general logarithm is given by
where k is the excess of the number of times the path in (4.2.1) crosses the negative real axis in the positive sense over the number of times in the negative sense.
In the DLMF we allow a further extension by regarding the cut as representing two sets of points, one set corresponding to the “upper side” and denoted byz=x+i0, the other set corresponding to the “lower side” and denoted by z=x−i0. Again see Figure 4.2.1. Then
| 4.2.7 | ln(x±i0)=ln|x|±iπ, | | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ | ------------------------ | | −∞<x<0, | | | ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,i: imaginary unit,lnz: principal branch of logarithm function andx: real variable Permalink: http://dlmf.nist.gov/4.2.E7 Encodings: TeX, pMML, png See also: Annotations for §4.2(i),§4.2 andCh.4 | |
with either upper signs or lower signs taken throughout. Consequentlylnz is two-valued on the cut, and discontinuous across the cut. We regard this as the closed definition of the principal value.
In contrast to (4.2.5) the closed definition is symmetric. As a consequence, it has the advantage of extending regions of validity of properties of principal values. For example, with the definition (4.2.5) the identity (4.8.7) is valid only when|phz|<π, but with the closed definition the identity (4.8.7) is valid when |phz|≤π. For another example see (4.2.37).
In the DLMF it is usually clear from the context which definition of principal value is being used. However, in the absence of any indication to the contrary it is assumed that the definition is the closed one. For other examples in this chapter see §§4.23,4.24, 4.37, and 4.38.
§4.2(ii) Logarithms to a General Base a
With a,b≠0 or 1,
| 4.2.8 | logaz | =lnz/lna, |
|---|---|---|
| ⓘ Symbols: logaz: logarithm to general base,lnz: principal branch of logarithm function,a: real or complex constant andz: complex variable A&S Ref: 4.1.18 Permalink: http://dlmf.nist.gov/4.2.E8 Encodings: TeX, pMML, png See also: Annotations for §4.2(ii),§4.2 andCh.4 | ||
| 4.2.9 | logaz | =logbzlogba, |
| ⓘ Symbols: logaz: logarithm to general base,a: real or complex constant andz: complex variable A&S Ref: 4.1.19 Permalink: http://dlmf.nist.gov/4.2.E9 Encodings: TeX, pMML, png See also: Annotations for §4.2(ii),§4.2 andCh.4 | ||
| 4.2.10 | logab | =1logba. |
| ⓘ Symbols: logaz: logarithm to general base anda: real or complex constant A&S Ref: 4.1.20 Permalink: http://dlmf.nist.gov/4.2.E10 Encodings: TeX, pMML, png See also: Annotations for §4.2(ii),§4.2 andCh.4 |
Natural logarithms have as base the unique positive number
such that
Equivalently,
Thus
logex=lnx is also called the Napierian or_hyperbolic_ logarithm. log10x is the common or_Briggs_ logarithm.
§4.2(iii) The Exponential Function
The function exp is an entire function of z, with no real or complex zeros. It has period 2πi:
Also,
The general value of the phase is given by
| 4.2.23 | ph(expz)=ℑz+2kπ, |
|---|---|
| k∈ℤ. | |
| ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,∈: element of,expz: exponential function,ℑ: imaginary part,ℤ: set of all integers,ph: phase,k: integer andz: complex variable A&S Ref: 4.2.14 (modified) Permalink: http://dlmf.nist.gov/4.2.E23 Encodings: TeX, pMML, png See also: Annotations for §4.2(iii),§4.2 andCh.4 |
§4.2(iv) Powers
Powers with General Bases
The general ath power of z is defined by
| 4.2.26 | za=exp(aLnz), |
|---|---|
| z≠0. | |
| ⓘ Symbols: expz: exponential function,Lnz: general logarithm function,a: real or complex constant andz: complex variable Permalink: http://dlmf.nist.gov/4.2.E26 Encodings: TeX, pMML, png See also: Annotations for §4.2(iv),§4.2(iv),§4.2 andCh.4 |
In particular, z0=1, and if a=n=1,2,3,…, then
In all other cases, za is a multivalued function with branch point atz=0. The principal value is
This is an analytic function of z on ℂ∖(−∞,0], and is two-valued and discontinuous on the cut shown in Figure 4.2.1, unless a∈ℤ.
where phz∈[−π,π] for the principal value of za, and is unrestricted in the general case. When a is real
| 4.2.31 | |za| | =|z|a, | | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | --------- | -------- | | ph(za) | =aphz. | | | ⓘ Symbols: ph: phase,a: real or complex constant andz: complex variable Permalink: http://dlmf.nist.gov/4.2.E31 Encodings: TeX, TeX, pMML, pMML, png, png See also: Annotations for §4.2(iv),§4.2(iv),§4.2 andCh.4 | | |
Unless indicated otherwise, it is assumed throughout the DLMF that a power assumes its principal value. With this convention,
but the general value of ez is
| 4.2.33 | ez=(expz)exp(2kzπi), |
|---|---|
| k∈ℤ. | |
| ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,∈: element of,expz: exponential function,e: base of natural logarithm,i: imaginary unit,ℤ: set of all integers,k: integer andz: complex variable Permalink: http://dlmf.nist.gov/4.2.E33 Encodings: TeX, pMML, png See also: Annotations for §4.2(iv),§4.2(iv),§4.2 andCh.4 |
If za has its general value, with a≠0, and if w≠0, then
This result is also valid when za has its principal value, provided that the branch of Lnw satisfies
Another example of a principal value is provided by
Again, without the closed definition the ≥ and ≤ signs would have to be replaced by > and <, respectively.