Handbook of Integral Equations (original) (raw)

	EqWorld The World of Mathematical Equations

Home Page Exact Solutions Methods Software Education For Authors Math Forums

Information >Mathematical Books >Handbook of Integral Equations, Second Edition > Contents

| | | | A. D. Polyanin and A. V. Manzhirov Handbook of Integral EquationsSecond Edition, Updated, Revised and Extended Publisher: Chapman & Hall/CRC Press Publication Date: 14 February 2008 Number of Pages: 1144 Summary Preface Features Contents Index References | | ---------------------------------------------------------------------------------------------------- | | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |

Authors
Preface
Some Remarks and Notation

Part I. Exact Solutions of Integral Equations

1. Linear Equations of the First Kind with Variable Limit of Integration

1.1. Equations Whose Kernels Contain Power-Law Functions
1.2. Equations Whose Kernels Contain Exponential Functions
1.3. Equations Whose Kernels Contain Hyperbolic Functions
1.4. Equations Whose Kernels Contain Logarithmic Functions
1.5. Equations Whose Kernels Contain Trigonometric Functions
1.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
1.7. Equations Whose Kernels Contain Combinations of Elementary Functions
1.8. Equations Whose Kernels Contain Special Functions
1.9. Equations Whose Kernels Contain Arbitrary Functions
1.10. Some Formulas and Transformations

2. Linear Equations of the Second Kind with Variable Limit of Integration

2.1. Equations Whose Kernels Contain Power-Law Functions
2.2. Equations Whose Kernels Contain Exponential Functions
2.3. Equations Whose Kernels Contain Hyperbolic Functions
2.4. Equations Whose Kernels Contain Logarithmic Functions
2.5. Equations Whose Kernels Contain Trigonometric Functions
2.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
2.7. Equations Whose Kernels Contain Combinations of Elementary Functions
2.8. Equations Whose Kernels Contain Special Functions
2.9. Equations Whose Kernels Contain Arbitrary Functions
2.10. Some Formulas and Transformations

3. Linear Equations of the First Kind with Constant Limits of Integration

3.1. Equations Whose Kernels Contain Power-Law Functions
3.2. Equations Whose Kernels Contain Exponential Functions
3.3. Equations Whose Kernels Contain Hyperbolic Functions
3.4. Equations Whose Kernels Contain Logarithmic Functions
3.5. Equations Whose Kernels Contain Trigonometric Functions
3.6. Equations Whose Kernels Contain Combinations of Elementary Functions
3.7. Equations Whose Kernels Contain Special Functions
3.8. Equations Whose Kernels Contain Arbitrary Functions
3.9. Dual Integral Equations of the First Kind

4. Linear Equations of the Second Kind with Constant Limits of Integration

4.1. Equations Whose Kernels Contain Power-Law Functions
4.2. Equations Whose Kernels Contain Exponential Functions
4.3. Equations Whose Kernels Contain Hyperbolic Functions
4.4. Equations Whose Kernels Contain Logarithmic Functions
4.5. Equations Whose Kernels Contain Trigonometric Functions
4.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
4.7. Equations Whose Kernels Contain Combinations of Elementary Functions
4.8. Equations Whose Kernels Contain Special Functions
4.9. Equations Whose Kernels Contain Arbitrary Functions
4.10. Some Formulas and Transformations

5. Nonlinear Equations of the First Kind with Variable Limit of Integration

5.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
5.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
5.3. Equations with Nonlinearity of General Form

6. Nonlinear Equations of the Second Kind with Variable Limit of Integration

6.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
6.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
6.3. Equations with Power-Law Nonlinearity
6.4. Equations with Exponential Nonlinearity
6.5. Equations with Hyperbolic Nonlinearity
6.6. Equations with Logarithmic Nonlinearity
6.7. Equations with Trigonometric Nonlinearity
6.8. Equations with Nonlinearity of General Form

7. Nonlinear Equations of the First Kind with Constant Limits of Integration

7.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
7.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
7.3. Equations with Power-Law Nonlinearity That Contain Arbitrary Functions
7.4. Equations with Nonlinearity of General Form

8. Nonlinear Equations of the Second Kind with Constant Limits of Integration

8.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
8.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
8.3. Equations with Power-Law Nonlinearity
8.4. Equations with Exponential Nonlinearity
8.5. Equations with Hyperbolic Nonlinearity
8.6. Equations with Logarithmic Nonlinearity
8.7. Equations with Trigonometric Nonlinearity
8.8. Equations with Nonlinearity of General Form

Part II. Methods for Solving Integral Equations

9. Main Definitions and Formulas. Integral Transforms

9.1. Some Definitions, Remarks, and Formulas
9.2. Laplace Transform
9.3. Mellin Transform
9.4. Fourier Transform
9.5. Fourier Cosine and Sine Transforms
9.6. Other Integral Transforms

10. Methods for Solving Linear Equations of the Form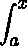K(x,t) y(t) dt = f(x)

10.1. Volterra Equations of the First Kind
10.2. Equations with Degenerate Kernel: K(x,t) = _g_1(x)_h_1(t) + ... + g n(x)h n(t)
10.3. Reduction of Volterra Equations of the First Kind to Volterra Equations of the Second Kind
10.4. Equations with Difference Kernel: K(x,t) = K(x − t)
10.5. Method of Fractional Differentiation
10.6. Equations with Weakly Singular Kernel
10.7. Method of Quadratures
10.8. Equations with Infinite Integration Limit

11. Methods for Solving Linear Equations of the Form_y_(x) − 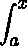K(x,t) y(t) dt = f(x)

11.1. Volterra Integral Equations of the Second Kind
11.2. Equations with Degenerate Kernel: K(x,t) = _g_1(x)_h_1(t) + ... + g n(x)h n(t)
11.3. Equations with Difference Kernel: K(x,t) = K(x − t)
11.4. Operator Methods for Solving Linear Integral Equations
11.5. Construction of Solutions of Integral Equations with Special Right-Hand Side
11.6. Method of Model Solutions
11.7. Method of Differentiation for Integral Equations
11.8. Reduction of Volterra Equations of the Second Kind to Volterra Equations of the First Kind
11.9. Successive Approximation Method
11.10. Method of Quadratures
11.11. Equations with Infinite Integration Limit

12. Methods for Solving Linear Equations of the Form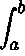K(x,t) y(t) dt = f(x)

12.1. Some Definition and Remarks
12.2. Integral Equations of the First Kind with Symmetric Kernel
12.3. Integral Equations of the First Kind with Nonsymmetric Kernel
12.4. Method of Differentiation for Integral Equations
12.5. Method of Integral Transforms
12.6. Krein's Method and Some Other Exact Methods for Integral Equations of Special Types
12.7. Riemann Problem for the Real Axis
12.8. Carleman Method for Equations of the Convolution Type of the First Kind
12.9. Dual Integral Equations of the First Kind
12.10. Asymptotic Methods for Solving Equations with Logarithmic Singularity
12.11. Regularization Methods
12.12. Fredholm Integral Equation of the First Kind as an Ill-Posed Problem

13. Methods for Solving Linear Equations of the Form_y_(x) − 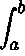K(x,t) y(t) dt = f(x)

13.1. Some Definition and Remarks
13.2. Fredholm Equations of the Second Kind with Degenerate Kernel. Some Generalizations
13.3. Solution as a Power Series in the Parameter. Method of Successive Approximations
13.4. Method of Fredholm Determinants
13.5. Fredholm Theorems and the Fredholm Alternative
13.6. Fredholm Integral Equations of the Second Kind with Symmetric Kernel
13.7. Integral Equations with Nonnegative Kernels
13.8. Operator Method for Solving Integral Equations of the Second Kind
13.9. Methods of Integral Transforms and Model Solutions
13.10. Carleman Method for Integral Equations of Convolution Type of the Second Kind
13.11. Wiener–Hopf Method
13.12. Krein's Method for Wiener–Hopf Equations
13.13. Methods for Solving Equations with Difference Kernels on a Finite Interval
13.14. Method of Approximating a Kernel by a Degenerate One
13.15. Bateman Method
13.16. Collocation Method
13.17. Method of Least Squares
13.18. Bubnov–Galerkin Method
13.19. Quadrature Method
13.20. Systems of Fredholm Integral Equations of the Second Kind
13.21. Regularization Method for Equations with Infinite Limits of Integration

14. Methods for Solving Singular Integral Equations of the First Kind

14.1. Some Definitions and Remarks
14.2. Cauchy Type Integral
14.3. Riemann Boundary Value Problem
14.4. Singular Integral Equations of the First Kind
14.5. Multhopp–Kalandiya Method
14.6. Hypersingular Integral Equations

15. Methods for Solving Complete Singular Integral Equations

15.1. Some Definitions and Remarks
15.2. Carleman Method for Characteristic Equations
15.3. Complete Singular Integral Equations Solvable in a Closed Form
15.4. Regularization Method for Complete Singular Integral Equations
15.5. Analysis of Solutions Singularities for Complete Integral Equations with Generalized Cauchy Kernels
15.6. Direct Numerical Solution of Singular Integral Equations with Generalized Kernels

16. Methods for Solving Nonlinear Integral Equations

16.1. Some Definitions and Remarks
16.2. Exact Methods for Nonlinear Equations with Variable Limit of Integration
16.3. Approximate and Numerical Methods for Nonlinear Equations with Variable Limit of Integration
16.4. Exact Methods for Nonlinear Equations with Constant Integration Limits
16.5. Approximate and Numerical Methods for Nonlinear Equations with Constant Integration Limits
16.6. Existence and Uniqueness Theorems for Nonlinear Equations
16.7. Nonlinear Equations with a Parameter: Eigenfunctions, Eigenvalues, Bifurcation Points

17. Methods for Solving Multidimensional Mixed Integral Equations

17.1. Some Definition and Remarks
17.2. Methods of Solution of Mixed Integral Equations on a Finite Interval
17.3. Methods of Solving Mixed Integral Equations on a Ring-Shaped Domain
17.4. Projection Method for Solving Mixed Equations on a Bounded Set

18. Application of Integral Equations for the Investigation of Differential Equations

18.1. Reduction of the Cauchy Problem for ODEs to Integral Equations
18.2. Reduction of Boundary Value Problems for ODEs to Volterra Integral Equations. Calculation of Eigenvalues
18.3. Reduction of Boundary Value Problems for ODEs to Fredholm Integral Equations with the Help of the Green's Function
18.4. Reduction of PDEs with Boundary Conditions of the Third Kind to Integral Equations
18.5. Representation of Linear Boundary Value Problems in Terms of Potentials
18.6. Representation of Solutions of Nonlinear PDEs in Terms of Solutions of Linear Integral Equations (Inverse Scattering)

Supplements

Supplement 1. Elementary Functions and Their Properties

1.1. Power, Exponential, and Logarithmic Functions
1.2. Trigonometric Functions
1.3. Inverse Trigonometric Functions
1.4. Hyperbolic Functions
1.5. Inverse Hyperbolic Functions

Supplement 2. Finite Sums and Infinite Series

2.1. Finite Numerical Sums
2.2. Finite Functional Sums
2.3. Infinite Numerical Series
2.4. Infinite Functional Series

Supplement 3. Tables of Indefinite Integrals

3.1. Integrals Involving Rational Functions
3.2. Integrals Involving Irrational Functions
3.3. Integrals Involving Exponential Functions
3.4. Integrals Involving Hyperbolic Functions
3.5. Integrals Involving Logarithmic Functions
3.6. Integrals Involving Trigonometric Functions
3.7. Integrals Involving Inverse Trigonometric Functions

Supplement 4. Tables of Definite Integrals

4.1. Integrals Involving Power-Law Functions
4.2. Integrals Involving Exponential Functions
4.3. Integrals Involving Hyperbolic Functions
4.4. Integrals Involving Logarithmic Functions
4.5. Integrals Involving Trigonometric Functions
4.6. Integrals Involving Bessel Functions

Supplement 5. Tables of Laplace Transforms

5.1. General Formulas
5.2. Expressions with Power-Law Functions
5.3. Expressions with Exponential Functions
5.4. Expressions with Hyperbolic Functions
5.5. Expressions with Logarithmic Functions
5.6. Expressions with Trigonometric Functions
5.7. Expressions with Special Functions

Supplement 6. Tables of Inverse Laplace Transforms

6.1. General Formulas
6.2. Expressions with Rational Functions
6.3. Expressions with Square Roots
6.4. Expressions with Arbitrary Powers
6.5. Expressions with Exponential Functions
6.6. Expressions with Hyperbolic Functions
6.7. Expressions with Logarithmic Functions
6.8. Expressions with Trigonometric Functions
6.9. Expressions with Special Functions

Supplement 7. Tables of Fourier Cosine Transforms

7.1. General Formulas
7.2. Expressions with Power-Law Functions
7.3. Expressions with Exponential Functions
7.4. Expressions with Hyperbolic Functions
7.5. Expressions with Logarithmic Functions
7.6. Expressions with Trigonometric Functions
7.7. Expressions with Special Functions

Supplement 8. Tables of Fourier Sine Transforms

8.1. General Formulas
8.2. Expressions with Power-Law Functions
8.3. Expressions with Exponential Functions
8.4. Expressions with Hyperbolic Functions
8.5. Expressions with Logarithmic Functions
8.6. Expressions with Trigonometric Functions
8.7. Expressions with Special Functions

Supplement 9. Tables of Mellin Transforms

9.1. General Formulas
9.2. Expressions with Power-Law Functions
9.3. Expressions with Exponential Functions
9.4. Expressions with Logarithmic Functions
9.5. Expressions with Trigonometric Functions
9.6. Expressions with Special Functions

Supplement 10. Tables of Inverse Mellin Transforms

10.1. Expressions with Power-Law Functions
10.2. Expressions with Exponential and Logarithmic Functions
10.3. Expressions with Trigonometric Functions
10.4. Expressions with Special Functions

Supplement 11. Special Functions and Their Properties

11.1. Some Coefficients, Symbols, and Numbers
11.2. Error Functions. Exponential and Logarithmic Integrals
11.3. Sine Integral and Cosine Integral. Fresnel Integrals
11.4. Gamma Function, Psi Function, and Beta Function
11.5. Incomplete Gamma and Beta Functions
11.6. Bessel Functions (Cylindrical Functions)
11.7. Modified Bessel Functions
11.8. Airy Functions
11.9. Confluent Hypergeometric Functions
11.10. Gauss Hypergeometric Functions
11.11. Legendre Polynomials, Legendre Functions, and Associated Legendre Functions
11.12. Parabolic Cylinder Functions
11.13. Elliptic Integrals
11.14. Elliptic Functions
11.15. Jacobi Theta Functions
11.16. Mathieu Functions and Modified Mathieu Functions
11.17. Orthogonal Polynomials
11.18. Nonorthogonal Polynomials

Supplement 12. Some Notions of Functional Analysis

12.1. Functions of Bounded Variation
12.2. Stieltjes Integral
12.3. Lebesgue Integral
12.4. Linear Normed Spaces
12.5. Euclidean and Hilbert Spaces. Linear Operators in Hilbert Spaces

References

Index

The EqWorld website presents extensive information on solutions to various classes of ordinary differential equations, partial differential equations, integral equations, functional equations, and other mathematical equations.