pagenorm - Page-wise matrix or vector norm - MATLAB (original) (raw)

Page-wise matrix or vector norm

Since R2022b

Syntax

Description

[N](#mw%5F017e6732-ce4c-40d4-ad16-c2d7c813b071) = pagenorm([X](#mw%5F73e04791-dabc-42f3-97c7-647239a53e54)) returns the 2-norm of each matrix page of N-D array X. Each page of the output array N is given by N(1,1,i) = norm(X(:,:,i)).

If X has more than three dimensions, thenpagenorm returns an N-D array with the same dimensions, as inN(1,1,i,j,k) = norm(X(:,:,i,j,k)).

example

[N](#mw%5F017e6732-ce4c-40d4-ad16-c2d7c813b071) = pagenorm([X](#mw%5F73e04791-dabc-42f3-97c7-647239a53e54),[p](#mw%5F6c624c93-1927-4037-8d9c-f9b8507c56db)) returns the _p_-norm of each page of X, wherep is 1, 2, orInf.

If p = 1, then N contains the maximum absolute column sum of each page of X.
If p = 2, then N contains the maximum singular value of each page of X.
If p = Inf, then N contains the maximum absolute row sum of each page of X.

example

[N](#mw%5F017e6732-ce4c-40d4-ad16-c2d7c813b071) = pagenorm([X](#mw%5F73e04791-dabc-42f3-97c7-647239a53e54),"fro") returns the Frobenius norm of each page of X.

example

[N](#mw%5F017e6732-ce4c-40d4-ad16-c2d7c813b071) = pagenorm([V](#mw%5F3221c2b4-0aab-4217-81f4-aaf45b2229e3)), whereV is an array with a vector on each page, returns the 2-norm of each page of N-D array V. Each page of the output array N is given by N(1,1,i) = norm(V(:,1,i)) or N(1,1,i) = norm(V(1,:,i)), depending on the orientation of the vectors.

example

[N](#mw%5F017e6732-ce4c-40d4-ad16-c2d7c813b071) = pagenorm([V](#mw%5F3221c2b4-0aab-4217-81f4-aaf45b2229e3),[p](#mw%5F6c624c93-1927-4037-8d9c-f9b8507c56db)) returns the generalized vector _p_-norm of each page ofV, where p is any positive real value orInf.

example

Examples

collapse all

Create a 3-D array with a matrix on each of two pages.

a = magic(3); b = pascal(3); A = cat(3,a,b);

Calculate the 2-norm of each page. This command returns the maximum singular value of each matrix.

N = N(:,:,1) =

N(:,:,2) =

7.8730

Now calculate the infinity norm of each page. This command returns the maximum absolute row sum of each matrix.

Ninf = Ninf(:,:,1) =

Ninf(:,:,2) =

When each page of a multidimensional array contains a vector, you can use pagenorm to calculate vector norms of each page.

Create a 3-D array with a vector on each of three pages.

a = 1:10; b = 11:20; c = 21:30; V = cat(3,a,b,c);

Calculate the 2-norm of each page in the array. This command returns the magnitude of each vector.

N = N(:,:,1) =

19.6214

N(:,:,2) =

49.8498

N(:,:,3) =

81.1480

Now calculate the 1-norm of each page. This command returns the sum of the element magnitudes for each vector.

N1 = N1(:,:,1) =

N1(:,:,2) =

155

N1(:,:,3) =

255

Create a 3-D array with a matrix on each of three pages.

a = randi(10,3,3); b = hilb(3); c = pascal(3); A = cat(3,a,b,c);

Calculate the Frobenius norm of each page.

N = N(:,:,1) =

21.9089

N(:,:,2) =

1.4136

N(:,:,3) =

7.9373

Input Arguments

collapse all

Input array with matrix pages, specified as a matrix or multidimensional array.

Data Types: single | double
Complex Number Support: Yes

Input array with vector pages, specified as a vector or multidimensional array.

Data Types: single | double
Complex Number Support: Yes

Norm type, specified as 2 (default), a positive real scalar, orInf. The valid values of p and what they return depend on whether each page of the input array is a matrix or vector, as shown in the table. See norm for definitions of each norm type.

Note

This table does not reflect the actual algorithms used in calculations.

p	Matrix pages	Vector pages
1	max(sum(abs(A)))	sum(abs(u))
2	max(svd(A))	sum(abs(u).^2)^(1/2)
Positive, real-valued numeric scalar	—	sum(abs(u).^p)^(1/p)
Inf	max(sum(abs(A')))	max(abs(u))

Example: pagenorm(X,Inf) returns the maximum absolute row sum of each matrix page in X.

Example: pagenorm(V,2) returns the magnitude of each vector page in V.

Output Arguments

collapse all

Norm value, returned as a scalar or multidimensional array. The norm gives a measure of the magnitude of the elements. By convention, pagenorm returnsNaN if the input contains any NaN values on a page.

More About

collapse all

Page-wise functions like pagenorm operate on 2-D matrices that have been arranged into a multidimensional array. For example, the elements in the third dimension of a 3-D array are commonly called pages because they stack on top of each other like pages in a book. Each page is a matrix that the function operates on.

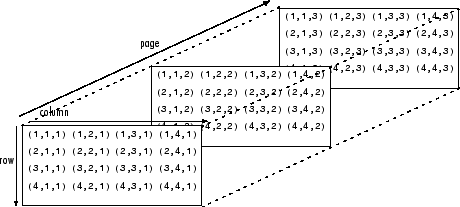
3-D array with several matrices stacked on top of each other as pages in the third dimension

You can also assemble a collection of 2-D matrices into a higher dimensional array, like a 4-D or 5-D array, and in these cases pagenorm still treats the fundamental unit of the array as a 2-D matrix that the function operates on, such asX(:,:,i,j,k,l).

The cat function is useful for assembling a collection of matrices into a multidimensional array, and the zeros function is useful for preallocating a multidimensional array.

Tips

The squeeze function is useful to reshape results from pagenorm as a column vector.
Results obtained using pagenorm are numerically equivalent to computing the norm of each of the same matrices in a for-loop. However, the two results might differ slightly due to floating-point round-off error.

Extended Capabilities

expand all

The pagenorm function supports GPU array input with these usage notes and limitations:

Pages larger than 32x32 are not supported when calculating the 2-norm of each matrix page using pagenorm(X) or pagenorm(X,2).

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2022b