pagesvd - Page-wise singular value decomposition - MATLAB (original) (raw)

Page-wise singular value decomposition

Since R2021b

Syntax

Description

[S](#mw%5Fc7e6d682-10b0-49f8-b1be-9db0cc20f842) = pagesvd([X](#mw%5Fbda08fbd-8a08-4357-ad86-555df3d2f60b)) returns the singular values of each page of a multidimensional array. Each page of the output S(:,:,i) is a column vector containing the singular values of X(:,:,i) in decreasing order. If each page of X is anm-by-n matrix, then the number of singular values returned on each page of S is min(m,n).

example

[[U](#mw%5Fceb8696c-e787-4a20-8a12-057267840c00),[S](#mw%5Fc7e6d682-10b0-49f8-b1be-9db0cc20f842),[V](#mw%5Fdb01df1e-c826-4b82-aac1-b21424a90b49)] = pagesvd([X](#mw%5Fbda08fbd-8a08-4357-ad86-555df3d2f60b)) computes the singular value decomposition of each page of a multidimensional array. The pages in the output arrays satisfy: U(:,:,i) * S(:,:,i) * V(:,:,i)' = X(:,:,i).

S has the same size as X, and each page ofS is a diagonal matrix with nonnegative singular values in decreasing order. The pages of U and V are unitary matrices.

If X has more than three dimensions, thenpagesvd returns arrays with the same number of dimensions:U(:,:,i,j,k) * S(:,:,i,j,k) * V(:,:,i,j,k)' = X(:,:,i,j,k)

example

[___] = pagesvd([X](#mw%5Fbda08fbd-8a08-4357-ad86-555df3d2f60b),"econ") produces an economy-size decomposition of the pages of X using either of the previous output argument combinations. If X is anm-by-n-by-p array, then:

m > n — Only the first n columns of each page of U are computed, and S has sizen-by-n-by-p.
m = n — pagesvd(X,"econ") is equivalent to pagesvd(X).
m < n — Only the first m columns of each page of V are computed, and S has sizem-by-m-by-p.

The economy-size decomposition removes extra rows or columns of zeros from the pages of singular values in S, along with the columns in eitherU or V that multiply those zeros in the expressionU(:,:,i) * S(:,:,i) * V(:,:,i)'. Removing these zeros and columns can improve execution time and reduce storage requirements without compromising the accuracy of the decomposition.

example

[___] = pagesvd(___,[outputForm](#mw%5F3f7af09c-d961-4021-a954-a24fd0117faa)) specifies the output format for the singular values returned in S. You can use this option with any of the previous input or output argument combinations. Specify"vector" to return each page of S as a column vector, or "matrix" to return each page of S as a diagonal matrix.

example

Examples

collapse all

Create two 6-by-6 matrices. Use the cat function to concatenate them along the third dimension into a 6-by-6-by-2 array.

A = magic(6); B = hilb(6); X = cat(3,A,B);

Calculate the singular values of each page by calling pagesvd with one output.

S = S(:,:,1) =

111.0000 50.6802 34.3839 10.1449 5.5985 0.0000

S(:,:,2) =

Create two 5-by-5 matrices. Use the cat function to concatenate them along the third dimension into a 5-by-5-by-2 array.

A = magic(5); B = hilb(5); X = cat(3,A,B);

Calculate the singular values of each array page.

s = s(:,:,1) =

65.0000 22.5471 21.6874 13.4036 11.9008

s(:,:,2) =

Perform a complete singular value decomposition on each array page.

U = U(:,:,1) =

-0.4472 -0.5456 -0.5117 -0.1954 -0.4498 -0.4472 -0.4498 0.1954 0.5117 0.5456 -0.4472 -0.0000 0.6325 -0.6325 0.0000 -0.4472 0.4498 0.1954 0.5117 -0.5456 -0.4472 0.5456 -0.5117 -0.1954 0.4498

U(:,:,2) =

-0.7679 0.6019 -0.2142 0.0472 0.0062 -0.4458 -0.2759 0.7241 -0.4327 -0.1167 -0.3216 -0.4249 0.1205 0.6674 0.5062 -0.2534 -0.4439 -0.3096 0.2330 -0.7672 -0.2098 -0.4290 -0.5652 -0.5576 0.3762

S = S(:,:,1) =

65.0000 0 0 0 0 0 22.5471 0 0 0 0 0 21.6874 0 0 0 0 0 13.4036 0 0 0 0 0 11.9008

S(:,:,2) =

1.5671         0         0         0         0
     0    0.2085         0         0         0
     0         0    0.0114         0         0
     0         0         0    0.0003         0
     0         0         0         0    0.0000

V = V(:,:,1) =

-0.4472 -0.4045 -0.2466 0.6627 0.3693 -0.4472 -0.0056 -0.6627 -0.2466 -0.5477 -0.4472 0.8202 0.0000 0.0000 0.3568 -0.4472 -0.0056 0.6627 0.2466 -0.5477 -0.4472 -0.4045 0.2466 -0.6627 0.3693

V(:,:,2) =

-0.7679 0.6019 -0.2142 0.0472 0.0062 -0.4458 -0.2759 0.7241 -0.4327 -0.1167 -0.3216 -0.4249 0.1205 0.6674 0.5062 -0.2534 -0.4439 -0.3096 0.2330 -0.7672 -0.2098 -0.4290 -0.5652 -0.5576 0.3762

Verify the relation X=U S VH for each array page, within machine precision.

e1 = norm(X(:,:,1) - U(:,:,1)*S(:,:,1)*V(:,:,1)',"fro")

e2 = norm(X(:,:,2) - U(:,:,2)*S(:,:,2)*V(:,:,2)',"fro")

Alternatively, you can use pagemtimes to check the relation for both pages simultaneously.

US = pagemtimes(U,S); USV = pagemtimes(US,"none",V,"ctranspose"); e = max(abs(X - USV),[],"all")

Create two 6-by-6 matrices. Use the cat function to concatenate them along the third dimension into a 6-by-6-by-2 array.

A = magic(6); B = hilb(6); X = cat(3,A,B);

Calculate the SVD of each array page. By default, pagesvd returns each page of singular values as a diagonal matrix when you specify multiple outputs.

U = U(:,:,1) =

-0.4082 0.5574 0.0456 -0.4182 0.3092 0.5000 -0.4082 -0.2312 0.6301 -0.2571 -0.5627 0.0000 -0.4082 0.4362 0.2696 0.5391 0.1725 -0.5000 -0.4082 -0.3954 -0.2422 -0.4590 0.3971 -0.5000 -0.4082 0.1496 -0.6849 0.0969 -0.5766 0.0000 -0.4082 -0.5166 -0.0182 0.4983 0.2604 0.5000

U(:,:,2) =

-0.7487 0.6145 -0.2403 -0.0622 0.0111 -0.0012 -0.4407 -0.2111 0.6977 0.4908 -0.1797 0.0356 -0.3207 -0.3659 0.2314 -0.5355 0.6042 -0.2407 -0.2543 -0.3947 -0.1329 -0.4170 -0.4436 0.6255 -0.2115 -0.3882 -0.3627 0.0470 -0.4415 -0.6898 -0.1814 -0.3707 -0.5028 0.5407 0.4591 0.2716

S = S(:,:,1) =

111.0000 0 0 0 0 0 0 50.6802 0 0 0 0 0 0 34.3839 0 0 0 0 0 0 10.1449 0 0 0 0 0 0 5.5985 0 0 0 0 0 0 0.0000

S(:,:,2) =

1.6189         0         0         0         0         0
     0    0.2424         0         0         0         0
     0         0    0.0163         0         0         0
     0         0         0    0.0006         0         0
     0         0         0         0    0.0000         0
     0         0         0         0         0    0.0000

V = V(:,:,1) =

-0.4082 0.6234 -0.3116 0.2495 0.2511 0.4714 -0.4082 -0.6282 0.3425 0.1753 0.2617 0.4714 -0.4082 -0.4014 -0.7732 -0.0621 -0.1225 -0.2357 -0.4082 0.1498 0.2262 -0.4510 0.5780 -0.4714 -0.4082 0.1163 0.2996 0.6340 -0.3255 -0.4714 -0.4082 0.1401 0.2166 -0.5457 -0.6430 0.2357

V(:,:,2) =

Specify the "vector" option to return each page of singular values as a column vector.

[U,S,V] = pagesvd(X,"vector")

U = U(:,:,1) =

U(:,:,2) =

S = S(:,:,1) =

111.0000 50.6802 34.3839 10.1449 5.5985 0.0000

S(:,:,2) =

V = V(:,:,1) =

V(:,:,2) =

If you specify one output argument, such as S = pagesvd(X), then pagesvd switches behavior to return each page of singular values as a column vector by default. In that case, you can specify the "matrix" option to return each page of singular values as a diagonal matrix.

Create a 10-by-3 matrix with random integer elements.

Perform both a complete decomposition and an economy-size decomposition on the matrix.

U = 10×10

-0.2554 -0.1828 0.6086 -0.6120 -0.0623 -0.2365 -0.1841 0.0165 -0.2369 -0.0792 -0.3408 0.4291 0.0365 0.1237 -0.2953 0.3040 0.0346 -0.3966 -0.3014 -0.5041 -0.3018 -0.3274 -0.6272 -0.0847 -0.3313 -0.3920 -0.2374 -0.2006 -0.1896 0.0717 -0.3560 -0.2919 0.3996 0.7531 -0.0136 -0.1963 -0.1046 0.0518 -0.0521 0.0788 -0.3711 -0.0109 -0.1957 -0.0519 0.8784 0.0025 -0.0413 -0.1224 -0.1273 -0.1289 -0.1298 -0.5635 -0.0331 -0.0842 -0.0685 0.7933 -0.1005 0.0004 -0.0259 0.1119 -0.2002 -0.2327 -0.0099 -0.0782 -0.0595 -0.0962 0.9398 -0.0274 -0.0524 0.0117 -0.3278 0.1769 -0.1847 -0.0238 -0.0987 0.0714 -0.0078 0.8775 -0.1186 -0.1662 -0.4273 0.0534 0.0145 -0.1222 -0.0872 -0.0131 -0.0467 -0.0828 0.8772 -0.1140 -0.3408 0.4291 0.0365 -0.0661 -0.0416 0.1247 0.0203 -0.0831 -0.1055 0.8114

S = 10×3

10.9594 0 0 0 4.6820 0 0 0 3.4598 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

V = 3×3

-0.6167 0.3011 0.7274 -0.6282 0.3686 -0.6852 -0.4744 -0.8795 -0.0382

[Ue,Se,Ve] = pagesvd(X,"econ")

Ue = 10×3

-0.2554 -0.1828 0.6086 -0.3408 0.4291 0.0365 -0.3018 -0.3274 -0.6272 -0.3560 -0.2919 0.3996 -0.3711 -0.0109 -0.1957 -0.1298 -0.5635 -0.0331 -0.2002 -0.2327 -0.0099 -0.3278 0.1769 -0.1847 -0.4273 0.0534 0.0145 -0.3408 0.4291 0.0365

Se = 3×3

10.9594 0 0 0 4.6820 0 0 0 3.4598

Ve = 3×3

-0.6167 0.3011 0.7274 -0.6282 0.3686 -0.6852 -0.4744 -0.8795 -0.0382

With the economy-size decomposition, pagesvd only calculates the first 3 columns of Ue, and Se is 3-by-3.

Input Arguments

collapse all

Input array, specified as a matrix or multidimensional array.

Data Types: single | double
Complex Number Support: Yes

Output format of singular values, specified as one of these values:

"vector" — Each page of S is a column vector. This is the default behavior when you specify one output, as in S = pagesvd(X).
"matrix" — Each page of S is a diagonal matrix. This is the default behavior when you specify multiple outputs, as in[U,S,V] = pagesvd(X).

Example: [U,S,V] = pagesvd(X,"vector") returns the pages ofS as column vectors instead of diagonal matrices.

Example: S = pagesvd(X,"matrix") returns the pages ofS as diagonal matrices instead of column vectors.

Data Types: char | string

Output Arguments

collapse all

Left singular vectors, returned as a multidimensional array. Each pageU(:,:,i) is a matrix whose columns are the left singular vectors ofX(:,:,i).

For an m-by-n matrixX(:,:,i) with m > n, the economy-size decomposition pagesvd(X,"econ") computes only the firstn columns of each page of U. In this case, the columns of U(:,:,i) are orthogonal andU(:,:,i) is an m-by-n matrix that satisfies UHU=In.
Otherwise, pagesvd(X) returns each pageU(:,:,i) as an m-by-m unitary matrix satisfying UUH=UHU=Im. The columns of U(:,:,i) that correspond to nonzero singular values form a set of orthonormal basis vectors for the range ofX(:,:,i).

Different machines and releases of MATLAB® can produce different singular vectors that are still numerically accurate. Corresponding columns in U(:,:,i) andV(:,:,i) can flip their signs, since this does not affect the value of the expression U(:,:,i) * S(:,:,i) * V(:,:,i)'.

Singular values, returned as a multidimensional array. Each pageS(:,:,i) contains the singular values ofX(:,:,i) in decreasing order.

For an m-by-n matrixX(:,:,i):

The economy-size decomposition [U,S,V] = pagesvd(X,"econ") returns S(:,:,i) as a square matrix of ordermin([m,n]).
The complete decomposition [U,S,V] = pagesvd(X) returnsS with the same size as X.

Additionally, the singular values on each page of S are returned as column vectors or diagonal matrices depending on how you callpagesvd and whether you specify theoutputForm option:

If you call pagesvd with one output or specify the"vector" option, then each page of S is a column vector.
If you call pagesvd with multiple outputs or specify the"matrix" option, then each page of S is a diagonal matrix.

Right singular vectors, returned as a multidimensional array. Each pageV(:,:,i) is a matrix whose columns are the right singular vectors of X(:,:,i).

For an m-by-n matrixX(:,:,i) with m < n, the economy-size decomposition pagesvd(X,"econ") computes only the firstm columns of each page of V. In this case, the columns of V(:,:,i) are orthogonal andV(:,:,i) is an n-by-m matrix that satisfies VHV=Im.
Otherwise, pagesvd(X) returns each pageV(:,:,i) as an n-by-n unitary matrix satisfying VVH=VHV=In. The columns of V(:,:,i) that do_not_ correspond to nonzero singular values form a set of orthonormal basis vectors for the null space of X(:,:,i).

Different machines and releases of MATLAB can produce different singular vectors that are still numerically accurate. Corresponding columns in U(:,:,i) andV(:,:,i) can flip their signs, since this does not affect the value of the expression U(:,:,i) * S(:,:,i) * V(:,:,i)'.

More About

collapse all

Page-wise functions like pagesvd operate on 2-D matrices that have been arranged into a multidimensional array. For example, the elements in the third dimension of a 3-D array are commonly called pages because they stack on top of each other like pages in a book. Each page is a matrix that the function operates on.

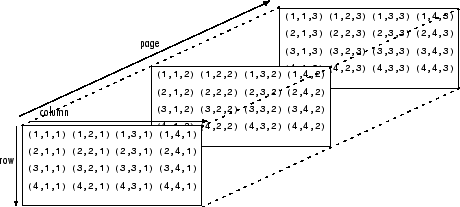
3-D array with several matrices stacked on top of each other as pages in the third dimension

You can also assemble a collection of 2-D matrices into a higher dimensional array, like a 4-D or 5-D array, and in these cases pagesvd still treats the fundamental unit of the array as a 2-D matrix that the function operates on, such asX(:,:,i,j,k,l).

The cat function is useful for assembling a collection of matrices into a multidimensional array, and the zeros function is useful for preallocating a multidimensional array.

Tips

Results obtained using pagesvd are numerically equivalent to computing the singular value decomposition of each of the same matrices in afor-loop. However, the two results might differ slightly due to floating-point round-off error.

Extended Capabilities

expand all

The pagesvd function supports GPU array input with these usage notes and limitations:

The row and column sizes of the input array must not be larger than 32.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2021b