Assembly Language (original) (raw)


music

| OSdata.com: assembly language | | OSdata.com | | ------------------------------------------------------------------------------------------ | | ---------- |

This web page examines assembly languages in a general manner. Specific examples of addressing modes and instructions from various processors are used to illustrate the general nature of assembly language.

This summary is now explained in more patient detail in a series of web pages starting at Introduction to Assembly Language.

OSdata.com is used in more than 300 colleges and universities around the world

Find out how to get similar high web traffic and search engine placement.

NOTE: If you have a slow connection, you may want to allow the entire web page to load before attempting to use any of the following in-page links:

general

Unlike the other programming languages catalogued here, assembly language is not a single language, but rather a group of languages. Each processor family (and sometimes individual processors within a processor family) has its own assembly language.

In contrast to high level languages, data structures and program structures in assembly language are created by directly implementing them on the underlying hardware. So, instead of catalogueing the data structures and program structures that can be built (in assembly language you can build any structures you so desire, including new structures nobody else has ever created), we will compare and contrast the hardware capabilities of various processor families.

This web page does not attempt to teach how to program in assembly language. Because of the close relationship between assembly languages and the underlying hardware, this web page will discuss hardware implementation as well as software.

If you aren’t fairly familiar with how computers work, you should probably first read basics of computer hardware or this page won’t make any sense at all.

history

history: The oldest non-machine language, allowing for a more human readable method of writing programs than writing in binary bit patterns (or even hexadecimal patterns).

comparison of assembly and high level languages

Assembly languages are close to a one to one correspondence between symbolic instructions and executable machine codes. Assembly languages also include directives to the assembler, directives to the linker, directives for organizing data space, and macros. Macros can be used to combine several assembly language instructions into a high level language-like construct (as well as other purposes). There are cases where a symbolic instruction is translated into more than one machine instruction. But in general, symbolic assembly language instructions correspond to individual executable machine instructions.

High level languages are abstract. Typically a single high level instruction is translated into several (sometimes dozens or in rare cases even hundreds) executable machine language instructions. Some early high level languages had a close correspondence between high level instructions and machine language instructions. For example, most of the early COBOL instructions translated into a very obvious and small set of machine instructions. The trend over time has been for high level languages to increease in abstraction. Modern object oriented programming languages are highly abstract (although, interestingly, some key object oriented programming constructs do translate into a very compact set of machine instructions).

Assembly language is much harder to program than high level languages. The programmer must pay attention to far more detail and must have an intimate knowledge of the processor in use. But high quality hand crafted assembly language programs can run much faster and use much less memory and other resources than a similar program written in a high level language. Speed increases of two to 20 times faster are fairly common, and increases of hundreds of times faster are occassionally possible. Assembly language programming also gives direct access to key machine features essential for implementing certain kinds of low level routines, such as an operating system kernel or microkernel, device drivers, and machine control.

High level programming languages are much easier for less skilled programmers to work in and for semi-technical managers to supervise. And high level languages allow faster development times than work in assembly language, even with highly skilled programmers. Development time increases of 10 to 100 times faster are fairly common. Programs written in high level languages (especially object oriented programming languages) are much easier and less expensive to maintain than similar programs written in assembly language (and for a successful software project, the vast majority of the work and expense is in maintenance, not initial development).

For information on how to interface high level languages and assembly languages, see[assembly/high level language interface](./asm/highlvl.htm #highlevelinterface)

availability

availability: Assemblers are available for just about every processor ever made. Native assemblers produce object code on the same hardware that the object code will run on. Cross assemblers produce object code on different hardware that the object code will run on.

structure

format: free form or column (depends on the assembly langauge)

nature: procedural language with one to one correspondence between language mnemonics and executable machine instructions.

“Assembler languages occupy a unique place in the computing world. Since most assmebler-language statements are symbolic of individual machine-language instructions, the assembler-language programmer has the full power of the computer at his disposal in a way that users of other languages do not. Because of the direct relationship between assembler language and machine language, assembler language is used when high efficiency of programs is needed, and especially in areas of application that are so new and amorphous that existing program-oriented languages are ill-suited for describing the procedures to be followed.” —Assembler Language Programming by George W. Struble, page viib1

“Perhaps the most glaring difference among the three types of languages [high level, assembly, and machine] is that as we move from high-level languages to lower levels, the code gets harder to read (with understanding). The major advantages of high-level languages are that they are easy to read and are machine independent. The instructions are written in a combination of English and ordinary mathematical notation, and programs can be run with minor, if any, changes on different computers.” —VAX-11 Assembly Language Programming by Sara Baase, page 1b2

“The second most visible difference among the different types of languages is that several lines of assembly language are needed to encode one line of a high-level language program.” —VAX-11 Assembly Language Programming by Sara Baase, page 2b2

“There are a number of situations in which it is very desirable to use assembler language routines to do part of a job, and use some higher-level language for other parts. It makes sense to use higher-level languages such as Fortran, COBOL, or PL/I for parts of procedures for which they are well-suited, and supplement with assembler language routines for those parts of procedures for which the higher-level language is awkward or inefficient.” —Assembler Language Programming by George W. Struble, page 427b1

“If one has a choice between assembly language and a high-level language, why choose assembly language? The fact that the amount of programming done in assembly language is quite small compared to the amount done in high-level languages indicates that one generally doesn’t choose assembly language. However, there are situations where it may not be convenient, efficient, or possible to write programs in hihg-level languages. … Programs to control and communicate with peripheral devices (input and output devices) are usually written in assembly language because they use special instructions that are not available in high-level languages, and they must be very efficient. Some systems programs are written in assembly language for similar reasons. In general, since high-level languages are designed without the features of a particular machine in mind and a compiler must do its job in a standardized way to accomodate all valid programs, there are situations where to take advantage of special features of a machine, to program some details that are inaccessible from a high-level language, or perhaps to increase the efficiency of a program, one may reasonably choose to write in assembly language.” —VAX-11 Assembly Language Programming by Sara Baase, page 3-4b2

“In situations where programming in a high-level language is not appropriate, it is clear that assembly language is to be preferred to machine language. Assembly language has a number of advantages over machine code aside from the obvious increase in readability. One is that the use of symbolic names for data and instruction labels frees the programmer from computing and recomputing the memory locations whenever a change is made in a program. Another is that assembly languages generally have a feature, called macros, that frees the [programmer] from having to repeat similar sections of code used in several places in a program. Assemblers fo many bookkeeping and other tasks for the user. Often compilers translate into assembly language rather than machine code.” —VAX-11 Assembly Language Programming by Sara Baase, page 3b2

kinds of processors

Processors can broadly be divided into the categories of: CISC, RISC, hybrid, and special purpose.

Complex Instruction Set Computers (CISC) have a large instruction set, with hardware support for a wide variety of operations. In scientific, engineering, and mathematical operations with hand coded assembly language (and some business applications with hand coded assembly language), CISC processors usually perform the most work in the shortest time.

Reduced Instruction Set Computers (RISC) have a small, compact instruction set. In most business applications and in programs created by compilers from high level language source, RISC processors usually perform the most work in the shortest time.

Hybrid processors are some combination of CISC and RISC approaches, attempting to balance the advantages of each approach.

Special purpose processors are optimized to perform specific functions. Digital signal processors and various kinds of co-processors are the most common kinds of special purpose processors.

Hypothetical processors are processors that don’t exist yet (and may never exist). Sometimes these are processors in the design phase. Sometimes these are processors used for theoretical work. The most famous hypothetical processor is MIX (or 1009), a hypothetical teaching processor created by Donald E. Knuth for presenting computer algorithms in his famous series “The Art of Computer Programming” (discussed in the Basic Concepts section of Volume I, Fundamental Algorithms).

data representation

Most data structures are abstract structures and are implemented by the programmer with a series of assembly language instructions. Many cardinal data types (bits, bit strings, bit slices, binary integers, binary floating point numbers, binary encoded decimals, binary addresses, characters, etc.) are implemented directly in hardware for at least parts of the instruction set. Some processors also implement some data structures in hardware for some instructions — for example, most processors have a few instructions for directly manipulating character strings.

An assembly language programmer has to know how the hardware implements these cardinal data types. Some examples: Two basic issues are bit ordering (big endian or little endian) and number of bits (or bytes). The assembly language programmer must also pay attention to word length and optimum (or required) addressing boundaries. Composite data types will also include details of hardware implementation, such as how many bits of mantissa, characteristic, and sign, as well as their order. In many cases there are machine specific encodings for some data types, as well as choice of character codes (such as ASCII or EBCDIC) for character and string implementations.

data size

The basic building block is the bit, which can contain a single piece of binary data (true/false, zero/one, north/south, positive/negative, high/low, etc.).

Bits are organized into larger groupings to store values encoded in binary bits. The most basic grouping is the byte. A byte is the smallest normally addressable quantum of main memory (which can be different than the minimum amount of memory fetched at one time). In modern computers this is almost always an eight bit byte, so much so that many skilled programmers believe that a byte is defined as being always eight bits. In the past there have been computers with seven, eight, twelve, and sixteen bits. There have also been bit slice computers where the common memory addressing approach is by single bit; in these kinds of computers the term byte actually has no meaning, although eight bits on these computers are likely to be called a byte. Throughout the rest of this discussion, assume the standard eight bit byte applies unless specifically stated otherwise.

A nibble is half a byte, or four bits.

A word is the default data size for a processor. The default size does not apply in all cases. The word size is chosen by the processor’s designer(s) and reflects some basic hardware issues (such as internal or external buses). The most common word sizes are 16 and 32, but words have ranged from 16 to 60 bits. Typically there will be additional data sizes that are defined relative to the size of a word: halfword, half the size of a word; longword, usually double the size of a word; doubleword, usually double the size of a word (sometimes double the size of a longword); and quadword, four times the size of a word. Whether or not there is a space between the size designation and “word” is designated by the manufacturer, and varies by processor.

Some processors require that data be aligned. That is, two byte quantities must start on byte addresses that are multiples of two; four byte quantities must start on byte addresses that are multiples of four; etc. The general rule follows a progression of exponents of two (2, 4, 8, 16, ƒ). Some processors allow data to be unaligned, but this usually results in a slow down in performance.

endian

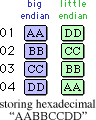
Endian is the ordering of bytes in multibyte scalar data. The term comes from Jonathan Swift’s Gulliver’s Travels. For a given multibyte scalar value, big- and little-endian formats are byte-reversed mappings of each other. While processors handle endian issues invisibly when making multibyte memory accesses, knowledge of endian is vital when directly manipulating individual bytes of multibyte scalar data and when moving data across hardware platforms.

Big endian stores scalars in their “natural order”, with most significant byte in the lowest numeric byte address. Examples of big endian processors are the IBM System 360 and 370, Motorola 680x0, Motorola 68300, and most RISC processors.

Little endian stores scalars with the least significant byte in the lowest numeric byte address. Examples of little endian processors are the Digital VAX and Intel x86 (including Pentium).

Bi-endian processors can run in either big endian or little endian mode under software control. An example is the Motorola/IBM PowerPC, which has two separate bits in the Machine State Register (MSR) for controlling endian: the ILE bit controls endian during interrupts and the LE bit controls endian for all other processes. Big endian is the default for the PowerPC.

number systems

Binary is a number system using only ones and zeros (or two states).

Decimal is a number system based on ten digits (including zero).

Hexadecimal is a number system based on sixteen digits (including zero).

Octal is a number system based on eight digits (including zero).

Duodecimal is a number system based on twelve digits (including zero).

binary octal decimal duodecimal hexadecimal
0 0 0 0 0
1 1 1 1 1
10 2 2 2 2
11 3 3 3 3
100 4 4 4 4
101 5 5 5 5
110 6 6 6 6
111 7 7 7 7
1000 10 8 8 8
1001 11 9 9 9
1010 12 10 A A
1011 13 11 B B
1100 14 12 10 C
1101 15 13 11 D
1110 16 14 12 E
1111 17 15 13 F
10000 20 16 14 10
10001 21 17 15 11
10010 22 18 16 12
10011 23 19 17 13
10100 24 20 18 14
10101 25 21 19 15
10110 26 22 1A 16
10111 27 23 1B 17
11000 30 24 20 18

number representations

integer representations

Sign-magnitude is the simplest method for representing signed binary numbers. One bit (by universal convention, the highest order or leftmost bit) is the sign bit, indicating positive or negative, and the remaining bits are the absolute value of the binary integer. Sign-magnitude is simple for representing binary numbers, but has the drawbacks of two different zeros and much more complicates (and therefore, slower) hardware for performing addition, subtraction, and any binary integer operations other than complement (which only requires a sign bit change).

In one’s complement representation, positive numbers are represented in the “normal” manner (same as unsigned integers with a zero sign bit), while negative numbers are represented by complementing all of the bits of the absolute value of the number. Numbers are negated by complementing all bits. Addition of two integers is peformed by treating the numbers as unsigned integers (ignoring sign bit), with a carry out of the leftmost bit position being added to the least significant bit (technically, the carry bit is always added to the least significant bit, but when it is zero, the add has no effect). The ripple effect of adding the carry bit can almost double the time to do an addition. And there are still two zeros, a positive zero (all zero bits) and a negative zero (all one bits).

In two’s complement representation, positive numbers are represented in the “normal” manner (same as unsigned integers with a zero sign bit), while negative numbers are represented by complementing all of the bits of the absolute value of the number and adding one. Negation of a negative number in two’s complement representation is accomplished by complementing all of the bits and adding one. Addition is performed by adding the two numbers as unsigned integers and ignoring the carry. Two’s complement has the further advantage that there is only one zero (all zero bits). Two’s complement representation does result in one more negative number (all one bits) than positive numbers.

Two’s complement is used in just about every binary computer ever made. Most processors have one more negative number than positive numbers. Some processors use the “extra” neagtive number (all one bits) as a special indicator, depicting invalid results, not a number (NaN), or other special codes.

In unsigned representation, only positive numbers are represented. Instead of the high order bit being interpretted as the sign of the integer, the high order bit is part of the number. An unsigned number has one power of two greater range than a signed number (any representation) of the same number of bits.

bit pattern sign-mag. one’s comp. two’s comp unsigned
000 0 0 0 0
001 1 1 1 1
010 2 2 2 2
011 3 3 3 3
100 -0 -3 -4 4
101 -1 -2 -3 5
110 -2 -1 -2 6
111 -3 -0 -1 7

floating point representations

Floating point numbers are the computer equivalent of “scientific notation” or “engineering notation”. A floating point number consists of a fraction (binary or decimal) and an exponent (bianry or decimal). Both the fraction and the exponent each have a sign (positive or negative).

In the past, processors tended to have proprietary floating point formats, although with the development of an IEEE standard, most modern processors use the same format. Floating point numbers are almost always binary representations, although a few early processors had (binary coded) decimal representations. Many processors (especially early mainframes and early microprocessors) did not have any hardware support for floating point numbers. Even when commonly available, it was often in an optional processing unit (such as in the IBM 360/370 series) or coprocessor (such as in the Motorola 680x0 and pre-Pentium Intel 80x86 series).

Hardware floating point support usually consists of two sizes, called single precision (for the smaller) and double precision for the larger. Usually the double precision format had twice as many bits as the single precision format (hence, the names single and double). Double precision floating point format offers greater range and precision, while single precision floating point format offers better space compaction and faster processing.

F_floating format (single precision floating), DEC VAX, 32 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 15 bits of an excess 128 binary exponent, followed by a normalized 24-bit fraction with the redundant most significant fraction bit not represented. Zero is represented by all bits being zero (allowing the use of a longword CLR to set a F_floating number to zero). Exponent values of 1 through 255 indicate true binary exponents of -127 through 127. An exponent value of zero together with a sign of zero indicate a zero value. An exponent value of zero together with a sign bit of one is taken as reserved (which produces a reserved operand fault if used as an operand for a floating point instruction). The magnitude is an approximate range of .29*10-38 through 1.7*1038. The precision of an F_floating datum is approximately one part in 223, or approximately seven (7) decimal digits).

32 bit floating format (single precision floating), AT&T DSP32C, 32 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 23 bits of a normalized two’s complement fractional part of the mantissa, followed by an eight bit exponent. The magnitude of the mantissa is always normalized to lie between 1 and 2. The floating point value with exponent equal to zero is reserved to represent the number zero (the sign and mantissa bits must also be zero; a zero exponent with a nonzero sign and/or mantissa is called a “dirty zero” and is never generated by hardware; if a dirty zero is an operand, it is treated as a zero). The range of nonzero positive floating point numbers is N = [1 * 2-127, [2-2-23] * 2127] inclusive. The range of nonzero negative floating point numbers is N = [-[1 + 2-23] * 2-127, -2 * 2127] inclusive.

40 bit floating format (extended single precision floating), AT&T DSP32C, 40 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 31 bits of a normalized two’s complement fractional part of the mantissa, followed by an eight bit exponent. This is an internal format used by the floating point adder, accumulators, and certain DAU units. This format includes an additional eight guard bits to increase accuracy of intermediate results.

D_floating format (double precision floating), DEC VAX, 64 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 15 bits of an excess 128 binary exponent, followed by a normalized 48-bit fraction with the redundant most significant fraction bit not represented. Zero is represented by all bits being zero (allowing the use of a quadword CLR to set a D_floating number to zero). Exponent values of 1 through 255 indicate true binary exponents of -127 through 127. An exponent value of zero together with a sign of zero indicate a zero value. An exponent value of zero together with a sign bit of one is taken as reserved (which produces a reserved operand fault if used as an operand for a floating point instruction). The magnitude is an approximate range of .29*10-38 through 1.7*1038. The precision of an D_floating datum is approximately one part in 255, or approximately 16 decimal digits).

address space

Address space is the maximum amount of memory that a processor can address. Some processors use a multi-level addressing scheme, with main memory divided into segments or pages and some or all instructions mapping into the current segment(s) or page(s).

register set

Registers are fast memory, almost always connected to circuitry that allows various arithmetic, logical, control, and other manipulations, as well as possibly setting internal flags.

Most early computers had only one data register that could be used for arithmetic and logic instructions. Often there would be additional special purpose registers set aside either for temporary fast internal storage or assigned to logic circuits to implement certain instructions. Some early computers had one or two address registers that pointed to a memory location for memory accesses (a pair of address registers typically would act as source and destination pointers for memory operations). Computers soon had multiple data registers, address registers, and sometimes other special purpose registers. Some computers have general purpose registers that can be used for both data and address operations. Every digital computer using a von Neumann architecture has a register (called the program counter) that points to the next executable instruction. Many computers have additional control registers for implementing various control capabilities. Often some or all of the internal flags are combined into a flag or status register.

accumulators

Accumulators are registers that can be used for arithmetic, logical, shift, rotate, or other similar operations. The first computers typically only had one accumulator. Many times there were related special purpose registers that contained the source data for an accumulator. Accumulators were replaced with data registers and general purpose registers. Accumulators reappeared in the first microprocessors.

data registers

Data registers are used for temporary scratch storage of data, as well as for data manipulations (arithmetic, logic, etc.). In some processors, all data registers act in the same manner, while in other processors different operations are performed are specific registers.

address registers

Address registers store the addresses of specific memory locations. Often many integer and logic operations can be performed on address registers directly (to allow for computation of addresses).

Sometimes the contents of address register(s) are combined with other special purpose registers to compute the actual physical address. This allows for the hardware implementation of dynamic memory pages, virtual memory, and protected memory.

The number of bits of an address register (possibly combined with information from other registers) limits the maximum amount of addressable memory. A 16-bit address register can address 64K of physical memory. A 24-bit address register can address address 16 MB of physical memory. A 32-bit address register can address 4 GB of physical memory. A 64-bit address register can address 1.8446744 x 1019 of physical memory. Addresses are always unsigned binary numbers. See number of bits.

general purpose registers

General purpose registers can be used as either data or address registers.

constant registers

Constant registers are special read-only registers that store a constant. Attempts to write to a constant register are illegal or ignored. In some RISC processors, constant registers are used to store commonly used values (such as zero, one, or negative one) — for example, a constant register containing zero can be used in register to register data moves, providing the equivalent of a clear instruction without adding one to the instruction set. Constant registers are also often used in floating point units to provide such value as pi or e with additional hidden bits for greater accuracy in computations.

floating point registers

Floating point registers are special registers set aside for floating point math.

index registers

Index registers are used to provide more flexibility in addressing modes, allowing the programmer to create a memory address by combining the contents of an address register with the contents of an index register (with displacements, increments, decrements, and other options). In some processors, there are specific index registers (or just one index register) that can only be used only for that purpose. In some processors, any data register, address register, or general register (or some combination of the three) can be used as an index register.

base registers

Base registers or segment registers are used to segment memory. Effective addresses are computed by adding the contents of the base or segment register to the rest of the effective address computation. In some processors, any register can serve as a base register. In some processors, there are specific base or segment registers (one or more) that can only be used for that purpose. In some processors with multiple base or segment registers, each base or segment register is used for different kinds of memory accesses (such as a segment register for data accesses and a different segment register for program accesses).

control registers

Control registers control some aspect of processor operation. The most universal control register is the program counter.

program counter

Almost every digital computer ever made uses a program counter. The program counter points to the memory location that stores the next executable instruction. Branching is implemented by making changes to the program counter. Some processor designs allow software to directly change the program counter, but usually software only indirectly changes the program counter (for example, a JUMP instruction will insert the operand into the program counter). An assembler has a location counter, which is an internal pointer to the address (first byte) of the next location in storage (for instructions, data areas, constants, etc.) while the source code is being converted into object code.

The VAX uses the 16th of 16 general purpose registers as the program counter (PC). Almost the entire instruction set can directly manipulate the program counter, allowing a very rich set of possible kinds of branching.

The program counter in System/360 and 370 machines is contained in bits 40-63 of the program status word (PSW), which is directly accessible by some instructions.

processor flags

Processor flags store information about specific processor functions. The processor flags are usually kept in a flag register or a general status register. This can include result flags that record the results of certain kinds of testing, information about data that is moved, certain kinds of information about the results of compations or transformations, and information about some processor states. Closely related and often stored in the same processor word or status register (although often in a privileged portion) are control flags that control processor actions or processor states or the actions of certain instructions.

A few typical result flags (with processors that include them):

Some conditions are determined by combining multiple flags. For example, if a processor has a negative flag and a zero flag, the equivalent of a positive flag is the case of both the negative and zero flags both simultaneously being cleared.

A few typical control flags (with processors that include them):

stack pointer

Stack pointers are used to implement a processor stack in memory. In many processors, address registers can be used as generic data stack pointers and queue pointers. A specific stack pointer or address register may be hardwired for certain instructions. The most common use is to store return addresses, processor state information, and temporary variables for subroutines.

subroutine return pointer

Some RISC processors include a special subroutine return pointer rather than using a stack in memory. The return address for subroutine calls is stored in this register rather than in memory. More than one level of subroutine calls requires storing and saving the contents of this register to and from memory.

address modes

The basic addressing modes are: register direct, moving date to or from a specific register; register indirect, using a register as a pointer to memory; program counter-based, using the program counter as a reference point in memory; absolute, in which the memory addressis contained in the instruction; and immediate, in which the data is contained in the instruction. Some instructions will have an inherent or implicit address (usually a specific register or the memory contents pointed to by a specific register) that is implied by the instruction without explicit declaration.

One approach to processors places an emphasis on flexibility of addressing modes. Some engineers and programmers believe that the real power of a processor lies in its addressing modes. Most addressing modes can be created by combining two or more basic addressing modes, although building the combination in software will usually take more time than if the combination addressing mode existed in hardware (although there is a trade-off that slows down all operations to allow for more complexity).

In a purely othogonal instruction set, every addressing mode would be available for every instruction. In practice, this isn’t the case.

Virtual memory, memory pages, and other hardware mapping methods may be layered on top of the addressing modes.

register direct

In register direct address mode, the source and/or destination is a register.

Many processors distinguish between data and address register operations (note, in some cases a general purpose register can act as eeither an address or data register).

In data register direct operations, flags are typically set or cleared. Data that is smaller than the register may be sign extended or zero filled to fill the entire register, or may be placed only in the portion of the register necessary for the size of the data, leaving the rest of the register unchanged.

In register to register (RR) operations, data is transferred from one register to another register or an instruction uses a source and destination register.

In address register direct operations, flags are not normally set or cleared. The address is usually sign extended to the full address size of the processor.

register indirect

In register indirect address mode, the contents of the designated register are used as a pointer to memory. Variations of register indirect include the use of post- or pre- increment, post- or pre- decrement, and displacements.

In address register indirect operations, the designated register is used as a pointer to memory.

In address register indirect with postincrement operations, the designated register is used as a pointer to memory, and then the register is incremented by the size of the operation. This is useful for a loop where the same or similar operations are performed on consecutive locations in memory. This address mode can be combined with a complimentary predecrement mode for stack and queue operations.

In address register indirect with predecrement operations, the designated register is decremented by the size of the operations, and then the designated register is used as a pointer to memory. This is useful for a loop where the same or similar operations are performed on consecutive locations in memory. This address mode can be combined with a complimentary postincrement mode for stack and queue operations.

In address register indirect with preincrement operations, the designated register is incremented by the size of the operations, and then the designated register is used as a pointer to memory. This is useful for a loop where the same or similar operations are performed on consecutive locations in memory. This address mode can be combined with a complimentary postdecrement mode for stack and queue operations.

In address register indirect with postdecrement operations, the designated register is used as a pointer to memory, and then the register is decremented by the size of the operation. This is useful for a loop where the same or similar operations are performed on consecutive locations in memory. This address mode can be combined with a complimentary preincrement mode for stack and queue operations.

In address register indirect with displacement operations, the contents of the designated register are modified by adding or subtracting a dispacement integer, then used as a pointer to memory. The displacement integer is stored in the instruction, and if shorter than the length of a the processor’s address space (the normal case), sign-extended before addition (or subtraction).

register indirect with index register

In a register indirect with index register mode, two registers are added together to form the effective address of a pointer to memory. These are sometimes called the base register and index register. Many processors will have limits on which registers can be used for the base register and/or which registers can be used for the index register.

In address/base register indirect with index register operations, the contents of the index register are added to the contents of the base address register to form an effective address in memory. Some processors allow for designating that less than the full size of the index register be used in the computation, with the designated low order portion of the index register being sign-extended for the effective address computation. Some processors require that a designated low order portion of the index register be used in the computation, with the designated low order portion of the index register being sign-extended for the effective address computation.

In address/base register indirect with index register and displacement operations, the contents of the index register are added to the contents of the base address register and then an integer displacement is added or subtracted to form an effective address in memory. Some processors allow for designating that less than the full size of the index register be used in the computation, with the designated low order portion of the index register being sign-extended for the effective address computation. Some processors require that a designated low order portion of the index register be used in the computation, with the designated low order portion of the index register being sign-extended for the effective address computation. The integer displacement is stored in the instruction, and if shorter than the length of a the processor’s address space (the normal case), sign-extended before addition (or subtraction).

absolute address with index register

In absolute address with index register operations, the contents of an index register are added to an absolute address to form an effective address in memory.

memory indirect

In memory indirect address mode, a location in memory contains a value that is used as a pointer (with or without additional effective address computations) to another location in memory.

In memory indirect postindexed operations, the processor calculates an intermediate memory address using a base register and a base displacement. The processor accesses the designated memory location, and adds the contents of the index register and an outer displacement to the memory value to yield the effective address. If either displacement and/or the index register is shorter than the length of a the processor’s address space (the normal case), each is sign-extended before addition (or subtraction). Base and outer displacements are stored in the instruction.

In memory indirect preindexed operations, the processor calculates an intermediate memory address using a base register, a base displacement, and an index register. The processor accesses the designated memory location, and adds an outer displacement to the memory value to yield the effective address. If either displacement and/or the index register is shorter than the length of a the processor’s address space (the normal case), each is sign-extended before addition (or subtraction). Base and outer displacements are stored in the instruction.

program counter indirect

In program counter indirect addressing, the program counter is used as a reference for the effective address computation. This is most commonly used for short branching relative to the current program counter, allowing for object code that can be placed anywhere in memory.

In program counter indirect with displacement operations, the effective address is the sum of the address in the program counter and the displacement integer stored in the instruction. If the displacement integer is shorter than the length of a the processor’s address space (the normal case), it is sign-extended before addition (or subtraction).

In program counter indirect with index and displacement operations, the effective address is the sum of the address in the program counter, the contents of the index register, and the displacement integer stored in the instruction. If the displacement integer or designated portion of the index register is shorter than the length of a the processor’s address space (the normal case), each is sign-extended before addition (or subtraction).

In program counter memory indirect postindexed operations, the processor calculates an intermediate indirect memory address by adding a base displacement to the contents of the program counter. The value accessed at this memory location is added to the scaled contents of the index register and the outer displacement to yield the effective address. If either the base or outer displacement integer or designated portion of the index register is shorter than the length of a the processor’s address space (the normal case), each is sign-extended before addition (or subtraction).

In program counter memory indirect preindexed operations, the processor calculates an intermediate indirect memory address by adding a base displacement and scaled contents of an index register to the contents of the program counter. The value accessed at this memory location is added to the outer displacement to yield the effective address. If either the base or outer displacement integer or designated portion of the index register is shorter than the length of a the processor’s address space (the normal case), each is sign-extended before addition (or subtraction).

absolute address

In absolute address mode, a pointer to the effective address in memory is part of the instruction. Some processors have full and short versions of absolute addressing (with short versions only pointing to a limited area in memory, normally starting at memory location zero). Unless overridden by hardware for virtual memory mapping, programs that use this address mode can not be moved in memory.

immediate data

In immediate data address mode, the actual data is stored in the instruction. The sizes allowed for immediate data vary by processor and often by instruction (with some instructions having specific implied sizes).

inherent address

Many instructions will have one or more inherent or implicit addresses. These are addresses that are implied by the instruction rather than explicitly stated. The two most common forms of inherent address are either a specific register or a memory location designated by the contents of a specific register.

executable instructions

Executable instructions can be divided into several broad categories of related operations.

There are four general classes of machine instructions. Some instructions may have characteristics of more than one major group. The four general classes of machine instructions are: computation, data transfer, sequencing, and environment control.

data movement

Data movement instructions move data from one location to another. The source and destination locations are determined by the addressing modes, and can be registers or memory. Some processors have different instructions for loading registers and storing to memory, while other processors have a single instruction with flexible addressing modes. Data movement instructions generally have the greatest options for addressing modes. Data movement instructions typically come in a variety of sizes. Data movement instructions destroy the previous contents of the destination. Data movement instructions typically set and clear processor flags. When the destination is a register and the data is smaller than the full register size, the data might be placed only in the low order bits (leaving high order bits unchanged), or might be zero- or sign-extended to fill the entire register (some processors only use one choice, others permit the programmer to choose how this is handled). Register to register operations can usually have the same source and destination register.

Earlier processors had different instructions and different names for different kinds of data movement, while most modern processors group data movement into a single symbolic name, with different kinds of data movement being indicated by address mode and size designation. A load instruction loads a register from memory. A store instruction stores the contents of a register into memory. A transfer instruction loads a register from another register. In processors that have separate names for different kinds of data moves, a memory to memory data move might be specially designated as a “move” instruction.

An exchange instruction exchanges the contents of two registers, two memory locations, or a register and a memory location (although some processors only have register-register exchanges or other limitations).

Some processors include versions of data movement instructions that can perform simple operations during the data move (such as compliment, negate, or absolute value).

Some processors include instructions that can save (to memory) or restore (from memory) a block of registers at one time (useful for implementing subroutines).

Some processors include instructions that can move a block of memory from one location to another at one time. If a processor includes string instructions, then there will usually be a string instruction that moves a string from one location in memory to another.

address movement

Address movement instructions move addresses from one location to another. The source and destination locations are determined by the addressing modes, and can be registers or memory. Address movement instructions can come in a variety of sizes. Address movement instructions destroy the previous contents of the destination. Address movement instructions typically do not modify processor flags. When the destination is a register and the address is smaller than the full register size, the data might be placed only in the low order bits (leaving high order bits unchanged), or might be zero- or sign-extended to fill the entire register (some processors only use one choice, others permit the programmer to choose how this is handled).

integer arithmetic

For most processors, integer arithmetic is faster than floating point arithmetic. This can be reversed in special cases such digital signal processors.

The basic four integer arithmetic operations are addition, subtraction, multiplication, and division. Arithmetic operations can be signed or unsigned (unsigned is useful for effective address computations). Some older processors don’t include hardware multiplication and division. Some processors don’t include actual multiplication or division hardware, instead looking up the answer in a massive table of results embedded in the processor.

A specialized, but common, form of addition is an increment instruction, which adds one to the contents of a register or memory location. For address computations, “increment” may mean the addition of a constant other than one. Some processors have “short” or “quick” addition instructions that extend increment to include a small range of positive values.

A specialized, but common, form of subtraction is an decrement instruction, which subtracts one from the contents of a register or memory location. For address computations, “decrement” may mean the subtraction of a constant other than one. Some processors have “short” or “quick” subtraction instructions that extend decrement to include a small range of values.

Compare instructions are used to examine one or more integers non-destructively. These are usually implemented by performing a subtraction in some shadow register or accumulator and then setting flags accordingly. Compare instructions can compare two integers, or can compare a single integer to zero. Triadic compare instructions compare a test value to an upper and lower limit, which can be useful for bounds and range checking.

Some processors have specific hardware support for large multi-byte integer arithmetic. Even if there is no specific support, generally carry and borrow flags can be used to implement software multi-byte arithmetic routines.

Some processors have other special integer arithmetic operations. A clear instruction sets a register or memory location to zero. Some processors have special instructions for setting a register to a special value (such as pi) with additional guard bits also being set appropriately. A sign extend operation takes a small value and sign extends it to a larger storage format (such as byte to word). An arithmetic complement gives the arithmetic complement of a number (one’s complement). An arithmetic negate gives the arithmetic inverse of a number (subtract from zero; two’s complement).

floating point arithmetic

On many processors, floating point arithmetic is in an optional unit or optional coprocessor rather than being included on the main processor. This allows the manufacturer to charge less for the business machines that don’t need floating point arithmetic.

The basic four floating point arithmetic operations are addition, subtraction, multiplication, and division. Some processors don’t include actual multiplication or division hardware, instead looking up the answer in a massive table of results embedded in the processor.

Compare instructions are used to examine one or more floating point numbers non-destructively. These are usually implemented by performing a subtraction in some shadow register or accumulator and then setting flags accordingly. Compare instructions can compare two floating point numbers, or can compare a single floating point number to zero.

binary coded decimals

Binary coded decimal (BCD) is a method for implementing lossless decimal arithmetic (including decimal fractions) on a binary computer. The most obvious uses involve money amounts where round-off error from using binary approximations is unacceptable.

BCD arithmetic includes BCD addition, BCD subtraction, BCD multiplication, BCD division, and BCD negate.

The Intel 80x86 series uses a two step approach for BCD arithmetic. Instead of having separate BCD instructions, the normal binary addition and subtraction instructions are used, then hardware instructions are used to adjust the results to correct BCD results. There are instuctions for both packed and unpacked adjustments.

Pack (Motorola 680x0) converts byte encoded numeric data (such as ASCII or EBCDIC characters) into binary coded decimals. Unpack (Motorola 680x0) converts binary coded decimals into byte encoded numeric data (such as ASCII or EBCDIC characters). The ASCII adjustment field is 3030;theEBCDICadjustmentfieldis3030; the EBCDIC adjustment field is 3030;theEBCDICadjustmentfieldisF0F0.

advanced math operations

data conversion

Data conversion instructions change data from one format to another.

A sign extension operation takes a small value and sign extends it to a larger storage format (such as byte to word).

A type conversion operation changes data from one format to another (such as signed two’s complement integer into binary coded decimal).

logical

Logical instructions typically work on a bit by bit basis, although some processors use the entire contents of the operands as whole flags (zero or not zero input, zero or negative one output). Typical logical operations include logical negation or logical complement (NOT), logical and (AND), logical inclusive or (OR or IOR), and logical exclusive or (XOR or EOR). Logical tests are a comparison of a value to a bit string (or operand treated as a bit string) of all zeros. Some processors have an instruction that sets or clears a bit or byte in registers or memory based on the processor condition codes.

shift and rotate

Shift and rotate instructions move bit strings (or operand treated as a bit string).

Shift instructions move a bit string (or operand treated as a bit string) to the right or left, with excess bits discarded (although one or more bits might be preserved in flags). In arithmetic shift left or logical shift left zeros are shifted into the low-order bit. In arithmetic shift right the sign bit (most significant bit) is shifted into the high-order bit. In logical shift right zeros are shifted into the high-order bit.

Rotate instructions are similar to shift instructions, ecept that rotate instructions are circular, with the bits shifted out one end returning on the other end. Rotates can be to the left or right. Rotates can also employ an extend bit for multi-precision rotates.

A swap instruction swaps the high and low order portions of a register or contents of a series of memory locations.

The carry bit typically receives the last bit shifted out of the operand. Sometimes an extend bit will receive the last bit shifted out also. Somtimes an overflow bit is used to indicate a sign change has occurred.

bit manipulation

Bit manipulation instructions manipulate a specific bit of a bit string (or operand treated as a bit string). Bit clear changes the specified bit to zero. Bit set changes the specified bit to one. Bit change modifies a specified bit, clearing a one bit to zero and setting a zero bit to one. In some processors, the value of the bit before modification is tested. Bit test examines the value of a specified bit.

Bit scan instructions search a bit string for the first bit that is set or cleared (depending on the processor).

bit field

Bit field instructions make modifications to bit fields (or operands treated as bit fields). Bit field insert inserts a value into a bit field. Bit field extract extracts a signed or unsigned value from a bit field. Bit field find first one finds the first bit that is set (one) in a bit field. Bit field test evaluates a bit field and sets or clears flags. Bit field test and setevaluates a bit field and set or clear flags then sets the bit field. Bit field test and clearevaluates a bit field and set or clear flags then clears the bit field. Bit field test and changeevaluates a bit field and set or clear flags then changes the bit field.

table operations

high level language support

Many processors have instructions designed to support constructs common in high level languages. Ironically, a few high level language constructs have been based on specific hardware instructions on specific processors. One famous example is the computed GOTO (three possible branches based on whether the tested value is positive, zero, or negative), which is based on a hardware instruction in an early IBM processor (and if anyone can loan or give me a data book on the processor, I sure would appreciate it).

Most modern processors have some kind of loop instructions. These are some variation on the theme of testing for a condition and/or making a count with a short branch back to complete a loop if the exit condition fails.

Many modern processors have some kind of hardware support for temporary data storage (for the temporary variables used in subroutines and functions), combining special hardware instructions with argument and/or frame and/or stack pointers.

Bounds check instructions are used to check if an array reference is out of bounds.

program control

Program control instructions change or modify the flow of a program.

The most basic kind of program control is the unconditional branch or unconditional jump. Branch is usually an indication of a short change relative to the current program counter. Jump is usually an indication of a change in program counter that is not directly related to the current program counter (such as a jump to an absolute memory location or a jump using a dynamic or static table), and is often free of distance limits from the current program counter.

The pentultimate kind of program control is the conditional branch or conditional jump. This gives computers their ability to make decisions and implement both loops and algorithms beyond simple formulas.

Most computers have some kind of instructions for subroutine call and return from subroutines.

There are often instructions for saving and restoring part or all of the processor state before and after subroutine calls. Some kinds of subroutine or return instructions will include some kinds of save and restore of the processor state.

Even if there are no explicit hardware instructions for subroutine calls and returns, subroutines can be implemented using jumps (saving the return address in a register or memory location for the return jump). Even if there is no hardware support for saving the processor state as a group, most (if not all) of the processor state can be saved and restored one item at a time.

NOP, or no operation, takes up the space of the smallest possible instruction and causes no change in the processor state other than an advancement of the program counter and any time related changes. It can be used to synchronize timing (at least crudely). It is often used during development cycles to temporarily or permanently wipe out a series of instructions without having to reassemble the surrounding code.

Stop or halt instructions bring the processor to an orderly halt, remaining in an idle state until restarted by interrupt, trace, reset, or external action.

Reset instructions reset the processor. This may include any or all of: setting registers to an initial value, setting the program counter to a standard starting location (restarting the computer), clearing or setting interrupts, and sending a reset signal to external devices.

condition codes

Condition codes are the list of possible conditions that can be tested during conditional instructions. Typical conditional instructions include: conditional branches, conditional jumps, and conditional subroutine calls. Some processors have a few additional data related conditional instructions, and some processors make every instruction conditional. Not all condition codes available for a processor will be implemented for every conditional instruction.

Zero is mathematically neither positive nor negative, but for processor condition codes, most processors treat zero as either a positive or a negative numbers. Processors that treat zero as a positive number include the Motorola 680x0 and Motorola 68300.

input/output

Input/Output (I/O) instructions are used to input data from peripherals, output data to peripherals, or read/write input/output controls. Early computers used special hardware to handle I/O devices. The trend in modern computers is to map I/O devices in memory, allowing the direct use of any instruction that operates on memory for handling I/O.

MIX devices

Information on the devices for the hypothetical MIX processor’s input/output instructions.

unit number peripheral block size control
t Tape unit no. i (0 i 7) 100 words M=0, tape rewound;M < 0, skip back M records;M > 0, skip forward M records
d Disk or drum unit no. d (8 d 15) 100 words position device according to X-register (extension)
16 Card reader 16 words
17 Card punch 16 words
18 Printer 24 words IOC 0(18) skips printer to top of following page
19 Typewriter and paper tape 14 words paper tape reader: rewind tape

system control

System control instructions control some basic element of the system or processor state.

Many system control instructions are privileged, meaning that only certain trusted routines are allowed to use them. This is implemented by having privilege states. The most simple version is two states: user and supervisor states. The user state can’t run any privileged instructions, while the supervisor state can run all instructions. Some processors have more than two privilege states, allowing greater granularity of freedom to increasingly trusted operations.

The most basic kind of system control instructions are those that modify the condition codes or user portion of a status register.

Closely related are instructions that modify an entire status word or status register. The more powerful version is a privileged instruction and includes access to portions of the status register that can control or modify other processes.

Machine control instructions directly affect the entire processor. Stop or halt instructions bring the processor to an orderly halt, remaining in an idle state until restarted by interrupt, trace, reset, or external action.

Reset instructions reset the processor. This may include any or all of: setting registers to an initial value, setting the program counter to a standard starting location (restarting the computer), clearing or setting interrupts, and sending a reset signal to external devices.

Trap generating instructions generate a system trap. This includes a transition to a privileged state and turns control over to a routine with supervisor permission. This allows user processes to communicate with and make requests of the operating system. Note that it is common for some parts of an operating system to run in normal user mode so as to limit potential damage if something goes wrong.

Memory management instructions control memory and how memory is mapped and accessed by user and system routines. These instructions are almost always privileged and vary greatly from processor to processor (although the general capabilities and effects are pretty standard).

coprocessor and multiprocessor operations

Multiprocessor instructions are used to coordinate activity between multiple processors.

Some multiprocessor instructions are designed to allow the processors to communicate with each other. A test and set instruction is used to implement flags or semaphores between processors. A compare and swap instruction is used to implement more sophsticated communications between multiple processors (such as counters or queue pointers) or secure updates of shared system control data structures in a multi-processing environment. Interlocked instructions are used to update counters, flags, and semaphores while locking out any other processors or devices from changing or reading the memory location while it is being updated.

trap generating

Trap generating instructions generate an exception that transfer control from software (usually application programs) to the operating system.

Operating system traps provide a mechanism to change to higher privilege levels (if they exist on the processor) and usually include a mechanism for identifying what kind of trap has occurred. This allows application programs to make requests of the operating system and may provide a hardware mechanism for switching from a user mode to a superviser, kernel, or other higher privilege level for the operating system response to the request.

A breakpoint instruction is used with external debugging hardware. The breakpoint instruction replaces an ordinary instruction (or the first part of an instruction) and relies on external debugging hardware to supply the missing instruction (or part of an instruction).

Various check instructions will test for conditions, trapping if the test fails. One common example is a check against bounds or limits.

Most processors have one or more illegal instructions. These are usually instructions that haven’t been implemented yet or instructions that have been dropped from a processor line. Many processors generate a trap or exception upon encountering an illegal instruction. Some processors will execute illegal instructions, which can lead to undocumented operations. Undocumented operations tend to change from one batch of processors to another and are highly unreliable. Some processors reserve an opcode that is guaranteed to always be illegal and always generate a trap or exception.

further reading: books:

If you want your book reviewed, please send a copy to: Milo, POB 1361, Tustin, CA 92781, USA.

Price listings are for courtesy purposes only and may be changed by the referenced businesses at any time without notice.

further reading: books: general

Structured Computer Organization, 4th edition; by Andrew S. Tanenbaum; Prentice Hall; October 1998; ISBN 0130959901; Paperback; 669 pages; $95.00; used by CS 308-273A (Principles of Assembly Languages) at McGill University School of Computer Science

Computers: An Introduction to Hardware and Software Design; by Larry L. Wear, James R. Pinkert (Contributor), William G. Lane (Contributor); McGraw-Hill Higher Education; February 1991; ISBN 0070686742; Hardcover; 544 pages; $98.60; used by CS 308-273A (Principles of Assembly Languages) at McGill University School of Computer Science

further reading: books: Motorola 680x0

68000 Family Assembly Language/Book and Disk (PWS Series in Engineering); by Alan Clements, B.Sc.; PWS Pub Co; August 1994; ISBN 0534932754; Hardcover; 720 pages; $98.95; used by CS 308-273A (Principles of Assembly Languages) at McGill University School of Computer Science

Assembly Language and Systems Programming for the M68000 Family, 2nd edition; by William Ford, William Topp; Jones & Bartlett Pub; November 1996; ISBN 0763703575; Hardcover; 890 pages; $78.95; used by CIS 260 (Honors: Machine Organization and Microcomputers) at University of Delaware Department of Department of Computer & Information Sciences

Macintosh Assembly System, version 2.0; by William Ford, William Topp; Jones & Bartlett Pub; January 1992; ISBN 0763705950; Textbook Binding; $37.50; used by CIS 260 (Honors: Machine Organization and Microcomputers) at University of Delaware Department of Department of Computer & Information Sciences

further reading: books: Motorola 68300

The Motorola Mc68332 Microcontroller: Product Design, Assembly Language Programming, and Interfacing; by Thomas L. Harman; Prentice Hall; March 1991; ISBN 0136031277; Paperback; 512 pages; $41.25; used by EE 380 (Introduction to Microprocessors) at University of Alberta Department of Electrical and Computer Engineering

further reading: books: IBM System 360/370

Assembler Language Programming The IBM System/360 and 370; 2nd edition; by George W. Struble (University of Oregon); Addison-Wesley Publishing Company; 1975, 1969; ISBN 0-201-07322-6; hardcover; 477 pages; special order

further reading: books: DEC VAX

VAX-11 Assembly Language Programming; by Sara Baase (San Diego State University); Prentice-Hall, Inc.; 1983; ISBN 0-13-940957-2; hardcover; 407 pages; special order

In Association with Amazon.com

If you want your book reviewed, please send a copy to: Milo, POB 1361, Tustin, CA 92781, USA.

Price listings are for courtesy purposes only and may be changed by the referenced businesses at any time without notice.

We are working on providing a second source.

Metrowerks CodeWarrior Discover Programming for Mac 5.0; C, C++, Java, and Pascal; PowerMac; $49.95

further reading: web sites

further reading: web sites: general

ProgramFiles.com — Programming — Assembly Language: a collection of assemblers, cross-assemblers, editors, debuggers, simulators, disassemblers, inspectors, shells, and other programs for assembly languages: 68000, 8085, MC68HC11, 80x86, 8748, and 8749

further reading: web sites: Motorola 680x0

Meet the 68000: Jack Powell’s May 1985 Digital Antic article introducing the 68000 as used in the Atari ST computers; although dated, still a valid introduction and overview of the 68000 processor

glossary of terms, symbols, and expressions: A. Clements’ gloassary of 68000 terms, symbols, and expressions

assembly language presentation: A. Clements’ presentation of the basics of 68000 assembly language programming with a simple programming example

Microprocessor Systems 1 (3D1) Notes: Michael Brady’s class notes on the basics of microprocessor systems using the 68000 as an example

Motorola M680x0 Macro Preprocessor: an SDSU student’s macro preprocessor for 680x0 assembly language

68000 Assembly Language Glossary: a UCI student’s guide to Motorola 680x0 terminology

further reading: web sites: other

Shopping for assembly language programming products; just a list of books

A web site on dozens of operating systems simply can’t be maintained by one person. This is a cooperative effort. If you spot an error in fact, grammar, syntax, or spelling, or a broken link, or have additional information, commentary, or constructive criticism, please e-mail Milo. If you have any extra copies of docs, manuals, or other materials that can assist in accuracy and completeness, please send them to Milo, PO Box 1361, Tustin, CA, USA, 92781.

Click here for our privacy policy.

home page

one level up

special topics

peer level

Made with Macintosh

This web site handcrafted on Macintosh computers using Tom Bender’s Tex-Edit Plus and served using FreeBSD .

Viewable With Any Browser

Names and logos of various OSs are trademarks of their respective owners.

Copyright © 2000, 2001, 2002, 2004 Milo

Last Updated: March 31, 2004

Created: July 9, 2000