effective refractive index (original) (raw)

Definition: a number quantifying the phase delay per unit length in a waveguide, relative to the phase delay in vacuum

Alternative term: modal index

Category: fiber optics and waveguides

• optical properties of materials

  • refractive index
    * effective refractive index
    * group index

• fiber properties

  • acceptance angle
  • bend losses
  • cut-off wavelength
  • differential mode delay
  • effective mode area
  • effective refractive index
  • group velocity dispersion
  • intermodal dispersion
  • modal bandwidth
  • mode radius
  • polarization beat length
  • propagation constant
  • propagation losses
  • V-number
  • waveguide dispersion
  • zero dispersion wavelength
  • (more topics)

Related: Mode Structure of a Multimode Fiberpropagation constantrefractive indexgroup indexwaveguidesEffective Refractive Index: Correcting a Common Belief

Units: (dimensionless)

Formula symbol: ($n_\textrm{eff}$)

Page views in 12 months: 10500

DOI: 10.61835/avr Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn

Content quality and neutrality are maintained according to our editorial policy.

What is an Effective Refractive Index?

For plane waves of light in homogeneous transparent media (e.g. in optical materials), the refractive index ($n$) can be used to quantify the increase in the wavenumber (phase change per unit length) caused by the medium: the wavenumber is ($n$) times higher than it would be in vacuum. The effective refractive index ($n_\rm{eff}$) has the analogous meaning for light propagation in a waveguide with restricted transverse extension: the ($\beta$) value (phase constant) of the waveguide (for some wavelength) is the effective index times the vacuum wavenumber: \beta = {n_{{\rm{eff}}}}\frac{{2\pi }}{\lambda }$$

The mode-dependent and frequency-dependent ($\beta$) values can be calculated with a mode solver software. (Relatively simple calculations are sufficient for LP modes, while a more general mode solver requires a rather sophisticated algorithm.) They depend on the refractive index profile of the waveguide. From frequency-dependent ($\beta$) values, one may also calculate chromatic dispersion, e.g. by numerical differentiation.

Note that the effective refractive index depends not only on the wavelength (or optical frequency) but also (for multimode waveguides) on the mode in which the light propagates. For that reason, it is also called modal index. Obviously, the effective index is not just a material property, but depends on the whole waveguide design. Its value can be obtained with numerical mode calculations, for example. It can vary substantially near a mode cut-off.

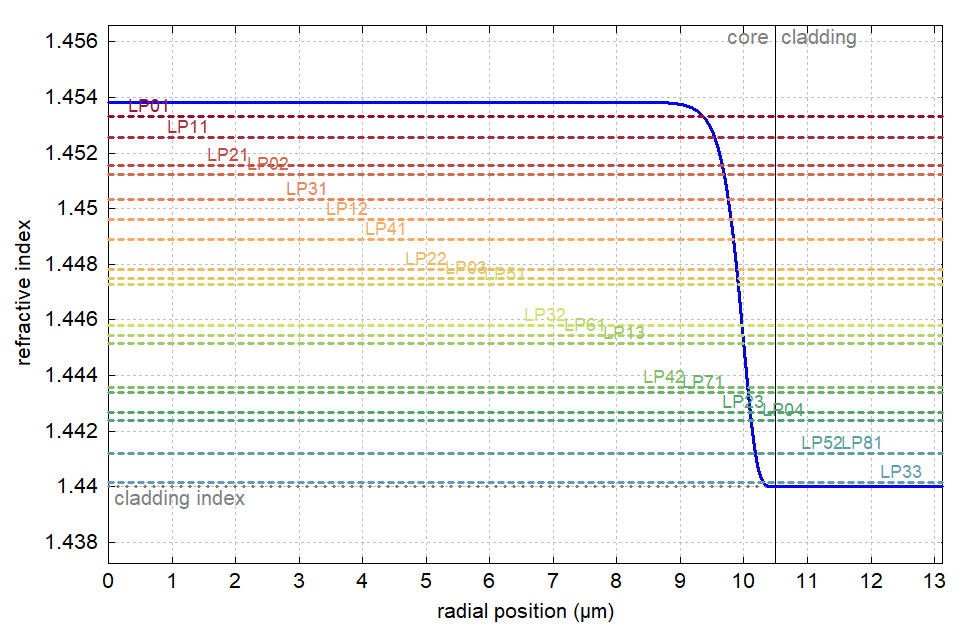
Figure 1: The effective mode indices (dashed horizontal lines) for a fiber with super-Gaussian refractive index profile (blue) at a fixed wavelength. The calculation has been done in a case study with the RP Fiber Power software.

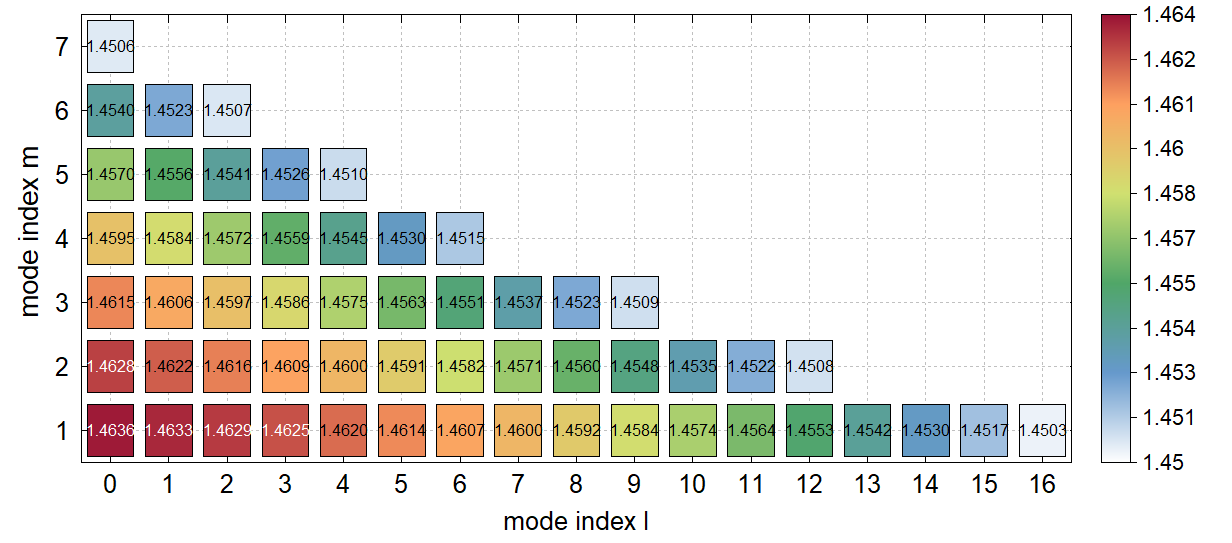
Figure 2: Distribution of effective indices in a multimode fiber.

Case Studies

Mode Structure of a Multimode Fiber

We explore various properties of guided modes of multimode fibers. We also test how the mode structure of such a fiber reacts to certain changes in the index profile, e.g. to smoothing of the index step.

Calculating Effective Indices

A mode solvermode solver is needed for calculating effective refractive indices and other properties of fiber modes. A flexible simulation tool like the RP Fiber Power software is ideal for such work.

The effective index may be a complex (rather than purely real) quantity. In that case, the imaginary part is related to gain or loss — see the article on refractive index for more details. In fiber amplifiers, for example, the imaginary part of the effective index is always far smaller than the real part — which implies that gain or loss does not have substantial effects on a length scale where diffraction and waveguiding start to become relevant.

The effective refractive index contains information on the phase velocity of light, but not on the group velocity; for the latter, one can similarly define an effective group index in analogy to the group index for plane waves in a homogeneous medium.

A common but wrong belief is that the effective refractive index is a kind of weighted average of the refractive index of core and cladding of the waveguide, with the weight factors determined by the fractions of the optical power propagating in the core and cladding. That impression may result from the common observation that higher-order modes, e.g. of a fiber, have a lower effective index and also a lower mode overlap with the core. However, consider e.g. a step-index multimode waveguide with a high numerical aperture and large core diameter. Here, all modes overlap to nearly 100% with the core (i.e. the mode overlaps are very similar), whereas the effective indices differ substantially. That demonstrates that the effective refractive index cannot be interpreted as a weighted average.

Frequently Asked Questions

What is an effective refractive index?

The effective refractive index ($n_{\rm eff}$) of a waveguide mode is a value used to quantify the phase change per unit length. It relates the mode's propagation constant ($\beta$) to the vacuum wavenumber ($2\pi/\lambda$) through the formula ($\beta = n_{\rm eff} \cdot (2\pi/\lambda)$), analogous to the refractive index for a bulk material.

Why is the effective refractive index also called the modal index?

It is also called the modal index because its value depends on the specific mode in which light propagates through the waveguide. Different modes, particularly in a multimode waveguide, will have different effective refractive indices.

What factors influence the effective refractive index?

The effective refractive index is not just a material property. It depends on the entire waveguide design (i.e., its refractive index profile), the wavelength of the light, and the specific propagation mode.

Is the effective refractive index an average of the core and cladding refractive indices?

No, that is a common misconception. The effective refractive index is not a weighted average based on the power distribution in the core and cladding. For example, in large-core fibers, different modes can have very different effective indices even when nearly 100% of their power is in the core.

How does the effective refractive index relate to the speed of light?

The effective refractive index is related to the phase velocity of a light wave in a waveguide, which describes how fast the phase of the wave propagates. It is not directly related to the group velocity, which describes the speed of a light pulse and is associated with the effective group index.

Questions and Comments from Users

Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.

Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.

By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.