A network-based gene-weighting approach for pathway analysis (original) (raw)
Introduction
Identifying biological pathways significantly regulated under various conditions has become one of the most common tasks in genome-wide expression profiling or association studies 1, 2, 3, 4. Biological pathways being investigated in such analyses can be obtained from various types of pathway databases. Several databases, such as KEGG 5, 6, WikiPathways 7 and Biocarta, manually create electronic graphs of structured pathways for cellular signaling and metabolic processes. Other databases, such as Gene Ontology (GO), PANTHER 8, 9, Reactome 10 and MSigDB 11, curate only gene composition information for pathways and usually do not provide graph representations. To develop general-purpose pathway analysis algorithms applicable to both types of pathway databases, it is a traditionally favored treatment to reduce “real” biological pathways featured with complex gene-gene linkages and topological arrangements into gene sets that are simply based on gene compositions of pathways.
The “gene set over-representation analysis” approach tests whether a gene set is over-represented in a given gene list 12. With Fisher's exact test or chi-square test, this approach holds a “competitive model” of significance assessment, in the sense that the gene set is tested against random genes from the genome 13. This approach is especially useful for studies with a very small sample size, though difficult in determining an optimal gene list from microarray data. Another approach, “gene set analysis (GSA)”, pioneered by Gene Set Enrichment Analysis (GSEA) 11, calculates a gene set statistically summarizing gene expression changes over the gene set, which are then compared to null distributions to evaluate significance. Gene set statistics proposed include the Kolmogorov-Smirnov type statistics in GSEA 11, the normalized mean of fold changes in Parametric Analysis of Gene Set Enrichment (PAGE) 14, the “maxmean” statistics in MAXMEAN-GSA 15, the quadratic sum of modified Student's T statistics in SAM-GS 16, the contrast between fold changes of genes within and outside gene sets in GAGE 17, as well as other choices such as mean 18, 19, absolute mean and mean of absolute (MeanAbs) of gene statistics 15. Choices of the null distributions are among a “competitive model”, a “self-contained model”, or a hybrid of the two 13, 15, 19. Unlike the “competitive model” where significance of a gene set is judged by comparing with the rest of genes in the genome, “self-contained model” tests whether the gene set itself is associated with the conditions under study. The “competitive model” has been adopted by Q1-test, PAGE and GAGE 14, 17, 19, the “self-contained model” by Q2-test 19, and a hybrid of the two models by GSEA and MAXMEAN-GSA 11, 15. These two approaches do not cover all gene set-based pathway analysis methods that have been proposed. For example, there are methods that test gene set association with sample conditions in logistic regression models 20, 21, 22, methods that focus on principal components of gene sets 23, 24, and methods that take only a core subset of genes for analysis 25.
Although reduction of “pathways” to “gene sets” seems inevitable to include pathway databases with gene compositions only, and also very convenient and fruitful for algorithm development, there are important issues worth critical consideration when examining carefully the difference between “pathways” and “gene sets”. In “gene sets”, the functional interactions among genes are ignored and all genes are completely equivalent to each other. This is not true in many “real” biological pathways, where some genes are indeed more “central” and “indispensable” than others, such as the p53 gene in the p53 signaling pathway. In addition, the potential curation errors in construction of pathway databases might have been misclassified into a pathway where some irrelevant genes should not be taken equivalently as other genes. Therefore, we realize that there is clearly a “constitutive non-equivalence” among genes in a pathway irrespective of the conditions under study, and that it is more appropriate to model a pathway with a set of genes with constitutively non-equivalent weights, rather than a set of essentially equivalent genes.
Here we constructed a gene functional association network based on protein-protein interactions (PPIs), co-annotations and co-expressions. We then used this network to determine the constitutive non-equivalence of genes and assign gene weights within pathways. These gene weights can be directly incorporated into classical GSA pipelines. We demonstrated that this gene-weighted GSA approach is reliable and reproducible for microarray data interpretation. We have implemented the network-based gene-weighting algorithm, as well as the gene-weighted version of GSA, in an open-source R package named GANPA (http://cran.r-project.org/web/packages/GANPA/index.html).
Results
Strategy of network-based gene weighting within pathways
Given the notion that genes are constitutively non-equivalent in pathways, we seek to develop a strategy to determine the gene non-equivalence in the form of gene weight. We reason that, if one gene is specifically associated with more genes in the pathway than expected, it is more likely to be functionally “important” in this pathway, and less likely to be randomly introduced into this pathway by curation errors. This association specificity could be estimated in a hypergeometric sampling model, and used to judge how strongly a gene is related to the pathway (Figure 1A, Materials and Methods).
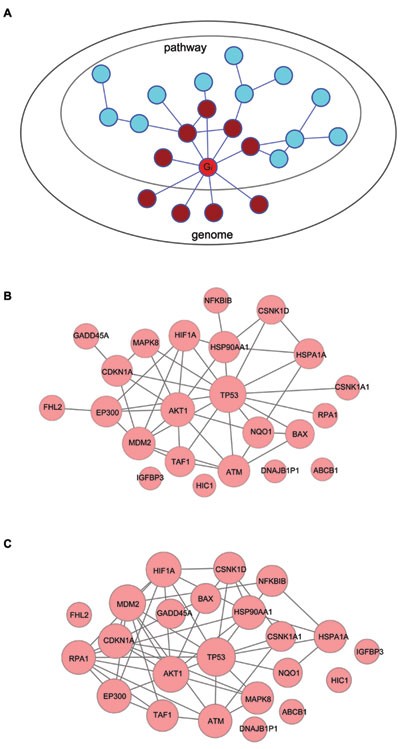
Figure 1
Network-based gene-weighting algorithm. (A) An illustration of the gene-weighting algorithm. A gene functional association network is required to provide inter-gene association linkages. For any gene G i (red) in a given pathway S of K genes, its M i functional associated genes (brown) are distributed within (X i) and outside (M _i_-X i) the pathway. A hypergeometric distribution model can be used to estimate the specific associations between G i and S, which reflects G i's contribution to the pathway (see Materials and Methods). (B) Inter-gene functional associations and gene weights determined with gNET for the p53 hypoxia pathway (Biocarta). Each node represents a gene and its size proportional to gene weight. Genes are linked by functional associations in gNET. Genes with no functional associations with other genes are also shown. (C) Inter-gene functional associations and gene weights determined with FunCoup for the p53 hypoxia pathway (Biocarta). Genes are linked by functional associations in FunCoup.
To achieve this goal, one practical way is to establish a gene functional association network 26, which could provide inter-gene linkages for evaluating gene-to-pathway associations. We have constructed a comprehensive gene functional association network, referred to as gNET hereafter, from three types of gene associations: PPIs, co-annotation in GO Biological Process (BP), and co-expression in large-scale gene expression microarray data (Materials and Methods, Supplementary information, Data S2). We have controlled the association specificity by filtering PPIs without PubMed references and BP terms that are too general to provide specific association information (Materials and Methods, Supplementary information, Data S1). Using a gene functional association network has several appealing features as compared with the inter-gene linkages recorded in certain databases such as KEGG (Supplementary information, Data S1).
Such a network-based gene-weighting strategy is general-purpose and suitable for almost all public pathway databases in that it requires no additional information except for gene compositions. We performed a number of tests and found that this strategy provided biologically consistent gene weights for various pathways and functional gene sets (Supplementary information, Tables S1 and S2, and Data S3). Taking p53 gene for example, the computed gene weights suggest that it acts as a core gene in pathways such as the p53 hypoxia signaling pathway (Figure 1B) and p53 signaling pathway (with a high weight ranking top 1), and it participates but not dominates in pathways such as Huntington's disease pathway and cell cycle checkpoint pathway (ranking 72 and 102, respectively; Supplementary information, Table S1). Another example is the EGFR gene, which is suggested to be a more central gene in some pathways (such as AT1R pathway 27 and EGF pathway 28) than others (such as calcium signaling pathway 29 and cytokine-cytokine receptor interaction 30) (Supplementary information, Table S2). We have tested another functional association network named FunCoup 31, which produced similar gene weights in the pathways, with p53 hypoxia signaling pathway again taken as an example (Figure 1C). For those genes that have no functional associations with other genes in the pathway, we simply assigned a minimum weight (Figure 1B and 1C, Materials and Methods). This way, the gene composition information from pathway databases is always retained even when the gene association network suggests a poor association with the pathway for some genes. Although this approach seems a bit conservative, it could help improve the stability of the gene weight estimates, since a gene association network might not be necessarily comprehensive and accurate enough for all pathways from various databases.
Stability and robustness of the network-based gene weights
We next addressed whether the gene weights determined from the above strategy are indeed stable, knowing the false positives that could have been introduced in the data sources of gNET, such as PPIs, co-annotation and co-expression. As a previous report on human PPI network has suggested, there was ∼85.5% verification rate of yeast-two hybrid protein pairs by co-affinity purifications, indicating ∼14.5% false positiveness 32. We performed two types of perturbation to gNET to re-calculate gene weights for 833 pathways (KEGG, Biocarta and Reactome) extracted from the MSigDB collection (version 3.0) at Broad Institute. First, 30% of the linkages in gNET were removed randomly for 1 000 times. Second, all the linkages in gNET were randomized, while retaining the original network topology (that is, we shuffled the node labels but retained topological properties such as node degree distribution). We again took the p53 hypoxia signaling pathway as an example. Compared with the nearly complete destruction of gene weights by edge randomization, the gene weights were only quite slightly affected by the 30% edge removal perturbation (Figure 2A and 2B). Overall, for all the 833 pathways, network randomizations have caused an average decrease of gene weights as dramatically as more than 40% for a majority of the 833 pathways, whereas the 30% linkage removals only have a very minor effect on gene weights (around 10% decrease) (Figure 2C). Further, we have tested another functional association network, FunCoup 31, on weighting genes in the pathways (Supplementary information, Data S1). The weights assigned by these two independently constructed networks are quite similar (Figure 1C and data not shown).
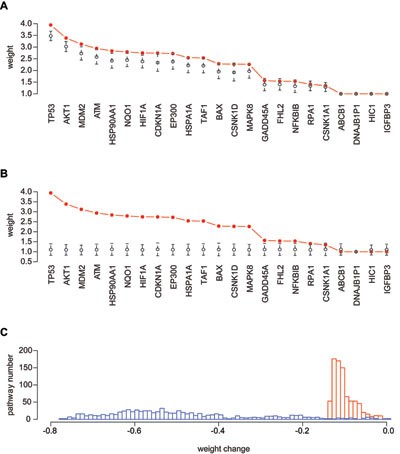
Figure 2
Robustness of network-based gene weights in pathways. (A) Gene weights in the p53 hypoxia pathway. Red: weights based on gNET. Black: weights after random removal of 30% network edges, 1 000 times to obtain the standard deviation. (B) Gene weights in the p53 hypoxia pathway. Red: weights based on gNET. Black: weights after topology-retaining network edge randomization, 1 000 times to obtain the standard deviation. (C) Distribution of average percentage of gene weight changes in all the 833 pathways. Blue: random removal of 30% network edge, 1 000 times. Red: topology-retaining network edge randomization, 1 000 times.
Taking the perturbation data here and the above weighting strategy design together, the network-based gene weights estimated in a hypergeometric model are generally stable and robust upon potential network perturbations, providing a strong support for development of pathway analysis methods with gene weights.
Incorporating gene weights into classical pathway analysis approaches
The gene weights determined from above accounting for the constitutive non-equivalence can be integrated into GSA pipelines to generate a weighted version that could potentially allow more specific evaluations of pathway significance (Figure 3, Materials and Methods). We have two motivations here for the validity of such a treatment. First, expression changes of core genes, as compared with other genes, can reasonably be considered as stronger evidences when deciding whether a pathway is regulated. Second, assigning smaller weights to less relevant genes present in a pathway allows a more reliable pathway significance assessment.
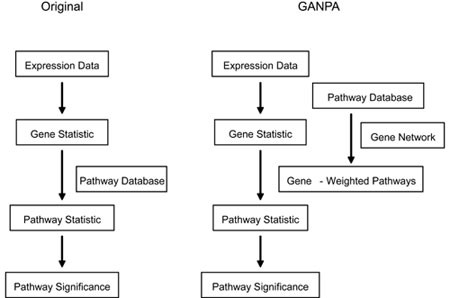
Figure 3
Schematic diagram of classical gene set analysis approaches and GANPA. Left: classical gene set analysis approach; Right: GANPA. See Results, and Materials and Methods for details.
To illustrate the benefits of weighted pathway analysis, we choose MeanAbs as the pathway statistic, which is not too complicated, yet still effective in demonstrating the reliability and characteristics of a gene-weighted GSA approach 15, 33 (see Materials and Methods for details). Briefly, Student's T statistic (also referred to as “T score”) is used as the gene statistic to summarize differential expression, and the pathway statistic MeanAbs is simply an average over absolute gene statistics, taking into account both up- and downregulations. In the corresponding weighted pathway analysis, the pathway statistic is a weighted average of absolute gene statistics, and for convenience it will be referred to as W-MeanAbs (weighted MeanAbs) below. To test the null hypothesis of no associations between a pathway and study conditions (“self-contained model”), sample permutations provide an empirical null distribution for significance evaluation. Nonetheless, the nominal pathway statistics are subject to properties of different gene sets (for instance, W-MeanAbs would be affected by pathway size, gene weights and inter-gene correlations), and therefore are not directly comparable across different pathways (Supplementary information, Data S1). To allow inter-pathway comparisons with pathway statistics, we standardize the nominal statistic to obtain a normalized pathway statistic (NS), which is in general comparable among pathways under the null hypothesis of no association (Materials and Methods, Supplementary information, Data S1). To correct for multiple comparisons, we use false discovery rate (FDR) along with permutation P values as the standard method.
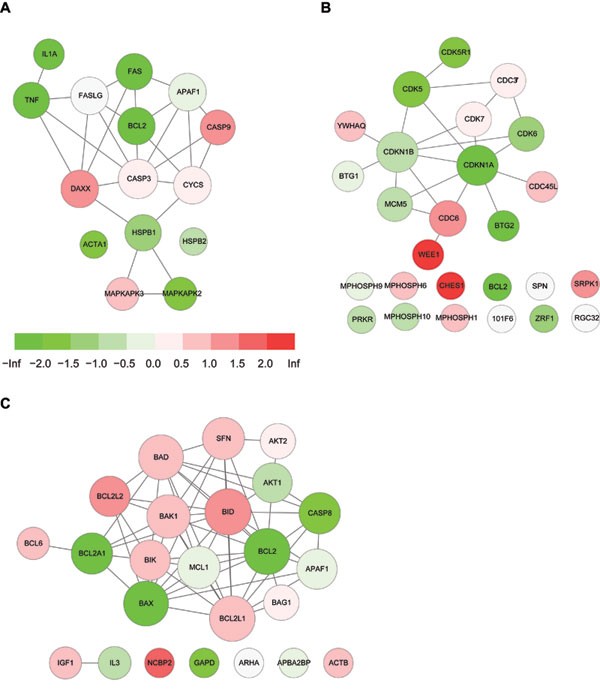
To test the effectiveness of W-MeanAbs, we first took the well-known p53 dataset for a comparative evaluation. The p53 dataset, consisting of gene expression profiling of 17 p53-wild-type (WT) and 33 p53-mutated (MUT) cancer cell lines, is an ideal benchmarking dataset for pathway analysis algorithms 11. We used the same gene sets from the original GSEA paper for p53 dataset 11, which were assigned gene weights based on gNET. We applied MeanAbs and W-MeanAbs to this dataset, with a 0.15 permutation FDR cutoff used to control error rates. Both methods have effectively identified p53-related pathways, yet with an obvious improvement in the significance from W-MeanAbs (Table 1). Several pathways well known to be related to p53 functions are only identified by W-MeanAbs: three apoptosis-related pathways (mitochondria pathway, ceramide pathway and BCL2 network), two cell cycle-related pathways (cell cycle regulator, cell cycle arrest), and one p53-related pathway (p53 signaling). Taking a look into these pathways would reveal features of the weighted approach. In cell cycle regulator pathway, high-weight genes such as CDKN1A, CDC6 and CDK5 showed strong expression changes (Figure 4B). In the BCL2 network, the high-weight genes such as BCL2, BCL2A1, BCL2L2, CASP8 and BID showed strong differential expression, whereas most of the low-weight genes such as IGF1, IL3, ARHA, APBA2BP and ACTB showed no significant expression changes (Figure 4C). Interestingly, HSP27 pathway was ranked after three p53 pathways (p53 UP pathway, p53 pathway, p53 hypoxia pathway) by W-MeanAbs, not as significant as that by MeanAbs, with a decrease in normalized statistic (NS) from 4.9 to 4.1. This seems to imply that the HSP pathway may be related to p53 functions, yet still not a central pathway. The central genes in this pathway, such as HSPB1, FASLG, APAF1, CASP3 and CYCS, did not have strong expression changes, whereas those heavily differentially expressed genes such as IL1A, FAS, BCL2, CASP9 and TNF are not quite specifically associated with HSP functions and thus only have a low weight (Figure 4A). To further verify the improvement of W-MeanAbs over MeanAbs, we reanalyzed the p53 dataset with gene sets weighted by another functional association network FunCoup. We observed very similar improvements, with the three apoptosis-related pathways and the two cell cycle-related pathways again identified only by W-MeanAbs, and a similar decrease in significance for the HSP27 pathway (Supplementary information, Table S3).
Table 1 Pathways significant in p53 dataset by MeanAbs and W-MeanAbs
Figure 4
Gene functional association networks for selected pathways in p53 dataset. Node color reflects expression changes in the p53 dataset. Red: upregulated expression. Green: downregulated expression. Gray: not covered by microarray data. (A) HSP27 pathway, with a color panel showing the mapping between T scores and node colors. (B) Cell cycle regulator pathway. (C) BCL2 network.
Although we mainly used MeanAbs as the demonstration statistic throughout this work, it should be emphasized that the pathway gene weights are conceptually reasonable to be integrated with other statistics in most, if not all, GSA methods. As an example, we integrated gene weights with the adapted KS statistic used by GSEA (see Materials and Methods). We then applied W-GSEA and standard GSEA to the p53 dataset, with gene weights assigned by gNET. GSEA/W-GSEA commonly identified the radiation sensitivity pathway and three p53 pathways as significant at a 0.15 FDR, similar to the MeanAbs/W-MeanAbs analysis described above (Supplementary information, Table S4). Nonetheless, most of the commonly top pathways showed an improvement in the normalized pathway enrichment score (NES) in W-GSEA as compared with GSEA, such as the p53 pathway, p53 UP, radiation sensitivity pathway and p53 signaling, which is a similar case in W-MeanAbs as compared with MeanAbs (Table 1, Supplementary information, Table S4). Further, the HSP27 pathway was not identified as significant as MeanAbs, also similar to its decreased significance in W-MeanAbs as compared with MeanAbs (Table 1, Supplementary information, Table S4), which can be similarly explained (Figure 4A). However, GSEA/W-GSEA indeed appeared to identify fewer significant pathways, probably a consequence of the low power issue related to GSEA methodology as suggested by several other research groups 13, 16, 19, 34. For this reason, we will just stress here that gene weights can be reasonably combined with statistics as complex as GSEA, and continue using W-MeanAbs/MeanAbs as our standard method in the following analysis.
Pathway identification in a relatively simple human disease
One of the important applications of pathway analysis is to interpret global gene expression patterns in human diseases. Thus, it would be essential to see whether a novel pathway analysis algorithm indeed works well for disease datasets. Here we took asthma as an example. The data that we used consisted of airway epithelial samples from seven healthy and nine asthmatic children 35.
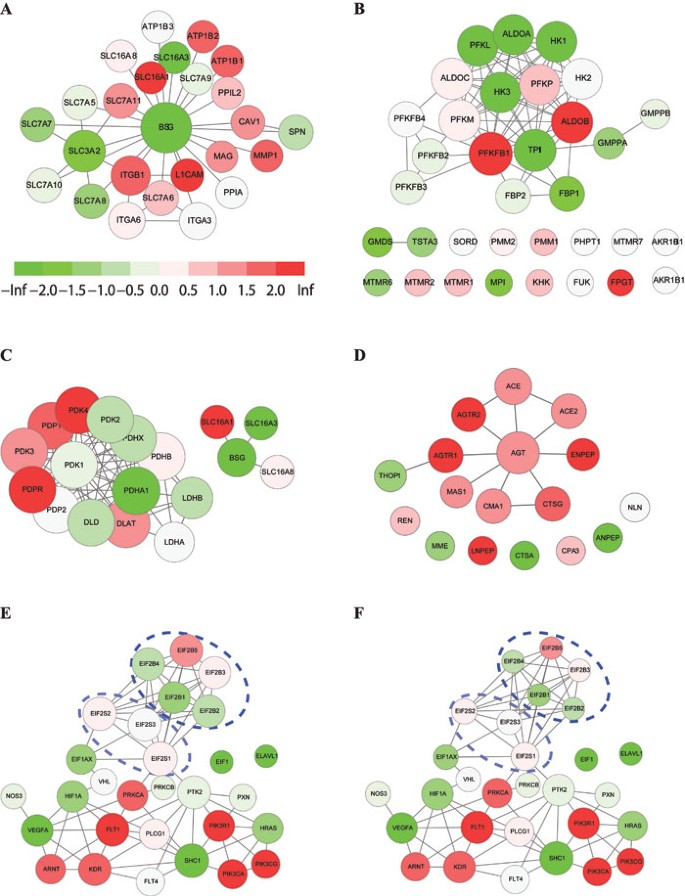
The MeanAbs and W-MeanAbs method identified 15 and 13 pathways, respectively, at a 0.05 permutation FDR, with 9 of them shared by two methods (Table 2). Among the shared pathways, RAC1 pathway, metabolism of carbohydrates, ECM pathway, CTCF pathway, Basigin interactions and glycolysis were ranked as the top 10 significant pathways in both methods (Table 2). Among them, Basigin interactions had a number of its genes differentially expressed, with ITGB1, L1CAM, SLC16A1 upregulated, and BSG, SLC3A1 and SLC16A3 downregulated (Figure 5A). In W-MeanAbs, Basigin interactions was reported to be even more significant in the sense that its core genes, such as BSG, SLC3A2 and ITGB1, were all dramatically differentially expressed (Figure 5A).
Table 2 Significant pathways in the asthma dataset by MeanAbs and W-MeanAbs
Figure 5
Gene functional association networks for selected pathways in asthma dataset. Node color reflects expression changes in the asthma dataset. Red: upregulated expression. Green: downregulated expression. Gray: not covered by microarray data. (A) Basigin interactions (Reactome), with a color panel showing the mapping between T scores and node colors. (B) Fructose and mannose metabolism (KEGG). (C) Pyruvate metabolism pathway (Reactome). (D) Renin-angiotensin system (KEGG). (E) VEGF pathway (Biocarta). (F) VEGF pathway (Biocarta), with gene weights computed after correcting for multi-subunit proteins. Gene weights in A-E are not corrected for multi-subunit proteins. Each circle in E, F indicates a cluster of genes encoding one multi-subunit protein.
Then it would be interesting to examine pathways that are ranked top by one method but not by the other methods, which should clearly reflect the different characteristics of the two methods. The fructose and mannose metabolism pathway (KEGG), ranked 40 by MeanAbs, was ranked as the top 6 significant pathways by W-MeanAbs. In its 11 highly weighted genes, 7 of them, including PFKFB1, TPI1, ALDOB, HK1, PFKL, HK3 and ALDOA, showed a strong differential expression in asthma (Figure 4C). On the contrary, the pyruvate metabolism pathway (Reactome) and renin-angiotensin system (KEGG), ranked as the top 10 and top 12 significant pathways by MeanAbs, were ranked 32 and 19 by W-MeanAbs, respectively, and did not pass the significance level (Table 2). For pyruvate metabolism pathway, the genes are distinctively clustered into two groups according to the functional associations, the “Basigin group” and the “Pyruvate group” (Figure 5C). The “Pyruvate group” is undoubtedly the desired group here in a pathway named “Pyruvate metabolism”; yet in asthma, it is the “Basigin group” that was more dramatically changed in expression (Figure 5C), recalling the top significant pathway Basigin Interactions by MeanAbs/W-MeanAbs that we have just mentioned (Figure 5A). Surely there are some biological concerns that Reactome experts have put the “Basigin group” together with “Pyruvate group” in the “pyruvate metabolism pathway”, but the point here is that W-MeanAbs can automatically “double-check” and reliably “re-adjust” the two subgroups for their relative “contributions” to the whole pathway. The renin-angiotensin pathway, where several highly expression-regulated genes, such as CTSA, LNPEP and ANPEP, are poorly associated with the majority of genes of the pathway, whereas several high-weight genes such as AGT, ACE2 and CMA1 do not show obvious expression changes, is therefore judged by W-MeanAbs as not significant at the 0.05 permutation FDR level (Figure 5D and Table 2).
Taken together, a functional association network-based gene-weighting approach has unique strength in determining pathway significance given expression data, especially for pathways consisting of heterogeneous subgroups with non-equivalent association confidences to the whole pathway.
Correction for genes encoding multi-subunit proteins
In the asthma data, the VEGF pathway, consistently identified to be altered in asthma according to a number of reports 36, 37, 38, 39, appeared to be less significant in W-MeanAbs as compared with MeanAbs (Table 2). When looking into this pathway, we noticed one issue that should be solved for more accurate gene weighting. This issue, referred to as the “over-counting” problem, is closely related to the genes encoding multi-subunit proteins. Since genes encoding subunits for multi-subunit proteins are usually considered to be different genes, a multi-subunit protein can artificially take a higher proportion in a pathway than a single-subunit protein. Although this issue should also affect classical GSA, it is more severe in our original network-based gene-weighted approach. As clearly depicted in the VEGF pathway (Biocarta), the 8 genes encoding EIF2B and EIF2S proteins take a proportion of nearly 30% of this 29-gene pathway, and the enriched inter-gene linkages among the subunit genes elevated the weight of each other in our network-based weighting strategy. The actually less close association of these two multi-subunit proteins with the VEGF pathway further exaggerated the side effect, leading to an unexpected masking of the otherwise central role of VEGFA and its receptor genes (Figure 5E).
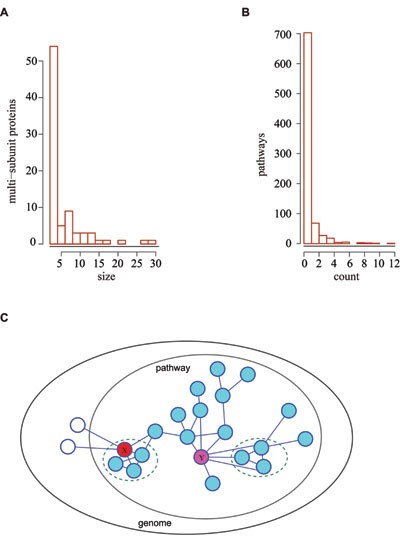
To determine whether this issue is prevalent enough for a specialized treatment, we prepared a collection of multi-subunit proteins and explored their prevalence in biological pathways. A list of genes encoding 82 multi-subunit proteins were extracted from human genes and provided as Supplementary information, Data S4. The majority of them have less than 5 subunits, yet few can have more than 10 (Figure 6A). 567 of the 833 pathways do not involve any of the 82 multi-subunit proteins, suggesting that a combination of subunit genes would not affect most of the pathways in an analysis (Figure 6B). Nonetheless, since as many as 266 pathways involve at least one multi-subunit protein, it is essential to design a refined version of the gene-weighting strategy so as to make the gene weights assigned for these pathways more accurate.
Figure 6
Combination of subunit genes encoding multi-subunit proteins for pathway analysis. (A) Distribution of subunit numbers (size) for multi-subunit proteins. (B) Distribution of multi-subunit proteins (count) in all the 833 pathways. (C) An illustration of the gene-weighting algorithm with a correction for multi-subunit proteins. In this example pathway, two multi-subunit proteins are present, as shown by the two dashed circles. X (red) and Y (violet) are subunit- and protein-encoding genes, respectively. In the original gene-weighting scheme subunit- and protein-encoding genes were not distinguished; whereas in this corrected version, to solve such confusion, we replaced gene-level association counting by protein-level association counting. Therefore, in this corrected version, the within-pathway associations of X and Y are counted as 4 and 5, respectively, rather than 6 and 7. Outside-pathway associations are also counted at protein level.
To correct this problem, our refinement is to add two extensions to the original gene weighting (Figure 6C). First, we do association counting on the whole-protein level for multi-subunit proteins rather than on each of its subunits. Second, genes encoding subunits and single proteins are both assessed by their associations with the pathway. The new weights of the 833 pathways after correction for multi-subunit proteins are provided as Supplementary information, Data S5. We reanalyzed the asthma dataset with the new gene weights and observed obvious changes in the significance evaluation of RAC1 pathway and VEGF pathway (Table 2). It can be clearly seen that the new weights in the VEGF pathway are now much more consistent with biological knowledge, which recaptured its significance in asthma (Figure 5F and Table 2). As the subunit combination of multi-subunit proteins has been seamlessly integrated with the gene-weighted GSA pipeline, for simplicity, we will still refer to this new version of W-MeanAbs with the subunit combination as W-MeanAbs hereafter.
Conserved pathways across three breast cancer datasets
To further test the multi-subunit combined weighted approach, we collected three breast cancer datasets from GEO database, each with cancer samples and normal controls. As the comparison between malignant cancer samples and normal tissues usually generates a large number of differential genes and pathways (at 0.1 permutation FDR level, the three breast cancer datasets have 661, 663 and 653 significant pathways for MeanAbs, respectively; and 654, 664 and 649 for W-MeanAbs, respectively), we took the top pathways from each dataset analysis to see how many pathways were conserved across all datasets, which might be a more appropriate metric to evaluate the performance of a pathway identification method, especially with respect to reproducibility. We tried serial cutoffs ranging from top 30 to top 80 and W-MeanAbs frequently identified more conserved pathways (Supplementary information, Figure S1). When setting top 80 as the cutoff, MeanAbs and W-MeanAbs identified 9 and 14 conserved pathways, respectively, with 8 of them being common to both methods (Table 3). The 8 conserved pathways are mainly related to cytoskeleton regulation, cell motion, cancer signaling, p53 signaling, and cellular synthesis (Table 3). The 6 pathways unique to W-MeanAbs are all known to be related to breast cancers or features common to cancers such as proliferation-related pathways: PDGF pathway 40, 41, pancreatic cancer, downstream signal transduction (related to PDGF signaling 40, 41, see Reactome 10 for details), G2-M transition 42, 43, metabolism of nucleotides 44, and regulation of APC activators between G1-S and early anaphase 45, 46, 47. The cell cycle checkpoint pathway unique to MeanAbs is also common to multiple cancers. Nonetheless, the reproducibility is obviously better in W-MeanAbs than in MeanAbs, which is essentially a required capability of pathway analysis methods.
Table 3 Conserved pathways in three breast cancer datasets
Throughout the applications to various real datasets, we have shown that a weighted approach indeed offers an improved accuracy for pathways consisting of core genes and less relevant genes, as well as pathways with heterogeneous subgroups that have non-equivalent associations to the pathway. The potential weighting bias due to involvement of multi-subunit proteins has been further corrected to improve reliability. With the breast carcinomas datasets, we have demonstrated the good reproducibility of our weighted approach, which would be useful for cross-dataset comparisons that are common in human disease studies.
Discussion
Unlike conventional pathway analysis approaches that reduced biological pathways to gene sets and adopted an implicit assumption on gene equivalence, we have recognized the prevalence of “constitutive non-equivalence” within biological pathways. Two types of “non-equivalence” might be involved: (1) biological non-equivalence: this is supported by the prevalent presence of genes with non-equivalent “contributions” or “association strengths” to pathways, such as p53 as core gene in the p53 hypoxia pathway, as well as by the presence of non-equivalent subgroups in pathways, such as the “Basigin group” and “Pyruvate group” in the “pyruvate metabolism pathway”; (2) technical non-equivalence: this specifically refers to the potential misclassification of irrelevant genes in the curation process, as well as false positives in computational classifications, such as predicting disease prognosis signature genes from high-throughput data. We took a relatively conservative way in retaining the pathway gene compositions even when some genes were poorly associated with other genes in the pathway, in case the network was not comprehensive and precise enough. This would improve the stability of gene weight estimations. A good robustness of the gene weights has been illustrated by network perturbations and topology-retaining network randomizations. Throughout this work, we have demonstrated that “a set of genes with non-equivalent weights” serves as a better model to account for the two types of intrinsic non-equivalence in both pathways and functional gene sets, as compared with the classical view of “a set of equivalent genes”. Integration of the constitutive gene weights into GSA allows us to develop a network-based gene-weighting approach for pathway analysis, as implemented in an R package named GANPA (http://cran.r-project.org/web/packages/GANPA/index.html).
Recently, several algorithms have tried to demonstrate the possibility of incorporating topological information in pathway graphs into gene set significance analysis, notably Pathway-Express 48, SPIA 49, SEPEA 50 and PWEA 51. Pathway-Express defines a pathway score summarizing gene set over-representation probability and a gene “perturbation factor” accounting for both expression alteration and directional linkages, which is revised in SPIA by removing the mingling effects of expression changes in the “perturbation factor” 48, 49. Unlike Pathway-Express and SPIA, SEPEA and PWEA omit linkage directions in KEGG pathways 50, 51. SEPEA adopts two types of topological information, distances to terminal genes and inter-pathway distances, whereas PWEA considers only inter-gene distances 50, 51. These represent a recent research shift from the completely reduced gene set view of pathways to a more structural and functional view that is closer to real biological pathways. From this perspective, our work can be seen as among the similar research stream.
However, GANPA is unique in several aspects. The above four algorithms mainly touch the question of designing a pathway statistic to combine structural information and gene expression changes, while our method asks the question of weighting the non-equivalence of genes within pathways using a gene functional association network based on multiple sources of datasets including protein-protein interactions, co-annotations and gene co-expressions. As a network-based gene-weighting method, GANPA offers several notable advantages over the above four algorithms that rely on curated gene-gene linkages in KEGG. First, it is more general-purpose and widely applicable, as both pathways with graph representations (KEGG, WikiPathways, etc.) and pathways with gene compositions alone (Reactome, MSigDB, GO BP, PANTHER, etc.) can be used for weighted GSA. Second, the potentially misclassified genes by curation errors in pathway databases are likely to be automatically identified and down-weighted by integrating gene functional associations. Third, genes with many non-specific associations to other genes across various pathways are statistically readjusted in these pathways, by considering the whole association network in a hypergeometric model. This specificity seems not directly targeted by other algorithms, although, from a different aspect, SEPEA uses a distance rule to make some control over genes with high non-specific associations 50.
It is also worth noting that GANPA provides a generally applicable solution to the “over-counting” issue associated with multi-subunit proteins, which is implicit in classical GSA. The fundamental cause of this problem is that subunit-encoding genes are regarded equivalent to protein-encoding genes in classical gene set significance analysis. This is especially critical when a pathway contains a not-so-relevant multi-subunit protein with a number of subunit genes, as illustrated in the VEGF pathway example in this work. By combining both expressions and associations of subunit-encoding genes as a single component, we showed that GANPA works well for this issue in pathway analysis.
With the simple but effective MeanAbs and its corresponding weighted form W-MeanAbs on various datasets ranging from the specific p53 data to a relatively simple asthma disease, and to three studies on the complex breast cancer diseases, we demonstrated that our gene-weighting approach is biologically sound and effective for diverse datasets, and highly reproducible for comparisons across different studies. Taken together, we designed a network-based statistical algorithm to account for the constitutive nonequivalence of genes within pathways, proposed a “weighted gene set” model for biological pathways that can be integrated with regular GSA methods, and demonstrated the feasibility of this novel general-purpose approach for pathway analysis, which is therefore of a methodological and biological significance for future research.
Materials and Methods
Microarray data and preprocessing
The p53 dataset was downloaded from GSEA website (http://www.broadinstitute.org/gsea/). The expression data were already collapsed to genes. If essential, we replaced negative or absent measures with the row median, and removed rows with non-positive values. We log transformed the scale for downstream analysis. Asthma (GSE18965) and breast cancer datasets (GSE14548, GSE10780 and GSE3744) were downloaded from NCBI GEO database (http://www.ncbi.nlm.nih.gov/geo/). Raw data were preprocessed with customized CDF 52 using the RMA method 53, 54, 55.
Gene sets and gene functional association networks
Gene sets were downloaded from GSEA website (http://www.broadinstitute.org/gsea/). To compare with pathways identified by other methods using the p53 data, we used the earlier version accompanied by the previous study 11, and for all other data, the version 3 gene sets (KEGG, Biocarta, Reactome) were used. Gene sets with inter-gene associations, gene weights and/or expression changes were visualized using Cytoscape 56, 57, an open-source project for network visualization and analysis (http://www.cytoscape.org/).
Gene association network FunCoup 31 version 1.1 was downloaded from website (http://funcoup.sbc.su.se). gNET was constructed de novo with PPIs, co-expressions and GO (gene ontology). For PPIs, the following databases are used: BioGrid (http://thebiogrid.org), HPRD (http://www.hprd.org), DIP (http://dip.doe-mbi.ucla.edu), MINT (http://mint.bio.uniroma2.it/mint), IntAct (http://www.ebi.ac.uk/intact) and Reactome (http://www.reactome.org). Only PPIs with at least one PubMed reference are used. For co-expressions, we collected the raw data of 73 human gene expression microarray datasets (each >20 samples, see Supplementary information, Data S2) consisting of 2 798 samples from NCBI GEO database, and only gene pairs with >0.8 (or <−0.8 for negative associations) Pearson's correlation coefficient in at least 5 datasets were extracted. None of the datasets used for pathway analysis throughout this work were included in generation of co-expressed gene pairs to avoid potential bias caused by data reuse (Supplementary information, Data S2). For GO BP annotation resources (GOA, September 2010), we discarded too general terms for specificity concerns, and extracted only gene pairs sharing at least one lowest-level BP term in the GO hierarchy graph (Supplementary information, Data S1). By integrating the three types of gene associations, we obtained 1 278 362 unique gene pairs.
Network-based gene weighting in pathways
Suppose that the genome contains N total genes. Given a gene functional association network of this genome and a pathway S consisting of K genes, we have two variables to characterize the functional property of any gene G i (_i_=1, 2, ..., K) in S: the number of associations between G i and the K genes in S, designated as X i, and the number of associations between G i and the N genes in the genome, designated as M i. Suppose that G i has no specific functional associations with genes in S; then X i is expected to follow a hypergeometric distribution,

with the expectation derived as

For gene G i (_i_=1, 2, ..., K), the observed number of associations between S and it (X i) is likely to be significantly larger than E(X i), when there is a specific functional association between G i and S. Therefore, we proposed to use a rescaled form of X i -E(Xi) to quantify the relative association strength W i between G i and S,

where I A is an indicator function for the positive subset A: (0, +∞) on R, and a is some appropriate scaling base for which we used 2. Notice that the weight W i defined in this way has a minimum value of 1, which is a basic-level weight for genes within a pathway (also see Results).
Non-weighted and weighted pathway significance tests
Gene expression microarray data are first summarized with a gene statistic, for example two-sample Student's T statistic, to evaluate differential expression. For a gene set S consisting of genes G i (_i_=1, 2, ..., K), the observed gene statistic can be obtained as T i. Pathway statistic can be derived from the gene statistics. The MeanAbs and corresponding W-MeanAbs statistics are the following:


The standard weighted form of GSEA (see original paper 11 for more details) and its corresponding W-GSEA statistics are as follows:


where,

and the maximum deviation function,

Note that the original GSEA also incorporates a “weight” |r i|, which is the correlation of G i's expression profile with the phenotype profile, and is therefore dataset-dependent. On the other hand, the pathway gene weights proposed by us are irrespective of datasets. Therefore, it should be sound to multiply these two types of gene weights and integrate them into the KS statistic to derive a new version of GSEA, referred to as W-GSEA.
For single hypothesis tests with GSEA and W-GSEA, we followed exactly the standard GSEA methodology. Briefly, we applied the following steps: generation of permutation distribution, normalization of pathway statistic, and calculation of permutation P values. For single-hypothesis tests with MeanAbs and W-MeanAbs, we will describe the methodology in detail below. Given a gene set S consisting of K genes, the gene randomization distributions of S MeanAbs are generated from 1 000 random gene sets of size K, and designated as S MeanAbs rand; the sample permutation distributions of S MeanAbs are generated from 1 000 times the sample label permutations, and designated as S MeanAbs perm. The randomization and permutation versions of S MeanAbs can be similarly obtained as S W-MeanAbs rand and S W-MeanAbs perm, respectively. Based on the randomization (or permutation) distribution, P values p rand (or p perm) can be computed by summarizing the probability of expecting a larger observation than the observed S MeanAbs. When sample size is sufficient, p perm is strict since inter-gene associations are retained by permutation. Throughout this work, we prefer to use p perm over p rand. It should be noted that the S MeanAbs perm distribution is dependent on gene set size K, and therefore the observed statistics are not directly comparable among gene sets of different sizes. To correct this, we applied a simple normalization (or standardization) step to the pathway statistic, by subtracting the median of S MeanAbs perm and dividing by the standard deviation of S MeanAbs perm. The normalized pathway statistic, designated as NS MeanAbs, can be shown to be roughly comparable among pathways and also comparable between statistics with and without gene weight incorporation (Supplementary information, Data S1).
During pathway analysis, it is quite common to involve a number of pathways, which requires a multiple-hypothesis testing procedure to control global error rates. We applied Benjamini-Hochberg FDR method 58 to account for false discoveries during all GSEA/W-GSEA or MeanAbs/W-MeanAbs analysis, generating FDR rand and FDR perm for p rand and p perm, respectively. Similarly, we prefer FDR perm over FDR rand.
Correction for multi-subunit proteins
Proteins that have multiple subunits each encoded by a different gene, causing an overestimated weight, should be considered and treated with some appropriate method. We took the combination approach, in which gene-gene linkages were mapped to the protein level, with subunit-encoding genes integrated into a single component. Both protein-encoding genes and subunit-encoding genes are weighted by calculating protein-level association strength between the gene and pathway, using exactly the same gene-weighting methodology described above.
References
- Wu MC, Lin XH . Prior biological knowledge-based approaches for the analysis of genome-wide expression profiles using gene sets and pathways. Stat Meth Med Res 2009; 18:577–593.
Article Google Scholar - Wang K, Li MY, Bucan M . Pathway-based approaches for analysis of genomewide association studies. Am J Hum Genet 2007; 81:1278–1283.
Article CAS PubMed PubMed Central Google Scholar - Perroud B, Lee J, Valkova N, et al. Pathway analysis of kidney cancer using proteomics and metabolic profiling. Mol Cancer 2006; 5:64.
Article PubMed PubMed Central Google Scholar - Medina I, Carbonell J, Pulido L, et al. Babelomics: an integrative platform for the analysis of transcriptomics, proteomics and genomic data with advanced functional profiling. Nucl Acids Res 2010; 38:W210–W213.
Article CAS PubMed PubMed Central Google Scholar - Kanehisa M, Araki M, Goto S, et al. KEGG for linking genomes to life and the environment. Nucl Acids Res 2008; 36:D480–D484.
Article CAS PubMed Google Scholar - Kanehisa M, Goto S, Furumichi M, Tanabe M, Hirakawa M . KEGG for representation and analysis of molecular networks involving diseases and drugs. Nucl Acids Res 2010; 38:D355–D360.
Article CAS PubMed Google Scholar - Pico AR, Kelder T, van Iersel MP, Hanspers K, Conklin BR, Evelo C . WikiPathways: pathway editing for the people. PLoS Biol 2008; 6:e184.
Article PubMed PubMed Central Google Scholar - Thomas PD, Campbell MJ, Kejariwal A, et al. PANTHER: a library of protein families and subfamilies indexed by function. Genome Res 2003; 13:2129–2141.
Article CAS PubMed PubMed Central Google Scholar - Mi H, Guo N, Kejariwal A, Thomas PD . PANTHER version 6: protein sequence and function evolution data with expanded representation of biological pathways. Nucl Acids Res 2006; 35:D247–D252.
Article PubMed PubMed Central Google Scholar - Vastrik I, D'Eustachio P, Schmidt E, et al. Reactome: a knowledge base of biologic pathways and processes. Genome Biol 2007; 8:R39.
Article PubMed PubMed Central Google Scholar - Subramanian A, Tamayo P . Mootha VK, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 2005; 102:15545–15550.
Article CAS PubMed PubMed Central Google Scholar - Draghici S, Khatri P, Martins RP, Ostermeier GC, Krawetz SA . Global functional profiling of gene expression. Genomics 2003; 81:98–104.
Article CAS PubMed Google Scholar - Goeman JJ, Buhlmann P . Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics 2007; 23:980–987.
Article CAS PubMed Google Scholar - Kim SY, Volsky DJ . PAGE: parametric analysis of gene set enrichment. BMC Bioinformatics 2005; 6:144.
Article PubMed PubMed Central Google Scholar - Efron B, Tibshiran R . On testing the significance of sets of genes. Ann Appl Stat 2007; 1:107–129.
Article Google Scholar - Dinu I, Potter JD, Mueller T, et al. Improving gene set analysis of microarray data by SAM-GS. BMC Bioinformatics 2007; 8:242.
Article PubMed PubMed Central Google Scholar - Luo WJ, Friedman MS, Shedden K, Hankenson KD, Woolf PJ . GAGE: generally applicable gene set enrichment for pathway analysis. BMC Bioinformatics 2009; 10:161.
Article PubMed PubMed Central Google Scholar - Smyth GK . Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat Appl Genet Mol Biol 2004; 3:Article3.
Article PubMed Google Scholar - Tian L, Greenberg SA, Kong SW, Altschuler J, Kohane IS, Park PJ . Discovering statistically significant pathways in expression profiling studies. Proc Natl Acad Sci USA 2005; 102:13544–13549.
Article CAS PubMed PubMed Central Google Scholar - Goeman JJ, Oosting J, Cleton-Jansen AM, Anninga JK, van Houwelingen HC . Testing association of a pathway with survival using gene expression data. Bioinformatics 2005; 21:1950–1957.
Article CAS PubMed Google Scholar - Goeman JJ, van de Geer SA, de Kort F, van Houwelingen HC . A global test for groups of genes: testing association with a clinical outcome. Bioinformatics 2004; 20:93–99.
Article CAS PubMed Google Scholar - Mansmann U, Meister R . Testing differential gene expression in functional groups – Goeman's global test versus an ANCOVA approach. Meth Inform Med 2005; 44:449–453.
Article CAS PubMed Google Scholar - Tomfohr J, Lu J, Kepler TB . Pathway level analysis of gene expression using singular value decomposition. BMC Bioinformatics 2005; 6:225.
Article PubMed PubMed Central Google Scholar - Ma S, Kosorok MR . Identification of differential gene pathways with principal component analysis. Bioinformatics 2009; 25:882–889.
Article CAS PubMed PubMed Central Google Scholar - Yan XT, Sun FZ . Testing gene set enrichment for subset of genes: Sub-GSE. BMC Bioinformatics 2008; 9:362.
Article PubMed PubMed Central Google Scholar - Hawkins T, Chitale M, Kihara D . Functional enrichment analyses and construction of functional similarity networks with high confidence function prediction by PFP. Bmc Bioinformatics 2010; 11:265.
Article PubMed PubMed Central Google Scholar - George AJ, Thomas WG, Hannan RD . The renin–angiotensin system and cancer: old dog, new tricks. Nat Rev Cancer 2010; 10:745–759.
Article CAS PubMed Google Scholar - Normanno N, De Luca A, Bianco C, et al. Epidermal growth factor receptor (EGFR) signaling in cancer. Gene 2006; 366:2–16.
Article CAS PubMed Google Scholar - Carafoli E . Calcium signaling: a tale for all seasons. Proc Natl Acad Sci USA 2002; 99:1115–1122.
Article CAS PubMed PubMed Central Google Scholar - Ihle JN . Cytokine receptor signalling. Nature 1995; 377:591–594.
Article CAS PubMed Google Scholar - Alexeyenko A, Sonnhammer ELL . Global networks of functional coupling in eukaryotes from comprehensive data integration. Genome Res 2009; 19:1107–1116.
Article CAS PubMed PubMed Central Google Scholar - Rual J-F, Venkatesan K, Hao T, et al. Towards a proteome-scale map of the human protein-protein interaction network. Nature 2005; 437:1173–1178.
Article CAS PubMed Google Scholar - Shahbaba B, Tibshirani R, Shachaf CM, Plevritis SK . Bayesian gene set analysis for identifying significant biological pathways. J R Stat Soc C-Appl 2011; 60:541–557.
Article Google Scholar - Damian D, Gorfine M . Statistical concerns about the GSEA procedure. Nat Genet 2004; 36:663–663.
Article CAS PubMed Google Scholar - Kicic A, Hallstrand TS, Sutanto EN, et al. Decreased fibronectin production significantly contributes to dysregulated repair of asthmatic epithelium. Am J Resp Crit Care Med 2010; 181:889–898.
Article CAS PubMed PubMed Central Google Scholar - Hoshino M, Takahashi M, Aoike N . Expression of vascular endothelial growth factor, basic fibroblast growth factor, and angiogenin immunoreactivity in asthmatic airways and its relationship to angiogenesis. J Allergy Clin Immunol 2001; 107:295–301.
Article CAS PubMed Google Scholar - Hoshino M, Nakamura Y, Hamid QA . Gene expression of vascular endothelial growth factor and its receptors and angiogenesis in bronchial asthma. J Allergy Clin Immunol 2001; 107:1034–1038.
Article CAS PubMed Google Scholar - Asai K, Kanazawa H, Kamoi H, Shiraishi S, Hirata K, Yoshikawa J . Increased levels of vascular endothelial growth factor in induced sputum in asthmatic patients. Clin Exp Allergy 2003; 33:595–599.
Article CAS PubMed Google Scholar - Chetta A, Zanini A, Foresi A, et al. Vascular endothelial growth factor up-regulation and bronchial wall remodelling in asthma. Clin Exp Allergy 2005; 35:1437–1442.
Article CAS PubMed Google Scholar - Dibb NJ, Dilworth SM, Mol CD . Switching on kinases: oncogenic activation of BRAF and the PDGFR family. Nat Rev Cancer 2004; 4:718–727.
Article CAS PubMed Google Scholar - Jechlinger M, Sommer A, Moriggl R, et al. Autocrine PDGFR signaling promotes mammary cancer metastasis. J Clin Invest 2006; 116:1561.
Article CAS PubMed PubMed Central Google Scholar - Collins K, Jacks T, Pavletich NP . The cell cycle and cancer. Proc Natl Acad Sci USA 1997; 94:2776–2778.
Article CAS PubMed PubMed Central Google Scholar - Hartwell L, Kastan M . Cell cycle control and cancer. Science 1994; 266:1821–1828.
Article CAS PubMed Google Scholar - Griffin JL, Shockcor JP . Metabolic profiles of cancer cells. Nat Rev Cancer 2004; 4:551–561.
Article CAS PubMed Google Scholar - Virmani AK, Rathi A . Sathyanarayana UG, et al. Aberrant methylation of the adenomatous polyposis coli (APC) gene promoter 1A in breast and lung carcinomas. Clin Cancer Res 2001; 7:1998–2004.
CAS PubMed Google Scholar - Jönsson M . Borg Å, Nilbert M, Andersson T . Involvement of adenomatous polyposis coli (APC)/beta-catenin signalling in human breast cancer. Eur J Cancer 2000; 36:242–248.
Article PubMed Google Scholar - Esteller M, Sparks A . Toyota M, et al. Analysis of Adenomatous Polyposis Coli promoter hypermethylation in human cancer. Cancer Res 2000; 60:4366–4371.
CAS PubMed Google Scholar - Draghici S, Khatri P, Tarca AL, et al. A systems biology approach for pathway level analysis. Genome Res 2007; 17:1537–1545.
Article CAS PubMed PubMed Central Google Scholar - Tarca AL, Draghici S, Khatri P, et al. A novel signaling pathway impact analysis. Bioinformatics 2009; 25:75–82.
Article CAS PubMed Google Scholar - Thomas R, Gohlke JM, Stopper GF, Parham FM, Portier CJ . Choosing the right path: enhancement of biologically relevant sets of genes or proteins using pathway structure. Genome Biol 2009; 10:R44.
Article PubMed PubMed Central Google Scholar - Hung JH, Whitfield TW, Yang TH, Hu Z, Weng Z, Delisi C . Identification of functional modules that correlate with phenotypic difference: the influence of network topology. Genome Biol 2010; 11:R23.
Article PubMed PubMed Central Google Scholar - Dai MH, Wang PL, Boyd AD, et al. Evolving gene/transcript definitions significantly alter the interpretation of GeneChip data. Nucl Acids Res 2005; 33:e175.
Article PubMed PubMed Central Google Scholar - Irizarry RA, Hobbs B, Collin F, et al. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 2003; 4:249–264.
Article PubMed Google Scholar - Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP . Summaries of affymetrix GeneChip probe level data. Nucl Acids Res 2003; 31:e15.
Article PubMed PubMed Central Google Scholar - Bolstad BM, Irizarry RA, Astrand M, Speed TP . A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003; 19:185–193.
Article CAS PubMed Google Scholar - Shannon P, Markiel A, Ozier O, et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res 2003; 13:2498–2504.
Article CAS PubMed PubMed Central Google Scholar - Cline MS, Smoot M, Cerami E, et al. Integration of biological networks and gene expression data using Cytoscape. Nat Protocols 2007; 2:2366–2382.
Article CAS PubMed Google Scholar - Benjamini Y, Hochberg Y . Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B Meth 1995; 57:289–300.
Google Scholar
Acknowledgements
We thank Lei Bao (University of California, San Diego, USA), Yun Li (SIBS, China), Tao Huang (SIBS, China), Micheal Wu (Harvard University, USA), Brad Efron (Stanford University, USA), Fei He (Shanghai Center for Bioinformatics Technology, China), Yan Feng, Zuoyun Wang, Wenjing Zhang, Jingqi Chen and Junrui Li (SIBS, China) for helpful communications or suggestions. We thank Yijun Gao and Chao Zheng for their help in manuscript preparation. This work was supported by the National Basic Research Program of China (2012CB910800, 2010CB912102), the National Natural Science Foundation of China (30871284, 30971461, 30971643 and 31071113), the Chinese Academy of Sciences (KSCX1-YW-22), and the Science and Technology Commission of Shanghai Municipality (09JC1416300, 09PJ1401000). HJ is a scholar of the Hundred Talents Program of the Chinese Academy of Sciences.
Author information
Authors and Affiliations
- State Key Laboratory of Cell Biology, Institute of Biochemistry and Cell Biology, Shanghai Institutes for Biological Sciences (SIBS), Chinese Academy of Sciences, 200031, Shanghai, China
Zhaoyuan Fang & Hongbin Ji - School of Life Sciences, Institute of Biostatistics, Fudan University, 200433, Shanghai, China
Weidong Tian
Authors
- Zhaoyuan Fang
You can also search for this author inPubMed Google Scholar - Weidong Tian
You can also search for this author inPubMed Google Scholar - Hongbin Ji
You can also search for this author inPubMed Google Scholar
Corresponding authors
Correspondence toWeidong Tian or Hongbin Ji.
Additional information
(Supplementary information is linked to the online version of the paper on the Cell Research website.)
Supplementary information
Supplementary information, Data S1
Gene functional association network-based pathway gene weighting (PDF 659 kb)
Supplementary information, Data S2
A list of GEO datasets used for gene co-expressions. (PDF 129 kb)
Supplementary information, Data S3
Gene weights for 833 pathways without correction for multi-subunit genes. (PDF 934 kb)
Supplementary information, Data S4
A list of multi-subunit proteins. (PDF 116 kb)
Supplementary information, Data S5
Gene weights for 833 pathways after correction for multi-subunit genes. (PDF 934 kb)
Supplementary information, Table S1
P53 weights in different pathways (PDF 129 kb)
Supplementary information, Table S2
EGFR weights in different pathways (PDF 67 kb)
Supplementary information, Table S3
Pathways significant in P53 dataset by MeanAbs and W-MeanAbs (PDF 67 kb)
Supplementary information, Table S4
Pathways significant in P53 dataset by GSEA and W-GSEA (PDF 126 kb)
Supplementary information, Figure S1
Conserved pathways across breast cancer datasets. (PDF 338 kb)
Rights and permissions
About this article
Cite this article
Fang, Z., Tian, W. & Ji, H. A network-based gene-weighting approach for pathway analysis.Cell Res 22, 565–580 (2012). https://doi.org/10.1038/cr.2011.149
- Received: 16 February 2011
- Revised: 25 May 2011
- Accepted: 28 July 2011
- Published: 06 September 2011
- Issue Date: March 2012
- DOI: https://doi.org/10.1038/cr.2011.149