Integrated elastomeric components for autonomous regulation of sequential and oscillatory flow switching in microfluidic devices (original) (raw)
Abstract
A critical need for enhancing the usability and capabilities of microfluidic technologies is the development of standardized, scalable and versatile control systems1,2. Electronically controlled valves and pumps typically used for dynamic flow regulation, although useful, can limit convenience, scalability and robustness3,4,5. This shortcoming has motivated the development of device-embedded non-electrical flow-control systems. Existing approaches to regulate operation timing on-chip, however, still require external signals such as timed generation of fluid flow, bubbles, liquid plugs or droplets or an alteration of chemical compositions or temperature6,7,8,9,10,11,12,13,14,15,16. Here, we describe a strategy to provide device-embedded flow switching and clocking functions. Physical gaps and cavities interconnected by holes are fabricated into a three-layer elastomer structure to form networks of fluidic gates that can spontaneously generate cascading and oscillatory flow output using only a constant flow of Newtonian fluids as the device input. The resulting microfluidic substrate architecture is simple, scalable and should be applicable to various materials. This flow-powered fluidic gating scheme brings the autonomous signal processing ability of microelectronic circuits to microfluidics where there is the added diversity in current information of having distinct chemical or particulate species and richness in current operation of having chemical reactions and physical interactions.
Similar content being viewed by others
Main
A limitation of microfluidic control is that unlike modern electronic systems where the controller and actuator circuits are all electrically driven, microfluidics typically requires peripheral electromechanical components for the control and actuation of fluid flow2,3,4. This more closely resembles the very early days of electrical circuitry where electromechanical relays carried out electrical switching. Two-phase flow interactions can regulate the movement of bubbles/droplets and carry out logic operations that direct the flow of trailing fluid on-chip10,11. This approach enables high-speed digital flow control, where the bubble/droplet represents a bit of information passing through logic gates. Although this approach may become useful for some high-throughput droplet assays, it is not suitable for applications that require filtration of physical objects or other two-phase flow-disrupting operations. In addition, the bubble/droplet approach requires dynamic input (dictating when bubbles/droplets should be created) to carry out time-varying operations; that is, they still require external controllers. Another approach, which aims to minimize the need for external control, is the use of elastomeric valves with tuned resonant frequencies that respond passively according to the frequency of external inputs14. Owing to the large bandwidth of each component’s resonant response, however, clean switching between different gates has not been achieved17. Thus, there is a lack of schemes for different fluids to regulate each other in either a cascading or feedback mechanism.
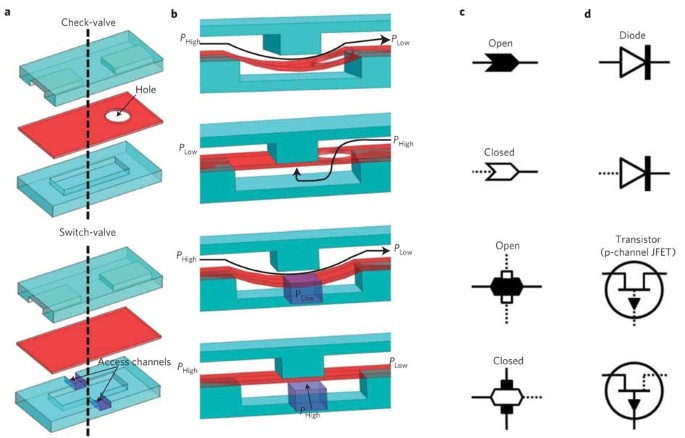
Control in a cascading electrical or fluidic circuit is dictated by two parameters, a switching mechanism and a time delay18. In our microfluidic circuitry, the switching action is enabled by check-valves and switch-valves that have geometrically regulated threshold pressures. These components translate a constant infusion of fluid into a transient outflow. The time-delay effect is realized by compliant components that gradually pressurize in response to steady infusion of fluid in a process that mimics the charging of a capacitor. All components in the fluidic circuits are made in a three-layer polydimethylsiloxane (PDMS) substrate (Fig. 1a). Both the check-valve and switch-valve consist of an interrupted microchannel in one layer, a cavity in the other layer and a deformable membrane in between that can deflect into the cavity to allow the interrupted channel to become connected (Fig. 1b). The check-valve also has a through-hole in the membrane layer to connect one of the ends of the interrupted microchannel with the cavity on the opposing layer. The position of this through-hole dictates the direction of flow allowed and effectively creates a diode-like function that negates any backflow and diffusion in its closed state (Fig. 1c, see also Supplementary Fig. S1). A switch-valve is flow-permissive in both directions but can have access channels to its cavity so that an alternative pressure can force the switch-valve into a closed ‘off’ state (Fig. 1b). A switch-valve with two access channels is shown in Fig. 1a; alternatively, it can have either zero or one access channel. The function of the switch-valve can be thought of as a gated transistor that functions as an electronically controlled switch (Fig. 1d). Specifically, we show a p-channel junction gate field-effect transistor (JFET) transistor because it functions similarly in that a positive gate voltage turns off the switch. It should be noted that the switch-valve is not capable of providing any nonlinear gain; however, the required ‘gate’ pressure (pressure in the cavity region) is lower than that of the source pressure (pressure in the top channel) owing to the contribution of the membrane elasticity in keeping the valve closed. This means that the opening differential pressure is higher than that of the closing differential pressure.
Figure 1: Elastomeric components for autonomously controlled microfluidic devices.
a, A three-layer composite of the check-valve and switch-valve. b, Cross-section schematic of the check-valve and switch-valve in both the open and closed state based on differential pressure. c, Corresponding component state symbol of the check-valve and switch-valve. Conducting current/flow is shown as solid lines and non-conducting current/flow is shown as dotted lines. d, The diode and p-channel JFET transistor shown as analogous electronic components to the check-valve and switch-valve, respectively.
To estimate the performance of the developed microfluidic system, a theoretical model based on an equivalent fluidic circuit concept was constructed and solved numerically in Labview 8.5 (National Instruments; see Supplementary Section S2). The underlying fluid model is based on the Navier–Stokes equation and mechanics. Three basic components are used to derive the model: fluid resistance, capacitance and inductance. Analogous to electrical resistance, fluid resistance is defined as the ratio of pressure drop over flow rate,

where Δ_P_ is the pressure difference, in N m−2, and Q is the volume flow rate, in m3 s−1.
For a microfluidic channel with a rectangular cross-section with width w, length l, depth h, channel aspect ratio ɛ, viscosity μ and assuming both laminar flow and Newtonian fluid, the resistance19 is

Compliant elements of a fluidic system show the fluidic equivalent of capacitance as a pressure-dependent volume change

The fluidic capacitance for a square membrane can be derived by plate theory as

where w is membrane width (m), E is Young’s modulus of the membrane (N m−2), t is membrane thickness (m) and ν is Poisson’s ratio of the membrane (dimensionless; refs 20, 21).
In a manner analogous to electrical inductance, the change in fluidic kinetic energy can directly affect the system pressure change, termed as fluidic inductance, H (in kg m−4; refs 21, 22)
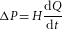
For incompressible and inert fluids in tubes of constant cross-section A, fluid density ρ and length L, the fluidic inductance is given by

It should be mentioned that fluidic inductance in microfluidics, despite having much smaller cross-sectional areas, is typically not a dominant factor because d_Q_/d_t_ and L are significantly smaller. However, for devices where valves are rapidly opening and closing pressurized flow, fluidic inductance could become more influential on the fluid dynamics of the system.
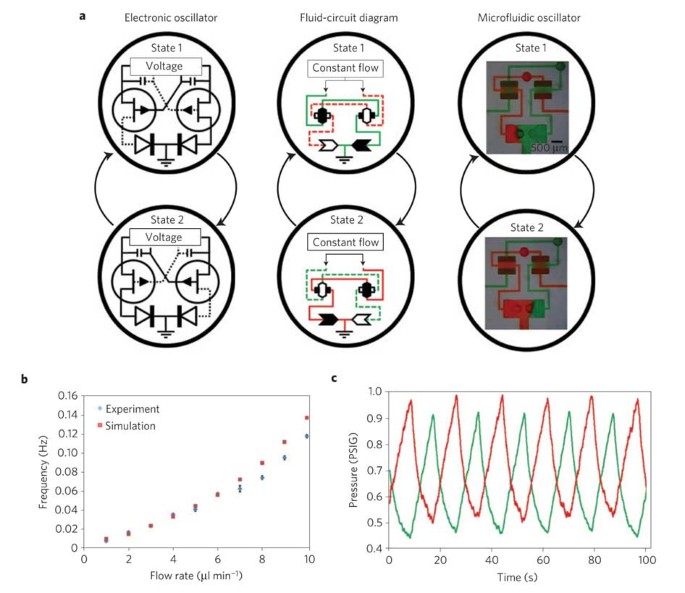
Components integrated in specific configurations enable dynamic auto-regulation of fluid flow. The microfluidic oscillator, comprising two switch-valves each connected to a check-valve, autonomously regulates two flows that are infused at a constant rate to have a distinctive alternating output that indefinitely oscillates between two states so that only one fluid is flowing at a given time (Fig. 2a; see also Supplementary Movie S1). There is only one steady oscillation frequency when a particular set of conditions is applied (that is, infusion rates of the two fluids and the channel and the component geometries in the circuit). Changing any one of these parameters will change the oscillation frequency, and therefore the fluidic circuit must be designed as a whole to achieve a desired autonomously regulating function. This switching scheme may be understood by an analogous electronic circuit shown in Fig. 2a where the transistor provides similar switching functions to the switch-valve. Although the diodes are not necessary for the electronic oscillator, the check-valves serve to negate backflow and mixing between the solutions in the microfluidic oscillator. For the microfluidic oscillator in Fig. 2a, when the red fluid reaches a threshold pressure, it breaks through and opens the right switch-valve. The red fluid then flows to the cavity chamber of the left switch-valve to close it and stop flow of the green fluid. The red fluid then flows out through a check-valve to the outlet where the pressure is released. Now the green fluid builds up pressure while the pressure of the red fluid decreases to repeat the process on the other side of the circuit. For a range of flow rates (Fig. 2b) determined by the response time of membrane deflection and the geometry of the components and channels, the frequency increases with flow rate (that is, the time for parameters _C_1/_Q_1, _C_2/_Q_2 to surpass a threshold pressure decreases with increasing flow rates, see Supplementary Information for description of a theoretical model). At flow rates beyond this operating range, the switching frequencies approach the response time of the valve opening and closings resulting in partially switching oscillations (see Supplementary Movie S2 and Section S2) and eventually no switching. Figure 2c shows the autonomous on-chip oscillation in pressure within the device, which has implications for signal processing and clock-signal generation (for example, see Fig. 3). Oscillations are also biologically relevant as flow of bodily fluids and release of biochemicals is often cyclic or pulsatile23,24,25. We note that continuous switching of low-Reynolds-number, single-phase, Newtonian fluid flows has previously been possible only by external control.
Figure 2: Interactive elastomeric components for oscillatory switching.
a, Comparison between a microfluidic oscillator and an electronic oscillator. The two states of a microfluidic oscillator automatically produce an alternating output flow between two distinct solutions being simultaneously infused at a constant rate. b, Graph of both the simulated and experimental data for the oscillator’s switching frequency for various flow rates within its operating range. The error bars represent the standard deviations from three measurements taken at each flow rate. c, Graph of pressure oscillations at solution inlets for an infusion rate of 10 μl min−1.
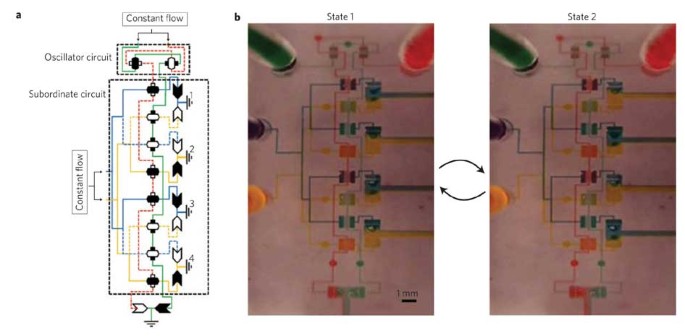
Figure 3: Microfluidic-oscillator control of flow in a subordinate fluid circuit.
a, Fluid-circuit diagram for state 1 of a microfluidic oscillator providing input signals (red and green solutions) to a subordinate fluid circuit that distributes the flow of two solutions (yellow and blue) to four outlets. b, Actual images of both states for the fluid circuit with an infusion rate of 100 μl min−1 that oscillates at 1 Hz.
Figure 3 demonstrates how the microfluidic oscillator (Fig. 2a) can serve as a controller to regulate the flow of different solutions in a subordinate fluidic circuit. The pressure changes shown in Fig. 2c are used as a clocking signal for the subordinate circuit. The subordinate circuit comprises eight switch-valves and eight check-valves that distribute the flow of two solutions (yellow and blue) to four outlets (Fig. 3a). The green and red controller solutions each activate four of the eight switch-valves of the subordinate circuit in an alternating serial arrangement. All solutions are infused simultaneously by a multi-syringe pump at a flow rate of 100 μl min−1. It can be seen that the distribution of flow to the four outlets alternates on the basis of the state of the oscillator circuit at a frequency of 1 Hz (Fig. 3b, see also Supplementary Movie S3). It is noted that the output flow of the oscillator circuit drops along its serial path. To compensate for this pressure loss, the two switch-valves in the oscillator circuit were designed with smaller widths for the output flow to be of sufficient pressure to properly regulate each valve of the subordinate circuit. Alternatively, the blue and yellow sample solutions could have been infused at a relatively lower flow rate than that of the green and red controller solutions.
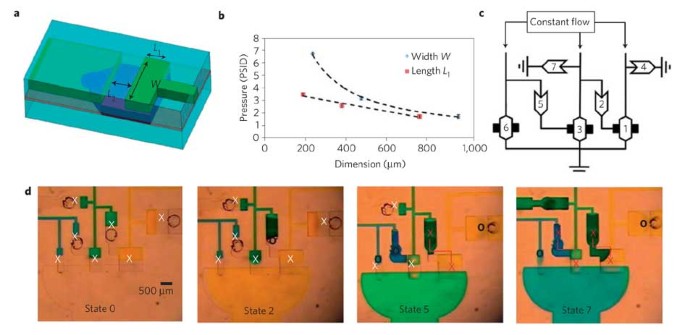
In addition to oscillations, another important class of fluidic control functions is automated sequential operations, as done in electronic finite-state machines. Figure 4 shows such an automatically reconfiguring channel network that enables a time-regulated discretization of flow conduction into on and off states. This network comprised three switch-valves and four check-valves arranged both in parallel and in series. Each component has a different threshold pressure dictated by its physical geometry so that each is activated at different times when being infused simultaneously (see Supplementary Section S3 for details of the cascading switching mechanism). Infusion can be carried out by a multi-syringe pump (see Supplementary Movie S4) or alternatively by the squeezing force of a clamp (see Supplementary Movie S5). Actual images of four of the seven states are shown in Fig. 4d; an ‘O’ or ‘X’ represents the component in an on or off state, respectively. A red ‘X’ designates a check-valve with a downstream channel linked to the cavity of a switch-valve. This combination of components locks in pressure, which subsequently maintains both components in an off state despite any subsequent release of pressure behind the check-valve. The sequential switching mechanism enables assays where multiple solutions are introduced into a channel sequentially, such as in an immunoassay (see Supplementary Fig. S5). Although the fluidic control shown here is relatively simple, consisting of only a few steps, electronic circuit analysis describes that every circuit or logic operation is possible using only a transistor component26. As a transistor’s directionally distinct switching properties are mimicked by having a switch-valve and check-valve in series, this suggests broad applicability of the developed elastomeric components for device-embedded flow control.
Figure 4: Automated fluid circuits for cascading operations.
a, The geometric parameters that dictate the component opening threshold pressure for the check-valve and diode. b, Graph showing the linear and nonlinear dependence of the check-valve’s geometries for varying _L_1 and W dimensions (while the other dimension is held constant), respectively. The error bars represent the standard deviations from measurements taken from three separate devices. c, Fluid-circuit diagram of a device that sequentially switches between three solutions being infused simultaneously at a constant flow rate. This circuit is a simple finite-state machine that carries out a predefined sequence of operations. The numbers in the components show the order of opening. d, Actual images of four of the seven states, with ‘X’ and ‘O’ representing closed and opened valves, respectively. Red ‘X’s connected by a line designate check-valve and switch-valve modules that lock in pressure to maintain the two linked valves closed once a threshold is surpassed.
Methods
Fabrication of device.
The device consists of three layers made from PDMS prepolymer and curing agent (Sylgard 184, Dow Corning) at a 10:1 ratio. The top and bottom layers are moulded against a master mould made by standard photolithography using the negative-photoresist SU-8 (SU-8, MicroChem). The master moulds were silanized in a desiccator for 2 h (United Chemical Tech.). The height of all top layer and bottom layer features is 100 μm except for those in the top layer of Fig. 3, which is 30 μm. The PDMS moulds of the top and bottom layers were cured in a 120 ∘C oven for over 2 h. The middle-layer membrane was made by spin-coating a 30 μm PDMS layer on a silanized silicon wafer at 1,500 rpm for 90 s and then curing in a 120 ∘C oven for 30 min. All layers were bonded together using oxygen plasma treatment (SPI Plasma-Prep II, Structure Probe) for 30 s.
The three layers of the device are bonded together using oxygen plasma for 30 s. In the first step, the thin PDMS membrane, while still on the silicon wafer (or any flat substrate), is bonded to either the top or bottom layer and then the two bonded layers are detached from the wafer. Access holes are made in the top layer with a biopsy punch. Holes are punched into the bonded middle layer, using a 350 μm biopsy punch (Ted Pella), for the check-valve and switch-valve components for all figures. For check-valve components, a hole is punched in the downstream region of the cavity directly after the gap. Switch-valves have holes punched to interface access channels of the top and bottom layers. To ensure efficacy of the components, the circular shape of the biopsy punch can be moulded into either or both the bottom layer and top layer so the hole is accurately punched every time (as shown in Fig. 4a). For the second step, the top layer and the bonded middle and bottom layers are bonded. The gap regions of the components are rendered unable to permanently bond to the middle membrane by placing a PDMS stamp that has extruding features that correspond to the gap regions negating exposure to oxygen plasma. Finally in step three, all layers are aligned and bonded together; the device is incubated at 60 ∘C for 1 min to enhance the bond strength. Solutions are then inserted in the access holes to fill the device. The device should not be used directly after being placed in a vacuum because it can cause some components to open; in which case waiting about 30 min allows air to penetrate back in. Tubing or other interfaces can be connected to access holes in the top layer.
Component pressure characterization.
The dependence of threshold pressure on the geometry of a component was characterized for three lengths of both _L_1 and W (as shown in Fig. 4b). The threshold pressure was determined by continuously measuring the differential pressure across the component with a differential pressure transducer (Model PX139-005D4V, Omega Eng.) as a syringe pump continuously pressurized the microchannel with a flow rate of 6 ml h−1. The pressure transducers were connected to access microchannels that were located directly before and after the component for quicker response timing and more accurate readings. The threshold pressure for a given trial was determined by the peak pressure in the pressure histogram as measured by the transducer as the component pressurized to a critical limit and opened. The average of three trials was plotted to give the relationship between the threshold pressure and the component dimension. Threshold pressures for components with a constant W of 1 mm with _L_1 values of 800,400 and 200 μm as well as for a constant _L_1 of 800 μm with W values of 1,000,500 and 250 μm are provided in Fig. 4b. For all components, _L_2 was maintained constant at 300 μm. The oscillator pressure measurements were carried out by measuring the gauge pressure of both inlets simultaneously using two pressure transducers (Model PX26-015DV, Omega Eng.). Measurements were taken every 100 ms and the graphs are the moving time-average of 50 minus the measured zero value for each sensor.
References
- Whitesides, G. M. The origins and the future of microfluidics. Nature 442, 368–373 (2006).
Article ADS Google Scholar - Pennathur, S. Flow control in microfluidics: Are the workhorse flows adequate? Lab Chip 8, 383–387 (2008).
Article Google Scholar - Unger, M. A., Chou, H. P., Thorsen, T., Scherer, A. & Quake, S. R. Monolithic microfabricated valves and pumps by multilayer soft lithography. Science 288, 113–116 (2000).
Article ADS Google Scholar - Gu, W., Zhu, X., Futai, N., Cho, B. S. & Takayama, S. Computerized microfluidic cell culture using elastomeric channels and Braille displays. Proc. Natl Acad. Sci. USA 101, 15861–15866 (2004).
Article ADS Google Scholar - Xie, J., Shih, J., Lin, Q., Yang, B. & Tai, Y. C. Surface micromachined electrostatically actuated micro peristaltic pump. Lab Chip 4, 495–501 (2004).
Article Google Scholar - Beebe, D. J. et al. Functional hydrogel structures for autonomous flow control inside microfluidic channels. Nature 404, 588–590 (2000).
Article ADS Google Scholar - Groisman, A., Enzelberger, M. & Quake, S. R. Microfluidic memory and control devices. Science 300, 955–958 (2003).
Article ADS Google Scholar - Madou, M. J., Lee, L. J., Daunert, S., Lai, S. & Shih, C-H. Design and fabrication of CD-like microfluidic platforms for diagnostics: Microfluidic functions. Biomed. Microdev. 3, 245–254 (2001).
Article Google Scholar - Fuerstman, M. J., Garstecki, P. & Whitesides, G. M. Coding/decoding and reversibility of droplet trains in microfluidic networks. Science 315, 828–832 (2007).
Article ADS Google Scholar - Prakash, M. & Gershenfeld, N. Microfluidic bubble logic. Science 315, 832–835 (2007).
Article ADS Google Scholar - Cheow, L. F., Yobas, L. & Kwong, D. L. Digital microfluidics: Droplet based logic gates. Appl. Phys. Lett. 90, 054107 (2007).
Article ADS Google Scholar - Toepke, M. W., Abhyankar, V. V. & Beebe, D. J. Microfluidic logic gates and timers. Lab Chip 7, 1449–1453 (2007).
Article Google Scholar - Kartalov, E. P., Walker, C., Taylor, C. R., Anderson, W. F. & Scherer, A. Microfluidic vias enable nested bioarrays and autoregulatory devices in Newtonian fluids. Proc. Natl Acad. Sci. USA 103, 12280–12284 (2006).
Article ADS Google Scholar - Leslie, D. C. et al. Frequency-specific flow control in microfluidic circuits with passive elastomeric features. Nature Phys. 5, 231–235 (2009).
Article ADS Google Scholar - Chen, P. J., Rodger, D. C., Humayun, M. S. & Tai, Y. C. MEMS 2008: 21st IEEE International Conference. Technical Digest 1080, 575–578 (2008).
Google Scholar - Langelier, S. M., Chang, D. S., Zeitoun, R. I. & Burns, M. A. Acoustically driven programmable liquid motion using resonance cavities. Proc. Natl Acad. Sci. USA 106, 12617–12622 (2009).
Article ADS Google Scholar - Stone, H. A. Tuned-in flow control. Nature Phys. 5, 178–179 (2009).
Article ADS Google Scholar - Hayes, J. P. Introduction to Digital Logic Design 391–479 (Addison-Wesley, 1993).
Google Scholar - Bahrami, M., Yovanovich, M. M. & Culham, J. R. Pressure drop of fully-developed, laminar flow in microchannels of arbitrary cross-section. J. Fluids Eng. 128, 1036–1044 (2006).
Article Google Scholar - Zengerle, R. & Richter, M. Simulation of microfluid systems. J. Micromech. Microeng. 4, 192–204 (1994).
Article ADS Google Scholar - Bourouina, T. & Grandchamp, J-P. Modeling micropumps with electrical equivalent networks. J. Micromech. Microeng. 6, 398–404 (1996).
Article ADS Google Scholar - Gerlach, T. Microdiffusers as dynamic passive valves for micropump applications. Sens. Actuat. A 69, 181–191 (1998).
Article Google Scholar - Gundelfinger, E. D., Kessels, M. M. & Qualmann, B. Temporal and spatial coordination of exocytosis and endocytosis. Natl Rev. Mol. Cell Biol. 4, 127–139 (2003).
Article Google Scholar - Weigle, D. S., Koerker, D. J. & Goodner, C. J. Pulsatile glucagon delivery enhances glucose production by perifused rat hepatocytes. Am. J. Physiol. 247, E564–E568 (1984).
Google Scholar - Robertson, A., Drage, D. J. & Cohen, M. H. Control of aggregation in Dictyostelium discoideum by an external periodic pulse of cyclic adenosine monophosphate. Science 175, 333–335 (1972).
Article ADS Google Scholar - Hayes, J. P. Introduction to Digital Logic Design 140–213 (Addison-Wesley, 1993).
Google Scholar
Acknowledgements
We thank the NIH (HL-084370) for financial support. B.M. acknowledges financial support from a GAANN fellowship supported by the US Department of Education and a TEAM training grant supported by the National Institute for Dental and Craniofacial Research.
Author information
Authors and Affiliations
- Department of Biomedical Engineering, University of Michigan, 2200 Bonisteel Boulevard, Ann Arbor, Michigan 48109-2099, USA
Bobak Mosadegh, Yi-Chung Tung, Yu-suke Torisawa, Tommaso Bersano-Begey, Hossein Tavana & Shuichi Takayama - Department of Mechanical Engineering, University of Michigan, 2350 Hayward Street, Ann Arbor, Michigan 48109-2125, USA
Chuan-Hsien Kuo - Macromolecular Science and Engineering Center, University of Michigan, 2300 Hayward Street, Ann Arbor, Michigan 48109, USA
Shuichi Takayama
Authors
- Bobak Mosadegh
You can also search for this author inPubMed Google Scholar - Chuan-Hsien Kuo
You can also search for this author inPubMed Google Scholar - Yi-Chung Tung
You can also search for this author inPubMed Google Scholar - Yu-suke Torisawa
You can also search for this author inPubMed Google Scholar - Tommaso Bersano-Begey
You can also search for this author inPubMed Google Scholar - Hossein Tavana
You can also search for this author inPubMed Google Scholar - Shuichi Takayama
You can also search for this author inPubMed Google Scholar
Contributions
B.M. conceived, designed and fabricated devices for all experiments and S.T. oversaw the complete project. B.M. and C-H.K. carried out component characterization experiments. Y-C.T. developed the computer model for the oscillation device. B.M., T.B-B., Y.T., H.T. and S.T. developed the framework and wrote the paper.
Corresponding author
Correspondence toShuichi Takayama.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Mosadegh, B., Kuo, CH., Tung, YC. et al. Integrated elastomeric components for autonomous regulation of sequential and oscillatory flow switching in microfluidic devices.Nature Phys 6, 433–437 (2010). https://doi.org/10.1038/nphys1637
- Received: 22 September 2009
- Accepted: 05 March 2010
- Published: 18 April 2010
- Issue Date: June 2010
- DOI: https://doi.org/10.1038/nphys1637