Testing the Infinitely Many Genes Model for the Evolution of the Bacterial Core Genome and Pangenome (original) (raw)
Journal Article
Origins Institute and Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, Canada
Search for other works by this author on:
Origins Institute and Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, Canada
Search for other works by this author on:
Cite
R. Eric Collins, Paul G. Higgs, Testing the Infinitely Many Genes Model for the Evolution of the Bacterial Core Genome and Pangenome, Molecular Biology and Evolution, Volume 29, Issue 11, November 2012, Pages 3413–3425, https://doi.org/10.1093/molbev/mss163
Close
Navbar Search Filter Mobile Enter search term Search
Abstract
When groups of related bacterial genomes are compared, the number of core genes found in all genomes is usually much less than the mean genome size, whereas the size of the pangenome (the set of genes found on at least one of the genomes) is much larger than the mean size of one genome. We analyze 172 complete genomes of Bacilli and compare the properties of the pangenomes and core genomes of monophyletic subsets taken from this group. We then assess the capabilities of several evolutionary models to predict these properties. The infinitely many genes (IMG) model is based on the assumption that each new gene can arise only once. The predictions of the model depend on the shape of the evolutionary tree that underlies the divergence of the genomes. We calculate results for coalescent trees, star trees, and arbitrary phylogenetic trees of predefined fixed branch length. On a star tree, the pangenome size increases linearly with the number of genomes, as has been suggested in some previous studies, whereas on a coalescent tree, it increases logarithmically. The coalescent tree gives a better fit to the data, for all the examples we consider. In some cases, a fixed phylogenetic tree proved better than the coalescent tree at reproducing structure in the gene frequency spectrum, but little improvement was gained in predictions of the core and pangenome sizes. Most of the data are well explained by a model with three classes of gene: an essential class that is found in all genomes, a slow class whose rate of origination and deletion is slow compared with the time of divergence of the genomes, and a fast class showing rapid origination and deletion. Although the majority of genes originating in a genome are in the fast class, these genes are not retained for long periods, and the majority of genes present in a genome are in the slow or essential classes. In general, we show that the IMG model is useful for comparison with experimental genome data both for species level and widely divergent taxonomic groups. Software implementing the described formulae is provided at http://github.com/rec3141/pangenome.
Introduction
One of the major surprises that has resulted from the analysis of large numbers of complete bacterial genomes over the past decade is that the gene content is highly variable, even among sets of closely related genomes. For any set of genomes analyzed, the core genome is the set of genes found in all genomes (i.e., the intersection of the gene sets on individual genomes), and the pangenome is the set of genes found on at least one of the genomes (i.e., the union of the sets of genes on individual genomes). For example, Welch et al. (2002) compared three genomes of Escherichia coli for which the mean number of genes was 4,769. They found only 2,996 genes in the core genome and 7,638 genes in the pangenome. This illustrates a general point that has now been observed with many groups of bacteria: the core genome is always substantially smaller than the mean genome size, and the pangenome is always substantially larger.
A more recent analysis of 17 E. coli genomes (Rasko et al. 2008) finds that the core genome is reduced to ∼ 2,200 genes. The number of genes in the core genome, which we will call _G_core(n), depends on the number of genomes in the sample, n. In the E. coli example, _G_core(n) continues to decrease slowly with n, which makes it difficult to estimate the limiting size of the core genome that would be reached if very large numbers of genomes were included. The number of genes in the pangenome, _G_pan(n), is ∼13,000 for the 17 E. coli genomes and increases rapidly as new genomes are added. If _G_pan(n) continues to increase with n for large n, the pangenome is said to be open, whereas if _G_pan(n) tends to a maximum limit for large n, the pangenome is said to be closed. The E. coli pangenome appears to be open, or least, _G_pan(n) is still far from reaching a limit with the available number of genomes. Open pangenomes have also been observed in Streptococcus agalactiae (Tettelin et al. 2005), Prochlorococcus (Kettler et al. 2007), a combination of E. coli and Shigella (Touchon et al. 2009), Listeria (den Bakker et al. 2010), and in a study taking representative genomes from across the full range of bacteria (Lapierre and Gogarten, 2009). A closed pangenome was found in Clostridium difficile (Scaria et al. 2010), where it was estimated that a sample of 26 genomes would be sufficient to capture the entire pangenome. However, this result may depend on the way the extrapolation to large n was done and may not indicate a qualitative difference between C. difficile and other bacteria.
A quantity related to the pangenome size is the number of “new” genes, _G_new(n), that are found for the first time in the _n_th genome sequenced. It was found by Tettelin et al. (2005) that both _G_core(n) and _G_new(n) could be fitted quite well by simple functions that decreased exponentially with n. No theoretical model was given to explain why this form of fitting function should apply, but we will show that their model implies an underlying star-shaped phylogeny. It is our objective in this article to consider ways of predicting the shape of the core and pangenome curves beginning from explicit evolutionary models.
An approach that we consider to be very promising is the infinitely many genes (IMG) model, introduced by Baumdicker et al. (2010). The name IMG is analogous to the infinitely many sites model, which is well known in population genetics (Hein et al. 2005). In the infinitely many sites model, it is assumed that there are an infinite number of possible sites at which a mutation could occur; hence, each new mutation occurs at a different site. Similarly, in the IMG model, it is assumed that an infinite number of possible genes might arise in a genome; hence, each new gene that arises is different from all previous genes. Baumdicker et al. (2010) consider a population of genomes evolving according to the neutral Wright–Fisher model (Wright 1969). New genes arise in each genome at a constant rate. Genes spread to new genomes when the lineages branch. It is also supposed that each gene currently in a genome can be deleted at constant rate. The model allows the functions _G_core(n) and _G_pan(n) to be calculated in an elegant way as a function of the evolutionary parameters (rate of origin and deletion and effective population size).
The original IMG model assumes that the genealogical tree of the population is a coalescent tree, as is the case in population genetics when we consider individuals within a species. Herein, we want to study groups of genomes that extend beyond the species level. The process of speciation/diversification giving rise to the genomes in the available data is not necessarily equivalent to a coalescent. We will derive a phylogenetic tree from the amino acid sequences of conserved proteins and then use the IMG model for genome evolution on this fixed tree. We wish to determine the extent to which the predicted behavior of the core and pangenomes depends on the shape of the tree. In addition to the coalescent tree and the fixed phylogenetic tree, we will consider the star phylogeny, where there is a radiation of lineages at the root. We will show that the IMG on the star tree gives a prediction for the pangenome size that corresponds to an empirical fitting function previously used by Tettelin et al. (2005), in which the pangenome size increases linearly with the number of genomes. However, we will also show that the prediction of the model with a coalescent tree or a fixed phylogenetic tree is usually much better than with a star tree.
In this article, we apply the IMG model at the level of gene families, which are groups of related genes within a genome. Genes in a sample of _n_g genomes are clustered into families according to sequence similarity. A family is considered present in a genome if at least one gene in that family is present. The number of gene families found in k genomes gives the gene family frequency spectrum, G(k|_n_g). The _G_core(n) and _G_pan(n) can then be calculated directly from the frequency spectrum for n ≤ _n_g. Typically G(k|_n_g) has a U-shaped distribution with many gene families found in one or only a few species, a substantial number of core gene families found in all (or nearly all) species, and relatively few gene families at intermediate values of k.
The IMG model has not yet been tested on many data sets. Our intention here is to test the model on a variety of sets of genomes and to compare the results with the predictions of several alternative evolutionary models that we derive here. As examples, we use taxonomic subsets of completely sequenced bacterial genomes within the Bacilli, a Class of Firmicutes that has important biomedical and environmental implications. Although it is unlikely that the fairly restrictive assumptions of the model are exactly true, we view the IMG model as a useful null model of neutral genome evolution. Building more complex models from this starting point should allow identification of any important additional factors. However, as we shall see later, the IMG model and the variants we consider here stand up surprisingly well to analysis of the large number of bacterial genome data sets investigated.
Methods
Gene Clustering
Complete nucleic acid and translated proteome sequences were obtained from the NCBI Genomes database for all 172 Bacteria from the Class Bacilli available in April 2011 (supplementary table S1, Supplementary Material online). Only complete genome sequences were used — no incomplete or draft genomes were included. Genes encoded on plasmids associated with each genome sequence were also included and were treated as part of the genome. Basic Local Alignment Search Tool (BLAST) databases were created for each genome with all amino acid sequences encoded by each genome, and all-against-all searches were performed using blastp (v. 2.221). For each pair of genomes, including self-pairs, each peptide sequence was used as a query against every peptide sequence in the paired genome, and the process was repeated in the reverse direction. A direct link was counted between two genes if the BLAST E value was less than 1_e_-30 for searches in both directions, and if the length of the locally aligned region found by BLAST was longer than 70% of the length of the longer of the two sequences. Sequences were grouped into clusters using the single-link cluster procedure, i.e., sequences are part of the same cluster if there is a direct link between them or if there is a chain of direct links that connects them. These clustering methods were implemented with custom Perl scripts that are freely available online (http://github.com/rec3141/genometools). We have previously used these clustering methods for analysis of other sets of genomes (Collins et al. 2011), and we have considered the effects of changing the cutoff E value and the minimum length criterion. In this article we present only one set of clusters obtained with conservative clustering parameters, but similar results were obtained for more relaxed clustering parameters as well.
The gene clusters calculated earlier may contain more than one gene from the same genome in some cases. We call a group of paralogous genes in the same genome a gene family. For the remainder of the analysis, we deal with gene families, not individual genes. Because the IMG model does not account for duplication or loss of genes within a genome, it is preferable to work at the family level from the point of view of model comparison. As an example, insertion sequences (ISs) are known to proliferate to high copy numbers in the genomes of some Bacilli, even though each IS likely arrived into any particular genome only once (Qiu et al. 2010). Furthermore, clustering to gene families avoids the problem of identification of orthologs, which is difficult to do by an automated procedure.
Genome Phylogeny
Gene families present in all genomes and having exactly one gene per genome were used to build a genome phylogeny. The translated amino acid sequences of genes from 55 such single-copy clusters (supplementary table S2, Supplementary Material online) were aligned using MUSCLE v3.7 (Edgar 2004) with parameter “-diags.” Each cluster was aligned independently; alignments were then concatenated and input into PhyML v3.0.1 (Guindon et al. 2010) for phylogenetic tree construction using default parameters. The multiple sequence alignment and phylogenetic trees are archived on TreeBASE (http://purl.org/phylo/treebase/phylows/study/TB2:S11647; Sanderson et al. 1994). The complete tree is shown in (supplementary figure S1, Supplementary Material online). From within this tree, we selected subsets of genomes for further analysis, as shown in (figure 1 and supplementary figure S1, Supplementary Material online). The selected clades are characterized by relatively long internal branches separating them from other parts of the tree and are strongly supported by the approximate likelihood ratio test (aLRT), obtained from the program PhyML (supplementary fig. S1, Supplementary Material online). The clades span multiple taxonomic levels, including species-specific groups (Bacillus cereus group, Staphylococcus aureus, Streptococcus pneumoniae, and Streptococcus pyogenes), genus-specific groups (Staphylococcus spp., Listeria spp., and Streptococcus spp.), and higher level groups: family “Bacillaceae 1” (Ludwig et al. 2009), family “Lactobacillaceae” (including relatives among the “Leuconostocaceae”), and class Bacilli. The definitions of taxonomic groups are far from settled within the Bacteria, and the gene trees may not be fully consistent with each other because of horizontal gene transfer (HGT), so our intention is not to produce a fully resolved tree for these genomes. However, the phylogenetic tree clearly shows that the selected groups are monophyletic and, except for the “Lactobacillaceae,” nearly ultrametric, making them particularly suitable for the evolutionary analyses presented in this study.

Fig. 1.
Phylogenetic tree of 172 Bacilli having complete genome sequences, annotated with the taxonomic groups used in this study. Tree topology and branch lengths were determined by maximum likelihood analysis (using PhyML) of concatenated alignments of amino acid sequences from 55 single-copy core genes (supplementary table S2, Supplementary Material online). The fully annotated tree is given in supplementary fig. S1, Supplementary Material online. The root points of the taxonomic groupings chosen for study are demarcated with stars (★). These groups were 100% supported by the approximate likelihood ratio test (as calculated in PhyML). Scale bar indicates expected number of amino acid substitutions per site.
A Model of Genome Evolution on a Coalescent Tree
In this section, we describe the IMG model of Baumdicker et al. (2010), which considers a set of n genomes evolving on a coalescent tree, as in figure 2a. The rate of origin of new gene families in each genome is u, the rate of deletion of each existing gene family is v, and the effective population size is N. A gene origin may be an evolutionary event within the lineage or may be an insertion of a horizontally transferred gene. Either way, it is assumed that each new gene is distinct from all existing genes in the data set. The quantities of interest depend on the rates of insertion and deletion in scaled coalescent units: θ = 2_Nu_ and ρ = 2_Nv_.

Fig. 2.
Schematic representation of (a) the shape of a coalescent tree, (b) the shape of a star tree, and (c) the calculation of the gene frequency spectrum on a fixed tree.
The gene family frequency spectrum, G(k|n), is the expected number of families that will be found in k genomes after sampling n.
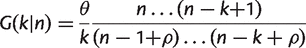
(1)
The number of clusters in the core genome is the number of families present in every genome:
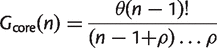
(2)
The number of clusters in the pangenome is the number of families that are present in at least one of the sampled genomes:
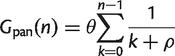
(3)
In the (supplementary Materials, Supplementary Material online), we provide a way of deriving the above results that may be simpler than that given by Baumdicker et al. (2010).
So far it was assumed that the same parameters, θ and ρ, apply for all gene families. Families are assumed to be “dispensable,” i.e., they can be inserted or deleted without affecting the fitness. In addition to dispensable families, we consider a second class of essential families that are present in all genomes and cannot be inserted and deleted. This introduces an extra parameter, _G_ess, the number of essential gene families. This changes the above formulations simply by adding the constant _G_ess to the equations for _G_core(n), _G_pan(n) and G(n|n). The gene family frequency spectrum G(k|n) is unaltered for k < n. We refer to the model with one class of dispensable genes plus a class of essential genes as “1D + E.” An extension of the model is to consider two classes of dispensable families with different parameters θ1, θ2, ρ1, and ρ2 in addition to the class of essential genes. We refer to this as “2D + E.” All the formulae for the case with two dispensable classes are simply the sum of two terms of the same form as the single class model.
A Model of Genome Evolution on a Star Tree
In this study, we will consider the star phylogeny shown in figure 2b, where there is a radiation of lineages at the root at a time t in the past. We choose the star phylogeny for three reasons. First, its shape is very different from a coalescent tree; therefore, if the results are dependent on the tree shape, we would expect a clear difference between these cases. Second, the star phylogeny is a simple case for which an analytical solution is easy to obtain. Third, we are motivated by the observation of Tettelin et al. (2005) that the pangenome size appears to increase linearly with n for large n, whereas according to equation (3), the pangenome should increase approximately as ln(n) for large n. We will now show that if evolution occurs on a star phylogeny instead of a coalescent tree, then the pangenome does in fact increase linearly with n.
Consider a set of genomes evolving according to the IMG model with a single class of dispensable gene families with deletion rate v per family and overall origination rate u as before. Suppose that the genome at the root of the star phylogeny is a typical genome described by this model. It therefore contains _G_0 = u/v gene families. The probability that a dispensable family is retained on one branch for time t without deletion is e_−_vt. The core families are those that are retained on all n branches. Therefore, the number of core families is
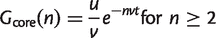
(4)
For a single genome, all families are in the core by definition, so _G_core(1) = _G_0. The probability that a dispensable family is retained on at least one of the n branches is one minus the probability that it is deleted on all branches. Hence, the number of dispensable families retained since the root is
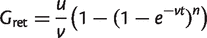
(5)
Let _G_gain be the number of families that were not present at the root and are gained along one branch of length t. We may write
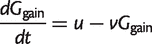
(6)
from which
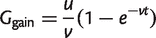
(7)
There will be _G_gain gene families gained on each of the n branches. Hence, the size of the pangenome is
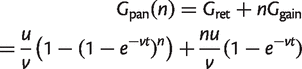
(8)
From this, the number of new families found for the first time in the _n_th genome is
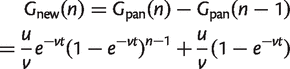
(9)
To facilitate comparison between the star phylogeny and the coalescent, it is useful to define θ = ut and ρ = vt. The time to the root in the star is t, whereas the typical time to the root in a coalescent tree is 2_N_; hence, θ and ρ mean almost the same thing in the two cases; however, the shape of the tree affects the way the core and pangenome depend on θ and ρ. As with the coalescent case, it is possible to add a number _G_ess of essential gene families or to consider two classes of dispensable families with insertion and deletion rates θ1, θ2, ρ1, and ρ2.
There is a connection between the star phylogeny model and the work of Tettelin et al. (2005), who found that the numbers of new and core gene families in Streptococcus can be fitted by simple exponential decay functions:
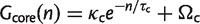
(10)
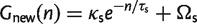
(11)
Equations (10) and (11) are equivalent to those given in the captions to figures 2 and 3 of Tettelin et al. (2005). We have used the notation Ωs in equation (11) instead of tg(θ), which was used by Tettelin et al., to avoid confusion with the parameter θ in the IMG model. If we write the results from equations (4) and (9) in terms of θ and ρ, and we explicitly include the essential families in the core, we obtain:
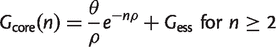
(12)
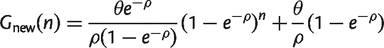
(13)

Fig. 3.
Fitting evolutionary models to the core and pangenome curves for 14 sequenced Streptococcus pneumoniae genomes. Models used a coalescent tree with one class of essential gene families and either one (1D+E; dashed lines) or two (2D+E; solid lines) dispensable classes. The shaded region demarcates the maximum range observed during 500 permutations of the data.
It can be seen that, as in equation (10), equation (12) is a simple exponential decay if we identify the parameters as Ωc = G_ess, κc = θ/ρ, and 1/τc = ρ. If we identify the parameters Ωs, κs and τ_s in a suitable way, equation (13) is also equivalent to equation (11). Note that the number of new families approaches a constant for large n, so the pangenome increases linearly with n for large n. The exponential decay functions were originally given as empirical fitting functions with no theoretical model to justify them. We now see that these fitting functions are the expected results for an IMG model on a star phylogeny. However, in our interpretation, there are only three independent parameters _G_ess, θ and ρ, and all six parameters in equations (10) and (11) depend on these three.
A Model of Genome Evolution on a Fixed Tree
A real phylogenetic tree is neither a coalescent nor a star tree. For a real tree, the gene family frequency spectrum is not simply a smooth curve but has structure which is indicative of the shape of the particular tree on which the genomes evolved. Herein, we will show that it is possible to calculate the expected gene family frequency spectrum for the IMG model on any given fixed tree with branch lengths that are specified in advance. In the case we analyze in the Results section, we use the maximum likelihood tree derived from protein sequence evolution (fig. 1), and the branch lengths are measured in amino acid substitutions per site.
Let a be a node in the fixed tree, let t a be the length of the branch leading to node a, and let n a be the number of genomes in the data that descend from node a, as shown in figure 2c. We may write
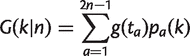
(14)
where g(t a) is the expected number of families present in a that arose on the branch leading to a, and p a(k) is the probability that a family present at a is present in k out of n a genomes that descend from a. The sum goes over n tip nodes (current genomes) and n − 1 internal nodes, i.e., 2_n_ − 1 nodes in total.
For a single class of dispensable gene families in the IMG model,
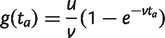
(15)
as in equation (7). If a is the root node, then g(t a) = u/v. If a is a tip node, then p a(1) = 1 and p a(k) = 0 for k_≠1. If a is an internal node, p a(k) = 0 for k > n a and we can calculate p a(k) for 0 ≤ k ≤ n a using the following recursion. Let the probability that a family is retained for a time t be r(t) = e_−_vt, and the probability that it is lost during time t be l(t) = 1−_e_−_vt. Let c be the parent node of a and b, as in figure 2c. Then, for k ≥ 1, we may write
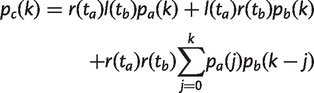
(16)
and for k = 0,
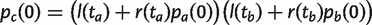
(17)
Once these probabilities have been calculated for every node, equation (14) gives the gene family frequency spectrum. If there is more than one class of dispensable family, then the spectrum is the sum of the spectra for the two classes. If there is a class of essential families, then a constant _G_ess is added to G(n|n). The core genome and pangenome curves can then be calculated from the gene family frequency spectrum, as below.
Calculating the Mean Core Genome and Pangenome
For a data set of _n_g genomes, we can plot _G_core(n) and _G_pan(n) as n increases from 1 to _n_g. This result depends on the order in which the genomes are added to the set. Therefore, it is useful to consider the mean values for _G_core(n) and _G_pan(n) averaged over the different permutations of the genomes. These mean functions can be obtained directly from the gene family frequency spectrum, G(k|_n_g), which is a function of the full data set and does not depend on the permutation. Consider a family that is present in k genomes out of _n_g. If n genomes are sampled, the probability that the family is present in all n is
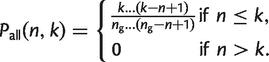
(18)
Therefore, the mean size of the core genome is
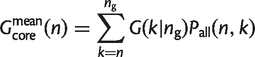
(19)
The probability that the family is absent in all n is
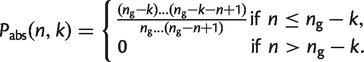
(20)
The probability that this family is in at least one of the n is 1 − _P_abs(n,k). Therefore, the mean size of the pangenome is
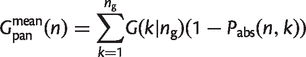
(21)
Fitting the Models
Each theoretical model was fitted to the data using the Nelder–Mead least-squares optimization routine in the open-source statistical software package R (R Development Core Team 2009). For each model, we imposed a constraint on the parameters, such that the mean number of families per genome, _G_0, is the same in the theory as the data. This reduces the number of free parameters by one in each model and means that the theory curve passes exactly through the mean of the data for the n = 1 point in _G_pan(n) and _G_core(n).
The parameters for the core and pangenome curves were chosen by minimizing the root mean square (RMS) deviation per point between the fitted model and the mean, as calculated below. Both the core and the pangenome data were used in the minimization because a good model should be able to fit both curves at the same time. The superscript “theory” denotes any one of the theoretical models.
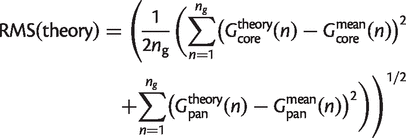
(22)
To compare the quality of fit among models, we relate the fit to the inherent uncertainty in the data, represented by permutations of the data. For each of the data sets in table 1, we considered 500 random permutations of the _n_g genomes and calculated the core and the pangenome curves for each. We denote the core and pangenome curves for any one particular permutation of the genomes in the data as _G_coreperm(n) and _G_panperm(n). The RMS deviation per point between the permutation and the mean is
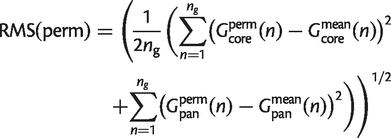
(23)
Table 1.
Comparison of properties of subsets of genomes of Bacilli.
| Taxonomic group | _n_g | _N_genes | _G_0 | 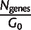 |
_G_core | 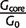 |
_G_pan |  |
_d_prot |
|---|---|---|---|---|---|---|---|---|---|
| Staphylococcus aureus | 15 | 2,668 | 2,212 | 1.21 | 1,532 | 0.69 | 5,522 | 2.50 | 0.0031 |
| Streptococcus pyogenes | 13 | 1,853 | 1,593 | 1.16 | 1,043 | 0.65 | 4,096 | 2.57 | 0.0064 |
| Streptococcus pneumoniae | 14 | 2,129 | 1,787 | 1.19 | 1,141 | 0.64 | 5,509 | 3.08 | 0.0076 |
| Bacillus cereus group | 19 | 5,502 | 4,333 | 1.27 | 2,246 | 0.52 | 18,111 | 4.18 | 0.0248 |
| Listeria spp. | 9 | 2,888 | 2,330 | 1.24 | 1,718 | 0.74 | 4,430 | 1.90 | 0.0571 |
| Staphylococcus spp. | 22 | 2,620 | 2,185 | 1.20 | 994 | 0.45 | 9,473 | 4.34 | 0.3297 |
| Streptococcus spp. | 50 | 2,000 | 1,693 | 1.18 | 487 | 0.29 | 16,583 | 9.79 | 0.3553 |
| “Bacillaceae 1” | 38 | 4,684 | 3,718 | 1.26 | 929 | 0.25 | 32,260 | 8.68 | 0.4261 |
| “Lactobacillaceae” | 31 | 2,152 | 1,736 | 1.24 | 356 | 0.21 | 16,357 | 9.42 | 0.8991 |
| Bacilli | 172 | 2,984 | 2,417 | 1.23 | 143 | 0.06 | 97,860 | 40.49 | 1.1359 |
| Taxonomic group | _n_g | _N_genes | _G_0 | 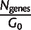 |
_G_core | 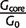 |
_G_pan |  |
_d_prot |
|---|---|---|---|---|---|---|---|---|---|
| Staphylococcus aureus | 15 | 2,668 | 2,212 | 1.21 | 1,532 | 0.69 | 5,522 | 2.50 | 0.0031 |
| Streptococcus pyogenes | 13 | 1,853 | 1,593 | 1.16 | 1,043 | 0.65 | 4,096 | 2.57 | 0.0064 |
| Streptococcus pneumoniae | 14 | 2,129 | 1,787 | 1.19 | 1,141 | 0.64 | 5,509 | 3.08 | 0.0076 |
| Bacillus cereus group | 19 | 5,502 | 4,333 | 1.27 | 2,246 | 0.52 | 18,111 | 4.18 | 0.0248 |
| Listeria spp. | 9 | 2,888 | 2,330 | 1.24 | 1,718 | 0.74 | 4,430 | 1.90 | 0.0571 |
| Staphylococcus spp. | 22 | 2,620 | 2,185 | 1.20 | 994 | 0.45 | 9,473 | 4.34 | 0.3297 |
| Streptococcus spp. | 50 | 2,000 | 1,693 | 1.18 | 487 | 0.29 | 16,583 | 9.79 | 0.3553 |
| “Bacillaceae 1” | 38 | 4,684 | 3,718 | 1.26 | 929 | 0.25 | 32,260 | 8.68 | 0.4261 |
| “Lactobacillaceae” | 31 | 2,152 | 1,736 | 1.24 | 356 | 0.21 | 16,357 | 9.42 | 0.8991 |
| Bacilli | 172 | 2,984 | 2,417 | 1.23 | 143 | 0.06 | 97,860 | 40.49 | 1.1359 |
Abbreviations are as follows: _n_g, number of genomes in taxonomic group; _N_genes, average number of genes per genome; _G_0, average number of gene families per genome; _G_core, number of clusters of gene families in core genome; _G_pan, number of clusters in pangenome; _d_prot, average number of amino acid substitutions per site expected since the most recent common ancestor of the taxa group.
Table 1.
Comparison of properties of subsets of genomes of Bacilli.
| Taxonomic group | _n_g | _N_genes | _G_0 | 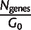 |
_G_core | 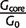 |
_G_pan |  |
_d_prot |
|---|---|---|---|---|---|---|---|---|---|
| Staphylococcus aureus | 15 | 2,668 | 2,212 | 1.21 | 1,532 | 0.69 | 5,522 | 2.50 | 0.0031 |
| Streptococcus pyogenes | 13 | 1,853 | 1,593 | 1.16 | 1,043 | 0.65 | 4,096 | 2.57 | 0.0064 |
| Streptococcus pneumoniae | 14 | 2,129 | 1,787 | 1.19 | 1,141 | 0.64 | 5,509 | 3.08 | 0.0076 |
| Bacillus cereus group | 19 | 5,502 | 4,333 | 1.27 | 2,246 | 0.52 | 18,111 | 4.18 | 0.0248 |
| Listeria spp. | 9 | 2,888 | 2,330 | 1.24 | 1,718 | 0.74 | 4,430 | 1.90 | 0.0571 |
| Staphylococcus spp. | 22 | 2,620 | 2,185 | 1.20 | 994 | 0.45 | 9,473 | 4.34 | 0.3297 |
| Streptococcus spp. | 50 | 2,000 | 1,693 | 1.18 | 487 | 0.29 | 16,583 | 9.79 | 0.3553 |
| “Bacillaceae 1” | 38 | 4,684 | 3,718 | 1.26 | 929 | 0.25 | 32,260 | 8.68 | 0.4261 |
| “Lactobacillaceae” | 31 | 2,152 | 1,736 | 1.24 | 356 | 0.21 | 16,357 | 9.42 | 0.8991 |
| Bacilli | 172 | 2,984 | 2,417 | 1.23 | 143 | 0.06 | 97,860 | 40.49 | 1.1359 |
| Taxonomic group | _n_g | _N_genes | _G_0 | 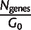 |
_G_core | 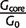 |
_G_pan |  |
_d_prot |
|---|---|---|---|---|---|---|---|---|---|
| Staphylococcus aureus | 15 | 2,668 | 2,212 | 1.21 | 1,532 | 0.69 | 5,522 | 2.50 | 0.0031 |
| Streptococcus pyogenes | 13 | 1,853 | 1,593 | 1.16 | 1,043 | 0.65 | 4,096 | 2.57 | 0.0064 |
| Streptococcus pneumoniae | 14 | 2,129 | 1,787 | 1.19 | 1,141 | 0.64 | 5,509 | 3.08 | 0.0076 |
| Bacillus cereus group | 19 | 5,502 | 4,333 | 1.27 | 2,246 | 0.52 | 18,111 | 4.18 | 0.0248 |
| Listeria spp. | 9 | 2,888 | 2,330 | 1.24 | 1,718 | 0.74 | 4,430 | 1.90 | 0.0571 |
| Staphylococcus spp. | 22 | 2,620 | 2,185 | 1.20 | 994 | 0.45 | 9,473 | 4.34 | 0.3297 |
| Streptococcus spp. | 50 | 2,000 | 1,693 | 1.18 | 487 | 0.29 | 16,583 | 9.79 | 0.3553 |
| “Bacillaceae 1” | 38 | 4,684 | 3,718 | 1.26 | 929 | 0.25 | 32,260 | 8.68 | 0.4261 |
| “Lactobacillaceae” | 31 | 2,152 | 1,736 | 1.24 | 356 | 0.21 | 16,357 | 9.42 | 0.8991 |
| Bacilli | 172 | 2,984 | 2,417 | 1.23 | 143 | 0.06 | 97,860 | 40.49 | 1.1359 |
Abbreviations are as follows: _n_g, number of genomes in taxonomic group; _N_genes, average number of genes per genome; _G_0, average number of gene families per genome; _G_core, number of clusters of gene families in core genome; _G_pan, number of clusters in pangenome; _d_prot, average number of amino acid substitutions per site expected since the most recent common ancestor of the taxa group.
The mean value of RMS(perm) averaged over permutations is defined as RMS(data), measured in units of gene families. After the parameters are chosen to minimize RMS(theory), the ratio RMS(theory)/RMS(data) is a useful measure of the quality of fit of a theoretical model to the data. The smaller the ratio, the better the fit. If the ratio is less than 1, the theory deviates less from the mean than does a typical permutation, i.e., the curve falls within the spread of points generated by the permutations. A well-fitting model should have this ratio less than 1.
As an alternative to fitting the _G_pan(n) and _G_core(n) curves, we also fitted the gene family frequency spectrum. This was done by minimizing the χ2 function:
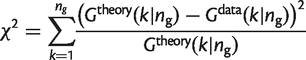
(24)
The χ2 function fits the data across the full range of k, whereas if a simple least squares fit is done, the fit is dominated by the high-frequency classes at either end of the U-shaped distribution, and a poor fit is obtained to the overall shape of the curve.
Software
Many of the formulae described in this study are available as functions written in the R statistical programming language, and are downloadable at http://github.com/rec3141/pangenome. A helper script provides example usage and plotting for each of the functions using an example data set. Users can compute the gene family frequency spectrum from a matrix of gene clusters or using various models on a coalescent or fixed tree. The mean core genome and pangenome curves can be calculated from the gene family frequency spectrum or using the models on a coalescent tree, a star tree, or a fixed tree provided by the user. Permutations of these curves may be computed from gene cluster data. Fitting functions are also defined to allow users to fit each model to their own data.
Results
Properties of the Core Genome and Pangenome
Before considering fits of the models to the data, we present some statistics with which to compare the different subsets of genomes (table 1). Most of the taxonomic groups examined have mean genome sizes of ∼2,000 gene families, excepting many members of the “Bacillaceae 1,” which have experienced significant genome expansions to well over 4,000 gene families each. Nonetheless, the mean number of genes per family is close to 1.2 in every case, indicating that most genes are in single gene families even in large genomes, as previously observed (Collins et al. 2011).
The numbers of gene clusters in the core and pangenomes for each data set were measured relative to the mean number of gene families per genome (table 1). The core ratio, _G_core/_G_0, is substantially less than 1 even for genomes nominally in the same species. For the full set of Bacilli, the core ratio is only 0.06, indicating that relatively few genes are conserved across the whole group at the level of sequence similarity used here. The pangenome ratio, _G_pan/_G_0, is in the range 2–4 for the species-level data sets and increases to more than 40 for the full set of Bacilli.
The mean phylogenetic distance on the protein evolution tree (_d_prot) was measured from the common ancestor of the group to the tips of the branches for each genome (fig. 1 and supplementary fig. S1, Supplementary Material online). The data sets in table 1 are listed in order of increasing distance, demonstrating that _G_pan/_G_0 increases, and _G_core/_G_0 decreases, as _d_prot increases. This is to be expected if the set of genomes becomes more diverse as the time since the common ancestor increases. The mean phylogenetic distance for the full set of Bacilli was greater than 1 amino acid substitution per site, indicating that the size of the core genome for the full data set might be underestimated due to core gene sequences evolving beyond recognition by the similarity criteria used here. The Listeria data set is unusual in having a higher _G_core/_G_0 and a lower _G_pan/_G_0 than expected given the observed amount of protein sequence evolution.
Fitting the Core and Pangenomes
For each data set, the models 1D + E and 2D + E were fitted (representing one or two classes of dispensable genes plus a class of essential genes) and the three types of tree (coalescent, star, and fixed) were compared. Here, we describe how the number of dispensable gene classes used, the shape of the underlying tree, and the taxonomic group chosen each affect the ability of the IMG model to fit real genomic data.
We first tested the effect of including an additional class of dispensable genes in the original IMG model on a coalescent tree. Figure 3 compares model 2D+E with model 1D+E on the coalescent tree for S. pneumoniae and shows that addition of the second class of dispensable genes clearly improves the fit. The 1D+E model fails to fit the pangenome and core genome curves simultaneously. The 2D+E model on the coalescent tree is a good fit for every case tested, with a fitting ratio RMS(theory)/RMS(data) much less than one for every data set (table 2). In contrast, model 1D+E is a much worse fit than 2D+E in every case, and the fitting ratio is often greater than 1. The median gain in quality of fit of model 2D+E over model 1D+E was 38×, even though only a single additional class of genes has been added.
Table 2.
Comparison of quality-of-fit for four models using root mean squared (RMS) values.
| Taxonomic Group | RMS (data) | RMS(theory)/RMS(data) | |||
|---|---|---|---|---|---|
| Coalescent | Star | Fixed | |||
| 1D+E | 2D+E | 2D+E | 2D+E | ||
| Staphylococcus aureus | 87 | 1.418 | 0.088 | 0.244 | 0.023 |
| Streptococcus pyogenes | 74 | 1.021 | 0.027 | 0.322 | 0.066 |
| pneumoniae pneumoniae | 71 | 1.318 | 0.034 | 0.375 | 0.071 |
| Bacillus cereus group | 299 | 1.506 | 0.040 | 0.426 | 0.019 |
| Listeria spp. | 88 | 0.538 | 0.003 | 0.179 | 0.008 |
| Staphylococcus spp. | 225 | 1.428 | 0.035 | 0.344 | 0.310 |
| Streptococcus spp. | 253 | 1.538 | 0.119 | 2.247 | 0.123 |
| “Bacillaceae 1” | 492 | 1.834 | 0.020 | 1.785 | 0.030 |
| ”Lactobacillaceae” | 254 | 1.076 | 0.078 | 1.928 | 0.078 |
| Bacilli | 1,425 | 0.863 | 0.065 | 2.497 | 0.040 |
| Taxonomic Group | RMS (data) | RMS(theory)/RMS(data) | |||
|---|---|---|---|---|---|
| Coalescent | Star | Fixed | |||
| 1D+E | 2D+E | 2D+E | 2D+E | ||
| Staphylococcus aureus | 87 | 1.418 | 0.088 | 0.244 | 0.023 |
| Streptococcus pyogenes | 74 | 1.021 | 0.027 | 0.322 | 0.066 |
| pneumoniae pneumoniae | 71 | 1.318 | 0.034 | 0.375 | 0.071 |
| Bacillus cereus group | 299 | 1.506 | 0.040 | 0.426 | 0.019 |
| Listeria spp. | 88 | 0.538 | 0.003 | 0.179 | 0.008 |
| Staphylococcus spp. | 225 | 1.428 | 0.035 | 0.344 | 0.310 |
| Streptococcus spp. | 253 | 1.538 | 0.119 | 2.247 | 0.123 |
| “Bacillaceae 1” | 492 | 1.834 | 0.020 | 1.785 | 0.030 |
| ”Lactobacillaceae” | 254 | 1.076 | 0.078 | 1.928 | 0.078 |
| Bacilli | 1,425 | 0.863 | 0.065 | 2.497 | 0.040 |
RMS(data) is the RMS of 500 replicate permutations of the pangenome and core genome data points compared with calculated means. RMS(theory) is the RMS of the best fit line for evolutionary models based on two different tree shapes (star tree and coalescent tree), one essential gene class, and either one (1D+E) or two dispensable gene classes (2D+E). Bold values indicate best fitting model in each taxonomic group.
Table 2.
Comparison of quality-of-fit for four models using root mean squared (RMS) values.
| Taxonomic Group | RMS (data) | RMS(theory)/RMS(data) | |||
|---|---|---|---|---|---|
| Coalescent | Star | Fixed | |||
| 1D+E | 2D+E | 2D+E | 2D+E | ||
| Staphylococcus aureus | 87 | 1.418 | 0.088 | 0.244 | 0.023 |
| Streptococcus pyogenes | 74 | 1.021 | 0.027 | 0.322 | 0.066 |
| pneumoniae pneumoniae | 71 | 1.318 | 0.034 | 0.375 | 0.071 |
| Bacillus cereus group | 299 | 1.506 | 0.040 | 0.426 | 0.019 |
| Listeria spp. | 88 | 0.538 | 0.003 | 0.179 | 0.008 |
| Staphylococcus spp. | 225 | 1.428 | 0.035 | 0.344 | 0.310 |
| Streptococcus spp. | 253 | 1.538 | 0.119 | 2.247 | 0.123 |
| “Bacillaceae 1” | 492 | 1.834 | 0.020 | 1.785 | 0.030 |
| ”Lactobacillaceae” | 254 | 1.076 | 0.078 | 1.928 | 0.078 |
| Bacilli | 1,425 | 0.863 | 0.065 | 2.497 | 0.040 |
| Taxonomic Group | RMS (data) | RMS(theory)/RMS(data) | |||
|---|---|---|---|---|---|
| Coalescent | Star | Fixed | |||
| 1D+E | 2D+E | 2D+E | 2D+E | ||
| Staphylococcus aureus | 87 | 1.418 | 0.088 | 0.244 | 0.023 |
| Streptococcus pyogenes | 74 | 1.021 | 0.027 | 0.322 | 0.066 |
| pneumoniae pneumoniae | 71 | 1.318 | 0.034 | 0.375 | 0.071 |
| Bacillus cereus group | 299 | 1.506 | 0.040 | 0.426 | 0.019 |
| Listeria spp. | 88 | 0.538 | 0.003 | 0.179 | 0.008 |
| Staphylococcus spp. | 225 | 1.428 | 0.035 | 0.344 | 0.310 |
| Streptococcus spp. | 253 | 1.538 | 0.119 | 2.247 | 0.123 |
| “Bacillaceae 1” | 492 | 1.834 | 0.020 | 1.785 | 0.030 |
| ”Lactobacillaceae” | 254 | 1.076 | 0.078 | 1.928 | 0.078 |
| Bacilli | 1,425 | 0.863 | 0.065 | 2.497 | 0.040 |
RMS(data) is the RMS of 500 replicate permutations of the pangenome and core genome data points compared with calculated means. RMS(theory) is the RMS of the best fit line for evolutionary models based on two different tree shapes (star tree and coalescent tree), one essential gene class, and either one (1D+E) or two dispensable gene classes (2D+E). Bold values indicate best fitting model in each taxonomic group.
Another factor to consider is the shape of the underlying evolutionary tree. Figure 4 compares the three kinds of tree for the 2D+E model in the case of the “Bacillaceae 1” data set. The model fits the data well using either the coalescent tree or the fixed tree, but the fit using the star tree is clearly much worse, with fitting ratios greater than 1 in a number of cases (table 2). The median gain in quality of fit of the coalescent tree over the star tree was 15×. The result for the fixed tree is sometimes slightly better than that for the coalescent and sometimes slightly worse, but in general, there is not much difference. This illustrates that the core and pangenome curves are not very sensitive to the difference between a fixed phylogenetic tree and a coalescent tree, whereas a star tree is noticeably different from either of these (as is also seen in fig. 4).

Fig. 4.
Fitting model 2D+E to the core and pangenome curves for 38 sequenced “Bacillaceae 1” genomes. Models were based on three different tree shapes: the coalescent tree (solid line), the star tree (dashed line), or the fixed tree (solid line; overlaps coalescent). The shaded region demarcates the maximum range observed during 500 permutations of the data.
Fitting the Gene Frequency Spectrum
When fitting the gene frequency spectrum, we see similar trends as when fitting the core and pangenome curves. The χ2 fit for the 2D+E model on the coalescent is always much better than for the 1D+E, as shown in table 3. Figure 5 shows this graphically for the case of Strep. pneumoniae, where the 2D+E model gives the shape of the U-shaped curve much better than the 1D+E model.

Fig. 5.
The gene family frequency spectrum, G(k), for 14 sequenced Streptoccocus pneumoniae genomes. Observed data are shown as gray bars. The frequency spectrum was calculated with the optimized parameters from fitting model 1D+E (dashed line) or 2D+E (solid line) to the G(k) using a coalescent tree.
Table 3.
Comparison of quality-of-fit for three models using χ2 values of the best fit line for evolutionary models based on two different tree shapes (fixed tree and coalescent tree), one essential gene class, and either one (1D+E) or two dispensable gene classes (2D+E).
| Taxonomic Group | Coalescent | Fixed | |
|---|---|---|---|
| 1D+E | 2D+E | 2D+E | |
| Staphylococcus aureus | 3,897 | 119 | 252 |
| Streptococcus pyogenes | 1,941 | 91 | 587 |
| Streptococcus pneumoniae | 2,972 | 47 | 233 |
| Bacillus cereus group | 17,525 | 230 | 1,167 |
| Listeria spp. | 921 | 21 | 268 |
| Staphylococcus spp. | 10,668 | 173 | 2,375 |
| Streptococcus spp. | 31,107 | 1,080 | 1,388 |
| “Bacillaceae 1” | 39,590 | 1,731 | 1,573 |
| “Lactobacillaceae” | 17,944 | 1,220 | 746 |
| Bacilli | 951,192 | 11,532 | 14,847 |
| Taxonomic Group | Coalescent | Fixed | |
|---|---|---|---|
| 1D+E | 2D+E | 2D+E | |
| Staphylococcus aureus | 3,897 | 119 | 252 |
| Streptococcus pyogenes | 1,941 | 91 | 587 |
| Streptococcus pneumoniae | 2,972 | 47 | 233 |
| Bacillus cereus group | 17,525 | 230 | 1,167 |
| Listeria spp. | 921 | 21 | 268 |
| Staphylococcus spp. | 10,668 | 173 | 2,375 |
| Streptococcus spp. | 31,107 | 1,080 | 1,388 |
| “Bacillaceae 1” | 39,590 | 1,731 | 1,573 |
| “Lactobacillaceae” | 17,944 | 1,220 | 746 |
| Bacilli | 951,192 | 11,532 | 14,847 |
Bold values indicate best fitting model in each taxonomic group.
Table 3.
Comparison of quality-of-fit for three models using χ2 values of the best fit line for evolutionary models based on two different tree shapes (fixed tree and coalescent tree), one essential gene class, and either one (1D+E) or two dispensable gene classes (2D+E).
| Taxonomic Group | Coalescent | Fixed | |
|---|---|---|---|
| 1D+E | 2D+E | 2D+E | |
| Staphylococcus aureus | 3,897 | 119 | 252 |
| Streptococcus pyogenes | 1,941 | 91 | 587 |
| Streptococcus pneumoniae | 2,972 | 47 | 233 |
| Bacillus cereus group | 17,525 | 230 | 1,167 |
| Listeria spp. | 921 | 21 | 268 |
| Staphylococcus spp. | 10,668 | 173 | 2,375 |
| Streptococcus spp. | 31,107 | 1,080 | 1,388 |
| “Bacillaceae 1” | 39,590 | 1,731 | 1,573 |
| “Lactobacillaceae” | 17,944 | 1,220 | 746 |
| Bacilli | 951,192 | 11,532 | 14,847 |
| Taxonomic Group | Coalescent | Fixed | |
|---|---|---|---|
| 1D+E | 2D+E | 2D+E | |
| Staphylococcus aureus | 3,897 | 119 | 252 |
| Streptococcus pyogenes | 1,941 | 91 | 587 |
| Streptococcus pneumoniae | 2,972 | 47 | 233 |
| Bacillus cereus group | 17,525 | 230 | 1,167 |
| Listeria spp. | 921 | 21 | 268 |
| Staphylococcus spp. | 10,668 | 173 | 2,375 |
| Streptococcus spp. | 31,107 | 1,080 | 1,388 |
| “Bacillaceae 1” | 39,590 | 1,731 | 1,573 |
| “Lactobacillaceae” | 17,944 | 1,220 | 746 |
| Bacilli | 951,192 | 11,532 | 14,847 |
Bold values indicate best fitting model in each taxonomic group.
For the closely related sets of genomes, the frequency spectrum is a smooth curve, as in the example of figure 5, and the 2D+E coalescent model explains this shape quite well. For more diverse data sets, however, the data show an irregular structure that is a result of the shape of the underlying phylogenetic tree. As an example, when the frequency spectrum is calculated for “Bacillaceae 1,” a prominent peak is observed at k = 20 (fig. 6). The phylogenetic tree (fig. 1) shows that there are 20 closely related genomes in the B. cereus group that have very short branch lengths in comparison with the rest of the genomes in the “Bacillaceae 1.” There will thus be many genes present in this group of 20 that are not present in the others. The resulting peak at k = 20 is thus seen in the calculated curve for the fixed tree and not for the smooth curve that results from the coalescent model. The result from the fixed tree predicts the other peaks and troughs in the data fairly well, and by the χ2 criterion, the fit is slightly better for the fixed tree than for the coalescent (table 3).

Fig. 6.
The gene family frequency spectrum, G(k), for 38 sequenced “Bacillaceae 1” genomes. Observed data are shown as gray bars. The frequency spectrum was calculated with the optimized parameters from fitting model 2D+E to the G(k) using either a coalescent tree (smooth solid line) or the fixed phylogenetic tree (jagged solid line). Additionally, the frequency spectrum was calculated with the optimized parameters from fitting model 2D+E to the core and pangenome curves using the fixed phylogenetic tree (jagged dotted line).
In fact, the fit for the fixed tree is better than the coalescent only for two of the most diverse groups, whereas for some of the less diverse groups, the fixed tree gives a noticeably worse fit by the χ2 criterion. One possible reason for this is that the branch lengths on the fixed tree (which were calculated from the protein sequence phylogeny of the conserved genes) are not optimal for fitting the data for presence and absence of dispensable genes. It would clearly be possible to improve this fit by treating the branch lengths as variable parameters to be estimated. It may be that a generic coalescent tree gives a better fit to the data than a slightly incorrect fixed tree. It should also be borne in mind that the IMG model does not allow more than one gene origin per gene family. If multiple origins did occur, the effect would be to smooth out some of the peaks in the frequency spectrum.
Another point that is illustrated by figure 6 is that the 2D+E model is able to fit the core and pangenome curves at the same time as the frequency spectrum. Two different theory curves are shown for the fixed tree 2D+E model. One of these comes from directly fitting the frequency spectrum, and the other comes from fitting the core and pangenome curves (as previously shown in fig. 4) and using these parameters to calculate the frequency spectrum. The two theory curves are very similar, and this gives us confidence that the model is explaining several aspects of the data simultaneously. It is also clear from figure 6 that the frequency spectrum is sensitive to the shape of the fixed tree, whereas the predicted core and pangenome curves for the coalescent and fixed tree are almost indistinguishable from one another (fig. 4).
Using the Three Gene Classes to Extrapolate to Larger Numbers of Genomes
The average number of genes per genome in the three classes are _G_ess, _G_slow = θ1/ρ1, and _G_fast = θ2/ρ2. These values are shown in a phylogenetic context in figure 7. The fraction of genes in the fast category, _f_fast = _G_fast/_G_0, is only 10–20% in most data sets (table 4). However, θ2 is very much greater than θ1, which means that most of the new genes that arise are in the fast evolving category. There is thus a very high rate of appearance of new fast-evolving genes in genomes, but most of these disappear very rapidly, because ρ2 is also very large. As ρ2 ≫ 1, the fast evolving genes are lost on a time scale that is rapid compared with that of speciation and coalescence. Therefore, most of the fast evolving genes are only present in a very small number of genomes.

Fig. 7.
The fraction of gene families in each class as predicted by model 2D+E on the coalescent tree, fit to the G(k). The symbol • shows the observed size of the core genome (_G_core); black bars indicate the predicted number of gene families in the essential class (_G_ess), gray bars indicate the slow class of dispensable families (_f_slow); and white bars the fast class (_f_fast).
Table 4.
Fitted parameters for model 2D+E on a coalescent tree fit to the gene family frequency spectrum.
| Taxonomic group | _G_ess | θ1 | ρ1 | θ2 | ρ2 | _f_ess | _f_slow | _f_fast | _G_new(k) | _G_pan(k) | _G_core(k) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1,000 | 100 | 1,000 | 100 | 1,000 | |||||||||
| Sta. aureus | 0 | 188 | 0.093 | 92,978 | 471 | 0 | 0.911 | 0.089 | 165 | 63 | 20,887 | 109,374 | 1,251 | 1,008 |
| Str. pyogenes | 713 | 208 | 0.293 | 21,450 | 126 | 0.448 | 0.446 | 0.107 | 97 | 19 | 14,959 | 49,894 | 879 | 798 |
| Str. pneumoniae | 951 | 250 | 0.425 | 28,346 | 114 | 0.532 | 0.329 | 0.139 | 136 | 26 | 20,604 | 67,994 | 1,024 | 978 |
| B. cereus group | 999 | 658 | 0.248 | 116,573 | 171 | 0.230 | 0.612 | 0.157 | 439 | 100 | 60,658 | 232,977 | 1,766 | 1,432 |
| Listeria spp. | 0 | 157 | 0.075 | 6,540 | 27 | 0 | 0.895 | 0.105 | 54 | 7 | 13,164 | 27,234 | 1,418 | 1,192 |
| Sta. spp. | 0 | 347 | 0.185 | 79,800 | 262 | 0 | 0.860 | 0.140 | 225 | 64 | 29,447 | 130,018 | 741 | 484 |
| Str. spp. | 298 | 825 | 0.748 | 29,579 | 101 | 0.176 | 0.651 | 0.173 | 156 | 28 | 25,398 | 77,636 | 331 | 304 |
| “Bacillaceae 1” | 704 | 2,337 | 0.973 | 145,738 | 238 | 0.189 | 0.646 | 0.164 | 455 | 120 | 64,095 | 258,733 | 731 | 707 |
| “Lactobacillaceae” | 249 | 656 | 0.782 | 17,048 | 26 | 0.143 | 0.483 | 0.374 | 143 | 17 | 30,954 | 68,242 | 270 | 252 |
| Bacilli | 43 | 2,250 | 1.254 | 204,501 | 353 | 0.018 | 0.742 | 0.240 | 475 | 154 | 62,016 | 291,143 | 50 | 44 |
| Taxonomic group | _G_ess | θ1 | ρ1 | θ2 | ρ2 | _f_ess | _f_slow | _f_fast | _G_new(k) | _G_pan(k) | _G_core(k) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1,000 | 100 | 1,000 | 100 | 1,000 | |||||||||
| Sta. aureus | 0 | 188 | 0.093 | 92,978 | 471 | 0 | 0.911 | 0.089 | 165 | 63 | 20,887 | 109,374 | 1,251 | 1,008 |
| Str. pyogenes | 713 | 208 | 0.293 | 21,450 | 126 | 0.448 | 0.446 | 0.107 | 97 | 19 | 14,959 | 49,894 | 879 | 798 |
| Str. pneumoniae | 951 | 250 | 0.425 | 28,346 | 114 | 0.532 | 0.329 | 0.139 | 136 | 26 | 20,604 | 67,994 | 1,024 | 978 |
| B. cereus group | 999 | 658 | 0.248 | 116,573 | 171 | 0.230 | 0.612 | 0.157 | 439 | 100 | 60,658 | 232,977 | 1,766 | 1,432 |
| Listeria spp. | 0 | 157 | 0.075 | 6,540 | 27 | 0 | 0.895 | 0.105 | 54 | 7 | 13,164 | 27,234 | 1,418 | 1,192 |
| Sta. spp. | 0 | 347 | 0.185 | 79,800 | 262 | 0 | 0.860 | 0.140 | 225 | 64 | 29,447 | 130,018 | 741 | 484 |
| Str. spp. | 298 | 825 | 0.748 | 29,579 | 101 | 0.176 | 0.651 | 0.173 | 156 | 28 | 25,398 | 77,636 | 331 | 304 |
| “Bacillaceae 1” | 704 | 2,337 | 0.973 | 145,738 | 238 | 0.189 | 0.646 | 0.164 | 455 | 120 | 64,095 | 258,733 | 731 | 707 |
| “Lactobacillaceae” | 249 | 656 | 0.782 | 17,048 | 26 | 0.143 | 0.483 | 0.374 | 143 | 17 | 30,954 | 68,242 | 270 | 252 |
| Bacilli | 43 | 2,250 | 1.254 | 204,501 | 353 | 0.018 | 0.742 | 0.240 | 475 | 154 | 62,016 | 291,143 | 50 | 44 |
The columns _f_slow and _f_fast are the fractions of gene families in each rate class. Extrapolations to large numbers of genomes were performed to predict the number of new gene families (_G_new), pangenome clusters (_G_pan), and core clusters (_G_core) detected when k genomes are sequenced.
Table 4.
Fitted parameters for model 2D+E on a coalescent tree fit to the gene family frequency spectrum.
| Taxonomic group | _G_ess | θ1 | ρ1 | θ2 | ρ2 | _f_ess | _f_slow | _f_fast | _G_new(k) | _G_pan(k) | _G_core(k) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1,000 | 100 | 1,000 | 100 | 1,000 | |||||||||
| Sta. aureus | 0 | 188 | 0.093 | 92,978 | 471 | 0 | 0.911 | 0.089 | 165 | 63 | 20,887 | 109,374 | 1,251 | 1,008 |
| Str. pyogenes | 713 | 208 | 0.293 | 21,450 | 126 | 0.448 | 0.446 | 0.107 | 97 | 19 | 14,959 | 49,894 | 879 | 798 |
| Str. pneumoniae | 951 | 250 | 0.425 | 28,346 | 114 | 0.532 | 0.329 | 0.139 | 136 | 26 | 20,604 | 67,994 | 1,024 | 978 |
| B. cereus group | 999 | 658 | 0.248 | 116,573 | 171 | 0.230 | 0.612 | 0.157 | 439 | 100 | 60,658 | 232,977 | 1,766 | 1,432 |
| Listeria spp. | 0 | 157 | 0.075 | 6,540 | 27 | 0 | 0.895 | 0.105 | 54 | 7 | 13,164 | 27,234 | 1,418 | 1,192 |
| Sta. spp. | 0 | 347 | 0.185 | 79,800 | 262 | 0 | 0.860 | 0.140 | 225 | 64 | 29,447 | 130,018 | 741 | 484 |
| Str. spp. | 298 | 825 | 0.748 | 29,579 | 101 | 0.176 | 0.651 | 0.173 | 156 | 28 | 25,398 | 77,636 | 331 | 304 |
| “Bacillaceae 1” | 704 | 2,337 | 0.973 | 145,738 | 238 | 0.189 | 0.646 | 0.164 | 455 | 120 | 64,095 | 258,733 | 731 | 707 |
| “Lactobacillaceae” | 249 | 656 | 0.782 | 17,048 | 26 | 0.143 | 0.483 | 0.374 | 143 | 17 | 30,954 | 68,242 | 270 | 252 |
| Bacilli | 43 | 2,250 | 1.254 | 204,501 | 353 | 0.018 | 0.742 | 0.240 | 475 | 154 | 62,016 | 291,143 | 50 | 44 |
| Taxonomic group | _G_ess | θ1 | ρ1 | θ2 | ρ2 | _f_ess | _f_slow | _f_fast | _G_new(k) | _G_pan(k) | _G_core(k) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1,000 | 100 | 1,000 | 100 | 1,000 | |||||||||
| Sta. aureus | 0 | 188 | 0.093 | 92,978 | 471 | 0 | 0.911 | 0.089 | 165 | 63 | 20,887 | 109,374 | 1,251 | 1,008 |
| Str. pyogenes | 713 | 208 | 0.293 | 21,450 | 126 | 0.448 | 0.446 | 0.107 | 97 | 19 | 14,959 | 49,894 | 879 | 798 |
| Str. pneumoniae | 951 | 250 | 0.425 | 28,346 | 114 | 0.532 | 0.329 | 0.139 | 136 | 26 | 20,604 | 67,994 | 1,024 | 978 |
| B. cereus group | 999 | 658 | 0.248 | 116,573 | 171 | 0.230 | 0.612 | 0.157 | 439 | 100 | 60,658 | 232,977 | 1,766 | 1,432 |
| Listeria spp. | 0 | 157 | 0.075 | 6,540 | 27 | 0 | 0.895 | 0.105 | 54 | 7 | 13,164 | 27,234 | 1,418 | 1,192 |
| Sta. spp. | 0 | 347 | 0.185 | 79,800 | 262 | 0 | 0.860 | 0.140 | 225 | 64 | 29,447 | 130,018 | 741 | 484 |
| Str. spp. | 298 | 825 | 0.748 | 29,579 | 101 | 0.176 | 0.651 | 0.173 | 156 | 28 | 25,398 | 77,636 | 331 | 304 |
| “Bacillaceae 1” | 704 | 2,337 | 0.973 | 145,738 | 238 | 0.189 | 0.646 | 0.164 | 455 | 120 | 64,095 | 258,733 | 731 | 707 |
| “Lactobacillaceae” | 249 | 656 | 0.782 | 17,048 | 26 | 0.143 | 0.483 | 0.374 | 143 | 17 | 30,954 | 68,242 | 270 | 252 |
| Bacilli | 43 | 2,250 | 1.254 | 204,501 | 353 | 0.018 | 0.742 | 0.240 | 475 | 154 | 62,016 | 291,143 | 50 | 44 |
The columns _f_slow and _f_fast are the fractions of gene families in each rate class. Extrapolations to large numbers of genomes were performed to predict the number of new gene families (_G_new), pangenome clusters (_G_pan), and core clusters (_G_core) detected when k genomes are sequenced.
As ρ1 is of order 1 or less than 1 in most data sets, the slowly evolving genes are retained in genomes for a time that is longer than the speciation time scale. Thus, these genes have a reasonable probability of being present in multiple genomes. The slow category fits the frequency spectrum across the moderate and high range of k. The fast evolving category fits the peak in the gene frequency spectrum close to k = 1. The essential class fits only the peak at k = _n_g. In some cases, the best fit parameters of the 2D+E model actually have _G_ess = 0. In these cases, the slow category fits the shape of the high-k end of the spectrum without needing an extra parameter for k = _n_g. This indicates that in some cases, e.g., within the Staphylococcus clade, model 2D+E overfits the data and a simpler 2D model would suffice. These exceptions tend to occur in groups that have relatively large fractions of nearly core gene families, i.e., gene families that are not essential but are lost very slowly relative to the speciation time of the clade (fig. 7).
One question that is relevant to bacterial genome sequencing projects is to estimate how diverse is the pangenome for a given species or taxonomic group and to determine how many genome sequences would be required to adequately describe the diversity of genes within the group. The 2D+E model on the coalescent is useful for this purpose, because it gives a prediction that can be extrapolated to larger numbers of genomes, whereas the fixed tree model cannot be extrapolated.
The fitted parameters for the 2D+E model (table 4) were used to predict the sizes of the pangenome and core genome when extrapolated to _n_g = 100. This is substantially bigger than the current value of _n_g for all the individual data sets, although the combined data set already has 172 genomes, as shown in table 1. The predicted size of the core genome continues to slowly decrease well beyond the number of genomes currently available, eventually converging on _G_ess. Substantial numbers of new families are expected to be found even if very many genomes are sequenced (table 4). For example, the predicted _G_new is in the range of dozens to hundreds even after sequencing 100 genomes and still always > 1 after 1,000 genomes. It should be remembered that the pangenome is open according to these models, so there will always be new families however many genomes are sequenced.
Conclusions
The Meaning of Dispensable and Essential Genes
The original version of the IMG introduced by Baumdicker et al. (2010) used a single class of dispensable gene families plus a class of essential families and corresponds to our model 1D+E on the coalescent tree. These authors gave an example where the gene family frequency spectrum from nine Prochlorococcus genomes was well fitted with this model. In our data sets, however, we always found that model 2D+E, with two dispensable classes and an essential class, gave a much better fit than the 1D+E model. This corresponds to the Koonin and Wolf (2008) conceptual genome model that includes a “core” of essential gene families, a “shell” of conserved families that are gained and lost rather slowly, and a “cloud” of dispensable families that are rapidly gained and lost.
In our interpretation, genes in the fast evolving class would probably not be beneficial to the genome and may even be deleterious. Hence, rapid deletion is to be expected. Genes in the slowly evolving category would be beneficial to at least some of the genomes, possibly depending on the lifestyle of the organism. Hence, these genes would stand a reasonable chance of being retained for longer times. Genes that are essential will be retained indefinitely. However, it should be remembered that genes that appear essential in narrow taxonomic groups may not be retained in broader groups, so the meaning of essential depends on the data set considered.
For all the data sets we considered, we found that most of the new genes that arise are in the fast evolving class (θ2 ≫ θ1). However, a relatively small proportion of the genes in a genome at one time belong to the fast evolving class (_f_fast < _f_slow + _f_ess). The presence of fast evolving families means that there can be rapid divergence between genomes that are closely related (such as the species level data sets considered here). However, the fact that the majority of families are in the slow and essential classes explains why significant numbers of conserved families are still found in the more diverse data sets. It was previously observed that gain and loss of families in the B. cereus group appeared to be much faster than in the wider set of Bacilli (Hao and Golding 2006). This is because the fast changes are dominant when considering the short branch lengths in closely related groups, whereas changes at slower time scales are relevant for the longer branches, and it is not possible to see this with a model that has only a single rate class.
Open and Closed Pangenomes and the Effect of HGT
The IMG model touches on fundamental questions about the mechanisms of bacterial genome evolution, including the processes by which new genes arise in genomes and the possibility of exchange of genes between genomes by HGT. The assumption of the IMG model is that a given gene can be introduced into a population of genomes only once. There are several reasons to think that this might often be true. The origin of a new open reading frame from a noncoding region is presumed to be rare, but if it occurs, it will lead to a new sequence that is unlikely to have similarity to previous genes; hence, it will fit the IMG assumption. A new gene might also be created by modification of an existing gene by a rapid burst of substitutions, by a substantial insertion or deletion, or by shuffling of domains within the gene. If the gene becomes sufficiently divergent from the other related sequences, it will no longer be classed as belonging to the same gene family by the similarity criteria we used for clustering. Thus, a new gene will have arisen de novo within a single lineage.
As an alternative to de novo gene origin, new genes can also arise by HGT of a gene from outside the genomes of interest. If the diversity of genes in the environment is sufficiently large, it will be unlikely that the same type of gene is inserted more than once into the group being studied, and this will again fit the assumptions of the IMG model. On the other hand, if the pool of genes available for HGT contains a smaller number of genes of high frequency, it is possible that a gene of the same type could get inserted more than once into the set of genomes under study. This should show up in systematic deviations from the predictions of the IMG model. One recent study concluded that the majority of gene gains in multigene families arise from within-group HGT rather than by gene duplication (Treangen and Rocha 2011). Gain of additional members of gene families is not visible in our analysis because we worked at the level of presence/absence of whole gene families. However, if genes in large families have an unusually high rate of HGT, but the majority of genes have a very low rate, the model of Treangen and Rocha (2011) would still be consistent with the IMG assumption.
In the supplementary materials, Supplementary Material online, we consider a finitely many genes (FMG) model, in which each new gene that arises in a genome is one of a finite number M of possible gene families. The rate of origination of each type of gene is a, and the overall rate of origination of genes is u = Ma. We derive the core and pangenome sizes and the gene frequency spectrum for the FMG model and show that the IMG is a limiting case of the FMG when M tends to infinity with u kept constant. In the FMG, it is possible for the same kind of gene to originate more than once, as would be the case if the gene originates by horizontal transfer and the number of types of genes in the pool available for HGT is limited.
The pangenome is closed in the FMG model because there cannot be more than M genes. However, it seems to us that the pangenome must almost certainly be open in real cases. As long as there is some nonzero rate of origination of gene families within individual lineages or there is a high diversity of families available for HGT, then there will always be some constant rate of origination of gene families that have not been seen before. This means that there are at least some types of families that fit the IMG assumption, and so the pangenome must be open. It is also possible that there are other families that have a high rate of repeated HGT and which would fit an FMG model better. These could be present at the same time as gene families of the IMG type. In the future, we intend to look for genes whose presence/absence pattern is very unlikely according to an IMG model and that would be better explained by multiple insertions. Our expectation is that such multiple insertions are rare and that the majority of gene originations are either occurring within the lineage or by unique HGT events. Hence, we expect the IMG model to be a useful starting point for genome analysis.
Our main reason for introducing the star phylogeny calculations was the fact that the pangenome increases linearly with n on the star phylogeny, which corresponds to claims made for real data in some of the original work with pangenomes (Tettelin et al. 2005). However, our results show rather poor agreement with predictions based on a star phylogeny. On a star phylogeny, the length of each new branch is constant, no matter how many genomes are added, and the number of new genes arising on that branch is constant. Hence, the prediction of a linearly increasing pangenome. In contrast, on a coalescent tree, the length of the branch leading to the last genome added gets shorter and shorter, and this leads to a pangenome that increases approximately logarithmically with n, which seems to be a good fit to the data here. For a fixed phylogenetic tree, the pangenome size will depend on the shape of the tree and on which genomes are included in the phylogeny. However, the major branches of a phylogeny and the position of the root will become established with only a few genomes, and after this point, the branches leading to newly added genomes will become shorter and shorter, as with the coalescent tree. Thus, genome evolution seems to occur on a tree that resembles a coalescent more than a star.
Another connection with the star tree is the finite supragenome model (FSM), developed in a recent series of papers (Hogg et al. 2007; Donati et al. 2010; Boissy et al. 2011), which is used to calculate the core and pangenome sizes. This model supposes that a finite number of gene families are present in each genome with probability μ (and absent with probability 1 − μ). The families are divided among K classes with different values of μ for each class. The FSM can be interpreted as a star tree model with multiple classes of genes. However, the FSM starts from the assumption that the pangenome is closed, whereas our interpretation is that the pangenome is open, as explained earlier.
Rates of Genome Evolution Vary among Taxonomic Clades
The microorganisms included in our analysis live enormously varied lifestyles and inhabit diverse niches, so the ease with which genes may be gained and lost might be expected to differ among organisms. It was shown in table 1 that Listeria stands out as having a rather slow rate of gene gain and loss in comparison with its rate of protein sequence evolution. This also shows up in table 4, where Listeria has the smallest pangenome size and the smallest expected number of new genes when extrapolated to _n_g = 100.
den Bakker et al. (2010) also found that the pangenome of Listeria had experienced limited introductions of genetic material from external gene pools, but neither the evolutionary nor mechanistic reasons for this are apparent. Possible mechanistic explanations for the small Listeria pangenome revolve around limitations in the acquisition or invention of novel genes: Listeria spp. are host to prophages (Nelson et al. 2004), transducing phages (Hodgson 2000) and conjugative elements (Charpentier et al. 1999), but they have not been reported to become naturally competent for transformation; a few stable transposable elements are present in each genome (Nelson et al. 2004), but only one family of IS has been reported (ISFinder database, Siguier et al. 2006). So although limited gene acquisition and innovation may result from a sparsity of mobile genetic elements in Listeria spp., the underlying evolutionary principle remains unknown.
Limitations of this Analysis
In this article, we began by considering the sizes of the core and pangenomes because these are quantities that are often measured in genome sequencing projects. The 2D+E IMG model on the coalescent works well for these quantities. This amounts to saying that we cannot reject the IMG as a null model, based only on the core and pangenome curves. The gene frequency spectrum is more sensitive to details of the model. We found that the difference between the fixed tree and the coalescent tree shows up in the gene frequency spectrum (e.g., in fig. 6) but not in the core and pangenome curves. However, the fit using the fixed tree is not always better than using the coalescent. This suggests that it will be useful to consider optimization of the tree topology and branch lengths in future, and it also highlights that there is a lot of information in the gene presence/absence patterns that is not present in the gene frequency spectrum. In a maximum likelihood phylogenetic analysis, the likelihood of a pattern depends on which species possess the gene and where these species are on the tree. It would, therefore, be useful to consider the IMG model in a full phylogenetic context in the future.
In a recent article, Baumdicker et al. (2012) present a statistical test of neutrality for the IMG based on simulations of the gene family frequency spectrum on random coalescent trees. Although the test seems conservative, they indicate that the statistical power of their test would be improved with the additional information not available in the frequency spectrum.
In conclusion, we have found that variants of the IMG model make good predictions of the sizes of the core and pangenomes and the shape of the gene family frequency spectrum in many groups of bacterial genomes. The model has a sound basis in population genetics and is derived from an explicit evolutionary model. Therefore, it is more useful for interpretation of experimental data than alternative approaches that are simply empirical fitting functions or statistical models for distributions that are not associated with an evolutionary mechanism.
Acknowledgments
This work was supported by the Origins Institute at McMaster University and Compute Canada, which provided essential CPU resources through the SHARCNET high performance computing center.
References
, , . ,
The diversity of a distributed genome in bacterial populations
,
Ann Appl Prob.
,
2010
, vol.
20
(pg.
1567
-
1606
)
, , . ,
The infinitely many genes model for the distributed genome of bacteria
,
Genome Biol Evol.
,
2012
, vol.
4
(pg.
443
-
456
)
, , , et al. ,
(16 co-authors)
. ,
Comparative supragenomic analyses among the pathogens Staphylococcus aureus, Streptococcus pneumoniae, and Haemophilus influenzae using a modification of the finite supragenome model
,
BMC Genomics
,
2011
, vol.
12
pg.
187
, , . ,
Conjugative mobilization of the rolling-circle plasmid pIP823 from Listeria monocytogenes BM4293 among gram-positive and gram-negative bacteria
,
J Bacteriol.
,
1999
, vol.
181
(pg.
3368
-
74
)
, , . ,
Origin and evolution of gene families in Bacteria and Archaea
,
BMC Bioinformatics
,
2011
, vol.
12
pg.
S14
, , , , , , , , , . ,
Comparative genomics of the bacterial genus Listeria: genome evolution is characterized by limited gene acquisition and limited gene loss
,
BMC Genomics
,
2010
, vol.
11
pg.
688
, , , et al. ,
(18 co-authors)
. ,
Structure and dynamics of the pan-genome of Streptococcus pneumoniae and closely related species
,
Genome Biol.
,
2010
, vol.
11
pg.
R107
. ,
MUSCLE: multiple sequence alignment with high accuracy and high throughput
,
Nucl Acids Res.
,
2004
, vol.
32
(pg.
1792
-
1797
)
, , , , , . ,
New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0
,
Sys Biol.
,
2010
, vol.
59
(pg.
307
-
21
)
, . ,
The fate of laterally transferred genes: Life in the fast lane to adaptation or death
,
Genome Res.
,
2006
, vol.
16
(pg.
636
-
643
)
, , . ,
Gene genealogies, variation and evolution: a primer in coalescent theory
,
2005
Oxford
Oxford University Press
. ,
Generalized transduction of serotype 1/2 and serotype 4b strains of Listeria monocytogenes
,
Mol Microbiol.
,
2000
, vol.
35
(pg.
312
-
323
)
, , , , , , , . ,
Characterization of the Haemophilus influenzae core and supragenomes based on the complete genomic sequences of Rd and 12 clinical nontypeable strains
,
Genome Biol.
,
2007
, vol.
8
pg.
R103
, , , et al. ,
(14 co-authors)
. ,
Patterns and implications of gene gain and loss in the evolution of Prochlorococcus
,
PLoS Genet.
,
2007
, vol.
3
pg.
e231
, . ,
Genomics of bacteria and archaea: the emerging dynamic view of the prokaryotic world
,
Nucleic Acids Res.
,
2008
, vol.
36
(pg.
6688
-
6719
)
, . ,
Estimating the size of the bacterial pan-genome
,
Trends Genet.
,
2009
, vol.
25
(pg.
107
-
110
)
, . ,
Revised road map to the phylum Firmicutes
,
2009
, , , et al. ,
(30 co-authors)
. ,
Whole genome comparisons of serotype 4b and 1/2a strains of the foodborne pathogen Listeria monocytogenes reveal new insights into the core genome components of this species
,
Nucl Acids Res.
,
2004
, vol.
32
(pg.
2386
-
2395
)
, , , , , , . ,
Prevalence and diversity of insertion sequences in the genome of Bacillus thuringiensis YBT-1520 and comparison with other Bacillus cereus group members
,
FEMS Microbiol Lett.
,
2010
, vol.
310
(pg.
9
-
16
)
R Development Core Team
,
R: A language and environment for statistical computing. [Internet]
,
2009
Vienna, Austria
R Foundation for Statistical Computing
R version 2.10.1 (2009-12-14). ISBN 3-900051-07-0. [cited 2012 Jul 9]. Available at: http://www.R-project.org
, , , et al. ,
(13 co-authors)
. ,
The pangenome structure of Escherichia coli: Comparative genomic analysis of E. coli commensal and pathogenic isolates
,
J Bacteriol.
,
2008
, vol.
190
(pg.
6881
-
6893
)
, , , . ,
Tree-BASE: a prototype database of phylogenetic analyses and an interactive tool for browsing the phylogeny of life
,
Am J Bot.
,
1994
, vol.
81
pg.
183
, , , , , . ,
Analysis of ultra-low genome conservation in Clostridium difficile
,
PLoS One
,
2010
, vol.
5
pg.
e15147
, , , , . ,
ISfinder: the reference centre for bacterial insertion sequences
,
Nucleic Acids Res.
,
2006
, vol.
34
(pg.
D32
-
D36
)
, , , et al. ,
(46 co-authors)
. ,
Genome analysis of multiple pathogenic isolates of Streptococcus agalactiae: Implications for the microbial pangenome
,
Proc Nat Acad Sci USA.
,
2005
, vol.
102
(pg.
13950
-
13955
)
, , , et al. ,
(41 co-authors)
. ,
Organized genome dynamics in the Escherichia coli species results in highly diverse adaptive paths
,
PLoS Genet.
,
2009
, vol.
5
pg.
e1000344
, . ,
Horizontal transfer, not gene duplication, drives the expansion of gene families in prokaryotes
,
PLoS Genet.
,
2011
, vol.
7
pg.
e1001284
, , , et al. ,
(19 co-authors)
. ,
Extensive mosaic structure revealed by the complete genome sequence of uropathogenic E. coli
,
Proc Nat Acad Sci U S A.
,
2002
, vol.
99
(pg.
17020
-
17024
)
. ,
Evolution and the genetics of populations. Vol. II. The theory of gene frequencies
,
1969
Chicago
University of Chicago Press
Author notes
Associate editor: Jeffrey Thorne
© The Author 2012. Published by Oxford University Press on behalf of the Society for Molecular Biology and Evolution. All rights reserved. For permissions, please e-mail: [email protected]
Supplementary data
Citations
Views
Altmetric
Email alerts
Email alerts
Citing articles via
More from Oxford Academic