Modeling formalisms in Systems Biology (original) (raw)
- Mini-Review
- Open access
- Published: 05 December 2011
AMB Express volume 1, Article number: 45 (2011)Cite this article
- 19k Accesses
- 148 Citations
- 3 Altmetric
- Metrics details
Abstract
Systems Biology has taken advantage of computational tools and high-throughput experimental data to model several biological processes. These include signaling, gene regulatory, and metabolic networks. However, most of these models are specific to each kind of network. Their interconnection demands a whole-cell modeling framework for a complete understanding of cellular systems. We describe the features required by an integrated framework for modeling, analyzing and simulating biological processes, and review several modeling formalisms that have been used in Systems Biology including Boolean networks, Bayesian networks, Petri nets, process algebras, constraint-based models, differential equations, rule-based models, interacting state machines, cellular automata, and agent-based models. We compare the features provided by different formalisms, and discuss recent approaches in the integration of these formalisms, as well as possible directions for the future.
Introduction
Living organisms are complex systems that emerge from the fundamental building blocks of life. Systems Biology (SB) is a field of science that studies these complex phenomena currently, mainly at the cellular level (Kitano 2002). Understanding the mechanisms of the cell is essential for research in several areas such as drug development and biotechnological production. In the latter case, metabolic engineering approaches are applied in the creation of microbial strains with increased productivity of compounds with industrial interest such as biofuels and pharmaceutical products (Stephanopoulos 1998). Using mathematical models of cellular metabolism, it is possible to systematically test and predict manipulations, such as gene knockouts, that generate (sub)optimal phenotypes for specific applications (Burgard et al. 2003, Patil et al. 2005). These models are typically built in an iterative cycle of experiment and refinement, by multidisciplinary research teams that include biologists, engineers and computer scientists.
The interconnection between different cellular processes, such as metabolism and genetic regulation, reflects the importance of the holistic approach introduced by the SB paradigm in replacement of traditional reductionist methods. Although most cellular components have been studied individually, the behavior of the cell emerges at the network-level and requires an integrative analysis.
Recent high-throughput experimental methods generate the so-called omics data (e.g.: genomics, transcriptomics, proteomics, metabolomics, fluxomics) that have allowed the reconstruction of many biological networks (Feist et al. 2008). However, despite the great advances in the area, we are still far from a whole-cell computational model that integrates and simulates all the components of a living cell. Due to the enormous size and complexity of intracellular biological networks, computational cell models tend to be partial and focused on the application of interest. Also, due to the multidisciplinarity of the field, these models are based on several different kinds of formalisms, including those based on graphs, such as Boolean networks, and equation-based ones, such as ordinary differential equations (ODEs). This diversity can lead to the fragmentation of modeling efforts as it hampers the integration of models from different sources. Therefore, the whole-cell simulation goals of SB would benefit with the development of a framework for modeling, analysis and simulation that is based on a single formalism. This formalism should be able to integrate the entities and their relationships, spanning all kinds of biological networks.
This work reviews several modeling formalisms that have been used in SB, comparing their features and relevant applications. We opted to focus on the formalisms rather than the tools as they are the essence of the modeling approach. For the software tools implementing the formalisms, the interested reader may use the respective references. Note that besides the intracellular level, several studies in SB also address the cellular population level. Therefore, formalisms for modeling the dynamics of cellular populations that have received attention in the field were also considered in this work.
There are some interesting reviews already published in the literature. However they usually focus only on particular biological processes. An excellent review regarding the modeling of signaling pathways was elaborated by Aldridge et al. (2006). They address the model design process, as well as, model validation and calibration. They highlight the application of ODE and rule-based models, but do not mention other formalisms. Another recent review on the modeling of signaling networks can be found in Morris et al. (2010). Two remarkable reviews on the modeling of gene regulatory networks are presented by Schlitt and Brazma (2007) and by Karlebach and Shamir (2008). Both give examples of several applications of different formalisms for modeling this kind of networks. A few reviews with broader scope can also be found in the literature. Two excellent examples are Fisher and Henzinger (2007) and Materi and Wishart (2007). Both give a critical discussion on the application of different formalisms for computational modeling of cellular processes. The former covers Boolean networks, interacting state machines, Petri nets, process algebras and hybrid models, whereas the latter covers differential equations, Petri nets, cellular automata, agent-based models and process algebras. The lack of a single comprehensive review that compares a larger spectrum of formalisms motivated the development of this work.
Biological Networks
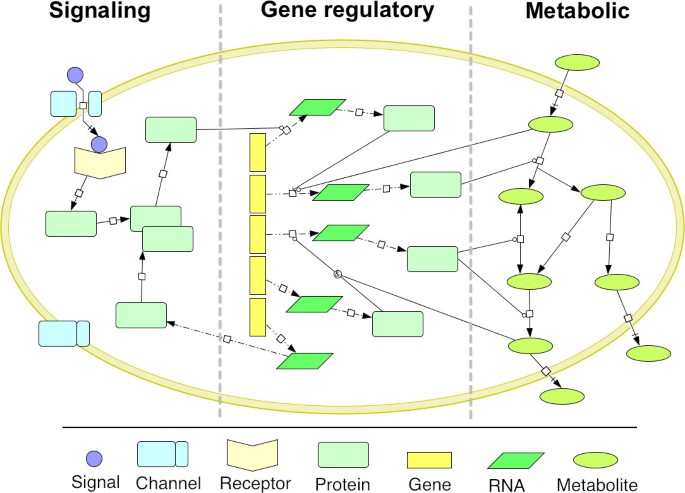
Cells are composed by thousands of components that interact in a myriad of ways. Despite this intricate interconnection, it is usual to divide and classify these networks according to their biological function. A very simplistic example can be found in Figure 1 (created with the free software tool CellDesigner (Funahashi et al. 2003), that uses the graphical notations defined in (Kitano et al. 2005)). The main types of networks are signaling, gene regulatory and metabolic (although some authors also classify protein-protein interactions as another type of network).
Figure 1
The main cellular processes. Conceptual representation of the main cellular processes that occur inside the cell. Signaling cascades receive external signals from the environment, either by binding to an extracellular receptor or, as illustrated, by passing through a channel and binding to an internal receptor. This signal is then propagated through a signaling cascade that involves the sequential phosphorylation of several proteins, leading to gene activations. Gene regulatory networks control the transcription level of genes. Genes are transcribed into RNA molecules, which are subsequently translated into proteins. These proteins are involved in all cellular functions. Some proteins are enzymes involved in the catalysis of metabolic reactions. Metabolic networks obtain energy and carbon from external sources using internal conversion steps. The internal metabolites can be used for cellular growth, or converted into by-products that are excreted by the cell. Their concentration level can also influence gene regulation.
Signaling networks
Signal transduction is a process for cellular communication where the cell receives (and responds to) external stimuli from other cells and from the environment. It affects most of the basic cell control mechanisms such as differentiation and apoptosis. The transduction process begins with the binding of an extracellular signaling molecule to a cell-surface receptor. The signal is then propagated and amplified inside the cell through signaling cascades that involve a series of trigger reactions such as protein phosphorylation. The output of these cascades is connected to gene regulation in order to control cell function. Signal transduction pathways are able to crosstalk, forming complex signaling networks (Gomperts et al. 2009, Albert and Wang 2009).
Gene regulatory networks
Gene regulation controls the expression of genes and, consequently, all cellular functions. Although all of the cell functionality is encoded in the genome through thousands of genes, it is essential for the survival of the cell that only selected functions are active at a given moment. Gene expression is a process that involves transcription of the gene into mRNA, followed by translation to a protein, which may be subject to post-translational modification. The transcription process is controlled by transcription factors (TFs) that can work as activators or inhibitors. TFs are themselves encoded by genes and subject to regulation, which altogether forms complex regulatory networks (Schlitt and Brazma 2007, Karlebach and Shamir 2008).
Metabolic networks
Metabolism is a mechanism composed by a set of biochemical reactions, by which the cell sustains its growth and energy requirements. It includes several catabolic and anabolic pathways of enzyme-catalyzed reactions that import substrates from the environment and transform them into energy and building blocks required to build the cellular components. Metabolic pathways are interconnected through intermediate metabolites, forming complex networks. Gene regulation controls the production of enzymes and, consequently, directs the metabolic flux through the appropriate pathways in function of substrate availability and nutritional requirements (Steuer and Junker 2008, Palsson 2006).
Modeling Requirements
Due to the different properties and behavior of the biological networks, they usually require different modeling features (although some desired features such as graphical visualization are common). For instance, features such as stochasticity and multi-state components may be important for signaling but not for metabolic networks. A summary of the major modeling features required by these networks is presented next.
Network visualization
Biological models should be expressed as intuitively as possible and easily interpreted by people from different areas. For that matter, graph and diagram based formalisms can be more appealing than mathematical or textual notations. Such formalisms can take advantage of state of the art network visualization tools that, when compared to traditional textbook diagrams, allow a much better understanding of the interconnections in large-scale networks, as well as the integration of heterogeneous data sources (Pavlopoulos et al. 2008).
Topological analysis
A considerable amount of the work in this field is based on topological analysis of biological networks. In this case, graph-based representations also play a fundamental role. The analysis of the topological properties of these graphs, such as degree distribution, clustering coefficient, shortest paths or network motifs can reveal crucial information from biological networks, including organization, robustness and redundancy (Jeong et al. 2000, Barabási and Oltvai 2004, Assenov et al. 2008).
Modularity and hierarchy
Despite its great complexity, the cell is organized as a set of connected modules with specific functions (Hartwell et al. 1999, Ravasz et al. 2002). Taking advantage of this modularity can help to alleviate the complexity burden, facilitating the model analysis. Compositionality is a related concept meaning that two modeling blocks can be aggregated together into one model without changes to any of the submodels. This property can be of special interest for applications in Synthetic Biology (Andrianantoandro et al. 2006).
While modularity represents the horizontal organization of the cell, living systems also present vertical organization (Cheng and Hu 2010). Molecules, cells, tissues, organs, organisms, populations and ecosystems reflect the hierarchical organization of life. A modeling formalism that supports hierarchical models and different levels of abstraction will cope with models that connect vertical organization layers using top-down, bottom-up or middle-out approaches (Noble 2002).
Multi-state components
Some compounds may have multiple states, for example, a protein may be modified by phosphorylation. This is a very common case in signaling networks. The state of a protein can affect its functionality and consequently the reactions in which it participates. Therefore, different states are represented by different entities. However, a protein with n binding sites will have 2_n_possible states, which results in a combinatorial explosion of entities and reactions (Hlavacek et al. 2003, Blinov et al. 2004). To avoid this problem, a suitable modeling formalism should consider entities with internal states and state-dependent reactions.
Spatial structure and compartmentalization
On its lowest level, the cell can be seen as a bag of mixed molecules. However, this bag is compartmentalized and requires transport processes for some species to travel between compartments. Furthermore, in some compartments, including the cytosol, the high viscosity, slow diffusion and amount of molecules may not be sufficient to guarantee a spatial homogeneity (Takahashi et al. 2005). Spatial localization and concentration gradients are actually important mechanisms in biological processes such as morphogenesis (Turing 1952).
Qualitative analysis
Experimental determination of kinetic parameters to build quantitative models is a cumbersome task. Furthermore, they are dependent on the experimental conditions, and there is generally no guarantee that the in vitro values will match the in vivo conditions (Teusink et al. 2000). Therefore, several models are only qualitative. Although these models do not allow for quantitative simulations, they allow us to ask qualitative questions about the system and to learn valuable knowledge. For instance, elementary mode analysis is used for calculating all possible pathways through a metabolic network (Schuster et al. 1999).
Dynamic simulation
Dynamic simulation allows the prediction of the transient behavior of a system under different conditions. For each model, the particular simulation approach depends on the type of components included, which depend on the nature of the involved interactions and also on the available information for their characterization.
In regulatory networks, genes are activated and deactivated through the transcription machinery. Due to their complexity and the lack of kinetic information, the transcriptional details are usually not considered. Instead, genes are modeled by discrete (typically boolean) variables that change through discrete time steps. This is the simplest simulation method and requires models with very little detail.
Signaling cascades are triggered by a low number of signaling molecules. Therefore, it is important to take into consideration the inherent stochasticity in the diffusion of these molecules. Stochastic simulation is a common approach for simulation of signaling networks (Costa et al. 2009). This approach requires the attribution of probability functions for each reaction in the model.
Metabolic reactions, on the other hand, comprise large quantities of metabolites. Therefore, their behavior can be averaged and modeled by continuous variables governed by deterministic rate laws (Chassagnole et al. 2002). This requires a significant amount of experimental data for estimation of the kinetic parameters.
Standardization
Biological models need to be represented in a common format for exchange between different tools. The Systems Biology Markup Language (SBML) has become the de facto standard of the SB community, and is currently supported by over two hundred tools (Hucka et al. 2003). It is an XML-based language for representation of species, compartments, reactions and their specific properties such as concentrations, volumes, stoichiometry and rate laws. It also facilitates the storage of tool specific data using appropriate tags. SBML was initially focused on biochemical reaction networks such as metabolic and signaling pathways, therefore it is not so well-suited for modeling other kinds of processes such as regulatory networks which are better described by logical models. Nevertheless, these and other limitations are being addressed in the development of future releases (Finney and Hucka 2003, Hucka et al. 2010).
CellML is another XML-based language with a similar purpose to SBML albeit more generic (Lloyd et al. 2004). The Systems Biology Graphical Notation (SBGN) (Le Novère et al. 2009) is a standard that focuses on the graphical notation and may be seen as a complement to SBML. It addresses the visualization concerns discussed previously, specially the creation of graphical models with a common notation that can be shared and unambiguously interpreted by different people.
Modeling Formalisms
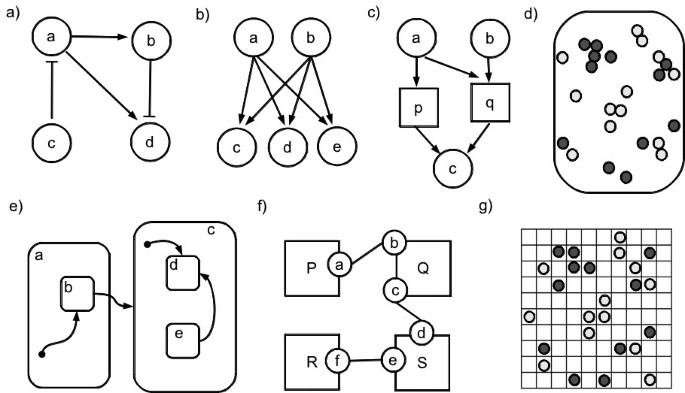
Many formalisms have been used to model biological systems, in part due to the diversity of phenomena that occur in living systems, and also due to the multidisciplinarity of the research teams. Biologists may be more familiar with mathematical modeling and computer scientists may be religious to their computational formalism of choice. The dichotomy between mathematical and computational models has been discussed elsewhere (Hunt et al. 2008). Although they follow different approaches (denotational vs operational), it has been questioned if there is such a clear separation between mathematical and computational models. Therefore, we will briefly describe several formalisms regardless of such distinction. Table 1 summarizes some of the literature references reviewed herein, classified by type of intracellular process implemented. Toy examples of the formalisms with graphical notation are depicted in Figure 2.
Table 1 Literature references grouped by formalism
Figure 2
Formalisms with visual representation Toy examples of the formalisms with visual representation. a) Boolean network: genes are represented by nodes (a, b, c, d) and the arrows represent activation and repression; b) Bayesian network: the value of the output nodes (genes c, d, e) are given by a probability function that depends on the value of the input nodes (genes a and b); c) Petri net: places represent substances (a, b, c), transitions represent reactions (p, q) and the arrows represent consumption and production; d) Agent-based model: two types of agents, representing two different kinds of cells (or two kinds of molecules) can move freely and interact within the containing space; e) Interacting state machine: systems are represented by their state (a, b), where each state may contain one or more internal sub-states (b, d, e), arrows represent the transition between different states of the system; f) Rule-based model (represented by a contact map): agents represent proteins (P, Q, R, S), which may contain different binding sites (a to f ), the connections represent the rules for possible interactions (such as phosphorylation); g) Cellular automata: a grid where the value of each element can represent different kinds of cells (or molecules), that can change by interaction with their immediate neighbors.
Boolean networks
Boolean networks (Figure 2a) were introduced by Kauffman in 1969 to model gene regulatory networks (Kauffman 1969). They consist on networks of genes, modeled by boolean variables that represent active and inactive states. At each time step, the state of each gene is determined by a logic rule which is a function of the state of its regulators. The state of all genes forms a global state that changes synchronously. For large network sizes (n nodes) it becomes impractical to explore all possible states (2_n_). This type of model can be used to find steady-states (called attractors), and to analyze network robustness (Li et al. 2004). Boolean networks can be inferred directly from experimental gene expression time-series data (Akutsu et al. 1999, D'haeseleer et al. 2000). They have also been applied in some studies to model signaling pathways (Gupta et al. 2007, Saez-Rodriguez et al. 2007). To cope with the inherent noise and the uncertainty in biological processes, stochastic extensions like Boolean networks with noise (Akutsu et al. 2000) and Probabilistic Boolean networks (Shmulevich et al. 2002) were introduced.
Bayesian networks
Bayesian networks (Figure 2b) were introduced in the 80's by the work of Pearl (Pearl 1988). They are a special type of probabilistic graphs. Their nodes represent random variables (discrete or continuous) and the edges represent conditional dependencies, forming a directed acyclic graph. Each node contains a probabilistic function that is dependent on the values of its input nodes. There are learning methods to infer both structure and probability parameters with support for incomplete data. This flexibility makes Bayesian networks specially interesting for biological applications. They have been used for inferring and representing gene regulatory (Friedman 2004, Pena et al. 2005, Grzegorczyk et al. 2008, Auliac et al. 2008) and signaling networks (Sachs et al. 2002; 2005). One disadvantage of Bayesian networks is the inability to model feedback loops, which is a common motif in biological networks. This limitation can be overcome by dynamic Bayesian networks (Husmeier 2003, Kim et al. 2003, Zou and Conzen 2005, Dojer et al. 2006). In this case, the variables are replicated for each time step and the feedback is modeled by connecting the nodes at adjacent time steps.
Petri nets
Petri nets (Figure 2c) were created in the 60's by Carl Adam Petri for the modeling and analysis of concurrent systems (Petri 1962). They are bipartite graphs with two types of nodes, places and transitions, connected by directed arcs. Places hold tokens that can be produced (respectively, consumed) when an input (respectively, output) transition fires. The execution of a Petri net is non-deterministic and specially suited for distributed systems with concurrent events. Their application to biological processes began in 1993, by the work of Reddy and coworkers, to overcome the limitations in quantitative analysis of metabolic pathways (Reddy et al. 1993).
There are currently several Petri net extensions (e.g.: coloured, timed, stochastic, continuous, hybrid, hierarchical, functional), forming a very versatile framework for both qualitative and quantitative analysis. Due to this versatility, they have been used in metabolic (Küffner et al. 2000, Zevedei-Oancea and Schuster 2003, Koch et al. 2005), gene regulatory (Chaouiya et al. 2004; 2008), and signaling networks (Sackmann et al. 2006, Chen et al. 2007, Breitling et al. 2008, Hardy and Robillard 2008). Also, they are suited for integrating different types of networks, such as gene regulatory and metabolic (Simao et al. 2005).
Process algebras
Process algebras are a family of formal languages for modeling concurrent systems. They generally consist on a set of process primitives, operators for sequential and parallel composition of processes, and communication channels. The Calculus of Communicating Systems (CCS) was one of the first process algebras, developed during the 70's by Robin Milner (Milner 1980), and later gave origin to the more popular _π_-calculus (Milner et al. 1992). In SB the application of process algebras has been mainly focused on signaling pathways due to their similarity to communication processes. About a decade ago, Regev and coworkers published their pioneer work on the representation of signaling pathways with _π_-calculus (Regev et al. 2000; 2001). They later extended their work using stochastic _π_-calculus (BioSpi) to support quantitative simulations (Priami et al. 2001) and using Ambient calculus (BioAmbients) for representation of compartments (Regev et al. 2004). Other relevant biological applications of process algebras include Bio-calculus (Nagasaki et al. 1999), _κ_-calculus (for protein-protein interactions) (Danos and Laneve 2004), CCS-R (Danos and Krivine 2007), Beta binders (Priami and Quaglia 2005), Brane Calculi (Cardelli 2005), SpacePi (John et al. 2008), Bio-PEPA (Ciocchetta and Hillston 2008; 2009) and BlenX (Dematte et al. 2008, Priami et al. 2009).
Constraint-based models
Constraint-based models for cellular metabolism began spreading during the 90's, mainly influenced by the work of Palsson and coworkers (Varma and Palsson 1994). Assuming that cells rapidly reach a steady-state, these models overcome the limitations in lack of experimental data for parameter estimation inherent in fully detailed dynamic models. They are based on stoichiometric, thermodynamic and enzyme capacity constraints (Reed and Palsson 2003, Price et al. 2003). Instead of a single solution, they define a space of possible solutions representing different phenotypes that comply with the constraints. The simplicity in this formulation allows its application to genome-scale metabolic models comprising thousands of reactions, such as the most recent metabolic reconstruction of E. coli (Orth et al. 2011).
Constraint-based models have been used in metabolic engineering strategies for the determination of flux distributions (metabolic flux analysis (Wiechert 2001), flux balance analysis (Kauffman et al. 2003)), knockout phenotype predictions (minimization of metabolic adjustment (Segrè et al. 2002), regulatory on/off minimization (Shlomi et al. 2005)) or enumerating all possible pathways (extreme pathways (Schilling et al. 2000), elementary flux modes (Schuster et al. 1999)). Although their main application has been on metabolic networks, there are recent efforts towards application on gene regulatory and signaling networks (Papin et al. 2005, Gianchandani et al. 2009, Lee et al. 2008a).
Differential equations
Differential equations describe the rate of change of continuous variables. They are typically used for modeling dynamical systems in several areas. Systems of non-linear ordinary differential equations (ODEs) have been used in SB to describe the variation of the amount of species in the modeled system as a function of time. They have been applied to all kinds of biological pathways (Chassagnole et al. 2002, Tyson et al. 2003, Chen et al. 1999, Rizzi et al. 1997). With a fully detailed kinetic model, one can perform time-course simulations, predict the response to different inputs and design system controllers. However, building ODE models requires insight into the reaction mechanisms to select the appropriate rate laws, and experimental data to estimate the kinetic parameters. The lack of kinetic data has limited the size of the modeled networks to pathway size, with exception for the human red blood cell model (Jamshidi et al. 2001).
Approximative rate laws such as generalized mass action (GMA) (Horn and Jackson 1972), S-systems (Savageau and Voit 1987), lin-log (Visser and Heijnen 2003), and convenience kinetics (Liebermeister and Klipp 2006), have compact standard formulations that can facilitate the development and analysis of large-scale models (Heijnen 2005, Costa et al. 2010). This opens the possibility for kinetic modeling at the genome-scale (Smallbone et al. 2010).
Other types of differential equations, such as stochastic differential equations (SDEs) and partial differential equations (PDEs) can be used respectively to account for stochastic effects and spatial distribution (Turner et al. 2004). Piecewise-linear differential equations (PLDEs) have been used to integrate discrete and continuous features in gene regulatory networks (De Jong et al. 2004, Batt et al. 2005).
Rule-based models
Rule-based (Figure 2f) modeling comprises a recent approach to the problem of multi-state components in biological models. In rule-based formalisms the species are defined in a structured manner and support multiple states. The reaction rules are defined as transformations of classes of species, avoiding the need for specifying one reaction per each possible state of a species. This high-level specification is then automatically transformed into a biochemical network with the set of species and reactions generated by the specification. This kind of formalism is implemented in BioNetGen (Blinov et al. 2004) which generates an ODE model or a stochastic simulation from the ruled-based specification. It has been applied in the modeling of different signaling pathways (Blinov et al. 2006, Barua et al. 2007; 2008; 2009). A similar rule-based formalism used for this kind of pathways is the κ language, where the species are defined by agents that have a structured interface for interaction with other agents (Danos et al. 2007; 2009, Feret et al. 2009). The possible interactions are defined by a set of rules, which can be visualized by a contact map. BIOCHAM implements a rule-based approach for model specification which is complemented with a temporal logic language for the verification of the properties the biological models (Calzone et al. 2006).
The main advantage of the rule-based approach is that it can avoid the combinatorial explosion problem in the generation and simulation of the complete reaction network by performing stochastic simulations that only instantiate the species and reactions as they become available (Colvin et al. 2009; 2010) or by the generation of coarse-grained ODE systems (Feret et al. 2009). Spatial simulation has been addressed recently by the inclusion of geometric information as part of the structure of the species (Gruenert et al. 2010).
Interacting state machines
Interacting state (Figure 2e) machines are diagram-based formalisms that describe the temporal behavior of a system based on the changes in the states of its parts. They are suited to model biological behavior in a qualitative way as they require little quantitative data. They differ from other approaches as they define a system in terms of its states rather than its components. They are typically used for model checking and interactive execution.
One such formalism is Statecharts, developed by David Harel during the 80's (Harel 1987) that was first applied in biology for modeling the T-cell activation process (Kam et al. 2001, Efroni et al. 2003) and more recently in pancreatic organogenesis (Setty et al. 2008). In this formalism, the state of a system may contain sub-states at multiple levels, allowing an hierarchical view of the system and the relation between events at smaller and larger scales. Other related formalisms are Reactive Modules (Alur and Henzinger 1999) and Live Sequence Charts (Damm and Harel 2001), which, along with the former, have been applied in the modelling of C. elegans vulval development (Fisher et al. 2005; 2007).
Cellular automata
Cellular automata (Figure 2g) were created by von Neumann and Ulam in the 40's (Von Neumann and Burks 1966). They are discrete dynamic models that consist on a grid of cells with a finite number of states. A cellular automaton has an initial configuration that changes at each time step through a predefined rule that calculates the state of each cell as a function of the state of its neighbors at the previous step. They are specially suited for modeling complex phenomena in a scale-free manner and have been used in biological studies for a long time (Ermentrout and Edelstein-Keshet 1993). Due to their spatial features their main applications are related to molecular dynamics and cellular population dynamics.
Application examples at the molecular level include enzyme reaction networks that account for spatial diffusion (Weimar 2002) and signaling pathways (Wurthner et al. 2000, Kier et al. 2005). At the cellular level they were used for models such as those of bacterial aggregation (Sozinova et al. 2005) and HIV infection (Zorzenon dos Santos and Coutinho 2001, Corne and Frisco 2008). Dynamic cellular automata are a variation of cellular automata that allows for movement of the cell contents inside the grid, mimicking brownian motion. They were used to model enzyme kinetics, molecular diffusion and genetic circuits (Wishart et al. 2005).
Agent-based models
Agent-based models (Figure 2d) describe the interactions among multiple autonomous agents. They are similar in concept to cellular automata, except in this case, instead of using a grid and synchronized time steps, the agents move freely within the containing space. Likewise, they are used to study complex phenomena and emergent dynamics using populations of agents with simple rules. At the molecular level they have been mainly used to build models of signaling pathways that account for spatial distribution and the structural properties of the cell (Gonzalez et al. 2003, Pogson et al. 2006; 2008, An 2009). Recently, they have also been applied to metabolic reactions (Klann et al. 2011). However, their main application is at the multi-cellular level, where they have been used to study granuloma formation (Segovia-Juarez et al. 2004), tumor growth (Zhang et al. 2007, Engelberg et al. 2008), morphogenesis (Grant et al. 2006), chemotaxis (Emonet et al. 2005), immune responses (Lollini et al. 2006, Li et al. 2008), and several others (Thorne et al. 2007, Merelli et al. 2007).
Other formalisms
There are other modeling formalisms that have been used in SB which are worth mentioning. Cybernetic modeling is one of the earliest approaches for dynamic modeling that was used in bioprocess applications (Kompala et al. 1984, Dhurjati et al. 1985). A recent approach combines cybernetic variables with elementary flux modes (Young et al. 2008, Kim et al. 2008). Hybrid automata addressed the integration of discrete and continuous components in the Delta-Notch signaling pathway (Ghosh and Tomlin 2001; 2004). Artificial neural networks were used to model gene expression (Vohradsky 2001). Molecular interaction maps are a popular graph-based formalism created by Kohn in 1999 (Kohn 1999, Kohn et al. 2006, Luna et al. 2011) that influenced the SBGN standard (Le Novère et al. 2009). Other graph-based formalisms include modular interaction networks (Yartseva et al. 2007) and logical interaction hypergraphs (Klamt et al. 2006). The P systems formalism created by Paun in 1998, inspired the area of membrane computing (Paun 2000) and has been recently applied in SB (Pérez-Jiménez and Romero-Campero 2006, Cao et al. 2010). Chemical organization theory is a recent approach for modeling biochemical reaction networks that uses set theory to analyze how they can be decomposed into self-maintaining subnetworks called organizations, that reveal dynamic properties of the system (Dittrich and Di Fenizio 2007). It has been used to analyze different types of networks including signaling pathways and regulated metabolic networks (Centler et al. 2007; 2008, Kaleta et al. 2008; 2009).
Formalisms conversion
The inability of the formalisms to fit all purposes has driven the development of methodologies to convert between different formalisms. Two different methods have been proposed to convert Boolean networks to Petri nets (Chaouiya et al. 2004, Steggles et al. 2007). Boolean networks have also been converted to constraint-based models (Gianchandani et al. 2006) and to ODEs (Wittmann et al. 2009). Other formalisms have also been converted to ODEs, including constraint-based models (Smallbone et al. 2007), Petri nets (Gilbert and Heiner 2006), process algebras (Calder et al. 2005) and rule-based models (Feret et al. 2009). When the mappings are made from abstract to more detailed models they usually require some assumptions and insight into the reaction mechanisms. The language for biochemical systems (LBS) is a recent language that integrates a rule-based approach with process calculus, and supports the generation of Petri nets, ODEs and continuous time Markov chains (Pedersen and Plotkin 2010).
Formalisms integration
Along with the conversion between formalisms, there is also a recent trend for developing methods that support integrated simulation of different formalisms in order to integrate different kinds of biological networks, where each network is modeled in its own formalism. Extensions of flux balance analysis (FBA) (Kauffman et al. 2003), such as regulated FBA (rFBA) (Covert and Palsson 2002) and steady-state regulated FBA (SR-FBA) (Shlomi et al. 2007) incorporate boolean rules into constraint-based models for integrated simulation of regulatory and metabolic networks. Integrated FBA (iFBA) extends rFBA by integrating kinetic information from ODE models (Covert et al. 2008). Integrated dynamic FBA (idFBA) aims to integrate signaling, regulatory and metabolic networks by modeling all networks in the constraint-based formulation (Lee et al. 2008b). Biochemical systems theory (BST) has been recently integrated with Hybrid Functional Petri Nets (HFPN) in order to integrate metabolic, regulatory and signaling networks, in a framework that accounts for different time-scales as well as discrete, stochastic and continuous effects (Wu and Voit 2009a;b).
Comparison of the Formalisms
The diversity of problems studied in SB gave rise to the application of several different types of formalisms. A comparison of the amount of literature references for each formalism, classified by the type of biological process described, is given in Table 1. We can observe that only four formalisms (Petri nets, constraint-based models, differential equations and cellular automata) have been applied to all three types of biological networks, which makes them potential candidates as a suitable integrative formalism for whole-cell modeling. However, this should not exclude other formalisms from this possibility as well. Another interesting observation is that metabolism is the biological process with the smaller number of formalisms applied. This is likely due to the fact that its two main frameworks (differential equations and constraint-based) are well suited for modeling metabolic networks. On the other hand, all of the formalisms have been applied to signaling pathways. One possible reason is that they require the largest number of modeling features, including spatial localization and multi-state components.
The modeling features provided by the formalisms reviewed in this work are compared in Table 2. Some of the features are only available in extensions of the formalisms. We can observe that no single formalism covers the whole spectrum of features desired for modeling all kinds of biological components. Petri nets and rule-based models are among the formalisms that cover most features. Petri nets have several extensions available, and although none of the extensions alone fulfills all requisites, altogether they form a very versatile modeling framework. Rule-based models present a high level of abstraction and can be used for stochastic simulation and automatic generation of lower level ODE-based representations. Therefore, they take advantage of the analytic power of abstract representations, preserving the ability to generate stochastic and deterministic simulations.
Table 2 Modeling formalisms and implemented features
Although none of the formalisms implements all the required features, this is not necessarily a limitation, since different formalisms can be used at different stages of the modeling process. The model construction process begins with biochemical knowledge and experimental data that allow an enumeration of the components and connections in the system. Graph-based models, such as Boolean networks, Bayesian networks and Petri nets can be used for modeling this map of interactions. This allows a deeper understanding of the organization of the system through topological analysis, and drives new experiments by finding gaps in the models. This kind of models also allows qualitative descriptions of system behavior and coarse simulation capabilities. If the reactions' stoichiometry and directionality are known, one may analyze the steady-states of the system using constraint-based models. Finally, if extensive experimental data is available to infer the kinetics of the reactions, probabilistic or deterministic rate laws can be used to create dynamic models. These are used to generate time-course simulations under different sets of initial conditions. Stochastic process algebras, stochastic Petri nets, continuous Petri nets, rule-based models and differential equations, would all be ideal candidates for this purpose.
Cellular automata and agent-based models account for the individual replicas of each component in the system. When applied at the molecular level, this paradigm provides accurate simulations of small sets of biochemical reactions that account for spatial diffusion. However, it becomes infeasible to perform simulations at the genome-scale network level, as this would imply modeling every copy of all substances present in the cell. Nevertheless, this approach is very convenient for modeling at the cell population level, as it allows to track changes in individual cells and to study the emergent properties of cellular communities.
In search for a proper formalism perhaps the most important aspect to consider is the balance between simplicity and expressiveness. There is a price to pay for the amount of features provided by a formalism, which may come at the cost of increased model complexity. The complexity of the representation and the number of parameters determines the amount of experimental data required for model construction. This is the reason why the most simple formalisms such as Boolean networks and constraint-based models have been used to build, respectively, gene regulatory and metabolic networks at the genome scale. This concern is most critical when not only the parameters but also the network structure are unknown. Model inference (also known as reverse engineering) methods are applied in these cases. They have been used to infer Boolean networks (Akutsu et al. 1999, D'haeseleer et al. 2000), Bayesian networks (Friedman 2004, Auliac et al. 2008), Petri nets (Nummela and Julstrom 2005, Durzinsky et al. 2011) and ODEs (Kimura et al. 2005, Iba 2008) from experimental data. However, the scalability of these methods is greatly dependent on the simplicity of the underlying formalism.
Perspective
With the myriad of formalisms that have been applied in SB, we face the challenge of choosing the proper formalism for the problem in hands. As more data become available for network reconstruction, we move towards integration of all kinds of biological networks, namely signaling, gene regulatory and metabolic. Although some formalisms like Petri nets, constraint-based models and differential equations have been applied for all these networks, no single formalism covers the whole spectrum of functionalities reviewed in this work. Petri nets have several extensions available, covering most of the features analyzed, with the exception of compartments and spatial localization. Rule-based models are another strong candidate as they also cover a great part of the modeling features. These are definitely two formalisms to keep under consideration in the near future.
The model building process is based on iterative steps of refinement and validation. Recent approaches for genome-scale kinetic modeling of metabolism, begin with the network topology, modeled in the constraint-based framework, and then refine the models by adding the kinetic structure in order to generate ODE models (Jamshidi and Palsson 2010, Smallbone et al. 2010). Petri nets seem to be a promising formalism for this purpose, given that discrete Petri nets can model the network topology, and can then be used as a scaffold for the generation of dynamic models based on continuous or stochastic Petri nets. The fact that the same kind of formalism is used during the whole model refinement process, helps the creation of more straightforward methods for automatic mapping and validation of the models.
A common problem in the analysis of biological networks is the combinatorial explosion that originates from the complexity of large models. A typical example is the computation of elementary flux modes at the genome-scale, requiring modular decomposition of the networks (Schuster et al. 2002). This problem will aggravate as we get closer to whole-cell modeling. The solution may reside in the application of hierarchical formalisms to represent an intermediate level between the reaction and the cell. As stated elsewhere, one should not "model bulldozers with quarks" (Goldenfeld 1999). Hierarchical Petri nets, BioAmbients and Statecharts are formalisms that support hierarchical modeling.
Models of cell populations are also becoming more frequent. They are used to study scenarios like cell differentiation, chemotaxis, infections or tumor growth. This kind of models depends on the internal dynamics of the cells as well as population dynamics. Therefore, they require modeling of interactions across organizational scales (Walker and Southgate 2009). It is possible that in the future, we will have multi-scale models that integrate formalisms. For instance, the evolution of a population of cells may be modeled by an agent-based model, where each agent has a boolean network for internal representation of its gene expression.
In order to convert between different formalisms it is important to have a standard representation format that preserves most of the features in the models. SBML is the most popular standard in the SB community, currently supported by over two hundred tools (Hucka et al. 2003). Most of the modeling features covered herein have been proposed for future versions of SBML (Finney and Hucka 2003). These include hierarchical model composition, rule-based modeling, spatial geometry and alternative mathematical representations. The compatibility with the SBML representation will dictate which formalisms will prevail in the future.
Many of the proposed formalisms, such as Petri nets or process algebras, were originally created by the computational community for the specification of software systems, where the final system has to comply to the model. The biological community faces the opposite problem, where the model has to mimic the system's behavior, and where most components cannot even be measured directly. Therefore, a proper framework for SB must provide not only a suitable formalism with attractive features and simulation methods, but also methods for model inference and parameter estimation that are sufficiently robust to handle experimental data that are incomplete and prone to measurement error.
References
- Akutsu T, Miyano S, Kuhara S: Identification of genetic networks from a small number of gene expression patterns under the Boolean network model. In Pacific Symposium on Biocomputing. Volume 4. World Scientific Computing, Singapore; 1999:17–28.
Google Scholar - Akutsu T, Miyano S, Kuhara S: Inferring qualitative relations in genetic networks and metabolic pathways. Bioinformatics 2000,16(8):727–734.
CAS Google Scholar - Albert R, Wang R: Discrete dynamic modeling of cellular signaling networks. Methods Enzymol 2009, 467: 281–306.
CAS Google Scholar - Aldridge B, Burke J, Lauffenburger D, Sorger P: Physicochemical modelling of cell signalling pathways. Nat Cell Biol 2006,8(11):1195–1203.
CAS Google Scholar - Alur R, Henzinger T: Reactive modules. Lect Notes Comput Sc 1999,15(1):7–48.
Google Scholar - An G: A model of TLR4 signaling and tolerance using a qualitative, particle-event-based method: introduction of spatially configured stochastic reaction chambers (SCSRC). Math Biosci 2009,217(1):43–52.
CAS Google Scholar - Andrianantoandro E, Basu S, Karig D, Weiss R: Synthetic biology: new engineering rules for an emerging discipline. Mol Syst Biol 2006.,2(1):
- Assenov Y, Ramirez F, Schelhorn S, Lengauer T, Albrecht M: Computing topological parameters of biological networks. Bioinformatics 2008,24(2):282–284.
CAS Google Scholar - Auliac C, Frouin V, Gidrol X, D'Alché-Buc F, et al.: Evolutionary approaches for the reverse-engineering of gene regulatory networks: A study on a biologically realistic dataset. BMC Bioinf 2008,9(1):91.
Google Scholar - Barabási A, Oltvai Z: Network biology: understanding the cell's functional organization. Nat Rev Genet 2004,5(2):101–113.
Google Scholar - Barua D, Faeder J, Haugh J: Structure-based kinetic models of modular signaling protein function: focus on Shp2. Biophys J 2007,92(7):2290–2300.
CAS PubMed Central Google Scholar - Barua D, Faeder J, Haugh J: Computational models of tandem Src homology 2 domain interactions and application to phosphoinositide 3-kinase. J Biol Chem 2008,283(12):7338–7345.
CAS PubMed Central Google Scholar - Barua D, Faeder J, Haugh J: A Bipolar Clamp Mechanism for Activation of Jak-Family Protein Tyrosine Kinases. PLoS Comput Biol 2009,5(4):e1000364.
PubMed Central Google Scholar - Batt G, Ropers D, De Jong H, Geiselmann J, Mateescu R, Page M, Schneider D: Validation of qualitative models of genetic regulatory networks by model checking: Analysis of the nutritional stress response in Escherichia coli. Bioinformatics 2005,21(Suppl 1):i19-i28.
CAS Google Scholar - Blinov M, Faeder J, Goldstein B, Hlavacek W: BioNetGen: software for rule-based modeling of signal trans-duction based on the interactions of molecular domains. Bioinformatics 2004,20(17):3289–3291.
CAS Google Scholar - Blinov M, Faeder J, Goldstein B, Hlavacek W: A network model of early events in epidermal growth factor receptor signaling that accounts for combinatorial complexity. Biosystems 2006,83(2–3):136–151.
CAS Google Scholar - Breitling R, Gilbert D, Heiner M, Orton R: A structured approach for the engineering of biochemical network models, illustrated for signalling pathways. Brief Bioinform 2008,9(5):404–421.
CAS Google Scholar - Burgard A, Pharkya P, Maranas C: Optknock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol Bioeng 2003,84(6):647–657.
CAS Google Scholar - Calder M, Gilmore S, Hillston J: Automatically deriving ODEs from process algebra models of signalling pathways. In Computational Methods in Systems Biology. Springer, Berlin Heidelberg; 2005:204–215.
Google Scholar - Calzone L, Fages F, Soliman S: BIOCHAM: an environment for modeling biological systems and formalizing experimental knowledge. Bioinformatics 2006,22(14):1805.
CAS Google Scholar - Cao H, Romero-Campero F, Heeb S, Cámara M, Krasnogor N: Evolving cell models for systems and synthetic biology. Syst Synth Biol 2010,4(1):55–84.
PubMed Central Google Scholar - Cardelli L: Brane calculi. In Computational Methods in Systems Biology. Springer, Berlin Heidelberg; 2005:257–278.
Google Scholar - Centler F, Fenizio P, Matsumaru N, Dittrich P: Chemical organizations in the central sugar metabolism of Escherichia coli. Math Model Biol Syst 2007,1(2):105–119.
Google Scholar - Centler F, Kaleta C, Di Fenizio P, Dittrich P: Computing chemical organizations in biological networks. Bioinformatics 2008,24(14):1611–1618.
CAS Google Scholar - Chaouiya C, Remy E, Ruet P, Thieffry D: Qualitative modelling of genetic networks: From logical regulatory graphs to standard petri nets. Lect Notes Comput Sc 2004, 3099: 137–156.
Google Scholar - Chaouiya C, Remy E, Thieffry D: Petri net modelling of biological regulatory networks. J Discrete Algorithms 2008,6(2):165–177.
Google Scholar - Chassagnole C, Noisommit-Rizzi N, Schmid J, Mauch K, Reuss M: Dynamic modeling of the central carbon metabolism of Escherichia coli. Biotechnol Bioeng 2002,79(1):53–73.
CAS Google Scholar - Chen L, Qi-Wei G, Nakata M, Matsuno H, Miyano S: Modelling and simulation of signal transductions in an apoptosis pathway by using timed Petri nets. J Biosci 2007,32(1):113–127.
Google Scholar - Chen T, He H, Church G: Modeling Gene Expression with Differential Equations. In Pacific Symposium on Biocomputing. World Scientific Computing, Singapore; 1999:29–40.
Google Scholar - Cheng C, Hu Y: Extracting the abstraction pyramid from complex networks. BMC Bioinf 2010,11(1):411.
Google Scholar - Ciocchetta F, Hillston J: Bio-PEPA: an extension of the process algebra PEPA for biochemical networks. Electron Notes Theor Comput Sci 2008,194(3):103–117.
Google Scholar - Ciocchetta F, Hillston J: Bio-PEPA: a framework for the modelling and analysis of biological systems. Theor Comput Sci 2009,410(33–34):3065–3084.
Google Scholar - Colvin J, Monine M, Faeder J, Hlavacek W, Von Hoff D, Posner R: Simulation of large-scale rule-based models. Bioinformatics 2009,25(7):910–917.
CAS PubMed Central Google Scholar - Colvin J, Monine M, Gutenkunst R, Hlavacek W, Von Hoff D, Posner R: RuleMonkey: software for stochastic simulation of rule-based models. BMC Bioinf 2010,11(1):404.
Google Scholar - Corne D, Frisco P: Dynamics of HIV infection studied with cellular automata and conformon-P systems. Biosystems 2008,91(3):531–544.
CAS Google Scholar - Costa M, Radhakrishnan K, Wilson B, Vlachos D, Edwards J, Jonsson H: Coupled stochastic spatial and non-spatial simulations of ErbB1 signaling pathways demonstrate the importance of spatial organization in signal transduction. PLoS ONE 2009, 4: e6316.
PubMed Central Google Scholar - Costa R, Machado D, Rocha I, Ferreira E: Hybrid dynamic modeling of Escherichia coli central metabolic network combining Michaelis-Menten and approximate kinetic equations. Biosystems 2010,100(2):150–157.
CAS Google Scholar - Covert M, Palsson B: Transcriptional regulation in constraints-based metabolic models of Escherichia coli. J Biol Chem 2002,277(31):28058–28064.
CAS Google Scholar - Covert M, Xiao N, Chen T, Karr J: Integrating metabolic, transcriptional regulatory and signal transduction models in Escherichia coli. Bioinformatics 2008,24(18):2044–2050.
CAS Google Scholar - Damm W, Harel D: LSCs: Breathing life into message sequence charts. Lect Notes Comput Sc 2001,19(1):45–80.
Google Scholar - Danos V, Feret J, Fontana W, Harmer R: Rule-Based Modelling of Cellular Signalling. In CONCUR 2007 - Concurrency Theory. Volume 4703. Springer, Berlin Heidelberg; 2007:17–41.
Google Scholar - Danos V, Feret J, Fontana W, Harmer R, Krivine J: Rule-based modelling and model perturbation. T Comput Syst Biol XI 2009, 5750: 116–137.
Google Scholar - Danos V, Krivine J: Formal molecular biology done in CCS-R. Electron Notes Theor Comput Sci 2007,180(3):31–49.
Google Scholar - Danos V, Laneve C: Formal molecular biology. Theor Comput Sci 2004,325(1):69–110.
Google Scholar - De Jong H, Gouzé J, Hernandez C, Page M, Sari T, Geiselmann J: Qualitative simulation of genetic regulatory networks using piecewise-linear models. Bull Math Biol 2004,66(2):301–340.
Google Scholar - Dematte L, Priami C, Romanel A, Soyer O: Evolving BlenX programs to simulate the evolution of biological networks. Theor Comput Sci 2008,408(1):83–96.
Google Scholar - D'haeseleer P, Liang S, Somogyi R: Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics 2000,16(8):707–726.
Google Scholar - Dhurjati P, Ramkrishna D, Flickinger M, Tsao G: A cybernetic view of microbial growth: modeling of cells as optimal strategists. Biotechnol Bioeng 1985,27(1):1–9.
CAS Google Scholar - Dittrich P, Di Fenizio P: Chemical organisation theory. Bull Math Biol 2007,69(4):1199–1231.
CAS Google Scholar - Dojer N, Gambin A, Mizera A, Wilczyński B, Tiuryn J: Applying dynamic Bayesian networks to perturbed gene expression data. BMC Bioinf 2006,7(1):249.
Google Scholar - Durzinsky M, Wagler A, Marwan W: Reconstruction of extended Petri nets from time series data and its application to signal transduction and to gene regulatory networks. BMC Syst Biol 2011,5(1):113.
PubMed Central Google Scholar - Efroni S, Harel D, Cohen I: Toward rigorous comprehension of biological complexity: modeling, execution, and visualization of thymic T-cell maturation. Genome Res 2003,13(11):2485–2497.
CAS PubMed Central Google Scholar - Emonet T, Macal C, North M, Wickersham C, Cluzel P: AgentCell: a digital single-cell assay for bacterial chemotaxis. Bioinformatics 2005,21(11):2714.
CAS Google Scholar - Engelberg J, Ropella G, Hunt C: Essential operating principles for tumor spheroid growth. BMC Syst Biol 2008,2(1):110.
PubMed Central Google Scholar - Ermentrout G, Edelstein-Keshet L: Cellular Automata Approaches to Biological Modeling. J Theor Biol 1993,160(1):97–133.
CAS Google Scholar - Feist A, Herrgård M, Thiele I, Reed J, Palsson B: Reconstruction of biochemical networks in microorganisms. Nat Rev Microbiol 2008,7(2):129–143.
PubMed Central Google Scholar - Feret J, Danos V, Krivine J, Harmer R, Fontana W: Internal coarse-graining of molecular systems. Proc Natl Acad Sci USA 2009,106(16):6453.
CAS PubMed Central Google Scholar - Finney A, Hucka M: Systems biology markup language: Level 2 and beyond. Biochem Soc Trans 2003, 31: 1472–1473.
CAS Google Scholar - Fisher J, Henzinger T: Executable cell biology. Nat Biotechnol 2007,25(11):1239–1249.
CAS Google Scholar - Fisher J, Piterman N, Hajnal A, Henzinger T: Predictive Modeling of Signaling Crosstalk during C. elegans Vulval Development. PLoS Comput Biol 2007,3(5):e92.
PubMed Central Google Scholar - Fisher J, Piterman N, Hubbard E, Stern M, Harel D: Computational insights into Caenorhabditis elegans vulval development. Proc Natl Acad Sci USA 2005,102(6):1951–1956.
CAS PubMed Central Google Scholar - Friedman N: Inferring cellular networks using probabilistic graphical models. Science 2004,303(5659):799–805.
CAS Google Scholar - Funahashi A, Morohashi M, Kitano H, Tanimura N: CellDesigner: a process diagram editor for gene-regulatory and biochemical networks. BIOSILICO 2003,1(5):159–162.
Google Scholar - Ghosh R, Tomlin C: Lateral inhibition through delta-notch signaling: A piecewise affine hybrid model. Lect Notes Comput Sc 2001, 2034: 232–246.
Google Scholar - Ghosh R, Tomlin C: Symbolic reachable set computation of piecewise affine hybrid automata and its application to biological modelling: Delta-Notch protein signalling. Syst Biol 2004,1(1):170–183.
CAS Google Scholar - Gianchandani E, Joyce A, Palsson B, Papin J: Functional States of the Genome-Scale Escherichia coli Tran-scriptional Regulatory System. PLoS Comput Biol 2009,5(6):e1000403.
PubMed Central Google Scholar - Gianchandani E, Papin J, Price N, Joyce A, Palsson B: Matrix Formalism to Describe Functional States of Transcriptional Regulatory Systems. PLoS Comput Biol 2006,2(8):e101.
PubMed Central Google Scholar - Gilbert D, Heiner M: From Petri Nets to Differential Equations-An Integrative Approach for Biochemical Network Analysis. In Petri nets and other models of concurrency, ICATPN 2006. Volume 4024. Springer, Berlin Heidelberg; 2006:181–200.
Google Scholar - Goldenfeld N: Simple lessons from complexity. Science 1999,284(5411):87–89.
Google Scholar - Gomperts B, Kramer I, Tatham P: Signal transduction. Academic Press; 2009.
Google Scholar - Gonzalez P, Cardenas M, Camacho D, Franyuti A, Rosas O, Lagunez-Otero J: Cellulat: an agent-based intracellular signalling model. Biosystems 2003,68(2–3):171–185.
Google Scholar - Grant M, Mostov K, Tlsty T, Hunt C: Simulating Properties of in vitro Epithelial Cell Morphogenesis. PLoS Comput Biol 2006,2(10):e129.
PubMed Central Google Scholar - Gruenert G, Ibrahim B, Lenser T, Lohel M, Hinze T, Dittrich P: Rule-based spatial modeling with diffusing, geometrically constrained molecules. BMC Bioinf 2010,11(1):307.
Google Scholar - Grzegorczyk M, Husmeier D, Edwards K, Ghazal P, Millar A: Modelling non-stationary gene regulatory processes with a non-homogeneous Bayesian network and the allocation sampler. Bioinformatics 2008,24(18):2071–2078.
CAS Google Scholar - Gupta S, Bisht S, Kukreti R, Jain S, Brahmachari S: Boolean network analysis of a neurotransmitter signaling pathway. J Theor Biol 2007,244(3):463–469.
CAS Google Scholar - Hardy S, Robillard P: Petri net-based method for the analysis of the dynamics of signal propagation in signaling pathways. Bioinformatics 2008,24(2):209–217.
CAS Google Scholar - Harel D: Statecharts: A visual formalism for complex systems. Sci Comput Program 1987,8(3):231–274.
Google Scholar - Hartwell L, Hopfield J, Leibler S, Murray A: From molecular to modular cell biology. Nature 1999, 402: C47-C52.
CAS Google Scholar - Heijnen J: Approximative kinetic formats used in metabolic network modeling. Biotechnol Bioeng 2005,91(5):534–545.
CAS Google Scholar - Hlavacek W, Faeder J, Blinov M, Perelson A, Goldstein B: The complexity of complexes in signal transduction. Biotechnol Bioeng 2003,84(7):783–794.
CAS Google Scholar - Horn F, Jackson R: General mass action kinetics. Arch Ration Mech An 1972,47(2):81–116.
Google Scholar - Hucka M, Bergmann F, Hoops S, Keating S, Sahle S, Schaff J, Smith L, Wilkinson D: The Systems Biology Markup Language (SBML): Language Specification for Level 3 Version 1 Core. Nat Precedings 2010.
Google Scholar - Hucka M, Finney A, Sauro H, Bolouri H, Doyle J, Kitano H, Arkin A, Bornstein B, Bray D, Cornish-Bowden A, et al.: The Systems Biology Markup Language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 2003,19(4):524–531.
CAS Google Scholar - Hunt C, Ropella G, Park S, Engelberg J: Dichotomies between computational and mathematical models. Nat Biotechnol 2008,26(7):737–738.
CAS Google Scholar - Husmeier D: Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics 2003,19(17):2271–2282.
CAS Google Scholar - Iba H: Inference of differential equation models by genetic programming. Inf Sci 2008,178(23):4453–4468.
Google Scholar - Jamshidi N, Edwards J, Fahland T, Church G, Palsson B: Dynamic simulation of the human red blood cell metabolic network. Bioinformatics 2001,17(3):286–287.
CAS Google Scholar - Jamshidi N, Palsson B: Mass action stoichiometric simulation models: Incorporating kinetics and regulation into stoichiometric models. Biophys J 2010, 98: 175–185.
CAS PubMed Central Google Scholar - Jeong H, Tombor B, Albert R, Oltvai Z, Barabási A: The large-scale organization of metabolic networks. Nature 2000,407(6804):651–654.
CAS Google Scholar - John M, Ewald R, Uhrmacher A: A spatial extension to the π-Calculus. Electron Notes Theor Comput Sci 2008,194(3):133–148.
Google Scholar - Kaleta C, Centler F, Di Fenizio P, Dittrich P: Phenotype prediction in regulated metabolic networks. BMC Syst Biol 2008,2(1):37.
PubMed Central Google Scholar - Kaleta C, Richter S, Dittrich P: Using chemical organization theory for model checking. Bioinformatics 2009,25(15):1915–1922.
CAS PubMed Central Google Scholar - Kam N, Cohen I, Harel D: The Immune System as a Reactive System: Modeling T Cell Activation With Stat-echarts. In Proceedings of the IEEE 2001 Symposia on Human Centric Computing Languages and Environments (HCC'01). Stresa, Italy; 2001:15–22.
Google Scholar - Karlebach G, Shamir R: Modelling and analysis of gene regulatory networks. Nat Rev Mol Cell Biol 2008,9(10):770–780.
CAS Google Scholar - Kauffman K, Prakash P, Edwards J: Advances in flux balance analysis. Curr Opin Biotechnol 2003,14(5):491–496.
CAS Google Scholar - Kauffman S: Metabolic stability and epigenesis in randomly constructed genetic nets. J Theor Biol 1969,22(3):437–467.
CAS Google Scholar - Kier L, Bonchev D, Buck G: Modeling biochemical networks: a cellular-automata approach. Chem Biodivers 2005,2(2):233–243.
Google Scholar - Kim J, Varner J, Ramkrishna D: A hybrid model of anaerobic E. coli GJT001: Combination of elementary flux modes and cybernetic variables. Biotechnol Prog 2008,24(5):993–1006.
CAS Google Scholar - Kim S, Imoto S, Miyano S: Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief Bioinform 2003,4(3):228–235.
CAS Google Scholar - Kimura S, Ide K, Kashihara A, Kano M, Hatakeyama M, Masui R, Nakagawa N, Yokoyama S, Kuramitsu S, Kon-agaya A: Inference of S-system models of genetic networks using a cooperative coevolutionary algorithm. Bioinformatics 2005,21(7):1154–1163.
CAS Google Scholar - Kitano H: Systems Biology: A Brief Overview. Science 2002,295(5560):1662–1664.
CAS Google Scholar - Kitano H, Funahashi A, Matsuoka Y, Oda K: Using process diagrams for the graphical representation of biological networks. Nat Biotechnol 2005,23(8):961–966.
CAS Google Scholar - Klamt S, Saez-Rodriguez J, Lindquist J, Simeoni L, Gilles E: A methodology for the structural and functional analysis of signaling and regulatory networks. BMC Bioinf 2006,7(1):56.
Google Scholar - Klann M, Lapin A, Reuss M: Agent-based simulation of reactions in the crowded and structured intracellular environment: Influence of mobility and location of the reactants. BMC Syst Biol 2011,5(1):71.
PubMed Central Google Scholar - Koch I, Junker B, Heiner M: Application of Petri net theory for modelling and validation of the sucrose breakdown pathway in the potato tuber. Bioinformatics 2005,21(7):1219–1226.
CAS Google Scholar - Kohn K: Molecular interaction map of the mammalian cell cycle control and DNA repair systems. Mol Biol Cell 1999,10(8):2703–2734.
CAS PubMed Central Google Scholar - Kohn K, Aladjem M, Kim S, Weinstein J, Pommier Y: Depicting combinatorial complexity with the molecular interaction map notation. Mol Syst Biol 2006.,2(51):
- Kompala D, Ramkrishna D, Tsao G: Cybernetic modeling of microbial growth on multiple substrates. Biotech-nol Bioeng 1984,26(11):1272–1281.
CAS Google Scholar - Küffner R, Zimmer R, Lengauer T: Pathway analysis in metabolic databases via differential metabolic display (DMD). Bioinformatics 2000,16(9):825–836.
Google Scholar - Le Novère N, Hucka M, Mi H, Moodie S, Schreiber F, Sorokin A, Demir E, Wegner K, Aladjem M, Wimalaratne S, et al.: The systems biology graphical notation. Nat Biotechnol 2009,27(8):735–741.
Google Scholar - Lee J, Gianchandani E, Eddy J, Papin J: Dynamic Analysis of Integrated Signaling, Metabolic, and Regulatory Networks. PLoS Comput Biol 2008,4(5):e1000086.
Google Scholar - Lee J, Gianchandani E, Eddy J, Papin J: Dynamic analysis of integrated signaling, metabolic, and regulatory networks. PLoS Comput Biol 2008,4(5):e1000086.
Google Scholar - Li F, Long T, Lu Y, Ouyang Q, Tang C: The yeast cell-cycle network is robustly designed. Proc Natl Acad Sci USA 2004,101(14):4781–4786.
CAS PubMed Central Google Scholar - Li N, Verdolini K, Clermont G, Mi Q, Rubinstein E, Hebda P, Vodovotz Y: A patient-specific in silico model of inflammation and healing tested in acute vocal fold injury. PLoS ONE 2008,3(7):e2789.
PubMed Central Google Scholar - Liebermeister W, Klipp E: Bringing metabolic networks to life: convenience rate law and thermodynamic constraints. Theor Biol Med Model 2006,3(1):1–13.
Google Scholar - Lloyd C, Halstead M, Nielsen P: CellML: its future, present and past. Prog Biophys Mol Biol 2004,85(2–3):433–450.
CAS Google Scholar - Lollini P, Motta S, Pappalardo F: Discovery of cancer vaccination protocols with a genetic algorithm driving an agent based simulator. BMC Bioinf 2006,7(1):352.
Google Scholar - Luna A, Karac E, Sunshine M, Chang L, Nussinov R, Aladjem M, Kohn K: A formal MIM specification and tools for the common exchange of MIM diagrams: an XML-Based format, an API, and a validation method. BMC Bioinf 2011,12(1):167.
Google Scholar - Materi W, Wishart D: Computational systems biology in drug discovery and development: methods and applications. Drug Discov Today 2007,12(7–8):295–303.
CAS Google Scholar - Merelli E, Armano G, Cannata N, Corradini F, d'Inverno M, Doms A, Lord P, Martin A, Milanesi L, Moller S, et al.: Agents in bioinformatics, computational and systems biology. Brief Bioinform 2007,8(1):45–59.
CAS Google Scholar - Milner R: A calculus of communicating systems. Springer; 1980.
Google Scholar - Milner R, Parrow J, Walker D: A calculus of mobile processes. I. Inf Comput 1992,100(1):1–40.
Google Scholar - Morris M, Saez-Rodriguez J, Sorger P, Lauffenburger D: Logic-based models for the analysis of cell signaling networks. Biochemistry 2010,49(15):3216–3224.
CAS PubMed Central Google Scholar - Nagasaki M, Onami S, Miyano S, Kitano H: Bio-calculus: Its Concept and Molecular Interaction. In Genome informatics. Workshop on Genome Informatics. Volume 10. Universal Academic Press, Tokyo; 1999:133–143.
Google Scholar - Noble D: The rise of computational biology. Nat Rev Mol Cell Biol 2002,3(6):459–463.
Google Scholar - Nummela J, Julstrom B: Evolving petri nets to represent metabolic pathways. In Proceedings of the 2005 conference on genetic and evolutionary computation. ACM, New York; 2005:2133–2139.
Google Scholar - Orth J, Conrad T, Na J, Lerman J, Nam H, Feist A, Palsson B: A comprehensive genome-scale reconstruction of Escherichia coli metabolism -- 2011. Mol Syst Biol 2011.,7(1):
- Palsson B: Systems Biology: Properties of Reconstructed Networks. Cambridge University Press; 2006.
Google Scholar - Papin J, Hunter T, Palsson B, Subramaniam S: Reconstruction of cellular signalling networks and analysis of their properties. Nat Rev Mol Cell Biol 2005,6(2):99–111.
CAS Google Scholar - Patil K, Rocha I, Forster J, Nielsen J: Evolutionary programming as a platform for in silico metabolic engineering. BMC Bioinf 2005,6(1):308.
Google Scholar - Paun G: Computing with membranes. J Comput Syst Sci 2000,61(1):108–143.
Google Scholar - Pavlopoulos G, Wegener A, Schneider R: A survey of visualization tools for biological network analysis. Biodata mining 2008,1(1):12.
PubMed Central Google Scholar - Pearl J: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann Publishers Inc; 1988.
Google Scholar - Pedersen M, Plotkin G: A language for biochemical systems: Design and formal specification. T Comput Syst Biol XII 2010, 5945: 77–145.
Google Scholar - Pena J, Bjorkegren J, Tegnér J: Growing Bayesian network models of gene networks from seed genes. Bioin-formatics 2005,21(Suppl 2):224–229.
Google Scholar - Pérez-Jiménez M, Romero-Campero F: P systems, a new computational modelling tool for systems biology. T Comput Syst Biol VI 2006, 4220: 176–197.
Google Scholar - Petri C: Kommunikation mit Automaten. Ph.D. thesis, Rheinisch-Westfälisches Institut f. instrumentelle Mathematik an d. Univ; 1962.
Google Scholar - Pogson M, Holcombe M, Smallwood R, Qwarnstrom E: Introducing Spatial Information into Predictive NF-κB Modelling-An Agent-Based Approach. PLoS ONE 2008,3(6):e2367.
PubMed Central Google Scholar - Pogson M, Smallwood R, Qwarnstrom E, Holcombe M: Formal agent-based modelling of intracellular chemical interactions. Biosystems 2006,85(1):37–45.
CAS Google Scholar - Priami C, Ballarini P, Quaglia P: BlenX4Bio-BlenX for Biologists. In Computational Methods in Systems Biology. Springer, Berlin Heidelberg; 2009:26–51.
Google Scholar - Priami C, Quaglia P: Beta binders for biological interactions. In Computational Methods in Systems Biology. Springer, Berlin Heidelberg; 2005:20–33.
Google Scholar - Priami C, Regev A, Shapiro E, Silverman W: Application of a stochastic name-passing calculus to representation and simulation of molecular processes. Inf Process Lett 2001,80(1):25–31.
Google Scholar - Price N, Papin J, Schilling C, Palsson B: Genome-scale microbial in silico models: the constraints-based approach. Trends Biotechnol 2003,21(4):162–169.
CAS Google Scholar - Ravasz E, Somera A, Mongru D, Oltvai Z, Barabási A: Hierarchical organization of modularity in metabolic networks. Science 2002,297(5586):1551–1555.
CAS Google Scholar - Reddy V, Mavrovouniotis M, Liebman M: Petri Net Representations in Metabolic Pathways. In: Proceedings of the 1st International Conference on Intelligent Systems for Molecular Biology. AAAI/MIT Press, Menlo Park, CA; 1993:328–336.
Google Scholar - Reed J, Palsson B: Thirteen years of building constraint-based in silico models of Escherichia coli. J Bacteriol 2003,185(9):2692–2699.
CAS PubMed Central Google Scholar - Regev A, Panina E, Silverman W, Cardelli L, Shapiro E: BioAmbients: an abstraction for biological compartments. Theor Comput Sci 2004,325(1):141–167.
Google Scholar - Regev A, Silverman W, Shapiro E: Representing biomolecular processes with computer process algebra: π-calculus programs of signal transduction pathways. In Proceedings of Pacific Symposium of Biocomputing. World Scientific Press, Singapore; 2000.
Google Scholar - Regev A, Silverman W, Shapiro E: Representation and simulation of biochemical processes using the-calculus process algebra. In Pacific Symposium on Biocomputing. Volume 6. World Scientific Press, Singapore; 2001:459–470.
Google Scholar - Rizzi M, Baltes M, Theobald U, Reuss M: In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: II. mathematical model. Biotechnol Bioeng 1997,55(4):592–608.
CAS Google Scholar - Sachs K, Gifford D, Jaakkola T, Sorger P, Lauffenburger D: Bayesian network approach to cell signaling pathway modeling. Sci STKE 2002,2002(148):pe38.
Google Scholar - Sachs K, Perez O, Pe'er D, Lauffenburger D, Nolan G: Causal protein-signaling networks derived from multi-parameter single-cell data. Science 2005,308(5721):523–529.
CAS Google Scholar - Sackmann A, Heiner M, Koch I: Application of Petri net based analysis techniques to signal transduction pathways. BMC Bioinf 2006,7(1):482.
Google Scholar - Saez-Rodriguez J, Simeoni L, Lindquist J, Hemenway R, Bommhardt U, Arndt B, Haus U, Weismantel R, Gilles E, Klamt S, Schraven B: A logical model provides insights into T cell receptor signaling. PLoS Comput Biol 2007,3(8):e163.
PubMed Central Google Scholar - Savageau M, Voit E: Recasting nonlinear differential equations as S-systems: a canonical nonlinear form. Math Biosci 1987,87(1):83–115.
Google Scholar - Schilling C, Letscher D, Palsson B: Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J Theor Biol 2000,203(3):229–248.
CAS Google Scholar - Schlitt T, Brazma A: Current approaches to gene regulatory network modelling. BMC Bioinf 2007,8(Suppl 6):S9.
Google Scholar - Schuster S, Dandekar T, Fell D: Detection of elementary flux modes in biochemical networks: a promising tool for pathway analysis and metabolic engineering. Trends Biotechnol 1999,17(2):53–60.
CAS Google Scholar - Schuster S, Pfeiffer T, Moldenhauer F, Koch I, Dandekar T: Exploring the pathway structure of metabolism: decomposition into subnetworks and application to Mycoplasma pneumoniae. Bioinformatics 2002,18(2):351–361.
CAS Google Scholar - Segovia-Juarez J, Ganguli S, Kirschner D: Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J Theor Biol 2004,231(3):357–376.
CAS Google Scholar - Segrè D, Vitkup D, Church G: Analysis of optimality in natural and perturbed metabolic networks. Proc Natl Acad Sci USA 2002,99(23):15112–15117.
PubMed Central Google Scholar - Setty Y, Cohen I, Dor Y, Harel D: Four-dimensional realistic modeling of pancreatic organogenesis. Proc Natl Acad Sci USA 2008,105(51):20374–20379.
CAS PubMed Central Google Scholar - Shlomi T, Berkman O, Ruppin E: Regulatory on/off minimization of metabolic flux changes after genetic perturbations. Proc Natl Acad Sci USA 2005,102(21):7695–7700.
CAS PubMed Central Google Scholar - Shlomi T, Eisenberg Y, Sharan R, Ruppin E: A genome-scale computational study of the interplay between transcriptional regulation and metabolism. Mol Syst Biol 2007.,3(1):
- Shmulevich I, Dougherty E, Kim S, Zhang W: Probabilistic Boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002,18(2):261–274.
CAS Google Scholar - Simao E, Remy E, Thieffry D, Chaouiya C: Qualitative modelling of regulated metabolic pathways: application to the tryptophan biosynthesis. E coli Bioinformatics 2005,21(suppl 2):190–196.
Google Scholar - Smallbone K, Simeonidis E, Broomhead D, Kell D: Something from nothing - bridging the gap between constraint-based and kinetic modelling. FEBS J 2007,274(21):5576–5585.
CAS Google Scholar - Smallbone K, Simeonidis E, Swainston N, Mendes P: Towards a genome-scale kinetic model of cellular metabolism. BMC Syst Biol 2010,4(1):6.
PubMed Central Google Scholar - Sozinova O, Jiang Y, Kaiser D, Alber M: A three-dimensional model of myxobacterial aggregation by contact-mediated interactions. Proc Natl Acad Sci USA 2005,102(32):11308–11312.
CAS PubMed Central Google Scholar - Steggles L, Banks R, Shaw O, Wipat A: Qualitatively modelling and analysing genetic regulatory networks: a Petri net approach. Bioinformatics 2007,23(3):336–343.
CAS Google Scholar - Stephanopoulos G: Metabolic engineering. Biotechnol Bioeng 1998,58(2–3):119–120.
CAS Google Scholar - Steuer R, Junker B: Computational models of metabolism: Stability and regulation in metabolic networks. Volume 142. John Wiley & Sons, Inc; 2008.
Google Scholar - Takahashi K, Arjunan S, Tomita M: Space in systems biology of signaling pathways-towards intracellular molecular crowding in silico. FEBS Lett 2005,579(8):1783–1788.
CAS Google Scholar - Teusink B, Passarge J, Reijenga C, Esgalhado E, Van Der Weijden C, Schepper M, Walsh M, Bakker B, Van Dam K, Westerhoff H, et al.: Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur J Biochem 2000,267(17):5313–5329.
CAS Google Scholar - Thorne B, Bailey A, Peirce S: Combining experiments with multi-cell agent-based modeling to study biological tissue patterning. Brief Bioinform 2007,8(4):245–257.
CAS Google Scholar - Turing A: The Chemical Basis of Morphogenesis. Philos Trans R Soc Lond B Biol Sci 1952,237(641):37–72.
Google Scholar - Turner T, Schnell S, Burrage K: Stochastic approaches for modelling in vivo reactions. Comput Biol Chem 2004,28(3):165–178.
CAS Google Scholar - Tyson J, Chen K, Novak B: Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol 2003,15(2):221–231.
CAS Google Scholar - Varma A, Palsson B: Metabolic flux balancing: basic concepts, scientific and practical use. Nat Biotechnol 1994,12(10):994–998.
CAS Google Scholar - Visser D, Heijnen J: Dynamic simulation and metabolic re-design of a branched pathway using linlog kinetics. Metab Eng 2003,5(3):164–176.
CAS Google Scholar - Vohradsky J: Neural network model of gene expression. FASEB J 2001,15(3):846–854.
CAS Google Scholar - Von Neumann J, Burks A: Theory of self-reproducing automata. University of Illinois Press; 1966.
Google Scholar - Walker D, Southgate J: The virtual cell -- a candidate co-ordinator for 'middle-out' modelling of biological systems. Brief Bioinform 2009,10(4):450.
CAS Google Scholar - Weimar J: Cellular automata approaches to enzymatic reaction networks. Cellular Automata 2002, 2493: 294–303.
Google Scholar - Wiechert W: 13C metabolic flux analysis. Metab Eng 2001,3(3):195–206.
CAS Google Scholar - Wishart D, Yang R, Arndt D, Tang P, Cruz J: Dynamic cellular automata: an alternative approach to cellular simulation. Silico Biol 2005,5(2):139–161.
CAS Google Scholar - Wittmann D, Krumsiek J, Saez-Rodriguez J, Lauffenburger D, Klamt S, Theis F: Transforming Boolean models to continuous models: methodology and application to T-cell receptor signaling. BMC Syst Biol 2009,3(1):98.
PubMed Central Google Scholar - Wu J, Voit E: Hybrid modeling in biochemical systems theory by means of functional petri nets. J Bioinform Comput Biol 2009,7(1):107–34.
CAS Google Scholar - Wu J, Voit E: Integrative biological systems modeling: challenges and opportunities. Front Comput Sci Chin 2009,3(1):92–100.
Google Scholar - Wurthner J, Mukhopadhyay A, Peimann C: A cellular automaton model of cellular signal transduction. Comput Biol Med 2000,30(1):1–21.
CAS Google Scholar - Yartseva A, Klaudel H, Devillers R, Képès F: Incremental and unifying modelling formalism for biological interaction networks. BMC Bioinf 2007,8(1):433.
Google Scholar - Young J, Henne K, Morgan J, Konopka A, Ramkrishna D: Integrating cybernetic modeling with pathway analysis provides a dynamic, systems-level description of metabolic control. Biotechnol Bioeng 2008,100(3):542–559.
CAS Google Scholar - Zevedei-Oancea I, Schuster S: Topological analysis of metabolic networks based on Petri net theory. In Silico Biol 2003,3(3):323–345.
CAS Google Scholar - Zhang L, Athale C, Deisboeck T: Development of a three-dimensional multiscale agent-based tumor model: simulating gene-protein interaction profiles, cell phenotypes and multicellular patterns in brain cancer. J Theor Biol 2007,244(1):96–107.
CAS Google Scholar - Zorzenon dos Santos R, Coutinho S: Dynamics of HIV infection: A cellular automata approach. Phys Rev Lett 2001,87(16):168102.
CAS Google Scholar - Zou M, Conzen S: A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics 2005,21(1):71–79.
CAS Google Scholar
Acknowledgements
Research supported by grants SFRH/BD/35215/2007 and SFRH/BD/25506/2005 from the Fundação para a Ciência e a Tecnologia (FCT) and the MIT-Portugal Program through the project "Bridging Systems and Synthetic Biology for the development of improved microbial cell factories" (MIT-Pt/BS-BB/0082/2008).
Author information
Authors and Affiliations
- IBB-Institute for Biotechnology and Bioengineering/Centre of Biological Engineering, University of Minho, Campus de Gualtar, 4710-057, Braga, Portugal
Daniel Machado, Rafael S Costa, Eugénio C Ferreira & Isabel Rocha - Department of Informatics/CCTC, University of Minho, Campus de Gualtar, 4710-057, Braga, Portugal
Miguel Rocha - Department of Biological Engineering/Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, 02139, USA
Bruce Tidor
Authors
- Daniel Machado
- Rafael S Costa
- Miguel Rocha
- Eugénio C Ferreira
- Bruce Tidor
- Isabel Rocha
Corresponding author
Correspondence toDaniel Machado.
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Machado, D., Costa, R.S., Rocha, M. et al. Modeling formalisms in Systems Biology.AMB Expr 1, 45 (2011). https://doi.org/10.1186/2191-0855-1-45
- Received: 18 November 2011
- Accepted: 05 December 2011
- Published: 05 December 2011
- DOI: https://doi.org/10.1186/2191-0855-1-45