Geometric Centroid (original) (raw)

Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology

Alphabetical Index New in MathWorld

The centroid is center of mass of a two-dimensional planar lamina or a three-dimensional solid. The mass of a lamina with surface density function sigma(x,y) is

M=intintsigma(x,y)dA, (1)

and the coordinates of the centroid (also called the center of gravity) are

The centroid of a lamina is the point on which it would balance when placed on a needle. The centroid of a solid is the point on which the solid would "balance."

The geometric centroid of a region can be computed in the Wolfram Language using RegionCentroid[_reg_].

The centroid of a set of n point masses m_i located at positions x_i is

x^_=(sum_(i=1)^(n)m_ix_i)/(sum_(i=1)^(n)m_i), (4)

which, if all masses are equal, simplifies to

x^_=(sum_(i=1)^(n)x_i)/n. (5)

For a closed lamina of uniform density with boundary specified by (x(t),y(t)) for t in [t_0,t_1] and the lamina on the left as the curve is traversed,Green's theorem can be used to compute the centroid as

The positions of the geometric centroid of a planar non-self-intersecting polygon with vertices (x_1,y_1), ..., (x_n,y_n) are

where A is the polygon area and x_(n+1)=x_1 and y_(n+1)=y_1 (Bourke 1988, Nürnberg 2013).

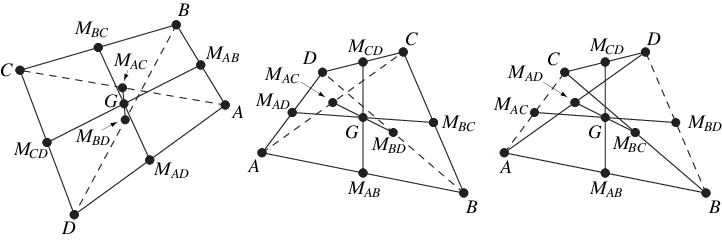
QuadrilateralCentroid

The centroid of the vertices of a quadrilateral occurs at the point of intersection of the bimedians (i.e., the lines M_(AB)M_(CD) and M_(AD)M_(BC) joining pairs of opposite midpoints) (Honsberger 1995, pp. 36-37). In addition, it is the midpoint of the line M_(AC)M_(BD) connecting the midpoints of the diagonals AC and BD (Honsberger 1995, pp. 39-40).

Given an arbitrary hexagon, connecting the centroids of each consecutive three sides gives the so-called centroid hexagon, a hexagon with equal and parallel sides (Wells 1991).

The centroid of a semicircle of radius R is given by

x^_=(2R)/pi. (10)

The centroids of several common laminas bounded by the following curves along the nonsymmetrical axis are summarized in the following table.

In three dimensions, the mass of a solid with density function rho(x,y,z) is

M=intintintrho(x,y,z)dV, (11)

and the coordinates of the center of mass are

See also

Centroid Hexagon, Circumcenter of Mass, Pappus's Centroid Theorem,Polygon Centroid, Polyhedron Centroid

Explore with Wolfram|Alpha

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 132, 1987.Bourke, P. "Calculating the Area and Centroid of a Polygon." July 1988. http://paulbourke.net/geometry/polygonmesh/.Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., 1995.Kern, W. F. and Bland, J. R. "Center of Gravity." §39 in Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 110, 1948.McLean, W. G. and Nelson, E. W. "First Moments and Centroids." Ch. 9 in Schaum's Outline of Theory and Problems of Engineering Mechanics: Statics and Dynamics, 4th ed. New York: McGraw-Hill, pp. 134-162, 1988.Nürnberg, R. "Calculating the Area and Centroid of a Polygon in 2D." 2013. https://www.ma.imperial.ac.uk/~rn/centroid.pdf.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 53-54, 1991.

Referenced on Wolfram|Alpha

Geometric Centroid

Cite this as:

Weisstein, Eric W. "Geometric Centroid." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/GeometricCentroid.html

Subject classifications