Emergent patterns of growth controlled by multicellular form and mechanics (original) (raw)

Abstract

Spatial patterns of cellular growth generate mechanical stresses that help to push, fold, expand, and deform tissues into their specific forms. Genetic factors are thought to specify patterns of growth and other behaviors to drive morphogenesis. Here, we show that tissue form itself can feed back to regulate patterns of proliferation. Using microfabrication to control the organization of sheets of cells, we demonstrated the emergence of stable patterns of proliferative foci. Regions of concentrated growth corresponded to regions of high tractional stress generated within the sheet, as predicted by a finite-element model of multicellular mechanics and measured directly by using a micromechanical force sensor array. Inhibiting actomyosin-based tension or cadherin-mediated connections between cells disrupted the spatial pattern of proliferation. These findings demonstrate the existence of patterns of mechanical forces that originate from the contraction of cells, emerge from their multicellular organization, and result in patterns of growth. Thus, tissue form is not only a consequence but also an active regulator of tissue growth.

Keywords: morphogenesis, pattern formation, micropatterning, cytoskeleton, mechanotransduction

Spatial patterning of the behaviors of individual cells generates global changes in tissue architecture that drive morphogenesis (1, 2). Several morphogenic mechanisms likely collaborate to direct tissue form, including local changes in cell adhesion, cell shape, and cell proliferation. Qualitative and quantitative differences in cellular adhesiveness can lead to the segregation and layering of tissues (3); ordered changes in cell shape appear to direct gastrulation (4), epithelial folding (5), and tubulogenesis (6); and differentials in cell growth can locally alter tissue form (7, 8). Although the molecular basis for these behaviors has been under intense study, the mechanical nature of morphogenesis also has been recognized since the late 19th century (9): Specific patterns of cellular growth (in which some cells proliferate but other cells do not) create mechanical stresses that help drive the buckling, budding, pinching, and branching processes of morphogenesis. Complex forms, such as the regular fractal structure of the branching organs, can thus arise from simple embryonic sheets (reviewed in refs. 10 and 11).

What causes such localized patterns is one of the central puzzles of biology and has fascinated scientists from numerous disciplines for at least two millennia (12). Perhaps most well described are concentration gradients of diffusible factors, known as morphogens, which can drive spatial patterns of cellular behaviors (13–15). In addition to soluble factors, adhesion to extracellular matrix and mechanical forces also are known to modulate cell functions, including proliferation (10, 16, 17).

Although spatial patterning of these cues can certainly explain spatial patterning of cellular behaviors, it remains unclear what initiates or maintains patterns. One theory suggests that these gradients (e.g., of morphogens) are entirely driven by prespecified genetic programs. A more tractable alternative suggests that the highly ordered architectures of mature tissues and the evolution of ever more complex structures from simpler ones arise as a result of feedback mechanisms, whereby tissue form regulates patterned growth to ensure that certain structures are encouraged and elaborated upon while others are eliminated (18). Indeed, in some instances, it has been observed that changes in tissue form precede rather than follow changes in proliferation. During lung bud outgrowth, bud formation precedes the proliferation of cells in the bud (19). Similarly, capillary sprouting often precedes angiogenic proliferation (20). Although the spatial organization of cells in theory may give rise to spatial templates of soluble and mechanical stimuli that could feed back to sustain patterns of proliferation (21, 22), such feedback has never been demonstrated experimentally. We therefore set out to ask whether the spatial organization of a population of cells could initiate patterns of spatial asymmetries in cellular proliferation.

Here, we demonstrate that gradients of mechanical stresses generated within multicellular aggregates and organized by aggregate geometry can act in a morphogenic capacity to induce spatial patterning of cellular proliferation. These data suggest that tissue form and mechanics are deeply entangled within the causal web of structure–function relationships that drive developmental processes and indicate that our models of morphogenesis should take into account tissue geometry and mechanical stress as inductive cues.

Materials and Methods

Cell Culture and Proliferation Assay. Bovine pulmonary artery endothelial cells were cultured as described in ref. 23. Normal rat kidney epithelial cells (American Type Culture Collection no. CRL-1571) were cultured in DMEM supplemented with 10% FCS/100 units/ml penicillin/100 μg/ml streptomycin. Cells were seeded on substrates, allowed to form a confluent monolayer, exposed to BrdUrd-containing growth media for 48 h, and fixed and stained for BrdUrd incorporation as described in ref. 23.

Substrate Fabrication. Micropatterned substrata containing fibronectin-coated islands were fabricated as described in ref. 24. Briefly, glass coverslips were coated by electron beam evaporation with 2.0 nm of Ti, followed by 15 nm of Au. Elastomeric stamps containing a relief of the desired pattern were inked in an ethanolic solution of 2 mM hexadecanethiol (Sigma), dried under nitrogen, and placed in conformal contact for 2 s with the Au-coated coverslips. The unstamped regions of the coverslips were rendered nonadhesive by immersing them in an ethanolic solution of 2 mM tri(ethylene glycol)-terminated alkanethiol (Prochimia, Golansk, Poland) for 1 h. Substrata were rinsed, sterilized in ethanol, and incubated in 25 μg/ml fibronectin in PBS for 2 h.

Reagents. Recombinant adenoviruses encoding RhoAV14 and human vascular endothelial (VE)-cadherin lacking the β-catenin binding domain (VEΔ) were prepared as described in refs. 23 and 25. Recombinant adenovirus encoding human E-cadherin lacking the β-catenin-binding domain (the N-terminal 35 amino acids) (EΔ) was PCR-amplified from pcDNA3-hE-cadherin [a generous gift from C. Gottardi (Northwestern University, Chicago) and B. Gumbiner (University of Virginia, Charlottesville)] by using the primers 5′-GAGGCGGCCGCACCATGGGCCCTTGGAGCCGC-3′ and 5′-GAGCTCGAGTCAGGAGCTCAGACTAGCAGC-3′ and cloned into pShuttle-IRES-hrGFP-1 (AdEasy XL system, Stratagene) by using NotI and XhoI restriction sites. The shuttle vector was linearized with Pme I and transformed into BJ5183-AD-1-competent cells to generate recombinant adenoviral plasmids, which were then purified and transfected into HEK293 cells. To infect monolayers of cells, a solution of recombinant adenovirus was mixed with culture medium, and cells were exposed to the virus with a multiplicity of 10–100 viral particles per cell for 3 h. Cells were then washed and exposed to BrdUrd-containing medium. Under these conditions, >95% of the cells were infected. To disrupt tension, cells were treated with 10 μM Y-27632 (Calbiochem), 10 μM ML-7 (Calbiochem), or 5 μM blebbistatin (Tocris Cookson, Ellisville, MO) at the time of exposure to BrdUrd.

Immunofluorescence Microscopy, Image Processing, and Statistical Analysis. Samples were fixed and stained as described in ref. 23 and then visualized by using an Orca charge-coupled device camera (Hamamatsu, Middlesex, NJ) attached to an inverted Nikon TE200 microscope. Images were obtained with ip lab 3.0. Total cumulative data were presented by stacking images from 50 samples, obtaining relative pixel frequency with ip lab, and color-coding the stacked image by using photoshop (Adobe Systems, San Jose, CA). Experiments were conducted at least three times; statistical significance of the individual data sets was calculated by using Student's t test and is compiled in Fig. 5, which is published as supporting information on the PNAS web site.

Modeling. A three-dimensional finite-element model of the cell monolayer was constructed (with abaqus 6.3) with two components, a contractile layer and a passive layer (with a fixed bottom surface), by using physical parameters reported previously (26–28). Computationally, contractility was introduced by prescribing a thermal strain. The contractile layer (20-μm height; other dimensions prescribed as indicated) was treated as an isotropic elastic material with a Young's modulus of 500 Pa, a Poisson's ratio of 0.499 (incompressible), a thermal conductivity of 10 W·m–1·K–1, and a coefficient of expansion of 0.05 K–1. The passive layer (4-μm height) was treated as an isotropic elastic material with values of 100 Pa and 0.499 for the Young's modulus and Poisson's ratio, respectively. To simulate monolayer contraction, isotropic zero-stress length was reduced in the contractile layer by using a temperature drop of 5 K. All simulations, with the exception of the two-dimensional “pyramid,” were three-dimensional, with finite-element mesh density corresponding to a spacing of 4–10 μm per node. Stress and strain tensors were calculated throughout the structures. The maximum principal stress at the bottom fixed surface was reported; similar patterns were observed in von Mises stress as well. Convergence of results was confirmed by using multiple mesh densities and values for mechanical properties of materials.

Posts. Microfabricated post array detectors were used to measure traction forces as described in ref. 29. Briefly, post arrays (3-μm diameter, 11-μm height, and 6-μm spacing) were micropatterned with fibronectin to form the indicated monolayer geometries. Cells were seeded onto the substrata and allowed to form and maintain a confluent monolayer for several days. Samples were fixed, stained, and visualized under confocal microscopy. Over a representative patch of cells, a series of eight captured images was taken. Over each field of view, quantification of forces was performed as described in ref. 29. The traction fields were then stitched together and shown as a single vector or magnitude map. Central vectors were excluded from the vector map for clarity; the sum of traction forces was found to be within the expected experimental error.

Results and Discussion

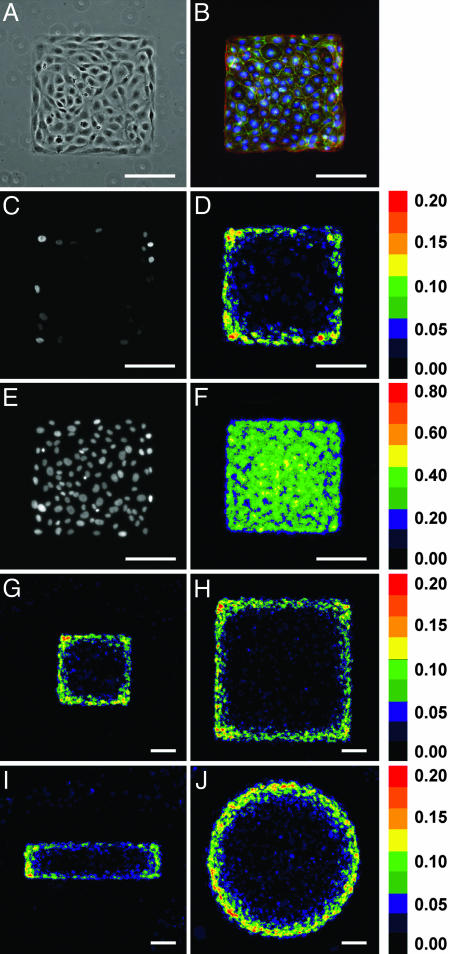
To address whether multicellular form could direct patterns of proliferation, we used a microfabrication technique to generate microcultures of defined shape and size (24). Endothelial cells were attached and spread on adhesive islands micropatterned onto glass coverslips, and, during a period of several days, they proliferated uniformly over the adhesive surface to form a confluent monolayer conforming to the shape of the island (Fig. 1 A and B). The proliferation rate decreased to nearly undetectable levels after cells reached confluence. However, around the perimeter of the cellular sheet, proliferation persisted for an additional several weeks, as indicated by continued DNA synthesis (Fig. 1_C_). To represent this effect statistically, we stacked images of 50 samples in registration such that the stacked image showed the spatial distribution of the rate of proliferation across these samples (Fig. 1_D_). This analysis not only confirmed that cells on the edges of the islands proliferated more than cells in the center but revealed that corners of the square islands proliferated more than edges (Fig. 5). Staining all nuclei (Fig. 1_E_) and similarly stacking images (Fig. 1_F_) demonstrated a uniform distribution of cells within the geometrically constrained monolayers.

Fig. 1.

Fig. 1.

Method for detecting spatial variations in proliferation in sheets of cells. (A) Phase contrast image of cells on a small (250-μm edge) square island. (B) Fluorescence image of monolayer showing actin (red), VE-cadherin (green), and nuclei (blue). (C) Fluorescence image of cell proliferation (BrdUrd incorporation) in one island of cells. (D) Colorimetric stacked image of cell proliferation. A pixel value of 0.20 indicates that 20% of cells at that location proliferated. (E) Fluorescence image of all nuclei (stained with DAPI) in one island of cells. (F) Colorimetric stacked image of all nuclei showing a uniform distribution of cells in the monolayers. The pattern of proliferation is defined by the geometry of the island of cells. (G_–_J) Colorimetric stacked images of cell proliferation in small (250-μm edge) square (G), large (500-μm edge) square (H), small (125 × 500 μm) rectangular (I), and large (564-μm diameter) circular (J) islands. Statistical analysis is presented in Fig. 5. (Scale bars, 100 μm.)

Interestingly, the geometry of the monolayers appeared to influence the resulting patterns of localized proliferation. Increasing the area of square islands increased the magnitude of proliferation at both the edge and the corners (from 2.2% to 3.4% per island per mm of edge), indicating that the proliferative effect scales with the size of the island (Fig. 1 G and H). When cells were cultured on rectangular islands, short edges were found to proliferate more than long edges (Fig. 1_I_). Culturing monolayers on large circular islands with a radius of curvature much greater than the cellular length scale resulted in a statistically significant uniformly high rate of proliferation around the periphery of the circle (Figs. 1_J_ and 5). Together, these findings suggested that stable foci of proliferation could be maintained at the edges of monolayers and that the pattern and rate of proliferation depended on the geometry of the monolayer.

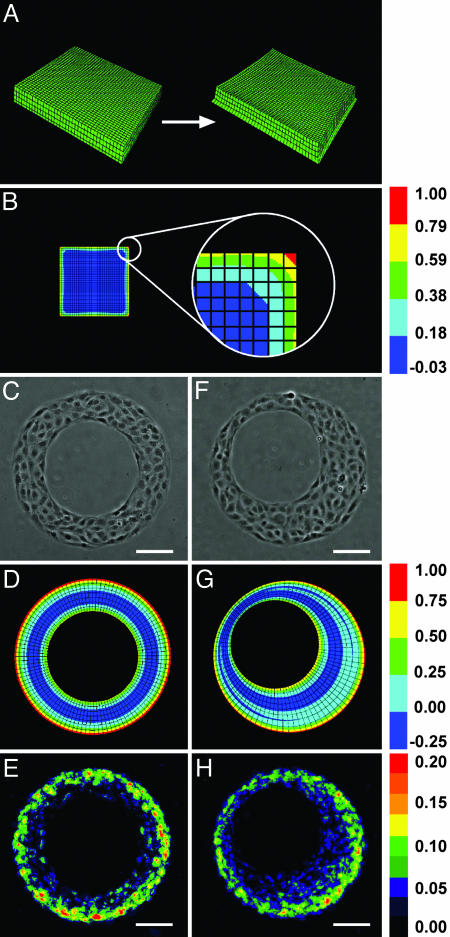
The increased proliferation at the edge of the monolayers might have been either induced directly by these edges (for example, from decreased cell–cell adhesion relative to the cells in the interior of the monolayer) or propagated outward to the edge from the bulk tissue mass (for example, from contractile tension). However, the differences in magnitude of proliferation from geometry to geometry observed in Fig. 1 G_–_J are inconsistent with direct signaling from the edge itself. The significantly lower proliferation along the long edges of rectangles as compared with squares with the same edge length suggests that the proliferative signal emanates from the bulk tissue rather than the edges. To examine this possibility further, we explored whether patterns of mechanical stress could be generated by the contraction of cells within a monolayer. We first constructed a computational model by using the finite-element method (FEM) to simulate a sheet of cells contracting against a matrix-coated substratum (Fig. 2_A_). A contractile layer was connected onto a thin, compliant passive layer with a fixed bottom surface. We simulated contraction by decreasing the resting length of the contractile layer (equivalent to generating isotropic contractile stress) and computed the resulting maximum principal stress produced by the monolayer against the underlying fixed surface. For a square monolayer, contraction of the simulated cellular sheet increased traction stress at the edges relative to the interior and produced a concentrated maximum at the corners (Fig. 2_B_). In circular and rectangular monolayers, patterns of traction stress predicted by the FEM similarly corresponded to the observed patterns of proliferation and were relatively insensitive to the parameters used to define the model (Fig. 6, which is published as supporting information on the PNAS web site).

Fig. 2.

Fig. 2.

The pattern of proliferation corresponds to predicted local mechanical stresses. (A) FEM mesh of contracting monolayer. (B) FEM calculations of relative maximum principal tractional stress exerted by cells in a small square island. (C_–_E) Cells cultured on annulus. Shown are phase contrast (C), FEM results (D), and colorimetric stacked image of cell proliferation (E). (F_–_H) Cells cultured on asymmetric annulus. Shown are phase contrast (F), FEM results (G), and colorimetric stacked image of cell proliferation (H). Outer diameter is 346 μm; inner diameter is 200 μm; center of asymmetric hole is 30 μm from the center of the island. Statistical analysis is presented in Fig. 5. (Scale bars, 100 μm.)

These computational data suggested the possibility that the organization of cells defines patterns of mechanical stresses that, in turn, may drive the observed patterns of proliferation. To test this hypothesis, we asked whether proliferation would decrease in geometries having edges with decreased predicted stress. One such geometry is an annulus, where contractile activity is predicted by the FEM to be lower at the concave inner edge formed by the hole than at the convex outer edge of the monolayer (Fig. 2 C and D). Consistent with the predicted distribution of mechanical stress, the proliferation rate of cells surrounding the inner edge of the annulus was low compared with that of cells at the outer edge (Fig. 2_E_). In annuli with eccentrically placed holes, the predicted mechanical stresses varied along the perimeter of the outer edge, with maxima farthest from the hole (Fig. 2_F_; see also Fig. 7, which is published as supporting information on the PNAS web site). In this geometry, proliferation remained restricted to the outer edge but exhibited asymmetry that again mirrored the predicted patterns of mechanical stress (Fig. 2 G and H). Thus, even in the absence of any local difference in edge geometry or curvature (comparing symmetric and asymmetric annuli), foci of proliferation emerge. These foci appear to occur in regions of greatest traction stresses generated by the cellular sheet.

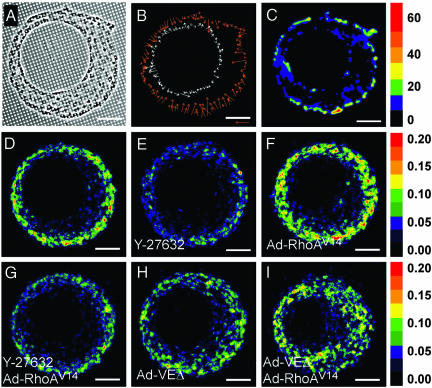
Our mechanical model predicts that the geometry of a multicellular structure defines patterns of mechanical stress. To test these predictions experimentally, we cultured monolayers of cells on an elastomeric force sensor array (29) to directly measure traction forces within the asymmetric annulus. The sensor contains a high-density array of vertical microneedles that act as cantilevers (Fig. 3_A_); the deflection of each cantilever reports the force exerted by cells at that position with subcellular resolution. Plotting the magnitude and direction of traction forces generated at the edges of the annulus confirmed that cells on the outer edge exerted significantly more force than did cells on the inner edge and that asymmetric placement of the hole caused the predicted asymmetry in the distribution of force (Fig. 3 B and C). Cells on the rectangular geometry also produced the predicted patterns of force, with stresses higher along the short edge than along the long edge and highest at the corners. Therefore, the geometry of the monolayer directly affected the pattern of forces exerted and experienced by the cells; this pattern of tension can be generated from a homogeneous, isotropic contraction of the monolayer.

Fig. 3.

Fig. 3.

Mechanical forces generated by cytoskeletal contraction cause the patterns of proliferation. (A_–_C) Cells cultured on elastomeric force sensor array. Shown are phase contrast image (A), vector map of traction forces measured at edges (B), and colorimetric map of traction forces measured over the entire monolayer (nN) (C). (D_–_I) Colorimetric images of cell proliferation for cells cultured on asymmetric annulus and left untreated (D), treated with Y-27632 (E), infected with Ad-RhoAV14 (F), simultaneously treated with Y-27632 and infected with Ad-RhoAV14 (G), infected with Ad-VEΔ (H), or coinfected with Ad-VEΔ and Ad-RhoAV14 (I). Reference arrow in B indicates 50 nN of force. Statistical analysis is presented in Fig. 5. (Scale bars, 100 μm.)

To investigate directly whether this tension within the monolayer is responsible for the corresponding pattern of proliferation, we then altered cellular mechanics by using pharmacological and molecular approaches. Mechanical stresses within monolayers arise from tension generated by the actomyosin cytoskeleton, which is regulated in part by signaling through RhoA, its downstream effector Rho kinase (ROCK), and myosin light chain kinase (30, 31). Decreasing contractile tension throughout the monolayer by inhibiting ROCK with Y-27632 (32) (Fig. 3 D and E), inhibiting myosin light chain kinase with ML-7 (33) (Fig. 8, which is published as supporting information on the PNAS web site), or inhibiting nonmuscle myosin II ATPase activity with blebbistatin (34) (Fig. 8) significantly reduced the gradient of proliferation at the outer edge of the asymmetric annulus at concentrations that did not affect proliferation of cells at submonolayer densities. Conversely, increasing cellular tension throughout the monolayer by using a recombinant adenovirus to express constitutively active RhoAV14 (Ad-RhoAV14) (29) increased and enhanced the gradient of proliferation in the asymmetric annulus (Fig. 3_F_); this increase was abrogated by simultaneous addition of either contractility inhibitor (Y-27632 or blebbistatin) to the cells (Figs. 3_G_ and 8). Together, these findings indicate that cytoskeletal tension is directly involved in generating the patterns of proliferation in the monolayers.

To cooperate and contract as a mechanically coupled monolayer, individual cells must transmit tension to and from their neighbors, likely through cadherin-mediated intercellular adhesion (30, 31). To disrupt the transfer of tension between cells, we used an adenovirus encoding a cytoplasmic-deletion mutant of VE-cadherin (Ad-VEΔ) that acts as a dominant negative by blocking the formation of cadherin-mediated adhesions between cells, inhibiting the cell–cell localization of β-catenin, and blocking connection to the actin cytoskeleton (23, 35). Expressing VEΔ in our endothelial cells inhibited intercellular adhesive interactions, as expected, and substantially reduced the gradient of proliferation in the asymmetric annulus (Fig. 3_H_) but had no effect on the proliferation of cells at submonolayer densities. Coinfection with Ad-RhoAV14 and Ad-VEΔ, causing increased contraction while mechanically decoupling the cells, induced uniform rather than patterned proliferation over the entire monolayer (Fig. 3_I_). Although these findings were initially demonstrated in endothelial cells, monolayers of epithelial cells also exhibited the mechanically templated spatial patterning of proliferation (Fig. 9, which is published as supporting information on the PNAS web site). Together, these data demonstrate that cytoskeletal tension propagated through the sheet of cells regulates the emergent pattern of proliferation.

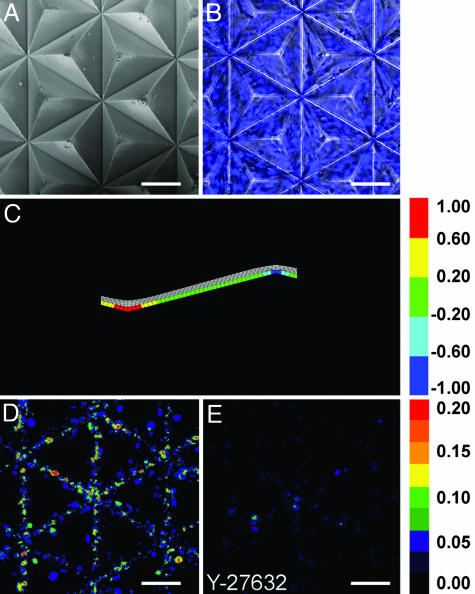
These findings suggest that mechanical stresses can trigger patterned growth at the edges of cellular sheets, as seen during wound healing (36) and development (37, 38), but patterns of proliferation also exist in many tissues that lack an edge [for example, in angiogenesis (39), epithelial branching morphogenesis (11), intestinal crypt renewal (40), and neural tube morphogenesis (41)]. Is the presence of an edge required for the mechanically induced proliferation, or is it simply one of several mechanisms that concentrates gradients of stress? That is, could these edge-free patterns also be driven in part by multicellular mechanics? To increase stress within monolayers that lack edges, we cultured sheets of cells on an undulating surface of tetrahedral pyramids (Fig. 4 A and B). In this geometry, the cells in the valleys between tetrahedrons were predicted by the FEM to experience more tractional stress than those at the peaks (Fig. 4_C_). Proliferation in the monolayer was concentrated in the valleys, again mirroring the predicted pattern of mechanical stresses (Fig. 4_D_). Inhibition of contractility generated in the monolayer eliminated the focal increase in proliferation in the valleys (Fig. 4_E_). These results indicate that patterns of stress, rather than simply the presence or absence of edges, regulate growth.

Fig. 4.

Fig. 4.

Patterned proliferation corresponds to mechanical stresses in cellular aggregates that lack edges. (A_–_E) Monolayer of cells on pyramidal array. Shown are scanning electron microscopy of substratum surface (A), phase contrast merged with fluorescence image of nuclei (B), FEM results (C), colorimetric stacked image of cell proliferation (D), and colorimetric image of cell proliferation when treated with Y-27632 (E). Tetrahedrons are pointed upward. Statistical analysis is presented in Fig. 5. (Scale bars, 100 μm.)

Spatial patterning of cellular behavior is a critical feature of both the developing embryo and the adult. Although there are a number of morphogenic hypotheses, such patterning is largely thought to be genetically prespecified by means of the coordinated expression of numerous extracellular morphogens (15, 42). Here, we show that the long-range transmission and local concentration of mechanical stresses dictated by the spatial organization of cells also provide an important mechanism for templating patterns of cell proliferation: Through mechanics, cells continuously sense the geometry of the tissue mass, as well as their location within it, and respond accordingly by changing tissue geometry. The concept that forces distributed by cells within multicellular tissues feed back to control growth locally and thus drive morphogenic patterning has been proposed by others (21, 43, 44), but, to our knowledge, this controversial idea had never before been experimentally demonstrated. Mechanical force transmitted across cells and matrix during morphogenesis (45) may have several purposes: not only to physically sculpt tissue form (9) but also to biochemically drive the changes in patterns of cellular proliferation and function.

It is well appreciated that mechanical stresses forge the patterns that define the nonliving natural world (1, 46). Our data and recent theoretical studies (18) support a similar role for mechanical stress in the morphogenesis of biological tissue and suggest a need for further work to determine the relative roles of mechanical and chemical gradients in patterning the dynamic behaviors of individual cells during the evolution of tissue form in vivo. Indeed, patterns of mechanical cues are present throughout life and may affect many developmental processes in addition to proliferation. The shear forces of fluid flow were recently shown to modulate the expression of developmental patterning genes in endothelial cells, including TIE-2, Ang-1, and Ang-2 (47, 48). In the Drosophila embryo, patterns of mechanical stress have also recently been implicated in the spatial regulation of developmental gene expression (49) and the migrations of sheets of cells during dorsal closure (50). These multiple causal linkages among growth, mechanics, and tissue form highlight the importance of epigenetic factors in tissue morphogenesis and suggest that spatial organization may be not only a product of development but also an initiating template for it.

Supplementary Material

Supporting Figures

Acknowledgments

We thank B. Harris for assistance with scanning electron microscopy and D. Pirone, M. Shockley, A. Popel, J. Tien, and G. Whitesides for insightful discussions. This work was supported in part by grants from the National Institutes of Health, the Whitaker Foundation, the Defense Advanced Research Projects Agency, and the Army Research Office Multidisciplinary University Research Initiative. C.M.N., R.P.J., and J.L.T. acknowledge financial support from the Whitaker Foundation; W.F.L. was supported by the National Science Foundation; and N.J.S. was supported by a Ruth L. Kirschstein National Research Service Award.

Author contributions: C.M.N. and C.S.C. designed research; C.M.N., R.P.J., J.L.T., W.F.L., N.J.S., and A.A.S. performed research; C.M.N. and C.S.C. analyzed data; and C.M.N. and C.S.C. wrote the paper.

This paper was submitted directly (Track II) to the PNAS office.

Abbreviations: VE, vascular endothelial; FEM, finite-element method.

See Commentary on page 11571.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Figures