Recent developments in phasing and structure refinement for macromolecular crystallography (original) (raw)
. Author manuscript; available in PMC: 2010 Oct 1.
Published in final edited form as: Curr Opin Struct Biol. 2009 Aug 21;19(5):566–572. doi: 10.1016/j.sbi.2009.07.014
Summary
Central to crystallographic structure solution is obtaining accurate phases in order to build a molecular model, ultimately followed by refinement of that model to optimize its fit to the experimental diffraction data and prior chemical knowledge. Recent advances in phasing and model refinement and validation algorithms make it possible to arrive at better electron density maps and more accurate models.
Introduction
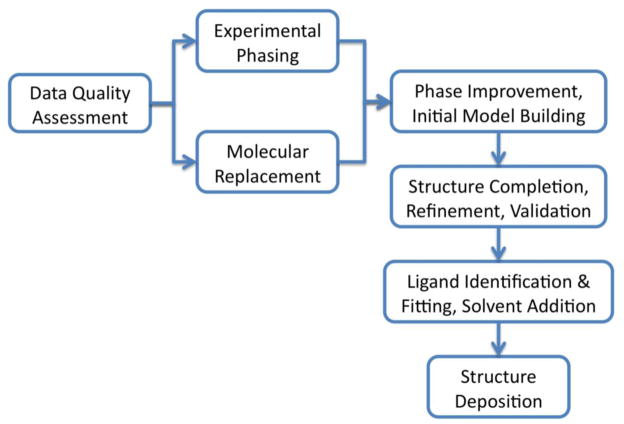
X-ray crystallography is one of the most content-rich methods available for providing high resolution information about biological macromolecules. The goal of the crystallographic experiment is to obtain a three-dimensional map of the electron density in the macromolecular crystal. Given sufficient resolution this map can be interpreted to build an atomic model of the macromolecule (Figure 1 summarizes the process of crystallographic structure solution). To calculate the distribution of electron density in the crystal requires a Fourier synthesis using complex numbers derived from the diffraction experiment. Each complex number is composed of a diffraction amplitude and an associated phase (i.e. the magnitude and direction of a vector in a complex plane). However, experimentally it is only possible to measure the amplitude; the phase information is lost. Therefore, one of the central problems in the crystallographic experiment is the indirect derivation of phase information. Multiple methods have been developed to obtain phase information. In the article we review recent advances in the computational aspects of phase determination.
Figure 1.
Overview of the crystallographic structure solution process for macromolecules.
After a map has been obtained and an atomic model built it is necessary to optimize the model with respect to the experimental diffraction data and prior chemical knowledge, achieved by multiple cycles of refinement and model rebuilding. Efficient and accurate optimization of the atomic model is desirable in order to rapidly generate the best models for biological interpretation. We review the recent advances in the computational methods used to optimize atomic models with respect to X-ray diffraction data.
Experimental phase determination
Experimental, and associated computational, methods have been developed to obtain phase information for structures with no prior structural information. These isomorphous replacement and anomalous scattering methods rely on information that can be derived from small differences between diffraction datasets. The first step in both methods is the location of the heavy atoms or anomalous scatterers, generally termed the substructure, in the crystallographic asymmetric unit.
Substructure location
The location of heavy atoms in isomorphous replacement or the location of anomalous scatterers was traditionally performed by manual inspection of Patterson maps. However, in recent years labeling techniques such as seleno-methionyl incorporation have become widely used. This leads to an increase in the number of atoms to be located, rendering manual interpretation of Patterson maps extremely difficult. As a result automated heavy atom location methods have proliferated, including automated Patterson methods [1]. The most successful substructure location methods today are dual-space recycling algorithms [2,3,4,5]. These algorithms are characterized by the use of Fourier transforms to switch between crystal (direct) space and diffraction (reciprocal) space, with a variety of modification procedures working in both spaces. The dual-space recycling procedures are designed to converge to a self-consistent state. The likelihood that this is a correct solution depends on the quality of the experimental data and the size of the problem. Some algorithms combine Patterson and dual-space recycling methods [2,3]. In the recent work of Dumas and van der Lee [5], the charge flipping method of Oszlányi & Süto [6**] is used instead of the more traditional squaring method [7] underlying the direct methods steps in the other dual-space recycling programs. The new charge-flipping approach is promising and appears to be competitive.
Phasing
After successful substructure location complex structure factors for the substructure can be calculated. This information can be used to bootstrap the calculation of phase information for the whole contents of the asymmetric unit in a process termed phasing. In macromolecular crystallography a thorough statistical treatment of errors is crucial. The magnitudes of structure factors are measured relatively accurately but the phases are not measured directly at all. This leads to combinations of experimental and model errors that are not simple Gaussian distributions. In the phasing step, maximum-likelihood based methods (MLPHARE [8], CNS [9], SHARP [10]), have for some time been the most effective techniques for modeling the crystallographic experiment.
The development of tractable likelihood targets for experimental phasing generally requires some assumptions to be made about the independence of sources of error [11]. However, the case of single-wavelength anomalous diffraction (SAD) can be handled without such assumptions [12]. SAD phasing has recently undergone a renaissance, due to a combination of more sensitive detectors measuring data more precisely, the absence of non-isomorphism, and SAD’s reduced problems with radiation damage compared to MAD phasing [13]. However, in cases of weak anomalous signal or a single scattering site in polar space groups it may still be advantageous to perform a MAD experiment, to maximize the amount of information obtained and resolve phase ambiguities. Clearly, the likelihood of success decreases as crystal sensitivity to radiation damage increases, which at an extreme can require the merging of data from multiple, possibly non-isomorphous, crystals.
Initial substructures supplied to phasing programs are generally incomplete, so effective substructure completion is an essential element of an optimal phasing strategy. Log-likelihood-gradient maps are highly sensitive in detecting new sites or signs of anisotropy, whether for general experimental phasing methods [10] or specifically for the SAD target in Phaser [14].
In addition to the intrinsic complication of modelling errors in crystallography due to not measuring phases directly, there are significant complications due to the physics of the diffraction process and to damage of the sample during the experiment. Recently statistical methods have been developed that account for these effects and in some cases even make virtues of them. The correlations of errors in the modelling of the anomalously-scattering atoms at various wavelengths in a MAD experiment and of non-isomorphism errors in various heavy-atom derivatives are included in experimental phasing with SOLVE [1]. The radiation-induced damage at heavy-atom sites in MAD and SAD experiments is used as a source of phase information in the RIP (radiation-damage-induced phasing) method [15]. The interactions between the polarization of synchrotron X-ray beams and the anisotropy of anomalous diffraction have long been recognized but only recently has a systematic and practical treatment been developed that allows a full use of this source of phase information [16*].
Molecular Replacement: phase determination using known structures
The method of molecular replacement is commonly used to solve structures for which a homologous structure is already known. As the database of known structures increases, the number of new folds drops and the proportion of structures that can be solved by molecular replacement increases. About two-thirds of structures deposited in the PDB are currently solved by molecular replacement, and the proportion could probably be higher [17*].
The introduction of likelihood targets [18,19,20] has increased the sensitivity of molecular replacement searches, thus allowing structures to be solved with more distant homologues. These targets, implemented in Phaser [14], allow the information from partial solutions to be exploited, which improves success in solving structures of complexes or crystals containing multiple copies.
Automation is also playing a major role. Even within a single program such as Phaser, the ability to test multiple choices of model for multiple choices of possible space group, following a tree of potential solutions, allows problems to be solved when they would exhaust the patience of a user. Molecular replacement pipelines can extend this power even further, by testing alternative strategies for model preparation (CaspR [21], MrBUMP [22*]) or building up models using automated databases of domains (BALBES [17*]). In some cases, the target structure differs from the molecular replacement model by deformations that can be modeled by a normal modes calculation (elNemo [23]).
As the level of sequence identity drops below about 30%, the success rate of molecular replacement drops precipitously. It might be expected that homology modelling could improve distant templates for molecular replacement, but until recently this was not the case. The best strategy was to use sensitive profile-profile alignment techniques to determine which parts of the template would not be preserved, and then to trim off loops and side chains [24]. However, modelling techniques have now matured to the point where value can be added to the template, and it is possible to improve homology models or NMR structures for use in molecular replacement [25**]. At least in favorable circumstances, similar modelling techniques can generate ab initio models that are sufficiently accurate to succeed in molecular replacement calculations [25**,26].
Phase Improvement
Once experimental or molecular replacement phase information is available, electron density maps can be calculated. Often these initial maps are very noisy, but powerful density modification techniques can be used to greatly improve their quality [27,28,29]. The essence of density modification procedures is that electron density maps have recognizable features such as a flat solvent region, and that enhancing these features generally improves the accuracy of the crystallographic phases. Key to this process is the fact that improving one region in a map (flattening the solvent) improves the phases, which then improves other parts of the map as well (the image of the macromolecule). Recently density modification procedures have been greatly improved through statistical treatments that reduce bias towards the starting map by solvent flipping [30] or maximum-likelihood techniques [31,32,33].
Structure Refinement
With an electron density map of sufficient resolution and quality it is possible to build an atomic model. Traditionally this has been a time consuming subjective manual process prone to human error [34]. More recently, automated methods have been developed that work at higher and lower resolution limits [35*,36*]. These methods iterate automated model building, model refinement, and, in the case of the Phenix [37] Autobuild procedure, density modification [36*]. This method has been extended to calculate minimally biased electron density maps by iterative build omit maps [38**]. In general an atomic model obtained by automatic or manual methods contains some errors and must be optimized to best fit the experimental data and prior chemical information. In addition, the initial model is often incomplete and refinement is carried out to generate improved phases that can then be used to compute a more accurate electron density map.
Over the last ten years there have been great improvements in the targets for refinement of incomplete, error-containing models by making use of the more general maximum likelihood formulation [39,40]. The resulting maximum likelihood refinement targets have been successfully combined with the powerful optimization method of simulated annealing to provide a very robust and efficient refinement scheme [41]. For many structures, some initial experimental phase information is available from either isomorphous heavy atom replacement or anomalous diffraction methods. These phases represent additional observations that can be incorporated in the refinement target. Tests have shown that the addition of experimental phase information greatly improves the results of refinement [42]. Recently there have been efforts to use phasing targets in structure refinement, thus more correctly accounting for the anomalous scattering and the relationship between structure factors [43]. Results indicate that improved models and electron density maps are produced.
Of central importance in model refinement is the parameterization of the atomic model. The two main features of the model that are optimized are the coordinates (position of the atoms) and atomic displacement parameters (movements of the atoms from their average position). In both cases restraints may be used to provide additional information, or constraints applied to reduce the number of parameters being refined. The application of constraints to anisotropic displacement parameters, using the Translation-Libration-Screw (TLS) formalism [44], is now widely used to refine the displacements of large rigid bodies. This method typically improves the fit between the model and experimental data, as judged by the free R-factor, although significant improvements in the electron density maps are typically less common. Very recently an alternative approach to modeling concerted atomic displacements has been introduced: refinement of normal modes against the experimental diffraction data [45**]. Although only applied to a few structures to date the method has demonstrated improvements in models and in some challenging cases sufficient changes in the electron density maps to permit correction of model errors [46*].
The refinement of molecular models is particularly challenging when the upper limit of diffraction is low, 4Å or worse. At this resolution atomic features are typically not visible, although secondary structure elements are usually recognizable. However, by application of the collection of tools currently available, researchers have been able to push the limits of meaningful refinement to 4.7Å resolution [47,48**]. To achieve this, it was essential to include experimental phase information in the refinement target, apply B-factor sharpening to the data, apply non-crystallographic symmetry restraints, and optimize the bulk solvent scattering model [49]. As more and more crystallographic experiments are focused on large molecular complexes, increasing the likelihood of poor diffraction, tools for low resolution refinement and validation are becoming more important.
Macromolecular crystals can also be studied using neutron diffraction. The neutrons interact with the nucleus of the atoms rather than the electrons. This allows neutron diffraction experiments to provide information about the position of hydrogen atoms, something usually not possible with X-ray diffraction methods unless ultra high resolution diffraction is obtained. Recent work has demonstrated that the joint (simultaneous) refinement of a single model against X-ray and neutron data leads to an improved model, as judged by both X-ray and neutron R-factors [50**]. In addition the electron density maps are improved for both types of data. The method has been successfully applied to the high resolution structure of aldose reductase leading to a quantum model of catalysis that depends on accurate modeling of the hydrogen atoms in the structure [51*].
Structure Validation
Since the inception of Rfree for model-to-data fit [52] and ProCheck for model quality assessment [53] in the early 1990’s, structure validation has been considered a necessary final step before deposition, occasionally prompting correction of an individual problem but chiefly serving a gatekeeping function to ensure professional standards for publication of crystal structures. For true cross-validation, the criteria should be independent of the refinement target function, as engineered into the definition of Rfree and nearly always true for the Ramachandran measure important in ProCheck. However, local measures are typically more important to end users than global ones, since no level of global quality can protect against a large local error at the specific region of interest. Local measures can also enable the crystallographer to make specific local corrections to the model.
In the intervening years, further measures of model-to-data agreement have been developed, for example in WhatCheck [54], SFCheck [55], and the Electron-Density Server [56]. Stereochemical validation such as rotamer [57] and Ramachandran [58] criteria have benefitted from great increases in high-resolution data, B-factor filtering at the residue level, and evaluation as multi-dimensional distributions. All-atom contacts [59] contributed a new major source of independent information by adding, optimizing, and analyzing the other half of the atoms – the hydrogens – and analyzing their steric clashes as well as their H-bonding.
Recently, validation criteria have been developed for carbohydrates [60] and for RNA backbone [61**], as well as a promising new evaluation of under-packing in proteins [62*]. The MolProbity validation web site [63**] combines all-atom contacts (especially the “clashscore”) with geometric and dihedral-angle criteria for proteins, nucleic acids, and ligands, to produce numerical and graphical local evaluations as well as global scores. The local results can guide manual [64,65] or automated [66**] rebuilding to correct systematic errors such as backward-fit sidechains trapped in the wrong local minimum, thereby improving refinement behavior, electron density quality, and chemical reasonableness, and also lowering R and Rfree by small amounts. Such procedures have become standard in many structural genomics and industrial labs that do high-throughput crystallography, and are being built into software such as ARP/wARP [35*], Coot [65], Buster [67], and PHENIX [36*,37]. In general, there are now many fewer “false alarms”, and outliers flagged by validation are nearly always worth examining.
The most significant overall development currently happening in the area of validation is the application of these local criteria much earlier in the structure solution process, their integration into a cycle of repeated refinement, correction, and re-refinement, and the gradual automation of more aspects of that cycle. A useful level of independence for cross-validation can still be preserved, for stereochemistry by the wealth of interdependent criteria that must be satisfied simultaneously with data match, and for all-atom steric clashes by avoiding refinement of explicit hydrogen contacts. The benefits are a significant increase in the accuracy of structures treated in this new manner.
Impact of New Methods
The advances in data collection hardware, development of anomalous diffraction-based phasing methods, and new structure solution, refinement and validation algorithms have made it easier to arrive at high quality macromolecular structures. Routine structures can often be solved rapidly using a variety of automated tools. Many challenging structures can now be solved that otherwise would be intractable using the tools available 15 years ago. While the availability of better validation tools makes the existence of local conformational, steric, and geometric errors less likely, the global fit of models to the experimental data has not improved substantially, as judged by a criterion such as the R-free value. A brief inspection of the Protein Data Bank reveals that structures solved at a typical resolution of 2.2Å still routinely have final R and R-free values in the range of 20% to 30%, which is much larger than the data measurement errors. Inasmuch as a cross-validated measure such as R-free reflects the degree to which the atomic model adequately models the true contents of the crystal, we can suppose that our current atomic models are still in some way deficient. The most likely culprit is motion and multiple conformations, at all size scales. This highlights the need for yet more sophisticated model parameterizations. There have been recent advances in the modeling of domain motion using TLS [44] and normal mode methods [45**], both of which have been observed to decrease R and R-free values. However, obvious areas for further improvement are in the modeling of alternate conformations, domain motion/disorder, local macromolecular disorder, ordered solvent disorder, and the current relatively crude bulk solvent models in use. Unfortunately, as the resolution of the experimental data worsens these features become less and less easy to detect and model but are still present in the crystal, probably to an even greater degree. In addition, our current harmonic parameterizations are in many cases approximate; progress will require the use of anharmonic models to better capture the underlying molecular reality. One of the main challenges of developing better models will be arriving at efficient parameterizations that provide improved physical meaning while only requiring a small number of refinable parameters.
Conclusions
The last ten years has seen a dramatic improvement in the computational tools available for the determination of macromolecular crystal structures. The routine inclusion of likelihood-based algorithms in experimental phasing, molecular replacement, and structure refinement serve to generate better electron density maps and atomic models. These in turn serve to improve the efficiency and success rate of automated model building methods. Structure validation methods are starting to be applied throughout the crystallographic process, further improving the quality of models. Many challenges still remain. In particular, the generation of accurate structures when only low resolution data are available, and improved parameterizations of macromolecular models and their motions to best fit the experimental data at all resolutions.
Acknowledgments
The authors would like to thank the NIH for their support (1P01 GM063210). This work was partially supported by the US Department of Energy under Contract No. DE-AC02–05CH11231. RJR is supported by a Principal Research Fellowship from the Wellcome Trust (UK).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References and recommended reading
- 1.Terwilliger TC, Berendzen J. Automated MAD and MIR structure solution. Acta Cryst. 1999;D55:849–861. doi: 10.1107/S0907444999000839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schneider TR, Sheldrick GM. Substructure solution with SHELXD. Acta Cryst. 2002;D58:1772–1779. doi: 10.1107/s0907444902011678. [DOI] [PubMed] [Google Scholar]
- 3.Grosse-Kunstleve RW, Adams PD. Substructure search procedures for macromolecular structures. Acta Cryst. 2003;D59:1966–1973. doi: 10.1107/s0907444903018043. [DOI] [PubMed] [Google Scholar]
- 4.Xu H, Weeks CM, Hauptman HA. Optimizing statistical Shake-and-Bake for Se-atom substructure determination. Acta Cryst. 2005;D61:90–96. doi: 10.1107/S0907444905011558. [DOI] [PubMed] [Google Scholar]
- 5.Dumas C, van der Lee A. Macromolecular structure solution by charge flipping. Acta Cryst. 2008;D64:864–873. doi: 10.1107/S0907444908017381. [DOI] [PubMed] [Google Scholar]
- 6**.Oszlányi G, Süto A. The charge flipping algorithm. Acta Cryst. 2008;A64:123–134. doi: 10.1107/S0108767307046028. A charge flipping algorithm is described, related to previous solvent flipping methods, which can be used to recover phase information from random or poor initial phase estimates. [DOI] [PubMed] [Google Scholar]
- 7.Sayre D. The squaring method: a new method for phase determination. Acta Cryst. 1952;5:60–65. [Google Scholar]
- 8.Otwinowski Z. Isomorphous Replacement and Anomalous Scattering, Proc. Daresbury Study Weekend. Warrington: SERC Daresbury Laboratory; 1991. pp. 80–85. [Google Scholar]
- 9.Brunger AT, Adams PD, Clore GM, Gros P, Grosse Kunstleve RW, Jiang J-S, Kuszewski J, Nilges M, Pannu NS, Read RJ, Rice LM, Simonson T, Warren GL. Crystallography & NMR system (CNS): A new software system for macromolecular structure determination. Acta Cryst. 1998;D54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]
- 10.de La Fortelle E, Bricogne G. Maximum-Likelihood Heavy-Atom Parameter Refinement in the MIR and MAD Methods. Methods Enzymol. 1997;276:472–494. doi: 10.1016/S0076-6879(97)76073-7. [DOI] [PubMed] [Google Scholar]
- 11.Read RJ. New ways of looking at experimental phasing. Acta Cryst. 2003;D59:1891–1902. doi: 10.1107/s0907444903017918. [DOI] [PubMed] [Google Scholar]
- 12.McCoy AJ, Storoni LC, Read RJ. Simple algorithm for a maximum-likelihood SAD function. Acta Cryst. 2004;D60:1220–1228. doi: 10.1107/S0907444904009990. [DOI] [PubMed] [Google Scholar]
- 13.Dauter Z, Dauter M, Dodson EJ, Jolly SAD. Acta Cryst. 2002;D58:494–506. doi: 10.1107/s090744490200118x. [DOI] [PubMed] [Google Scholar]
- 14.McCoy AJ, Grosse-Kunstleve RW, Adams PD, Winn MD, Storoni LC, Read RJ. Phaser crystallographic software. J. Appl. Cryst. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ravelli RB, Leiros HK, Pan B, Caffrey M, McSweeney S. Specific radiation damage can be used to solve macromolecular crystal structures. Structure. 2003;11:217–224. doi: 10.1016/s0969-2126(03)00006-6. [DOI] [PubMed] [Google Scholar]
- 16*.Schiltz M, Bricogne G. Exploiting the anisotropy of anomalous scattering boosts the phasing power of SAD and MAD experiments. Acta Cryst. 2008;D64:711–729. doi: 10.1107/S0907444908010202. Most researchers are unaware of the changes in the anomalous scattering dependent on the orientation of the scatterer with respect to the incident radiation. Here this effect is exploited to improve the quality of phases derived from SAD and MAD experiments. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17*.Long F, Vagin AA, Young P, Murshudov GN. BALBES: a molecular-replacement pipeline. Acta Cryst. 2008;D64:125–132. doi: 10.1107/S0907444907050172. An automated pipeline for molecular replacement phasing is described which uses a local structure database to solve complex molecular replacement problems. The whole system is coordinated using the Python scripting language. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Read RJ. Pushing the boundaries of molecular replacement with maximum likelihood. Acta Cryst. 2001;D57:1373–1382. doi: 10.1107/s0907444901012471. [DOI] [PubMed] [Google Scholar]
- 19.Storoni LC, McCoy AJ, Read RJ. Likelihood-enhanced fast rotation functions. Acta Cryst. 2004;D60:432–438. doi: 10.1107/S0907444903028956. [DOI] [PubMed] [Google Scholar]
- 20.McCoy AJ, Grosse-Kunstleve RW, Storoni LC, Read RJ. Likelihood-enhanced fast translation function. Acta Cryst. 2005;D61:458–464. doi: 10.1107/S0907444905001617. [DOI] [PubMed] [Google Scholar]
- 21.Claude J-B, Suhre K, Notredame C, Claverie J-M, Abergel C. CaspR: a web server for automated molecular replacement using homology modeling. Nucleic Acids Res. 2004;32:W606–W609. doi: 10.1093/nar/gkh400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22*.Keegan RM, Winn MD. Automated search-model discovery and preparation for structure solution by molecular replacement. Acta Cryst. 2007;D63:447–457. doi: 10.1107/S0907444907002661. An automated pipeline for molecular replacement phasing is described which tries multiple search models including possible domains identified from the target amino acid sequence. [DOI] [PubMed] [Google Scholar]
- 23.Suhre K, Sanejouand YH. On the potential of normal mode analysis for solving difficult molecular replacement problems. Acta Cryst. 2004;D60:796–799. doi: 10.1107/S0907444904001982. [DOI] [PubMed] [Google Scholar]
- 24.Schwarzenbacher R, Godzik A, Grzechnik SK, Jaroszewski L. The importance of alignment accuracy for molecular replacement. Acta Cryst. 2004;D60:1229–1236. doi: 10.1107/S0907444904010145. [DOI] [PubMed] [Google Scholar]
- 25**.Qian B, Raman S, Das R, Bradley P, McCoy AJ, Read RJ, Baker D. High-resolution structure prediction and the crystallographic phase problem. Nature. 2007;450:176–177. Ab initio model prediction, using purely computational methods, is combined with molecular replacement to solve novel structures. This approach is likely to be exploited more in the future as the prediction methods improve. [Google Scholar]
- 26.Das R, Baker D. Prospects for de novo phasing with de novo protein models. Acta Cryst. 2009;D65:169–175. doi: 10.1107/S0907444908020039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bricogne G. Geometric sources of redundancy in intensity data and their use for phase determination. Acta Cryst. 1974;A30:395–405. [Google Scholar]
- 28.Wang BC. Resolution of phase ambiguity in macromolecular crystallography. Methods Enzymol. 1985;115:90–112. doi: 10.1016/0076-6879(85)15009-3. [DOI] [PubMed] [Google Scholar]
- 29.Cowtan K, Main P. Phase Combination and Cross Validation in Iterated Density Modification Calculations. Acta Cryst. 1996;D52:43–48. doi: 10.1107/S090744499500761X. [DOI] [PubMed] [Google Scholar]
- 30.Abrahams JP, Leslie AWG. Methods used in the structure determination of bovine mitochondrial F1 ATPase. Acta Cryst. 1996;D52:30–42. doi: 10.1107/S0907444995008754. [DOI] [PubMed] [Google Scholar]
- 31.Terwilliger TC. Maximum likelihood density modification. Acta Cryst. 2000;D56:965–972. doi: 10.1107/S0907444900005072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cowtan K. Generic representation and evaluation of properties as a function of position in reciprocal space. J Appl Cryst. 2002;35:655–663. [Google Scholar]
- 33.Terwilliger TC. Using prime-and-switch phasing to reduce model bias in molecular replacement. Acta Cryst. 2004;D60:2144–2149. doi: 10.1107/S0907444904019535. [DOI] [PubMed] [Google Scholar]
- 34.Mowbray SL, Helgstrand C, Sigrell JA, Cameron AD, Jones TA. Errors and reproducibility in electron-density map interpretation. Acta Cryst. 1999;D55:1309–1319. doi: 10.1107/s0907444999005211. [DOI] [PubMed] [Google Scholar]
- 35*.Langer G, Cohen SX, Lamzin VS, Perrakis A. Automated macromolecular model building for X-ray crystallography using ARP/wARP version 7. Nature Protocols. 2008;3:1171–1179. doi: 10.1038/nprot.2008.91. The current version of the ARP/wARP package is described including new features designed to extend the applicability of the system to lower resolution data. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36*.Terwilliger TC, Grosse-Kunstleve RW, Afonine PV, Moriarty NW, Zwart PH, Hung L-W, Read RJ, Adams PD. Iterative model building, structure refinement and density modification with the PHENIX AutoBuild wizard. Acta Cryst. 2008;D64:61–69. doi: 10.1107/S090744490705024X. The automated model building method in the Phenix package is described, including the integration of density modification into the rebuilding process. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Adams PD, Grosse-Kunstleve RW, Hung L-W, Ioerger TR, McCoy AJ, Moriarty NW, Read RJ, Sacchettini JC, Sauter NK, Terwilliger TC. PHENIX: building new software for automated crystallographic structure determination. Acta Cryst. 2002;D58:1948–1954. doi: 10.1107/s0907444902016657. [DOI] [PubMed] [Google Scholar]
- 38**.Terwilliger TC, Grosse-Kunstleve RW, Afonine PV, Moriarty NW, Adams PD, Read RJ, Zwart PH, Hung L-W. Iterative-build OMIT maps: map improvement by iterative model building and refinement without model bias. Acta Cryst. 2008;D64:515–524. doi: 10.1107/S0907444908004319. The Phenix automated model building methods are extended to generate minimally unbiased electron density maps by building complete atomic models outside of omitted regions, which are combined to provide a complete map for the asymmetric unit which has never been biased by a model. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pannu NS, Read RJ. Improved Structure Refinement Through Maximum Likelihood. Acta Cryst. 1996;A52:659–668. [Google Scholar]
- 40.Murshudov GN, Vagin AA, Dodson EJ. Refinement of macromolecular structures by the maximum-likelihood method. Acta Cryst. 1997;D53:240–255. doi: 10.1107/S0907444996012255. [DOI] [PubMed] [Google Scholar]
- 41.Adams PD, Pannu NS, Read RJ, Brunger AT. Extending the limits of molecular replacement through combined simulated annealing and maximum likelihood refinement. Acta Cryst. 1999;D55:181–190. doi: 10.1107/S0907444998006635. [DOI] [PubMed] [Google Scholar]
- 42.Pannu NS, Murshudov GM, Dodson EJ, Read RJ. Incorporation of prior phase information strengthens maximum-likelihood structure refinement. Acta Cryst. 1998;D54:1285–1294. doi: 10.1107/s0907444998004119. [DOI] [PubMed] [Google Scholar]
- 43.Skubak P, Murshudov GN, Pannu NS. Direct incorporation of experimental phase information in model refinement. Acta Cryst. 2004;D60:2196–2201. doi: 10.1107/S0907444904019079. [DOI] [PubMed] [Google Scholar]
- 44.Winn MD, Isupov MN, Murshudov GN. Use of TLS parameters to model anisotropic displacements in macromolecular refinement. Acta Cryst. 2001;D57:122–133. doi: 10.1107/s0907444900014736. [DOI] [PubMed] [Google Scholar]
- 45**.Poon BK, Chen X, Lu M, Vyas NK, Quiocho FA, Wang Q, Ma J. Normal Mode Refinement of Anisotropic Thermal Parameters for A Supramolecular Complex at 3.42-Å Crystallographic Resolution. Proc Natl Acad Sci USA. 2007;104:7869–7874. doi: 10.1073/pnas.0701204104. An alternative approach to the modeling of atomic displacements in crystals is described, based on the concept of normal modes. The amplitudes of multiple modes are refined against the experimental diffraction data to fit approximately rigid body displacements. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46*.Chen X, Poon BK, Dousis A, Wang Q, Ma J. Normal Mode Refinement of Anisotropic Thermal Parameters for Potassium Channel KcsA at 3.2Å Crystallographic Resolution. Structure. 2007;15:955–962. doi: 10.1016/j.str.2007.06.012. The application of the normal modes method to another structure, which shows enough improvements in the electron density map to permit rebuilding of parts of the structure. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.DeLaBarre B, Brunger AT. Complete Structure of p97/Valosin-Containing Protein Reveals Communication Between Nucleotide Domains. Nature Structural Biology. 2003;10:856–863. doi: 10.1038/nsb972. [DOI] [PubMed] [Google Scholar]
- 48**.Brunger AT, DeLaBarre B, Davies JM, Weis WI. X-ray structure determination at low resolution. Acta Cryst. 2009;D56:128–133. doi: 10.1107/S0907444908043795. The methods used to solve a collection of structures at low resolution are described. In addition, comparison with a recently solved high resolution structure enable an analysis of the errors introduced at low resolution. Starting model building from an available high resolution structure is shown to significantly improve results. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Afonine PV, Grosse-Kunstleve RW, Adams PD. A robust bulk-solvent correction and anisotropic scaling procedure. Acta Cryst. 2005;D61:850–855. doi: 10.1107/S0907444905007894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50**.Adams PD, Mustyakimov M, Afonine PV, Langan P. Generalized X-ray and neutron crystallographic analysis: more accurate and complete structures for biological macromolecules. Acta Cryst. 2009 doi: 10.1107/S0907444909011548. in press The computational methods implemented for the joint use of X-ray and neutron diffraction data are described. The improvements in model quality, with respect to both kinds of data, are significant and more chemically reasonable models are produced. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51*.Blakeley MP, Ruiz F, Cachau R, Hazemann I, Meilleur F, Mitschler A, Ginell S, Afonine P, Ventura ON, Cousido-Siah A, Haertlein M, Joachimiak A, Myles D, Podjarny A. Quantum model of catalysis based on a mobile proton revealed by subatomic x-ray and neutron diffraction studies of h-aldose reductase. Proc Natl Acad Sci USA. 2008;105:1844–1848. doi: 10.1073/pnas.0711659105. Very high resolution X-ray data and medium resolution neutron data are used to determine a model with experimentally derived hydrogen atom positions. This model is combined with computational studies to create a quantum model for catalysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brunger AT. Free R-value – a novel statistical quantity for assessing the accuracy of crystal structures. Nature. 1992;355:472–475. doi: 10.1038/355472a0. [DOI] [PubMed] [Google Scholar]
- 53.Laskowski RA, MacArthur MW, Moss DS, Thornton JM. ProCheck – A program to check the stereochemical quality of protein structures. J Appl Crystallogr. 1993;26:283–291. [Google Scholar]
- 54.Hooft RWW, Vriend G, Sander C, Abola EE. Errors in crystal structures. Nature. 1996;381:272. doi: 10.1038/381272a0. [DOI] [PubMed] [Google Scholar]
- 55.Vaguine AA, Richelle J, Wodak SJ. SFCheck. Acta Crystallogr. 1999;D55:191–205. doi: 10.1107/S0907444998006684. [DOI] [PubMed] [Google Scholar]
- 56.Kleywegt GJ, Harris MR, Zou JY, Taylor TC, Wahlby A, Jones TA. The Uppsala electron-density server. Acta Crystallogr. 2004;60:2240–2249. doi: 10.1107/S0907444904013253. [DOI] [PubMed] [Google Scholar]
- 57.Dunbrack RL., Jr Rotamer libraries in the 21st century. Curr Opin Struct Biol. 2002;12:431–440. doi: 10.1016/s0959-440x(02)00344-5. [DOI] [PubMed] [Google Scholar]
- 58.Lovell SC, Davis IW, Arendall WB, III, de Bakker PIW, Word JM, Prisant MG, Richardson JS, Richardson DC. Structure validation by Cα geometry: φ, ψ and Cβ deviation. Proteins Struct Funct Genetics. 2003;50:437–450. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 59.Word JM, Lovell SC, LaBean TH, Zalis M, Presley BK, Richardson JS, Richardson DC. Visualizing and Quantitating Molecular Goodness-of-Fit: Small-Probe Contact Dots with Explicit Hydrogens. J Mol Biol. 1999;285:1711–33. doi: 10.1006/jmbi.1998.2400. [DOI] [PubMed] [Google Scholar]
- 60.Frank M, Lütteke T, von der Lieth CW. GlycoMapsDB: a database of the accessible conformational space of glycosidic linkages. Nucleic Acids Res. 2007;35:287–290. doi: 10.1093/nar/gkl907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61**.Richardson JS, Schneider B, Murray LW, Kapral GJ, Immormino RM, Headd JJ, Richardson DC, Ham D, Hershkovits E, Williams LW, Keating K, Pyle AM, Micallef D, Westbrook J, Berman HM. RNA backbone: Consensus all-angle conformers and modular string nomenclature (an RNA Ontology Consortium Contribution) RNA. 2008;14:465–81. doi: 10.1261/rna.657708. A new system for the classification of RNA backbone structure is described, accompanied by a geometric analysis of local conformation for common structural motifs. This information provides a basis for the development of improved RNA structure validation tools in the future, and improved geometric target functions for structure refinement. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62*.Sheffler W, Baker D. RosettaHoles: Rapid assessment of protein core packing for structure prediction, refinement, design, and validation. Protein Sci. 2009;18:229–239. doi: 10.1002/pro.8. A method for analyzing the internal packing of proteins is described. Using a set of spherical cavity balls to fill the empty volume between atoms in the protein interior a numerical value is assigned to the degree of under-packing. This method, although developed for ab initio protein design and optimization, may become a valuable validation tool in the field of crystallography. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63**.Davis IW, Leaver-Fay A, Chen VB, Block JN, Kapral GJ, Wang X, Murray LJ, Arendall WB, III, Snoeyink JS, Richardson JS, Richardson DC. MolProbity: All-atom contacts and structure validation for proteins and nucleic acids. Nucleic Acids Research. 2007:W375–W383. doi: 10.1093/nar/gkm216. 35 (Web server issue) This state-of-the-art model validation tool is described. The use of all atom contacts, including hydrogen atoms, is very powerful in revealing local errors in protein models. Visualization of the poor contacts typically enables rapid correction of the underlying problem. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Arendall WB, III, Tempel W, Richardson JS, Zhou W, Wang S, Davis IW, Liu Z-J, Rose JP, Carson M, Luo M, Richardson DC, Wang B-C. A test of enhancing model accuracy in high-throughput crystallography. J Struct Func Genomics. 2005;6:1–11. doi: 10.1007/s10969-005-3138-4. [DOI] [PubMed] [Google Scholar]
- 65.Emsley P, Cowtan K. Coot: Model-building tools for molecular graphics. Acta Crystallogr. 2004;D60:2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- 66**.Headd JJ, Immormino RM, Keedy DA, Emsley P, Richardson DC, Richardson JS. Autofix for backward-fit sidechains: using MolProbity and real-space refinement to put misfits in their place. J Struct Func Genomics. 2008;10:83–93. doi: 10.1007/s10969-008-9045-8. The contact analysis methods developed in the MolProbity system are combined with local refinement of the atomic model to fix problematic side chain conformations. The use of validation criteria to automatically correct model errors is likely to be an area of algorithm development in the near future. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Blanc E, Roversi P, Vonrhein C, Flensburg C, Lea SM, Bricogne G. Refinement of severely incomplete structures with maximum likelihood in BUSTER-TNT. Acta Crystallogr. 2004;D60:2210–21. doi: 10.1107/S0907444904016427. There is currently a new release of Buster, not yet described in print. [DOI] [PubMed] [Google Scholar]