Integrative approaches for large-scale transcriptome-wide association studies (original) (raw)
. Author manuscript; available in PMC: 2017 Mar 1.
Published in final edited form as: Nat Genet. 2016 Feb 8;48(3):245–252. doi: 10.1038/ng.3506
Abstract
Many genetic variants influence complex traits by modulating gene expression, thus altering the abundance levels of one or multiple proteins. Here, we introduce a powerful strategy that integrates gene expression measurements with summary association statistics from large-scale genome-wide association studies (GWAS) to identify genes whose cis-regulated expression is associated to complex traits. We leverage expression imputation to perform a transcriptome wide association scan (TWAS) to identify significant expression-trait associations. We applied our approaches to expression data from blood and adipose tissue measured in ~3,000 individuals overall. We imputed gene expression into GWAS data from over 900,000 phenotype measurements to identify 69 novel genes significantly associated to obesity-related traits (BMI, lipids, and height). Many of the novel genes are associated with relevant phenotypes in the Hybrid Mouse Diversity Panel. Our results showcase the power of integrating genotype, gene expression and phenotype to gain insights into the genetic basis of complex traits.
Introduction
Although a large proportion of variability in complex human traits is due to genetic variation, the mechanistic steps between genetic variation and trait are generally not understood1–7. Many genetic variants influence complex traits by modulating gene expression, thus altering the abundance levels of one or multiple proteins8–12. Such relationships between expression and trait could be investigated through association scans in individuals for which both measurements are available8,13,14. Unfortunately, studies that measure gene expression have been held back by specimen availability and cost, with the few published studies of expression and complex trait being orders of magnitude smaller than studies of trait alone. Consequently, many expression-trait associations cannot be detected, especially those with small effects. To mitigate the reduced power from small sample size, alternative approaches examined the overlap of genetic variants that impact gene expression (eQTLs) with trait-associated variants identified in large, independent genome-wide association studies (GWAS)5,6,8,9,11–13,15. However, this approach is also likely to miss expression-trait associations of small effect.
We developed a new approach to identify genes whose expression is significantly associated to complex traits in individuals without directly measured expression levels (Methods). We leveraged a relatively small set of reference individuals for whom both gene expression and genetic variation (single nucleotide polymorphisms, SNPs) have been measured to impute the cis-genetic component of expression into a much larger set of phenotyped individuals from their SNP genotype data (Figure 1). The imputed expression can be viewed as a linear model of genotypes with weights based on the correlation between SNPs and gene expression in the training data while accounting for linkage disequilibrium (LD) among SNPs. We then correlated the imputed gene expression to the trait to perform a transcriptome-wide association study (TWAS) and identify significant expression-trait associations (Methods). Work in parallel to ours has also proposed to find expression-trait associations through imputation of gene expression when GWAS at an individual level is available16(see Discussion). However, a critical limitation is that large-scale GWAS data are typically only publicly available at the level of summary association statistics (e.g. individual SNP effect sizes)2–4. To capitalize on the largest GWAS to date (typically available only at the summary level), we extended our approach to impute the expression-trait association statistics directly from GWAS summary statistics (Methods). In contrast to expression imputation from individual-level data16, imputation of expression-trait association from GWAS summary statistics can exploit publically available data from hundreds of thousands of samples. Linear predictors naturally extend to indirect imputation of the standardized effect of the cis-genetic component on the trait starting from only the GWAS association statistics2–4 (Methods). This allowed us to increase the effective sample size for expression-trait association testing to hundreds of thousands of individuals. By focusing only on the genetic component of expression, we avoid instances of expression-trait associations that are not a consequence of genetic variation but are driven by variation in trait (Figure 2). Our approach can be conceptualized as a test for significant cis-genetic correlation between expression and trait (see Results).
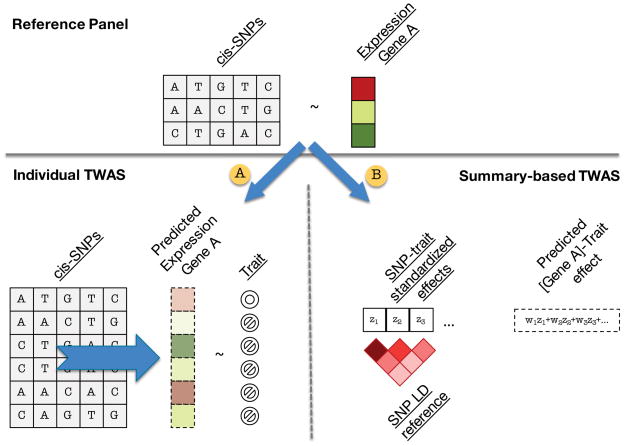
Figure 1. Overview of methods.
Cartoon representation of TWAS approach. In the reference panel (top) estimate gene expression effect-sizes: directly (i.e. eQTL); modeling LD (BLUP); or modeling LD and effect-sizes (BSLMM). A: Predict expression directly into genotyped samples using effect-sizes from the reference panel and measure association between predicted expression and trait. B: Indirectly estimate association between predicted expression and trait as weighted linear combination of SNP-trait standardized effect sizes while accounting for LD among SNPs.
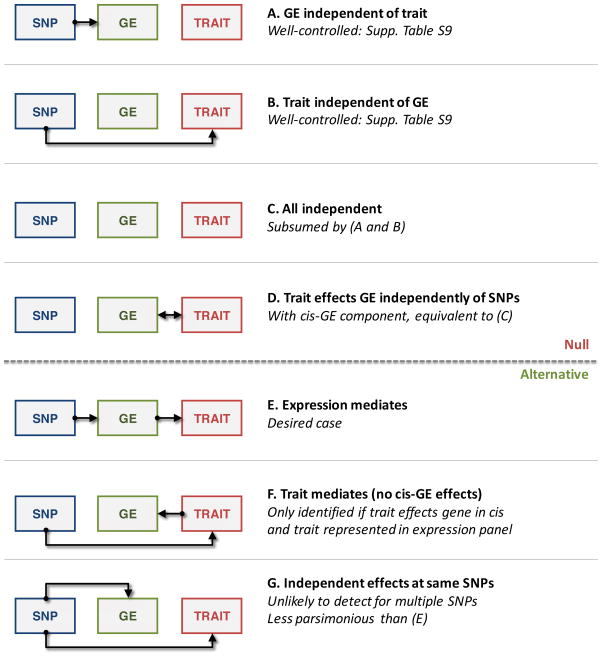
Figure 2. Modes of expression causality.
Diagrams are shown for the possible modes of causality for the relationship between genetic markers (SNP, blue), gene expression (GE, green), and trait (red). A–D describes scenarios that would be considered null by the TWAS model; E–G describes scenarios that could be identified as significant.
We applied our approaches to expression data from blood and adipose tissue measured in ~3,000 individuals overall. Through extensive simulations and real data analyses we show that our proposed approach increases performance over standard GWAS or eQTL-guided GWAS. Furthermore, we reanalyzed a 2010 lipid GWAS17 to find 25 new expression-trait associations in that data. 19 out of 25 contained genome-wide significant SNPs in the more recent and expanded lipids study5 thus showcasing the power of our approach to find robust associations. We imputed gene expression into GWAS data from over 900,000 phenotype measurements5–7 to identify 69 novel genes significantly associated to obesity-related traits (BMI, lipids, and height). Many of the novel genes were associated with relevant phenotypes in the Hybrid Mouse Diversity Panel. Overall our results showcase the power of integrating genotype, gene expression and phenotype to gain insights into the genetic basis of complex traits.
Results
SNP-heritability of gene expression
To investigate the potential utility of a transcriptome-wide association (TWAS) based on imputed gene expression we first estimated the cis- (1Mb window around the gene) and trans- (rest of the genome) SNP-heritability (hg,cis2,hg,trans2) for each gene in our data18,19. These metrics quantify the maximum possible accuracy (in terms of R2) of a linear predictor from the corresponding set of SNPs20,21 (Methods). We used 3,234 individuals for whom genome-wide SNP data and expression measurements were available from METSIM (adipose), YFS (blood), and NTR (blood) data sets22–24 (Methods, Supplementary Table 1). All expression measurements were adjusted for batch confounders, and array probes were merged into a single expression value for each gene where possible (Methods). Consistent with previous work24,25, we observed significantly non-zero estimates of heritability across all three studies, with mean hg,cis2 ranging from 0.01–0.07 and mean hg,trans2 ranging from 0.04–0.06 in genes where estimates converged (Supplementary Figure 1, Supplementary Table 1). Although we observed large differences in the average hg,cis2 estimates between the two blood cohorts, the estimates were strongly correlated across genes (Pearson _ρ_=0.47 for YFS-NTR, as compared to _ρ_=0.15 and _ρ_=0.26 for METSIM-NTR and METSIM-YFS respectively). This is consistent with a common but not identical genetic architecture. The hg,cis2 was significantly non-zero for 6,924 genes after accounting for multiple hypotheses (1,985 for METSIM, 3,836 for YFS, and 1,103 for NTR) (Supplementary Figure 1) whereas current sample sizes where too small to detect individually significant trans heritable genes. As expected, we also observed a high overlap of genes with significant hg,cis2 across cohorts (Supplementary Table 2, Supplementary Figure 2). We focused subsequent analyses on the 6,924 cis-heritable genes as such genes are typically enriched for trait associations7,9,13,24–29.
TWAS performance in simulation and cross-validation
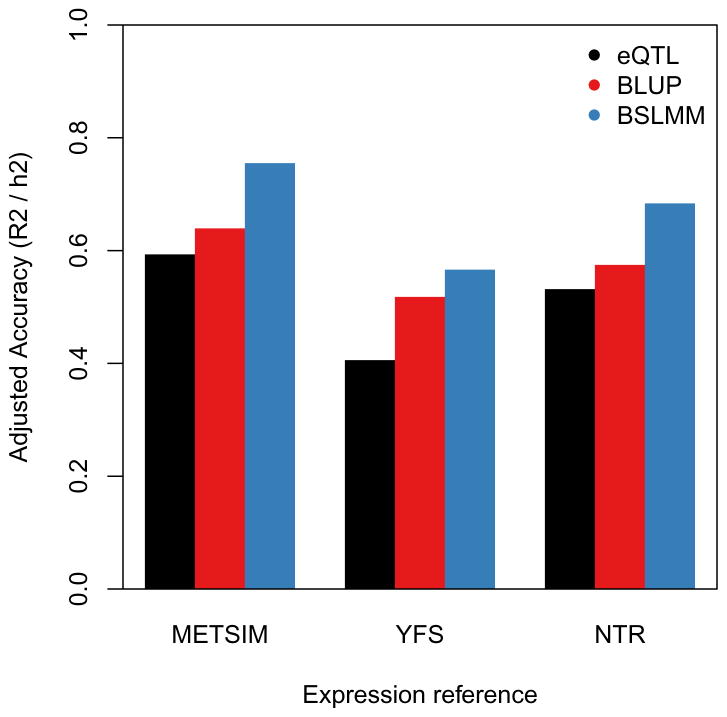
We evaluated whether the expressions of the 6,924 highly heritable genes could be accurately imputed from cis-SNP genotype data alone in these three cohorts. In each tissue, we used cross-validation to compare predictions from the best cis-eQTL to those from all SNPs at the locus either in a best linear unbiased predictor (BLUP) or in a Bayesian model30,31 (Methods). On average, the Bayesian linear mixed model (BSLMM)31, which uses all cis-SNPs and estimates the underlying effect-size distribution, attained the best performance with a 32% gain in prediction R2 over a prediction computed using only the top cis-eQTL (Figure 4, Supplementary Figure 3). The BSLMM exhibited a long tail of increased accuracy, more than doubling the prediction R2 for 25% of genes (Supplementary Figure 4). In contrast to complex traits where hundreds of thousands of training samples are required for accurate prediction32,33, a substantial portion of variance in expression can be predicted at current sample sizes due to the much smaller number of independent SNPs in the cis region21. Furthermore, larger training sizes will continue to increase the total number of genes that can be accurately predicted (Figure 3). We further evaluated cross-cohort prediction of these genes in the YFS and NTR, which were roughly equally sized and had expression measured in whole-blood by microarray, but were genotyped on different platforms and from different Scandinavian populations. After accounting for cis-heritability in the test cohort, our cross-cohort standardized accuracy (i.e. r2/hg,cis2) was broadly consistent with in-cohort cross-validation accuracy (Supplementary Table 3). The BSLMM was again the most accurate predictor, with an average cross-cohort r2/hg,cis2 of 72%, outperforming the best eQTL by an average 1.17x.
Figure 4. Accuracy of direct expression imputation algorithms.
Adjusted accuracy was estimated using cross-validation R^2 between prediction and true expression, and normalized by corresponding cis-h2g. Bars show mean estimate across three cohorts and three methods: eQTL – single best cis-eQTL in the locus; BLUP using all SNPs in the locus; BSLMM using all SNPs in the locus and non-infinitesimal priors.
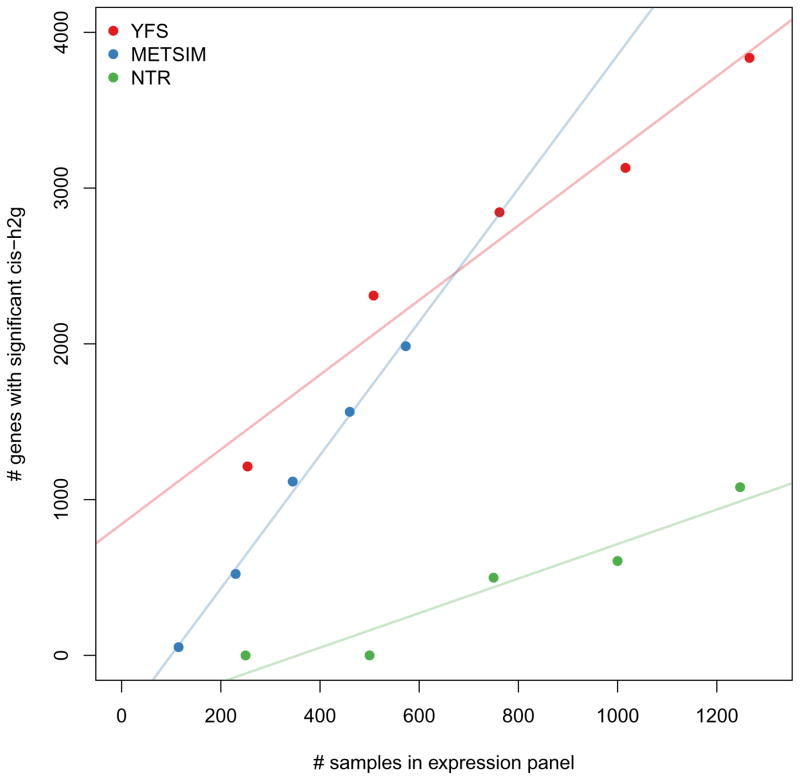
Figure 3. Number of genes with significant cis-heritability observed at varying sample sizes.
The number of genes with significant cis-heritability was estimated by down-sampling each cohort (YFS, METSIM, and NTR/Wright et al.) into quintiles.
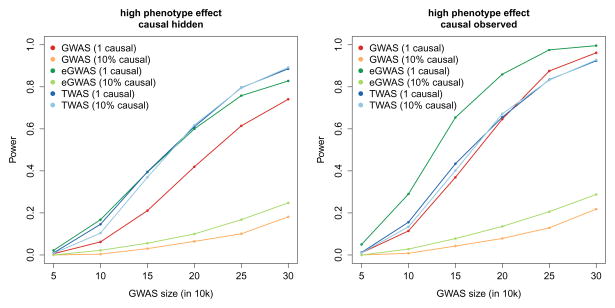
Next, we focused on evaluating the power of the TWAS approach to detect significant expression-trait associations using GWAS summary data from complex traits (equivalent to TWAS from individual level data; Methods, Supplementary Figure 5). For comparison, we also measured power to detect significant SNP-trait associations through standard GWAS (testing each SNP individually) and eQTL-based GWAS (eGWAS, where the best eQTL in each gene is the only variant tested for association to trait), with all three tests corrected for their genome-wide testing burdens. Using real genotype data, we simulated a causal SNP-expression-trait model with realistic effect-sizes and measured the power of each strategy to identify genome-wide significant variants (accounting for 1 million SNPs for GWAS and 15,000 expressed genes using family-wise error rate control). Over many diverse disease architectures TWAS substantially increased power when the expression-causing variants were un-typed or poorly tagged by an individual SNP (Figure 5, Supplementary Figures 6–11). The greatest power gains were observed in the case of multiple causal variants: 92% power for TWAS compared to 18% and 25% for GWAS and eGWAS. This scenario would correspond to expression caused by allelic heterogeneity9,34,35, or “apparent” heterogeneity at common variants (due to tagging of unobserved causal variant)36. TWAS was comparable to other approaches when a single causal variant was directly typed, in which case combining the effects of neighboring SNPs does not add signal. Under the null where expression was completely independent of phenotype (with either being heritable, Figure 2A–D), the TWAS false positive rate was well controlled (Supplementary Table 4). As expected, all methods were confounded in the case where the same causal variants had independent effects on trait and expression (Figure 2F–G; Supplementary Figures S8, 12).
Figure 5. Power of summary-based expression imputation algorithms.
Realistic disease architectures were simulated and power to detect a genome-wide significant association evaluated across three methods (accounting for 15,000 eGWAS/TWAS tests, and 1,000,000 GWAS tests). Colors correspond number of causal variants simulated and methods used: GWAS where every SNP in the locus is tested; eGWAS where only the best cis-eQTL is tested; and TWAS computed using summary-statistics. Expression reference panel was fixed at 1,000 out-of-sample individuals and simulated GWAS sample size designated by x-axis. Power was computed as the fraction of 500 simulations where significant association was identified.
Our approach can be conceptually viewed as a test for the correlation between the genetic component of expression and the genetic component of trait (Methods). Since several recent methods have been proposed that measure genetic correlation between summary statistics37, we sought to evaluate this relationship empirically. We compared TWAS to the recently proposed cross-trait LD-score regression (LDSC) that estimates genome-wide genetic correlation between traits37. Although LDSC is not intended for local analyses due to model assumptions on polygenicity and use of block-jackknife across loci for estimating standard errors, we performed the evaluation using expression and phenotype (height) from the YFS cohort, using the results over individual data as the “gold standard” (Methods). We find that LDSC estimate of genetic correlation between height and expression from summary data is highly correlated with the gold standard (correlation=0.7, Supplementary Figure 13), but the relationship is much noisier than that of TWAS (correlation=0.99, Supplementary Figure 5, 13). This suggests that TWAS attains more power in relating expression to complex traits.
TWAS is also conceptually similar a test for co-localization of signal between expression and complex trait38,39, and we compared to a recently proposed method, COLOC38, that evaluates co-localization of expression at known GWAS risk loci. After matching the false-discovery rate of the two methods in simulations (Methods), TWAS and COLOC had similar power under the single typed causal variant scenario (with slightly lower COLOC power at small GWAS sizes), but TWAS has superior performance when the causal variant was un-typed or in the presence of allelic heterogeneity (Supplementary Figure 10). This is likely due the fact that TWAS explicitly models LD to better capture the un-typed variants.
Finally, we investigated the effect of the expression reference panel size on performance of TWAS (Supplementary Figure 9). In general, TWAS always outperforms eGWAS when multiple variants are causal. Interestingly, power for either approaches does not increase substantially beyond 1,000 expression samples, suggesting that the expression panels analyzed in this manuscript nearly saturate the available imputation accuracy. This was further reflected in an analysis of real data where merging cohorts did not substantially change the distribution of TWAS statistics for the same gene set (Supplementary Figure 14). Although these results come with caveats (e.g. standard assumptions of additive effects and normal residuals), they suggest that the main benefit of larger expression reference panels is in increasing the total number of significant cis-heritable genes available for imputation (Figure 3).
TWAS performance in GWAS summary data
We employed TWAS to identify expression-trait associations at the 697 known GWAS risk loci for height7 using the YFS data for which height was also measured. At each locus, we considered three strategies for selecting a single causal gene: 1) the gene nearest to the top GWAS SNP; 2) the gene for which the index SNP is the strongest eQTL in the training data; 3) the most significant TWAS gene. For each strategy, we then constructed a risk-score using the genetic value of expression for the selected genes and correlated the risk score with height measurements in the YFS individuals (an independent sample from the original height GWAS, Supplementary Note). The R2 between the risk score and height was 0.038 (nearest); 0.031 (eQTL); and 0.054 (TWAS); with TWAS significantly higher than the others in a joint model (Supplementary Table 5, Methods). When we re-computed the risk scores using TWAS values for expression from the NTR cohort (which introduces additional noise due to heterogeneity between the cohorts), TWAS remained significantly higher than the eQTL strategy, but was comparable to selecting the nearest gene (Supplementary Table 5). This indicates that using expression from a different study to select genes still significantly explains variance, but is complementary (rather than superior) to selecting the nearest gene. Working from the assumption that genes with a higher cis-genetic correlation to phenotype are more likely to be causal, these results motivate the use of TWAS to prioritize putative risk genes at known GWAS loci.
Across all known risk loci in our data, 77% of genome-wide significant loci (defined as lead SNP +/−500kb) overlapped at least one gene with significant hg,cis2, and 36% overlapped at least one significant TWAS association (Supplementary Table 6). These results suggest that cis regulation of expression in blood and adipose tissue is an important mechanism through which genetic variation at known risk loci alters obesity related traits. We expect that expression studies from other tissues relevant to obesity-related traits will further increase the overlap. Focusing specifically on the 282 TWAS genes that were within 500kb of the lead SNP, 187 (66%) are not the nearest gene with many residing more than 100kb away from the lead GWAS SNP (Supplementary Figure 15). Since GWAS usually reports the nearest gene, these 187 genes can be considered new candidates for follow-up at known risk loci. We note that gene-trait associations at known risk loci will not be found by TWAS either due to a causal mechanism that does not involve cis-expression of the tested genes, or lack of power to identify and detect all cis-heritable genes at the locus.
Next, we employed TWAS to identify novel expression-trait associations using summary association statistics from a 2010 lipid GWAS17 (~100,000 samples), i.e. associations more than 500Kb away from any genome-wide significant SNPs in that study. We used all three studies (METSIM, YFS, and NTR;) as separate SNP-expression training panels. We then looked for genome-wide significant SNPs at these loci in the larger 2013 lipid GWAS5 (expanded to ~189,000 samples). We identified 25 such expression-trait associations in the 2010 study (Supplementary Table 7), of which 19/25 contained genome-wide significant SNPs in the 2013 study (P=1×10−24 by hypergeometric test, Methods) and 24/25 contained a more significant SNP (P=1×10−04), a highly significant validation of the identified loci. The validation remained significant after conservatively accounting for sample overlap across the studies (binomial P=3×10−16; Methods, Supplementary Table 7). As a sanity check, we compared direct and summary-level TWAS in the METSIM cohort, and found the two sets of imputed expression-trait Z-scores to be nearly identical, with summary-level TWAS slightly under-estimating the effect (Pearson _ρ_=0.96, Supplementary Figure 16). Overall, we find the TWAS approach to be highly predictive of robust phenotypic associations.
TWAS identifies novel expression-trait associations
Having established the utility of TWAS, we applied the approach to identify novel expression-trait associations using summary data from three recent GWAS over more than 900,000 phenotype measurements: lipid measures (high-density lipoproteins [HDL] cholesterol, low-density lipoprotein [LDL] cholesterol, total cholesterol [TC], and triglycerides [TG])5; height7; and BMI6. Significantly cis-heritable genes across the three expression data sets were tested individually (6,924 tests) and together in an omnibus test that accounts for predictor correlation (1,075 tests; Methods), and we conservatively corrected for the 8,000 total tests performed for each trait. Overall, we identified 665 significant gene-trait associations (Supplementary Table 8). Of these, 69 gene-trait associations did not overlap a genome-wide significant SNP in the corresponding GWAS, residing in 60 physically non-overlapping cis-loci (Table 1, Supplementary Table 9). Averaging over the novel genes, the Z2 statistics from TWAS were 1.5x higher than the strongest eQTL SNP for the same gene(though this may be slightly inflated due to winner’s curse). Our previous simulations suggest that the substantial gain over testing the cis-eQTL is an indication of pervasive allelic heterogeneity40 at these loci, and analyses of the expression showed strong evidence for allelic heterogeneity at the TWAS genes (Supplementary Figure 17).
Table 1.
TWAS significant genes with no known GWAS risk variants within 500Kb.
| GWAS | trainingexpression | gene | chr | locus start | locus end | p-value | |||
|---|---|---|---|---|---|---|---|---|---|
| TWAS | permuted | bestcis-SNP | |||||||
| LOCKE.BMI | omnibus | INO80E | 16 | 29506615 | 30517114 | 3E-09 | 3E-07 | 3E-06 | * |
| LOCKE.BMI | omnibus | FTSJ3 | 17 | 61396793 | 62407372 | 1E-07 | 5E-06 | 9E-07 | * |
| LOCKE.BMI | omnibus | PAM | 5 | 101589685 | 102866809 | 3E-07 | 4E-09 | 3E-03 | * |
| LOCKE.BMI | YFS | GGNBP2 | 17 | 34400737 | 35446278 | 1E-06 | 7E-05 | 3E-06 | * |
| LOCKE.BMI | YFS | MYO19 | 17 | 34351477 | 35399284 | 3E-06 | 4E-05 | 3E-06 | * |
| LOCKE.BMI | omnibus | OPRL1 | 20 | 62211526 | 63231996 | 3E-06 | 9E-05 | 2E-05 | * |
| LOCKE.BMI | NTR | RABGAP1 | 9 | 125203287 | 126367145 | 4E-06 | 3E-05 | 1E-05 | * |
| LOCKE.BMI | YFS | SMARCD2 | 17 | 61409444 | 62420425 | 5E-06 | 9E-05 | 9E-07 | * |
| LOCKE.BMI | METSIM | AL049840.1 | 14 | 103677607 | 104679149 | 5E-06 | 5E-05 | 1E-07 | * |
| LOCKE.BMI | omnibus | LPAR2 | 19 | 19234477 | 20239739 | 6E-06 | 3E-05 | 4E-06 | * |
| WILLER.HDL | YFS | MRPS18B | 6 | 30085486 | 31094172 | 1E-07 | 2E-02 | 4E-06 | |
| WILLER.LDL | omnibus | PAM | 5 | 101589685 | 102866809 | 4E-15 | 9E-12 | 2E-03 | * |
| WILLER.LDL | omnibus | ITIH4 | 3 | 52346991 | 53365495 | 8E-09 | 4E-06 | 3E-05 | * |
| WILLER.LDL | omnibus | WARS | 14 | 100300125 | 101343142 | 1E-08 | 6E-07 | 3E-05 | * |
| WILLER.LDL | omnibus | MAN2C1 | 15 | 75148133 | 76160971 | 1E-08 | 1E-05 | 6E-05 | * |
| WILLER.LDL | YFS | DHRS13 | 17 | 26724799 | 27730089 | 6E-07 | 4E-04 | 2E-06 | * |
| WILLER.LDL | YFS | ERAL1 | 17 | 26681956 | 27688085 | 8E-07 | 9E-04 | 2E-06 | |
| WILLER.LDL | YFS | HCG27 | 6 | 30665537 | 31671745 | 2E-06 | 7E-03 | 7E-08 | |
| WILLER.LDL | YFS | VARS2 | 6 | 30376019 | 31394236 | 3E-06 | 2E-02 | 1E-05 | |
| WILLER.LDL | omnibus | PEX6 | 6 | 42431608 | 43446958 | 5E-06 | 3E-05 | 4E-04 | * |
| WILLER.LDL | omnibus | CSK | 15 | 74574398 | 75595539 | 6E-06 | 1E-04 | 1E-05 | * |
| WILLER.TC | omnibus | PAM | 5 | 101589685 | 102866809 | 9E-15 | 3E-13 | 5E-03 | * |
| WILLER.TC | omnibus | WARS | 14 | 100300125 | 101343142 | 2E-08 | 4E-06 | 2E-05 | * |
| WILLER.TC | omnibus | MAN2C1 | 15 | 75148133 | 76160971 | 3E-07 | 7E-05 | 2E-06 | * |
| WILLER.TC | omnibus | ITIH4 | 3 | 52346991 | 53365495 | 6E-07 | 2E-05 | 5E-05 | * |
| WILLER.TC | NTR | CDK2AP1 | 12 | 123245552 | 124256687 | 6E-07 | 2E-04 | 5E-06 | * |
| WILLER.TC | YFS | TBKBP1 | 17 | 45271447 | 46289416 | 9E-07 | 3E-04 | 2E-07 | * |
| WILLER.TC | METSIM | RPP25 | 15 | 74746757 | 75749805 | 2E-06 | 2E-04 | 9E-07 | * |
| WILLER.TC | omnibus | CSK | 15 | 74574398 | 75595539 | 2E-06 | 9E-05 | 9E-07 | * |
| WILLER.TC | YFS | MPI | 15 | 74682346 | 75691798 | 2E-06 | 2E-04 | 5E-06 | * |
| WILLER.TC | omnibus | DAGLB | 7 | 5948757 | 7023821 | 2E-06 | 8E-05 | 7E-06 | * |
| WILLER.TC | NTR | TOM1 | 22 | 35195267 | 36243985 | 2E-06 | 2E-06 | 1E-06 | * |
| WILLER.TC | METSIM | HMGXB4 | 22 | 35153445 | 36191800 | 3E-06 | 4E-05 | 4E-07 | * |
| WILLER.TC | NTR | C17orf68 | 17 | 7628139 | 8651413 | 3E-06 | 6E-06 | 2E-07 | * |
| WILLER.TG | YFS | PABPC4 | 1 | 39526488 | 40542462 | 1E-08 | 1E-04 | 8E-08 | * |
| WILLER.TG | omnibus | PACS1 | 11 | 65337834 | 66512218 | 5E-08 | 3E-04 | 1E-05 | * |
| WOOD.HEIGHT | omnibus | INO80E | 16 | 29506615 | 30517114 | 2E-10 | 2E-05 | 1E-07 | * |
| WOOD.HEIGHT | NTR | INPP5B | 1 | 37825435 | 38912729 | 2E-09 | 1E-06 | 1E-06 | * |
| WOOD.HEIGHT | omnibus | MEGF9 | 9 | 122863091 | 123976748 | 3E-09 | 2E-04 | 1E-07 | * |
| WOOD.HEIGHT | omnibus | ATF1 | 12 | 50657493 | 51714905 | 6E-09 | 4E-05 | 1E-06 | * |
| WOOD.HEIGHT | omnibus | PAM | 5 | 101589685 | 102866809 | 2E-08 | 8E-06 | 1E-05 | * |
| WOOD.HEIGHT | omnibus | CNIH4 | 1 | 224044552 | 225067161 | 3E-08 | 2E-05 | 6E-08 | * |
| WOOD.HEIGHT | omnibus | PLEKHA1 | 10 | 123634212 | 124691867 | 1E-07 | 3E-05 | 6E-07 | * |
| WOOD.HEIGHT | NTR | PDXDC1 | 16 | 14568832 | 15632186 | 1E-07 | 3E-03 | 7E-06 | |
| WOOD.HEIGHT | YFS | MSRB2 | 10 | 22884435 | 23910942 | 2E-07 | 2E-04 | 3E-06 | * |
| WOOD.HEIGHT | YFS | ZNF213 | 16 | 2679778 | 3692806 | 2E-07 | 1E-03 | 6E-07 | |
| WOOD.HEIGHT | NTR | YWHAB | 20 | 43014185 | 44037354 | 5E-07 | 3E-04 | 4E-06 | * |
| WOOD.HEIGHT | NTR | ITM2B | 13 | 48307273 | 49336451 | 5E-07 | 4E-05 | 1E-06 | * |
| WOOD.HEIGHT | omnibus | WDSUB1 | 2 | 159592304 | 160643310 | 7E-07 | 3E-04 | 5E-06 | * |
| WOOD.HEIGHT | NTR | STAT6 | 12 | 56989190 | 58005129 | 8E-07 | 3E-03 | 8E-06 | |
| WOOD.HEIGHT | omnibus | PLCL1 | 2 | 198169426 | 199937305 | 9E-07 | 4E-03 | 6E-07 | |
| WOOD.HEIGHT | YFS | H2AFJ | 12 | 14427270 | 15430936 | 1E-06 | 4E-04 | 6E-07 | * |
| WOOD.HEIGHT | YFS | FAM8A1 | 6 | 17100586 | 18111950 | 1E-06 | 2E-03 | 1E-07 | |
| WOOD.HEIGHT | METSIM | AC016995.3 | 2 | 38133861 | 39242882 | 1E-06 | 3E-04 | 4E-05 | * |
| WOOD.HEIGHT | omnibus | CDA | 1 | 20415441 | 21445401 | 1E-06 | 3E-04 | 6E-07 | * |
| WOOD.HEIGHT | YFS | ECHDC2 | 1 | 52861656 | 53892884 | 1E-06 | 3E-03 | 1E-05 | |
| WOOD.HEIGHT | YFS | NFATC3 | 16 | 67618654 | 68763162 | 2E-06 | 4E-03 | 4E-07 | |
| WOOD.HEIGHT | YFS | SH3YL1 | 2 | −282270 | 766398 | 2E-06 | 1E-04 | 6E-07 | * |
| WOOD.HEIGHT | omnibus | PABPC4 | 1 | 39526488 | 40542462 | 3E-06 | 4E-04 | 6E-06 | * |
| WOOD.HEIGHT | METSIM | RP11-473M20.14 | 16 | 2666043 | 3684883 | 3E-06 | 4E-03 | 1E-07 | |
| WOOD.HEIGHT | omnibus | HEBP1 | 12 | 12627798 | 13653207 | 3E-06 | 7E-04 | 1E-06 | * |
| WOOD.HEIGHT | YFS | KBTBD2 | 7 | 32407784 | 33433743 | 3E-06 | 4E-03 | 1E-07 | |
| WOOD.HEIGHT | METSIM | LRRC69 | 8 | 91614060 | 92731464 | 3E-06 | 6E-04 | 6E-07 | * |
| WOOD.HEIGHT | YFS | RAB23 | 6 | 56553607 | 57587078 | 4E-06 | 4E-03 | 6E-07 | |
| WOOD.HEIGHT | YFS | PPP4C | 16 | 29587299 | 30596698 | 5E-06 | 1E-03 | 1E-07 | |
| WOOD.HEIGHT | NTR | B3GALNT2 | 1 | 235110442 | 236167884 | 5E-06 | 5E-04 | 1E-06 | * |
| WOOD.HEIGHT | YFS | PSRC1 | 1 | 109322178 | 110325808 | 5E-06 | 3E-04 | 1E-07 | * |
| WOOD.HEIGHT | YFS | ACSS1 | 20 | 24486868 | 25539616 | 5E-06 | 6E-04 | 1E-06 | * |
| WOOD.HEIGHT | omnibus | GGPS1 | 1 | 234990665 | 236007847 | 5E-06 | 4E-04 | 3E-07 | * |
We further sought to quantify the significance of the expression-trait associations conditional on the SNP-trait effects at the locus with a permutation test (Methods). Comparing to this null assesses how much signal is added by the true expression given the specific architecture of the locus. Of the 69 genes, this permutation test was significant for 54 (after accounting for 69 tests). After excluding these individually significant genes, the P-values were still substantially elevated with λGC of 19 (ratio of median _χ_2 to the expected null). For these 54 genes, we can confidently conclude that integration of expression data significantly refined the association to trait. As before, more evidence of allelic heterogeneity of expression was observed at the loci that passed permutation (Supplementary Figure 17). Our results are consistent with a model of causality where these genes harbor inherited causal variants that modulate expression, which in turn has a complex effect on the cell and downstream impact on complex traits6.
Next, we evaluated the contribution to heritability of all expression-trait associations, including those that were not genome-wide significant (Methods,29,30). We estimated the variance in trait explained by all METSIM+YFS imputed genes (hGE2) to be 3.4% averaged over six traits (Supplementary Table 10). We assumed independence between the two cohorts, and did not include the NTR genes because of its strong correlation with YFS. Height had the most variance attributable to the heritable genes at hGE2=7.1%. These combined estimates were consistently higher than a corresponding analysis using predictions from permuted expression (Supplementary Table 10). For the four traits with individual-level genotype and phenotype data in the METSIM (BMI, TG, WHR, INS), we estimated hGE2 directly using variance-components over the imputed expression values (Methods). On average, all significantly heritable genes in adipose + blood explained 4–6% of the trait variance (16–19% of the total trait hg2), and were largely orthogonal between the two predictions (Supplementary Table 11). The imputed expression consistently explained more trait variance than the best cis-eQTL in each gene and did not strongly depend on the cis-window size (Supplementary Table 12).
Re-evaluation using other expression cohorts
To replicate the 69 novel expression-trait associations, we re-evaluated the GWAS summary statistics with expression data from two external studies: eQTLs from ~900 samples in the MuTHER study25 of fat, LCL, and skin cells; and separate eQTL data from 5,311 samples across in whole blood11 (Methods). These expression studies only consist of summary-level associations, and are expected to be much noisier as reference. In the relatively smaller MuTHER sample, 20 out of 55 available genes replicated significantly in at least one tissue (after accounting for 55 tests, Supplementary Table 9). This is substantial given the apparent heterogeneity between cohorts we previously observed (Methods). Importantly, the correlations between discovery and replication Z-scores were strongest for associations found in the corresponding tissue (_ρ_=0.60, P=1.5×10−05 for blood/LCL; _ρ_=0.66, P=0.05 for adipose, Supplementary Table 13); a significant aggregate replication and further evidence for the tissue-specific nature of our findings. Using the larger, but heterogeneous, training sample from ref.11, 24 out of 37 available genes replicated significantly (Supplementary Table 9). Although these replications are not strictly independent (they use the same GWAS data), they demonstrate that many of the novel loci are consistently significant across diverse expression cohorts.
Functional analysis of the novel associations
To better understand their functional consequences, we evaluated the 69 novel genes in the Hybrid Mouse Diversity Panel (HMDP) for correlation with multiple obesity-related traits. This panel includes 100 inbred mice strains with extensive collection of obesity-related phenotypes from ~12,000 genes. Of the 69 novel TWAS genes previously identified, 40 were present in the panel and could be evaluated for effect on phenotype. Of these, 26 were significantly associated with at least one obesity-related trait (after accounting for genes tested) and 14 remained significant after accounting for 36 phenotypes tested (very conservatively assuming the phenotypes were independent) (Supplementary Table 14). 77% of the genes with an association were associated with multiple phenotypes. For example, expression of Ftsj3 was significantly correlated with fat mass, glucose-to-insulin ratio, and body weight in both liver and adipose tissue, with R2 ranging from 0.20–0.28. Another candidate, Iih4, was significantly correlated with LDL and TC levels in liver. In humans, this gene is also linked to hypercholesterolemia in OMIM and was previously associated with BMI in East Asians41. Due to complex correlation of phenotypes, it is difficult to assess whether this gene set is significant in aggregate and genes in the HMDP are typically expected to have strong effects. We could not perform enough random selections of genes to establish significance for this set. However, we consider the 26 individually significant genes to be fruitful targets for follow-up studies.
The BMI and height GWAS evaluated functional enrichment at identified loci, and we performed similar analyses for the novel genes that we identified. We tested the 10 novel BMI genes and 33 novel height genes for tissue-specific enrichment using DEPICT42, a method based on large-scale gene co-expression analyses, following the protocol of the original GWAS studies6,7. Analysis of BMI identified significant enrichment for hypothalamus and neurosecretory systems (P=2.6×10−4, significant at FDR<5%). This enrichment is consistent with the landmark finding in the original study6 showing enrichment in these and other central nervous system tissues. Notably, we recapitulated this result using only novel genes that did not overlap any genome-wide significant SNPs. In analysis of height, DEPICT did not identify any tissue-specific enrichment.
Discussion
In this work we proposed methods that integrate genetic and transcriptional variation to identify genes with expression associated to complex traits. Using imputed gene expression to guide GWAS has three potential advantages. First, the gene is a more interpretable biological unit than an associated locus, which often contains multiple significant SNPs in LD that may not lie in genes and/or tag variants in multiple genes. Second, the lower total number of genes (or cis-heritable genes) means the multiple-testing burden is substantially reduced relative to all SNPs. Lastly, combining cis-SNPs into a single predictor may capture heterogeneous signal better than individual SNPs or cis-eQTLs. Focusing the prediction on the genetic component of expression also avoids confounding from environmental differences caused by the trait that may impact expression. Our approach builds upon the wealth of GWAS data in massive cohorts to directly implicate the gene-based mechanisms underlying complex traits.
Our proposed method shares conceptual similarities with 2-sample Mendelian randomization approaches that aim to identify causal relations between traits using genetic variation predictions as a randomizer43–45. However, while Mendelian randomization is intended to quantify the total causal effect, our method has the less strict goal of identifying significant associations and can operate on summary GWAS data. Importantly, our approach maintains the attractive feature of not being confounded by effects on expression and trait that are independent of the SNPs. Other recent work proposed to leverage summary statistics to estimate the underlying genetic correlation between traits at the genome-wide level37, but cannot be applied locally as it requires multiple loci to estimate standard errors (Methods). Recent work in parallel to ours also proposes gene expression imputation from individual-level data to find expression-trait associations and observes benefits from a reduced multiple-testing burden and increased interpretability16. In contrast, our approach does not require individual GWAS data and is applicable directly to GWAS summary data of very large sample sizes thus increasing discovery power.
Unlike current methods, which focus on individually significant eQTL and SNP associations5,6,8,9,11,13,26,29, our approach captures the full cis-SNP signal and does not require any individual marker to be significant. This is underscored by the fact that TWAS substantially outperformed its cis-eQTL analog both in imputing expression and in association to trait. Our results show that the imputation approach is especially effective when multiple variants influence expression (which in turn influences trait). The large number of new associations identified in real data supports this phenomenon and suggests that it may be a strong contributor to common phenotypes46. Therefore, our approach can be seen as complementary to GWAS by identifying expression-trait associations that are not well explained by individual tagging SNPs. Future work could leverage the difference in performances of TWAS and GWAS to explicitly detect allelic heterogeneity. We note that it is still possible for some loci to have an independent SNP-phenotype and SNP-expression association driven by the same underlying variant though we consider this to be an infrequent biological model.
We conclude with several limitations of our approach. First, disease-impacting variants that are independent of cis-expression – in general or in the training data – will not be identified. Second, as with any prediction, the number of genes that can be accurately imputed is still limited by the training cohort size and the quality of the training data. In particular, we found that prediction accuracy did not correspond to theoretical expectations and is likely driven by data quality. The impact of these weaknesses could be better quantified as expression from larger sample sizes and a more diverse set of tissues becomes available. Although in this work we utilized both microarray and RNA-seq as measure of gene expression thus showcasing the applicability of our approach to diverse data sets, the accuracy of our method intrinsically depends on the quality of the expression measurements. For the associated genes, it remains possible that the effect is actually mediated by phenotype (i.e. SNP → phenotype → cis-expression, Figure 2F). We attempted to quantify this in the YFS data by conditioning the heritability analyses on all the evaluated phenotypes (height, BMI, and lipids) but observed no significant change at individual genes or in the mean cis-hg2. These results suggest that confounding from phenotype does not substantially affect the tested cis expression, though at the current sample size we cannot completely rule out such confounders for individual genes. An alternative confounder arises from independent effects on phenotype and expression at the same SNP/tag (Figure 2G, Methods). Such instances could be indistinguishable from the desired causal model (Methods) without analyzing individual-level data, though we believe they are still biologically interesting cases of co-localization. Both types of confounding could potentially be quantified by training the SNP-expression relationships in control individuals where phenotype is fixed, or by interrogating the gene experimentally. Lastly, the summary-based TWAS cannot account for rare variants that are poorly captured by the LD reference panel, or optimally capture non-linear relationships between SNPs and expression. Additional sources of information could potentially be incorporated to improve the prediction, including significant trans-associations11,28; allele-specific expression47,48; splice-QTLs effecting individual exons10; haplotype effects; and SNP-specific functional priors20,49–51.
Online Methods
Data sets
In this study, we included 11,484 participants from two Finnish population cohorts, the METabolic Syndrome in Men (METSIM, n=10,197)52,53 and the Young Finns Study (YFS, n=1,414)22,23. 1,400 randomly selected individuals from the 10,197 METSIM participants underwent a subcutaneous abdominal adipose biopsy of which 600 RNA samples were analyzed using RNA-seq (Supplementary Note). Traits BMI, TG, WHR, and INS were inverse rank transformed and adjusted for age and age-square. INS was additionally adjusted for T1D and T2D. 1,414 individuals (638 men with a median age of 43 years and 776 women with a median age of 43) with gene expression, phenotype, and genotype data available were included in the blood expression analysis. Traits height, BMI, TG, TC, HDL, and LDL were inverse rank transformed and adjusted for age, age-square, and sex. TC was also adjusted for Statin intake. The biochemical lipid, glucose, and other clinical and metabolic measurements of METSIM and YFS were performed as described previously22,52,54. Complete details on the pipeline and quality control procedures can be found in Supplementary Note.
Heritability estimation with individual data
Cis and trans variance components were estimated using the REML algorithm implemented in GCTA19. As in previous studies, estimates were allowed to converge outside the expected 0–1 bound on variance to achieve unbiased mean estimates across all genes24. Standard error across gene sets was estimated by dividing the observed standard deviation by the square root of the number of genes that converged (this will lead to underestimation due to correlated genes, but is presented for completeness). Genome-wide h2g for the four traits in the GWAS cohort was estimated with GCTA from a single relatedness matrix constructed over all post-QC SNPs in the strictly unrelated individuals. For estimating expression-wide h2GE, each predicted expression value was standardized to mean=0 and variance=1, and sample covariance across these values used to define the relatedness matrix. The hGE2 was then estimated from this component with GCTA, with P-values for difference from zero computed using a likelihood ratio test. 20 principal components (PCs) were always included as fixed-effects to account for ancestry. Genetic correlation between traits in the GWAS cohort was estimated from all post-QC SNPs in the full set of 10,000 individuals with GEMMA31 (Supplementary Table 15). For the YFS, we quantified the mediating effects of trait on cis-expression by separately re-estimating cis-h2g with all analyzed traits (height, BMI, TC, TG, HDL, LDL) included as fixed-effects in addition to PCs. We did not observe significant differences in any individual gene (after accounting for 3,836 genes tested) nor in the mean estimate of cis-h2g.
Heritability estimation with summary data
As shown in ref.51,55, for an association study of N independent samples, the expected χ2 statistic is E[χ2] = 1 + Nlh2GE/M, where l is the LD-score accounting for correlation, M is the number of markers, and h2GE is the variance in trait explained by the imputed expression. We estimated l directly from the genetic values of expression to be close to independence (1.4, 1.5 for METSIM, YFS) allowing us to solve for h2GE from the observed distribution of χ2 (or, asymptotically equivalent Z2) statistics. We did not compute this value for the BMI GWAS because the conservative multiple GC-correction applied in that study would yield a severe downwards bias6.
Imputing expression into genotyped samples
We evaluated three prediction schemes: i. cis-eQTL, the single most significantly associated SNP in the training set was used as the predictor; ii. the best linear predictor (BLUP)30, estimates the causal effect-sizes of all SNPs in the locus jointly using a single variance-component; iii. The Bayesian linear mixed model (BSLMM)31, which estimates the underlying effect-size distribution and then fits all SNPs in the locus jointly. For the BLUP and BSLMM, prediction was done over all post-QC SNPs using GEMMA31. We note that the BLUP/BSLMM both perform shrinkage of the SNP weights but not variable selection, so all SNPs are included in the predictor. Recent work in parallel to ours also evaluated expression imputation using polygenic risk scores, LASSO, and elastic net16.
Evaluating prediction accuracy
Within-study prediction accuracy was measured by five-fold cross-validation in a random sampling of 1,000 of the highly heritable genes (i.e. significant non zero cis-heritability) for each study. Cross-study prediction accuracy was measured by merging the YFS/NTR genotyped individuals and predicting from all individuals in one cohort into all individuals in the other. In all instances, the R2 between predicted and true expression across all predicted folds was used to evaluate accuracy (see Supplementary Note).
Imputing expression into GWAS summary statistics
Summary-based imputation was performed using the ImpG-Summary algorithm4 extended to train on the cis-genetic component of expression. Let Z be a vector of standardized effect sizes (z-scores) of SNP on trait at a given cis-locus (i.e. Wald statistics β/se(β) ). We impute the z-score of the expression and trait as a linear combination of elements of Z with weights W (these weights are precompiled from the reference panel as Σ_e,s_Σ_−1s,s_ for ImpG-Summary or directly from BSLMM). Σ_e,s_ is the covariance matrix between all SNPs at the locus and gene expression and Σ_s,s_ is the covariance among all SNPs (i.e. linkage disequilibrium). Under null data (no association) and a multi-variate normal assumption Z ~ N(0,Σ_s,s_). It follows that imputed z-score of expression and trait (WZ) has variance W Σ_s,s W_t; therefore, we use WZ/(W Σ_s,s W_t )1/2 as the imputation Z-score of cis-genetic effect on trait. In practice, for each gene, all SNPs within 1Mb of the gene present in the GWAS study were selected, and Σ_s,s_ and Σ_e,s_ were computed in the reference panel (i.e. expression and SNP data). To account for finite sample size and instances where Σ_s,s_ is not invertible, we adjusted the diagonal of the matrix using a technique similar to ridge regression with λ=0.1 (as evaluated in Pasaniuc et al4). This regularization, as well as noise in the estimation of W, can translate to lower power for association but yield conservative imputed Z-statistics.
We used the YFS samples that were assayed for SNPs, phenotype, and expression to assess the consistency of individual-level and summary-based TWAS. We first computed GWAS association statistics between phenotype (height) and SNP and used them in conjunction with the expression data to impute summary-based TWAS statistics. The TWAS statistics were compared to those from the simple regression of (height ~ expression) in the YFS data. We observed a correlation of 0.415 (Supplementary Figure 5), consistent with an average cis-h2g of 0.17 (≈0.415^2) observed for these genes. When restricting to a regression of (height ~ cis component of expression) we observed a correlation of 0.998 to the summary based TWAS, demonstrating the equivalence of the two approaches when using in-sample LD.
Power analysis of summary-based method
Simulations to evaluate the summary-based method were performed in 6,000 unrelated METSIM GWAS individuals. 100 genes and the SNPs in the surrounding 1MB were randomly selected for testing. For each gene, normally distributed gene expression was simulated as E = Xβ + ε; where X is a matrix of the desired number of causal genotypes, sampled randomly from the locus; β is a vector of normally distributed effect-sizes for each causal variant; and ε is a vector of normally distributed noise to achieve a cis-h2g of 0.17 (corresponding to the mean observed in our significant gene sets). 1,000 individuals with SNPs and simulated expression were then withheld for training the predictors. For the remaining 5,000 individuals, normally distributed noise was applied to the expression to generate a heritable phenotype where expression explained 0.10/180 or 0.20/180 of the phenotypic variance (the former corresponding to the average effect-sizes for associated genes observed in a large GWAS of height56 and the latter to high-effect loci). Association between SNP and phenotype was estimated in the 5,000 individuals (standard Z-score), and the phenotype generation repeated with different environmental noise (up to 60 times) to generate results from multiple GWAS sub-studies. Association statistics from each run were then meta-analyzed to reach precision corresponding to a larger GWAS of desired size (up to 300,000) (Supplementary Note).
Detecting a locus was defined as follows. The single most significant trait associated SNP was taken as the GWAS association, considered detected if GWAS significance was <5×10−8. The single most significant eQTL in the training set was taken as the eQTL-guided association (eGWAS), and considered detected if GWAS significance was <0.05/15,000. The TWAS association was measured by training the imputation algorithm on the 1,000 held-out samples with expression and imputing into the GWAS summary statistics, and considered detected if significance was <0.05/15,000. The entire procedure was repeated 500 times (5 per gene) and power was estimated by counting the fraction of instances where each method detected the locus. As in the cross-validation analysis, training on the genetic component of expression instead of the overall expression consistently increased TWAS power by ~10% (Supplementary Figure 7). Two null expression models were tested by generating gene expression for the 1,000 held-out samples that was standard normal as well as heritable expression (cis-h2g=0.17) with GWAS Z-scores drawn from the standard normal (Supplementary Table 4). See Supplementary Note for detailed simulation setup.
Power comparison to COLOC
COLOC uses summary data from eQTL and GWAS studies and a Bayesian framework to identify the subset of GWAS signals that co-localize with eQTLs. We sought to compare TWAS to the COLOC-estimated posterior probability of association (PPA) being shared for both phenotypes (PP4 in the COLOC implementation). COLOC additionally evaluates the hypothesis of multiple independent associations (PP3), but this is more general than the proposed TWAS model and was not tested. Because COLOC relies on priors of association to produce posterior probabilities of co-localization, we sought to identify a significance threshold that would make a fair comparison to the TWAS p-value-based threshold. Specifically, we ran both methods on a realistic null expression simulation (with the generative model described previously): the expression was sampled from a null standard normal for 1,000 individuals and eQTLs computed; the trait associations were derived from a simulated 300,000 GWAS with a single typed causal variant that explained 0.001 variance of the trait (high effect). We believe this scenario is both realistic and consistent with the GWAS assumptions of COLOC. We then empirically identified the statistical threshold for COLOC and TWAS that would yield a 5% false discovery rate: co-localization statistic PP4 > 0.17 for COLOC, and P<0.05 for TWAS. We note that this empirical COLOC threshold is much less stringent than PP4>0.8 used in the COLOC paper (PP4>0.8 would yield lower power for COLOC in our simulations). These thresholds were subsequently to evaluate the power to detect an expression-trait association in simulations with a true effect (Supplementary Figures S10, 12). The reported power is for a single locus and we did not attempt to quantify genome/transcriptome-wide significance.
Individual-level analysis of METSIM GWAS
We imputed the significantly heritable genes into the METSIM GWAS cohort of 5,500 unrelated individuals with individual-level genotypes (and unmeasured expression). We then tested the imputed expression for obesity-related traits: body mass index (BMI); triglycerides (TG); waist-hip-ratio (WHR); and fasting insulin levels (INS). Overall, the evaluated traits exhibited high phenotypic and genetic correlation as well as highly significant genome-wide h2g ranging from 23–36% (Supplementary Table 15) consistent with common variants having a major contribution to disease risk1. Association was assessed using standard regression as well as a mixed-model that accounted for relatedness and phenotypic correlation31 with similar results. The effective number of tests for each trait was estimated by permuting the phenotypes 10,000 times and, for each permutation, re-running the association analysis on all predicted genes. For each trait P_perm_, the P-value in the lowest 0.05 of the distribution, was computed and the effective number of tests was 0.05/P_perm_, reported in Supplementary Table 16. All phenotypes were shuffled together, so any phenotypic correlation was preserved. The effective number of tests corresponded to 88–95% of the total number of genes, indicating a small amount of statistical redundancy (Supplementary Note). To evaluate the TWAS approach, we computed phenotype association statistics for the 5,500 unrelated individuals and re-ran the analysis using only these summary statistics and the same expression reference panels. The resulting TWAS associations were nearly identical to the direct TWAS associations across the four traits (Pearson _ρ_=0.96). Reassuringly, the TWAS was generally more conservative than the direct estimates (Supplementary Figure 16).
Refining trait-associated genes at known loci
We focused on GWAS data from height7 that identified 697 genome-wide significant variants in 423 loci, and conducted the summary-based TWAS over all genes in these loci using YFS and NTR as expression training data. Because the YFS individuals had been phenotyped for height and not tested in the GWAS, we could directly evaluate whether selected genes were associated with phenotype. At each locus, we considered three strategies for selecting a single causal gene: 1) the gene nearest to the most significantly associated SNP; 2) the gene for which the index SNP is the strongest eQTL in the training data; 3) the most significant TWAS gene. For each strategy, we then constructed a risk-score using the genetic value of expression for the selected gene weighted by the corresponding TWAS Z-score. The same procedure was then re-evaluated using TWAS values trained in the NTR cohort (which introduces additional noise due to heterogeneity between the cohorts, Supplementary Table 5).We separately used GCTA to estimate the heritability of height explained by all of the genes selected by each algorithm by constructing a GRM from the selected genes. In contrast to the risk score, this does not assume pre-defined weights on each gene but allows them to be fit by the REML model. Results were comparable, with only the TWAS-selected genes explaining significantly non-zero heritability (Supplementary Table 5).
Validation analysis in lipid GWAS data
We evaluated the performance of TWAS by identifying significantly associated genes in the 2010 lipid study that did not overlap a genome-wide significant SNP, and looking for newly genome-wide significant SNPs in the expanded 2013 study. The P-value for the number of genes with increased significance and genome-wide significance in the 2013 study was computed by a hypergeometric test, with background probabilities estimated from the set of significantly heritable genes. Of the genes not overlapping a significant locus in the 2010 study, 70% had a more significant SNP in the 2013 study and 3.5% overlapped a genome-wide significant SNP (P<5×10−08).
Meta-analysis of imputed expression from multiple tissues
We proposed a novel omnibus test for significant association across predictions from all three cohorts. Because the imputation is made into the same GWAS cohort, correlation between predictors must be accounted for. For each gene i, we estimated a correlation matrix Ci by predicting from the three tissues into the ~5,500 unrelated METSIM GWAS individuals (though any large panel from the study population could be used). This correlation includes both the genetic correlation of expression as well as any correlated error in the predictors, thus capturing all redundancy. On average, a correlation of 0.01, 0.01, and 0.43 was observed between YFS:METSIM, NTR:METSIM, and YFS:NTR, highlighting the same tissue of origin the last pair. We then used the three-entry vector of TWAS predictions, Z_i_, to compute the statistic omnibusi = Z_i_′ Ci_−1 Z_i which is approximately χ2 (3-dof) distributed and provides an omnibus test for effect in any tissue while accounting for correlation57,58. Though the correlation observed in our data was almost entirely driven by the YFS:NTR blood datasets, we expect this to be an especially useful strategy for future studies with many correlated tissues. An alternative approach would be to perform traditional meta-analysis across the three cohorts and then predict the TWAS effect. However, this would lose power when true eQTL effect-sizes (or LD) differ across the cohorts, which we have empirically observed to be the case looking at predictor correlations above. The proposed omnibus test aggregates different effects across the studies, at the cost of additional degrees of freedom.
Gene permutation test
The standard TWAS Z-score is a test against the null of no SNP-trait association; that is ZTWAS = WZ/(W Σ_s,s W_t )1/2 is well calibrated (i.e. has a 0 mean and unit variance) only under the null model of Z ~ N(0,Σ_s,s_). In the alternate model where Z is drawn from a non-zero mean distribution59,60, ZTWAS has a distribution that depends both on Z as well as the weights W. To quantify the impact of the weights on ZTWAS regardless of whether Z is null or non-null we conduct permutations conditional on the observed Z vector. For each gene, the expression labels were randomly shuffled and the summary-based TWAS analysis trained on the resulting expression to compute a permuted new null for ZTWAS. Testing against this permuted null distribution is equivalent to testing for an expression-trait association (or genetic correlation between expression and trait, see below) conditional on the observed GWAS statistics at the locus (which may not be drawn from the null of no association). The permutation test empirically computes this distribution of ZTWAS values conditional on the observed Z and asks how extreme is the observed ZTWAS among all possible W coming from permuted expression data. Note that failing the permutation test may be an indication of lack of power to show that the expression significantly refines the direct SNP-trait signal. In practice, the permutation test was run 1,000 times for each TWAS gene and a p-value computed by Z-test against this null.
Relationship to genetic covariance/correlation
Our tests relate to previously defined estimators of genetic correlation and covariance between traits. We consider two definitions of genetic covariance at a locus: 1) the covariance between the genetic component of expression and the genetic component of trait; 2) the covariance between the causal effect sizes for expression and the causal effect-sizes for trait. Under assumptions of independent effect-sizes, these definitions yield asymptotically identical quantities37. Assuming a substantially large training set where the genetic component of expression can be perfectly predicted, the direct TWAS tests for a significant association between the genetic component of expression and the trait; equivalent to testing definition #1 for a polygenic trait. Likewise, the summary-based TWAS tests for a significant sum of products of the causal expression effect sizes and the causal trait effect sizes; equivalent to definition #2 up to a scaling factor. The TWAS approach therefore fits naturally with the broader study of shared genetic etiology of multiple phenotypes. At the sample sizes evaluated in this study, the TWAS approach is substantially better powered than an LD-based estimate of local genetic correlation (Supplementary Note).
Supplementary Material
Supplementary Figures
Supplementary Note
Supplementary Tables
Acknowledgments
We thank the individuals who participated in the study. We also acknowledge Liming Yang for helpful discussions that have improved the quality of this manuscript. We would also like to thank Karen Mohlke, Michael Boehnke and Francis Collins for help with the METSIM data. This work was funded in part by NIH grants F32 GM106584 (A.G.), R1 GM053725 (B.P.), R01 GM105857 (A.L.P., A.G., G.B.), HL-28481 (P.P., A.J.L., M.C.), HL-095056 (P.P., B.P.), and by the NIH training grant in Genomic Analysis and Interpretation T32 HG002536 (A.K.)
Footnotes
Author Contributions
AG and BP conceived and designed the experiments. AG, AK HS performed the experiments and analyzed the data. GB WC BJP RJ EdG DB FW PS EN MA MC AL TL ER MK IS OR JK ML generated data/reagents/materials and analysis tools. AG ALP PP and BP wrote the paper. All authors reviewed, revised and wrote feedback for the manuscript.
The authors declare no competing financial interests.
Data access.
The predictor weights computed from all three expression studies, as well as software to perform individual and summary-level prediction are available at: http://bogdan.bioinformatics.ucla.edu/software/twas/.
NTR expression data and genotypes are available in dbGaP under accession phs000486.v1.p1.
References
- 1.Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. Am J Hum Genet. 2012;90:7–24. doi: 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang J, et al. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat Genet. 2012;44:369–75. S1–3. doi: 10.1038/ng.2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lee D, Bigdeli TB, Riley BP, Fanous AH, Bacanu SA. DIST: direct imputation of summary statistics for unmeasured SNPs. Bioinformatics. 2013;29:2925–7. doi: 10.1093/bioinformatics/btt500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pasaniuc B, et al. Fast and accurate imputation of summary statistics enhances evidence of functional enrichment. Bioinformatics. 2014;30:2906–14. doi: 10.1093/bioinformatics/btu416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Global Lipids Genetics C et al. Discovery and refinement of loci associated with lipid levels. Nat Genet. 2013;45:1274–83. doi: 10.1038/ng.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Locke AE, et al. Genetic studies of body mass index yield new insights for obesity biology. Nature. 2015;518:197–206. doi: 10.1038/nature14177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wood AR, et al. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat Genet. 2014;46:1173–86. doi: 10.1038/ng.3097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Musunuru K, et al. From noncoding variant to phenotype via SORT1 at the 1p13 cholesterol locus. Nature. 2010;466:714–9. doi: 10.1038/nature09266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lappalainen T, et al. Transcriptome and genome sequencing uncovers functional variation in humans. Nature. 2013;501:506–11. doi: 10.1038/nature12531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang X, et al. Identification of common genetic variants controlling transcript isoform variation in human whole blood. Nat Genet. 2015 doi: 10.1038/ng.3220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Westra HJ, et al. Systematic identification of trans eQTLs as putative drivers of known disease associations. Nat Genet. 2013;45:1238–43. doi: 10.1038/ng.2756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Albert FW, Kruglyak L. The role of regulatory variation in complex traits and disease. Nat Rev Genet. 2015 doi: 10.1038/nrg3891. [DOI] [PubMed] [Google Scholar]
- 13.Raj T, et al. Polarization of the effects of autoimmune and neurodegenerative risk alleles in leukocytes. Science. 2014;344:519–23. doi: 10.1126/science.1249547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Letourneau A, et al. Domains of genome-wide gene expression dysregulation in Down’s syndrome. Nature. 2014;508:345–50. doi: 10.1038/nature13200. [DOI] [PubMed] [Google Scholar]
- 15.Davis LK, et al. Partitioning the heritability of Tourette syndrome and obsessive compulsive disorder reveals differences in genetic architecture. PLoS Genet. 2013;9:e1003864. doi: 10.1371/journal.pgen.1003864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gamazon ER, et al. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet. 2015;47:1091–8. doi: 10.1038/ng.3367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Teslovich TM, et al. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466:707–13. doi: 10.1038/nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang J, et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42:565–9. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gusev A, et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am J Hum Genet. 2014;95:535–52. doi: 10.1016/j.ajhg.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wray NR, et al. Pitfalls of predicting complex traits from SNPs. Nat Rev Genet. 2013;14:507–15. doi: 10.1038/nrg3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nuotio J, et al. Cardiovascular risk factors in 2011 and secular trends since 2007: the Cardiovascular Risk in Young Finns Study. Scand J Public Health. 2014;42:563–71. doi: 10.1177/1403494814541597. [DOI] [PubMed] [Google Scholar]
- 23.Raitakari OT, et al. Cohort profile: the cardiovascular risk in Young Finns Study. Int J Epidemiol. 2008;37:1220–6. doi: 10.1093/ije/dym225. [DOI] [PubMed] [Google Scholar]
- 24.Wright FA, et al. Heritability and genomics of gene expression in peripheral blood. Nat Genet. 2014;46:430–7. doi: 10.1038/ng.2951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Grundberg E, et al. Mapping cis- and trans-regulatory effects across multiple tissues in twins. Nat Genet. 2012;44:1084–9. doi: 10.1038/ng.2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nicolae DL, et al. Trait-associated SNPs are more likely to be eQTLs: annotation to enhance discovery from GWAS. PLoS Genet. 2010;6:e1000888. doi: 10.1371/journal.pgen.1000888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Torres JM, et al. Cross-tissue and tissue-specific eQTLs: partitioning the heritability of a complex trait. Am J Hum Genet. 2014;95:521–34. doi: 10.1016/j.ajhg.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Buil A, et al. Gene-gene and gene-environment interactions detected by transcriptome sequence analysis in twins. Nat Genet. 2015;47:88–91. doi: 10.1038/ng.3162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nica AC, et al. Candidate causal regulatory effects by integration of expression QTLs with complex trait genetic associations. PLoS Genet. 2010;6:e1000895. doi: 10.1371/journal.pgen.1000895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Robinson GK. That BLUP is a good thing: the estimation of random effects. Statistical science. 1991:15–32. [Google Scholar]
- 31.Zhou X, Carbonetto P, Stephens M. Polygenic modeling with bayesian sparse linear mixed models. PLoS Genet. 2013;9:e1003264. doi: 10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dudbridge F. Power and predictive accuracy of polygenic risk scores. PLoS Genet. 2013;9:e1003348. doi: 10.1371/journal.pgen.1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chatterjee N, et al. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nat Genet. 2013;45:400–5. 405e1–3. doi: 10.1038/ng.2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brown CD, Mangravite LM, Engelhardt BE. Integrative modeling of eQTLs and cis-regulatory elements suggests mechanisms underlying cell type specificity of eQTLs. PLoS Genet. 2013;9:e1003649. doi: 10.1371/journal.pgen.1003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wen X, Luca F, Pique-Regi R. Cross-population joint analysis of eQTLs: fine mapping and functional annotation. PLoS Genet. 2015;11:e1005176. doi: 10.1371/journal.pgen.1005176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wood AR, et al. Another explanation for apparent epistasis. Nature. 2014;514:E3–5. doi: 10.1038/nature13691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bulik-Sullivan B, et al. An atlas of genetic correlations across human diseases and traits. Nat Genet. 2015;47:1236–41. doi: 10.1038/ng.3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Giambartolomei C, et al. Bayesian test for colocalisation between pairs of genetic association studies using summary statistics. PLoS Genet. 2014;10:e1004383. doi: 10.1371/journal.pgen.1004383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lee D, et al. JEPEG: a summary statistics based tool for gene-level joint testing of functional variants. Bioinformatics. 2015;31:1176–82. doi: 10.1093/bioinformatics/btu816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pritchard JK, Cox NJ. The allelic architecture of human disease genes: common disease-common variant...or not? Hum Mol Genet. 2002;11:2417–23. doi: 10.1093/hmg/11.20.2417. [DOI] [PubMed] [Google Scholar]
- 41.Wen W, et al. Meta-analysis of genome-wide association studies in East Asian-ancestry populations identifies four new loci for body mass index. Hum Mol Genet. 2014;23:5492–504. doi: 10.1093/hmg/ddu248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pers TH, et al. Biological interpretation of genome-wide association studies using predicted gene functions. Nat Commun. 2015;6:5890. doi: 10.1038/ncomms6890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Smith GD, Ebrahim S. ‘Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease? Int J Epidemiol. 2003;32:1–22. doi: 10.1093/ije/dyg070. [DOI] [PubMed] [Google Scholar]
- 44.Pickrell J. Fulfilling the promise of Mendelian randomization. 2015. [Google Scholar]
- 45.Pierce BL, Burgess S. Efficient design for Mendelian randomization studies: subsample and 2-sample instrumental variable estimators. Am J Epidemiol. 2013;178:1177–84. doi: 10.1093/aje/kwt084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gusev A, et al. Quantifying missing heritability at known GWAS loci. PLoS Genet. 2013;9:e1003993. doi: 10.1371/journal.pgen.1003993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dimas AS, et al. Common regulatory variation impacts gene expression in a cell type-dependent manner. Science. 2009;325:1246–50. doi: 10.1126/science.1174148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Montgomery SB, et al. Transcriptome genetics using second generation sequencing in a Caucasian population. Nature. 2010;464:773–7. doi: 10.1038/nature08903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pickrell JK. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am J Hum Genet. 2014;94:559–73. doi: 10.1016/j.ajhg.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kichaev G, et al. Integrating functional data to prioritize causal variants in statistical fine-mapping studies. PLoS Genet. 2014;10:e1004722. doi: 10.1371/journal.pgen.1004722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Finucane HK, et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat Genet. 2015;47:1228–35. doi: 10.1038/ng.3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Stancakova A, et al. Hyperglycemia and a common variant of GCKR are associated with the levels of eight amino acids in 9,369 Finnish men. Diabetes. 2012;61:1895–902. doi: 10.2337/db11-1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Stancakova A, et al. Changes in insulin sensitivity and insulin release in relation to glycemia and glucose tolerance in 6,414 Finnish men. Diabetes. 2009;58:1212–21. doi: 10.2337/db08-1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Turchin MC, et al. Evidence of widespread selection on standing variation in Europe at height-associated SNPs. Nat Genet. 2012;44:1015–9. doi: 10.1038/ng.2368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bulik-Sullivan BK, et al. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet. 2015;47:291–5. doi: 10.1038/ng.3211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lango Allen H, et al. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467:832–8. doi: 10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bolormaa S, et al. A multi-trait, meta-analysis for detecting pleiotropic polymorphisms for stature, fatness and reproduction in beef cattle. PLoS Genet. 2014;10:e1004198. doi: 10.1371/journal.pgen.1004198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhu X, et al. Meta-analysis of correlated traits via summary statistics from GWASs with an application in hypertension. Am J Hum Genet. 2015;96:21–36. doi: 10.1016/j.ajhg.2014.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zaitlen N, Pasaniuc B, Gur T, Ziv E, Halperin E. Leveraging genetic variability across populations for the identification of causal variants. Am J Hum Genet. 2010;86:23–33. doi: 10.1016/j.ajhg.2009.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Han B, Kang HM, Eskin E. Rapid and accurate multiple testing correction and power estimation for millions of correlated markers. PLoS Genet. 2009;5:e1000456. doi: 10.1371/journal.pgen.1000456. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures
Supplementary Note
Supplementary Tables