Mathematical modeling identifies Smad nucleocytoplasmic shuttling as a dynamic signal-interpreting system (original) (raw)
Abstract
TGF-β-induced Smad signal transduction from the membrane into the nucleus is not linear and unidirectional, but rather a dynamic network that couples Smad phosphorylation and dephosphorylation through continuous nucleocytoplasmic shuttling of Smads. To understand the quantitative behavior of this network, we have developed a tightly constrained computational model, exploiting the interplay between mathematical modeling and experimental strategies. The model simultaneously reproduces four distinct datasets with excellent accuracy and provides mechanistic insights into how the network operates. We use the model to make predictions about the outcome of fluorescence recovery after photobleaching experiments and the behavior of a functionally impaired Smad2 mutant, which we then verify experimentally. Successful model performance strongly supports the hypothesis of a dynamic maintenance of Smad nuclear accumulation during active signaling. The presented work establishes Smad nucleocytoplasmic shuttling as a dynamic network that flexibly transmits quantitative features of the extracellular TGF-β signal, such as its duration and intensity, into the nucleus.
Keywords: systems biology, TGF-β, computational modeling, signaling network
In response to TGF-β, the prototypic member of a large superfamily of growth factors, the R-Smads, Smad2 and Smad3 are phosphorylated by the type I receptor kinase on two serine residues at their extreme C termini, which creates the interaction interface that enables them to form either homomeric complexes or heteromeric complexes with Smad4 (1). Smad complexes accumulate in the nucleus, where they are directly involved in the regulation of target gene transcription (2). Signaling is turned off by negative feedback triggering receptor inactivation (3, 4). Thus, the events involved in Smad-dependent gene regulation in response to TGF-β can be viewed as four functional modules: receptor activation, Smad nucleocytoplasmic dynamics, transcriptional regulation by Smads, and feedback control. Here, we focus on Smad nucleocytoplasmic dynamics, the evolutionarily conserved core module that is the basis of signal transmission from the membrane into the nucleus (5–7). Smads continuously enter and exit the nucleus in the absence, but also in the presence of TGF-β. This observation has led us to propose that established nuclear Smad accumulation during active signaling is not static, but is in fact dynamically maintained by continuous phosphorylation of cytoplasmic R-Smads and counteracting R-Smad dephosphorylation in the nucleus (8) (Fig. 1A). Experimentally, it is impossible to determine whether such a hypothesis is consistent with the observed kinetics of nuclear accumulation of activated Smad complexes and their behavior after receptor inactivation, as many individual key reactions within this complex signaling network are not amenable to experimental investigation. Also, it is difficult to determine which reactions are rate-limiting and are thus potential points for therapeutic intervention. To overcome these problems, we have developed a mathematical rate equation model of Smad nucleocytoplasmic dynamics that has allowed us to explore these issues at the level of the entire network.
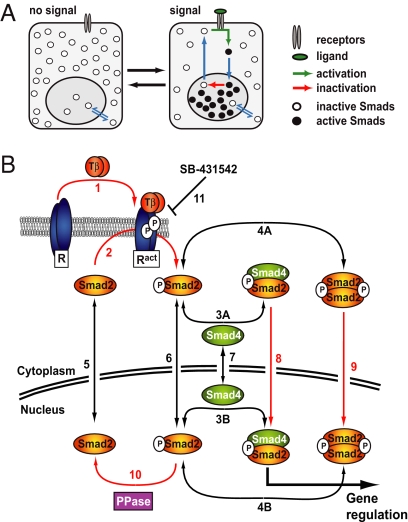
Fig. 1.
Smad nucleocytoplasmic dynamics. (A) A cartoon of Smad nucleocytoplasmic dynamics. Inactive Smads shuttle between the nucleus and cytoplasm. Receptor-activated Smads reside preferentially in the nucleus and accumulate there. Slow inactivation of active Smads in the nucleus, however, continuously releases inactivated Smads into the cytoplasm. In the presence of a signal, reactivation of cytoplasmic Smads dynamically maintains nuclear accumulation. As soon as receptor activity ceases, this mechanism restores the system back to the uninduced state. (B) Network topology used for model construction. Red arrows indicate irreversible reactions. Black arrows indicate reversible reactions. TGF-β binding converts inactive receptors (R) irreversibly into active receptors (Ract) with a rate constant _k_TGFβ (1). Active receptors irreversibly phosphorylate cytoplasmic Smad2 with a rate constant _k_phos (2). In both the nucleus and the cytoplasm, phospho-Smad2 forms heteromeric complexes with Smad4 (3A and 3B) and homomeric complexes (4A and 4B). These reversible reactions are described by the off-rate _k_off and the dissociation constant _K_diss. Smad2 (5), monomeric phospho-Smad2 (6), and Smad4 (7) shuttle reversibly between nucleus and cytoplasm with the rate constants _k_in and _k_ex. Heteromeric complexes (8) and homomeric complexes (9) are imported into the nucleus with a rate constant _k_in times CIF (complex import factor), but cannot be exported. The Smad2 phosphatase (PPase) is nuclear and irreversibly dephosphorylates monomeric phospho-Smad2 with a rate constant _k_dephos (10). Finally, the receptor kinase is reversibly blocked by the inhibitor SB-431542 (11), which is described by the interaction's off-rate, _k_offSB, and dissociation constant, _K_dissSB. For further details see SI Text and Fig. S2.
Results
The model is based on experimental evidence (Fig. 1B) and was implemented in the freely available software COPASI (9). For details on the underlying assumptions, the kinetic reaction parameters, and the implementation and calibration of the model, see supporting information (SI) Text. Experimental data were obtained in a cell line stably expressing EGFP-Smad2 at levels equivalent to endogenous Smad2/3 levels (7, 10) (SI Text, Table S1, and Fig. S1_B_). We have previously performed a thorough analysis of this cell line and have shown that EGFP–Smad2 behaves in an experimentally indistinguishable way from endogenous Smad2 (7, 10).
Two Mechanisms Can Be Envisaged to Account for TGF-β-Induced Smad Nuclear Accumulation.
How TGF-β-induced Smad complex formation causes Smad accumulation in the nucleus is under debate. Pronounced inhibition of nuclear export of Smad complexes is clearly required for nuclear Smad accumulation in vivo (6, 7, 11) and is perhaps also sufficient (7). Smad nuclear import has been suggested to occur through direct interaction with the nuclear pore complex (12, 13). Because Smad affinities for nuclear pore components were found to be similar independently of the Smad activation status, similar import rates for active and inactive Smad were expected (13). By contrast, in vitro evidence has suggested faster import of pseudophosphorylated R-Smads compared with wild-type unphosphorylated R-Smads (14). More recently, activated R-Smads have been shown to require the nuclear import receptors importin-7 and importin-8 for their nuclear accumulation in response to a signal, while these importins are dispensable for nuclear import of inactive Smads (15). These findings suggest distinct import mechanisms depending on the activation status of the Smads, possibly giving rise to distinct import rates. To clarify whether or not accelerated nuclear import of activated Smads is required to explain the kinetic data, we developed two variations of the rate equation model (for mathematical details, see SI Text, Fig. S2, and Fig. S3) and compared their performance. In both versions of the model, nuclear Smad complexes are required to dissociate before nuclear export of their subunits. However, whereas the retention-only (RO) model assumes that Smad complexes and monomeric Smads are imported into the nucleus with identical rates, the alternative retention/enhanced complex import (RECI) model allows Smad complexes to be imported faster.
The RECI Model Outperforms the RO Model.
Each model was simultaneously fitted to four experimental datasets (Fig. 2), which were obtained in HaCaT cells expressing low levels of EGFP-tagged Smad2 (EGFP-Smad2) (7, 10). The datasets used were: nuclear accumulation kinetics of EGFP-Smad2 in response to TGF-β (Fig. 2A), kinetics of nuclear clearance of accumulated EGFP-Smad2 after receptor inhibition by SB-431542 (16) (Fig. 2A), phosphorylation kinetics of Smad2 (Fig. 2B), and the nucleocytoplasmic distribution of phosphorylated Smad2 at maximal response to TGF-β (Fig. 2C). Both models fitted the nuclear accumulation and nuclear clearance data with excellent accuracy (Fig. 2D). The best fit of the phosphorylation data (Fig. 2E), however, required the RO model to overestimate the cytoplasmic fraction of phosphorylated Smad2 at steady state by nearly a factor of three compared with the experimental value (Fig. 2F and SI Text). The RECI model by contrast not only fitted the phosphorylation time course slightly better than the RO model (Fig. 2E), but also correctly predicted the experimentally observed cytoplasmic fraction of phosphorylated Smad2 at steady state (Fig. 2F). The superior performance of the RECI model strongly suggests that TGF-β-induced nuclear accumulation of activated Smads requires not only an inhibition of nuclear export of Smad complexes, but also their enhanced nuclear import. We therefore rejected the RO model and further analyzed the RECI model. The best-fit parameter set (Fig. 2G and SI Text) was used for all subsequent RECI model simulations. All optimized parameters are defined within narrow, biologically meaningful ranges. For the statistical analysis and a parameter correlation analysis, see SI Text.
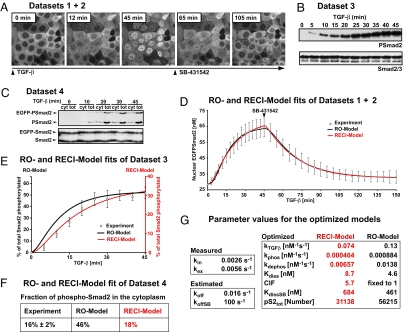
Fig. 2.
The RECI model is superior in fitting experimental datasets. (A) Live cell imaging in HaCaT EGFP-Smad2 cells in response to TGF-β and SB-431542 yielded Dataset 1 and Dataset 2, the kinetics of Smad2 nuclear accumulation and nuclear Smad2 clearance, respectively. Images of a subset of the sampled time course are shown. (B) Dataset 3. Kinetics of TGF-β-induced Smad2 phosphorylation. Representative immunoblots probed with anti-phospho-Smad2 and anti-Smad2/3 antibodies are shown. (C) Dataset 4. The nucleocytoplasmic distribution of total phospho-Smad2 immunoreactivity. Cytoplasmic (cyt) and total extracts (tot) were immunoblotted as in B. Double amounts of cytoplasmic extracts were loaded compared with total cell extracts. (D) Both models fit the average nuclear accumulation and average nuclear clearance data equally well. Images as in A were analyzed by measuring nuclear fluorescence (○; ± SD, n = 10 cells). The black line is the RO model fit, and the red line is RECI model fit. (E) Experimental phosphorylation data from immunoblots as shown in B (○; ± SD, n = 3). The black line and black ordinate indicate RO model fit. The red line and red ordinate indicate RECI model fit. The RECI model is superior in fitting the phosphorylation data and predicts a lesser extent of Smad2 phosphorylation. (F) Quantification of the levels of phosphorylated EGFP-Smad2 and endogenous Smad2 in the cytoplasm at maximal response to TGF-β derived from experiments like those shown in C compared with the predicted levels from the RO and RECI models. In contradiction to the experimental value, the RO model predicts high levels of cytoplasmic phospho-Smad2. The RECI model agrees well with the experimental value. (G) The best-fit parameter sets for the RECI and RO models. For a detailed description see SI Text.
The RECI Model Correctly Reproduces the Result of an Experiment Not Used in Its Conception.
Fluorescence recovery after photobleaching (FRAP) data were used to challenge the RECI model with an independent dataset that had not been used in model conception. Photobleaching of the whole nuclear pool of EGFP-Smad2 was performed in TGF-β-treated cells that had reached maximal nuclear accumulation of Smad2 (Fig. 3A). The FRAP data recorded (Fig. 3B) describe the system's trajectory after a perturbation at maximal response to TGF-β and are thus entirely independent from the previous datasets, which correspond to the initial response of the system to TGF-β and the response to receptor inactivation after 1 h of TGF-β signaling. A RECI model simulation and, for comparison, an RO model simulation of these experiments were calculated by using the best-fit parameter set for each model as previously obtained by fitting the datasets shown in Fig. 2. The RECI model simulation accurately reproduced the shape of the experimental, multiphasic FRAP curve and was superior to the RO model fit (Fig. 3B). The behavior of all of the EGFP-Smad2 species in the cell contributes to the experimental FRAP curve (Fig. 3C). Thus, the fact that the RECI model can reproduce this curve provides a strong verification of the validity of the assumptions and the parameter estimations made.
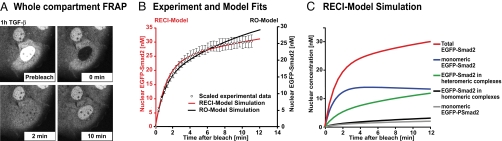
Fig. 3.
The RECI model correctly recapitulates a FRAP experiment. (A) After 1 h of TGF-β treatment, nuclear EGFP-Smad2 was photobleached and nuclear fluorescence recovery was monitored. Representative pictures of a recovery time course are shown. (B) To model the FRAP recovery, simulations were run for both models until maximal response to TGF-β was reached. The simulation was stopped, and from these initial conditions (RECI model: 68 nM EGFP-Smad2 in the nucleus, 42 nM in the cytoplasm; RO model: 64 nM in the nucleus, 45 nM in the cytoplasm), a photobleach was simulated by converting all nuclear species containing EGFP-Smad2 into the corresponding species containing endogenous, i.e., “invisible” Smad2. The simulation was continued, and the sum of the concentrations of all nuclear fluorescent species was plotted. Because the experimental data were measured in arbitrary units, a least-square method was used to scale the experimental dataset (○; ± SD, n = 10) such that maximal overlap with either the RECI model (red line and red ordinate) or the RO model (black line, black ordinate) was achieved. Note the superior performance of the RECI model when compared with the RO model in capturing the shape of the recovery curve. (C) The recovery curve (red line) is a sum of the recovery behavior of all species containing EGFP-Smad2, whose concentrations were calculated by using the RECI model.
The RECI Model Correctly Predicts the Phosphorylation and Dephosphorylation Kinetics and the Nucleocytoplasmic Distribution of Smad2 D300H.
For a model to be useful it should be able to make testable predictions (17). We therefore used the parameter-optimized RECI model to predict the behavior of a functionally compromised point mutant, Smad2 D300H. This mutant exhibits constitutive nucleocytoplasmic shuttling similar to wild-type Smad2 (data not shown). Although it is phosphorylated and does traffic through the nucleus, it cannot form complexes with either itself or Smad4 and hence does not accumulate in the nucleus in response to TGF-β (7). RECI model simulation of the behavior of Smad2 D300H in response to TGF-β predicted that the mutant would be phosphorylated and dephosphorylated with very similar kinetics to wild-type Smad2 (Fig. 4A). The corresponding experiment was carried out in a HaCaT cell line expressing EGFP-Smad2 D300H. Consistent with the model predictions, phosphorylation and dephosphorylation kinetics of EGFP-Smad2 D300H were found to be experimentally indistinguishable from the kinetics of endogenous Smad2 (Fig. 4B).
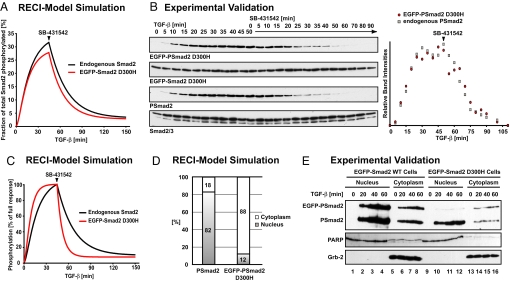
Fig. 4.
The RECI model correctly predicts the behavior of a mutant Smad2 unable to form Smad complexes. (A) EGFP-Smad2 D300H is predicted to be phosphorylated and dephosphorylated with highly similar kinetics to endogenous Smad2. (B) Representative immunoblots showing a time course of phosphorylation and dephosphorylation of EGFP-Smad2 D300H and of endogenous Smad2 in response to TGF-β and subsequent receptor inhibition. Total EGFP-Smad2 D300H and Smad2/3 are shown as loading controls. Note that EGFP-Smad2 D300H is expressed at lower levels compared with endogenous Smad2, and films showing EGFP-Smad2 D300H were exposed for a longer time to allow for direct comparison of the kinetics. The quantification shows that phosphorylation and dephosphorylation of mutant and wild-type Smad2 proceed with indistinguishable kinetics. (C) Phosphorylation and dephosphorylation kinetics of endogenous Smad2 and EGFP-Smad2 D300H assuming that 20% of the total phosphatase activity is cytoplasmic. Note the dramatic increase in the dephosphorylation rate of EGFP-Smad2 D300H on SB-431542 treatment compared with Smad2, differences that are not observed experimentally (B). (D) Even at full response, phosphorylated EGFP-Smad2 D300H is predicted to reside mainly in the cytoplasm. (E) Immunoblot of nuclear and cytoplasmic fractions of HaCaT EGFP-Smad2 cells and HaCaT EGFP-Smad2 D300H cells. Wild-type phosphorylated EGFP-Smad2 shows the same distribution as endogenous phospho-Smad2 (lanes 1–8). Phosphorylated EGFP-Smad2 D300H is enriched in the cytoplasm (lanes 9–16). Note that EGFP-Smad2 D300H HaCaT cells express lower levels of the transgene than EGFP-Smad2 HaCaT cells (7, 10). PARP and Grb-2 were used as fractionation and loading controls. The PARP antibody shows a cross-reaction with unrelated proteins of slightly lower mobility in the cytoplasm.
There Is No Substantial Cytoplasmic Phosphatase Activity Targeting Smads.
Based on the original nucleocytoplasmic shuttling hypothesis (8), the model assumes that the Smad phosphatase is restricted to the nucleus. To test whether a predominantly nuclear localization of phosphatase activity is essential to explain the observed dephosphorylation kinetics of wild-type and mutant Smad2, we modified the model such that a small amount of phosphatase activity (20% of total) was cytoplasmic. A partially cytoplasmic phosphatase activity had very little effect on the behavior of wild-type Smad2, but Smad2 D300H was now predicted to be dephosphorylated much more rapidly upon treatment with SB-431542 than was endogenous Smad2 (Fig. 4C). The fact that wild-type and mutant Smad2 are dephosphorylated with similar kinetics (Fig. 4B) thus indicates that dephosphorylation of R-Smads occurs almost exclusively in the nucleus.
Such similar dephosphorylation kinetics for mutant and wild-type Smad2 seems counterintuitive at first, because in contrast to wild-type phospho-Smad2, phospho-Smad2 D300H cannot form complexes to protect its C-terminal serine phosphates and would be expected to be dephosphorylated more rapidly than the wild type. However, a RECI model simulation of the behavior of Smad2 D300H not only predicts that this mutant would have the same phosphorylation and dephosphorylation kinetics as WT Smad2, but also provides an explanation. The Smad phosphatase is predicted to be strongly enriched in the nucleus. In contrast to wild-type phospho-Smad2, which is predominantly nuclear, the simulation indicates that phospho-Smad2 D300H resides mainly in the cytoplasm even at full response (Fig. 4D), a prediction that could be verified experimentally (Fig. 4E). Thus, phospho-Smad2 D300H, although more prone to dephosphorylation, is protected from the nuclear phosphatase as a result of its predominantly cytoplasmic localization and can only be dephosphorylated while trafficking through the nucleus. Wild-type phospho-Smad2 by contrast, although strongly enriched in the nucleus and thus exposed to the phosphatase, is protected from dephosphorylation by Smad complex formation. Overall, positive and negative contributions cancel out for both proteins and they exhibit similar dephosphorylation kinetics. In summary, the RECI model predictions concerning the behavior of Smad2 D300H and their successful experimental verification strongly support the notion of a predominantly nuclear Smad phosphatase targeting monomeric phospho-Smads, but not Smad complexes.
At Full Response, Smad2/Smad4 Complexes Are the Predominant Species in the Nucleus.
Having established that the RECI model fits the experimental data, performs well when challenged, and makes correct predictions, we used it to calculate concentrations of reaction species that cannot be determined experimentally. In the RECI model simulation, cytoplasmic concentrations of unphosphorylated Smad2 and monomeric Smad4 decrease only moderately upon TGF-β treatment (Fig. 5A). Thus, throughout the signaling period, a sufficiently large pool of Smad2 is available for phosphorylation by the receptor kinase. As Smad2/Smad4 complexes are the transcriptionally active species (18), their nuclear concentration is a major determinant of the outcome of TGF-β signaling. In line with this notion, Smad2/Smad4 complexes are the dominating nuclear Smad species in the RECI model simulation during active signaling (Fig. 5A). The concentration of homomeric Smad2/Smad2 complexes, the biological role of which remains elusive, is low in both compartments. Thus, despite the simplifying assumptions of dimeric complexes and equal stabilities of homodimers and heterodimers (see SI Text), the RECI model predicts preferential formation of heteromeric complexes.
Fig. 5.
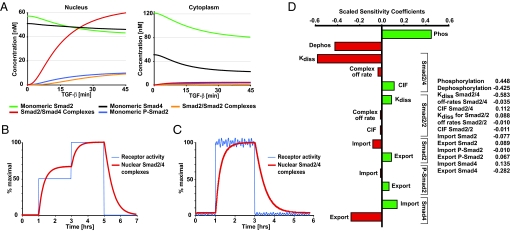
Predictions from the RECI model and parameter sensitivity analysis. (A) Calculated concentrations of Smad species in the nucleus and cytoplasm during TGF-β stimulation. Concentrations given refer to the sum of Smad2 and EGFP-Smad2. (B) As an input function, receptor activity was changed according to a double step function (blue line). The effect on the nuclear concentration of Smad2/Smad4 complexes (red line) was calculated. (C) As in B, except receptor activity is represented by a step function with added rapid fluctuations. (D) Sensitivity analysis. Scaled sensitivity coefficients for the plateau concentration of nuclear Smad2/Smad4 complexes to variations in the individual reaction rates are given. CIF, complex import factor for the respective complex (defined as import rate of Smad complexes over the import rate of monomeric Smads, see SI Text).
Smad Nucleocytoplasmic Dynamics Act as a Signal Interpretation System.
We have speculated previously that continuous nucleocytoplasmic shuttling of the Smads might allow the system to continuously adjust the amount of nuclear active Smad complexes in accordance with the degree of receptor activation (8). The RECI model allows direct testing of this hypothesis. To investigate the quantitative relationship between nuclear Smad2/Smad4 complexes (system output) and receptor activity (system input), we simulated the system's response to a theoretical activation of receptors in two steps, first, to half maximal activity, and then to maximal activity (Fig. 5B). This simulation demonstrates that Smad nucleocytoplasmic shuttling couples the amount of nuclear Smad2/Smad4 complexes to receptor activity, although with a time delay. In the simulation, the concentration of nuclear Smad2/Smad4 complexes becomes half-maximal ≈10 min after a step receptor activation (characteristic activation time). Provided that receptor activity is constant for much longer than the characteristic activation time, the system can reach a steady state in which the amount of nuclear Smad2/Smad4 complexes reflects receptor activity. Because of its inherent time delay, the system is also able to filter noise. Transient fluctuations in receptor activity, whose duration is short compared with the characteristic activation time, are strongly dampened and do not cause a corresponding fluctuation in the concentration of nuclear Smad2/Smad4 complexes (Fig. 5C). Thus, the system is robust against rapid fluctuations in receptor activity.
Sensitivity Analysis.
To conclude, we performed a sensitivity analysis and calculated the susceptibility of the peak concentration of Smad2/Smad4 complexes to changes in model parameters. This analysis identifies the reactions steps that, when modulated, affect system output most significantly and are thus the most appropriate targets for therapeutic intervention. Scaled sensitivity coefficients (defined in SI Text) are shown in Fig. 5D. The peak concentration of nuclear Smad2/Smad4 complexes is strongly influenced in a positive manner by the Smad2 phosphorylation rate and in a negative manner by the Smad2 dephosphorylation rate, the dissociation rate of Smad2/Smad4 complexes, and the nuclear export rate of Smad4. By contrast, the system is very robust to changes in, for instance, the complex off-rates for both homomeric and heteromeric complexes.
Discussion
Here, we present a parsimonious mathematical model of Smad nucleocytoplasmic dynamics, which is tightly constrained and allows hypothesis testing. The RECI model fits four datasets simultaneously with excellent accuracy. It correctly predicts the system's trajectory after a steady-state perturbation and the behavior of the system under conditions where a component is functionally compromised (Smad2 D300H). The RECI model requires Smad complexes to be imported faster than monomeric Smads and indicates that R-Smad dephosphorylation occurs in the nucleus. The successful performance of the model not only verifies the plausibility and mechanistic relevance of the underlying network topology and the assumptions made, but also leads to conclusions with regard to mechanistic details of Smad nucleocytoplasmic dynamics. Our analysis now explains how Smad phosphorylation, Smad complex formation, Smad nucleocytoplasmic shuttling, and Smad dephosphorylation act together as a system to transduce TGF-β signals into the nucleus.
The model describes intracellular Smad signal transduction in response to TGF-β in tissue culture cells. However, Smad nucleocytoplasmic dynamics operate in early Xenopus and zebrafish embryos and the reaction network seems to be identical (5). Smad nucleocytoplasmic shuttling has also been demonstrated in Drosophila embryos (6). In developmental systems, Smad signaling transmits signals from morphogenic ligands such as Nodals and Activins in frog embryos and Decapentaplegic (Dpp) in flies (19). To achieve a ligand concentration-dependent response, the quantitative and temporal characteristics of the extracellular signal have to be preserved and transmitted into the nucleus. The present work demonstrates that Smad nucleocytoplasmic dynamics can achieve this by adjusting the amount of active nuclear Smad complexes in a dynamic and strictly signal-dependent manner. Thus, Smad nucleocytoplasmic dynamics act as an intracellular interpretation system of the duration and magnitude of extracellular TGF-β superfamily signals. Moreover, our simulations indicate that, because of the inherent delay between input and output, the system only reacts to sustained changes in receptor activity and is thus able to dampen transient fluctuations in receptor activity. Interestingly, maximal nuclear accumulation of Smads occurs more rapidly in frog embryos than in tissue culture cells (5). Some developmental systems might thus exhibit a shorter delay time and be more sensitive to rapid changes in receptor activity than tissue culture cells, which might be relevant for gradient interpretation. Therefore, the numerical results of this study cannot be transferred directly to developmental systems. However, the general principles and conclusions are expected to be valid also in early development. Once kinetic data of sufficiently high quality are available, our model will provide a powerful tool for analyzing the kinetics of Smad signal transduction in developmental systems.
To date, mathematical descriptions of morphogen gradients have largely ignored the kinetics of downstream signal transduction (20), a gap we aim to fill with the model presented here. However, because of the lack of quantitative kinetic data, we had to approximate the complex process of TGF-β-induced receptor activation by a comparably simple function. Thus, to fully appreciate both gradient formation and gradient interpretation models that integrate extracellular and intracellular events are required. Merging our model with mathematical descriptions of other modules of TGF-β signaling, most notably descriptions of upstream events like ligand gradient formation and receptor biology (21, 22), will be the next challenge toward this goal. By itself, our work is an example of how modularity of signal transduction pathways can be exploited to obtain powerful, identifiable models of individual modules, such as nucleocytoplasmic dynamics as presented here.
Materials and Methods
Cell Lines, Immunoblotting, and Live Cell Imaging.
The HaCaT EGFP-Smad2 and HaCaT EGFP-Smad2 D300H cell lines were as described (7). Whole-cell extracts (23) and nuclear/cytoplasmic extracts (24) were prepared as described. Immunoblotting was performed with anti-phospho-Smad2 (Cell Signaling Technology), anti-Grb-2 (BD Biosciences), and anti-poly(ADP)-ribose-polymerase (PARP) (Roche) antibodies. Live cell imaging was performed as described (7, 10). Average fluorescence intensities and immunoblot band intensities were quantified by using ImageJ 1.37v software. In both experiments and simulations, TGF-β was used at 2 ng/ml, and the receptor kinase inhibitor SB-431542 (10 μM; Tocris) was added 45 min later.
Computational Modeling.
The system of ordinary differential equations (ODEs) was numerically solved by using the free software COPASI (9). All simulations, data fitting, and model analyses were performed in COPASI. Curve fitting and parameter optimization are described in SI Text. The statistical analysis of the best-fit parameter set is shown in Fig. S4_A_. The parameter correlation analysis is shown in Fig. S4_B_.
Incorporation of EGFP-Smad2 into the Model.
To specifically simulate the behavior of EGFP-Smad2 in bleaching experiments, EGFP-Smad2 was incorporated into the models as a separate species, resulting in additional chemical reactions and modifications in the system of ODEs. For simplicity and readability, the basic systems of chemical reactions and ODEs are given separately, describing a wild-type cell without EGFP-Smad2 expression (SI Text and Fig. S2). This system is sufficient to appreciate the mathematical structure of the model. For completeness, the full system of chemical equations and ODEs describing a cell additionally expressing EGFP-Smad2 is given (SI Text and Fig. S3). All modeling is based on this full system. EGFP-Smad2 D300H was implemented in the model by setting all complex on-rates for this protein to zero, whereas endogenous Smad2 was allowed to form complexes as usual.
Supplementary Material
Supporting Information
Acknowledgments.
We thank Eva Grönroos, Mike Howell, Laurence Levy, Julian Lewis, Nic Tapon, and Richard Treisman for helpful comments on the manuscript; Stefan Hoops for COPASI support; and Yasmine Mamnun for networking. This work was funded by Cancer Research UK, Erwin-Schrödinger Fellowship J2397-B12 from the Austrian Science Foundation (to B.S.), European Union Marie Curie Fellowship 515294 (to B.S.), and a European Molecular Biology Organization Fellowship (to A.L.T.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Shi Y, Massagué J. Mechanisms of TGF-β signaling from cell membrane to the nucleus. Cell. 2003;113:685–700. doi: 10.1016/s0092-8674(03)00432-x. [DOI] [PubMed] [Google Scholar]
- 2.Massagué J, Seoane J, Wotton D. Smad transcription factors. Genes Dev. 2005;19:2783–2810. doi: 10.1101/gad.1350705. [DOI] [PubMed] [Google Scholar]
- 3.Kavsak P, et al. Smad7 binds to Smurf2 to form an E3 ubiquitin ligase that targets the TGF-β receptor for degradation. Mol Cell. 2000;6:1365–1375. doi: 10.1016/s1097-2765(00)00134-9. [DOI] [PubMed] [Google Scholar]
- 4.Shi W, et al. GADD34-PP1c recruited by Smad7 dephosphorylates TGF-β type I receptor. J Cell Biol. 2004;164:291–300. doi: 10.1083/jcb.200307151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Batut J, Howell M, Hill CS. Kinesin-mediated transport of Smad2 is required for signaling in response to TGF-β ligands. Dev Cell. 2007;12:261–274. doi: 10.1016/j.devcel.2007.01.010. [DOI] [PubMed] [Google Scholar]
- 6.Dudu V, et al. Postsynaptic Mad signaling at the Drosophila neuromuscular junction. Curr Biol. 2006;16:625–635. doi: 10.1016/j.cub.2006.02.061. [DOI] [PubMed] [Google Scholar]
- 7.Schmierer B, Hill CS. Kinetic analysis of Smad nucleocytoplasmic shuttling reveals a mechanism for TGF-β-dependent nuclear accumulation of Smads. Mol Cell Biol. 2005;25:9845–9858. doi: 10.1128/MCB.25.22.9845-9858.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Inman GJ, Nicolás FJ, Hill CS. Nucleocytoplasmic shuttling of Smads 2, 3, and 4 permits sensing of TGF-β receptor activity. Mol Cell. 2002;10:283–294. doi: 10.1016/s1097-2765(02)00585-3. [DOI] [PubMed] [Google Scholar]
- 9.Hoops S, et al. COPASI: A complex pathway simulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 10.Nicolás FJ, De Bosscher K, Schmierer B, Hill CS. Analysis of Smad nucleocytoplasmic shuttling in living cells. J Cell Sci. 2004;117:4113–4125. doi: 10.1242/jcs.01289. [DOI] [PubMed] [Google Scholar]
- 11.Chen HB, Rud JG, Lin K, Xu L. Nuclear targeting of TGF-β-activated Smad complexes. J Biol Chem. 2005;280:21329–21336. doi: 10.1074/jbc.M500362200. [DOI] [PubMed] [Google Scholar]
- 12.Xu L, Alarcon C, Col S, Massagué J. Distinct domain utilization by Smad3 and Smad4 for nucleoporin interaction and nuclear import. J Biol Chem. 2003;278:42569–42577. doi: 10.1074/jbc.M307601200. [DOI] [PubMed] [Google Scholar]
- 13.Xu L, Kang Y, Col S, Massagué J. Smad2 nucleocytoplasmic shuttling by nucleoporins CAN/Nup214 and Nup153 feeds TGF-β signaling complexes in the cytoplasm and nucleus. Mol Cell. 2002;10:271–282. doi: 10.1016/s1097-2765(02)00586-5. [DOI] [PubMed] [Google Scholar]
- 14.Kurisaki A, Kose S, Yoneda Y, Heldin CH, Moustakas A. TGF-β induces nuclear import of Smad3 in an importin-β1 and Ran-dependent manner. Mol Biol Cell. 2001;12:1079–1091. doi: 10.1091/mbc.12.4.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xu L, et al. Msk is required for nuclear import of TGF-β/BMP-activated Smads. J Cell Biol. 2007;178:981–994. doi: 10.1083/jcb.200703106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Inman GJ, et al. SB-431542 is a potent and specific inhibitor of TGF-β superfamily type I activin receptor-like kinase (ALK) receptors ALK4, ALK5, and ALK7. Mol Pharmacol. 2002;62:65–74. doi: 10.1124/mol.62.1.65. [DOI] [PubMed] [Google Scholar]
- 17.Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK. Physicochemical modeling of cell signaling pathways. Nat Cell Biol. 2006;8:1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- 18.Feng XH, Derynck R. Specificity and versatility in TGF-β signaling through Smads. Annu Rev Cell Dev Biol. 2005;21:659–693. doi: 10.1146/annurev.cellbio.21.022404.142018. [DOI] [PubMed] [Google Scholar]
- 19.Schmierer B, Hill CS. TGF-β-SMAD signal transduction: Molecular specificity and functional flexibility. Nat Rev Mol Cell Biol. 2007;8:970–982. doi: 10.1038/nrm2297. [DOI] [PubMed] [Google Scholar]
- 20.Reeves GT, Muratov CB, Schupbach T, Shvartsman SY. Quantitative models of developmental pattern formation. Dev Cell. 2006;11:289–300. doi: 10.1016/j.devcel.2006.08.006. [DOI] [PubMed] [Google Scholar]
- 21.Vilar JM, Jansen R, Sander C. Signal processing in the TGF-β superfamily ligand-receptor network. PLoS Comput Biol. 2006;2:e3. doi: 10.1371/journal.pcbi.0020003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zi Z, Klipp E. Constraint-based modeling and kinetic analysis of the Smad dependent TGF-β signaling pathway. PLoS ONE. 2007;2:e936. doi: 10.1371/journal.pone.0000936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Germain S, Howell M, Esslemont GM, Hill CS. Homeodomain and winged-helix transcription factors recruit activated Smads to distinct promoter elements via a common Smad interaction motif. Genes Dev. 2000;14:435–451. [PMC free article] [PubMed] [Google Scholar]
- 24.Wong C, et al. Smad3-Smad4 and AP-1 complexes synergize in transcriptional activation of the c-Jun promoter by TGF-β. Mol Cell Biol. 1999;19:1821–1830. doi: 10.1128/mcb.19.3.1821. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information