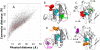Signal propagation in proteins and relation to equilibrium fluctuations - PubMed (original) (raw)

Signal propagation in proteins and relation to equilibrium fluctuations

Chakra Chennubhotla et al. PLoS Comput Biol. 2007 Sep.

Erratum in

Abstract

Elastic network (EN) models have been widely used in recent years for describing protein dynamics, based on the premise that the motions naturally accessible to native structures are relevant to biological function. We posit that equilibrium motions also determine communication mechanisms inherent to the network architecture. To this end, we explore the stochastics of a discrete-time, discrete-state Markov process of information transfer across the network of residues. We measure the communication abilities of residue pairs in terms of hit and commute times, i.e., the number of steps it takes on an average to send and receive signals. Functionally active residues are found to possess enhanced communication propensities, evidenced by their short hit times. Furthermore, secondary structural elements emerge as efficient mediators of communication. The present findings provide us with insights on the topological basis of communication in proteins and design principles for efficient signal transduction. While hit/commute times are information-theoretic concepts, a central contribution of this work is to rigorously show that they have physical origins directly relevant to the equilibrium fluctuations of residues predicted by EN models.

PubMed Disclaimer

Conflict of interest statement

Competing interests. The authors have declared that no competing interests exist.

Figures

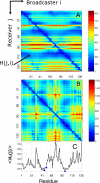
Figure 1

Figure 1. Distribution of Hitting Times and Commute Times for Phospholipase A2 (1bk9 [20])

(A) Hitting time H(j,i) distribution shows more variation between rows than between columns, indicating that residues differ in their ability to receive signals, while their broadcasting properties are more uniform. (B) Shows commute time C(i,j) distribution. (C) Displays the average hitting times evaluated from (A). All three catalytic residues (blue dots) exhibit short hitting times.

Figure 2

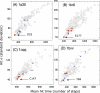
Figure 2. Average Hit Times < _Hr_(_j_) > versus Their Standard Deviations σ(Hr(j))

Catalytic residues (red crosses) are fast and precise, being located at the lower left end of the plot. Ligand-binding residues are indicated by black +.

Figure 3

Figure 3. Results from Hitting Time Analysis for Four Enzymes

(A) HIV-1 protease (1a30, [21]), (B) Ricin (1br6, [22]), (C) Human rhinovirus 3C protease (1cqq, [23]), and (D) Endo-1,4-xylanase (1bvv, [24]). The plots reveal the tendency of catalytic residues (D25 and D30 in (A), Y80, V81, G121, Y123, E177, and R180 in (B), H40, E71, G145, and C147 in (C), and Y69, E78, and E172 in (D); red dots) to exhibit fast and precise communication, in accord with the results for phospholipase A2 (Figure 2). Ligand-binding residues are shown by blue dots. The catalytic residues with the highest communication propensity are labeled.

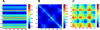
Figure 4

Figure 4. Physical Meaning of Hitting Times

Decomposing the hitting time H(j,i) matrix from Figure 1A into (A) one-body, (B) two-body, and (C) three-body terms, such that summation of these three matrices will reproduce the matrix in Figure 1A. The one-body term involves the fluctuations of only the destination node, apparent by the horizontal stripes seen (A). From the scale of this plot, it is easy to infer that the one-body term dominates the overall computation of the hitting time. However, the source node can modulate the hitting time to the destination node depending on the cross-correlations between the fluctuations of the two nodes (B). (C) reveals the contribution from the three-body terms to be negligibly small.

Figure 5

Figure 5. Correlation of Effective Communication Distances with Physical Distances

(A) Comparison of efficient communication distances (ordinate) and physical distances (abscissa) for all residue pairs in phospholipase A2. The points colored red refer to pairs involving the catalytic residue His48. (B) and (C) illustrate the differences in communication times, for residue pairs separated by similar distances, and the opposite situation of comparable communication times despite significant differences in inter-residue distances, (D) and (E). See text for more details.

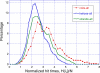
Figure 6

Figure 6. Importance of Secondary Structure in Defining Effective Means of Communication

Probability distribution of hitting times H(j,i) for the cases where residue j is located on (A) α-helices, (B) _β_-strands, and (C) loops or disordered regions. A total set of 49,929, 64,732, and 79,444 pairs contribute to the three respective curves, derived from the examined five enzymes. The abscissa represents the hitting time divided by the number of residues, which permits a normalization of the data collected for different proteins. The histograms are based on bins of size 0.2 in the interval [0, 10].

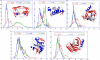
Figure 7

Figure 7. Effect of Secondary Structure on the Hitting Time Distributions for Individual Proteins, Each Shown in a Separate Panel

The ribbon diagrams are colored by the secondary structure, namely helices (red), strands (blue), and coils/disordered regions (white). For each enzyme, the probability distribution of hitting times H(j,i), where j is located on (A) α-helices, (B) _β_-strands, and (C) loops or disordered regions is shown in blue, red, and green respectively. The distributions from α-helices and loops/disordered regions have roughly the same shape as the ones shown in Figure 6. However, the distributions for the _β_-strands exhibit significant variations, pointing to a dependency on their spatial location in the 3-D structure of the proteins.

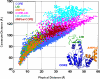
Figure 8

Figure 8. Comparison of Effective (Commute) Distances and Physical Distances between Residue Pairs in E. coli Adenylate Kinase (PDB: 4ake)

Effective (ordinate) and physical (abscissa) distances between residues in the CORE, LID, and AMPbd domains (see inset), grouped as intradomain and interdomain distances and shown in different colors for each group. Note that communication between residues in the same domain is more efficient than that between residues in two different domains. This is evidenced by the longer commute distance corresponding to interdomain pairing for a given physical distance, compared with that of intradomain pairs. The inset gives a schematic overview of the distance distributions for intradomain and interdomain pairings.

Similar articles

Cited by

References

    1. Bahar I, Atilgan A, Erman B. Direct evaluation of thermal fluctuations in protein using a single parameter harmonic potential. Folding Design. 1997;2:173–181. - PubMed
    1. Haliloglu T, Bahar I, Erman B. Gaussian dynamics of folded proteins. Phys Rev Lett. 1997;79:3090–3093.
    1. Bahar I, Atilgan AR, Demirel MC, Erman B. Vibrational dynamics of proteins: Significance of slow and fast modes in relation to function and stability. Phys Rev Lett. 1998;80:2733–2736.
    1. Cui Q, Bahar I, editors. Normal Mode Analysis: Theory and applications to biological and chemical systems. Boca Raton (Florida): CRC Press; 2006.
    1. Bahar I, Rader AJ. Coarse-grained normal modes in structural biology. Curr Opin Struct Bio. 2005;15:1–7. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources