GTPase cycle of dynamin is coupled to membrane squeeze and release, leading to spontaneous fission - PubMed (original) (raw)
GTPase cycle of dynamin is coupled to membrane squeeze and release, leading to spontaneous fission
Pavel V Bashkirov et al. Cell. 2008.
Abstract
The GTPase dynamin is critically involved in membrane fission during endocytosis. How does dynamin use the energy of GTP hydrolysis for membrane remodeling? By monitoring the ionic permeability through lipid nanotubes (NT), we found that dynamin was capable of squeezing NT to extremely small radii, depending on the NT lipid composition. However, long dynamin scaffolds did not produce fission: instead, fission followed GTPase-dependent cycles of assembly and disassembly of short dynamin scaffolds and involved a stochastic process dependent on the curvature stress imposed by dynamin. Fission happened spontaneously upon NT release from the scaffold, without leakage. Our calculations revealed that local narrowing of NT could induce cooperative lipid tilting, leading to self-merger of the inner monolayer of NT (hemifission), consistent with the absence of leakage. We propose that dynamin transmits GTP's energy to periodic assembling of a limited curvature scaffold that brings lipids to an unstable intermediate.
Figures
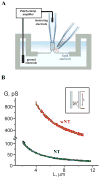
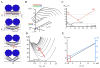
Figure 1. Formation of NT and wNT from a planar phospholipid bilayer
A. Illustration of a nanotube formation from planar bilayer by patch-pipette. Nanotube conductance (GNT) is determined by measuring the current resulting from application of a constant potential between measuring and ground electrodes (Frolov et al., 2003b); a pipette used to deliver chemicals directly to the nanotube is shown on the right. B. GNT measured in picosiemens (pS), depends hyperbolically on nanotube length (L); the fitting function G(L)=π_RL_2/(σ·(L+Loffset)) (where σ=100 Ohm·cm is the specific resistance of the ionic buffer used and Loffset is the length offset due to pipette positioning) was used to determine the luminal radius (RL) of nanotubes of different lipid composition (NT, black, and wNT, red; the fit results shown in green); insert outlines nanotube geometry.
Figure 2. Interaction of dynamin with NT
A. Decrease of normalized conductance (Gn) of NT upon application of dynamin. Gn=(G−G0)/(Ginit−Go), where Ginit is the nanotube conductance before dynamin application, G0 is the background conductance and G is the measured conductance; upon reaching steady-state, an attempt to shorten NT (↓L arrow) resulted in NT breakage. B. Immediate decrease of the NT conductance (black) formed in the presence of dynamin; blue curve illustrates the behavior of NT without dynamin. C. Extension of NT “squeezed” by dynamin (↑L) caused two effects: first, a new piece of a bare NT was added seen as initial conductance drop; second, this new part of NT was slowly squeezed by dynamin producing additional conductance decrease (ΔGdyn). D. Fluorescence micrographs showing outcomes of dynamin adsorption on a nanotube pulled from a GUV containing 0.5 mol% of Rh-DOPE. The pulling pipette is outlined in the first panel; t=0 corresponds to the dynamin application; bar 5 μm. E. Fluorescent micrographs showing adsorption of BODIPY-Fl-labeled dynamin on a nanotube pulled from a GUV containing Rh-DOPE; images of BODIPY-Fl (left) and Rh (right) fluorescence taken before and 5 minutes after protein application; bar 5 μm.
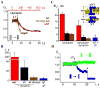
Figure 3. Lipid dependence and critical character of the squeezing of lipid nanotubes by dynamin
A. Dynamin-induced decrease of normalized conductance (Gn, see Figure 2) of NT and NT containing 1 mol% PI(4,5)P2 (black and brown curves respectively, lower time scale) and wNT (red, upper time scale). B. Histogram showing characteristic times of nanotube squeezing by dynamin (black bars for NT, n=17; red bars for wNT, n=6; brown bars for NT with PI(4,5)P2, n=3) and hydrostatic pressure (blue bar for NT, n=5); error bars represent SD. C. Histogram demonstrating the averaged luminal radius of bare nanotubes and nanotubes squeezed by dynamin or osmotic pressure estimated from their conductance (black bars for NT, n=12; red bars for wNT, n=6; brown bars for NT with PI(4,5)P2, n=3; blue bar for NT squeezed by osmotic pressure, n=5), error bars show SD; insert demonstrates scaled shapes of NT and wNT squeezed by dynamin. Geometrical parameters of the dynamin spiral are from Sweitzer and Hinshaw, 1998, bilayer thickness is 4nm. D. Effect of osmotic pressure on NT conductance; blue curve –negative pressure inside tube (~0.8 Osm), green curve – positive pressure (~0.2 Osm).
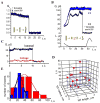
Figure 4. Non-leaky fission of NT by dynamin and GTP
A. Simultaneous addition of dynamin and GTP to NT caused a small gradual decrease of NT normalized conductance followed by instantaneous NT breakage. B. Waves of conductance fluctuations preceding the fission of NT shortened to ~1 μm length in the presence of dynamin and GTP; fission is seen as an abrupt conductance drop; NT shortened to similar length without dynamin was stable (blue curve). C. Simultaneous measurements of the GNT (integral conductance through NT lumen, black curve) and the conductance of its membrane corresponding to leakage through NT wall (red curve). D. Scatter plot showing the dependence of NT lifetime (upon the dynamin and GTP application) on NT length and radius. E. Life time distribution of shortened NT (as in 4B) in the presence of dynamin and GTP (red), compared to the distribution of the characteristic time of NT squeezing by dynamin (blue).
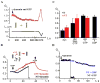
Figure 5. Relaxation of pre-assembled dynamin scaffold by GTP
A. Simultaneous addition of dynamin and GTP caused a slight gradual narrowing of wNT (red). At the new steady-state a decrease of wNT length (black) leads to the increase of its normalized conductance (Gn) indicating that wNT is not constrained by dynamin (see Figure 1C); B. Addition of GTP to “squeezed” nanotubes triggers an increase of both NT (black) and wNT (red) conductances. NT broke after a period of expansion, while wNT remained stable and was rapidly squeezed upon removal of GTP. C. Histogram showing steady-state conductance of NT (black) and wNT (red) upon addition of dynamin alone (dyn), GTP to nanotubes squeezed by dynamin (dyn, then GTP), dynamin and GTP (dyn+GTP) and dynamin and GDP (dyn+GDP); for dynamin and GTP the NT conductance was averaged near the fission point, error bars show SE. D. Effect of dynamin on the NT conductance is nucleotide-dependent: GTP stimulates fast fission of NT (black); GDP impairs both fission and curvature activities of dynamin.
Figure 6. Theoretical analysis of local membrane rearrangements by dynamin
A. The pathway of membrane rearrangement leading to the fission of a short membrane neck detached from a dynamin scaffold (blue) upon GTP hydrolysis; upper half of the neck membrane is shown. The neck constriction is followed by rearrangement of the thinnest part of the neck: lipids, by synchronous tilting, expose a small part of the hydrophobic membrane interior (hydrophobic belt). If the radius of the neck at the mid-point (Rmid) is small enough, expansion of the belt correlated with thinning of the neck (see 6D) becomes possible and the neck closes completely. The neutral surface (Kozlovsky and Kozlov, 2003) of the inner monolayer of the neck membrane is shown by the red line. The function R(L) describes the shape of this surface in the coordinate system (R, L); the coordinate center is placed in the midst of the neck (where Rmid is measured), so that the total length of the detached neck is 2_L0_. This length and the radius of the neck at both ends (R0) are fixed by the dynamin scaffold (note that R0 equals the radius of the nanotube in the dynamin-squeezed state and is about 0.5nm bigger than the luminal radius, R_L_). B. Calculated shapes of necks (R(L)) detached from the dynamin scaffold of different initial length (L0). Necks shorter than a critical length Lc (see 6C) narrow (Rmid<R0) while longer necks bulge; calculated 3D shapes of shortest and longest necks are shown. C. Numerically calculated dependence of the Rmid of the neck length L0 for NT and wNT. From this dependence the minimal radius of the neck (Rmin) and the critical length Lc (at which _Rmid_=R0) are determined. D. Energy diagram showing the dependence of free energy of the neck (_R0_=2nm) upon the width (H) and the radius (Rmid) of the hydrophobic belt. The energy barrier along the pathway indicated by the red arrow is ~35kBT. E. Dependence of the critical length, Lc, (blue) and the neck radius in the narrowest place, Rmin, (black) on R0.
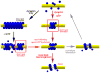
Figure 7. Pathway of non-leaky membrane fission mediated by dynamin
Dynamin polymerizes into a cylindrical scaffold: short in the presence of GTP (red arrows) and long when preassembled in the absence of GTP (black arrows). GTP hydrolysis causes detachment of the nanotube membrane from the dynamin scaffold so that fission becomes possible, but only for short membrane necks held by a dynamin scaffold. If fission is not immediate, the scaffold ultimately softens and disassembles allowing expansion of the nanotube (grey arrows). Thus, multiple rounds of assembly and disassembly of the scaffold can produce cyclic squeezing and relaxation of the nanotube.
Comment in
- The long and short of membrane fission.
Roux A, Antonny B. Roux A, et al. Cell. 2008 Dec 26;135(7):1163-5. doi: 10.1016/j.cell.2008.12.003. Cell. 2008. PMID: 19109885
Similar articles
- Real-time visualization of dynamin-catalyzed membrane fission and vesicle release.
Pucadyil TJ, Schmid SL. Pucadyil TJ, et al. Cell. 2008 Dec 26;135(7):1263-75. doi: 10.1016/j.cell.2008.11.020. Epub 2008 Dec 11. Cell. 2008. PMID: 19084268 Free PMC article. - Dynamin: functional design of a membrane fission catalyst.
Schmid SL, Frolov VA. Schmid SL, et al. Annu Rev Cell Dev Biol. 2011;27:79-105. doi: 10.1146/annurev-cellbio-100109-104016. Epub 2011 May 18. Annu Rev Cell Dev Biol. 2011. PMID: 21599493 Review. - Geometric catalysis of membrane fission driven by flexible dynamin rings.
Shnyrova AV, Bashkirov PV, Akimov SA, Pucadyil TJ, Zimmerberg J, Schmid SL, Frolov VA. Shnyrova AV, et al. Science. 2013 Mar 22;339(6126):1433-6. doi: 10.1126/science.1233920. Science. 2013. PMID: 23520112 Free PMC article. - Membrane shape at the edge of the dynamin helix sets location and duration of the fission reaction.
Morlot S, Galli V, Klein M, Chiaruttini N, Manzi J, Humbert F, Dinis L, Lenz M, Cappello G, Roux A. Morlot S, et al. Cell. 2012 Oct 26;151(3):619-29. doi: 10.1016/j.cell.2012.09.017. Cell. 2012. PMID: 23101629 Free PMC article. - Building a fission machine--structural insights into dynamin assembly and activation.
Chappie JS, Dyda F. Chappie JS, et al. J Cell Sci. 2013 Jul 1;126(Pt 13):2773-84. doi: 10.1242/jcs.108845. Epub 2013 Jun 18. J Cell Sci. 2013. PMID: 23781021 Free PMC article. Review.
Cited by
- Membrane fission is promoted by insertion of amphipathic helices and is restricted by crescent BAR domains.
Boucrot E, Pick A, Çamdere G, Liska N, Evergren E, McMahon HT, Kozlov MM. Boucrot E, et al. Cell. 2012 Mar 30;149(1):124-36. doi: 10.1016/j.cell.2012.01.047. Cell. 2012. PMID: 22464325 Free PMC article. - FisB mediates membrane fission during sporulation in Bacillus subtilis.
Doan T, Coleman J, Marquis KA, Meeske AJ, Burton BM, Karatekin E, Rudner DZ. Doan T, et al. Genes Dev. 2013 Feb 1;27(3):322-34. doi: 10.1101/gad.209049.112. Genes Dev. 2013. PMID: 23388828 Free PMC article. - Poplar extrafloral nectaries: two types, two strategies of indirect defenses against herbivores.
Escalante-Pérez M, Jaborsky M, Lautner S, Fromm J, Müller T, Dittrich M, Kunert M, Boland W, Hedrich R, Ache P. Escalante-Pérez M, et al. Plant Physiol. 2012 Jul;159(3):1176-91. doi: 10.1104/pp.112.196014. Epub 2012 May 9. Plant Physiol. 2012. PMID: 22573802 Free PMC article. - The tilted helix model of dynamin oligomers.
Kadosh A, Colom A, Yellin B, Roux A, Shemesh T. Kadosh A, et al. Proc Natl Acad Sci U S A. 2019 Jun 25;116(26):12845-12850. doi: 10.1073/pnas.1903769116. Epub 2019 Jun 12. Proc Natl Acad Sci U S A. 2019. PMID: 31189604 Free PMC article. - Hepatocytes internalize trophic receptors at large endocytic "Hot Spots".
Cao H, Krueger EW, McNiven MA. Cao H, et al. Hepatology. 2011 Nov;54(5):1819-29. doi: 10.1002/hep.24572. Hepatology. 2011. PMID: 21793030 Free PMC article.
References
- Allain JM, Storm C, Roux A, Ben Amar M, Joanny JF. Fission of a multiphase membrane tube. Phys Rev Lett. 2004;93:158104. - PubMed
- Angelova MI, Dimitrov DS. A mechanism of liposome electroformation. Prog Colloid Polym Sci. 1988;76:59–67.
- Bar-Ziv R, Moses E. Instability and “pearling” states produced in tubular membranes by competition of curvature and tension. Phys Rev Lett. 1994;73:1392–1395. - PubMed
- Bashkirov PV. Membrane nanotubes in the electric field as a model for measurement of mechanical parameters of the lipid bilayer. Biochemistry (Moscow) Supplement Series A: Membrane and Cell Biology. 2007;1:176–184.
- Chernomordik LV, Kozlov MM. Protein-lipid interplay in fusion and fission of biological membranes. Annu Rev Biochem. 2003;72:175–207. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R37 MH061345/MH/NIMH NIH HHS/United States
- Z01 HD001415-17/ImNIH/Intramural NIH HHS/United States
- R01GM42455/GM/NIGMS NIH HHS/United States
- Z01 HD001409-22/ImNIH/Intramural NIH HHS/United States
- R01 GM042455/GM/NIGMS NIH HHS/United States
- R01 MH061345/MH/NIMH NIH HHS/United States
- Z99 HD999999/ImNIH/Intramural NIH HHS/United States
- R37MH61345/MH/NIMH NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials