Accurate macromolecular structures using minimal measurements from X-ray free-electron lasers - PubMed (original) (raw)
doi: 10.1038/nmeth.2887. Epub 2014 Mar 16.
Nathaniel Echols 1, Rosalie Tran 1, Jan Kern 1, Richard J Gildea 2, Aaron S Brewster 1, Roberto Alonso-Mori 3, Carina Glöckner 4, Julia Hellmich 4, Hartawan Laksmono 5, Raymond G Sierra 5, Benedikt Lassalle-Kaiser 1, Alyssa Lampe 1, Guangye Han 1, Sheraz Gul 1, Dörte DiFiore 4, Despina Milathianaki 3, Alan R Fry 3, Alan Miahnahri 3, William E White 3, Donald W Schafer 3, M Marvin Seibert 3, Jason E Koglin 3, Dimosthenis Sokaras 6, Tsu-Chien Weng 6, Jonas Sellberg 7, Matthew J Latimer 6, Pieter Glatzel 8, Petrus H Zwart 1, Ralf W Grosse-Kunstleve 1, Michael J Bogan 9, Marc Messerschmidt 3, Garth J Williams 3, Sébastien Boutet 3, Johannes Messinger 10, Athina Zouni 11, Junko Yano 1, Uwe Bergmann 3, Vittal K Yachandra 1, Paul D Adams 1, Nicholas K Sauter 1
Affiliations
- PMID: 24633409
- PMCID: PMC4008696
- DOI: 10.1038/nmeth.2887
Accurate macromolecular structures using minimal measurements from X-ray free-electron lasers
Johan Hattne et al. Nat Methods. 2014 May.
Erratum in
- Nat Methods. 2015 Jul;12(7):692
Abstract
X-ray free-electron laser (XFEL) sources enable the use of crystallography to solve three-dimensional macromolecular structures under native conditions and without radiation damage. Results to date, however, have been limited by the challenge of deriving accurate Bragg intensities from a heterogeneous population of microcrystals, while at the same time modeling the X-ray spectrum and detector geometry. Here we present a computational approach designed to extract meaningful high-resolution signals from fewer diffraction measurements.
Conflict of interest statement
Competing Financial Interests
The authors declare no competing financial interests.
Figures
Figure 1. Thermolysin structure determination at 2.1 Å resolution
(a) _2mF_o−_DF_celectron density contoured at 1 σ (gray mesh) with water molecules shown as red spheres. (b)mF_o−_DF_c difference density map contoured at +3 σ (green mesh) and −3_σ (red mesh) showing binding sites for two of the four Ca ions and (c) the single Zn ion. (d) Detail of two crystal lattices found on the same diffraction image. Modeled spot positions assigned to the different lattices are shown in red and blue, respectively. The sample-detector distance of 135 mm corresponds to a resolution of 2.15 Å at the edges. (e) Detail from a different diffraction image. Increasing radial spot elongation is observed with distance from the beam center (blue cross).
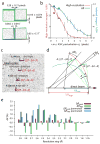
Figure 2. Calibration and validation
(a) Aggregate relative positions (top) and rotations (bottom) of 32 pairs of application-specific integrated circuits (ASICs), each pair bump-bonded to a pixel array sensor of the CSPAD detector. The two ASICs on each sensor are manufactured to be aligned along the long axis, separated by a 3.0-pixel gap. These calibration results bear out this expectation within the tolerances shown. (b) Impact of positional accuracy on the indexing and integration success rate. Perturbing the ASICs away from their true positions reduces both the total number of indexed images (blue) and the number of images that contain successfully integrated reflections at high (1.8–2.2 Å) resolution (red). Error bars are the standard deviation from five different sets of perturbations drawn from a twodimensional normal distribution with a standard deviation_σr_. Separate perturbations were drawn for each ASIC. Squares: failure to apply final subpixel corrections from iterative least squares refinement. Circles: failure to apply nearest-whole pixel corrections. (c) Detail of four Bragg reflections on a thermolysin diffraction pattern, showing pronounced (seven pixel) radial elongation for the [27 –34 –7] reflection and lesser elongation for those nearby. Solution of Bragg’s law for each pixel (black arrows) identifies the spread of photon energies that contribute to each reflection. Red disks delineate integration masks from a three-parameter model with wavelength limits λ_high= 1.297 (9.556 keV) and λ_low = 1.313 (9.443 keV), and full-width mosaic spread δ = 0.174°. (d) Reciprocal space diagram indicating how different-shaped reflections arise. Reciprocal lattice points (arcs) all have a constant angular extent_δ due to their mosaic spread. Points are in reflecting condition if they are within the zone between the high-energy (red) and low-energy (blue) Ewald spheres. Therefore, a greater fraction of the [27 –34 –7] mosaic distribution is within the reflecting condition, leading to a reflection that subtends a greater radial angle Δ_θ. (e) Paired refinements of the thermolysin structure. Red and green bars indicate the change in_R_work and _R_free, respectively, as higher-resolution data are added to the refinement. Dark and light blue bars show changes to the _R_-factors when the newly added high-resolution structure factors are randomly permuted. The data are interpreted as containing statistically significant signal for the resolution shells where Δ_R_free is continuously negative,i.e. out to 2.1 Å.
Similar articles
- Enabling X-ray free electron laser crystallography for challenging biological systems from a limited number of crystals.
Uervirojnangkoorn M, Zeldin OB, Lyubimov AY, Hattne J, Brewster AS, Sauter NK, Brunger AT, Weis WI. Uervirojnangkoorn M, et al. Elife. 2015 Mar 17;4:e05421. doi: 10.7554/eLife.05421. Elife. 2015. PMID: 25781634 Free PMC article. - Diverse application platform for hard X-ray diffraction in SACLA (DAPHNIS): application to serial protein crystallography using an X-ray free-electron laser.
Tono K, Nango E, Sugahara M, Song C, Park J, Tanaka T, Tanaka R, Joti Y, Kameshima T, Ono S, Hatsui T, Mizohata E, Suzuki M, Shimamura T, Tanaka Y, Iwata S, Yabashi M. Tono K, et al. J Synchrotron Radiat. 2015 May;22(3):532-7. doi: 10.1107/S1600577515004464. Epub 2015 Apr 16. J Synchrotron Radiat. 2015. PMID: 25931065 Free PMC article. - A Bright Future for Serial Femtosecond Crystallography with XFELs.
Johansson LC, Stauch B, Ishchenko A, Cherezov V. Johansson LC, et al. Trends Biochem Sci. 2017 Sep;42(9):749-762. doi: 10.1016/j.tibs.2017.06.007. Epub 2017 Jul 18. Trends Biochem Sci. 2017. PMID: 28733116 Free PMC article. Review. - X-Ray Free-Electron Lasers for the Structure and Dynamics of Macromolecules.
Chapman HN. Chapman HN. Annu Rev Biochem. 2019 Jun 20;88:35-58. doi: 10.1146/annurev-biochem-013118-110744. Epub 2019 Jan 2. Annu Rev Biochem. 2019. PMID: 30601681 Review. - Radiation Damage in Macromolecular Crystallography.
Garman EF, Weik M. Garman EF, et al. Methods Mol Biol. 2017;1607:467-489. doi: 10.1007/978-1-4939-7000-1_20. Methods Mol Biol. 2017. PMID: 28573586 Review.
Cited by
- XFEL diffraction: developing processing methods to optimize data quality.
Sauter NK. Sauter NK. J Synchrotron Radiat. 2015 Mar;22(2):239-48. doi: 10.1107/S1600577514028203. Epub 2015 Jan 29. J Synchrotron Radiat. 2015. PMID: 25723925 Free PMC article. Review. - IOTA: integration optimization, triage and analysis tool for the processing of XFEL diffraction images.
Lyubimov AY, Uervirojnangkoorn M, Zeldin OB, Brewster AS, Murray TD, Sauter NK, Berger JM, Weis WI, Brunger AT. Lyubimov AY, et al. J Appl Crystallogr. 2016 May 11;49(Pt 3):1057-1064. doi: 10.1107/S1600576716006683. eCollection 2016 Jun 1. J Appl Crystallogr. 2016. PMID: 27275148 Free PMC article. - A quantum spin-probe molecular microscope.
Perunicic VS, Hill CD, Hall LT, Hollenberg LC. Perunicic VS, et al. Nat Commun. 2016 Oct 11;7:12667. doi: 10.1038/ncomms12667. Nat Commun. 2016. PMID: 27725630 Free PMC article. - Improving signal strength in serial crystallography with DIALS geometry refinement.
Brewster AS, Waterman DG, Parkhurst JM, Gildea RJ, Young ID, O'Riordan LJ, Yano J, Winter G, Evans G, Sauter NK. Brewster AS, et al. Acta Crystallogr D Struct Biol. 2018 Sep 1;74(Pt 9):877-894. doi: 10.1107/S2059798318009191. Epub 2018 Sep 3. Acta Crystallogr D Struct Biol. 2018. PMID: 30198898 Free PMC article. - An outlook on using serial femtosecond crystallography in drug discovery.
Mishin A, Gusach A, Luginina A, Marin E, Borshchevskiy V, Cherezov V. Mishin A, et al. Expert Opin Drug Discov. 2019 Sep;14(9):933-945. doi: 10.1080/17460441.2019.1626822. Epub 2019 Jun 11. Expert Opin Drug Discov. 2019. PMID: 31184514 Free PMC article. Review.
References
- Neutze R, et al. Nature. 2000;406:752–757. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R01 GM102520/GM/NIGMS NIH HHS/United States
- GM055302/GM/NIGMS NIH HHS/United States
- GM095887/GM/NIGMS NIH HHS/United States
- R56 GM055302/GM/NIGMS NIH HHS/United States
- R01 GM110501/GM/NIGMS NIH HHS/United States
- P41GM103393/GM/NIGMS NIH HHS/United States
- GM102520/GM/NIGMS NIH HHS/United States
- R01 GM055302/GM/NIGMS NIH HHS/United States
- R01 GM095887/GM/NIGMS NIH HHS/United States
- P41 GM103393/GM/NIGMS NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources