Print level order traversal line by line (original) (raw)

Last Updated : 01 Oct, 2024

Try it on GfG Practice

Given a **Binary Tree, the task is to print the nodes level-wise, each level on a new line.

**Example:

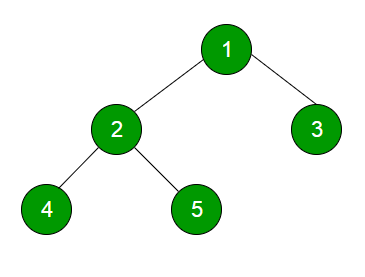
**Input:

**Output:
1
2 3
4 5

Table of Content

• [Naive Approach] - Using Recursion - O(n^2) Time and O(n) Space
• [Expected Approach – 1] Using Queue with delimiter – O(n) Time and O(n) Space
• [Expected Approach – 2] Using Queue without delimiter – O(n) Time and O(n) Space

[Naive Approach] - Using Recursion - O(n^2) Time and O(n) Space

A simple solution to perform level order traversal is to first calculate the **height of the tree. After obtaining the **height, we can use a **recursive function to store the nodes at each level into a container. For each level from **1 to the height, we traverse the tree using depth-first search while maintaining the current height. Instead of printing the nodes directly, we store them in a 2d container, where each inner corresponds to a **level in the **tree.

Below is the implementation of the above approach:

C++ `

// C++ Program to print level Order // traversal of Binary Tree #include <bits/stdc++.h> using namespace std;

class Node { public: int data; Node *left, *right;

Node(int key) {
    data = key;
    left = nullptr;  
    right = nullptr; 
}

};

// Print nodes at a given level void printGivenLevel(Node *root, int level, vector &levelNodes) { if (root == nullptr) return; if (level == 1) { levelNodes.push_back(root->data); } else if (level > 1) { printGivenLevel(root->left, level - 1, levelNodes); printGivenLevel(root->right, level - 1, levelNodes); } }

// Compute the "height" of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node *node) { if (node == nullptr) return 0;

// Compute the height of each subtree
int lheight = height(node->left);
int rheight = height(node->right);

// Use the larger one without the ternary operator
if (lheight > rheight) {
    return lheight + 1;
}
else {
    return rheight + 1;
}

}

// Function to return level order traversal as // a vector of vectors vector<vector> levelOrder(Node *root) { vector<vector> result; int h = height(root); for (int i = 1; i <= h; i++) { vector levelNodes; printGivenLevel(root, i, levelNodes); result.push_back(levelNodes); } return result; }

int main() {

// Binary Tree Representation
//
//       1
//     /   \
//    2     3
//   / \
//  4   5

Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);

vector<vector<int>> result = levelOrder(root);
for (const auto &level : result) {
    for (int val : level) {
        cout << val << " ";
    }
    cout << endl;
}

return 0;

}

Java

// Java Program to print level Order // traversal of Binary Tree

import java.util.ArrayList; import java.util.List;

class Node { int data; Node left, right;

Node(int key) {
    data = key;
    left = null;
    right = null;
}

}

class GfG {

// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node.
static int height(Node node) {
    if (node == null)
        return 0;
    else {
      
        // compute the height of each subtree
        int lheight = height(node.left);
        int rheight = height(node.right);

        // use the larger one
        return Math.max(lheight, rheight) + 1;
    }
}

static void printGivenLevel(Node root, int level,
                            List<Integer> levelNodes) {
    if (root == null)
        return;
    if (level == 1)
        levelNodes.add(root.data);
    else if (level > 1) {
        printGivenLevel(root.left, level - 1, levelNodes);
        printGivenLevel(root.right, level - 1, levelNodes);
    }
}

// Function to return level order traversal as a list of
// lists
static List<List<Integer> > levelOrder(Node root) {
    List<List<Integer> > result = new ArrayList<>();
    int h = height(root);
    for (int i = 1; i <= h; i++) {
        List<Integer> levelNodes = new ArrayList<>();
        printGivenLevel(root, i, levelNodes);
        result.add(levelNodes);
    }
    return result;
}

public static void main(String[] args) {

    // Binary Tree Representation
    //
    //       1
    //     /   \
    //    2     3
    //   / \
    //  4   5

    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
  
    List<List<Integer> > result = levelOrder(root);

    for (List<Integer> level : result) {
        for (int val : level) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}

}

Python

Python Program to print level Order

traversal of Binary Tree

class Node: def init(self, key): self.data = key self.left = None self.right = None

def height(node): if node is None: return 0 else:

    # compute the height of each subtree
    lheight = height(node.left)
    rheight = height(node.right)

    # use the larger one
    return (lheight + 1) if lheight > rheight else (rheight + 1)

def printGivenLevel(root, level, levelNodes): if root is None: return if level == 1: levelNodes.append(root.data) elif level > 1: printGivenLevel(root.left, level - 1, levelNodes) printGivenLevel(root.right, level - 1, levelNodes)

def levelOrder(root): result = [] h = height(root) for i in range(1, h + 1): levelNodes = [] printGivenLevel(root, i, levelNodes) result.append(levelNodes) return result

Binary Tree Representation

1

/ \

2 3

/ \

4 5

root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)

result = levelOrder(root)

for level in result: for val in level: print(val, end=" ") print()

C#

// C# Program to print level Order traversal // of Binary Tree

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int key) {
    data = key;
    left = null;
    right = null;
}

}

class GfG {

// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node.
static int Height(Node node) {
    if (node == null)
        return 0;
    else {
      
        // compute the height of each subtree
        int lheight = Height(node.left);
        int rheight = Height(node.right);

        // use the larger one
        return Math.Max(lheight, rheight) + 1;
    }
}

static void PrintGivenLevel(Node root, int level, 
                            List<int> levelNodes) {
    if (root == null)
        return;
    if (level == 1)
        levelNodes.Add(root.data);
    else if (level > 1) {
        PrintGivenLevel(root.left, level - 1, levelNodes);
        PrintGivenLevel(root.right, level - 1, levelNodes);
    }
}

// Function to return level order traversal 
  // as a list of lists
static List<List<int>> LevelOrder(Node root) {
    List<List<int>> result = new List<List<int>>();
    int h = Height(root);
    for (int i = 1; i <= h; i++) {
        List<int> levelNodes = new List<int>();
        PrintGivenLevel(root, i, levelNodes);
        result.Add(levelNodes);
    }
    return result;
}

static void Main() {
  
    // Binary Tree Representation
    //
    //       1
    //     /   \
    //    2     3
    //   / \
    //  4   5
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);

    List<List<int>> result = LevelOrder(root);

    foreach (var level in result) {
        foreach (var val in level) {
            Console.Write(val + " ");
        }
        Console.WriteLine();
    }
}

}

JavaScript

// JavaScript Program to print level Order // traversal of Binary Tree

class Node { constructor(key) { this.data = key; this.left = null; this.right = null; } }

function height(node) { if (node === null) { return 0; } else {

    // compute the height of each subtree 
    const lheight = height(node.left);
    const rheight = height(node.right);

    // use the larger one 
    return Math.max(lheight, rheight) + 1;
}

}

function printGivenLevel(root, level, levelNodes) { if (root === null) { return; } if (level === 1) { levelNodes.push(root.data); } else if (level > 1) { printGivenLevel(root.left, level - 1, levelNodes); printGivenLevel(root.right, level - 1, levelNodes); } }

function levelOrder(root) { const result = []; const h = height(root); for (let i = 1; i <= h; i++) { const levelNodes = []; printGivenLevel(root, i, levelNodes); result.push(levelNodes); } return result; }

// Binary Tree Representation // // 1 // /
// 2 3 // /
// 4 5

const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5);

const traversal = levelOrder(root); for (const level of traversal) { console.log(level.join(" ")); }

`

**Time complexity: O(n^2) where **n is the number of node of binary tree.
**Auxiliary Space: O(n), recursion stack space used is **O(n).

[Expected Approach – 1] Using Queue with delimiter – O(n) Time and O(n) Space

The idea is to use **single queues anddelimiter to traverse in Level order manner. First insert the **root and a null into the queue. NULL acts as a **delimiter. Next, **pop from the top of the **queue and add its **left and **right nodes to the end of the **queue and then add the **top element of the queue into **container. When we find the top element of the queue as **NULL, it indicates the occurrence of **next level. Continue this process till the queues become empty. Please refer to Level order traversal line by line (Using One Queue) for implementation.

[Expected Approach – 2] Using Queue without delimiter – O(n) Time and O(n) Space

To perform a level order traversal of a binary tree, use a **queue to process nodes level by level. Start by **enqueuing the root node, then iterate while the queue is not empty. For each level, determine the number of nodes to process, **dequeue each node, **store in the container , and **enqueue its children. After processing all nodes at the **current level, finally **push the current level stored in the **result before moving to the next level. Please refer to Level order traversal line by line (Using One Queue) for implementation.

**Related articles:

• Level Order Traversal (Breadth First Search or BFS) of Binary Tree