Placental mammal diversification and the Cretaceous–Tertiary boundary (original) (raw)
Abstract
Competing hypotheses for the timing of the placental mammal radiation focus on whether extant placental orders originated and diversified before or after the Cretaceous-Tertiary (K/T) boundary. Molecular studies that have addressed this issue suffer from single calibration points, unwarranted assumptions about the molecular clock, and/or taxon sampling that lacks representatives of all placental orders. We investigated this problem using the largest available molecular data set for placental mammals, which includes segments of 19 nuclear and three mitochondrial genes for representatives of all extant placental orders. We used the Thorne/Kishino method, which permits simultaneous constraints from the fossil record and allows rates of molecular evolution to vary on different branches of a phylogenetic tree. Analyses that used different sets of fossil constraints, different priors for the base of Placentalia, and different data partitions all support interordinal divergences in the Cretaceous followed by intraordinal diversification mostly after the K/T boundary. Four placental orders show intraordinal diversification that predates the K/T boundary, but only by an average of 10 million years. In contrast to some molecular studies that date the rat–mouse split as old as 46 million years, our results show improved agreement with the fossil record and place this split at 16–23 million years. To test the hypothesis that molecular estimates of Cretaceous divergence times are an artifact of increased body size subsequent to the K/T boundary, we also performed analyses with a “K/T body size” taxon set. In these analyses, interordinal splits remained in the Cretaceous.
Keywords: Mammalia‖molecular clock‖Placentalia‖phylogeny
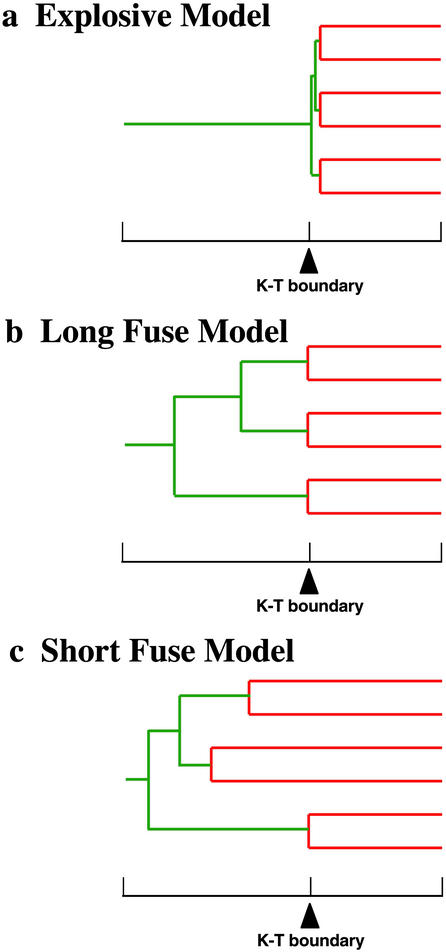
Archibald and Deutschman (1) suggested the Explosive, Long Fuse, and Short Fuse models as competing hypotheses for placental mammal diversification (Fig. 1). Differences between these models focus on the timing of the placental mammal radiation relative to the Cretaceous–Tertiary (K/T) boundary, which marked the abrupt extinction of dinosaurs. Discriminating among these models is critical for understanding the historical context of placental mammal diversification and for deriving accurate estimates of genomic and morphological rates of evolution.
Figure 1.
Simplified versions of three models (1) for the timing and diversification of placental mammals. Red branches indicate intraordinal diversification; green branches indicate interordinal divergences. A simplified time scale is shown below each tree, with an arrow marking the K/T boundary.
The Explosive Model (Fig. 1a) postulates ordinal originations and intraordinal diversification mostly or entirely after the K/T boundary. Some paleontologists favor this model (2–5, §), in large part because essentially all fossils with characters specific to modern placental orders occur after the K/T boundary. The Long Fuse Model (Fig. 1b) agrees with the Explosive Model in placing most intraordinal diversifications after the K/T boundary. However, in this scenario, interordinal divergences are placed well back in the Cretaceous. Archibald (6), Nessov et al. (7), and Archibald et al. (8) have interpreted 85- to 90-million-year-old fossils from Uzbekistan as crown-group placentals that provide support for the Long Fuse Model. Finally, the Short Fuse Model (Fig. 1c) postulates interordinal and some intraordinal divergences in excess of 100 million years ago (mya), “before or shortly after the appearance of eutherians in the fossil record” (1). Although molecular studies provide almost unanimous support for Cretaceous interordinal divergences (9–15), a finding that is compatible with both the Long Fuse and Short Fuse models, some molecular studies agree with the Short Fuse Model by placing some intraordinal divergences (e.g., rodents, eulipotyphlan insectivores) in excess of 100 mya (9, 11, 12).
Previous molecular studies that have addressed the timing of the placental mammal radiation (reviewed in ref. 16) have shortcomings that include the use of single calibration points, an unwarranted molecular clock assumption even when there is lineage-specific rate variation, limited taxon sampling that fails to include all orders of placental mammals, either because molecular sequences were unavailable or because violations of the molecular clock limited comparisons to reduced sets of taxa [e.g., linearized tree results of Murphy _et al._ (14)], and failure to address the proposed negative correlation between body size and the rate of molecular evolution, which is potentially important because mean body size increased in placental mammals subsequent to the K/T boundary (17). Here, we address these issues using the Murphy et al. (14) data set in conjunction with recently developed Bayesian approaches for estimating posterior probabilities of divergence times (18, 19). Taxon sampling includes representatives from each of the 18 modern placental orders (20), as well as taxa within most of these orders that diverged early after ordinal definition. Furthermore, the Bayesian approach (18, 19) avoids the molecular clock assumption and permits the incorporation of multiple constraints from the fossil record. Our results, including an analysis that addressed the potential problem of increasing body size subsequent to the K/T boundary and analyses that used different data partitions, are generally compatible with the Long Fuse Model and support interordinal diversification in the Cretaceous followed by intraordinal diversification that is mostly after the K/T boundary.
Materials and Methods
Gene and Taxon Sampling.
The Murphy et al. (14) data set totals 16,397 aligned nucleotide positions and indexes segments of 19 nuclear and three mitochondrial genes for 42 placental mammals. Taxon sampling comprises representatives of all extant placental orders, including taxa that index the presumed deepest splits in Afrosoricida (Tenrecidae + Chrysochloridae), Carnivora, Cetartiodactyla, Chiroptera, Eulipotyphla, Lagomorpha, Perissodactyla, Primates, Rodentia, and Xenarthra. We performed analyses with the complete data set and with the following partitions: nuclear genes (14,750 bp); exons (12,988 bp); first and second codon positions (8,658 bp); third codon positions (4,330 bp); UTRs (1,762 bp); and mitochondrial RNA genes (1,647 bp). For the complete data set, see Data Set 1, which is published as supporting information on the PNAS web site, www.pnas.org.
Branch Length Estimation.
Branch lengths were estimated with the estbranches program of Thorne et al. (18) for the complete data set and each partition thereof. In each case, we used the maximum likelihood topology from Murphy et al. (ref. 14; supporting information). In addition, we investigated the potential effect of increased body size on estimates of placental divergence times by performing separate analyses with a pruned set of 16 placental taxa (denoted with asterisks in Fig. 2) that included only lineages that have maintained small body sizes, in the range of Alroy's (21) calculations for the 67–66 mya (mean ± SD mass = 4.40 ± 1.98 natural log grams) and 65–64 mya (mean ± SD = 6.42 ± 1.88 natural log grams) “bins” of fossil mammals. This was denominated the “K/T body size” set of taxa. We used Felsenstein's (22) model of sequence evolution and an allowance for a Γ distribution of rates with four discrete rate categories. The transition/transversion parameter and estimates of the rate categories of the gamma distribution were calculated with PAUP 4.0 (23) for each data set. The Murphy et al. (14) data set included two marsupial outgroups (opossum and diprotodontian). We arbitrarily chose opossum, but also performed an analysis with the diprotodontian to examine the sensitivity of our results to outgroup choice. To examine the impact of topological variation, we performed an analysis using the unrooted Murphy et al. (14) tree for placental mammals, which was alternatively rooted at the base of myomorph rodents. This root renders Rodentia, Glires, Euarchontoglires, and Boreoeutheria paraphyletic. Although the maximum likelihood results of Murphy et al. (14) provide 100% bootstrap support for each of these clades, other studies based on both mitochondrial and nuclear DNA sequences have suggested rooting at or near the base of myomorph rodents (ref. 15 and figure 1B of ref. 24).
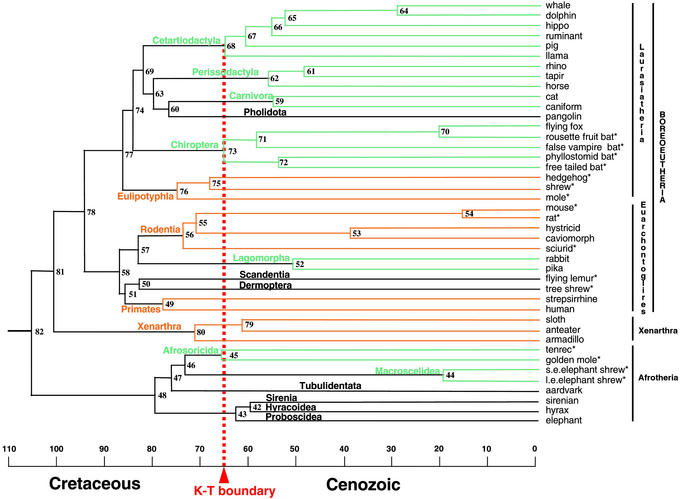
Figure 2.
Molecular time scale for the orders of placental mammals based on the 16,397-bp data set and maximum likelihood tree of ref. 14 with an opossum outgroup (data not shown), 13 fossil constraints (Materials and Methods), and a mean prior of 105 mya for the placental root. Ordinal designations are listed above the branches. Orange and green lines denote orders with basal diversification before or after the K/T boundary, respectively. Black lines depict orders for which only one taxon was available. Asterisks denote placental taxa included in the “K/T body size” taxon set. The composition of chimeric taxa, including caniform, caviomorph, strepsirrhine, and sirenian, is indicated elsewhere (14). Numbers for internal nodes are cross-referenced in the supporting information.
Divergence Time Estimation.
Divergence times were estimated using the program divtime5b (18, 19). Markov Chain Monte Carlo analyses were run for 1 million generations after a burnin of 100,000 generations to allow Markov chains to approach stationarity before states are sampled; chains were sampled every 100 generations. Application of the DIVTIME5B program requires an input value for the mean of the prior distribution of the root of the ingroup tree. We used 105 mya, which is the mean of two extremes that were selected from the literature. First, Penny et al. (12) obtained a value of 146 mya for the placental root based on an analysis of mtDNA amino acid sequences. Second, 65 mya is based on a strict interpretation of the Explosive Model. To ascertain the sensitivity of our results to this prior, we also performed supplementary analyses with mean priors of 146 and 65 mya. Analyses with the “K/T body size” taxon set were performed with mean priors of 65, 105, and 146 mya for the base of Placentalia. We used the following fossil constraints on divergence times (node numbers are for cross-referencing with Fig. 2):
Minimum of 60 mya for armadillo to sloth/anteater (node 80) based on the occurrence of cingulatan fossils from the late Paleocene (25, 26).
Minimum of 50 mya and maximum of 63 mya for the split between feliform and caniform carnivores (node 59) (25, 26). Viverravids from the early Paleocene are usually regarded as stem-group carnivores, but McKenna and Bell (26) suggest that they are crown-group carnivores. Given the latter possibility, we used a conservative maximum of 63 mya for the base of Carnivora.
Minimum of 54 mya and maximum of 58 mya for the split between hippomorph and ceratomorph perissodactyls (node 62) (24–27).
We followed Waddell et al. (24) and assigned a minimum of 52 mya for the hippo–cetacean divergence (node 65). The recent discovery of the early cetacean Himalayacetus allows for a slightly older minimum (53–54 mya) (28).
Although the oldest artiodactyls are ≈55 mya, controversial phylogenetic relationships among the major cetartiodactyl lineages, and of these to extinct mesonychids, suggest that the base of Cetartiodactyla (node 68) has a maximum of 65 mya (29), which was used here.
Minimum of 54 mya for the base of Paenungulata (node 43) based on the oldest proboscidean fossil (30). A maximum age for the base of Paenungulata (node 43) is difficult to establish, but a value of 65 mya is reasonable given that most estimates are less than this (e.g., ref. 31). At the same time, we tested the paenungulate maximum by performing an analysis that omitted this constraint.
Minimum of 12 mya for Mus to Rattus (node 54) (32).
In Chiroptera, we used a minimum of 43 mya and a maximum of 60 mya for Pteropodidae (flying fox and rousette fruit bat) to the false vampire bat (node 71) (26, 33, 34). The former is based on an approximate age for the earliest rhinolophoid bats (26, 34); the latter allows for views such as that of Sigé (33), though we recognize that Sigé (33) did not advocate the same topology for bats as recent molecular studies (14, 35–37).
In Eulipotyphla, we used a minimum of 63 mya for the split between shrew and hedgehog (node 75) based on the occurrence of soricoids (i.e., Carnilestes, Prosarcodon) from the early Paleocene (26) and erinaceids (i.e., Litolestes) that may be as old as early Paleocene (26).
Additional analyses omitted the carnivore, perissodactyl, paenungulate, bat, eulipotyphlan, and all cetartiodactyl constraints, respectively, to examine whether similar estimates were recovered when these constraints were not used. In analyses with the “K/T body size” taxon set, only the rat–mouse, pteropodid–megadermatid, and shrew–hedgehog constraints were available because of limited taxon sampling.
Results
Analyses with the Complete Data Set, Different Priors, and Different Outgroups.
Fig. 2 depicts a time scale for placental mammal evolution based on the 16,397-bp data set with the opossum outgroup and the 105 mya prior for the base of the placental tree. Results of a second analysis, which used different starting states for the Markov chain, were almost identical and always within one million years (see supporting information). Similarly, switching to the diprotodontian marsupial outgroup had minimal impact: divergence estimates were always within one million years of those shown in Fig. 2 (see supporting information). Employing a mean value of 65 or 146 mya for the prior distribution of the root of the placental tree had minimal impact; divergence dates shown in Fig. 2 changed by no more than two million years (Table 1; see supporting information for complete results).
Table 1.
Comparison of divergence estimates obtained with different data sets, varying prior probability distributions for the age of the placental root, and two different topologies (see supporting information)
| Group | 16,397-bp data set; 105 mya prior; Murphy (14) root | 16,397-bp data set; 65 mya prior; Murphy (14) root | 16,397-bp data set; 146 mya prior; Murphy (14) root | 16,397-bp data set; 105 mya prior; myomorph root | 16,397-bp K/T “body size” data set; 105 mya prior; Murphy (14) root |
|---|---|---|---|---|---|
| Base of Placentalia (node 82) | 107 (98–117) | 105 (96–115) | 108 (99–119) | 131 (116–148) | 102 (91–116) |
| Xenarthra–Boreoeutheria (node 81) | 102 (94–111) | 101 (93–109) | 103 (95–112) | NA | NA |
| Base of Boreoeutheria (node 78) | 94 (88–101) | 93 (87–100) | 95 (88–102) | NA | 90 (83–101) |
| Base of Laurasiatheria (node 77) | 85 (80–90) | 85 (80–90) | 85 (81–91) | 89 (84–95) | 82 (76–90) |
| Base of Euarchontoglires (node 58) | 87 (81–94) | 87 (81–93) | 88 (82–94) | NA | 85 (77–94) |
| Base of Paenungulata (node 43) | 62 (57–65) | 62 (57–65) | 62 (57–65) | 57 (54–62) | NA |
| Base of Cetartiodactyla (node 68) | 64 (62–65) | 64 (62–65) | 64 (62–65) | 64 (63–65) | NA |
| Base of Perissodactyla (node 62) | 56 (54–58) | 56 (54–58) | 56 (54–58) | 56 (54–58) | NA |
| Base of Carnivora (node 59) | 55 (51–60) | 55 (51–60) | 55 (50–60) | 56 (51–61) | NA |
| Base of Chiroptera (node 73) | 65 (62–68) | 65 (62–68) | 65 (62–68) | 66 (63–69) | 65 (61–69) |
| Base of Lagomorpha (node 52) | 51 (43–59) | 51 (42–58) | 51 (43–59) | 71 (57–81) | NA |
| Base of Afrosoricida (node 45) | 66 (60–73) | 66 (59–72) | 66 (59–73) | 58 (53–64) | 76 (66–87) |
| Base of Eulipotyphla (node 76) | 76 (71–81) | 75 (71–80) | 76 (71–81) | 79 (74–84) | 73 (69–75) |
| Base of Rodentia (node 56) | 74 (68–81) | 73 (67–80) | 74 (68–81) | NA | 70 (63–79) |
| Base of Primates (node 49) | 77 (71–84) | 77 (70–83) | 77 (71–84) | 95 (86–105) | NA |
| Base of Xenarthra (node 80) | 71 (63–79) | 72 (64–79) | 71 (63–79) | 66 (60–73) | NA |
| Hystricidae–Caviomorpha (node 53) | 38 (31–46) | 38 (30–46) | 38 (31–46) | 71 (57–85) | NA |
| Mus–Rattus (node 54) | 16 (13–21) | 16 (13–21) | 16 (13–21) | 35 (26–46) | 16 (12–20) |
The deepest split among placentals is between Afrotheria and other taxa at 107 mya (Fig. 2). The split between Euarchontoglires and Laurasiatheria was estimated at 94 mya. Interordinal splits within Euarchontoglires are in the range of 82–87 mya; those within Laurasiatheria are in the range of 77–85 mya. Among interordinal splits, only divergences within Paenungulata occurred after the K/T boundary, and only when constrained with a maximum of 65 mya. Within orders, subsequent basal splits are approximately at the K/T boundary for Afrosoricida, Chiroptera, and Cetartiodactyla. These are followed by basal splits within Carnivora, Lagomorpha, and Perissodactyla at ≈10–15 mya after the K/T boundary. Eulipotyphla, Primates, Rodentia, and Xenarthra show basal splits that are 5–12 million years before the K/T boundary. Of these, the oldest split is within Primates at 77 mya. The earliest divergence within Rodentia was estimated at 74 mya, and the rat-mouse split was dated at 16 mya.
Analyses with the Complete Data Set and a Myomorph Root.
Select results of an analysis that used a myomorph root for the placental tree are depicted in Table 1. Dates were older for the root of the placental tree (131 mya) and several clades with more basal positions on the myomorph root tree including rat to mouse (35 mya), hystricid to caviomorph (71 mya), Primates (95 mya), and Lagomorpha (71 mya). Similarly, dates were younger for some clades with more derived positions on the tree, such as Afrosoricida (58 mya) and Xenarthra (66 mya).
Analyses with Reduced Constraints.
When constraints on basal cladogenesis in Paenungulata were relaxed, the point estimate for this node changed from ≈63 mya to 72 mya. Estimated dates for some of the other nodes also increased, including 112 mya for the base of Placentalia, 98 mya for Euarchontoglires to Laurasiatheria, and 17 mya for rat to mouse. Omitting the minimum constraint of 63 mya for shrew–hedgehog had minimal impact on estimates of dates in Eulipotyphla; hedgehog–shrew remained at 68 mya and the split between these two and mole remained at 76 mya. When the basal carnivore and basal perissodactyl constraints were relaxed, these divergence events were still estimated in the early Cenozoic (carnivores at 55 mya; perissodactyls at 59 mya). Basal cladogenesis for Chiroptera shifted from 65 to 70 mya when constraints on the megadermatid–pteropodid split were omitted. Omitting the minimum for hippo to Cetacea and the maximum for the base of Cetartiodactyla resulted in younger estimates for both splits (55 mya for base of Cetartiodactyla; 40 mya for hippo-Cetacea). Detailed results are given in the supporting information.
Analyses with Nuclear and Mitochondrial Data Partitions.
Select results of analyses based on individual data partitions are given in Table 2. Complete results and confidence intervals for all analyses are given in the supporting information. The analysis with the nuclear genes data set (14,750 bp) yielded dates that were always within two million years of those illustrated in Fig. 2 for the complete data set. Among different partitions of the nuclear data, older dates were consistently estimated with exons than with UTRs. Similarly, first and second codon positions recovered younger estimates than third codon positions of exons. All interordinal splits were estimated in the Cretaceous with all of the data partitions except for Paenungulata, which was constrained, and the Scandentia–Dermoptera split, which was estimated at 58 mya with the mitochondrial RNA data partition. Estimates for intraordinal cladogenesis remained in the Late Cretaceous for Eulipotyphla, Primates, Rodentia, and Xenarthra with both the nuclear and mitochondrial partitions. However, some estimates were only slightly older than the K/T boundary. For example, analysis of just first and second codon positions produced an estimate of 67 mya for the base of Xenarthra. Analyses based on the mitochondrial RNA data partition recovered a placental root at 97 mya, whereas the majority of the additional estimates did not depart considerably from results of the other partitions.
Table 2.
Comparison of divergence estimates obtained with different data partitions (see supporting information)
| Group | Nuclear genes only | First and second codon positions | Third codon positions | Exons only | 3′ UTRs only | Mitochondrial RNA |
|---|---|---|---|---|---|---|
| Base of Placentalia (node 82) | 107 (98–119) | 103 (94–113) | 109 (99–121) | 108 (98–119) | 97 (87–110) | 97 (86–109) |
| Xenarthra–Boreoeutheria (node 81) | 103 (95–112) | 100 (92–110) | 103 (94–114) | 103 (95–113) | 94 (84–107) | 94 (84–106) |
| Base of Boreoeutheria (node 78) | 95 (88–102) | 91 (84–98) | 98 (90–107) | 96 (89–104) | 87 (79–97) | 88 (80–99) |
| Base of Laurasiatheria (node 77) | 85 (81–91) | 82 (78–88) | 87 (81–93) | 86 (81–91) | 83 (76–91) | 84 (76–93) |
| Base of Euarchontoglires (node 58) | 88 (82–95) | 85 (79–92) | 90 (83–99) | 89 (82–96) | 82 (73–92) | 84 (73–95) |
| Base of Paenungulata (node 43) | 62 (57–65) | 61 (55–65) | 62 (55–65) | 62 (56–65) | 62 (56–65) | 62 (56–65) |
| Base of Cetartiodactyla (node 68) | 64 (62–65) | 63 (60–65) | 64 (62–65) | 64 (62–65) | 63 (59–65) | 62 (57–65) |
| Base of Perissodactyla (node 62) | 56 (54–58) | 57 (54–58) | 56 (54–58) | 56 (54–58) | 56 (54–58) | 56 (54–58) |
| Base of Carnivora (node 59) | 56 (51–61) | 56 (51–61) | 56 (51–62) | 55 (51–61) | 56 (50–62) | 54 (50–61) |
| Base of Chiroptera (node 73) | 65 (62–68) | 62 (59–65) | 69 (65–73) | 66 (62–68) | 58 (50–64) | 65 (57–74) |
| Base of Lagomorpha (node 52) | 50 (42–58) | 48 (39–56) | 55 (45–64) | 52 (43–60) | 41 (28–57) | 56 (44–70) |
| Base of Afrosoricida (node 45) | 67 (60–73) | 60 (52–68) | 72 (63–80) | 66 (58–73) | 70 (59–82) | 61 (47–76) |
| Base of Eulipotyphla (node 76) | 76 (72–81) | 71 (67–75) | 81 (75–87) | 76 (72–81) | 76 (69–85) | 74 (66–85) |
| Base of Rodentia (node 56) | 74 (67–81) | 72 (65–79) | 76 (68–85) | 75 (67–82) | 73 (62–84) | 73 (61–85) |
| Base of Primates (node 49) | 77 (71–84) | 74 (67–82) | 80 (72–88) | 78 (71–86) | 69 (57–81) | 74 (62–87) |
| Base of Xenarthra (node 80) | 70 (62–78) | 67 (61–75) | 71 (62–81) | 70 (62–79) | 68 (60–82) | 81 (68–96) |
| Hystricidae–Caviomorpha (node 53) | 37 (30–45) | 36 (28–44) | 37 (28–45) | 37 (29–45) | 44 (33–57) | 52 (38–67) |
| Mus–Rattus (node 54) | 16 (12–21) | 15 (12–20) | 17 (13–22) | 16 (13–21) | 14 (12–20) | 24 (15–34) |
Analyses with the “K/T Body Size” Taxon Set.
The “K/T body size” taxon set was used to determine if analyses that only included smaller taxa resulted in younger divergence estimates. Some divergence estimates were slightly younger with this pruned taxon set relative to the full-taxon data set; however, the overall results were similar. The placental root was estimated at 100–104 mya. The split between Euarchontoglires and Laurasiatheria was estimated at 89–91 mya. Although comparisons were limited, all interordinal divergences were estimated in the Cretaceous, including 84–86 mya for Afrosoricida to Macroscelidea, 81–82 mya for the base of Laurasiatheria, and 83–85 mya for the base of Euarchontoglires. As with the full-taxon data set, results of analyses that used mean priors of 65, 105, and 146 million years for the base of Placentalia were in excellent agreement with each other. Point estimates using the 65 and 146 mya priors differed by no more than three million years from estimates using the 105 prior (see supporting information).
Discussion
Molecular and Paleontological Support for the Long Fuse Model.
The fossil record has suggested to some paleontologists that the ordinal radiation and diversification of crown-group Placentalia is entirely or mostly post-Cretaceous, i.e., the Explosive Model (Fig. 1). This hypothesis regards most or all known species of Cretaceous eutherian mammals as stem eutherians. In contrast, McKenna and Bell (26) recognize 22 genera from the Late Cretaceous and one genus from the Early Cretaceous as crown-group Placentalia. Cladistic analyses that incorporate a diverse assemblage of Cretaceous eutherian fossils, as well as representatives of all extant orders, have not been reported. Lacking a robust phylogeny that integrates Cretaceous and early Cenozoic eutherian fossils into the emerging molecular tree (13, 14, 38–40), it is difficult to evaluate how compatible the fossil record is with Cretaceous interordinal divergences. Archibald et al.'s (8) cladistic study provides some support for the Long Fuse Model of placental diversification, but even this study samples only a few crown-group placentals.
Our results are generally compatible with the Long Fuse Model of placental diversification. Interordinal splits are concentrated in the Cretaceous, whereas basal cladogenesis within most orders is in the Cenozoic (Table 1; Fig. 2). Four orders show basal cladogenesis extending back into the Crtetaceous, but point estimates are only 1–16 million years before the K/T boundary. The suggestion that four orders have intraordinal cladogenesis in the Cretaceous exceeds Archibald and Deutschman's (1) depiction of a single order. However, we find no evidence for deep intraordinal splits in excess of 100 mya, as predicted by the Short Fuse Model.
These results are robust, having been obtained with three different priors (65, 105, and 146 mya) for the placental root, two different marsupial outgroups, different data partitions, and with a “K/T body size” taxon set (Table 1). Our estimates for a placental root at 97–112 mya, even with an allowance for rate variation among lineages and a mean prior that was set at 65 mya, demonstrate the difficulty of fitting molecular data to the Explosive Model, as do analyses with “K/T body size” taxa. These analyses resulted in slightly younger estimates of divergence times for most nodes, but all interordinal divergences were still placed in the Cretaceous. Therefore, the proposed negative correlation between body size and rate of molecular evolution (17) does not account for the apparent discrepancy between molecular dates and the Explosive Model.
To examine the cost of fitting these molecular data (14) to a strict interpretation of the Explosive Model, we added constraints for the base of Placentalia (minimum = 65 mya; maximum = 66 mya) and compared resulting interordinal and intraordinal rates of nucleotide substitution over the entire placental tree. The lowest interordinal rate was 72 times higher than the lowest intraordinal rate; the highest interordinal rate was 3.4 times higher than the highest intraordinal rate; the highest interordinal rate was 669 times higher than the lowest interordinal rate; and the median interordinal rate was 7 times higher than the median intraordinal rate (see supporting information). Additional results from this analysis further demonstrate the difficulties of fitting the Murphy et al. data to the Explosive Model. For example, the rate on the branch leading to Boreoeutheria was 19 times higher than the branch leading to rat and 30 times higher than the rate on the branch leading to mouse, even though murids have among the fastest rates among placental taxa (41). Indeed, the median rate on interordinal branches was 242 times higher than the median rate on terminal branches under the Explosive Model.
Intraordinal Divergences.
Of the four orders that consistently display intraordinal diversification in the Late Cretaceous, some interpretations of the fossil record suggest that lipotyphlan insectivores extend into the Cretaceous (1, 26). However, this issue remains contentious (4, 5, §). Given that molecular data suggest Lipotyphla is diphyletic (10, 14, 42), the phylogenetic affinities of Cretaceous insectivores are highly questionable and demand further scrutiny.
Rodentia, Primates, and Xenarthra first appear in the Paleocene (26). Our analyses suggest intraordinal diversification in the Late Cretaceous, but only 5–11 (rodents), 4–15 (primates), and 2–16 (xenarthrans) million years before the K/T boundary in different analyses and with different data sets. Further, 95% confidence intervals in some analyses extend into the Tertiary for each of these orders (e.g., 63 mya for rodents in “K/T body size” analysis). On the other hand, Tavaré et al. (43) estimated that living primates last shared a common ancestor 81.5 mya (95% confidence interval, 72.0–89.6 mya) based on a statistical analysis of the fossil record that takes into account fossil preservation rate.
Our sampling includes taxa that index basal or near basal divergences in 10 of 18 eutherian orders (Afrosoricida, Carnivora, Cetartiodactyla, Chiroptera, Eulipotyphla, Lagomorpha, Perissodactyla, Primates, Rodentia, Xenarthra). Taxa that represent basal crown-group cladogenesis were not indexed for the remaining orders: Tubulidentata, Hyracoidea, Proboscidea, Sirenia, Pholidota, Scandentia, Dermoptera, and Macroscelidea. However, available evidence suggests that none of these orders has crown-group cladogenesis as far back as the K/T boundary (supporting information).
Estimates Based on Different Data Partitions.
Dates based on different partitions were generally in good agreement, although dates based on UTRs and first and second codon positions were consistently younger than dates based on third codon positions. Whether the former two are underestimates or the latter are inflated deserves investigation. One potential problem with the latter is base-compositional heterogeneity. A χ2 test indicates base-compositional heterogeneity for third codon positions, but not for UTRs or first and second codon positions. Huchon et al. (44) also found significant base-compositional heterogeneity for third codon positions, but not for first and second codon positions. Huchon et al. (44) obtained a median estimate of 101 mya for the base of Placentalia by using quartet dating and first and second codon positions for three nuclear genes. This finding agrees with our estimate of 103 mya based on first and second codon positions.
Deep Rodent Dates.
A potential stumbling block for the acceptance of molecular dates is deep cladogenesis within Rodentia, either as a monophyletic or paraphyletic group (11, 15). Our 70–77 mya estimates for basal cladogenesis within this order are younger than molecular dates in the range of 112–125 mya (9, 11, 45, 46) and agree with Adkins et al.'s (47) study of rodent genes, which estimates the basal rodent split at 75 mya. Huchon et al. (44) obtained even younger dates (median = 56 mya) for the base of Rodentia by using quartet dating. In addition, paleontological evidence supports the view that Mus and Rattus diverged at 12–14 mya (32), whereas many molecular estimates have departed significantly from fossil evidence, ranging as high as 41–46 mya (11, 47). Our analyses with the Murphy et al. (14) maximum likelihood topology suggest dates (14–24 mya) that are more concordant with the fossil record. Our results also suggest a possible explanation for the deep split between rat and mouse that has emerged from some molecular studies. Specifically, placement of rodents at or near the base of the eutherian tree (46). In our analysis that rooted Placentalia at the base of myomorph rodents, we obtained an estimate of 35 mya for the rat–mouse split. However, this requires a topology that contradicts the monophyly of Rodentia, Glires, Euarchontoglires, and Boreoeutheria, all of which are supported by Bayesian posterior probabilities of 1.00 and bootstrap support scores of 100% (14). Further, the monophyly of Euarchontoglires is supported by two independent deletions (48). Nevertheless, this analysis highlights the sensitivity of molecular dates to the underlying topology.
Conclusions
Our analyses support interordinal diversification of placental mammals before the K/T boundary. Congruent results for basal placental cladogenesis have now been obtained by using linearized tree methods that assume a single rate, quartet dating methods allowing two rates, and new Bayesian methods that allow rate variation across the topology (11–14, 38, 44). Our results reveal the increasing difficulty of reconciling molecular interordinal dates with the Explosive Model of placental diversification (5, §). Instead, our data are generally more consistent with the Long Fuse Model, rather than the Short Fuse Model predicted by very early rodent and insectivore molecular divergences. Using the Thorne/Kishino (18, 19) algorithm ameliorates the effects of murid-specific rate acceleration, and brings molecular interordinal estimates into greater accord with putative 85- to 90-million-year-old placental fossils (6–8). Four placental orders (Eulipotyphla, Rodenta, Xenarthra, Primates) consistently showed pre-K/T divergence dates, even in the absence of fossil constraints and under a variety of different data partitions and priors for the root. However, these values only exceed the K-T boundary by an average of 10 million years, and are within 10 to 15 million years of the oldest Paleocene fossils reported for these taxa. Reliable fossil calibrations, large molecular data sets, and improved dating methods are shaping a molecular time scale for the evolution of placental mammals that is largely compatible with existing paleontological evidence.
Supplementary Material
Supporting Information
Abbreviations
K/T
Cretaceous–Tertiary
mya
million years ago
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
§
Novacek, M. J., Rougier, G. W., Dashzeveg, D. & McKenna, M. C. (2000) J. Vert. Paleontol. 3, 61A (abstr.).
References
- 1.Archibald J D, Deutschman D H. J Mammal Evol. 2001;8:107–124. [Google Scholar]
- 2.Gingerich P D. In: Patterns of Evolution as Illustrated by the Fossil Record. Hallam A, editor. Amsterdam: Elsevier; 1977. pp. 469–500. [Google Scholar]
- 3.Carroll R L. Patterns and Processes of Vertebrate Evolution. Cambridge, U.K.: Cambridge Univ. Press; 1997. [Google Scholar]
- 4.Foote M, Hunter J P, Janis C M, Sepkoski J J., Jr Science. 1999;283:1310–1314. doi: 10.1126/science.283.5406.1310. [DOI] [PubMed] [Google Scholar]
- 5.Benton M J. BioEssays. 1999;21:1045–1051. doi: 10.1002/(SICI)1521-1878(199912)22:1<1043::AID-BIES8>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 6.Archibald J D. Science. 1996;278:1438–1442. [Google Scholar]
- 7.Nessov L A, Archibald J D, Kielan-Jaworowska Z. Bull Carnegie Mus Nat Hist. 1998;34:40–88. [Google Scholar]
- 8.Archibald J D, Averianov A O, Ekdale E G. Nature. 2001;414:62–65. doi: 10.1038/35102048. [DOI] [PubMed] [Google Scholar]
- 9.Springer M S. J Mammal Evol. 1997;4:285–302. [Google Scholar]
- 10.Springer M S, Cleven G C, Madsen O, de Jong W W, Waddell V G, Amrine H M, Stanhope M J. Nature. 1997;388:61–64. doi: 10.1038/40386. [DOI] [PubMed] [Google Scholar]
- 11.Kumar S, Hedges S B. Nature. 1998;392:917–920. doi: 10.1038/31927. [DOI] [PubMed] [Google Scholar]
- 12.Penny D, Hasegawa M, Waddell P J, Hendy M D. Syst Biol. 1999;48:76–93. doi: 10.1080/106351599260454. [DOI] [PubMed] [Google Scholar]
- 13.Eizirik E, Murphy W J, O'Brien S J. J Hered. 2001;92:212–219. doi: 10.1093/jhered/92.2.212. [DOI] [PubMed] [Google Scholar]
- 14.Murphy W J, Eizirik E, O'Brien S J, Madsen O, Scally M, Douady C J, Teeling E, Ryder O A, Stanhope M J, de Jong W W, Springer M S. Science. 2001;294:2348–2351. doi: 10.1126/science.1067179. [DOI] [PubMed] [Google Scholar]
- 15.Arnason U, Adegoke J A, Bodin K, Born E W, Esa Y B, Gullberg A, Nilsson M, Short R V, Xu X, Janke A. Proc Natl Acad Sci USA. 2002;99:8151–8156. doi: 10.1073/pnas.102164299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Smith A B, Peterson K J. Annu Rev Earth Planet Sci. 2002;30:65–88. [Google Scholar]
- 17.Bromham L, Rambaut A, Harvey P H. J Mol Evol. 1996;43:610–621. doi: 10.1007/BF02202109. [DOI] [PubMed] [Google Scholar]
- 18.Thorne J L, Kishino H, Painter I S. Mol Biol Evol. 1998;15:1647–1657. doi: 10.1093/oxfordjournals.molbev.a025892. [DOI] [PubMed] [Google Scholar]
- 19.Kishino H, Thorne J L, Bruno W J. Mol Biol Evol. 2001;18:352–361. doi: 10.1093/oxfordjournals.molbev.a003811. [DOI] [PubMed] [Google Scholar]
- 20.Waddell P J, Okada N, Hasegawa M. Syst Biol. 1999;48:1–5. [PubMed] [Google Scholar]
- 21.Alroy J. Syst Biol. 1999;48:107–118. doi: 10.1080/106351599260472. [DOI] [PubMed] [Google Scholar]
- 22.Felsenstein J. Evolution (Lawrence, Kans) 1984;38:16–24. doi: 10.1111/j.1558-5646.1984.tb00255.x. [DOI] [PubMed] [Google Scholar]
- 23.Swofford D L. PAUP*: Phylogenetic Analysis Using Parsimony (* and Other Methods) Sunderland, MA: Sinauer; 1998. , Version 4. [Google Scholar]
- 24.Waddell P J, Kishino H, Ota R. Genome Informatics. 2001;12:141–154. [PubMed] [Google Scholar]
- 25.Benton M J. The Fossil Record 2. London: Chapman & Hall; 1993. [Google Scholar]
- 26.McKenna M C, Bell S K. Classification of Mammals Above the Species Level. New York: Columbia Univ. Press; 1997. [Google Scholar]
- 27.Bowen G J, Clyde W C, Koch P L, Ting S, Alroy J, Tsubamoto T, Wang Y, Wang Y. Science. 2001;295:2062–2065. doi: 10.1126/science.1068700. [DOI] [PubMed] [Google Scholar]
- 28.Bajpai S, Gingerich P D. Proc Natl Acad Sci USA. 1998;95:15464–15468. doi: 10.1073/pnas.95.26.15464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gatesy J, O'Leary M A. Trends Ecol Evol. 2001;16:562–570. [Google Scholar]
- 30.Gheerbrant E, Sudre J, Iarochene M, Moumni A. J Vert Paleontol. 2001;21:107–118. [Google Scholar]
- 31.Amrine H M, Springer M S. J Mammal Evol. 1999;6:161–176. [Google Scholar]
- 32.Jacobs L L, Downs W R. In: Rodent and Lagomorph Families of Asian Origins and Diversification. Tomida Y, Li C-K, Setoguchi T, editors. Tokyo: National Science Museum Monographs; 1994. pp. 149–156. [Google Scholar]
- 33.Sigé B. Geobios. 1991;13:231–236. [Google Scholar]
- 34.Simmons N B, Geisler J H. Bull Am Mus Nat Hist. 1998;235:1–182. [Google Scholar]
- 35.Teeling E C, Scally M, Kao D J, Romagnoli M L, Springer M S, Stanhope M J. Nature. 2000;403:188–192. doi: 10.1038/35003188. [DOI] [PubMed] [Google Scholar]
- 36.Teeling E C, Scally M, Kao D J, Romagnoli M L, Springer M S, Stanhope M J. Proc Natl Acad Sci USA. 2002;99:1431–1436. doi: 10.1073/pnas.022477199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Springer M S, Teeling E C, Madsen O, Stanhope M J, de Jong W W. Proc Natl Acad Sci USA. 2001;98:6241–6246. doi: 10.1073/pnas.111551998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Madsen O, Scally M, Douady C J, Kao D J, DeBry R W, Adkins R, Amrine H M, Stanhope M J, de Jong W W, Springer M S. Nature. 2001;409:610–614. doi: 10.1038/35054544. [DOI] [PubMed] [Google Scholar]
- 39.Murphy W J, Eizirik E, Johnson W E, Zhang Y P, Ryder O A, O'Brien S J. Nature. 2001;409:614–618. doi: 10.1038/35054550. [DOI] [PubMed] [Google Scholar]
- 40.Scally M, Madsen O, Douady C J, de Jong W W, Stanhope M J, Springer M S. J Mammal Evol. 2001;8:239–277. [Google Scholar]
- 41.Li W-H. Molecular Evolution. Sunderland, MA: Sinauer; 1997. [Google Scholar]
- 42.Stanhope M J, Waddell V G, Madsen O, de Jong W, Hedges S B, Cleven G C, Kao D, Springer M S. Proc Natl Acad Sci USA. 1998;95:9967–9972. doi: 10.1073/pnas.95.17.9967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tavaré S, Marshall C R, Will O, Soligo C, Martin R D. Nature. 2002;416:726–729. doi: 10.1038/416726a. [DOI] [PubMed] [Google Scholar]
- 44.Huchon D, Madsen O, Sibbald M J J B, Ament K, Stanhope M J, Catzeflis F, de Jong W W, Douzery E J P. Mol Biol Evol. 2002;19:1053–1065. doi: 10.1093/oxfordjournals.molbev.a004164. [DOI] [PubMed] [Google Scholar]
- 45.Janke A, Xu X, Arnason U. Proc Natl Acad Sci USA. 1997;94:1276–1281. doi: 10.1073/pnas.94.4.1276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Huelsenbeck J P, Larget B, Swofford D. Genetics. 2000;154:1879–1892. doi: 10.1093/genetics/154.4.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Adkins R M, Gelke E L, Rowe D, Honeycutt R L. Mol Biol Evol. 2001;18:777–791. doi: 10.1093/oxfordjournals.molbev.a003860. [DOI] [PubMed] [Google Scholar]
- 48.Poux C, van Rheede T, Madsen O, de Jong W W. Mol Biol Evol. 2002;19:2035–2037. doi: 10.1093/oxfordjournals.molbev.a004028. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information