Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model (original) (raw)

. Author manuscript; available in PMC: 2009 Jul 4.

Published in final edited form as: J Mol Biol. 2008 Apr 8;380(2):415–424. doi: 10.1016/j.jmb.2008.04.001

Summary

While the molecular-mechanics field has standardized on a few potential energy functions, computational protein design efforts are based on potentials that are unique to individual labs. Here we show that a standard molecular-mechanics potential energy function without any modifications can be used to engineer protein-ligand binding. A molecular-mechanics potential is used to reconstruct the coordinates of various binding sites with an average root mean square error of 0.61 Å, and to reproduce known ligand-induced side-chain conformational shifts. Within a series of 34 mutants, the calculation can always distinguish weak (Kd > 1 mM) and tight (Kd < 10 µM) binding sequences. Starting from partial coordinates of the ribose binding protein lacking the ligand and the ten primary contact residues, the molecular-mechanics potential is used to redesign a ribose binding site. Out of a search space of 2×1012 sequences, the calculation selects a point mutant of the native protein as the top solution (experimental Kd = 17 µM), and the native protein as the second best solution (experimental Kd = 210 nM). The quality of the predictions depends on the accuracy of the generalized Born electrostatics model, treatment of protonation equilibria, high resolution rotamer sampling, a final local energy minimization step, and explicit modeling of the bound, unbound, and unfolded states. The application of unmodified molecular-mechanics potentials to protein design links two fields in a mutually beneficial way. Design provides a new avenue to test molecular-mechanics energy functions, and future improvements in these energy functions will presumably lead to more accurate design results.

Keywords: protein design, generalized Born, force field, dissociation constant, structure prediction

Introduction

Computer-aided design of a ligand binding site is similar to solving a 3D jigsaw puzzle: it involves fitting together the right pieces (amino acid mutations) to create a properly shaped and functionalized pocket for a ligand. The inputs to the design procedure are the crystal structure of a scaffold protein, a ligand structure, and a set of amino-acid positions that will be mutated to create the binding site. The orientations of candidate jigsaw-puzzle pieces are determined by modeling the conformations that the ligand and surrounding amino acids can adopt, so as to identify the lowest energy arrangement. The design procedure searches through thousands of candidate sequences for one that optimizes the computed binding free energy of the ligand with the protein. The whole process depends heavily on the potential energy function (PEF), a mathematical expression embodying the physical laws that govern the protein-ligand and solvent system.

Over the past 30 years, potential energy functions have played a central role in the molecular-mechanics field. This field has converged on a small set of standard PEF’s that have been extensively tested.1 Identifying and correcting the limitations of these energy models is an area of active research.2–4 The modern molecular-mechanics potential energy functions (MM-PEF’s) treat proteins as a collection of atoms with partial charges and van der Waals parameters, connected by springs that maintain bond lengths and angles. The parameters are derived from quantum calculations and from experimental data on a wide range of systems.5 MM-PEF’s have been used to calculate binding constants6–10, protein folding kinetics11, protonation equilibria12, and active site coordinates8,13,14.

Perhaps surprisingly, standard MM-PEF’s are not used for protein design.15 The reason is that computing energies using MM-PEF’s requires significant computer time and is very sensitive to detailed atom positions, necessitating fine conformational sampling. When thousands of different sequences must be evaluated, the computation time per sequence becomes critical. In order to accelerate calculations, design algorithms typically use simplified PEFs with various ad hoc energy terms13,16–28 (heuristic potential energy functions are also often used to predict binding constants29,30 and to predict active site coordinates31). Water is treated in a simplified way, for example by inserting a distance dependent dielectric constant into Coulomb’s law, and by applying a surface-area based solvation energy.16,17 The van der Waals interaction is frequently smoothed so that it is less sensitive to spatial position, and thus can be optimized with coarse sampling.16–18 Rather than explicitly modeling reference states, such as the unfolded state, the reference states are typically treated implicitly by modifying the PEF.16–18 Statistical terms derived by counting how frequently different residues and functional groups interact in crystal structures, are included as well.16–18 Relative weights for the various energy terms are adjusted empirically so as to match experimental data.18,19 Similar approximations were used in the early days of molecular-mechanics calculations, but were replaced as better models and increased computational power became available.

There are several motivations for trying to identify a single, standardized energy function that is practically useful for protein design. First, design results from different labs could be compared, and those results would collectively address where the energy model had failed and how to improve it. Second, the practice of computational protein design would be simplified if PEF development were not required. Finally, a PEF that had been broadly validated might be expected to generalize better to new design problems than would a customized PEF.

One reasonable choice for a universal energy function would be an MM-PEF. MMPEF’s are the most broadly tested PEF’s,1 and a direct correspondence exists between them and more rigorous quantum-mechanical treatments of matter.5 A large group of scientists work on MM-PEF’s, and the advances they make would be directly applicable to design. Here, we test whether protein-ligand binding sites can be successfully designed based on a standard MM-PEF that does not include any heuristic corrections. We first describe how we directly apply an MM-PEF to the protein design problem, and then detail various tests applied to the ribose binding protein.

Results

Design scheme

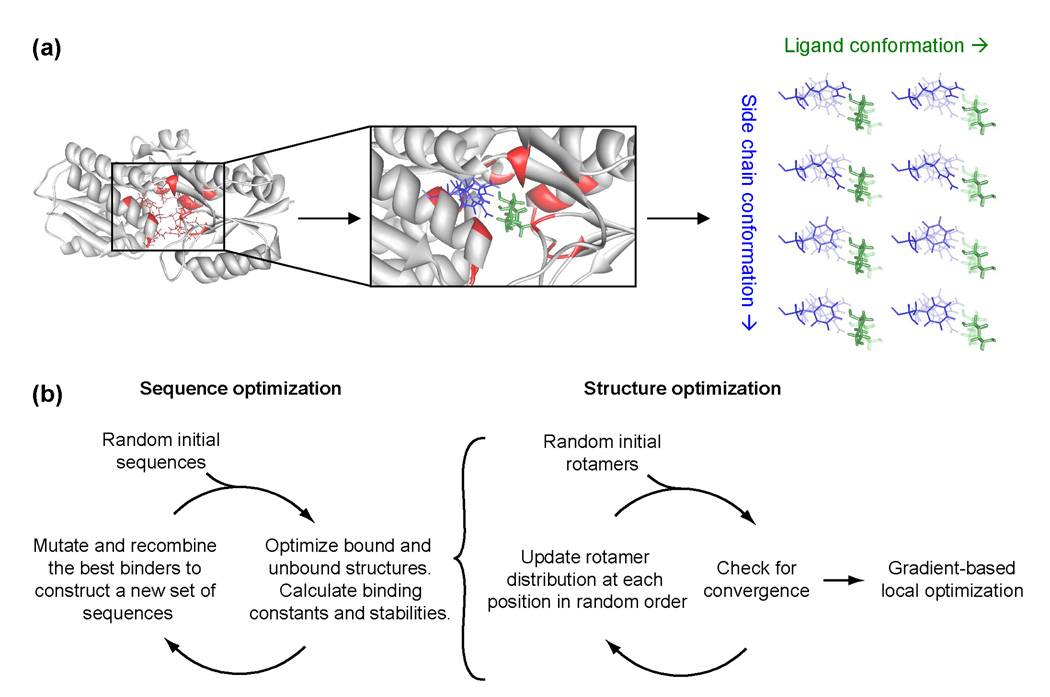
Using the genetic algorithm,32 we search through thousands of sequences to find one sequence that maximizes the calculated protein-ligand dissociation energy without destabilizing the protein by more than 5 kcal/mol. To evaluate dissociation and unfolding energies, the bound, unbound, and unfolded states are modeled, and their calculated energies are differenced. For each state, we use a mean field rotamer-repacking algorithm to find the atomic coordinates that minimize the energy. As part of the rotamer repacking, titratable residues are allowed to protonate or deprotonate depending on the local energetics. Good structural sampling is achieved by using extremely large rotamer libraries (≥5449 rotamers per position), and several thousand ligand poses that sample the translational, rotational, and internal degrees of freedom of the ligand. The optimal structure generated by rotamer repacking is then subjected to gradient-based energy minimization. The energies of each state are evaluated with the unmodified CHARMM22 molecular-mechanics potential energy function33 and the generalized Born solvation formalism34 developed by Lee et al.35 The design procedure is outlined in Figure 1. To evaluate the approach, we apply three tests: structural prediction, energetic prediction, and prediction of a binding site sequence.

Figure 1.

Figure 1

Simplified schematic of the protein design algorithm. (a) Setting up a design calculation. The design calculation is based on a scaffold protein (gray) with a known crystal structure, and a set of design positions (red). Possible ligand poses (green) and side chain conformations (blue) for each amino acid at each position are constructed. The right panel shows multiple side chain rotamers modeled at one design position, and two alternative ligand poses. Interaction energies between the possible ligand poses and the possible side chain conformations are precomputed. (b) Running a design calculation. The design procedure involves separate sequence optimization (to find sequences that bind ribose) and structural optimization (to determine the binding constant and stability of each sequence). In the RBP-ribose redesign, we search a space of 2×1012 sequences and an average of 5×1028 conformations per sequence.

Structural prediction

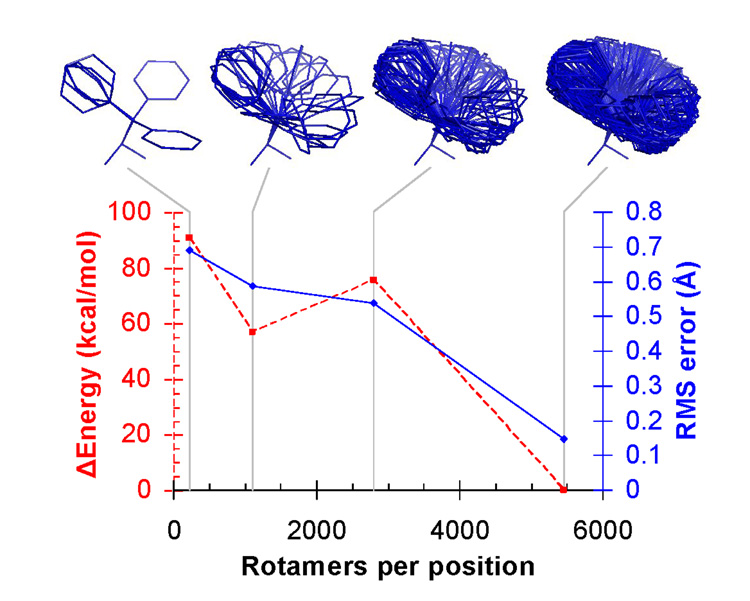
For structural predictions, we started with crystal structures and discarded the coordinates of the ligand and all contacting side chains. These coordinates were then predicted in the context of the rest of the protein. We first explored the effect of sampling resolution by predicting the structure of ribose binding protein (RBP) bound to ribose using four rotamer libraries of increasing size (Figure 2). With fewer than 5449 rotamers per position, the calculated energy of the predicted structure is less favorable than the calculated energy of the crystal structure, indicating that the crystal structure conformation is missed due to inadequate sampling resolution. At 5449 rotamers per position, the predicted structure has the same energy as the energy-minimized crystal structure, and the coordinates differ by a root mean square (RMS) error of 0.148 Å. This level of accuracy exceeds the experimental error in the crystallographic coordinates. This apparently surprising result likely occurs because the fixed portion of the crystallographic coordinates constrains the possible solutions at the modeled positions. However, this constraint alone is not sufficient to specify the binding site sequence and geometry (see below).

Figure 2.

Figure 2

Higher rotamer resolution improves structural predictions for the RBP binding site (PDB code: 2DRI). Δ Energy is the difference in potential energy between the calculated structure and the crystal structure, after both have been subjected to local energy minimization. RMS error is the root-mean-square deviation between the calculated and crystallographic coordinates of the repacked atoms, comprising the ligand and ten active site side chains. The phenylalanine rotamers from each rotamer library are shown to illustrate the sampling resolution. The lowest resolution rotamer library shown is the Richardson penultimate rotamer library51 with protonation states added for His, Asp, and Glu. The other rotamer libraries were derived by clustering side chain conformations in high resolution crystal structures from the Protein Data Bank (see Supporting Information).

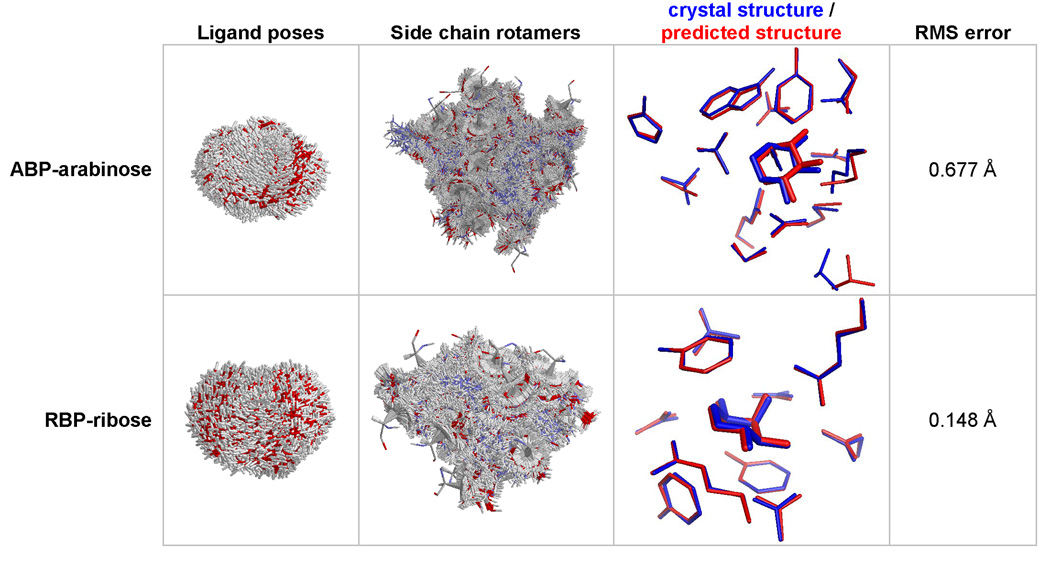
Using high resolution rotamer libraries (either 5449 or 6028 rotamers per position), side chains in the binding sites of 5 different structures were predicted with an average RMS error of 0.61 Å (Figure 3–Figure 4). The number of predicted residues ranged from 9 to 23. The error was generally larger for surface residues, and when more positions were predicted.

Figure 3.

Figure 3

Prediction of binding site coordinates. Starting from crystal structures stripped of the ligand and the contacting residues, the active site was reconstructed by finding the lowest energy arrangement of the ligand and side chains. For ABP-arabinose (PBD code: 6ABP), the coordinates of the arabinose and 15 contacting residues (10, 14, 16, 17, 64, 89, 90, 108, 145, 147, 151, 204, 205, 232, 259) were predicted using 6028 rotamers per position and 4111 ligand poses. For RBP-ribose (PDB code: 2DRI), the coordinates of ribose and 10 contacting residues (13, 15, 16, 89, 90, 141, 164, 190, 215, 235) were predicted using 5449 rotamers per position, and 4639 ligand poses.

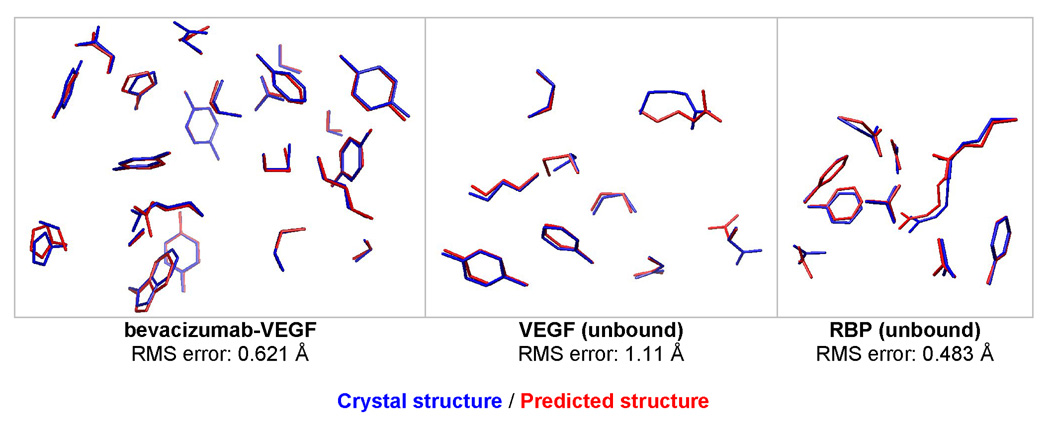
Figure 4.

Figure 4

Prediction of binding site coordinates for bevacizumab-VEGF (1BJ1), unbound VEGF (2VPF), and unbound RBP (1URP). For bevacizumab-VEGF, the following 23 residues were repacked, using 6028 rotamers per position: V17, V21, W48, W79, W81, W82, W83, W91, W93, H28, H30, H31, H32, H54, H55, H99, H101, H102, H103, H105, H106, H107, H108. V and W are VEGF chains, H and L are antibody heavy and light chains. For unbound VEGF and RBP, the same set of residues were predicted as the bound structure.

For the RBP-ribose calculations, we restricted the ligand poses to be within 1.8 Å RMS of the native pose, resulting in the 4639 poses shown in Figure 3. For the ABP-arabinose calculations, the ligand poses were restricted to be within 1.0 Å RMS of the native pose, resulting in the 4111 poses shown in Figure 3. Although we would have preferred to do the calculations without this filter, it was necessary to reduce the number of ligand poses to a manageable number (the precalculated interaction energy matrices had to be smaller than 2 GB to fit into memory).

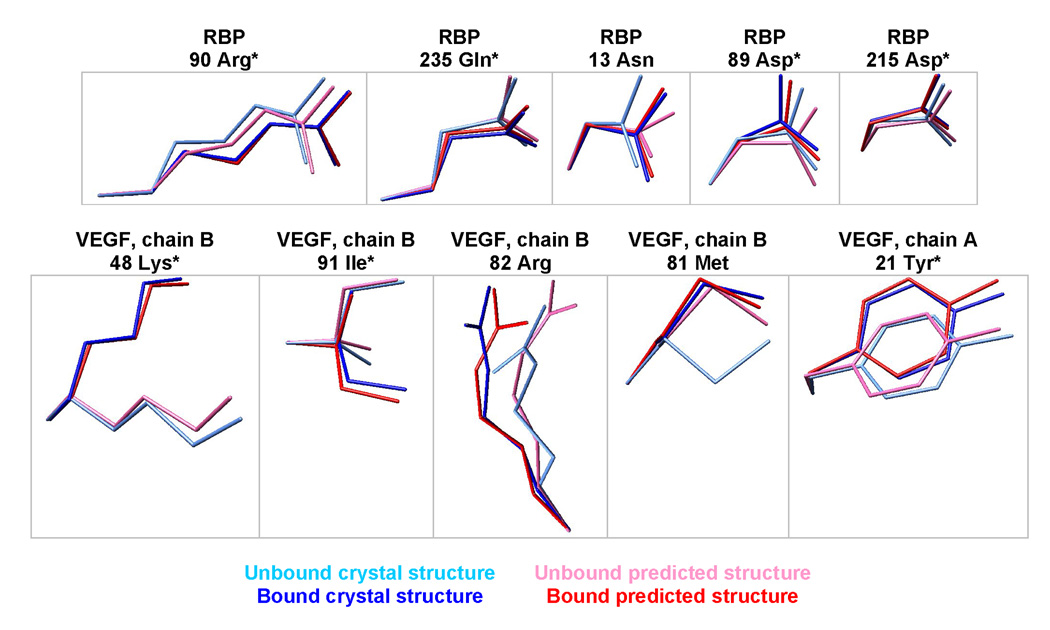
We explicitly model the bound and unbound states, providing predictions of side-chain conformational shifts upon binding. The predicted changes match the crystal structures in 70% of the residues with the largest conformational shifts (Figure 5). Single-state design algorithms ignore such conformational shifts, in contrast to a multi-state design framework.22 Note that we did not predict the backbone shift upon binding (4.1 Å RMS for RBP and 0.8 Å RMS for VEGF) because the bound and unbound backbone coordinates were used as inputs to the calculation.

Figure 5.

Figure 5

Prediction of side chain conformational shifts in RBP upon binding ribose, or VEGF upon binding bevacizumab. The five largest experimentally observed conformational shifts are shown for each protein. The residues were superimposed by aligning the backbone amide nitrogen, alpha carbon, and carbonyl carbon. * denotes correct predictions, where the unbound/bound predictions are closest to the unbound/bound crystallographic coordinates, respectively.

The calculation predicts that one aspartic acid and one glutamic acid in the binding site of ABP are protonated (Supporting Table 5). If these residues are not allowed to protonate, the structural prediction is degraded (Supporting Figure 7).

Energetic prediction

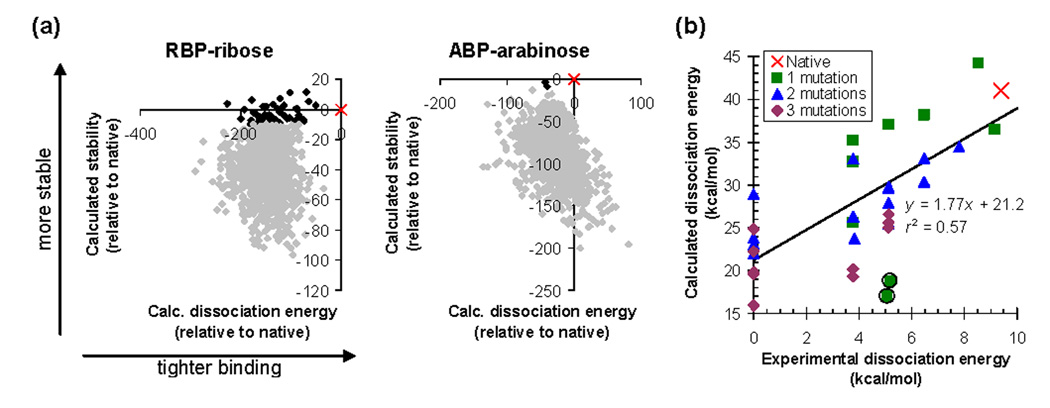
To test if the energy function can properly rank the binding affinities of different binding site sequences, we first computed ligand binding energies for the native ABP and RBP sequences and for 1000 scrambled sequences. As expected, none of the scrambled sequences have better predicted stability and dissociation energy than the native (Figure 6a).

Figure 6.

Figure 6

Predicting dissociation energies. (a) Calculated stability and dissociation energy distinguish the native sequence (×) from 1000 scrambled sequences (♦) for ABP and RBP. Sequences predicted to be more then 10 kcal/mol destabilized relative to the native are shown in gray. (b) Predicting relative dissociation energies of mutants. The graph shows data on mutants of ABP binding to arabinose. Experimental data are from reference 52 and from measurements reported in Supporting Table 6. An experimental dissociation energy of zero means that there was no detectable binding. Calculations were performed using 6ABP as the scaffold structure for both the bound and unbound states, with 6028 rotamers per position. Coordinates of the fifteen primary ligand contacts and of residues 20 and 235 were optimized. The circled points are predicted to be destabilized by more than 10 kcal/mol relative to the native.

Next, we calculated the relative binding energies of 34 mutants of ABP for which dissociation energies have been measured. Two sequences were predicted to destabilize the protein by more than 10 kcal/mol relative to native ABP, and presumably adopt alternative backbone conformations. The binding energies of the remaining sequences are predicted with a correlation coefficient of _r_2=0.57 (Figure 6b, Supporting Table 6). The predictions were performed without any adjustable parameters. As each calculation required about 1 minute of CPU time on a Pentium processor, the approach is fast enough for design applications. The data set includes single, double, and triple point mutants of wild type ABP, and covers a wide range of mutation types (hydrophobic to hydrophobic, hydrophobic to polar/charged, polar/charged to hydrophobic, and polar/charged to polar/charged).

Within the data set, the calculation can always distinguish weak (Kd > 1 mM) and tight (Kd < 10 µM) binding sequences. However, the absolute dissociation energies are not predicted correctly. One important possible source of error is that there is no published crystal structure of unbound ABP. We model the unbound protein backbone conformation based on the crystal structure of bound ABP. In reality, the unbound protein likely exists in an open conformation with better solvated binding-site residues.36 Our incorrect unbound state might explain the 21.2 kcal/mol offset in calculated dissociation energies. The slope of the regression line is greater than one, which is likely due to modes of structural relaxation (such as backbone motions) that were not modeled. The resulting clashes will exaggerate any energy differences between sequences. Another possibility is that we are not adequately modeling entropy losses upon binding.37

Binding site design

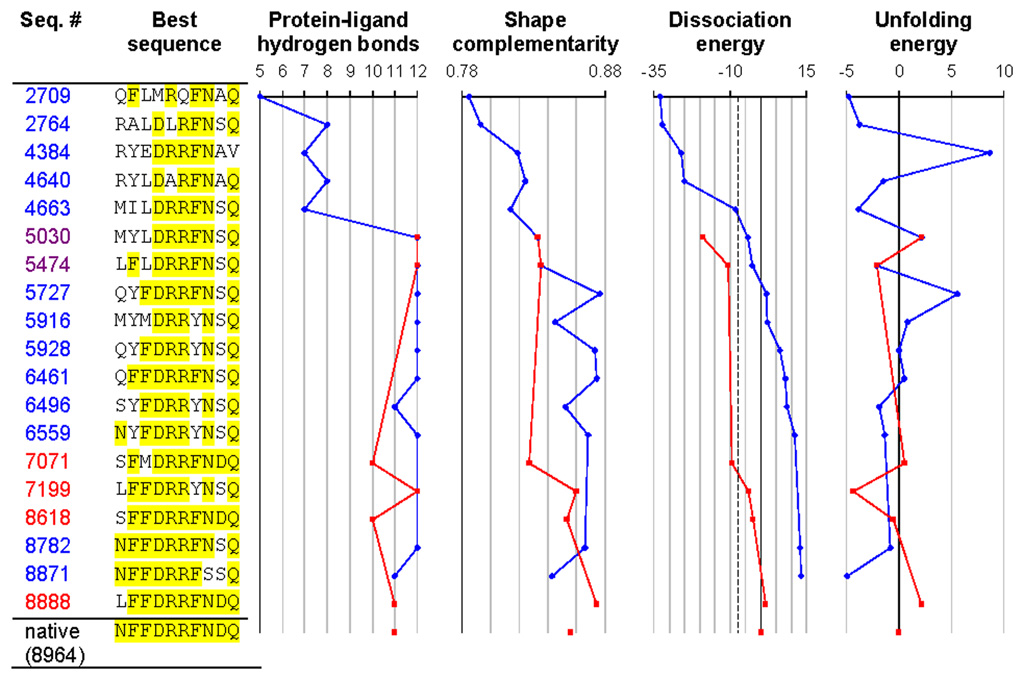
The final and most stringent test of the molecular mechanics energy model was a redesign of the binding site in RBP (Figure 7). We discarded the ligand coordinates, and the sequence and coordinates of the 10 residues contacting the ligand. The total size of the sequence space searched was 1710 = 2.0 × 1012 (Gly, Pro, and Cys were not allowed). The calculation was initiated from a population of random sequences. After evaluation of 8888 sequences, the energy function identified a point mutant (N13L) of native RBP as the tightest binding sequence. After 8964 sequences, it picked native RBP as the second tightest binding sequence. Evaluation of an additional 8879 sequences did not yield any further improvement. The entire process was repeated with a different random initial sequence population, and the same optimal sequences were selected. During the course of the design, first stability was achieved, then hydrogen bonding, and finally shape complementarity. The same pattern has been seen experimentally in the affinity maturation of antibodies against lysozyme.38

Figure 7.

Figure 7

Redesigning the ribose binding site in RBP. Positions identical to the native are highlighted in yellow. The figure shows the best sequence as a function of the number of sequences considered, using either the mean field dissociation energy as the criterion (blue trajectories) or alternatively the dissociation energy calculated using minimized structures (red trajectories). All sequences with a mean field dissociation energy greater than 30 kcal/mol (corresponding to −7.5 kcal/mol relative to the native sequence, dashed line) were locally energy minimized to generate the red trajectory. Sequence 8871 is the top sequence when ranked by mean field dissociation energy (corresponding to Table 1b), and sequence 8888 is the top sequence when ranked by minimized dissociation energy (corresponding to Table 1d). The native sequence was found out of a possible 2×1012 sequences after 8964 sequence evaluations. Dissociation and unfolding energies are reported in kcal/mol, relative to the native sequence. The number of protein-ligand hydrogen bonds was determined using bndlst.53 Shape complementarity (which ranges from 0 for perfectly non-complementary surfaces to 1 for perfectly complementary surfaces) was calculated using sc.54 Backbone coordinates for the bound state are from 2DRI, and backbone coordinates for the unbound state are from 1URP.

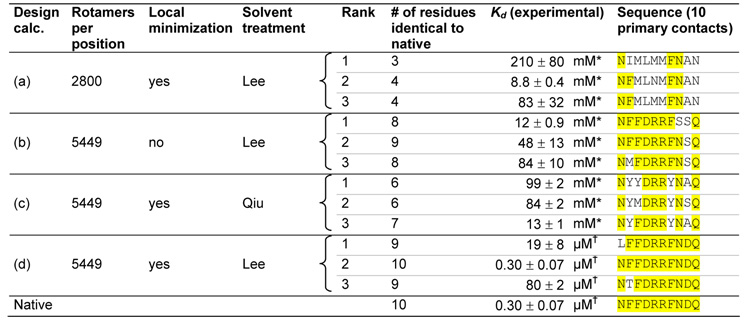
We experimentally tested the three top sequences from four different RBP-ribose redesign calculations to determine which aspects of the design algorithm were essential (Table 1). Decreasing the rotamer resolution (row a), omitting the final continuous minimization step (row b), or using a less accurate electrostatics model (row c) produces sequences that bind very weakly. Only when we use a high resolution rotamer library, a final continuous minimization step, and accurate electrostatics, does the design algorithm predict sequences that bind well (row d).

Table 1.

High resolution rotamer library, gradient-based local minimization, and an accurate solvation model are required to successfully redesign the ribose binding site in RBP. Multiple design calculations (a–d) were performed using different sampling resolutions and solvent models. The top three sequences from each calculation and their experimentally measured binding constants are shown. Parts of the sequence identical to the native sequence are highlighted in yellow. (a) Design calculation using a lower resolution rotamer library. (b) Design calculation without a gradient-based local minimization step. (c) Design calculation using a less accurate generalized Born solvent treatment55 (d) Design calculation using a high resolution rotamer library, gradient-based local minimization, and an accurate generalized Born solvation model35 Sequences are ranked by calculated dissociation energy, allowing 5 kcal/mol destabilization relative to the native sequence for 5449 rotamers / position, and 20 kcal/mol destabilization for 2800 rotamers / position. The native sequence was not within the top 100 sequences for design calculations A, B, or C.

graphic file with name nihms57945t1.jpg

Discussion

This paper reports the first successful redesign of an entire binding site based on an unmodified molecular-mechanics potential energy function. This is a stringent test of the energy function, because the native sequence and a point mutant are distinguished from 2.0 × 1012 alternative sequences. Good hydrogen bonds and steric complementarity were picked out directly by the energy function, without energy terms or selection criteria that specifically required these features. Given that the underlying physics is the same for the design of new proteins and for the simulation of known proteins, it is satisfying to see that the same energy models can be used as well.

We tested a number of simplifications commonly used in protein design calculations, and found that they all resulted in less successful predictions. For example, low sampling resolution or an inaccurate solvation model led to sequences that lacked critical hydrogen bonds. Scaling down the electrostatic energy (which is frequently done to compensate for a crude electrostatics model) reduced the accuracy of the energetic predictions. Eliminating the unfolded state resulted in unstable designed proteins. Softening the van der Waals interaction allowed atoms to pack together more closely, making hydrogen bonds and salt bridges appear artificially strong (Supporting Figure 8), and resulting in the burial of charged and polar functional groups.

An important conclusion from this work is that MM-PEF’s must be paired with an accurate continuum solvent model and with protonation equilibria in order to correctly redesign a polar binding site. Individual polar protein-ligand interactions can exhibit energies up to 100 kcal/mol (the Coulomb energy between unit charges separated by 3.3 Å). These energies are almost exactly counterbalanced by interactions with water in the unbound protein. Thus, small errors in the solvation energy grossly alter the design predictions. Finite difference algorithms are generally considered the most accurate methods to solve the Poisson-Boltzmann differential equation that defines the continuum solvent model, but they are currently too slow for protein design. Very accurate generalized Born approaches have been developed over the last few years,35 and produce solvation energies that differ from the finite difference result by only 2% (Supporting information). We have shown that this level of accuracy is both necessary and sufficient for protein design calculations.

The results in this paper suggest that the protein design and molecular-mechanics fields can work together on the same potential energy functions, and that future developments in MM-PEFs will be immediately applicable to protein design (although ad hoc terms may still be necessary for modeling aggregated and misfolded states). Currently, there are active efforts to develop polarizable potential energy functions that more accurately reproduce the physical characteristics of small molecules,2–4 and hybrid quantum mechanical / molecular mechanical potential energy functions that model charge transfer and changes in covalent bonding.39,40 It will be exciting to see how these improved energy models will impact the protein design problem.

Materials and methods

Calculations

Protein structures were predicted using a rotamer-based mean field algorithm.41 The energy was calculated as the sum of the CHARMM22 molecular-mechanics energy,33 a generalized Born surface-area solvation energy34,35 using a microscopic surface tension42 of 0.0072 kcal/mol/Å2, and a deprotonation energy.43 The most probable mean field structure was then locally minimized using the L-BFGS optimization algorithm44 in TINKER45 to obtain a final structure and energy. The unfolded protein energy was calculated by assuming that the protein backbone adopts an ensemble of random walk conformations in water (see 46,47 and Supporting Information) The stability of the protein was calculated as the energy difference between the unfolded protein and the folded unbound protein, and the dissociation energy was calculated as the energy difference between the uncomplexed and the complexed protein-ligand system. All calculations were performed at 25°C, pH 7.0, 100 mM monovalent salt. Ribose binding proteins were designed using a genetic algorithm32 that optimized the calculated ribose dissociation energy, given a 5 kcal/mol limit on protein destabilization. The genetic algorithm was initialized with a population of random sequences. Calculations were performed using CNSsolve48, TINKER45, and custom code written in C++, and run on a Pentium-based Linux cluster.

Protein purification and constructs

RBP without a periplasmic signal peptide was cloned into the NcoI/XhoI sites of pET28a (EMD Biosciences), generating a derivative with a C-terminal His6 tag. Mutants were made by Kunkel mutagenesis49 or by QuikChange (Stratagene). Protein was expressed in BL21 DE3 E. coli cells (Novagen) with 1 mM IPTG for 5 hr at 37°C. Cells were lysed with lysozyme and sonication in the presence of 1 mM phenylmethylsulfonyl fluoride. Protein was purified by immobilized metal affinity chromatography, followed by gel filtration chromatography in 20 mM potassium phosphate pH 7.0, 100 mM NaCl. The purified protein was then concentrated, and its final concentration determined by absorbance.50

Centrifugal concentrator radioligand binding assay

Proteins were diluted into 1 ml of 20 mM potassium phosphate pH 7.0, 100 mM NaCl, and 0.5 µCi 1-3H(N)-D-ribose (Moravek). After equilibration for 30 minutes, the samples were placed in centrifugal concentrators (Amicon Ultra, 5 kDa MWCO), and centrifuged until at least 500 µl of filtrate had crossed the membrane. Any filtrate in excess of 500 µl was returned to the retentate, and the quantity of radioligand in the filtrate and retentate were measured by scintillation counting. Dissociation constants were calculated as Kd=2Pr−1−2Lr+1, where r is the ratio of retentate to filtrate radioligand, P is the initial protein concentration, and L is the initial radioligand concentration. We chose conditions where P > Kd and r fell between 1.2 and 20. The analysis depends on the assumption that water and the ligand cross the membrane at equal rates. This assumption was tested by centrifuging a ribose solution across the membrane in the absence of protein; the specific activities of the retentate and filtrate were identical to within 4%.

Solid phase radioligand binding assay

A solid phase radioligand binding assay was used to detect binding with Kd_’s in the high millimolar range. Nickel-NTA agarose slurry (Qiagen) was washed and resuspended in buffer (20 mM potassium phosphate pH 7.0 and 100 mM NaCl) to form a 50% (v/v) slurry. Twenty microliters of the slurry were mixed with 5 nmol of His6-tagged protein and 1.0 µCi of radioligand in a final buffer volume of 50 µl. Following a 30 minute equilibration, the mixture was transferred to 0.45 µm centrifugal filter units (Millipore #UFC30HV0S) and centrifuged at 12000×g for 2 minutes to remove unbound ligand. The resin was washed three times by addition of 500 µl of 50 % ethanol and centrifugation at 12000×_g for 2 minutes. The bound ligand was eluted with 250 µl guanidinium HCl, and quantified by scintillation counting. Radioligand eluted from a no-protein control was included to account for non-specific binding to the resin, and a control of 0.5 µCi radioligand was used to determine counting efficiency. Dissociation constants were calculated as Kd=L−Lr−Pr+Pr2r, where r is the fraction of protein bound to radioligand, P is the initial protein concentration, and L is the initial ligand concentration.

Supplementary Material

01

Acknowledgments

We gratefully thank J.D. King, R.S. Fenn and S.R. Pfeffer for help with protein purification. We thank R.B. Altman, R.L. Baldwin, A.T. Brunger, R.S. Fenn, J.J. Havranek, D. Herschlag, M. Levitt, L.L. Looger, W.L. Martin, V.S. Pande, E.L. Raffauf, T.J. Wandless, R.M. Weisinger, and S.J. Wrenn for many helpful suggestions. This work was supported by NIH grants GM068126-01 and 1-DP1-0D000429 to P.B.H. F.E.B. was partially supported by a training grant from the National Institute of General Medical Sciences (5T32 GM07365-28).

Abbreviations

PEF

potential energy function

MM-PEF

molecular-mechanics potential energy function

PDB

Protein Data Bank

RMS

root mean square

ABP

arabinose binding protein

RBP

ribose binding protein

VEGF

vascular endothelial growth factor

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01