Analysis of Combinatorial cis-Regulation in Synthetic and Genomic Promoters (original) (raw)

. Author manuscript; available in PMC: 2009 Jul 8.

Published in final edited form as: Nature. 2008 Nov 23;457(7226):215–218. doi: 10.1038/nature07521

Abstract

Transcription factor binding sites (TFBS) are being discovered at a rapid pace1, 2. We must now begin to turn our attention towards understanding how these sites work in combination to influence gene expression. Quantitative models that accurately predict gene expression from promoter sequence3-5 will be a crucial part of solving this problem. Here we present such a model based on the analysis of synthetic promoter libraries in yeast. Thermodynamic models based only on the equilibrium binding of transcription factors to DNA and to each other captured a large fraction of the variation in expression in every library. Thermodynamic analysis of these libraries uncovered several phenomena in our system, including cooperativity and the effects of weak binding sites. When applied to the genome, a model of repression by Mig1, which was trained on synthetic promoters, predicts a number of Mig1 regulated genes that lack significant Mig1 binding sites in their promoters. The success of the thermodynamic approach suggests that the information encoded by combinations of cis-regulatory sites is interpreted primarily through simple protein-DNA and protein-protein interactions with complicated biochemical reactions, such as nucleosome modifications, being down stream events. Quantitative analyses of synthetic promoter libraries will be an important tool in unraveling the rules underlying combinatorial cis-regulation.

Thermodynamic models of gene regulation have shown promising results in Eukaryotic systems6, 7 when applied to small gene sets. Due to limitations in studying genomic promoters the number of observations in these studies is small compared to the number of molecular events that are modeled, and over fitting is therefore a serious concern. An approach that circumvents this limitation is to model the expression of synthetic promoters8-10. Since conceivably any promoter sequence can be created and analyzed, a large portion of possible regulatory element combinations can be evaluated.

We constructed synthetic promoter libraries consisting of random combinations of three to four transcription factor binding sites, or building blocks (Table 1 and Supplementary Information). In total, we analyzed 2807 promoters among 7 libraries using 18 different building blocks. All promoters were placed upstream of a medium strength basal promoter driving yellow fluorescent protein (YFP) (Supplementary Fig. S1) and integrated into the yeast genome at the TRP1 locus. The level of gene expression directed by each synthetic promoter was quantified by flow cytometry of 25,000 individual cells per promoter (Fig. 1A and 1B).

Table 1.

Summary of synthetic promoter libraries.

Library Building Blocks Number of Promoters Number of Parameters Fit Fraction of Variance Explained (R2)
L1 Mig1, Gcr1, Spacer 429 5 0.49
L1-Test Same as L1 83 0 0.44
L1-Weak Same as L1 plus a weak Mig1 site 266 1 0.44
L2 Mig1, Reb1, Rap1, Gcr1 (different from L1) 471 4 0.59
L3 Adr1, Hap2/3/4/5, CSRE, Rgt1 596 6 0.47
L4 Cbf1, Gcn4, Met31/32, Nrg1 381 10 0.54
L5 Msn2/4, Smp1, Xpb1 581 4 0.57

Figure 1.

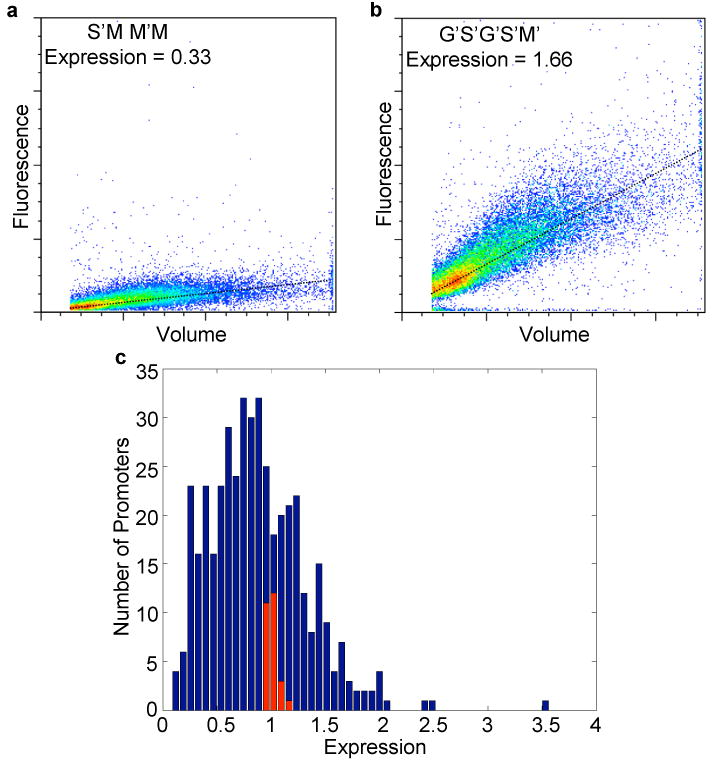
Figure 1

Gene expression measurements. Graphs of cell volume versus fluorescence for 25,000 individual cells containing the promoters A) S′MM′M and B) G′S′G′S′M′ where S = Spacer, G = Gcr1 site, M = Mig1 site and the ′ superscript indicates a site in the reverse orientation. C) Histogram of expression values for all L1 library members. Expression values were computed as the average fluorescence/volume ratio for 25,000 individual cells, and then normalized to plate controls. Control promoters with no library insert are shown in red.

Figure 1C shows the expression levels of 429 synthetic promoters from the L1 library (see Supplementary Tables S1-S7 for expression and sequence of all promoters). Basal promoter only controls (Fig. 1C, shown in red) were used to estimate the technical variance of our expression measurements, which is 1.3% of the total variance of the L1 library; the average technical variance for all libraries is 0.8% of the total variance. The biological replicate variance, which refers to the gene expression differences between independent transformants that have the same synthetic promoter by chance, is 35% of the total variance in the L1 library and 17% on average. Therefore, a perfect model relating promoter sequence to our expression data would explain 65% of the variance in expression driven by the different promoters in the L1 library.

We constructed a thermodynamic model of the relationship between promoter sequence and expression. The purpose of the model was to provide a formal mathematical framework for predicting the activity of novel combinations of cis-regulatory sites, and to gain insight into the mechanisms that generate diverse expression levels from different arrangements of the same cis-regulatory sites. We used a model first proposed by Shea and Ackers11, and later modified by Buchler et al.12 The main assumption of this model is that gene regulation is controlled completely by the equilibrium binding of proteins to DNA and to each other. Enzymatic events, such as chromatin modifications and polymerase phosphorylation, are not taken into account. The model consists of parameters that describe the changes in free energy of particular DNA-protein and protein-protein interactions that can occur on the promoters. These parameters are used to calculate the probability of RNA Polymerase (RNAP) being bound to each promoter in the library (See Supplementary Information). We then assume that the probability of RNAP being bound to a given promoter is directly proportional to the intensity of YFP fluorescence measured for that promoter.

In every library, thermodynamic models explained 44-59% of the variance in expression (Table 1), which is between 50% and 100% more variance explained than the best models of genome-wide expression data4, 5. The thermodynamic model for the L1 library captured 49% of the variance in expression (Supplementary Fig. S2; 75% of the available variance). The overall success of the thermodynamic approach indicates that expression driven by combinations of binding sites can be generally and accurately modeled by simply considering protein-DNA and protein-protein binding events.

To determine the predictive power of our model for the L1 library, we constructed the L1-Test library, which consists of novel combinations of the L1 building blocks. With the same parameter values from the L1 library the model still captures 44% of the variance in expression, implying that the model is not over fit. This lack of over fitting is not surprising considering that each model contains about 6 parameters fit to an average of over 400 promoters. The Mig1 parameter values found in the L1 library were held constant among three other libraries (L1-Test, L1-Weak and L2) that all exhibited high accuracy (see Supplementary Table S8 for all parameter values). Our model for the L1 library predicts that the Spacer building block, which we designed to contain no known or predicted regulatory sequence elements, can recruit RNAP to promoters. Since about half of the DNA binding proteins in yeast do not yet have an associated cis-regulatory motif 1, it is likely that the Spacer site is actually an unidentified cis-regulatory element. The ability of the model to incorporate an unknown sequence element and accurately predict its behavior points to a strength of the approach.

Analysis of the model for the L1 library suggests that Mig1 binds cooperatively to the synthetic promoters. Because nothing in the previous literature suggested cooperativity between Mig1 monomers we decided to analyze Mig1 cooperativity independent of the model. We fit a Hill equation relating percent repression to the number of Mig1 sites with the assumption that 100% repression occurs with five Mig1 binding sites. We found that a Hill coefficient of 3.4 ± 0.25 and _K_=1.8 (the number of Mig1 sites that causes half maximal repression) gives the best fit, suggesting cooperativity. Figure 2A shows that the observed data fits well to the Hill equation and that without cooperativity the fit is substantially worse. These results are consistent with the model and suggest that Mig1 acts cooperatively to repress transcription in our system, which lead us to examine the influence of low affinity TFBS on expression.

Figure 2.

Figure 2

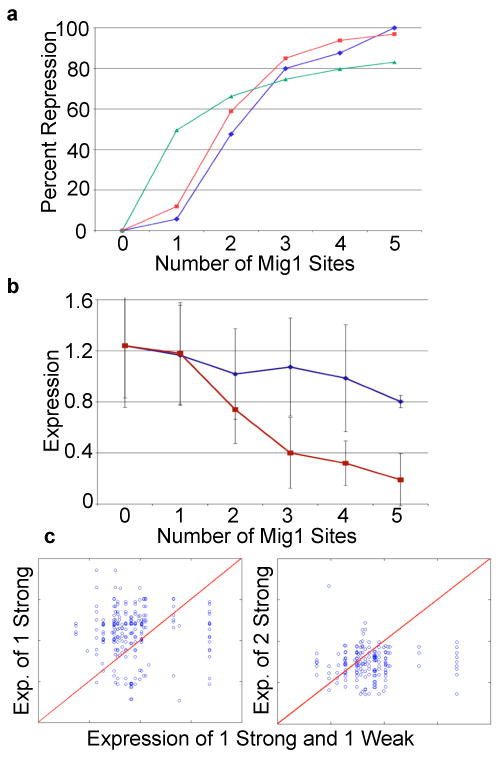
Mig1 sites act cooperatively and weak site represses weakly. A) Hill equation with _n_=3.4 and _K_=1.8 (red) fits the observed data (blue) well compared to _n_=1 (green). B) Plot of average expression versus the number of weak sites (blue), without strong sites, and strong sites (red), without weak sites. Error bars represent one standard deviation. C) Plots of expression for pairs of identical promoters except that either one strong Mig1 site or two strong Mig1 sites replace one strong and one weak Mig1 site. A blue circle represents one promoter pair and the red line represents equal expression.

Low affinity, or weak, TFBS are known to play important roles in prokaryotic promoters13 and have been postulated to play an important role in eukaryotic gene regulation14. However, their quantitative effect on gene expression is difficult to determine. To study the effects of weak TFBS we constructed a library (L1-weak) incorporating a building block matching a Mig1 binding site that was shown to have low affinity for Mig1 in vitro15. The sequence of this weak site scores below any reasonable cutoff in a genome scan for Mig1 sites based on a weight matrix derived from known Mig1 sites 16, 17. In our system the low affinity Mig1 site behaved as a weaker repressor than the strong site (Fig. 2B). However, when there are strong Mig1 sites present in a promoter the weak sites behave as strong sites. When comparing promoters with the same building block content except for the number of Mig1 sites, promoters with one weak and one strong Mig1 site exhibit lower expression compared to promoters with one strong Mig1 site (Fig. 2C; P<10-8, sign test, n=211) and the same expression as promoters with two strong Mig1 sites (Fig. 2C; _P_>10-2, sign test, n=177). This behavior suggests that strong and weak Mig1 sites interact cooperatively to repress transcription in our system. This interaction produces complex patterns of expression in the L1-Weak library.

The thermodynamic model of transcriptional regulation accurately captures many of the complexities of expression in the L1-Weak library by adding only one adjustable parameter to the L1 library model parameters, namely the relative affinity of Mig1 for the weak site. The optimal value of the new parameter is 1.9, which corresponds to a 6.7 fold lower relative affinity for Mig1 than the stronger Mig1 site. This value is in good agreement, and within a 95% confidence interval, with an independent computational analysis of a position specific weight matrix for Mig1, which predicted a 9.0-fold lower affinity of the weak site for Mig116, 18. The similarity of the R2 of this model with that of the L1 library model demonstrates that we are capturing the additional complexities caused by the effect of weak Mig1 sites on expression.

We next examined the possibility that weak sites contribute to Mig1 repression of genomic promoters. Weak Mig1 binding sites are over-represented in S. cerevisiae promoters compared to shuffled S. cerevisiae promoters (P<10-3, simulation, n=1000; Supplementary Fig. S3). Weak sites are found in 24% of all promoters, while 39% of promoters containing a significant match to a Mig1 weight matrix also contain a weak site (P<10-12, hypergeometric test), indicating that strong and weak sites tend to co-occur. Of 33 genes that are known to be regulated by Mig119, 20, and whose promoters contain a significant match to a Mig1 weight matrix, 20 also contain a weaker Mig1 site in their promoters compared to 8 genes expected by chance. According to our model of gene regulation promoters with one strong and one weak site are more sensitive to changes in Mig1 concentrations than promoters with either two strong or two weak sites and therefore may be best suited to respond to changes in available carbon sources (Supplementary Fig. S4). These results suggest that combinations of strong and weak Mig1 binding sites are commonly found together in genomic promoters and may provide a sensitive strategy for glucose repression.

We sought to determine if the properties of Mig1 repression found in the synthetic promoter libraries were informative when studying genomic promoters. 359 promoters in the S. cerevisiae genome have a significant match to a Mig1 weight matrix and 33 of these promoters correspond to one of 136 documented Mig1 regulated genes. To compare these results directly to our model we applied the thermodynamic model of Mig1 repression to genomic promoters (see Online Methods). Out of the top 359 promoters ranked by the thermodynamic model for the strength of Mig1 repression, 41 correspond to one of the 136 documented Mig1 regulated genes. Using the regulatory rules encoded in our thermodynamic model we explain eight (24%) more known Mig1 regulated genes (HXT9, HXT12, HXT13, GSY1, SOR1, ICS2, YIL172C, YOL153C) than by simply looking for promoters with a significant match to a Mig1 weight matrix. For example, the SOR1 promoter does not harbor a significant match to a Mig1 site but contains a number of weak sites that cluster together (Fig. 3A). Since cooperativity between Mig1 sites is an important part of our quantitative model, we correctly predicted that SOR1 is Mig1 regulated and also identified the likely binding sites of Mig1 in this promoter.

Figure 3.

Figure 3

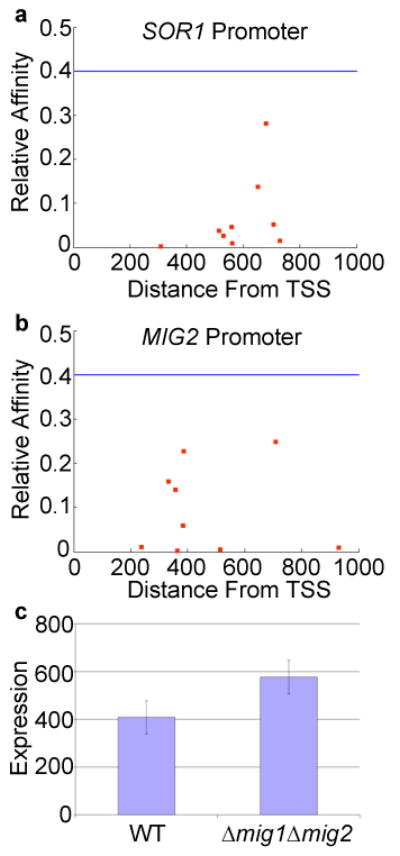
Thermodynamic model explains Mig1 repression in the genome. Mig1 binding sites in the promoters of SOR1 (A) and MIG2 (B) are shown. The affinity of Mig1 for the site based on a position weight matrix score relative to the strong site is plotted vs. the location upstream on the translation start site (TSS). The horizontal line represents the significance threshold for the weight matrix and each square represents a Mig1 site. C) MIG2 promoter activity in a wild-type (WT) strain and a mig1Δ mig2Δ strain, error bars represent one standard deviation.

Using the thermodynamic model we also predicted a number of Mig1 regulated genes that were not previously known to be Mig1 targets (Supplementary Table S9). MIG2, a paralog of MIG1 that represses and binds the same site as Mig115, was predicted by the model to be auto regulated based on its promoter sequence (Fig. 3B). To validate this prediction we measured MIG2 promoter activity (see Online Methods) in strains deleted for both MIG1 and MIG2. MIG2 promoter activity increased significantly in the mig1Δ mig2Δ strain as compared to wild-type (P<10-3, t-test, n=24), showing that MIG2 is auto-regulated by Mig1/Mig2 (Figure 3C). The prediction from the model was that MIG2 expression would increase 1.8-fold in a mig1Δ mig2Δ strain, and we observed a 1.5-fold change. The regulation of MIG2 by Mig1/Mig2 represents a previously unreported negative feedback loop in the glucose repression network that was identified based on our analysis of synthetic promoters.

Using a simple system we succeeded in constructing an accurate model of the relationship between promoter sequence and gene expression. In part this was because we sampled a much larger fraction of promoter space using our library than we could by sampling genomic promoters. Thus, we were able to fit models containing a small number of parameters to data containing large numbers of observations. We found that a completely thermodynamic model based on the equilibrium binding of the transcription factors and RNAP to each other, and to their cis-regulatory sites, was a reasonable way to capture the relationship between promoter sequence and gene expression in our system for all of the libraries examined. This does not imply that kinetic processes, such as histone or RNAP modification, are unimportant in gene regulation; however, it does suggest that the information encoded in a promoter is decoded primarily by the sequence specific binding of transcription factors. Our results support the idea that the complexity and variation in gene regulation could stem from very simple rules describing the binding of proteins to DNA and to each other 12, 13, 21.

Methods Summary

To create the building blocks that make up the synthetic promoters oligonucleotide pairs, each with a 5′ phosphate, were annealed by being boiled and then slowly cooled to room temperature (see Supplementary Information for building block sequences). 15 μL of 50 μM double stranded building blocks were then ligated with 200U of T4 DNA ligase (New England Biolabs) for 2 hours at 16°C. The ligation products were then purified using a microcon YM-100 column from Millipore (Billerica, MA) to reduce the number of short promoters. 15 ng of purified ligation product were then ligated into the BamH1 site of the integrating reporter plasmid pJG102 (20 ng) and transformed into E. coli. Transformants were scraped into Luria Broth plus carbinecillan, grown overnight and then maxipreped using the GenElute HP Plasmid Maxiprep kit from Sigma (St. Louis, MO). 130 μg of the maxiprep was digested with BglI, BamH1, Sal1 and EcoR1 (200U each) and transformed into yeast as described in 22. Colonies growing on medium lacking uracil were picked into 96 well plates and Trp- colonies were then identified by replica plating onto medium lacking tryptophan. We observed that some building blocks were represented slightly more than others, even though they were added at equal molar concentrations. The relative abundance of each building block in each library scaled similarly to the melting temperature of the building block.

Supplementary Material

1

Acknowledgments

The authors would like to thank Robi Mitra, Gary Stormo, Mark Johnston, Katherine Varley, Scott Doniger and members of the Cohen lab for discussion and suggestions as well as Jeff Sabina for technical help with LacZ experiments. B.A.C. and J.G. were supported by NIH grant R01 GM078222 and E.D.S. was supported by NSF grant DMR0129848. J.G. was also supported by NSF Graduate Research Fellowship DGE-0202737.

Footnotes

The sequence of the integrating reporter plasmid pJG100 has been deposited with GenBank under accession number FJ175377. Reprints and permissions information is available at www.nature.com/reprints.

Author Contributions J.G. performed all experiments and analysis. B.A.C. and J.G. designed the experiments and wrote the paper. E.D.S. conceived and contributed to the application of the thermodynamic model to the synthetic promoter libraries.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1