Dynamics of multiple myeloma tumor therapy with a recombinant measles virus (original) (raw)

. Author manuscript; available in PMC: 2010 Feb 15.

Published in final edited form as: Cancer Gene Ther. 2009 Jun 5;16(12):873. doi: 10.1038/cgt.2009.40

Abstract

Replication-competent viruses are being tested as tumor therapy agents. The fundamental premise of this therapy is the selective infection of the tumor cell population with the amplification of the virus. Spread of the virus in the tumor ultimately should lead to eradication of the cancer. Tumor virotherapy is unlike any other form of cancer therapy as the outcome depends on the dynamics that emerge from the interaction between the virus and tumor cell populations both of which change in time. We explore these interactions using a model that captures the salient biological features of this system in combination with in vivo data. Our results show that various therapeutic outcomes are possible ranging from tumor eradication to oscillatory behavior. Data from in vivo studies support these conclusions and validate our modeling approach. Such realistic models can be used to understand experimental observations, explore alternative therapeutic scenarios and develop techniques to optimize therapy.

Keywords: mathematical modeling, population dynamics, viruses, tumor therapy

Introduction

The field of cancer therapy with replication-competent viruses is gaining momentum. Several viruses have been tested in phase I and II clinical trials in patients with advanced neoplasms. The viruses tested include replication-competent adenoviruses,1 Newcastle disease virus,2 retroviruses, measles virus (MV) and herpes simplex viruses.3 Most of the studies have been primarily directed to evaluate the safety of these vectors with anti-tumor efficacy as a secondary outcome. So far, the therapeutic efficacy of these vectors has been limited, most likely because of the sub-optimal delivery of the virus to the target site, the low doses of the viruses used and the effect of the immune response that may contain the spread of the virus within the tumor. Fortunately, the various studies so far attest to the safety of these vectors and the approach to therapy.

Tumor therapy with replication-competent viruses presents a significant departure from chemo/radiotherapy; cancer eradication depends on the establishment of a viral infection within the tumor that turns them into virus production factories, amplifying the therapeutic agent. The newly generated virions proceed to infect additional tumor cells, producing a wave of virus propagation within the tumor.4 Tumor virotherapy is an exercise in applied population dynamics. Hence, modeling the dynamic interactions between the tumor, virus and immune system cells is essential to understand therapeutic outcomes and optimize therapy. Various investigators in the field have proposed models that capture essential elements of such biological dynamics,4–12 although most of these models were purely theoretical and not validated with in vivo data.

Our work has centered on recombinant viruses based on the Edmonston vaccine strain of MV as these vectors have potent and selective oncolytic activity against a broad range of tumors. 13–17 The vaccine has been given to more than a billion people with an excellent safety record. Moreover, MV can be engineered to enable entry through specific receptors (transductional targeting), increasing its safety margin even further.18, 19 Tumor cells infected with MV express the viral hemagglutinin and fusion proteins that induce fusion between the surrounding tumor cells with the formation of giant cell syncytia. Cells incorporated into syncytia ultimately die. This cell–cell fusion is considered an important therapeutic advantage of MV as it provides a significant bystander effect that eliminates uninfected cells that are incorporated in syncytia.20 Recombinant MV gene expression, viral amplification and propagation in vivo can be monitored non-invasively either by the use of secreted biomarkers, such as carcinoembryonic antigen (CEA) or human chorionic gonadotrophin (β-hCG) that are detectable in the bloodstream,21 or through molecular imaging using the sodium iodide symporter (NIS) as a reporter gene in combination with various iodide isotopes.22,23 To date, two recombinant measles viruses (MV-CEA21 and MV-NIS23) have entered phase I clinical trials for advanced ovarian carcinoma, glioma and multiple myeloma, respectively. Measles virus-based vectors can destroy every human tumor cell line in vitro, but the in vivo responses are more variable. Although some tumors are consistently eliminated, others persist with the virus and tumor cell populations reaching an equilibrium.24 To understand these observations, we have developed novel mathematical models that capture the salient biological properties and dynamics of the population interactions.5,25 In this work, we extend our modeling to (i) capture the detailed dynamics of the syncytium population and (ii) validate the model on a large data set that features various types of tumor behavior from curative therapy to oscillations.26 The implications of these dynamical behaviors on therapy are discussed.

Methods

In vivo tumor xenografts

The experimental design and tumor growth data in response to variable doses of MV-NIS injected intravenously have been reported elsewhere.26 Irradiated 6-week-old female CB17 severe combined immunodeficiency mice were injected in their right flank with washed KAS-6/1 cells (a human myeloma cell line that is interleukin-6 dependent)27 and observed for tumor growth. When tumor xenografts reached an average diameter of 5 mm, the mice were injected intravenously through the tail vein with MV-NIS (1 × 107 50% tissue culture infective dose (TCID50)) and serial tumor growth was monitored. A group of tumor bearing mice that was injected with ultraviolet-inactivated virus served as controls. Each cohort (control and treated) was composed of nine mice.

Mathematical model

Our mathematical model has to account for three populations: uninfected tumor cells, y(t), virus-infected tumor cells, x(t), and free virus, v(t), although taking into consideration that infected cells may be single or incorporated into syncytia. In the absence of virus, tumor growth is described by the generalized logistic (or Bertalanffy–Richards) model28:

where r is the effective growth rate, and y(t) is the total tumor burden, which cannot exceed the carrying capacity K. Parameter ε enables flexibility in the shape of the growth curve. When ε tends to zero (what seems to be the best fit for some tumor growth data; see below), one can show that the generalized logistic model becomes equivalent to the Gompertz model.29 In this case, Eq. (1) reads:

When the virus is administered, individual virions interact with the uninfected tumor cells with rate constant κ to generate a population of infected cells. The infected cells do not replicate (D Dingli et al., unpublished observations) but at a rate ρ they interact with neighboring uninfected cells to form syncytia. Infected cells (single or in syncytia) die at a rate δ. As pointed out in Bajzer et al.,25 the rate constant δ could also model some effects of the immune system, and possible low level of proliferation of infected cells. Cells that are infected release new virus particles at a rate α. However, for various reasons (including defective particle formation and complement inactivation) not all the released virus is available or able to infect tumor cells, and this is captured by rate constant ω. These biological considerations lead to a system of non-linear differential Eqs (3–6):

y′=ry[1−(y+x+s)ε/Kε]−kyv−ρxy, (3)

Each syncytium occupies a larger volume than a single infected cell, so we introduce a population of cells, s(t), representing the number of infected cells fused into syncytia, so that x + s can account for all the infected cell volume whether they are single cells or included in syncytia. (Note that if n is a number of cells in a syncytium then s = n_−1, because the syncytium itself is already counted as one member of population x.) The population of syncytia has been only implicitly accounted for in our previous models.5,25 The tumor burden is now given by y + x + s and considered proportional to the volume. In principle, an infected cell or syncytium may transfer the virus to an uninfected cell, which by certain probability λ becomes a single infected cell, whereas by probability (1−λ) fuses with the infected cell to form a syncytium or fuses to the already existing syncytium. The rate term, λρ_xy, is included in Eq. (4) to account for additional infected single cells. Cells that are included in syncytia die with the same rate constant δ (Eq. 6) and produce virus at the same rate constant α as single infected cells (Eq. 5). The term (1−λ)ρ_xy_ in Eq. (6) represents the rate by which uninfected cells fuse with infected cells (single or syncytia), yielding syncytia. In situations where tumor growth is best described by a Gompertz model, Eq. (3) becomes:

y′=ryln(K/(y+x+s))−kyv−ρxy, (7)

Data fitting and parameter estimation

The variability among nine measured untreated tumor growth curves, as well as nine treated tumor growth curves, required an elaborate approach to data fitting and parameter estimation. We used non-linear least-squares fitting procedure. First, untreated tumor data for available growth curves were fitted by generalized logistic and Gompertz growth models. The modified Akaike model selection criterion30,31 was used to determine that four out of nine growth curves were more adequately described by the Gompertz model. Data from one untreated tumor were excluded as inconsistent. In this way, to each of the nine tumor growth data a preferred model was assigned. Subsequently, every treated tumor growth curve was paired to each untreated control (nine pairings per treated mouse) and simultaneous fitting was performed for each pair. Within each pair, for untreated tumor growth data the generalized logistic or Gompertz models were used (as assigned earlier), and for treated tumor growth data the corresponding model given by Eqs (3–7) was used. In these fittings we assumed that model parameters, K, r, ε (if applied) and _y_0, (the initial tumor size before treatment) were global free parameters for both treated and untreated growth data, whereas the remaining parameters, κ, ρ, δ, α, ω and λ, were related only to the treated tumor growth data. The best pair for a given treated growth data was determined on the basis of the lowest χ2 for treated data and exclusion of those fits that yielded unacceptable parameter values.

It is significant that the estimates for parameters, K, r and ε, (if applied) in this second round of fitting were identical to the first fits (just to untreated data) up to the third decimal place showing that the fitting algorithm is robust. Least-squares fitting was performed using custom built software with the simplex induction hybrid minimizer32 and an adaptive Runge–Kutta solver. A tumor was considered cured if the total population y(t) + x(t) + s(t) was reduced to less than one cell. Similarly, any population was assumed extinct if it was reduced to less than one member. The virus was administered on day t = 1, whereas the tumor was measured 1 day before; therefore, _y_0 corresponds to the tumor size at t = 0. On the other hand, the initial conditions for Eqs (3–7) were: (a) for population of uninfected cells, y1–the predicted size of the untreated tumor at day 1 by generalized logistic (or Gompertz) model, (b) on the day of virus administration, we consider that there is at least one infected cell as the state without infected cells would artificially bring into effect the above mentioned condition and the infected population would automatically become extinct and (c) the initial virus population was 1 × 107. Tumor volumes were measured in mm3, although the model deals with populations of cells. We converted tumor volumes into cells by assuming that 1 mm3 contains 1 × 106 tumor cells.

Results

Parameter estimation

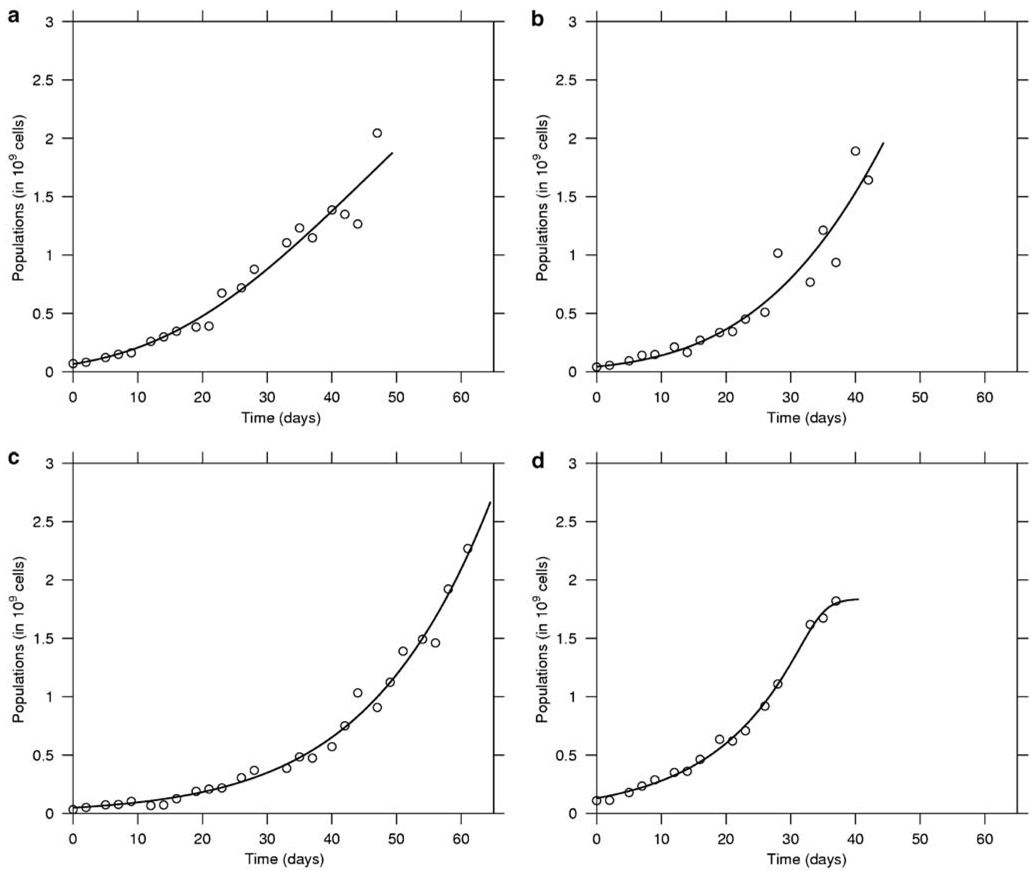
Tumor and virus-related parameters were determined as described in ‘Methods’. With respect to the nine untreated tumor growth curves, five were more adequately fitted with the generalized logistic model and four by the Gompertz model. In Figure 1 we show representative examples of the fits. The mean values and the standard deviations for the estimated parameters for each of the models are presented in Table 1. There was a good agreement between the two models with respect to the average carrying capacity of the tumors, but as expected, the growth rate, r, is different.

Figure 1.

Figure 1

In vivo growth of myeloma tumor xenografts. In this figure, the growth of four representative untreated tumors is depicted. Tumor growth data were fitted to the Gompertz (top panel: a, b) and general logistic model (bottom panel: c,d). Both models fit the experimental data well and the fitting enables parameter estimation. The best fit was determined using the modified Akaike selection criterion.

Table 1.

Parameter estimates for untreated tumor growth

Parameter/model General logistic Gompertz
r 0.076 ± 0.019 0.03 ± 0.0057
K 14.5 ± 12 13.8 ± 12.4
ε 14.6 ± 12 Not applicable

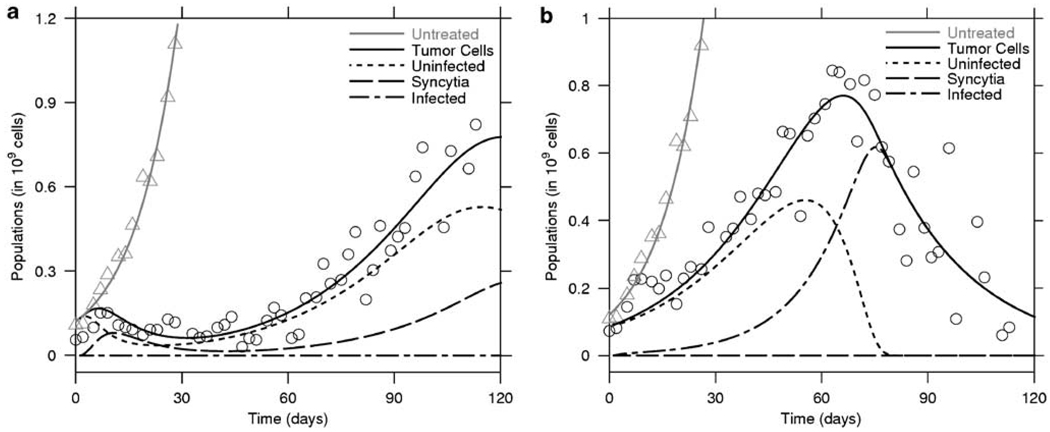
The estimation of virotherapy-specific parameters, κ, ρ, δ, α, ω and λ, resulted in considerable variability, as shown in Table 2. This parameter variability stems from the scatter in the data that leads to shallow minima in the least-squares fitting. Data scatter in turn relates to measurement errors and the intrinsic biological differences between the tumors. The estimated value for λ was <0.07, implying that when an infected cell or syncytium interacts with a non-infected cell, there is a high probability of fusion rather than simple virus transfer. We also observed that the death rate, δ, of infected cells tended to be smaller when therapy resulted in cure, whereas it was higher when therapy was unsuccessful in eradicating the tumor (see Table 2). In Figure 2 we illustrate the fits of our model to the data. Panel (a) shows unsuccessful therapy with the death rate, δ, estimated to be four times larger than δ estimated for another treated mouse (panel (b)) where therapy was a success.

Table 2.

Parameter estimates for the treated tumors

Mouse # Model κ δ α ω ρ λ Final state
1 GL 950.7 0.063 1.64 × 10−4 2.55 19.55 6.54 × 10−3 NC
2 GL 999.6 0.068 7.62 × 10−3 7.04 × 10−4 8.5 3.23 × 10−7 C
3 Gomp 0.621 0.152 6.97 × 10−6 2.14 × 10−2 147.3 6.6 × 10−3 NC
4 Gomp 0.06 0.084 9.61 × 10−3 1.13 × 10−5 1000 1.25 × 10−4 Con
5 GL 0.0092 0.146 1.42 × 10−8 8.36 × 10−2 988.1 7.85 × 10−4 NC
6 GL 0.067 0.155 1.02 × 10−7 3.51 × 10−2 596.7 5.11 × 10−4 NC
7 GL 2.49 0.039 1.12× 10−1 1.52 × 10−4 9.98 × 10−6 5.5 × 10−2 C
8 Gomp 0.382 0.068 1.99 × 10−1 3.2 × 10−3 46.04 6.37 × 10−4 Con

Figure 2.

Figure 2

Myeloma tumor therapy with MV-NIS. Two representative examples of therapy with MV-NIS are shown. In (a), is an example of a tumor that initially responds and then regrows while in (b), the tumor is eradication after a single injection of MV-NIS. The total tumor volume was measured and the model fitted to the data. MV-NIS always slows down tumor growth. Within each of these figures, the triangles represents the fit for the untreated tumor. The remainder of the lines correspond to the solutions of the system of equations (3)–(7) fitted to the virally treated mice (circles) with the measured tumor load y(t) + x(t) + s(t), and estimated values for uninfected cells (y(t)), infected cells (x(t)) and syncytium volume (s(t)), as in the legend.

Tumor and virus population dynamics

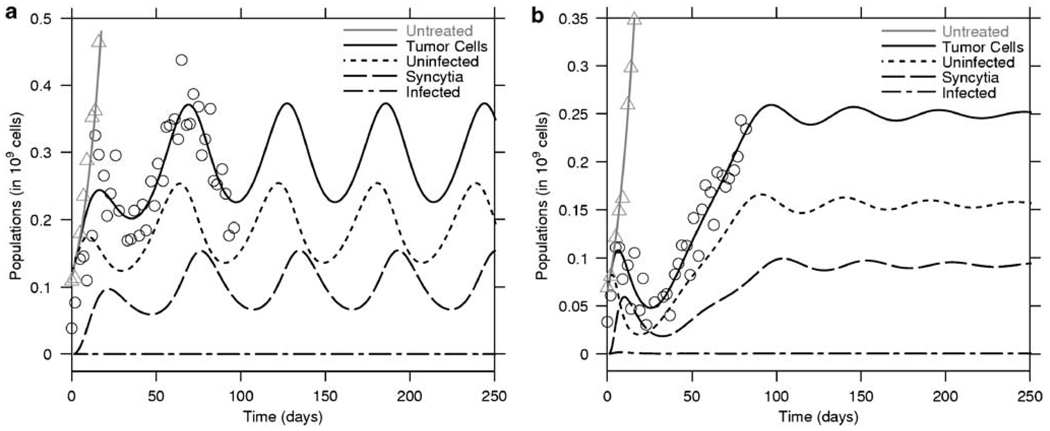
Therapy of myeloma tumor xenografts with MV-NIS (1 × 107 TCID50) exhibited three different outcomes: tumor eradication, therapeutic failure or oscillations in tumor size. In the presence of the virus, tumor growth is invariably slowed compared with that of untreated controls. As a result, survival of the mice improves with therapy. Tumor growth is initially slowed down and the tumor burden reaches a low maximum followed by oscillations around some mean, which in most cases is significantly lower than the carrying capacity. Examples of oscillatory behavior are provided in Figure 3. In Figure 3a we illustrate a case of sustained oscillations, whereas in Figure 3b we illustrate a case of damped oscillations, which decay to an equilibrium.

Figure 3.

Figure 3

In vivo population oscillations. The model predicts the occurrence of oscillations in the tumor and virus population. The figure presents two treated tumors that exhibit oscillations in size as a function of time. In (a), the oscillations are not damped and will persist, whereas in (b), the oscillations are damped and the populations will reach a steady state. Note that in (a), the peak of infected cells always follows that of the uninfected population.

The significant reduction of tumor to undetectable levels may occur rapidly or at a slower pace (Figure 4); in the observed data, all the cured tumors exhibited a monotonic decrease in size after a maximum (Figure 4). In all but one of the observed tumors, the population of single infected cells was very small, implying that most of the infected cells are incorporated into syncytia by fusing with surrounding cells. This is also compatible with the finding that the probability λ is small; the efficiency of cell-to-cell fusion is high compared with virus transfer between cells.

Figure 4.

Figure 4

Curative therapy with MV-NIS. Tumor virotherapy can lead to eradication of the xenograft. Tumor control can be relatively fast (a) or slow (b), but in all cases of tumor eradication observed, the tumor population exhibited a monotonic decrease in size without oscillations.

The fraction of tumor cells that were infected or fused into syncytia varies between tumors, and varies in time within the same tumor. However, in the case of tumors that persisted despite infection, less than half of the tumor cells were incorporated in syncytia and in most situations the fraction of cells that have fused in the tumor is between 1/3 and 1/2 (see Figure 3).

Simulations

In vivo experiments have a finite lifespan and mice are euthanized if a pre-specified time interval has passed since the intervention or the tumor reaches a size that necessitates euthanasia. Simulations may circumvent these experimental limitations and therefore, we carried out in silico studies to evaluate the dynamics of the various populations over a period of up to 1000 days, longer than the lifetime of the mouse. This enabled us to ensure that a mouse can die free of disease. The results of such simulations show that virotherapy invariably leads to a lower tumor burden compared with untreated animals. The system eventually reaches an equilibrium where the tumor and virus populations coexist (_y(t),x(t),v(t),s(t)_>0 and y(t) + x(t) + s(t) <K). Under certain conditions imposed on parameter values, this equilibrium is stable, which can be shown using the approach developed in Dingli et al.5 and Bajzer et al.25 Our simulations indicate that the tumor burden at this equilibrium state is independent of the initial virus dose for a range of 104−107 virions.

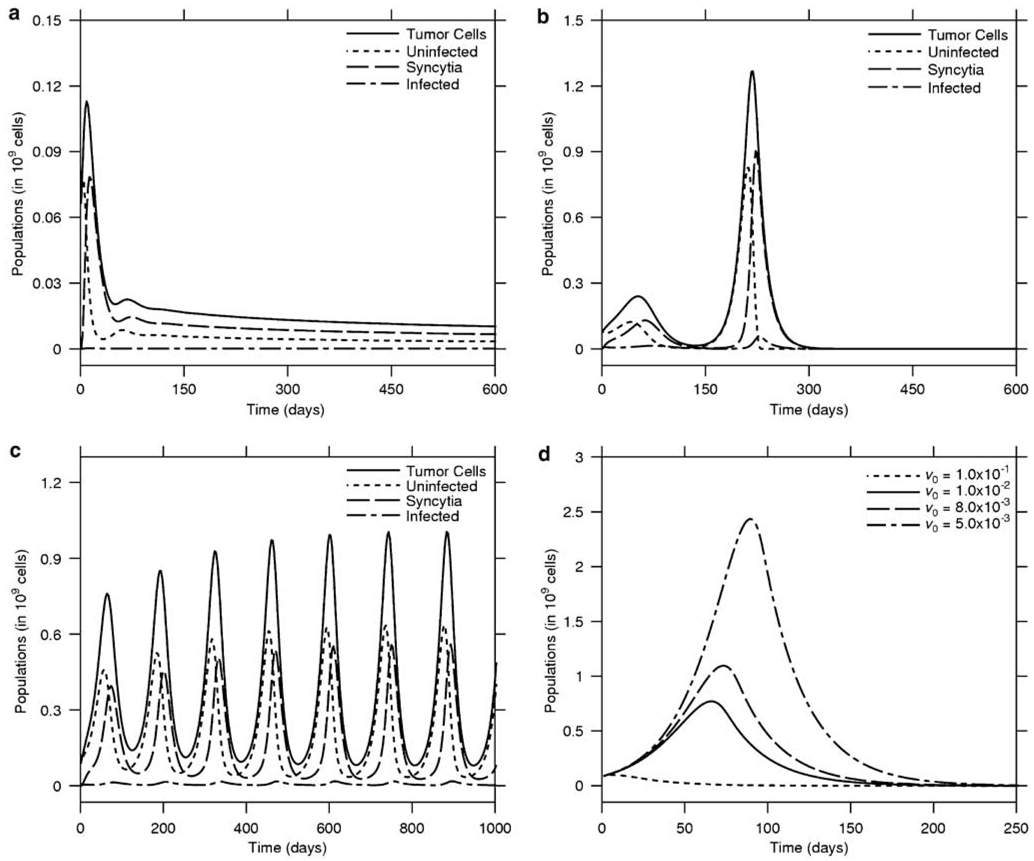
Our simulations suggest that for various mice that were considered to have failed therapy, continued observation would have shown tumor control (Figure 5a, b). In contrast, tumors that were ‘eradicated’ up to the point of animal killing would have recurred with extended follow-up (Figure 5b,d). Prolonged simulations of tumors often led to oscillatory behavior; the oscillations are almost always damped and the system may reach the equilibrium through different approaches: by increasing further after the first low maximum (Figure 3b) or by decreasing after the first maximum (Figure 6a). Tumors that initially responded to therapy can experience considerable regrowth, only to be eliminated as they increase rapidly in size (Figure 6b). Presumably, the second burst of tumor growth provides fertile ground for the amplification of the virus so that it can ‘catch’ up with the tumor and eliminate it. Other tumors exhibit oscillations of increasing amplitude (Figure 6c). It is interesting that, these oscillations could lead to tumor eradication as each swing is associated with a deeper trough that may lower the tumor burden to < 1 cell, and so by definition lead to cure as in Figure 6b. On the other hand, the simulation in Figure 6c shows that reduction of tumor load in deep valleys is not always sufficient for eradication during the assumed 1000 days lifespan.

Figure 5.

Figure 5

Tumor eradication is a time-dependent variable. Prolonged observation of the animals is essential to have reliable outcomes. In (a), therapy was considered a failure but longer observation would have shown tumor control (b). In contrast (c), a tumor that was considered eliminated would have recurred (d).

Figure 6.

Figure 6

Population oscillations and tumor eradication. Extended simulations show that as a result of virotherapy, the tumor may experience various types of oscillations. In (a), the tumor initially grows but then is rapidly controlled and monotonically decreases to very low levels. In (b), the tumor is reduced to low levels only to grow rapidly to a large size. The virus catches up with it and eliminates it. (c) Sometimes the virus cannot lower the tumor burden low enough and the population exhibits oscillations with increasing amplitude. (d) The impact of initial dose of virus on tumor eradication dynamics.

Subsequently, we evaluated the effect of initial virus dose on the outcome of therapy. As can be seen from Figure 6d, a larger dose of virus can lead to faster tumor eradication. However, even a dose of virus that is half of what was actually given would eventually lead to tumor eradication, assuming that the interim tumor burden can be tolerated.

Discussion

Replication-competent viruses are an exciting approach to cancer therapy for a variety of reasons. Viruses have evolved to be the ultimate parasites and usurp the cellular machinery for their own replication.4,33,34 To achieve this goal, they block the cell cycle, utilize ribosomes for their protein synthesis and leave the infected cell by lysis or else induce fusion between cells, ultimately leading to their death. Intriguingly, many viruses seem to replicate better in tumor cells as cancer cells are more permissive to virus entry and replication.4,33–36 However, tumor virotherapy presents a number of novel challenges because tumor eradication or control depends on the establishment of an infection and virus amplification in vivo.4,33,34 There is no other therapy in which the active agent is amplified in the body of the host. The interactions between the virus and the host, including the tumor and the immune response, present a non-linear dynamic system, and the outcomes of therapy are highly dependent on the interactions between these populations.4–12,25 Such a system may have different outcomes, including the potential for chaotic behavior. We believe that it is essential to understand the dynamics of such therapy for optimal use of these novel agents.

There is a perceived reluctance from experimentalists to consider the utility of such mathematical models. However, as it is clear from the experimental data, various behaviors can be observed even under controlled experimental conditions.24,26 Understanding the mechanisms behind such outcomes can be greatly facilitated with mathematical models that can unravel counter intuitive dynamic behaviors. Many of the previous attempts at modeling tumor virotherapy were by necessity based on guessed parameters, as there were no adequate experimental data at that time. These models already suggested the possibility of oscillatory behavior. In this work, we have developed a more refined mathematical model that is compatible with the specific biology of MV and is validated by experimental data,26 which showed the rich dynamics that this form of therapy provides. Apart from therapeutic success, oscillations were observed in the experimental animals and confirm the general validity of the population dynamics approach to modeling. Moreover, modeling and simulations enable the performance of ‘what if’ experiments so that many possible therapeutic scenarios can be evaluated in silico and then the most promising ones evaluated in vivo. This will minimize the use of laboratory animals and optimize the use of resources.

In our fitting, we considered the initial dose of virus administered (_v_0 = 1 × 107) to be constant. However, comparison of the parameter estimates for tumors that were eradicated with those of persistent tumors suggests that the initial virus dose is an important variable and determinant of the outcome of therapy. Given the small volume of virus injected, it is likely that even a small back-leak during the injection can lead to significant differences in this parameter, in part explaining the different outcomes in experiments with otherwise very limited variability. It is unlikely that the tumor cells from the different mice had significant variability in their CD46 receptor density, permissiveness to virus replication or MV oncolysis. Similarly, it is unlikely that the tumors would exhibit very different growth rates, so again the tumor growth parameters should be similar. Thus, the major variable is the initial dose of virus injected. This is supported by the observation that as the injected virus dose is reduced, the probability of observing tumor eradication decreases.26 However, as our modeling suggests25 in situations where both the tumor and the virus populations coexist, the equilibrium values for the various populations are independent of the starting tumor burden or virus administered. We performed simulations with the current model and found that this is true. Experimental data using various tumor models and MV derivatives support this conclusion.24

Tumor eradication with MV can only occur if the population of uninfected cells decays faster than the cells incorporated in syncytia. Indeed, only if at some point in its life history all the tumor cells are infected with MV-NIS, the tumor will be eliminated. Our model does not consider the potential immune response against the virus and/or the virus-infected tumor cells that could introduce additional nonlinearities in the dynamics. However, the experimental data modeled here were obtained from severe combined immunodeficiency mice that do not mount an immune response to the tumor and/or virus. Moreover, patients with advanced multiple myeloma often have profound immunosuppression, including very low levels of anti-measles virus antibodies.37,38 Hence, we believe that the model can be used to understand data from human clinical trials. In summary, we have presented a mathematical model of myeloma virotherapy with MV-NIS. These novel therapeutics, exhibit rich dynamic behavior because of the non-linear interactions between the populations of cells and viruses. Understanding these interactions will enable us to optimize our experimental approaches and more importantly therapy.

Acknowledgements

This project was possible through a career development award from Mayo Foundation to DD, Grant CA100634 (NCI) to SJR, the Mayo Santulli Fund to ZB, and NSF Grants DMS-0604429 and DMS-0817649 and a Texas ARP/ATP award to KJ.

Footnotes

Conflict of interest

The authors declare no conflict of interest.

References